Monitoring of fluid motion in a micromixer by dynamic NMR microscopy

Abstract

The velocity distribution of liquid flowing in a commercial micromixer has been determined directly by using pulsed-field gradient NMR. Velocity maps with a spatial resolution of 29 µm × 43 µm were obtained by combining standard imaging gradient units with a homebuilt rectangular surface coil matching the mixer geometry. The technique provides access to mixers and reactors of arbitrary shape regardless of optical transparency. Local heterogeneities in the signal intensity and the velocity pattern were found and serve to investigate the quality and functionality of a micromixer, revealing clogging and inhomogeneous flow distributions.

---

Introduction

The investigation of fluid transport in microstructured devices contains new challenges for the experimental techniques as compared to conventional, laboratory-scale or large-scale reactors. Introducing sensors without disturbing the flow behavior becomes exceedingly difficult due to the reduced dimensions and the growing importance of interfaces and structural obstacles; furthermore, they provide pointwise information only. Other methods for the determination of velocities rely on optically accessible media and thus usually require glass-made reactors or suitable windows; at the same time, tracers such as microscopic particles or dyes are necessary to visualize the flow paths. These tracers bear the risk of influencing the hydrodynamic properties which becomes an issue of increasing importance with reducing the channel dimensions. Moreover, they have limited applicability in the presence of multiphase and reacting systems as they can affect the mixing process or the reaction kinetics. Apart from the possibilities that a robust and non-invasive technique can provide for quality control and testing of mixer/reactor designs under varying conditions such as flow rates and temperature, a fundamental interest in flow dynamics on micrometer scales exists. The modeling and design of microreactors relies on the availability of quantitative data about the actual flow field, i.e. the velocity distribution of the fluids in the microstructured device, or of several fluids measured separately. Influences of local vorticity and turbulence, surface roughness and corrosion on the fluid dynamics need to be monitored in-situ. The particularly favorable properties of nuclear magnetic resonance (NMR) imaging techniques, namely its non-invasiveness and chemical selectivity, have made it the standard imaging technique in medical diagnostics, and it is gaining growing acceptance in non-medical fields, in particular Chemical Engineering.^1,2 However, the small-scale structures and related problems such as induced magnetic field inhomogeneities require some modification of the classical methods employing standard hardware and software. Significant progress has been achieved in recent years in NMR spectroscopy of small fluid volumes down to nanoliters.^3–5 The most straightforward approach is to make use of state-of-the-art spectrometers operating at high field strengths in combination with dedicated flow-through or cryoprobes, thus maximizing the sensitivity while keeping experimental times reasonably short. Stopped-flow and continuous-flow have been employed where the substrate is transported via tubing from a reaction chamber in the vicinity of the spectrometer to the measurement cell.^6–8 Mixing and reaction devices, however, possess geometries that do not allow the direct monitoring inside the named probes. In order to obtain spectroscopic information about the substances inside the microstructured device itself, dedicated coils have been designed,^9,10 such as wire-wound and etched surface coils^11–14 or multi-coil arrays.^15–18 Employing miniaturized coils, NMR spectroscopy was combined with microfluidic devices:¹⁹ for instance, Kakuta et al.²⁰ have investigated protein conformation changes, and Wensink et al.²¹ have demonstrated the quantitative monitoring of a reaction process in-situ.

Generating a signal with spatial resolution, or a complete image of the microstructured device, allows one to follow mixing and reaction processes in their spatial dependence; a prerequisite for achieving this goal is the understanding and quantification of flow processes in such a device. Similar to spectroscopy, the efficiency of an imaging experiment depends largely on the signal intensity, or rather the signal-to-noise ratio of the sample. For a given geometry, a matching coil which covers the region of interest best will meet this condition because it possesses the largest filling factor, i.e. fraction of sample volume compared to coil volume. Static imaging could be demonstrated to be feasible even for the visualization of single cells.²² While NMR velocity imaging is an established technique (see, for instance, ref. 2 and references therein), it remains mostly applied to larger structures which enable the use of commercial coil setups. In this study, we demonstrate, for the first time, the feasibility of generating flow maps inside a micromixer with 65 µm channel width, and present velocity fields for different flow conditions, highlighting the transport efficiency and local clogging in the mixer.

NMR velocity imaging

The image and velocity information in an NMR experiment both rely on the same principle of spatially dependent magnetic field strengths provided by pulsed field gradients (PFGs) (see, for instance, ref. 23 and 24). The spatial dependence of the Larmor frequency, ω, can generally be written by

ω(r) = γ|B(r)| = γ(|B₀| + g·r)

where g is the first derivative of the z (principal) component of the magnetic field strength B with respect to space, and B₀ is the constant main field. This provides one possibility to generate image information by acquiring the signal in the presence of a gradient so that the Fourier transform of the signal corresponds to the one-dimensional projection of the object onto the gradient axis. The second approach exploits the phase information which is acquired with the complex NMR signal. Applying a pulsed gradient g_phase for a duration δ generates a phase shift

ϕ(r) = (ω(r) − ω(r₀))δ = 2πk·r

relative to a reference value, where the wave vector is defined as k = (2π)⁻¹γg_phaseδ . The total signal intensity S(k)—normalized by its value in the absence of a gradient—can then be written as an integral over all spins in the sample,

S(k) = ∫ ρ(r) exp [i2πk·r] dr

Scanning k space evenly allows the reconstruction of the spin-density function ρ(r) following an inverse Fourier transformation. The scheme can be combined to obtain three-dimensional images, and a wide range of techniques have been developed that reduce the acquisition time of a full image considerably by either repeated refocusing of the signal or sectioning of the magnetization.

Velocity v, or rather displacement R during an interval Δ, is encoded in much the same way, by applying a pair of gradients of inverse sign but identical area. This gradient pair gives rise to a phase shift

ϕ(R) = 2πq·R = 2πq·vΔ

that is proportional to displacement, where q is identical to k but is conventionally used to distinguish between measurements of displacement and position. This encoding can also be carried out in combination with the mentioned imaging sequences. The velocity image is obtained by acquiring two datasets with different values of q, and computing the phase angle difference for each pixel, hereby eliminating spurious phase errors which are independent of the velocity information. The fact that the phase angle ϕ, which is obtained from the imaginary and real parts of the signal in the pixel, is only defined to a periodicity of 2π, determines the choice of q for a given maximum range of velocities.

Experimental

The interdigital micromixer (type MOH 030) was obtained from Mikroglas chemtech GmbH, Mainz, Germany (www.mikroglas.de). It consisted of a three-layer design with one cover plate on each side. The mixer was prepared for two liquids entering in rectangular flat channels, which are connected by a short vertical section to the third level containing channels of 65 µm width, 200 µm height and 45 µm separation at the end of the triangular section. Following this region, where channels were filled with the two liquids in an alternating fashion mixing occurs in another 25 mm long chamber.

The mixer was mounted into a PEEK holder and connected to inlet/outlet Teflon tubing. Water was used as the liquid in both compartments and was transported by two Pharmacia P-500 pumps with volume flow rates of 5 ml h⁻¹ each. From this we compute an average velocity inside the channels of 7.1 mm s⁻¹. Mixer and coil mounted at the probe body are shown in the photograph of Fig. 1.

Fig. 1 Photograph of mounted micromixer and rf coil. The homebuilt rectangular transmitter/receiver coil was designed to cover the central portion of the mixer.

Experiments were carried out on a 7 T horizontal super-widebore magnet equipped with a Bruker DMX 300 spectrometer. A Bruker Micro2.5 microimaging gradient set and probe body was used. Instead of the standard cylindrical birdcage resonator, a rectangular rf coil made from a single winding of 1.0 mm copper wire was installed and shielded in a copper foil casing. The coil was tuned to the proton resonance frequency of 300 MHz.

For the velocity images presented, a velocity encoded spin-echo sequence with a repetition time of 430 ms has been used. A standard spin-echo sequence was combined with a velocity encoding filter.²³ In the sequence, an excitation pulse of 90° is followed by the velocity encoding filter, consisting of a pair of bipolar gradients realized by two gradient pulses of the same sign with an inverting 180° rf pulse in between. The duration of the velocity encoding gradients was 1 ms and the separation of the gradient lobes was 15 ms and 8 ms for the x- and z- component, respectively (z denotes the axis of main flow, which was also parallel to the main magnetic field). Two images with two different values of the velocity encoding gradient were measured to obtain one velocity map. The gradient values were 0.65 G mm⁻¹ and 0 G mm⁻¹ for the x-component and 0.75 G mm⁻¹ and 0 G mm⁻¹ for the z-component. This velocity encoding part was followed by a conventional 2D imaging module containing read- and phase gradients.²³ Before acquisition the magnetization was refocused by a 180° rf pulse, the echo time in the imaging part was 8.2 ms for all images. The digital resolution has been 512 × 512 pixel for a field of view of 15 mm × 22 mm, which was subsequently zero-filled to generate a 2048 × 2048 matrix. Before zero-filling, the spatial resolution was 29 µm × 43 µm. Two velocity encoding steps were compared and the pixel-wise average velocity computed from the phase difference; q values where chosen such that the total velocity range covered was between ±12 and ±20 mm s⁻¹. The typical experimental duration for encoding velocity in one direction was 58 min using 16 signal accumulations, resulting in an estimated pixel-wise velocity error of below 2% of the total velocity range, but a minimum of two accumulations was found to be sufficient for acquiring velocity charts with acceptable signal-to-noise ratio. Data analysis was performed using PROSPA software (Magritek, Wellington, New Zealand).

Results and discussion

In Fig. 2, the water distribution inside the mixer is shown under static conditions, i.e. all channels were filled with water and the pumps were stopped. This image was obtained from the magnitude of the Fourier transformed 2D dataset in k space. An identical treatment was applied for all flow-encoded images, and the magnitude image was used as a mask for generating velocity information only from the desired regions and suppressing noise in the liquid-free regions outside the mixer and between the channels.

Fig. 2 Spin density image of the water-filled micromixer in the absence of flow. Insert: one-dimensional horizontal intensity profile across the central part of the upper (triangular) section of the mixer (indicated by the bar in the image), demonstrating the spatial resolution with respect to the channel size. A variation of local signal intensities between different channels is clearly seen (two such channels are indicated by arrows).

Fig. 2 covers the sensitive volume of the resonator coil which was placed on top of the region between fluid inlet and mixing chamber in order to make visualization of all channels possible. The left-hand main inlet is at the edge of the sensitive volume, resulting in a reduced signal intensity despite constant layer thickness in this part of the mixer. Note that despite this signal loss, the correct determination of the signal phase, required for the computation of the local velocity, is not compromised as long as the signal-to-noise ratio at any point in the image is sufficient.

Further to the reduction of signal intensity at the edges, regions of reduced signal intensity are also visible in the central part of the image, most notably inside the large areas of the inlet reservoirs. These “black areas” are atypical for NMR image artifacts, and must be attributed to local deviations of the B₀ magnetic field which are otherwise often found in the vicinity of interfaces. In this case, the most probable explanation for the black areas is an inhomogeneous distribution of either glue or air bubbles between the thin glass layers of between 0.2 and 0.3 mm thickness which affect the magnetic field at the location of the liquid. Surface impurities inside the chamber with direct contact to the fluid are also possible, but air bubbles can be ruled out due to the reproducibility of the features at varied conditions with and without flow. Note that, while it is possible to reduce the effect of field heterogeneities further by modifying the signal acquisition parameters or by performing the experiment at a lower magnetic field strength, NMR imaging can straightforward be employed to validate the quality of microstructured devices out of the production process.

The bright spots in Fig. 2 indicate the (vertical) transition channels where fluid is transferred from the feeder level to the mixer level; at these positions, the total thickness of the liquid columns is 0.8 mm compared to the 0.3 mm (inlet) and 0.2 mm (horizontal channels and mixing chamber), leading to a proportionally increased signal intensity. Brighter stripes appear where channels connected to the reservoir at the bottom of the figure are superposed above the second reservoir. Note that most channels possess similar signal intensity, hence complete filling and identical width and depth can be assumed. The insert of Fig. 2 highlights that there is indeed a variation in signal strength. While certain fluctuations at a given pixel may be of stochastic nature or are determined by magnetic field inhomogeneities such as the dark patches mentioned above, the reduced intensity of large channel sections must be attributed to a real reduction in amount of fluid (see, for example, the two channels in the upper region marked by arrows).

Fig. 3 shows the velocity component along x, i.e. perpendicular to the main flow axis. While in Fig. 3a, both pumps were switched on to provide identical volume flow rates of both liquids (resulting in identical velocities inside the channels since both total fluid volume and channel dimensions are identical), only one pump was running in Fig. 3b. The strength of the encoding gradients has been chosen such that the comparatively small velocities inside the reservoir chamber can be distinguished. The rather regular flow pattern in the bottom reservoir can immediately be identified (blue corresponds to leftward motion, red to rightward motion). Larger velocities toward the right are found in the upper chamber, and no velocity is detected when the pump is switched off (Fig. 3b). In the channels within the triangular section, the left- and rightward velocity components tend to grow toward the outer edge where the inclination angle relative to the main flow axis become larger. Due to the choice of velocity ranges, the outermost velocities are not depicted correctly (identifiable by an apparent change in sign where a phase wrap of 2π occurs in the velocity encoding angle). At the beginning of the mixing chamber, coherent flow structures are immediately lost.

Fig. 3 Transverse component of velocity (v_x, horizontal direction in the figure); (a) water flow driven by pumps in both inlets, (b) water flow driven only in the bottom inlet (other compartment contains static water). Velocity as indicated at the color bar is given in mm s⁻¹.

The results for the “upward” (z) velocity component are shown in Fig. 4. The only difference to the experiments in Fig. 3 has been the direction of the velocity encoding gradients, and their strength which have been adjusted to a somewhat wider range of velocities. The measurements were carried out under identical conditions as those of Fig. 3. From these measurements, some defects of the micromixer can immediately be identified. For instance, the leftmost channel of the triangular section does not contribute to flow as the velocity values oscillate randomly about zero (this can also be seen from Fig. 3a). Note, however, that this channel is indeed filled with liquid since it is clearly visible in Fig. 2. This channel must therefore contain a clog which is not directly visible by optical inspection or by static NMR imaging. In a similar fashion, the velocity distribution in the different channels appears uneven, but this mostly affects those channels connected to the lower reservoir. In both Fig. 4a and 4b, the channels with numbers 7, 9 and 14 of inlet A feature lower-than-average velocities throughout their length, which becomes most easily visible in the bottom (straight) part of the channels. (Note that in those places where channels and upper reservoir overlap, the measurement provides a velocity averaged over the whole fluid along the line-of-sight which leads to results of limited use.) In the still image (Fig. 2), two of these three channels were identified as having smaller signal intensity, i.e. possibly a smaller effective diameter. The contrast is obviously enhanced when velocities are determined directly. Considering a smaller diameter of a particular channel, this would lead to an increase of the pressure drop and thus to a lower velocity and smaller contribution to the net fluid transport.

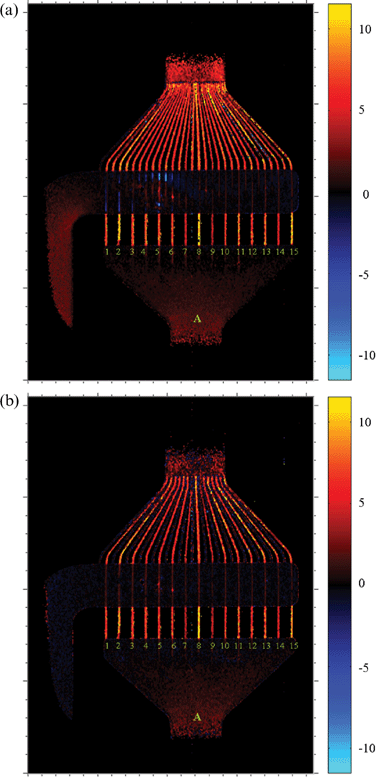Fig. 4 Longitudinal component of velocity (v_z, vertical direction in the figure); (a) water flow driven by pumps in both inlets, (b) water flow driven only in the bottom inlet (other compartment contains static water). Velocity as indicated at the color bar is given in mm s⁻¹.

In Fig. 5 we have combined the individual components of Fig. 3a and 4a to a plot of the magnitude of velocities, i.e. |v| = (v_x² + v_z²)^0.5, where v_x and v_z correspond to the components perpendicular and parallel to the main flow direction, respectively. Fig. 5 thus represents the actual fluid transport taking place in the mixer; the peculiarities mentioned above are observed again, the scatter of flow velocities becomes more obvious due to the particularly chosen contrast. In Fig. 6, the average velocities derived from integrating over the lower part of the channels (the rectangle in Fig. 5 indicates the integration range) are compared to each other. The velocities inside channels 7, 9 and 14 are indeed found to be significantly below average and thus do not contribute to the net fluid transport as efficiently as the other channels. Numbers 2, 8 and 15, on the other hand, are found to have considerably higher velocities than the overall average of 7.1 mm s⁻¹. The maximum deviation found in these averages amounts to about 35% above and 55% below the average of all channels, with even larger fluctuations occurring locally. Error bars are mainly determined by velocity fluctuations along the channels; with the chosen setup and measurement parameters, differences of average velocities (and thus, fluid transport) of 2–3% can be quantified, a number than can further be improved by increased signal averaging.

Fig. 5 Magnitude of velocities (speed) for water flow driven by pumps in both inlets, computed from data of Fig. 3a and 4a. Speed as indicated at the color bar is given in mm s⁻¹.

Fig. 6 Average velocity magnitudes inside channels, computed over the channel portions outlined in Fig. 5. The error bars correspond to the standard deviation within the integration volume.

Conclusions

Nuclear magnetic resonance (NMR) imaging and velocity imaging have been employed to provide access to quality control of microstructured devices by monitoring velocities with a spatial resolution that is sufficient to resolve the average flow properties in individual channels. This has been achieved with commercial hardware supplemented by a simple, homebuilt detector coil. Heterogeneities in the flow distribution and optically not detectable clogging could be identified, whereas image distortions could be interpreted in terms of large-scale imperfections stemming from the manufacturing process of the device itself. The spatial resolution has been deliberately chosen to cover a large fraction of the micromixer; it is entirely possible, by employing a smaller detector coil placed on top of the region of interest, to select more localized information of certain positions inside the mixer, for instance the mixing chamber. With limitations mainly given by diffusion and dispersion effects, channels of 10 µm width or less are easily accessible by the method. By reducing the encoding and acquisition times, a coverage of much higher flow velocities (several 100 mm s⁻¹) at comparable spatial resolution is feasible. Despite the presence of glass/fluid interfaces which are often detrimental to NMR imaging experiments, a substantial image distortion was not found, and the use of smaller magnetic field strengths—that might be of interest for routine and on-line monitoring—will further reduce these effects. Studies to combine the spatial resolution with chemical-shift resolved information are under way and will provide direct and unprecedented insight into the processes of mixing and chemical reactions inside microstructured devices.

Acknowledgements

S. A. thanks the Academy of Finland and the Finnish national graduate school of computational chemistry and molecular spectroscopy (LASKEMO) for funding.

References

1. L. F. Gladden and P. Alexander, Meas. Sci. Technol., 1996, 7, 423.
2. NMR Imaging in Chemical Engineering, ed. S. Stapf and S. Han, VCH-Wiley, Weinheim, 2005.
3. N. Wu, T. L. Peck, A. G. Webb, R. L. Magin and J. V. Sweedler, J. Am. Chem. Soc., 1994, 116, 7929.
4. B. Behnke, G. Schlotterbeck, U. Tallarek, S. Strohschein, L. H. Tseng, T. Keller, K. Albert and E. Bayer, Anal. Chem., 1996, 68, 1110.
5. A. M. Wolters, D. A. Jayawickrama and J. V. Sweedler, Curr. Opin. Chem. Biol., 2002, 6, 711.
6. K. Albert, M. Dachtler, T. Glaser, H. Handel, T. Lacker, G. Schlotterbeck, S. Strohschein, L. H. Tseng and U. Braumann, J. High Resolut. Chromatogr., 1999, 22, 135.
7. J. L. Wolfender, K. Ndjoko and K. Hostettmann, Curr. Org. Chem., 1998, 2, 575.
8. M. Maiwald, H. H. Fischer, Y. K. Kim, K. Albert and H. Hasse, J. Magn. Reson., 2004, 166, 135.
9. A. G. Webb, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 1.
10. K. R. Minard and R. A. Wind, Concepts Magn. Reson., 2001, 13, 128; K. R. Minard and R. A. Wind, Concepts Magn. Reson., 2001, 13, 190.
11. J. E. Stocker, T. L. Peck, A. G. Webb, M. Feng and R. L. Magin, IEEE Trans. Biomed. Eng., 1997, 44, 1122.
12. J. Dechow, A. Forchel, T. Lanz and A. Haase, Microelectron. Eng., 2000, 53, 517.
13. C. Massin, F. Vincent, A. Homsy, K. Ehrmann, G. Boero, P. A. Besse, A. Daridon, E. Verpoorte, N. F. de Rooij and R. S. Popovic, J. Magn. Reson., 2003, 164, 242.
14. S. Eroglu, B. Gimi, B. Roman, G. Friedman and R. L. Magin, Concepts Magn. Reson. B, 2003, 17, 1.
15. E. McNamara, T. Hou, G. Fisher, S. Williams and D. Raftery, Anal. Chim. Acta, 1999, 397, 9.
16. M. A. Mcnaughtan, T. Hou, J. Xu and D. Raftery, Anal. Chem., 2003, 75, 5116.
17. H. Wang, L. Ciobanu, A. S. Edison and A. G. Webb, J. Magn. Reson., 2004, 170, 206.
18. H. Wang, L. Ciobanu and A. G. Webb, J. Magn. Reson., 2005, 173, 134.
19. J. D. Trumbull, I. K. Glasgow, D. J. Beebe and R. L. Magin, IEEE Trans. Biomed. Eng., 2000, 47, 3.
20. M. Kakuta, D. A. Jayawickrama, A. M. Wolters, A. Manz and J. V. Sweedler, Anal. Chem., 2003, 75, 956.
21. H. Wensink, F. Benito-Lopez, D. C. Hermes, W. Verboom, Han J. G. E. Gardeniers, D. N. Reinhoudt and A. van den Berg, Lab Chip, 2004, 5, 280.
22. D. A. Seeber, L. Ciobanu and C. H. Pennington, Appl. Magn. Reson., 2002, 22, 139.
23. P. T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy, Clarendon Press, Oxford, 1991.
24. B. Blümich, NMR Imaging of Materials, Oxford University Press, Oxford, 2000.

---