Probing the mechanism of hypoxia selectivity of copper bis(thiosemicarbazonato) complexes: DFT calculation of redox potentials and absolute acidities in solution

Abstract

Density functional theory (DFT) calculations have been performed using the uB3LYP/6-31++G(d,p) model to calculate the solution phase one-electron reduction potentials (E_calc) and absolute pK_a values of a series of copper bis(thiosemicarbazonato) complexes. The effects of solvation in water and dimethylsulfoxide (DMSO) are incorporated as a self-consistent reaction field (SCRF) using the integral equation formalism polarisable continuum model (IEFPCM) and are found to be essential for quantitative agreement with an average error in E_calc of −0.02 V compared to experiment. The bonding and spin densities are examined through the use of Natural Bond Order analysis and the results used to rationalise the calculated and observed reduction potentials. Calculated estimates of pK_a values of several copper(II) species are presented and their implications for the mechanisms of transport and trapping within hypoxic cells are considered. Reduction is found to be a prerequisite for protonation of the complexes which suggests their transport in the blood stream as neutral species, and the mechanistic sequence is identified as a sequential electrochemical–chemical (EC) process. The complex equilibria of protonation, reoxidation and dissociation are discussed and the copper(I) diprotonated, cationic complex of diacetyl bis(4-methyl-3-thiosemicarbazonato)copper(II), Cu(I)ATSMH₂⁺, is identified as a possible candidate for the initial species trapped in hypoxic cells.

---

Introduction

Copper complexes of bis(thiosemicarbazonato) ligands have recently been the subject of intense research due to their potential as radiopharmaceuticals for the specific targeting of hypoxic tissue.^1–16 First synthesised^17–20 in the 1950s, they exhibit a wide range of biological activity including antibacterial, antimalarial, antitumour and superoxide dismutase-like radical scavenger properties.^5,21–26 However, it is their observed specific uptake in hypoxic cells, coupled with the possibility of using a radionuclide of copper that is driving their development as potential new generation selective imaging and therapeutic agents for hypoxia.^1,15,27

Hypoxia is a pathological condition where the partial pressure of oxygen in local tissue decreases to around pO₂ < 3 mmHg, the normal concentration being 20–80 mmHg, and has been associated with certain cancers, stroke and heart disease.^1,28 A decrease in the oxygen concentrations may arise from the insufficient blood supply to the affected tissue which in turn can lead to anaerobic respiration and the lowering of the cellular pH from accumulation of lactic acid. The ability to image and measure hypoxia non-invasively in vivo, through the use of techniques such as positron emission tomography (PET), single photon emission computerised tomography (SPECT) and fluorescence²⁹ would greatly assist in the clinical treatment of such diseases.⁷ Several radionuclides of copper have suitable decay properties for combination with these imaging techniques. For example, the positron, β⁺, emitting isotopes ⁶⁰Cu, ⁶¹Cu, ⁶²Cu and ⁶⁴Cu may be utilised in PET imaging. In addition to locating and visualising hypoxic regions, the hypoxia selectivity of copper bis(thiosemicarbazonato) complexes presents the possibility of delivering an in situ radiotherapeutic dose for the targeted therapy of diseases. Both the ⁶⁴Cu and ⁶⁷Cu radionuclides have β-emitting decay pathways with average non-penetrating radiation energies of 190 and 121 keV and half-lives, t_1/2 of 12.7 and 62 h, respectively. This corresponds to an average range in tissue of 1.4 and 0.6 mm, respectively.^13,30

Fujibayashi et al.¹⁵ demonstrated the selective uptake of diacetyl bis(4-methyl-3-thiosemicarbazonato)copper(II) (CuATSM) in hypoxic tissue, proposing a mechanism of trapping and selectivity based around the redox behaviour of the Cu(II)/Cu(I) couple. In an attempt to elucidate further this proposed mechanism, Blower et al.^1,2 conducted extensive structure–activity relationship (SAR) studies on a series on thirteen related complexes. They found that hypoxia selectivity strongly correlated with both the Cu(II)/Cu(I) reduction potential and the alkyl substitution pattern on the backbone of the ligand. On varying the concentration of oxygen supplied in vitro to a sample of mammalian EMT6 cells, CuATS and CuATSM showed decreased uptake with increasing oxygen concentration. The mechanism of selectivity and uptake is a complex one, dependent on many factors including lipophilicity, planarity, molecular weight, pK_a and redox potential.^4,16 This paper describes a computational investigation of the subtle variations in the Cu(II/I) redox potential when varying the ligand substituents and the implications this has for hypoxia selectivity. For the first time, calculated estimates of absolute pK_a values for a series of experimentally known copper(II) complexes are presented. The complexes studied computationally are shown in Fig. 1.

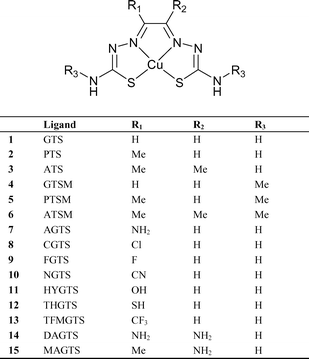Fig. 1 Structures of the copper bis(thiosemicarbazonato) complexes studied in this investigation.

Standard redox potentials, E^o, and relative acidity, pK_a, are two of the most fundamental properties of a molecule and are important in determining many factors including thermodynamic stability and chemical reactivity.^31–33 In the case of copper bis(thiosemicarbazonato) complexes, one-electron reduction potentials are proposed to be the controlling property regarding hypoxia selectivity and trapping.¹⁵ Therefore, their accurate calculation and prediction in solution phase would be of enormous benefit, not only in helping to explain observed trends but also in the rational design of more highly selective complexes. Many biological systems such as NiFe and Fe-only hydrogenases involve electron transfer steps which are accompanied by a proton transfer reaction.^34,35 For copper bis(thiosemicarbazonato) complexes, the effect of changing pH on the cyclic voltammetry and UV/vis spectroscopy in DMSO has been studied.⁴ However, it is not known experimentally whether reduction or protonation occurs first; a process which is crucial to the understanding of the mechanisms of transport, uptake and trapping in vivo. Identification of the electronic properties that control redox potentials and pK_a on a molecular level may also allow fine tuning of a system through computer-aided design. This is an area of growing importance not only for the radiopharmaceutical field but also in the optimisation of catalysts and the elucidation of enzymatic mechanisms.³⁶

Ever increasing computational power gives the quantum chemist the ability to conduct extensive screening of as yet unknown compounds for improved properties. This has been demonstrated in a study by Baik et al.³⁷ in which they calculated the one-electron oxidation potentials of minimally substituted DNA bases in a search for an analogue with a potential lower than that of guanine (E_1/2 = 1.29 eV). Subsequent synthesis of the most promising analogue, 5-amino-cytosine, which had a calculated oxidation potential of 0.72 V and experimental potential of ca. 0.75 V, vs. the standard hydrogen electrode (SHE) confirmed the calculations and reinforced the utility of theoretical quantum calculations of redox potentials in modern chemistry.

Computational details

All calculations were conducted using density functional theory^38,39 (DFT) as implemented in the Gaussian 03, Revision C.02 suite of ab initio quantum chemistry programs.⁴⁰ Geometry optimisations and vibrational frequency calculations were performed with an unrestricted scheme using the hybrid-DFT uB3LYP functional^41–46 and the double-ζ 6-31++G(d,p) basis set by Pople et al.^47–53 for all atoms. This method includes one set of polarisation functions and one set of diffuse functions on all atoms. Diffuse functions are essential for the accurate description of anions in which the electron density is remote from the nuclei due to increased electron–electron repulsions and the addition of polarisation functions improves the description of the metal–ligand bonds. Normal SCF and geometry convergence criteria were used throughout and no symmetry constraints were imposed. For all of the in vacuo calculations, harmonic frequency analysis based on analytical second derivatives was used to characterise the optimised geometries as local minima and to derive the zero-point energy (ZPE) and vibrational/rotational/translational contributions to the enthalpic and entropic corrections at standard temperature and pressure (298.15 K and 1.000 atm, respectively). Unscaled frequencies were used for the vibrational component to the entropy.

The effects of solvation were incorporated^54,55 iteratively by performing self-consistent reaction field (SCRF) calculations using the integral equation formalism polarisable continuum model (IEFPCM) initially developed by Tomasi and co-workers.⁵⁶ Geometry optimisations were performed in the presence of the reaction field using the optimised in vacuo coordinates as initial geometries. In this dielectric continuum model, the solute is placed in a cavity within the solvent continuum. The solute–solvent boundary has been defined using a solvent excluding surface (SES).⁵⁷ This is the surface traced by the solvent sphere as is rolls over the molecular surface of the solute defined using the United Atom Topological model (UAHF) for the radii of the solute atoms.⁵⁸ Two assumptions are made with the UAHF parameters which have been optimised for the 6-31G(d) basis set. Firstly, the hydrogen atoms do not have individual spheres but are included in the spheres of the heavy atoms to which they are bonded. Secondly, all elements in the same row of the periodic table have the same initial radius which is modified by the molecular environment. In the UAHF model the van der Waals radii of the solute atoms are scaled by a factor of f = 1.2. The actual radii used are corrected values which depend on the hybridisation and on the number of bonded hydrogens and heavy atoms. Therefore, the assignment of atomic radii is molecule specific. Two solvent models have been employed; water (ε = 78.39, R_solv = 1.385 Å) and DMSO (ε = 46.7, R_solv = 2.455 Å) where ε is the dielectric constant and R_solv is the sphere radius of the solvent. For the solute interior, a dielectric constant of 1.0 is used throughout. Frequency calculations have not been performed in solution phase as the entropy of the solvent is implicitly included in the dielectric continuum model. Their accuracy is also questionable given that no explicit solvent–solute interactions are accounted for by the continuum which may introduce large errors in the estimation of entropic terms due to inaccurate low frequency modes in solution. The choice of solvation models reflects the biological medium and the solvent used (DMSO) for the determination of experimental standard reduction potentials⁴ due to the insolubility of the copper complexes in water. The use of both water and DMSO also facilitates the assessment of the ability of the calculations to model the solvent effects accurately.

The standard one-electron reduction potential, E°/V, can be derived from the solution phase Gibbs free energy change of electron attachment, Δ_EAG° (sol), using eqn (1),

Δ_EAG°(sol) = −FE° (1)

Δ_EAH°(g) = Δε_SCF + Δε_trans + Δε_rot + Δε_vib + Δε_ZPE (2)

Δ_EAG°(g) = Δ_EAH° (g) − TΔS°(g) (3)

ΔΔ_solvG° = Δ_solvG°(A⁻) − Δ_solvG°(A) (4)

Δ_EAG°(sol) = Δ_EAG°(g) + ΔΔ_solvG° (5)

where F is the Faraday constant, 9.6485 × 10⁴ C mol⁻¹. Δ_EAG° (sol)/kJ mol⁻¹ can be readily derived from the calculations by using eqn (2)–(5), where ε is the energy.^59,60 The Gibbs free energy change of solvation of a species, Δ_solvG°/kJ mol⁻¹, is the sum of electrostatic and non-electrostatic contributions. The non-electrostatic terms include the cavitation, dispersion and repulsion energies associated with the formation of the cavity within the solvent continuum and the placement of the solute in this cavity. The electrostatic contribution is derived from the energy difference between the solute polarised by the reaction field of the solvent minus the non-polarised, in vacuo solute energy. In this work the electrostatic part includes the geometry relaxation energy, Δε_geom, incurred on moving from gas to solvent due to the full geometry optimisations in solution.^61–64

As experimental potentials are reported relative to the secondary standard calomel reference electrode (SCE), the computed absolute one-electron reduction potentials, E°, can be compared with the experiment by subtraction of 4.1888 V. This value is derived from the experimentally determined absolute potential of the standard hydrogen electrode, 4.43 V, minus the relative potential of the SCE, 0.2412 V. The method used to determine the reduction potentials is represented by the thermodynamic cycle shown in Scheme 1.^59,65

Scheme 1 Thermodynamic cycle used to determine the one-electron reduction potentials in solution.

The accurate calculation of absolute and relative acidities, pK_a, presents a significant technical and theoretical challenge in quantum chemistry.^66,67 For the general ionisation reaction, AH⁺ → A + H⁺, difficulties arise in the choice of reference and consequently, in the values used for the free energy of solvation of a proton, Δ_solvG°(H⁺)/kJ mol⁻¹. In aqueous solution, experimental values range from −1057.6 to −1099.0 kJ mol⁻¹, an uncertainty of around 41.4 kJ mol⁻¹. Given that an error of only 6.7 kJ mol⁻¹ in the free energy change in solution, Δ_dpG° (sol), leads to change of 1 pK_a unit, highly accurate calculations and experimental data are essential to achieve accurate values when determining the pK_a. The latest experimental data for solvation of a proton in water indicate Δ_solvG° (H⁺) to be −1105.3 kJ mol⁻¹. This agrees with most accurate calculations which converge on a value of −1107.0 kJ mol⁻¹.⁶⁸ Literature studies have found that the use of a theoretical model chemistry that accounts for electron correlation to be important in achieving the high degree of computational accuracy required. DFT coupled with the SCRF dielectric continuum models have demonstrated their ability quantitatively to reproduce experimental proton affinities and proton transfer reaction enthalpies.^69,70 Investigations in the literature include pK_a calculations on carboxylic acids,⁷¹ substituted uracils,⁷² pyrone and dihydropyrone inhibitors of HIV-1 protease⁷³ and substituted imidazoles⁷⁴ for which Topol et al. report an average absolute deviation of 0.8 pK_a units between calculated and experimental pK_a values.

The calculation of pK_a values for the copper bis(thiosemicarbazonato) complexes can be achieved using a thermodynamic cycle as shown in Scheme 2. The pK_a is related to the free energy change of deprotonation in solution, Δ_dpG° (sol) by eqn (6) and the energy decomposition in terms of the sum of free energies is given in eqn (7).⁷⁴

Δ_dpG°(sol) = Δ_dpG°(g) + Δ_solvG°(A) − Δ_solvG°(AH⁺) + Δ_solvG°(H⁺) (7)

Δ_dpG°(g) = Δε_SCF + Δε_trans + Δε_rot + Δε_vib + Δε_ZPE − T[S° (A) − S°(AH⁺)] −26.3 kJ mol⁻¹ (8)

Scheme 2 Thermodynamic cycle used to determine the pK_a of the copper bis(thiosemicarbazonato) complexes in solution, where (1) and (3) are the free energy change of solvation of the protonated and deprotonated complexes, Δ_solvG^o(AH⁺) and Δ_solvG^o(A), respectively. (2) and (4) are the solvation free energy changes associated with the water cluster model used as the reference.

At this point two approaches can be used for the value of Δ_solvG°(H⁺). The most commonly cited is to use a proton as the reference and insert the experimental free energy of solvation of H⁺ in water, under standard conditions (298.15 K and 1 M solution) into eqn (7). The gas phase translational entropy (32.5 kJ mol⁻¹) of the proton is accounted for by solving the Sackur–Tetrode equation at standard temperature and pressure. The increase in the number of in vacuo species (ΔpV) on deprotonation and the translational enthalpy of the proton are also included by the addition of 5/2RT. Combining these two gives the value −26.3 kJ mol⁻¹ in eqn (8). The choice of Δ_solvG°(H⁺) is crucial in obtaining accurate results.

The second approach (Scheme 2) is to eliminate the need for experimental values by changing the reference from a proton to a protonated water cluster, (H₉O₄⁺). This allows the calculation of all terms associated with in vacuo deprotonation and solvation via frequency calculations. The actual nature of a solvated proton is unclear and although the H₉O₄⁺ cluster may not be ideal, it is certainly more representative than an individual proton. Larger clusters may be used but the system quickly becomes conformationally complex. Eqn (9) shows the relationship between the two references.

Δ_solvG°(H⁺) ≡ Δ_solvG°(H₉O₄⁺) − Δ_solvG°(H₈O₄) (9)

Stabilisation energy due to full geometry relaxation is included in the SCF energy. One additional consideration is the energy stabilisation of the complex and the water cluster due to basis set superposition error, Δε_BSSE. In the case of proton transfer, this energy is expected to be small and in using the water cluster method the difference between the protonated complex and H₉O₄⁺, ΔΔε_BSSE, will be insignificant.⁶⁰

Relative pK_a values for the reaction AH⁺ + B → A + BH⁺, do not require a reference for the proton and can be determined using eqn (10),

where Δ_rG°(g) is the in vacuo free energy change for the proton transfer reaction between AH⁺ and B.

Results and discussion

Calculation of one-electron reduction potentials

In order to assess the initial accuracy of the calculations in modelling the complexes, the optimised geometries for oxidised Cu(II) species, 1–6, were compared to the experimental structures derived from X-ray crystallography.^3,75 Overall, the DFT calculations with the uB3LYP method show excellent agreement with the experiment. All Cu(II) complexes are predicted to have a distorted square-planar geometry and the carbon–carbon bond of the backbone lies in the plane with a dihedral angle d(N–C–C–N)/° which is very close to zero for all species. EPR experiments also support a d⁹ square-planar structure of the complexes. The metal–ligand bonds show the largest variance, being consistently overestimated in all complexes by 0.03–0.04 Å for r(N–Cu) bonds and 0.04–0.05 Å for r(Cu–S) bonds. This could be a consequence of using a double-ζ basis set and may be improved if a larger basis set were used. However, these values lie within the standard error for the B3LYP functional. The r(C–S) bonds are only slightly overestimated by around 0.01 Å. Crucially, all r(C–C) and r(C–N) bond lengths are very accurately reproduced and found to be within the experimental error for all structures. In addition, the r(N–N) bonds are underestimated by around only 0.01 Å. Therefore, all structures reproduce the alternating bond lengths in the ring which is indicative of the conjugation within the bis(thiosemicarbazonato) ligand system. This is particularly encouraging as the electron density within the system is being described to a high degree of accuracy and therefore, the substituent effects on the electronic structure should be well modelled. The bond angles around the metal are also well reproduced showing a small contraction from experimental values for the a(N–Cu–N) and a(N–Cu–S) angles which is countered by a corresponding increase in the a(S–Cu–S) angle of between 1 and 2°. More detailed information on the geometries of the complexes including Cartesian coordinates of all optimised structures can be found in the ESI†.

The different substituents at the R₁ and R₂ positions (Fig. 1) were chosen to investigate the effects of electron donating ability on the structure, orbitals and calculated reduction potentials of the copper bis(thiosemicarbazonato) complexes. If the reduction potentials are dependent on the electronic nature of the substituents on the backbone carbon atoms, then it is logical to surmise that more electron donating groups (EDG's) would stabilise the Cu(II) species, thereby lowering the reduction potential. The data in Table 1 shows the calculated changes in energy for electron attachment in vacuo, with the ZPE, thermal and entropy corrections included in accordance with eqn (2)–(5). The change in free energy of solvation, ΔΔ_solvG° (anion-neutral), in both water and DMSO are also given along with the calculated one-electron reduction potentials. The magnitude of the changes in solvation energy are very similar to the free energy of electron attachment which demonstrates the importance of including the effects of solvation in the calculations if quantitatively accurate results are to be obtained. As expected, the solvation of the anions in the polar solvents is more exothermic than solvation of the neutral Cu(II) complexes. The water model stabilises the complexes to a greater extent with the average values for Δ_solvG° of −66.4 and −241.0 kJ mol⁻¹ for the Cu(II) and Cu(I) respectively, compared to −30.8 and −191.2 kJ mol⁻¹ for the DMSO model. The average value of ΔΔ_solvG° are −174.6 and −160.4 kJ mol⁻¹ for water and DMSO, respectively. By performing single point calculations using the optimised in vacuo geometries of complexes 1–6 and including the effects of solvation with the DMSO model, the geometry relaxation energy, Δε_geom, obtained as a result of fully optimising the structures in solution can be determined. Using the electronic energy values, Δε_SCF, the average Δε_geom energies were found to be −40.9 and −58.3 kJ mol⁻¹ for Cu(II) and Cu(I) complexes, respectively. For the thermodynamic cycle used (Scheme 1), this results in an average overall change in geometry relaxation energy, ΔΔε_geom of −17.4 kJ mol⁻¹. Thus the contribution of geometry relaxation on solvation is non-negligible and these values demonstrate the requirement of performing full geometry optimisations in solution.

Table 1 Gas phase electron attachment energies in kJ mol⁻¹ including ZPE, thermal enthalpic and entropic corrections. Changes in the free energy of solvation for water and DMSO are also given along with the corresponding calculated one-electron reduction potentials, E_calc(SCE)/V, relative to the standard calomel reference electrode

	ΔεSCF/kJ mol^−1	ΔεZPE/kJ mol^−1	ΔEAH^o(g)/kJ mol^−1	ΔEAG^o(g)/kJ mol^−1	ΔΔsolvG^o (aq)/kJ mol^−1	ΔΔsolvG^o (DMSO)/kJ mol^−1	E calc(SCE)/V in H2O	E calc(SCE)/V in DMSO	Expt.^aE1/2(SCE)/V in DMSO
a Reference 4.
1	−204.2	−3.0	−207.7	−205.3	−178.0	−164.8	−0.218	−0.355	−0.428
2	−195.8	−2.3	−199.2	−194.5	−178.1	−163.1	−0.330	−0.486	−0.502
3	−186.0	−2.1	−189.7	−180.4	−178.4	−161.1	−0.473	−0.651	−0.587
4	−193.2	−5.9	−199.0	−196.6	−180.1	−163.9	−0.288	−0.456	−0.429
5	−184.0	−5.7	−189.8	−187.0	−179.7	−163.2	−0.391	−0.562	−0.510
6	−174.6	−6.3	−180.6	−177.4	−178.2	−161.6	−0.505	−0.678	−0.590
7	−184.2	−3.8	−187.9	−188.5	−181.7	−165.8	−0.355	−0.519	—
8	−227.1	−3.9	−230.5	−232.3	−168.5	−155.9	−0.038	−0.168	—
9	−222.2	−3.7	−225.7	−226.3	−172.2	−161.0	−0.061	−0.178	—
10	−250.6	−3.1	−253.9	−252.1	−155.9	−147.3	0.037	−0.052	—
11	−206.9	−3.7	−210.4	−210.9	−173.1	−161.6	−0.212	−0.331	—
12	−213.4	−3.0	−216.9	−214.6	−170.3	−157.0	−0.202	−0.340	—
13	−238.1	−3.5	−241.9	−238.8	−159.5	−149.6	−0.064	−0.166	—
14	−172.7	−5.0	−176.7	−179.4	−184.1	−166.7	−0.423	−0.604	—
15	−175.2	−3.6	−178.8	−178.6	−181.5	−163.4	−0.458	−0.647	—

---

Fig. 2 shows a plot of the calculated reduction potentials for complexes 1–6versus the experimental potentials, E_1/2/V measured in DMSO. Linear regression analysis indicates that the quality of the fit of calculation to experiment is very good with R values of 0.967 and 0.951 for the water and DMSO data, respectively. Within the consistent sets, (GTS, PTS, ATS) and (GTSM, PTSM, ATSM), a linear relationship may be expected between E_calc and the experiment and indeed is observed with R values >0.999 for both the sets of data in water and DMSO. The same trend is observed in both solvent models which demonstrates the consistency of the method and stability of the SCRF to functional group modification. Average deviations of calculated potentials from the experimental values measured in DMSO, are 0.14 V for water and −0.02 V for DMSO with maximum deviations of 0.21 V for GTS in water and 0.09 V for ATSM in DMSO. These results show the excellent agreement that can be obtained when the solvation model accurately reflects the solvent used in the cyclic voltammetry experiment, in this case DMSO. Again, the solvation model is observed to be highly influential in the quantitative accuracy of the results. The fact that in a water medium, the potentials are less negative by around 0.1–0.2 V may have consequences in designing the next generation of bis(thiosemicarbazonato) derivatives to be more compatible with the biologically accessible potentials in hypoxic cells.

Fig. 2 Calculated vs. experimental reduction potentials, E_1/2 (SCE)/V, for copper bis(thiosemicarbazonato) complexes 1–6 using water and DMSO solvation models.

By placing the backbone substituents in order of the calculated potentials, E_calc(DMSO)/V, the following trend is observed.

NGTS (10) < TFMGTS (13) < CGTS (8) < FGTS (9) < HYGTS (11) < THGTS (12) < GTS (1) < GTSM (4) < PTS (2) < AGTS (7) < PTSM (5) < DAGTS (14) < MAGTS (15) < ATS (3) < ATSM (6)

A strong positive correlation was found between the calculated reduction potentials and the Hammett σ_m substituent constants⁷⁶ with R values of 0.960 and 0.962 for water and DMSO, respectively. The calculations with the water model give a very similar substituent order; the only differences being the reversal of the THGTS and HYGTS positions and the shift of the TFMGTS complex to a higher potential than both CGTS and FGTS. This reveals several interesting features. The electron donating/withdrawing nature of the substituents determines the reduction potential with more electron donating groups leading to lower, E_calc. It was found that the amine substituent (7) gives a lower potential than the methyl substituent in PTS. Based on this observation the diamine and methyl-amine complexes (14 and 15) were investigated with the hypothesis that placing two amine substituents on the bis(thiosemicarbazonato) backbone may result in a calculated reduction potential lower than ATS (−0.651 V). However, from the data it can be seen that the effect of adding the second –NH₂ is to lower the potential by only 0.085 V. This is much smaller than the effect of adding a second methyl group which lowers the potential by 0.165 V.

The substituent order and Fig. 2 also reveal that in the calculations, the addition of methyl groups at the terminal nitrogen, R₃ positions lowers the potentials by 0.101, 0.076 and 0.027 V in comparison to where R₃ = H for GTSM, PTSM and ATSM, respectively. The experimental data suggests that substitution at the terminal nitrogen positions has a much smaller influence on the reduction potentials. This deviation from experiment indicates that the solvation model may not be sophisticated enough to account fully for the solvent–solute interactions associated with the methyl groups at the R₃ position. However, these effects are minor and substitution at the terminal nitrogen is not expected to have a large influence on the reduction potentials. A plot of calculated reduction potentials in water versus DMSO gives a linear correlation with an R value of 0.999 which shows that the errors are consistent between the two solvation models and overall, the qualitative results between the two models are comparable.

Table 2 contains the frontier molecular orbital (FMO) energies in electron volts from the unrestricted calculations on both the oxidised and reduced species in water and DMSO. Redox potentials are characterised by the nature of the orbitals involved in the process of either accepting or donating the electron. Hence, it can be supposed that the calculated one-electron reduction potentials may correlate with the energies of both the LUMO of the Cu(II) complexes and the HOMO of the reduced Cu(I) complexes. Fig. 3 shows the plots of the Cu(II) LUMO and the Cu(I) HOMO for the solution phase calculations versus E_calc/V including the linear regression analysis. The R values for the quality of the fit for water are 0.975 and 0.980 and for DMSO, 0.988 and 0.988 for the HOMO and LUMO, respectively. All four cases show excellent agreement between the orbital energies and the reduction potentials which supports the involvement of these orbitals in electron transfer processes. This linear relationship can be expressed in the form of eqn (11) where E_{Cu(I)HOMO/Cu(II)LUMO} is the calculated orbital energy in eV and E_calc,pred is the calculated prediction of the one-electron reduction potential in V. The constants, a and b, derived from the four sets of data are given in Table 3. These equations allow the prediction of reduction potentials of related copper bis(thiosemicarbazonato) complexes with backbone substitution from the calculated molecular orbital energies in solution phase. This should decrease the computational effort required by eliminating the need to conduct expensive in vacuo optimisations and frequency calculations. Assuming future complexes conform to the model used here, the prediction of reduction potentials can be achieved from the results of a single geometry optimisation calculation in solution.

Table 2 HOMO and LUMO molecular orbital energies/eV for both the oxidised Cu(II) and reduced Cu(I) complexes in H₂O and DMSO solutions

	Cu(II) complexes				Cu(I) complexes
	H2O		DMSO		H2O		DMSO
	β1 HOMO^a	β2 LUMO^b	β1 HOMO	β2 LUMO	β2 HOMO	α3 LUMO	β2 HOMO	α3 LUMO
a HOMO = highest occupied molecular orbital. b LUMO = lowest unoccupied molecular orbital.
1	−5.762	−3.208	−5.786	−3.251	−4.714	−1.845	−4.503	−1.671
2	−5.694	−3.132	−5.702	−3.164	−4.638	−1.737	−4.403	−1.544
3	−5.642	−3.021	−5.636	−3.038	−4.565	−1.552	−4.279	−1.312
4	−5.698	−3.108	−5.681	−3.113	−4.615	−1.744	−4.349	−1.514
5	−5.618	−3.025	−5.602	−3.026	−4.523	−1.629	−4.272	−1.414
6	−5.556	−2.914	−5.541	−2.916	−4.442	−1.432	−4.187	−1.239
7	−5.512	−3.038	−5.528	−3.070	−4.520	−1.478	−4.293	−1.320
8	−5.881	−3.388	−5.912	−3.446	−4.878	−1.940	−4.671	−1.779
9	−5.888	−3.397	−5.922	−3.458	−4.865	−1.885	−4.653	−1.741
10	−5.973	−3.468	−6.030	−3.548	−4.944	−2.386	−4.787	−2.231
11	−5.716	−3.207	−5.755	−3.267	−4.693	−1.646	−4.490	−1.507
12	−5.757	−3.255	−5.777	−3.297	−4.732	−1.788	−4.516	−1.600
13	−5.924	−3.404	−5.963	−3.465	−4.871	−2.180	−4.693	−2.012
14	−5.380	−2.904	−5.421	−2.963	−4.456	−0.960	−4.229	−0.850
15	−5.464	−2.944	−5.480	−2.972	−4.465	−1.319	−4.235	−1.151

---

Table 3 Values of the constants derived from Fig. 3, Table 2 and eqn (11)

	H2O		DMSO
Constant	HOMO	LUMO	HOMO	LUMO
a	−1.057	−0.937	−1.059	−0.991
b	−5.193	−3.228	−5.110	−3.584

---

Fig. 3 (a) HOMO and LUMO energies/eV of the Cu(I) and Cu(II) species, respectively, vs. the calculated reduction potentials, E_calc/V, with the water solvation model and (b) with DMSO solvation model.

E _calc,pred = aE_{Cu(I)HOMO/Cu(II)LUMO} + b (11)

Fig. 4 shows a schematic MO diagram of the relative one-electron orbital energies which is representative of all complexes studied. For the Cu(II) oxidation state, both the HOMO and LUMO are found to be beta spin–orbitals denoted β₁ and β₂, respectively. This situation occurs due to the energy splitting between differentially occupied α and β orbitals in the open-shell spin-unrestricted scheme. Fig. 5 shows the spatial distribution of electron density for Cu(II/I)ATSM again, representative of all the complexes studied. The axes are also shown in Fig. 5 where the yz plane is defined in the plane of the molecule with the x-axis perpendicular to the ligand.

Fig. 4 Schematic molecular orbital diagram for Cu(II/I) complexes showing the orbital degeneracy in the reduced state. Orbitals with similar spatial distribution are connected by dashed lines.

Fig. 5 Spatial distribution of the unrestricted molecular orbitals, α_1–3 and β_1–3 for Cu(II/I)ATSM. The orbitals are representative of complexes 1–15. For the Cu(II) complexes β₁ is the HOMO and β₂ the LUMO and for the reduced Cu(I) complexes, the α and β sets become degenerate with α₂/β₂ being the HOMO and α₃/β₃ the LUMO.

The Cu(II)ATSM HOMO (β₁), is a ligand based out-of-plane π/π* orbital with a small contribution from the metal d_xy orbital. The α spin spatial equivalent of the HOMO is the occupied α₂ orbital which is only 0.04 eV lower in energy than β₁. Below these two orbitals lies the singly occupied molecular orbital (SOMO) α₁ for which the β spin spatial partner is the LUMO β₂ orbital with a splitting energy of 2.84 eV. Therefore, the unpaired electron lies in the α₁ orbital, the characteristics of which are probed by EPR. This orbital has a large contribution from the copper d_yz orbital which is σ*-antibonding in character with respect to the orbital overlap between the ligand N/S donor atoms.

The EPR of Cu(II)ATSM has been studied by Hatfield et al.⁷⁷ and more recently by West et al.²⁶ The observed values for g_|| were found to be low; 2.113 and 2.121 in the solid state at room temperature and 77 K, respectively, and 2.130 in frozen DMF. According to Kivelson and Nieman values of g_|| < 2.3 indicate covalent character in the metal–ligand bonding.⁷⁸ This is supported further by the σ-bonding covalency parameter, α², determined from the empirical data to be 0.635 for the Cu(II) ion. A value of α² = 1.0 would indicate completely ionic bonding with all unpaired electron density localised on the Cu(II) ion and if the overlap integral between the copper and N/S donor ligand atoms was zero, a value of α² = 0.5 would correspond to purely covalent metal–ligand bonding. In addition the d-orbital spin density of the ground state was found to be 0.362. This value is in good agreement with the calculated Mulliken spin density of 0.408 and with the Natural Population Analysis (NPA) spin density of 0.436. The NPA spin densities on the nitrogen and sulfur donor atoms are found to be 0.113 and 0.158, respectively. Fig. 6 shows a spatial representation of the total spin density in Cu(II)ATSM. The major delocalisation of electron density in the copper d_yz orbital occurs in the sp² hybridised orbitals on the nitrogen donors and the in-plane p orbitals on the sulfur atoms. These spin density values are consistent with the splitting observed in the EPR spectra. Superhyperfine splitting lines in a 1 : 2 : 3 : 2 : 1 ratio are observed with A_N = 18 G, due to the coupling of the unpaired electron with the two equivalent donor nitrogen atoms. In addition, the high degree of covalency is a consequence of the presence two donor sulfur atoms in the coordination sphere which delocalise the electron density.²⁶ From the ligand field approach used in the description of bonding in the analysis of the EPR spectra, the metal orbital contributing the α₁ SOMO is assigned as the d_x²−y² orbital. As a result of the different orientation of the axes in our calculations the SOMO has copper d_yz orbital character. Thus the two analyses are consistent and the computation fully supports the conclusions drawn from the EPR experiment.

Fig. 6 Representation of the total Mulliken spin density calculated using the molecular orbital coefficients and mapped onto the structure of Cu(II)ATSM. The in-plane delocalisation of spin density to the nitrogen and sulfur donor atoms can be seen.

In order to investigate the intra-ligand and metal–ligand bonding within Cu(II)ATSM, a Natural Bond Order (NBO) analysis was performed using second order perturbation theory analysis of the Fock matrix.⁷⁹ The energies of the major stabilising interactions are shown in Fig. 7. Back-donation from the copper to the ligand π orbitals was found to be of negligible contribution to the stabilisation in the complex. In-plane σ- and π-donation from the N/S donor atoms to the copper accounts for 94.8% of the metal–ligand interaction. The nitrogen donor orbitals have sp^2.38 hybridisation constituting 48.6% ligand-to-metal donation whereas the sulfur atoms donate electrons (46.3%) to the copper via in-plane lone pair p orbitals. The remaining 5.1% of stabilisation arises from minor interactions with the ligand π system. Within the ligand strong π-donations from the lone pairs on both the sulfur atoms and the terminal nitrogen atoms into the C=N imine π-bonds are observed (150 and 273 kJ mol⁻¹, respectively). However, despite this large electron donation, the C=N bond does not directly stabilise the Cu(II) ion and therefore changing the R₃ group of the terminal-N position has little effect on the electronics of the metal. This supports the relatively small changes in redox potentials observed for different R₃ substituents. In contrast, the relatively small donation of only 57 kJ mol⁻¹ from the backbone methyl groups into the C=N_donor bond does have an effect on the electronics of the metal as the nitrogen atom donates electron density directly to the Cu(II) ion. Hence, changing the backbone substituents (R₁ and R₂) has a greater effect on the one-electron reduction potential than changing substituents at the R₃ position.

Fig. 7 Major stabilising interactions between occupied donor Natural Hybrid Orbitals (NHOs) and vacant acceptor antibonding NHOs. The arrows indicate the direction of the interaction from donor to acceptor orbitals and the values are the energies of stabilisation in kJ mol⁻¹ associated with the delocalisation.

In comparison, ligand donation from the bound nitrogen and sulfur atoms to the copper in Cu(II)GTS accounts for 49.7% and 46.1% of the ligand to metal stabilisation interactions. This picture of ligand-to-metal donation is very similar to Cu(II)ATSM which is consistent with the observed similarities in the EPR spectra.

The literature reports calculations on similar systems including Cu(II)ATSM and the selenium analogues have been performed.^3,8 However, significant differences are seen in the orbitals which were identified as the HOMO and LUMO. One previous report suggests that the HOMO is similar to the metal based Cu(II) α₁ orbital in Fig. 5 and the LUMO is actually a ligand based π/π* orbital similar to α₃. This has led to the suggestion that reduction may be ligand centred leading to the formation of a triplet state but no evidence has been found to support this from EPR experiments.^77,80 The triplet states were also calculated and found to be higher in energy by 45.1 and 57.0 kJ mol⁻¹ for Cu(I)GTS and Cu(I)ATSM, respectively. Although not conclusive, the lack of experimental evidence for a triplet state and the excellent agreement between calculations and the experimental electrochemistry presented in this paper (Fig. 3) suggest this new orbital assignment is correct.

The largest changes in geometry on reduction occur in the metal–ligand donor atom bond lengths which increase by an average of 0.11 Å for r(Cu–N) and 0.05 Å for r(Cu–S). This is consistent with the expected change on placing an electron in the σ*-antibonding β₂ LUMO of Cu(II) which would decrease the bond order and increase bond lengths. The magnitude of the increases also show that the additional electron has a larger influence on the electronic structure located around the nitrogen donors and the backbone of the ligand. The bond angles a(N–Cu–N)/° and a(N–Cu–S)/° contract by 3.8 and 2.7° whilst the a(S–Cu–S)/° angle expands by 16.7°. The C–C backbone decreases in length by 0.02 Å and is consistent with build up of electron density on the ligand due to the delocalisation in the Cu(I) α₂/β₂ HOMO. The pseudo-tetrahedral geometry of the Cu(I) species leads to a twist in the two branches of the bis(thiosemicarbazonato) ligand at two points: around the C–C and N–N bonds. The first dihedral angle, d(N1–C1–C2–N2)/° opens from zero degrees in all Cu(II) species to average values of −22.5° for the Cu(I)GTS(M)/PTS(M) complexes and −26.4° for Cu(I)ATS(M) complexes and the second dihedral, d(C–N–N–C)/°, also increases from zero degrees to an average of 26.2° in all complexes. For Cu(I)ATS(M), the ligands twist to a greater extent so as to reduce the steric repulsion between the backbone methyl groups. The crystal structure of the [Cu₂(ATSMH₂)₂]²⁺ dimer has been reported and shows an average d(N1–C1–C2–N2) dihedral angle of 51.5°.⁸¹

Reduction is metal centred leading to the formation of closed-shell Cu(I) d¹⁰ systems and the geometry changes from square-planar in the Cu(II) d⁹ complexes to pseudo-tetrahedral in the reduced state. The NPA analysis indicates that in Cu(II)ATSM the copper ion has a total (α plus β) electron configuration of [Ar]4s^0.473d^9.474p^0.034d^0.01 with a corresponding natural charge of +1.016e. For the geometry optimised Cu(I)ATSM species the electron configuration is [Ar]4s^0.413d^9.784p^0.024d^0.01 with a natural charge on the copper ion of +0.770e, a decrease of only 0.246e on reduction. Although reduction is metal centred, delocalisation of electron density onto the ligand occurs as shown in the α₂/β₂ HOMO orbitals of Cu(I)ATSM (Fig. 5).

Calculation of absolute pK_a values

Although the calculation of one-electron reduction potentials assist in understanding the molecular basis for the differences observed between CuGTS and CuATSM, considered alone they provide only limited insight into questions pertaining to the mechanism of transport, cellular uptake and trapping within hypoxic cells. When considering the in vivo activity of copper bis(thiosemicarbazonato) complexes one of the major factors that influences their potential use as radiopharmaceuticals for imaging and therapy is the pK_a. The ease of protonation and the stability of the protonated complexes, Cu(II)AH⁺, where A represents the dianionic bis(thiosemicarbazonato) ligands, will determine their biodistribution, localisation in different tissue phenotypes, cellular uptake and biological half-life. Therefore a knowledge of acidity along with other factors such as lipophilicity, is critical in understanding how the complexes behave in the body. Unfortunately, the very low water solubility of copper bis(thiosemicarbazonato) complexes has so far prevented reliable experimental determination of pK_a for species 1–6. Thus in order to provide a theoretical account of the effects of protonation both the absolute and relative acidities have been calculated for compounds 1–6.

When considering the protonation of a complex the first question to be addressed is; where is the most likely site for the addition of a proton? In order to investigate this, the structure of the Cu(II)GTSH⁺ complex was calculated with the proton in three different positions, shown in Fig. 8(a). It was found that the most stable conjugate acid results from protonation at the X position. Protonation at the Y and Z positions decreases the stability of the conjugate acids with free energies of 58.0 and 73.3 kJ mol⁻¹ relative to X. This is supported by the electrostatic potential map (ESP) of Cu(II)GTS in Fig. 8(b) which indicates that the region with the largest net negative charge is the nitrogen bonded to position X within the backbone followed by the sulfur atoms and finally the terminal nitrogen positions. However, when the effects of solvation are incorporated it was found that the acidity of the protonated terminal nitrogen and sulfur positions reversed with respect to X. Protonation at Y becomes less favourable than at position Z with relative free energies of 90.2 and 77.5 kJ mol⁻¹ in DMSO and 106.8 and 82.5 kJ mol⁻¹ in water, respectively. Although pK_a values were not explicitly determined in a previous study, a similar reversal in the order of conjugate acid stability has been found for Cu(II)ATSM.⁴ This is evidence of the dramatic effect solvation can have on the chemistry and electrochemistry of a system. If only in vacuo calculations are considered, the accurate prediction of chemical properties and behaviour may be restricted by the approximations made on extrapolation to solution phase systems.

The ESP map for Cu(II)ATSM, shown in Fig. 8(c), is very similar to that of Cu(II)GTS and consequently for complexes 2–6 only protonation at positions X and X′ (for Cu(II)PTS) have been considered.

Calculations performed on the water clusters H₈O₄ and H₉O₄⁺ using the uB3LYP/6–31++G(d,p) methodology result in a solvation free energy of a proton, Δ_solvG° (H⁺) of (−1134.3 + 26.3 = −1108.0 kJ mol⁻¹) viaeqn (7) and (8). This is close to the value determined from the most accurate experiments and high level calculations which indicates that the use of the cluster model as the reference does not introduce excessive errors that would affect the absolute pK_a values. It has been shown that to achieve the highest accuracy, the inclusion of contributions from vibrational anharmonicity to water cluster binding energies is essential.⁸² However, anharmonicity has not been included in this work as the effect is likely to be around 1 kJ mol⁻¹, within the standard error of DFT.

Fig. 8 (a) Structures of the three Cu(II)GTSH⁺ complexes protonated at the labelled sites X, Y and Z. The X′ site refers to the anti position in Cu(II)PTSH⁺. (b) Electrostatic potential (ESP) mapped onto the total electron density isosurface for the in vacuo Cu(II)GTS. Red indicates regions of net negative charge. (c) ESP map for Cu(II)ATSM.

Table 4 contains the in vacuo energetics with the ZPE, thermal and entropic corrections and the solvation free energies for the deprotonation reaction of the Cu(II)AH⁺ complexes in accordance with Scheme 2. The pK_a values are derived from eqn (6). Excluding the Y and Z protonated Cu(II)GTSH⁺ complexes, all the values lie within a narrow window of less than 3 pK_a units with absolute values centred around 0.0 pK_a. The Cu(II)AH⁺ complexes are all highly acidic and consequently will only be protonated in strongly acidic conditions. The lack of experimental data means that the accuracy of the absolute pK_a results cannot be assessed. However, this high acidity is supported by the one measure of pK_a reported in the literature. Petering found that for the related complex, Cu(II)KTS, where R₁ is the ether group—CH(CH₃)OC₂H₅, deprotonation of the Cu(II)KTSH⁺ complex has a pK_a of 2.75.¹⁴ The relative pK_a values reveal that within the homologous series, the order of acidity is Cu(II)—GTS(M) < PTS(M) < ATS(M). The addition of successive methyl substituents to the backbone increases the acidity of the protonated species (lower pK_a) by around 0.5 pK_a units when R₃ = H and by 1.1 pK_a units when methyl substituents are present at R₃.

Table 4 Cu(II)AH⁺in vacuo deprotonation energies and changes in free energy of solvation, ΔΔ_solvG^o/kJ mol⁻¹ in water. Both the absolute pK_a values and values relative to Cu(II)ATSM are also given. The energies for the H₉O₄⁺/H₈O₄ cluster are presented for reference and all energy values for the complexes include this correction

	ΔεSCF/kJ mol^−1	ΔεZPE/kJ mol^−1	ΔdpH^o(g)/kJ mol^−1	ΔdpG^o(g)/kJ mol^−1	ΔΔsolvG^o (aq)/kJ mol^−1	ΔdpG^o (sol)/kJ mol^−1	Calc. absolute pKa	Relative pKa (ATSMH^+)
a For the PTS(M) complexes syn refers to protonation on the same side as the methyl substituents at R1 and anti to the opposite side, corresponding to X and X′ in Fig. 8(a).
H8O4/H9O4^+	−930.9	22.4	−903.4	−918.2	−216.1	−1134.3	—	—
GTSH^+-X	39.4	−11.8	32.6	17.8	−8.8	9.0	1.6	2.9
GTSH^+-Y	−29.4	−16.4	−39.8	−55.6	−31.2	−86.7	−15.2	−13.9
GTSH^+-Z	−27.0	−3.5	−25.5	−40.3	−70.8	−111.1	−19.5	−18.2
PTSH^+-syn^a	49.1	−11.9	42.6	26.3	−20.3	6.0	1.1	2.4
PTSH^+-anti^a	44.8	−12.1	38.1	21.4	−12.4	9.0	1.6	2.9
ATSH^+	53.4	−12.3	46.9	26.0	−23.7	2.3	0.4	1.7
GTSMH^+	57.6	−11.0	50.8	37.7	−32.1	5.6	1.0	2.3
PTSMH^+-syn	66.4	−11.1	59.6	46.4	−47.3	−0.9	−0.2	1.1
ATSMH^+	69.9	−11.5	63.0	46.7	−53.9	−7.2	−1.3	0.0

---

In order to elucidate the mechanism with respect to the interplay between the electrochemical (E) and chemical (C) processes, the one-electron reduction potentials in water and DMSO for the reaction Cu(II)AH⁺ + e⁻ → Cu(I)AH have been calculated (Table 5). These reduction potentials follow the same trend as observed in reduction of the non-protonated complexes. However, as expected for cationic species, the values are all positive implying a facile electron attachment step. The pK_a results for the Cu(II)AH⁺ complexes indicate that the neutral copper(II) bis(thiosemicarbazonato) complexes do not protonate under normal biological conditions found in the blood stream, the extracellular interstitial fluid or within normoxic cells. The Cu(II)AH⁺ reduction potentials do not agree with the experimental data and it can be concluded that electrochemical reduction occurs first, facilitating the possible subsequent protonation reactions. Therefore, the mechanistic sequence is predicted to be electrochemical–chemical, EC.

Table 5 In vacuo free energies of electron attachment and changes in solvation free energy for water and DMSO are given in kJ mol⁻¹ for the reduction of the protonated Cu(II)AH⁺ species. The calculated one-electron reduction potentials, E_calc(SCE)/V, are also presented

	ΔEAG^o (g)/kJ mol^−1	ΔΔsolvG^o (DMSO)/kJ mol^−1	ΔΔsolvG° (aq)/kJ mol^−1	E calc(SCE)/V DMSO/H2O
GTSH-X	−581.5	139.1	155.0	0.39 / 0.23
GTSH-Y	−560.4	116.9	127.4	0.40 / 0.30
GTSH-Z	−604.0	134.8	152.1	0.67 / 0.49
PTSH-syn	−565.8	131.4	145.2	0.31 / 0.17
PTSH-anti	−570.7	153.1	153.1	0.14 / 0.14
ATSH	−552.9	130.5	141.3	0.19 / 0.07
GTSMH	−562.3	124.8	137.7	0.34 / 0.21
PTSMH-syn	−546.0	116.9	124.4	0.25 / 0.18
ATSMH	−536.5	116.3	121.0	0.16 / 0.11

---

Experimentally, the behaviour of copper(II) GTS, PTS and ATSM complexes differ on reduction and in the presence of acid in vitro.⁴ Addition of SnCl₂ to a red solution of Cu(II)GTS in DMSO does not alter the UV/vis spectrum. However, if acetic acid is also added the absorption at 497 nm disappears and a pale yellow solution forms with the same absorption as the free ligand GTSH₂ at 373 nm. No change occurred when acetic acid was added without the reductant. In contrast, the addition of the stronger reducing agent, sodium naphthalide, under anaerobic conditions is required to reduce Cu(II)ATSM in DMSO solution. The colour changes from orange to pale yellow but no absorption shoulder at 367 nm is observed showing that free ATSMH₂ is not present. The addition of acetic acid did not alter the spectrum. On standing in air, the original orange colour returned and the Cu(II)ATSM spectrum was restored. Studies into the effects of oxygen concentration showed that the radioactive ⁶⁴Cu may be washed out of the cells by the reintroduction of oxygen alone for CuATS(M) but that the trapping of CuGTS(M) and CuPTS(M) was relatively irreversible. Although the nature of the washout species was not identified it is reasonable to surmise that it may be the reoxidised Cu(II)ATS(M).²

The results presented concur with the observed experimental chemistry, CV, EPR and UV/vis data which supports the following conclusions. The mechanism of trapping within hypoxic cells and the fate of the species once reduced is dependent on the nature of the ligand. For all the complexes the low pK_a of [Cu(II)AH]⁺ prevents protonation in normal tissue and during transport in the blood system (pH 7.35–7.45). Therefore, the complexes remain neutral, which allows them to diffuse through the lipophilic cell membranes by passive, active or facilitated diffusion through intrinsic proteins embedded in the membranes. Once inside cells, the complexes may be reduced by various species such as thiols, NADH or mitochondrial components involved in the electron transport chain (ETC). From the UV/vis studies, Cu(II)GTS may undergo a concerted (EC) process, forming a dissociative species which releases the copper ion. In contrast, Cu(II)ATSM appears to undergo an initial reduction to form the anionic Cu(I)ATSM⁻ species. The fate and indeed existence of this species is uncertain, as the addition of the electron increases the basicity of the complex, which may then be stabilised by either mono- or diprotonation. The UV/vis data does not rule out either the anionic or diprotonated cationic complexes being the species trapped within hypoxic cells and both are consistent with the washout studies. However, the complete loss of reversibility of the Cu(II)/Cu(I) couple in the presence of water strongly suggests that protonation of the Cu(I) species occurs. A mono-protonated Cu(I)ATSMH species would remain neutral and presumably still able to diffuse in and out of the cell by the same mechanism by which Cu(II)ATSM entered. On the other hand a diprotonated Cu(I)ATSMH₂⁺ complex would carry a unit positive charge which is likely to prevent passive diffusion out of the cell through the lipophilic cell membrane.

A careful distinction must be made when considering the meaning of the term ‘stability’ in the context of the Cu(I) species. In the analysis above, stability refers to the difference in Gibbs free energy between the Cu(II) and Cu(I) complexes. The magnitude of Δ_EAG° (sol) is controlled by intrinsic effects of the ligand on the overall energy (stability) of the complex. However, the magnitude of the reduction potential does not necessarily reflect the chemical stability of the Cu(I) species both in vitro and in vivo. Reduction generates the Cu(I)A⁻ anion which may be unstable with respect to protonation, reoxidation or dissociation. Furthermore, the magnitude of the reduction potential gives no indication of the rate of reduction which depends on the reductant, the electron transfer kinetics and the structural rearrangement of the copper complexes from square planar to pseudo-tetrahedral geometry. The magnitude of E°/V indicates that at equilibrium, the concentrations of the initial Cu(I)A⁻ anion will be lower for CuATSM than for CuGTS. The relative amounts of Cu(II) to Cu(I) in the cell will be dependent on the rates of other processes (protonation, reoxidation and dissociation) which will be controlled by the bis(thiosemicarbazonato) ligand. Higher concentrations of Cu(I)GTS⁻ will increase the rate of for example, ligand dissociation which by the Le Chatelier Principle will displace the position of the equilibrium to the side of the Cu(I) species, driving the reduction process. In aqueous and mildly acidic conditions of the hypoxic cell, protonation is likely to be fast and therefore it will be the chemical stability of the mono- or diprotonated Cu(I) species with respect to ligand dissociation that determines the nature and lifetime of the species trapped within cells. This delicate balance of competing equilibria is complicated further in vivo by the role of enzyme catalysed reactions involved in the metabolism of copper.

Summary and conclusions

One-electron reduction potentials have been calculated for a series of copper bis(thiosemicarbazonato) complexes in good agreement with experimental data. The DFT calculations demonstrate the accuracy that is now possible in the quantitative prediction of chemical properties of a system and also their utility in the qualitative elucidation of mechanistic events. The inclusion of solvation effects is essential, leading to an excellent agreement between calculation and experiment with an average deviation of only −0.02 V for E_calc with the DMSO continuum model. The bonding in the copper bis(thiosemicarbazonato) complexes has been rationalised using Natural Bond Order analysis and through comparison with EPR results. Reduction is metal centred and the differences observed in the electrochemistry between CuGTS and CuATSM can be explained by considering the electronic and steric effects of the backbone substituents on the stability of the Cu(I) complexes. Electron donating groups at the R₁ and R₂ positions destabilise the Cu(I) α₂/β₂ HOMO by reducing the extent of delocalisation of electron density from the copper ion to the ligand. This raises the energy of the HOMO and destabilises the complex as a whole, thereby lowering the one-electron reduction potential of the Cu(II) partner. The chemical stability of the reduced species is complicated by the competing protonation, reoxidation and ligand dissociation equilibria, which are controlled by the bis(thiosemicarbazonato) ligand.

For the first time, numerical estimates of the absolute and relative acidities of complexes 1–6 are presented. In addition, differences in the protonated species predicted for the in vacuo and solution phase systems are highlighted. The mechanistic sequence with respect to one-electron reduction and protonation is identified as sequential electrochemical–chemical and the implications this may have with regard to the transport, localisation and trapping within hypoxic regions is discussed. In conjunction with experimental data, the reduction and pK_a calculations support the hypothesis that CuATSM is initially trapped within hypoxic cells as the cationic Cu(I)ATSMH₂⁺ species.

Acknowledgements

Thanks are due to all the members of the J. R. Dilworth and J. C. Green groups at the University of Oxford, Merton College and the EPSRC for a studentship. We would also like to thank Dr Philip Blower for helpful discussions and are very grateful for the support of the Oxford Supercomputing Centre.

References

1. J. L. J. Dearling, J. S. Lewis, G. E. D. Mullen, M. J. Welch and P. J. Blower, J. Biol. Inorg. Chem., 2002, 7, 249.
2. J. L. J. Dearling and P. J. Blower, Chem. Commun., 1998, 2531.
3. P. J. Blower, T. C. Castle, A. R. Cowley, J. R. Dilworth, P. S. Donnelly, E. Labisbal, F. E. Sowrey, S. J. Teat and M. J. Went, Dalton Trans., 2003, 4416.
4. R. I. Maurer, P. J. Blower, J. R. Dilworth, C. A. Reynolds, Y. Zheng and G. E. D. Mullen, J. Med. Chem., 2002, 45, 1420.
5. A. R. Cowley, J. R. Dilworth, P. S. Donnelly, A. D. Gee and J. M. Heslop, Dalton Trans., 2004, 2404.
6. D. X. West, A. E. Liberta, S. B. Padhye, R. C. Chikate, P. B. Sonawane, A. S. Kumbhar and R. G. Yerande, Coord. Chem. Rev., 1993, 123, 49.
7. J. S. Lewis and M. J. Welch, Technetium, Rhenium and Other Metals in Chemistry and Nuclear Medicine 6, ed. M. Nicolini and U. Mazzi, Servizi Grafici Editoriali, Padova, Italy, 2002, pp. 23–33.
8. T. C. Castle, R. I. Maurer, F. E. Sowrey, M. J. Went, C. A. Reynolds, E. J. L. McInnes and P. J. Blower, J. Am. Chem. Soc., 2003, 125, 10040.
9. L. J. Ashfield, A. R. Cowley, J. R. Dilworth and P. S. Donnelly, Inorg. Chem., 2004, 43, 4121.
10. M. Baldini, M. Belicchi-Ferrari, F. Bisceglie, G. Pelosi, S. Pinelli and P. Tarasconi, Inorg. Chem., 2003, 42, 2049.
11. M. Baldini, M. Belicchi-Ferrari, F. Bisceglie, P. P. Dall'Aglio, G. Pelosi, S. Pinelli and P. Tarasconi, Inorg. Chem., 2004, 43, 7170.
12. P. J. Blower, J. R. Dilworth, R. I. Maurer, G. E. D. Mullen, C. A. Reynolds and Y. Zheng, J. Inorg. Biochem., 2001, 85, 15.
13. P. McQuade, K. E. Martin, T. C. Castle, M. J. Went, P. J. Blower, M. J. Welch and J. S. Lewis, Nucl. Med. Biol., 2005, 32, 147.
14. D. H. Petering, Bioinorg. Chem., 1972, 1, 255.
15. Y. Fujibayashi, H. Taniuchi, Y. Yonekura, H. Ohtani, J. Konishi and A. Yokoyama, J. Nucl. Med., 1997, 38, 1155.
16. M. R. Taylor, E. J. Gabe, J. P. Glusker, J. A. Minkin and A. L. Patterson, J. Am. Chem. Soc., 1966, 88, 1845.
17. G. Bahr and G. Schleitzer, Z. Anorg. Allg. Chem., 1955, 280, 161.
18. G. Bahr and E. Schleitzer, Z. Anorg. Allg. Chem., 1955, 278, 136.
19. G. Bahr, E. Hess, E. Steinkopf and G. Schleitzer, Z. Anorg. Allg. Chem., 1953, 273, 325.
20. G. Bahr and E. Hess, Z. Anorg. Allg. Chem., 1952, 268, 351.
21. D. X. West, S. B. Padhye and P. B. Sonawane, Struct. Bonding, 1991, 76, 1.
22. K. Wada, Y. Fujibayashi, N. Tajima and A. Yokoyama, Biol. Pharm. Bull., 1994, 17, 701.
23. K. Wada, Y. Fujibayashi and A. Yokoyama, Arch. Biochem. Biophys., 1994, 310, 1.
24. P. J. Kostyniak, S. M. Nakeeb, E. M. Schopp, A. E. Maccubbin, E. K. John, M. A. Green and H. F. Kung, J. Appl. Toxicol., 1990, 10, 417.
25. E. K. John and M. A. Green, J. Med. Chem., 1990, 33, 1764.
26. D. X. West, J. S. Ives, G. A. Bain, A. E. Liberta, J. Valdes-Martinez, K. H. Ebert and S. Hernandez-Ortega, Polyhedron, 1997, 16, 1895.
27. Y. Fujibayashi, K. Wada, H. Taniuchi, Y. Yonekura, J. Konishi and A. Yokoyama, Biol. Pharm. Bull., 1993, 16, 146.
28. P. Burgman, J. A. O'Donoghue, J. S. Lewis, M. J. Welch, J. L. Humm and C. C. Ling, Nucl. Med. Biol., 2005, 32, 623.
29. A. R. Cowley, J. Davis, J. R. Dilworth, P. S. Donnelly, R. Dobson, A. Nightingale, J. M. Peach, B. Shore, D. Kerr and L. Seymour, Chem. Commun., 2005, 845.
30. P. J. Blower, J. S. Lewis and J. Zweit, Nucl. Med. Biol., 1996, 23, 957.
31. J. Li, C. L. Fisher, R. Konecny, D. Bashford and L. Noodleman, Inorg. Chem., 1999, 38, 929.
32. R. Konecny, J. Li, C. L. Fisher, V. Dillet, D. Bashford and L. Noodleman, Inorg. Chem., 1999, 38, 940.
33. G. Schuurmann, J. Chem. Phys., 1998, 109, 9523.
34. Z. Cao and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 3734.
35. E. J. Lyon, I. P. Georgakaki, J. H. Reibenspies and M. Y. Darensbourg, J. Am. Chem. Soc., 2001, 123, 3268.
36. V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759.
37. M.-H. Baik, J. S. Silverman, I. V. Yang, P. A. Ropp, V. A. Szalai, W. Yang and H. H. Thorp, J. Phys. Chem. B, 2001, 105, 6437.
38. P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, 864.
39. W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133.
40. R. C. Gaussian 03, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. VrevenK. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. NakatsujiM. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian, Inc., Wallingford, CT, 2004.
41. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
42. A. D. Becke, J. Chem. Phys., 1992, 96, 2155.
43. A. D. Becke, J. Chem. Phys., 1992, 97, 9173.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
45. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
46. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
47. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724.
48. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
49. P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209.
50. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213.
51. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654.
52. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223.
53. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976.
54. R. J. Hall, M. M. Davidson, N. A. Burton and I. H. Hillier, J. Phys. Chem., 1995, 99, 921.
55. J. L. Chen, L. Noodleman, D. A. Case and D. Bashford, J. Phys. Chem., 1994, 98, 11059.
56. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105(8), 2999.
57. M. L. Connolly, Science, 1983, 221, 709.
58. V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210.
59. M.-H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407.
60. J. Li, C. L. Fisher, J. L. Chen, D. Bashford and L. Noodleman, Inorg. Chem., 1996, 35, 4694.
61. R. A. Wheeler, J. Am. Chem. Soc., 1994, 116, 11048.
62. H. Kobayashi, T. Miura, Y. Shimodaira and A. Kudo, Chem. Lett., 2004, 33, 1176.
63. M. Namazian, H. A. Almodarresieh, M. R. Noorbala and H. R. Zare, Chem. Phys. Lett., 2004, 396, 424.
64. J. Langmaier, Z. Samec, E. Samcova, P. Hobza and D. Reha, J. Phys. Chem. B, 2004, 108, 15896.
65. H. Reiss and A. Heller, J. Phys. Chem., 1985, 89, 4207.
66. W. H. Richardson, C. Peng, D. Bashford, L. Noodleman and D. A. Case, Int. J. Quantum Chem., 1997, 61, 207.
67. C. Lim, D. Bashford and M. Karplus, J. Phys. Chem., 1991, 95, 5610.
68. M. W. Palascak and G. C. Shields, J. Phys. Chem. A, 2004, 108, 3692.
69. R. D'Auria, R. P. Turco and K. N. Houk, J. Phys. Chem. A, 2004, 108, 3756.
70. D. Asthagiri, L. R. Pratt and H. S. Ashbaugh, J. Chem. Phys., 2003, 119, 2702.
71. M. Namazian, S. Halvani and M. R. Noorbala, J. Mol. Struct. (THEOCHEM), 2004, 711, 13.
72. Y. H. Jang, L. C. Sowers, T. Cagin and W. A. Goddard, III, J. Phys. Chem. A, 2001, 105, 274.
73. I. A. Topol, S. K. Burt, A. A. Rashin and J. W. Erickson, J. Phys. Chem. A, 2000, 104, 866.
74. I. A. Topol, G. J. Tawa, S. K. Burt and A. A. Rashin, J. Phys. Chem. A, 1997, 101, 10075.
75. C. J. Mathias, M. J. Welch, M. E. Raichle, M. A. Mintun, L. L. Lich, A. H. McGuire, K. R. Zinn, E. K. John and M. A. Green, J. Nucl. Med., 1990, 31, 351.
76. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165.
77. L. E. Warren, S. M. Horner and W. E. Hatfield, J. Am. Chem. Soc., 1972, 94, 6392.
78. D. Kivelson and R. Neiman, J. Chem. Phys., 1961, 35, 149.
79. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
80. D. Getz and B. L. Silver, J. Chem. Phys., 1970, 52, 6449.
81. A. R. Cowley, J. R. Dilworth, P. S. Donnelly, E. Labisbal and A. Sousa, J. Am. Chem. Soc., 2002, 124, 5270.
82. K. Diri, E. M. Myshakin and K. D. Jordan, J. Phys. Chem. A, 2005, 109, 4005.

---

Footnote

† Electronic supplementary information (ESI) available: Selected geometric parameters for complexes 1–6 are given in Table S1 and the Cartesian coordinates for all geometry optimised structures are presented. The Hammett analysis is also given. See DOI: 10.1039/b512656h

---