Computational study of the energetics of ³Fe(CO)₄, ¹Fe(CO)₄ and ¹Fe(CO)₄(L), L = Xe, CH₄, H₂ and CO

Abstract

Large basis CCSD(T) calculations are used to calculate the energetics of ³Fe(CO)₄, ¹Fe(CO)₄ and ¹Fe(CO)₄(L), L = Xe, CH₄, H₂ and CO. The relative energy of the excited singlet state of Fe(CO)₄ with respect to the ground triplet state is not known experimentally, and various lower levels of theory predict very different results. Upon extrapolating to the infinite basis set limit, and including corrections for core–core and core–valence correlation, scalar relativity, and multi-reference character of the wavefunction, the best CCSD(T) estimate for the spin-state splitting in iron tetracarbonyl is 2 kcal mol⁻¹. Calculation of the dissociation energy of ¹Fe(CO)₄(L) into singlet fragments, taken together with known experimental behaviour of triplet Fe(CO)₄, provides independent evidence for the fact that the spin-state splitting is smaller than 3 kcal mol⁻¹. These calculations highlight some of the challenges involved in benchmark calculations on transition metal containing systems.

---

Introduction

In recent work,^1–9 we have explored the effect of spin-state changes on the kinetics and mechanisms of organometallic reactions. Because transition metal compounds very often have close-lying states with different spin, such reactions are quite common.^10–14 Reactivity in these cases is determined by two important factors, as shown in Fig. 1. The first is the strength of the spin–orbit coupling (SOC) between the two zeroth-order electronic wavefunctions corresponding to the pure spin states. By causing a mixing between initial and final wavefunctions, SOC can induce a spin-state change. The second factor is the energy required for the reactants to reach a geometry where the initial and final potential energy surfaces cross. Depending on the nature of the system, the lowest point on this crossing seam (which we refer to as the minimum energy crossing point or MECP) may be very energetically accessible or instead lie high in energy, thereby creating a significant spin-induced barrier to reaction.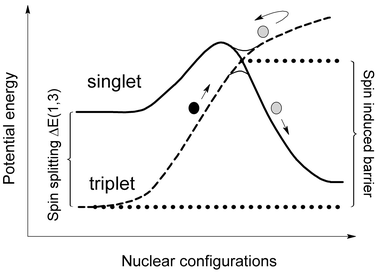

Fig. 1 Crossing between singlet and triplet states leading to a spin-induced energy barrier, whose height depends on the spin-state splitting.

As in any reaction, the magnitude of the energy barrier has a very large impact upon reactivity, so that the second of these factors is usually dominant in determining reactivity. For example, we have recently shown¹ that the contrasting kinetics of two much discussed spin-forbidden reactions can be rationalised qualitatively based on the relative energy of the MECP: Addition of dihydrogen to W[N(CH₂CH₂NSiMe₃)₃]H is slow,¹³ because the MECP between the reactant (triplet) and product (singlet) surfaces lies 15 kcal mol⁻¹ higher in energy than the separated reactants. In contrast, addition of CO to triplet Tp^i-Pr,MeCo(CO) leading to the singlet dicarbonyl is fast,¹⁴ because the MECP lies 12.4 kcal mol⁻¹ lower in energy than the reactants.

Despite the predominance of the energetic aspects in determining reactivity, both factors mentioned above play a role in determining the magnitude of rate coefficients, and their effect can in principle be described using a non-adiabatic version of TST.^15–18 To provide support for the qualitative description of reactivity given above, it is important to be able to show that such NA-TST calculations can give near-quantitative agreement with experimental rate coefficients for spin-forbidden organometallic reactions.¹⁹ Although relatively little experimental data of this type is available, one type of reaction, the gas phase addition of small molecules to triplet iron tetracarbonyl, has been studied extensively by Weitz et al.^20–28 We have already shown¹⁹ that NA-TST is able to predict the rate coefficient for addition of carbon monoxide to triplet Fe(CO)₄ to give singlet Fe(CO)₅ to within better than one order of magnitude, which is probably the best level of accuracy which can be expected using a statistical rate theory. This reaction^27,29 is roughly 500 times slower than the collisional rate, and we found that this is due partly to the fact that the MECP lies slightly (0.5 kcal mol⁻¹) higher in energy than the reactants, and partly to the fairly low (5%) probability of surface hopping upon reaching the MECP.

Iron tetracarbonyl is one of the simplest reactive intermediates in organometallic chemistry, and its reactions are of great interest both in their own right and as models for reactivity of larger systems. In more recent work, we have characterized the MECPs for the reaction of H₂ with Fe(CO)₄ as well as with related Fe(CO)₂(L)₂ and Fe(L)₄ species (L = phosphine).^2,5 The calculated potential energy surfaces accounted successfully for the qualitative aspects of reactivity in these systems. However, preliminary NA-TST calculations of the rate coefficients³⁰ for the reaction with iron tetracarbonyl gave a value which is four orders of magnitude smaller than the experimental²⁷ one (5.9 × 10⁻¹⁴ cm³ s⁻¹ molecule⁻¹). This is clearly a matter of concern given our stated aim of predicting rate coefficients with near quantitative accuracy. Although it is possible that the poor result is due to deficiencies in the NA-TST, the known difficulties in computing accurate potential energy surfaces for transition metal species suggest that it is possible that our calculated MECP properties^2,5 are inaccurate. This interpretation is plausible because preliminary work³⁰ shows that the computed energy of the MECP in the Fe(CO)₄ + H₂ system is strongly sensitive to the level of theory, considerably more so than for the Fe(CO)₄ + CO reaction for which the computed NA-TST rate coefficient is in much better agreement with experiment.

In particular, the MECP energy for the H₂ + Fe(CO)₄ reaction is very sensitive to the calculated singlet–triplet splitting in Fe(CO)₄. We have already shown¹⁹ that the latter varies quite significantly depending on the level of theory used to calculate it. For example, the B3LYP DFT method predicts a splitting of 9.8 kcal mol⁻¹, whereas with another commonly-used functional, BP86, the singlet lies only 0.9 kcal mol⁻¹ above the triplet. High-level CCSD(T) and CASPT2 calculations were used in our earlier study in a first attempt to determine this number accurately, which is not known directly from experiment (indeed, Poliakoff and Turner³¹ have highlighted the determination of this spin-state splitting as one of three “outstanding challenges” in relation to experimental studies of the photochemistry of Fe(CO)₄). However, this calibration work was not fully conclusive, due to the limitations in the basis set used, the sensitivity to the size of the active space in the CASPT2 calculations, and the neglect of effects such as core correlation and relativity.

We therefore decided to attempt to carry out benchmark calculations of the singlet–triplet spin-state splitting in Fe(CO)₄ taking into account all possible effects on this key energetic value, and report the results here. Although it is now possible to carry out calculations to within “chemical” accuracy³² (±1 kcal mol⁻¹ on bond energies) or better³³ on main group compounds, this is much more challenging for transition metal compounds. Because of effects such as multi-reference character, relativity and core–valence correlation, obtaining results of this accuracy is not at all straightforward.

As well as carrying out high-level calculations on iron tetracarbonyl itself, we have also calculated bond dissociation energies of several Fe(CO)₄(X) species, where X is CO, H₂, Xe and CH₄. The latter two bond energies can be combined with experimental observations on the behaviour of iron tetracarbonyl in low-temperature matrices^31,34–37 and room-temperature supercritical fluids³⁶ to give indirect insight into its singlet–triplet splitting. In supercritical argon or in an argon matrix, ³Fe(CO)₄ is stable and only decays upon addition of carbon monoxide or iron pentacarbonyl (leading in the latter case to diironenneacarbonyl). As argon is not expected to interact strongly with either state of the tetracarbonyl, this shows that the triplet state must be the ground state. On the other hand, ³Fe(CO)₄ is observed to convert into singlet Fe(CO)₄(L) (L = Xe or CH₄) adducts in a low-temperature matrix of L,^34,38 as well as in supercritical argon containing ca. 30 bar of L.³⁶ This implies that the BDE(3) and also the free energy of binding with respect to the triplet fragment of both of these ligands must be favourable under the experimental conditions. We have calculated binding energies and free energies of these ligands with respect to singlet Fe(CO)₄. These results, reported below, are expected to be more reliable than calculations of the binding energy with respect to the triplet state, or of the singlet–triplet splitting, as unlike these latter calculations, only closed-shell species with a similar electronic structure at iron are involved, so that much better error cancellation should occur. This enables us to place an upper limit on ΔE(1,3), as this value is equal to the difference between the singlet and triplet binding energies (Fig. 2), with the former accessible to accurate computation, and the experiments placing a lower limit on the latter.

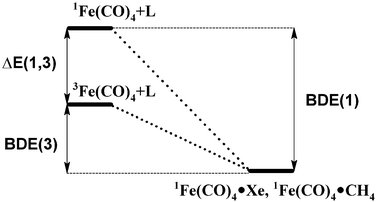Fig. 2 Thermochemical diagram showing the connection between Fe(CO)₄(L) (L = Xe or CH₄) bond energies and singlet–triplet spin state splitting.

Computational details

Density functional theory computations have been carried out using the Gaussian 03 program package,³⁹ mainly using the standard B3LYP functional. For these calculations, we use a flexible triple-zeta basis set, in particular, the all-electron basis sets of Ahlrichs et al.⁴⁰ as implemented in Gaussian. These are segmented contractions of the form (17s9p6d)/[6s3p3d] for Fe and (11s6p)/[5s3p] for C and O. A set of two diffuse, uncontracted 4p-like functions⁴¹ was added to the Fe basis (α = 0.134 915 and 0.041 843), as well as one f polarisation function (α = 1.0) on iron, one d function each on C and O (α = 0.8 and 1.2, respectively) and one p function (α = 0.8) on H. Where required, these basis sets are simply referred to as “TZV”. The Xe atom was described using a relativistic effective core potential⁴² to describe the innermost core electrons ([Kr] + 4d) together with an associated polarized VTZ basis set⁴³ of the form (14s,10p,2d,1f)/[3s,3p,2d,1f] to describe the valence 5s and 5p electrons. Full geometry optimisation was carried out for all species, followed by computation of frequencies within the harmonic approximation. All reported energies contain a correction for zero-point energy based on the B3LYP/TZV frequencies unless mentioned otherwise.

Coupled cluster single point calculations were carried out using the MOLPRO 2002.6 package,⁴⁴ at the B3LYP optimized geometry. The CCSD⁴⁵ and CCSD(T)^46–48 computations for singlet states and the RCCSD and RCCSD(T)^49–51 computations for triplet states had RHF and ROHF references respectively. For these calculations we used combinations of different basis sets. For C, O and H we use standard cc-pVDZ, cc-pVTZ and cc-pVQZ basis sets developed by Dunning et al.⁵² For xenon, we used the same⁴² ECP as in the DFT calculations, with the associated cc-pVTZ and cc-pVQZ basis sets,⁴³ in a fully uncontracted form. For iron, we used the cc-pVTZ, cc-pVQZ and cc-pV5Z all-electron basis sets developed by Ricca and Bauschlicher.⁵³ In all cases, these basis sets will be referred to as VXZ, where X = D,T,Q or 5. For most correlated calculations, the core Fe (1s2s2p3s3p), O (1s) and C (1s) orbitals were held frozen. However, the core–core and core–valence contributions from the outermost 3s and 3p electrons on iron can be significant, and we also carried out computations in which these electrons are correlated. In these calculations only, a core-valence (CV) cc-pCVTZ basis set⁵³ was used on Fe which includes additional tight primitives to describe this correlation. For some calculations a relativistic correction was included using Douglas–Kroll relativistic one-electron integrals,⁵⁴ as implemented in MOLPRO. In some cases, CCSD(T) calculations were carried out using an expansion in Kohn–Sham orbitals rather than the more usual Hartree–Fock reference.^19,55–57 Finally, some standard CCSD(T) and Brueckner orbital^58,59 coupled cluster (BD(T)) calculations were carried out using Gaussian 03. In this case, triplet Fe(CO)₄ is described using an UHF reference wave function as a reference for the BD(T) calculation. Basis set superposition errors on bond energies were evaluated using the counterpoise correction⁶⁰ with the fragments at their optimized geometries in the complexes.

Results and discussion

1. Direct calculation of ΔE(1,3) for Fe(CO)₄

Our initial aim is to carry out benchmark calculations of the spin-state splitting in iron tetracarbonyl, taking into account all relevant physical effects. For small molecules with main-group atoms, such benchmark computations can be carried out more or less straightforwardly to yield very accurate properties.³³ These calculations use the coupled-cluster method with full description of single and double excitations and a perturbative treatment of triples (CCSD(T)) in combination with Dunning’s correlation consistent basis sets⁵² and extrapolation to the basis set limit. For main-group compounds, this approach yields bond energies to within better than 1 kcal mol⁻¹. More thorough calculations including e.g. higher excitations⁶¹ improve the accuracy still further.

The situation for transition metal compounds (such as Fe(CO)₄) is much less favourable, for several reasons. First, this molecule is quite large (nine atoms, 82 electrons) so that calculations using the full cc-pVQZ basis on all atoms are not possible. Next, several effects which are small for simple main group compounds³³ need a priori to be taken into account in order to obtain kcal mol⁻¹ accuracy. These effects are core–core and core–valence correlation, scalar (and possibly spin–orbit) relativistic effects, and the importance of higher excitations. Our calculations set out to cover most of these effects.

We first calculate ΔE(1,3) for iron tetracarbonyl using a hierarchy of basis sets on the iron and carbonyl ligand at the CCSD(T) level (Table 1). The computed spin-state splitting ranges from 7.55 to 4.81 kcal mol⁻¹ after correction for zero-point energy at the B3LYP/TZV level (The zpe of triplet and singlet Fe(CO)₄ are respectively 19.68 and 20.47 kcal mol⁻¹). Larger basis sets on iron and on the carbonyl ligands both lead to a lower relative energy for the singlet state. Both the values and the trend upon increasing the basis set size are broadly the same as those found in our earlier work.¹⁹ However, the use of systematically optimized basis sets from the cc-pVXZ family enables us to extrapolate to the infinite basis limit, assuming that the correlation energy has an inverse cubic dependence on the basis set size, as shown in eqn (1).⁶²

We also assume that it is possible to make two separate extrapolations considering the increase in basis set size on the iron atom and the carbonyl groups.† This leads to a correction to ΔE(1,3) of −0.18 kcal mol⁻¹ for extrapolation from the X = 4 and X = 5 cases to the X = ∞ limit on iron (holding X = 3 constant on CO) and of −0.46 kcal mol⁻¹ for extrapolation from the X = 2 and X = 3 cases to the X = ∞ limit on the CO ligands (holding X = 5 constant on Fe). Taking these two corrections together, we have an initial best value for the spin-state splitting of 4.16 kcal mol⁻¹.

Table 1 Computed ΔE(1,3) between ³[Fe(CO)₄] and ¹[Fe(CO)₄] in kcal mol⁻¹ using different cc-pVXZ basis sets. All values include zero-point energy corrections at the B3LYP level

CO basis set	Fe∶VTZ	Fe∶VQZ	Fe∶V5Z
VDZ	7.55	6.39	5.67
VTZ	5.82	5.20	4.81

---

This value itself needs to be corrected for other effects. First, it is known that differential core–core and core–valence correlation effects in iron systems can lead to changes in relative energies of several kcal mol⁻¹.^63,64 We have therefore recomputed the spin-state splitting using the cc-pCVTZ basis set,⁵³ with additional primitives to treat 3s and 3p correlation, on iron (and cc-pVTZ on the carbonyl ligands). As can be seen in Table 2, this combination of basis sets leads as expected to a similar ΔE(1,3) to that obtained with the standard cc-pVTZ basis when the 3s and 3p electrons are kept in the core. However, upon including these electrons in the correlation treatment, the splitting is reduced by 1.25 kcal mol⁻¹.

Table 2 Comparison of computed BDE and ΔE(1,3) energies for the reaction ¹[Fe(CO)₅] → ³[Fe(CO)₄] + CO (in kcal mol⁻¹) using different approximations. All values include zero-point energy corrections at the B3LYP level

	VTZ	VTZ	(CV)VTZ	(CV)VTZ	VTZ	Fe∶VTZ, CO∶VDZ
System	CCSD(T)	Douglas–Kroll	CCSD(T)	CCSD(T)^a	KS-CCSD(T)	UHF-CCSD(T)	UHF-BD(T)
a Fe orbitals 3s and 3p are correlated.
ΔE(1,3)	5.82	3.34	6.21	4.96	7.72	6.54	7.68
BDE(3)	36.94	42.18	36.57	37.35	35.65	37.05	36.71
BDE(1)	42.76	45.53	42.79	42.30	43.37	43.59	44.40

---

This can be understood based on the nature of the frontier orbitals in Fe(CO)₄. In singlet Fe(CO)₄, the HOMO is a b₂ orbital which is a metal d orbital (with some CO character). In triplet Fe(CO)₄, this orbital is one of the two singly occupied MOs, together with an a₁ orbital, which has a mixture of metal d and s character (and some contributions from the ligands). The main contribution made by including a treatment of core-core and core-valence correlation in the calculation is likely to arise from the inclusion of correlation between “core” Fe 3s and 3p electrons and “valence” Fe 3d electrons, as these orbitals occupy similar regions of space. Species with a larger number of electrons in 3d orbitals are likely to lead to larger core-valence correlation contributions. In the present case, the singlet state of iron tetracarbonyl should have a larger core-valence correlation energy than the triplet state, because in the latter, one of the Fe valence electrons is in an orbital with partial 4s character, and hence will be less stabilised by core-valence correlation effects. This is indeed what is found.

We have next considered the effect of relativity on the singlet–triplet splitting, by comparing results obtained at the CCSD(T) level with normal one-electron integrals with those derived at the same level and with the same basis set, but using one-electron integrals which account for scalar relativistic effects using the Douglas–Kroll modified Hamiltonian. The basis set used is cc-pVTZ basis on all atoms. The scalar relativistic effects are fairly small, but definitely non-negligible, with the spin-state splitting ΔE(1,3) changing from 5.82 kcal mol⁻¹ when calculated using non-relativistic integrals to 3.34 kcal mol⁻¹ with the Douglas–Kroll integrals. The singlet state is thereby stabilized by roughly 2.5 kcal mol⁻¹ upon including relativistic effects. This is at first sight surprising because the triplet state, as mentioned above, contains an unpaired electron in an orbital with partial 4s character, which is expected to be stabilised upon including relativistic effects. However, stabilising the 4s orbital has a more important effect, which is to strengthen the ligand-metal interaction for all the carbonyl ligands. This interaction is due to donation from the lone pairs on the CO ligands into the empty 3d and 4s orbitals on Fe, and is stronger in the singlet state than in the triplet, as shown e.g. by the Fe–C bond lengths, which are of 1.79 and 1.83 Å at the B3LYP level for the singlet and 1.85 and 1.88 Å for the triplet. By lowering the energy of the 4s orbital, the relativistic effects stabilize both states, but especially the singlet, hence the decrease in spin-state splitting.

Another effect which needs to be taken into account is that CCSD(T) calculations may not be accurate enough for TM compounds such as iron tetracarbonyl, due to the occurrence of near-degeneracy effects. One traditional way to assess the applicability of coupled-cluster methods is the t₁ diagnostic⁶⁵ for the CCSD wavefunction, which is a measure of the importance of singly excited determinants. It has been suggested that values larger than 0.02 for CCSD, or perhaps 0.05 for CCSD(T), indicate excessive multi-reference character. In our case, all species give t₁ diagnostic values of 0.05 or lower, which taken at face value suggests that coupled-cluster results should be reliable. It should however be noted that the t₁ diagnostic is not totally meaningful for two reasons. First, it is not size-consistent and second, it focuses exclusively on single excitations, whereas large amplitudes for pair excitations are perhaps even more diagnostic of multi-reference character.⁶⁶ It is therefore possible that these systems display significant multi-reference character and that CCSD(T) is not applicable despite the low value of the t₁ diagnostic.

We have previously¹⁹ carried out extensive CASSCF and CASPT2 calculations on Fe(CO)₄ and Fe(CO)₅, and observed that (a) the CASSCF function is dominated by a single configuration, suggesting that multi-reference character is not excessive, and (b) that with a well-chosen active space, the CASPT2 calculated spin-state splitting is similar to that obtained with CCSD(T) using the same basis set. This suggests that both methods should be applicable. We have preferred CCSD(T) here because the CASPT2 result is sensitive to parameters such as the active space, level shift, and the nature of the perturbation Hamiltonian so that it is difficult to obtain quantitative results.

As a further test of the reliability of CCSD(T), we have carried out two different types of coupled-cluster calculations. First, we have expanded the wavefunction using Kohn–Sham orbitals (KS-CCSD(T) calculations^19,55–57). This can give a more balanced description as the shape of the orbitals in the reference state already incorporates the effects of electron correlation. These calculations give an increase in the triplet–singlet splitting, of 1.9 kcal mol⁻¹ compared to the value derived using the standard CCSD(T) method with the same basis set. This increase in the splitting energy is similar to that calculated using BP86 orbitals for the reference wavefunction with smaller basis sets,¹⁹ and is mainly due to a lower total energy for the triplet state, suggesting that this state is better described with the KS reference.

We also carried out Brueckner orbital (BD(T)) calculations^58,59 using the cc-pVTZ basis on iron and the cc-pVDZ basis on C and O. These calculations were carried out using the Gaussian program package, and use an unrestricted reference function, so we have also carried out corresponding CCSD(T) calculations with a UHF reference function. It has been shown that the orbital optimisation procedure in Brueckner coupled-cluster theory leads to significantly improved results over traditional CCSD(T) in cases with multi-reference character such as the NO₃ radical.⁶⁷ As shown in Table 2, these BD(T) calculations too lead to a larger spin-state splitting ΔE(1,3), by 1.15 kcal mol⁻¹ compared to the corresponding CCSD(T) calculation. Taken together, these KS-CCSD(T) and BD(T) calculations show that the coupled-cluster ansatz in general and the CCSD(T) method in particular is reasonably reliable for this transition-metal system, as all the results are comparable. However, the multi-reference character of the systems apparently leads the normal CCSD(T) method to slightly underestimate the stability of the triplet state.

Taking all these results together, it is possible to make a rough estimate of the “best” value for the spin-state splitting in Fe(CO)₄. The CCSD(T) calculation with the largest basis sets, cc-pV5Z on iron and cc-pVTZ on the CO ligands, gives a value of 4.81 kcal mol⁻¹. Basis set extrapolation leads to a value of 4.16, to which we add estimates of the effect of core-valence correlation, relativistic effects, and multi-reference character, based on the reported calculations with the cc-pCVTZ basis set, the Douglas–Kroll correction, and the KS-CCSD(T) method. These corrections are respectively of −1.25, −2.48 and +1.90 kcal mol⁻¹, so that our “best” value for ΔE(1,3) is of 2.33 kcal mol⁻¹. Of course, it is not clear that the corrections mentioned above are really additive, nor that the basis set extrapolation can be carried out separately for the iron and ligand basis sets, so the error bar on the above value is still fairly large—at least 2 kcal mol⁻¹.

One potential problem with these CCSD(T) calculations concerns the nature of the reference function. We have used the restricted coupled-cluster theory as implemented in Molpro.^45–51 In our calculations on triplet Fe(CO)₄, we noticed that when using different procedures to generate the initial guess, different converged ROHF wavefunctions could be obtained when using exactly the same basis set and the same geometry. These solutions are typically very close in energy (they differ by less than 0.5 kcal mol⁻¹) and are also identical in terms of orbital occupation per irreducible representation. However, they have somewhat different dipole moments and the orbital coefficients are slightly different. Tests suggest that these different wavefunctions correspond to different local minima within the SCF orbital optimization procedure.⁶⁸ As a consequence of obtaining different Hartree–Fock reference wavefunctions, we also observe different CCSD(T) energies. Again, these values are rather close to each other, with differences less than 1.52 kcal mol⁻¹. In principle, this makes it difficult to extrapolate from the results of calculations using different basis sets. However, we were able to ensure consistency within the results in Tables 1 and 2 by making sure that “the same” ROHF reference was used in all cases. This was done by using the same procedure to generate the initial guess in all cases, and by checking that the overall HF dipole moment and RCCSD(T) t₁ diagnostic value were similar, as these properties were observed to differ slightly from one solution to another. As this is a small effect, and as we have taken precautions to ensure that it does not affect the extrapolation procedure, we believe that it does not seriously affect the results discussed above, but the observation of such unusual behaviour does invite some caution in the context of an attempt to obtain highly accurate “benchmark” data.

2. Indirect experimental and computational route to an upper limit for ΔE(1,3) in Fe(CO)₄

In the previous section, we present benchmark calculations on the singlet and triplet states of iron tetracarbonyl in an attempt to determine as accurately as possible the spin-state splitting ΔE(1,3) in this intermediate. We obtain a best value of 2.33 kcal mol⁻¹. However, the need to use several corrections, so as to include the effects of extrapolation to infinite basis set size, of core-valence correlation, of relativity, and of multi-reference character mean that this value is still somewhat uncertain, with an error of at least 2 kcal mol⁻¹. For complementary insight into the spin-state splitting, we therefore consider the thermochemical situation for bonding of Xe and CH₄ to Fe(CO)₄. As discussed in the introduction, these weak ligands nevertheless form strong enough bonds to iron to induce conversion to the singlet adducts ¹Fe(CO)₄(L) both in rare gas matrices^34,38 and in supercritical argon.³⁶

This must mean that the free energy of bond dissociation of these ligands from iron tetracarbonyl must be positive under the relevant experimental conditions. At the low temperature of the matrix experiments, this is equivalent to saying that the bond dissociation energy of these ligands must be positive, as entropy effects are negligible. At the higher temperatures of the more recent experiments,³⁶ the free energy of bond dissociation will have a significant and favourable entropic contribution, such that the bond energy must be quite strongly positive in order for the free energy to be positive also. By computing the free energy of binding of these ligands to singlet iron tetracarbonyl under the conditions of the supercritical argon reactions, therefore, it is possible to obtain an upper bound to the singlet–triplet splitting in iron tetracarbonyl.

To calculate this free energy of binding, we first calculate the bond energy with respect to singlet fragments of Fe(CO)₄(Xe), Fe(CO)₄(CH₄), Fe(CO)₄(H)₂ and Fe(CO)₅ at the CCSD(T) level (Table 3), both with and without the BSSE correction. For comparison, we also include B3LYP-calculated bond energies.

Table 3 Computed BDE(1)s relative to ¹Fe(CO)₄ of the ¹[Fe(CO)₄]·L systems (in kcal mol⁻¹) using different methods and basis sets. All values include zero-point energy corrections at the B3LYP level. Values in parenthesis include the counterpoise correction of the basis set superposition error (BSSE). Numbers in bold are calculated bond dissociation free energies including 298 K thermal and entropic contributions as well as the BSSE correction

Method	B3LYP	CCSD(T)
Basis	TZV	VTZ(Fe), VDZ(CO), VTZ(L)	VQZ(Fe), VDZ(CO), VQZ(L)	VTZ	VQZ(Fe), VTZ(CO), VQZ(L)	(Extrapolated)
^1[Fe(CO)4·Xe]	1.25 (0.80) –6.37	8.11 (5.64)	8.55 (6.34)	8.46 (6.94)	8.46 (7.42)	8.46 (8.11) 0.94
^1[Fe(CO)4·CH4]	0.98(0.26) –7.59	8.54 (5.05)	9.80 (5.54)	7.67 (6.11)	—	10.43 (6.37) –1.48
^1[Fe(CO)4·H2]	13.78(12.93) 5.39	22.94 (18.53)	24.76 (19.38)	21.18 (19.04)	21.97 (19.72)	21.69 (20.40) 12.86
^1[Fe(CO)5]	35.69(34.29) 23.04	44.75 (38.55)	47.69 (40.47)	42.76 (39.21)	44.09 (40.81)	43.96 (42.03) 30.79

---

As can be seen, the DFT bond energies for the weakly bound xenon and methane fragments are much too small. This is because a large part of the bonding in these complexes is due to dispersion interactions, which are not described in the DFT method. The discrepancy is smaller but still present for the dihydride and pentacarbonyl complexes, despite the fact that bonding is in this case covalent, suggesting that the functional does not account well for exchange–correlation effects in these complexes.

The coupled-cluster results converge fairly rapidly as the basis sets on the metal and the ligand are enlarged. Both triple- and quadruple-zeta basis sets have been considered on these key atoms, whereas the spectator CO ligands have been treated using either the cc-pVDZ or cc-pVTZ basis, leading to similar results. In the case of Fe(CO)₄(CH₄), the calculation with the largest basis set combination (cc-pVQZ on iron and methane, cc-pVTZ on the CO ligands) was not possible due to computational limits. As above for the singlet–triplet splitting, we have extrapolated to the basis set limit using two separate additive corrections to the bond energies. The first correction comes from extrapolating the correlation energy obtained using the cc-pVTZ and cc-pVQZ basis sets on the metal and incoming ligand, whilst holding the basis set on the CO spectator ligands fixed as cc-pVTZ (fifth and sixth column in Table 3). The second correction is based on calculations with the cc-pVQZ basis on iron and the incoming ligand, and increasing the basis on CO from cc-pVDZ to cc-pVTZ (fourth and sixth columns). With the methane complexes, we instead extrapolate based on the third and fourth, and third and fifth columns, and the end result may not be as accurate. As can be seen, the final bsse-corrected bond dissociation energies are well above zero for all four ligands, as is needed for ligand addition to occur to Fe(CO)₄. Test calculations on the interaction with argon, however, show only a negligible energy gain at both the B3LYP and CCSD(T) levels of theory.

The CCSD(T) calculations have been carried out as single point energy computations at the B3LYP geometries. Given the very weak bond energies for Xe and CH₄ at the B3LYP level, it is possible that the geometries are poor also and that this introduces an error on the CCSD(T) bond energies. We have carried out geometry optimisation using other functionals, e.g. BP86, and do indeed observe shorter bond lengths to Xe and CH₄ in some cases. Also, we have carried out single point CCSD(T) computations using different Fe–Xe distances for the Fe(CO)₄(Xe) complex. The minimum of this rough CCSD(T) potential energy curve lies at a shorter Fe–Xe distance (ca. 2.80 Å) than the B3LYP minimum (2.98 Å), but the difference in total energy is negligible (<0.3 kcal/mol) so we have neglected this effect. Test calculations also show that core-core and core-valence correlation effects, relativistic effects, and correction to the CCSD(T) method only change the calculated bond energies for Xe and CH₄ by small amounts, so that the values in Table 3 should be fairly reliable. Note that the calculations on the xenon complex include scalar relativistic calculations due to the xenon nucleus.

Also shown in Table 3 are the calculated bond dissociation free energies at room temperature. For xenon, this value is just above zero, and for methane, where as already mentioned the extrapolation procedure is less reliable, it is slightly negative, meaning that the complex is thermodynamically unstable. Because triplet iron tetracarbonyl is lower in energy than the singlet (the free energy contribution to the singlet–triplet gap is small), the overall free energy of dissociation of Fe(CO)₄(Xe) and Fe(CO)₄(CH₄) to give triplet iron tetracarbonyl will be slightly negative in both cases. However, these free energies relate to standard conditions, i.e. to gaseous species at a pressure (fugacity) of 1 bar. Experimentally, binding is observed either in the neat supercritical fluid, or in supercritical argon in the presence of 20–30 bar of xenon or methane. Under these conditions, the ligand is present at a high concentration, which will shift the equilibrium towards the formation of adduct. Using equations for ideal gases, the free energy of xenon at 30 bar is 2 kcal mol⁻¹ higher than under standard conditions. Thermodynamic data⁶⁹ shows that the behaviour under supercritical conditions does not deviate too strongly from the ideal gas laws.

Taking all of these figures together, for xenon, the estimated upper bound for the singlet–triplet gap in iron tetracarbonyl which still gives a positive free energy of dissociation is 2.94 kcal mol⁻¹. The methane calculations suggest a lower value for this upper bound, but are less reliable. On the other hand, the fact that only triplet iron tetracarbonyl is observed in argon matrices shows that the triplet must be the ground state. This leads to a prediction that the singlet–triplet gap must lie somewhere between 0 and 3 kcal mol⁻¹. This overlaps very well with the predicted energy gap based on CCSD(T) calculations alone.

With a singlet–triplet energy gap of 2 kcal mol⁻¹, the calculated bond energies for dissociation of Fe(CO)₅ and Fe(CO)₄(H)₂ into triplet Fe(CO)₄ and CO or H₂ are in good agreement with experiment. For Fe(CO)₅, the best value (Table 3) for dissociation to give ¹Fe(CO)₄ is 42.03 kcal mol⁻¹, so that the adiabatic bond energy should be close to 40 kcal mol⁻¹, as compared to the experimental value⁷⁰ of 41 kcal mol⁻¹. For Fe(CO)₄(H)₂, the calculated adiabatic bond energy is 18 kcal mol⁻¹, which again compares favourably with the experimental value²⁵ of 20 kcal mol⁻¹.

Discussion and conclusions

We have carried out very large basis set CCSD(T) calculations on iron tetracarbonyl in both singlet and triplet states, as well as various adducts Fe(CO)₄(L). For example, the CCSD calculation using the cc-pVQZ basis on iron and cc-pVTZ basis on CO for Fe(CO)₅ involves 750 primitive functions, 450 contracted basis functions, 96 electrons and more than 17 million configurations. These calculations enable us to determine the singlet–triplet splitting in iron tetracarbonyl at the basis set limit. We have also calculated the effects of core-core and core-valence correlation, scalar relativistic effects and errors in the CCSD(T) method, to give a value of 2.33 kcal mol⁻¹. This value is significantly smaller than that predicted using B3LYP density functional theory (9.8 kcal mol⁻¹), and in fact much closer to values obtained using gradient-corrected functionals such as BP86 (0.9 kcal mol⁻¹).¹⁹ We have previously found¹ that the singlet–triplet splitting in CpCo(CO) (Cp = C₅H₅) and Tp′Co(CO) (where Tp′ is a tris(pyrazolyl)borate ligand) is better described using BP86 than with B3LYP. Other authors have pointed out^71,72 that for many coordination compounds, spin-state splittings depend strongly on the amount of exact exchange included in the functional, with increased exact exchange leading to relatively lower energies for high-spin states. This is certainly true for Fe(CO)₄, where very large differences in the spin-state splitting are found with different functionals (our previous calculations¹⁹ led to values varying from −6 to 22 kcal mol⁻¹). It has been suggested^71,72 that the best results are obtained using functionals with a reduced amount of exact exchange contribution (15%) compared to B3LYP (20%).

As suggested by us previously⁷³ the optimum amount of exact exchange may in fact depend upon the property considered and the target compound. The present results provide more support for this conclusion, since the low value of the singlet–triplet splitting is reproduced only by functionals such as B3PW91** or BP86 which contain little or no contribution from exact exchange.

Benchmark calculations on species such as Fe(CO)₄ remain highly challenging, and some uncertainties remain concerning our predicted singlet–triplet energy gap. For this reason, we have also resorted to an indirect method to estimate this key value. The observation³⁶ that triplet Fe(CO)₄ is quantitatively converted to singlet Fe(CO)₄(L) in supercritical fluids containing the ligand Xe or CH₄ means that the free energy of dissociation of the latter must be positive under the reaction conditions. Calculation of the free energy of dissociation of these adducts to form the free ligand and singlet Fe(CO)₄ is subject to fewer approximations than the direct calculation of the singlet–triplet gap in Fe(CO)₄. This free energy of dissociation is barely larger than zero, and in the case of xenon, leads to an upper bound for the spin-state splitting of 3 kcal mol⁻¹, consistent with the directly calculated value.

The calculations reported here provide a firm reference upon which to address the potential energy surfaces⁵ and kinetics of the reactions of H₂ and related species with Fe(CO)₄.

Acknowledgements

JNH acknowledges an Advanced Research Fellowship from EPSRC, and JLCM acknowledges support from Mexico’s National Council for Science and Technology (CONACYT). The authors thank Prof. Mike George for his helpful comments.

References

1. J. L. Carreon-Macedo and J. N. Harvey, J. Am. Chem. Soc., 2004, 126, 5789.
2. D. Schott, P. Callaghan, J. Dunne, S. B. Duckett, C. Godard, J. M. Goicoechea, J. N. Harvey, J. P. Lowe, R. J. Mawby, G. Mueller, R. N. Perutz, R. Poli and Michael K. Whittlesey, Dalton Trans., 2004, 3218.
3. R. Poli and J. N. Harvey, Chem. Soc. Rev., 2003, 32, 1.
4. J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2003, 238, 347.
5. J. N. Harvey and R. Poli, Dalton Trans., 2003, 4100.
6. J. C. Green, J. N. Harvey and R. Poli, J. Chem. Soc., Dalton Trans., 2002, 1861.
7. J. N. Harvey, in Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker, New York, 2001.
8. K. M. Smith, R. Poli and J. N. Harvey, New J. Chem., 2000, 24, 77.
9. K. M. Smith, R. Poli and J. N. Harvey, Chem.–Eur. J., 2001, 7, 1679.
10. R. Poli, J. Organomet. Chem., 2004, 689, 4291.
11. R. Poli, Chem. Rev., 1996, 96, 2135.
12. H. Schwarz, Int. J. Mass Spectrom., 2004, 237, 75.
13. R. R. Schrock, K. Y. Shih, D. A. Dobbs and W. M. Davis, J. Am. Chem. Soc., 1995, 117, 6609.
14. J. L. Detrich, O. M. Reinaud, A. L. Rheingold and K. H. Theopold, J. Am. Chem. Soc., 1995, 117, 11745.
15. J. C. Lorquet and B. Leyh-Nihant, J. Phys. Chem., 1988, 92, 4778.
16. K. Morokuma, Q. Cui and Z. W. Liu, Faraday Discuss., 1998, 110, 71.
17. Q. Cui, K. Morokuma, J. M. Bowman and S. J. Klippenstein, J. Chem. Phys., 1999, 110, 9469.
18. J. N. Harvey and M. Aschi, Phys. Chem. Chem. Phys., 1999, 1, 5555.
19. J. N. Harvey and M. Aschi, Faraday Discuss., 2003, 124, 129.
20. J. Q. Wang, G. T. Long and E. Weitz, J. Phys. Chem. A, 2001, 105, 3765.
21. D. L. Cedeno and E. Weitz, J. Phys. Chem. A, 2000, 104, 8011.
22. G. T. Long and E. Weitz, J. Am. Chem. Soc., 2000, 122, 1431.
23. P. G. House and E. Weitz, J. Phys. Chem. A, 1997, 101, 2988.
24. P. G. House and E. Weitz, Chem. Phys. Lett., 1997, 266, 239.
25. W. H. Wang, A. A. Narducci, P. G. House and E. Weitz, J. Am. Chem. Soc., 1996, 118, 8654.
26. S. J. Gravelle, L. J. Vandeburgt and E. Weitz, J. Phys. Chem., 1993, 97, 5272.
27. R. J. Ryther and E. Weitz, J. Phys. Chem., 1991, 95, 9841.
28. A. J. Ouderkirk and E. Weitz, J. Chem. Phys., 1983, 79, 1089.
29. T. A. Seder, A. J. Ouderkirk and E. Weitz, J. Chem. Phys., 1986, 85, 1977.
30. JLCM and JNH, unpublished work.
31. M. Poliakoff and J. J. Turner, Angew. Chem., Int. Ed., 2001, 40, 2809.
32. L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764.
33. T. Helgaker, T. A. Ruden, P. Jorgensen, J. Olsen and W. Klopper, J. Phys. Org. Chem., 2004, 17, 913.
34. M. Poliakoff and E. Weitz, Acc. Chem. Res., 1987, 20, 408.
35. N. Leadbeater, Coord. Chem. Rev., 1999, 188, 35.
36. P. Portius, J. X. Yang, X. Z. Sun, D. C. Grills, P. Matousek, A. W. Parker, M. Towrie and M. W. George, J. Am. Chem. Soc., 2004, 126, 10713.
37. S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, J. Phys. Chem. A, 2000, 104, 1997.
38. M. Poliakof and J. J. Turner, J. Chem. Soc., Dalton Trans., 1974, 2276.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, in ‘Gaussian 03’, Pittsburgh PA, 2003.
40. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
41. A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033.
42. A. Bergner, M. Dolg, W. Kuechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431.
43. J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408.
44. R. D. Amos, A. Bernhardsson, A. Berning, P. Celani, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, P. J. Knowles, T. Korona, R. Lindh, A. W. Lloyd, S. J. McNicholas, F. R. Manby, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, G. Rauhut, M. Schütz, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and H.-J. Werner, in MOLPRO, a package of ab initio programs designed by H.-J. Werner and P. J. Knowles, 2003.
45. C. Hampel, K. A. Peterson and H. J. Werner, Chem. Phys. Lett., 1992, 190, 1.
46. C. Hampel and H. J. Werner, J. Chem. Phys., 1996, 104, 6286.
47. M. Schutz, J. Chem. Phys., 2000, 113, 9986.
48. M. Schutz and H. J. Werner, J. Chem. Phys., 2001, 114, 661.
49. P. J. Knowles, C. Hampel and H. J. Werner, J. Chem. Phys., 1993, 99, 5219.
50. P. J. Knowles, C. Hampel and H. J. Werner, J. Chem. Phys., 2000, 112, 3106.
51. J. D. Watts, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1993, 98, 8718.
52. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
53. A. Ricca and C. W. Bauschlicher, Theor. Chem. Acc., 2001, 106, 314.
54. B. A. Hess, Phys. Rev. A, 1986, 33, 3742.
55. S. Villaume, C. Daniel, A. Strich, S. A. Perera and R. J. Bartlett, J. Chem. Phys., 2005, 122, 044313.
56. G. J. O. Beran, S. R. Gwaltney and M. Head-Gordon, Phys. Chem. Chem. Phys., 2003, 5, 2488.
57. D. C. Graham, G. J. O. Beran, M. Head-Gordon, G. Christian, R. Stranger and B. F. Yates, J. Phys. Chem. A, 2005, 109, 6762.
58. C. E. Dykstra, Chem. Phys. Lett., 1977, 45, 466.
59. N. C. Handy, J. A. Pople, M. Headgordon, K. Raghavachari and G. W. Trucks, Chem. Phys. Lett., 1989, 164, 185.
60. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
61. T. A. Ruden, T. Helgaker, P. Jorgensen and J. Olsen, J. Chem. Phys., 2004, 121, 5874.
62. T. H. Dunning, J. Phys. Chem. A, 2000, 104, 9062.
63. C. Heinemann, J. Schwarz, W. Koch and H. Schwarz, J. Chem. Phys., 1995, 103, 4551.
64. B. J. Persson, B. O. Roos and K. Pierloot, J. Chem. Phys., 1994, 101, 6810.
65. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Symp., 1989, 23, 199.
66. J. D. Watts, M. Urban and R. J. Bartlett, Theor. Chim. Acta, 1995, 90, 341.
67. J. F. Stanton, J. Gauss and R. J. Bartlett, J. Chem. Phys., 1992, 97, 5554.
68. T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, Wiley, Weinheim, 2000.
69. E. W. Lemmon, M. O. McLinden and D. G. Friend, in Thermophysical Properties of Fluid Systems, ed. P. J. Linstrom and W. G. Mallard, Gaithersburg, MD, June 2005 (see also NIST Database Number 69, http:/webbook.nist.gov).
70. K. E. Lewis, D. M. Golden and G. P. Smith, J. Am. Chem. Soc., 1984, 106, 3905.
71. O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729.
72. M. Reiher, Inorg. Chem., 2002, 41, 6928.
73. J. N. Harvey, Struct. Bonding, 2004, 112, 151.

---

Footnote

† Although this assumption is reasonable, it is certainly not exact. Also, it is unclear which value of X to use for the Fe cc-pVXZ basis sets. We use X = 3, 4, 5 for cc-pVTZ, cc-pVQZ and cc-pV5Z, respectively, although the largest angular momentum functions in these basis sets are respectively g, h, and i functions (l_max = 4, 5 and 6). Finally, unlike the cc-pVXZ basis sets for main group elements, the iron basis sets used here have not been tested using the inverse cubic extrapolation procedure – in fact, another extrapolation equation was used.⁵³ Therefore, the numerical value of our extrapolated spin-state splitting is perhaps not as reliable as it would otherwise be. However, the uncertainty caused by this extrapolation procedure is certainly smaller than that due to other effects.

---