Accuracy and limitations of second-order many-body perturbation theory for predicting vertical detachment energies of solvated-electron clusters

Abstract

Vertical electron detachment energies (VDEs) are calculated for a variety of (H₂O)_n⁻ and (HF)_n⁻ isomers, using different electronic structure methodologies but focusing in particular on a comparison between second-order Møller–Plesset perturbation theory (MP2) and coupled-cluster theory with noniterative triples, CCSD(T). For the surface-bound electrons that characterize small (H₂O)_n⁻ clusters (n ≤ 7), the correlation energy associated with the unpaired electron grows linearly as a function of the VDE but is unrelated to the number of monomers, n. In every example considered here, including strongly-bound “cavity” isomers of (H₂O)₂₄⁻, the correlation energy associated with the unpaired electron is significantly smaller than that associated with typical valence electrons. As a result, the error in the MP2 detachment energy, as a fraction of the CCSD(T) value, approaches a limit of about −7% for (H₂O)_n⁻ clusters with VDEs larger than about 0.4 eV. CCSD(T) detachment energies are bounded from below by MP2 values and from above by VDEs calculated using second-order many-body perturbation theory with molecular orbitals obtained from density functional theory. For a variety of both strongly- and weakly-bound isomers of (H₂O)₂₀⁻ and (H₂O)₂₄⁻, including both surface states and cavity states, these bounds afford typical error bars of ±0.1 eV. We have found only one case where the Hartree–Fock and density functional orbitals differ qualitatively; in this case the aforementioned bounds lie 0.4 eV apart, and second-order perturbation theory may not be reliable.

---

1. Introduction

Clusters comprised of closed-shell, polar molecules such as HF or H₂O can form stable (or at least metastable) supramolecular radical anions that are often termed dipole-bound anions,^1,2 a reference to the fact that the dipole moment μ₀ of the neutral cluster frequently provides an important stabilizing interaction for the excess electron. In many such systems, however, dispersion interactions contribute significantly to electron binding,^2–4 and even clusters with μ₀ ≈ 0 can bind an extra electron quite strongly within a cavity.⁵ As such, accurate calculation of vertical electron detachment energies (VDEs) for this type of cluster anion is a challenging problem for electronic structure theory, because electron correlation is responsible for a significant fraction of the electron binding energy.^1–3,6–9 Water cluster anions, in particular, have been intensely scrutinized by electronic structure theorists¹⁰ in the two decades since they were first observed in a molecular beam.^11,12 Recent experiments^13–16 have detected two new classes of (H₂O)_n⁻ isomers with VDEs that are significantly smaller, for a given n, than those of the dominant isomers observed in earlier experiments.¹⁷ These new data have rekindled an old controversy^15–24 regarding whether the excess electron is solvated within the cluster or at its surface, and how this solvation mechanism evolves as a function of n.

To this debate, we have recently contributed a benchmark study⁵ of electronic structure predictions of VDEs for small water cluster anions (n ≤ 6), demonstrating that second-order Møller–Plesset perturbation theory (MP2), in conjunction with a modest one-electron basis set, underestimates VDEs by 0.03–0.05 eV, an accuracy that is sufficient to assign the experimental photoelectron spectra.^13,25 A preliminary examination of selected isomers of (H₂O)₂₀⁻ and (H₂O)₂₄⁻, using the same methodology, cast considerable doubt on all previous electronic structure calculations for large water cluster anions, all of which utilize density functional theory (DFT) and probably overestimate VDEs by 0.2–0.4 eV.⁵ At the time, we speculated that these were probably the most accurate VDEs to date for cluster anions of this size, but it is difficult to quantify this statement absolutely since electronic structure calculations beyond the MP2 level are tremendously difficult (and rapidly become impossible) beyond six or seven water monomers. Moreover, for n > 6 there is no agreement as to which isomers of (H₂O)_n⁻ are actually interrogated in the experimental photoelectron spectra.

In the present study, we follow up on our previous work, with the goal of quantifying the accuracy of MP2 detachment energies for large water cluster anions. This can only be accomplished indirectly, for the reasons mentioned above; nevertheless, by extensively benchmarking MP2 detachment energies against coupled-cluster results, both for (H₂O)_n⁻ (with n ≤ 7) and also for (HF)_n⁻ (with n ≤ 8), we can establish whether, and to what extent, the accuracy of MP2 theory degrades as a function of cluster size. In fact, we find that it does not; rather, the error in MP2 detachment energy predictions is an approximately constant fraction of the VDEs themselves. Scaled MP2 results provide VDEs for large cluster anions with typical estimated errors of ±0.1 eV.

2. Technical details

Drawing upon what we learned in ref. 5, all calculations reported in this work employ the 6-31(1+,3+)G* basis set unless otherwise stated.²⁶ This basis augments the standard 6-31++G* basis with two additional diffuse s functions on each hydrogen atom, whose exponents are decremented by successive factors of 3.32. Comparison to larger and more diffuse basis sets indicates that this basis affords VDEs at both the MP2 and the CCSD(T) levels that are 0.01–0.02 eV below their respective complete-basis limits.⁵ For example, the cis-(H₂O)₂⁻, cyclic (H₂O)₃⁻, and linear (H₂O)₃⁻ clusters introduced below afford MP2/6-31(1+,3+)G* VDEs of 0.026, 0.007, and 0.141 eV, respectively, whereas the corresponding MP2/TZVPP+3s2p values²⁷ are 0.031, 0.021, and 0.139 eV.

Again consistent with our previous work,⁵ the calculations discussed here use drop tolerances of 10⁻¹²–10⁻¹⁴ au. Eigenvectors of the overlap matrix that correspond to eigenvalues smaller than the square root of the drop tolerance are projected out of the atomic orbital basis. Numerical integrations required for DFT exploit the SG-1 grid,²⁹ and all self-consistent field (SCF) calculations are converged to a maximum occupied-virtual Fock matrix element of 10⁻⁸ au. Except where noted, all geometries are optimized using the B3LYP^30,31 density functional with no constraints on point-group symmetry. Electronic structure calculations were performed using Q-Chem,³² and the Molden³³ and VMD³⁴ programs were used for visualization.

We have confirmed through numerous examples that sundry standard procedures for generating an SCF guess all lead to the same SCF solution, except in one high-symmetry case that is discussed in Section 3.2. In contrast, when converged molecular orbitals for (H₂O)_n are used as an initial guess for (H₂O)_n⁻ at the same geometry, we have found cases where the SCF calculation for the anion converges to a higher-energy (and qualitatively different) solution than that obtained with a standard SCF guess. For this reason, we never employ neutral molecular orbitals as an initial guess.

Fig. 1 depicts a catalogue of B3LYP/6-31(1+,3+)G* optimized geometries for (H₂O)_n⁻ isomers with n ≤ 7 and possessing CCSD(T)/6-31(1+,3+)G* detachment energies that range from nearly zero up to about 0.75 eV. This will serve as our test set for the calculations described in Section 3.1. In order to facilitate future benchmarking, the geometries and absolute energies (at various levels of theory) for all (H₂O)_n⁻ isomers discussed in this work are available as electronic supplementary information (ESI).†

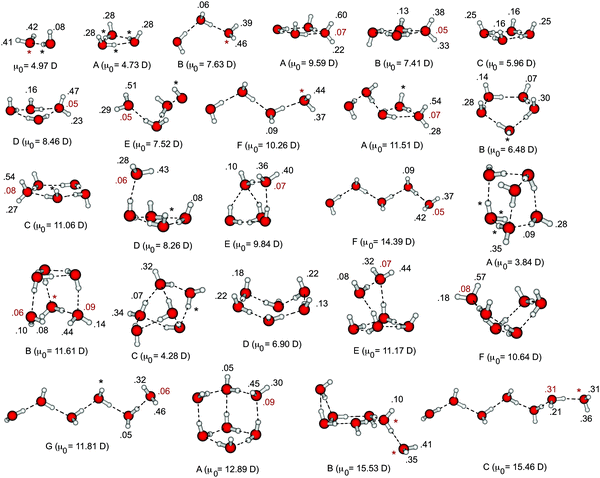Fig. 1 Isomers of (H₂O)_n⁻ considered in this work, optimized at the B3LYP/6-31(1+,3+)G* level. Also indicated for each isomer is the dipole moment μ₀ of the neutral cluster and the changes in natural atomic charges that accompany electron detachment, both calculated at the Hartree–Fock/6-31(1+,3+)G* level. The δq_i values in black correspond to hydrogen atoms while those in gray are for oxygen atoms.

3. Results and discussion

3.1. Benchmark results for small clusters

Natural population analysis^35,36 provides a convenient atomic partition of the singly-occupied molecular orbital (SOMO) coefficients from an SCF calculation, and is one way to assess and quantify which atoms are most directly responsible for solvating the extra electron. (Unlike Mulliken populations, natural populations are reasonably stable with respect to basis-set expansion.³⁵) In our catalogue of (H₂O)_n⁻ isomers, Fig. 1, we indicate the changes δq_i in natural atomic charges that accompany electron detachment. For clarity, δq_i is given explicitly only for those atoms i where |δq_i| ≥ 0.050, whereas atoms with 0.025 ≤ |δq_i| < 0.050 are indicated by asterisks, and cases where |δq_i| < 0.025 are omitted.

Except for certain weak-binding cyclic isomers, in which the excess electron is delocalized over many dangling hydrogen atoms, natural population analysis reveals that the excess electron is typically localized on two or three hydrogen atoms. In cases where the electron is bound to both hydrogen atoms on a single water molecule, this is accompanied by a small change in charge on the oxygen atom (δq ≈ 0.05–0.10). This is the so-called double hydrogen-bond acceptor or “AA” binding motif, and isomers of this sort represent the dominant feature in the dimer through hexamer photoelectron spectra.^14,25,37,38 This inherent localization of the SOMO is consistent with previous electronic structure results indicating that diffuse basis functions on the hydrogen atoms are much more important in VDE calculations than are diffuse functions on the oxygen atoms, at least in (H₂O)_n⁻ clusters.⁵

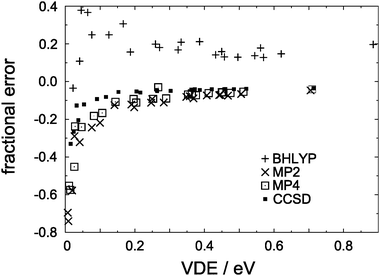
In Fig. 2, we plot both the absolute and the fractional errors in the MP2 detachment energies for each of the isomers in Fig. 1. Here and elsewhere in this work, we define “error” to mean the difference with respect to the CCSD(T) value in the same basis set. As the predicted VDE increases, so does the difference between the MP2 and the CCSD(T) detachment energies, but this error is apparently uncorrelated with the number of monomers, n. On the other hand, the fraction of the CCSD(T) detachment energy recovered at the MP2 level appears to approach an asymptotic limit as the VDE increases, and for the ten (H₂O)_n⁻ isomers in our data set that have VDEs greater than 0.4 eV, MP2 theory recovers an average of 93.3 ± 1.0% of the CCSD(T) detachment energy. (Uncertainties reported in this work represent one standard deviation.) Moreover, this asymptotic behavior appears to be rather general: as shown in Fig. 3, VDEs obtained from full fourth-order Møller–Plesset perturbation theory (MP4) as well as from coupled-cluster theory at the singles-doubles level (CCSD) also approach limiting fractions of the CCSD(T) detachment energy as the VDE increases. These data indicate that MP4 theory recovers a larger fraction of the VDE than does MP2 theory, with CCSD recovering a larger fraction still. As demonstrated below, the electron correlation contribution to the VDE increases as the VDE itself increases, hence we expect this trend to continue in larger, higher-binding isomers.

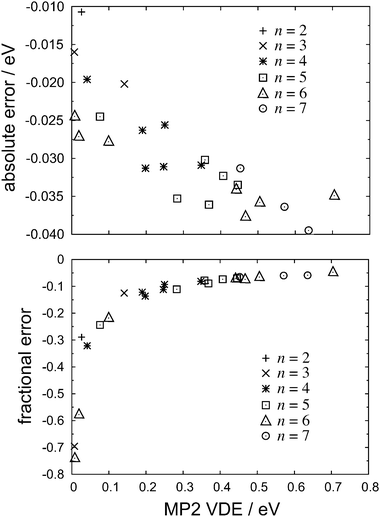Fig. 2 Absolute errors (upper panel) and fractional errors (lower panel) in MP2 detachment energies, with respect to CCSD(T) values, for various isomers of (H₂O)_n⁻. All calculations use the 6-31(1+,3+)G* basis set.

Trends in the MP2 error noted above can best be understood by examining trends in the correlation energy Δ associated with the unpaired electron,

Δ = E_corr(anion) − E_corr(neutral).

We will use the notation Δ_X to indicate a particular level of theory, X. Note that Δ_X is also the correction to the Hartree–Fock VDE. The quantities Δ_MP2 and Δ_CCSD(T) are plotted in Fig. 4, and again we find no correlation whatsoever with cluster size but a clear trend with increasing VDE, namely, Δ is an approximately linear function of the VDE. Hartree–Fock VDEs and Δ_CCSD(T) corrections for our catalogue of (H₂O)_n⁻ isomers are listed in Table 1.

Fig. 3 Fractional errors, with respect to CCSD(T) values, in VDEs calculated for the (H₂O)_n⁻ isomers in Fig. 1.

Table 1 Hartree–Fock VDEs and CCSD(T) corrections to the VDE, Δ_CCSD(T), for isomers of (H₂O)_n⁻

Isomer	Hartree–Fock VDE/eV	Δ CCSD(T)/eV
n = 2	0.000	0.037
n = 3(A)	−0.018	0.039
n = 3(B)	0.092	0.069
n = 4(A)	0.248	0.131
n = 4(B)	0.128	0.101
n = 4(C)	0.010	0.051
n = 4(D)	0.170	0.108
n = 4(E)	0.127	0.091
n = 4(F)	0.189	0.100
n = 5(A)	0.298	0.141
n = 5(B)	0.038	0.063
n = 5(C)	0.325	0.154
n = 5(D)	0.189	0.130
n = 5(E)	0.263	0.141
n = 5(F)	0.264	0.124
n = 6(A)	−0.019	0.052
n = 6(B)	0.513	0.227
n = 6(C)	−0.011	0.058
n = 6(D)	0.056	0.071
n = 6(E)	0.343	0.162
n = 6(F)	0.371	0.170
n = 6(G)	0.322	0.154
n = 7(A)	0.477	0.198
n = 7(B)	0.434	0.173
n = 7(C)	0.348	0.136

---

Averaging over all (H₂O)_n⁻ cluster sizes and isomers, we find that MP2 theory recovers 94.90 ± 0.07% of the CCSD(T) correlation energy, and 95.00 ± 0.07% in the case of the corresponding neutral clusters. (Uncertainties represent one standard deviation.) That these fractions are nearly geometry- and size-independent merely reflects the fact that the total correlation energy is dominated by the sum of monomer correlation energies, but together with the linear relationship between Δ and the VDE, this explains the asymptotic fractional error observed in Fig. 2. The increasing importance of electron correlation as a function of the VDE eventually overshadows any differences between isomers at the Hartree–Fock level, such that in strong-binding isomers, the error in the MP2 calculation is dominated solely by the difference between Δ_MP2 and Δ_CCSD(T).

In addition to wave function-based electronic structure methods, we also calculate VDEs using the BHLYP^5,39 density functional (E^BHLYP_XC = 0.5E^LDA_X + 0.5E^HF_X + E^LYP_C), which tends to be the least overbinding of the common density functionals. Fig. 3 suggests that, for (H₂O)_n⁻ isomers with VDEs in excess of about 0.4 eV, BHLYP overestimates the VDE by about 15%, though the scatter among data points in the asymptotic region is greater than in the case of wave function-based methods. Somewhat more consistent behavior is obtained when BHLYP molecular orbitals are used in second-order many-body perturbation theory (MBPT2), including single excitations. We refer to this procedure as the MBPT2(BHLYP) method.⁴⁰ As shown in Fig. 5, the CCSD(T) detachment energy is bounded from below by the MP2 value, which averages 93.2 ± 1.1% of the CCSD(T) detachment energy, and from above by MBPT2(BHLYP), at an average of 111.1 ± 1.4% of CCSD(T). In calculating these averages and standard deviations, we have included only those isomers whose CCSD(T) detachment energies exceed 0.4 eV, since we demonstrated above that it is only in these cases that MP2 affords an approximately constant fractional error. Our conclusions regarding the accuracy of second-order perturbation theory thus apply mainly to strongly-bound isomers (VDE ≳ 0.4 eV).

Fig. 4 Correlation energy Δ_X [X = MP2 or CCSD(T)] associated with the unpaired electron, for various isomers of (H₂O)_n⁻. Lines indicate best fits to the data.

Having only a small number of data points above 0.4 eV, we cannot be certain that the apparently asymptotic behavior observed in the 0.4–0.8 eV range persists to higher detachment energies. For additional data, we turn to (HF)_n⁻ clusters, since a relatively small number of HF molecules can bind an electron much more strongly than can a small water cluster. Optimized geometries for (HF)_n⁻, n = 3–8, are depicted in Fig. 6, and clearly show the evolution of a nascent cavity within the cluster, in which protons are oriented toward the excess electron. None of these isomers has a neutral dipole moment larger than 2.7 D and in most cases μ₀ is considerably smaller than the critical value (≈2.4 D; see ref. 2) necessary to obtain anionic states that are rigorously dipole-bound. Nevertheless, these clusters exhibit VDEs as large as 4.0 eV. Along with their cavity-like structures, this fact implies that these clusters are true “solvated electron” systems, in contrast to small water cluster anions, which are sometimes termed “wet electron” systems⁴¹ to emphasize that the electron is not solvated in the bulk sense. The existence of solvated electron or “cavity states” (as we shall call them) at such a small number of monomers is important because it allows us to perform coupled-cluster calculations for such species, which are anticipated to be important in large water cluster anions but cannot be located in clusters small enough to be treated with coupled-cluster theory.

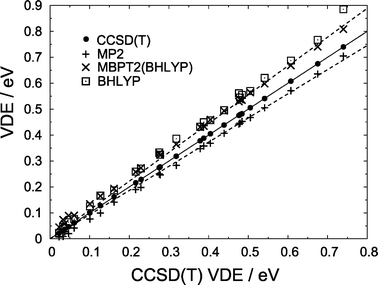Fig. 5 Predicted VDEs for the (H₂O)_n⁻ isomers shown in Fig. 1. CCSD(T) VDEs lie along the diagonal (solid line); the upper and lower broken lines represent 111.1% and 93.2% of the CCSD(T) VDE, which represent the average fractions recovered by the MBPT2(BHLYP) and MP2 methods, respectively.

We digress briefly here to discuss some technical details related to electronic structure calculations for (HF)_n⁻. First of all, we observe that these clusters are not quite as insensitive to basis sets effects as are (H₂O)_n⁻ clusters. In (HF)₃⁻, for example, expansion of the basis from 6-31(m+,n+)G* to 6-311(m+,n+)G** decreases the MP2 detachment energy by about 0.06 eV, while additional diffuse shells added to the fluorine atoms increase the VDE by about 0.02 eV. The fact that basis set effects of this magnitude are not observed in (H₂O)_n⁻ is consistent with our earlier explanation⁵ that the bent geometry of a water molecule allows the SOMO (essentially an sp hybrid) to acquire p character by mixing together two s functions on different hydrogen atoms; as such, diffuse p functions are not absolutely required in the case of (H₂O)_n⁻. The same argument does not apply to (HF)_n⁻, and for these systems it appears that p functions on the hydrogen atoms have an important effect. Furthermore, as demonstrated by the natural charge differences given in Fig. 6, the excess electron density is shared by a far greater number of atoms in the (HF)_n⁻ cavity states than in most of the (H₂O)_n⁻ isomers shown in Fig. 1. Despite these considerations, we will stick to the 6-31(1+,3+)G* basis set for consistency and because our primary interest lies in (H₂O)_n⁻, keeping in mind that our calculated VDEs for (HF)_n⁻ isomers likely lie further below the complete-basis limit than they do in the case of (H₂O)_n⁻.

With this in mind, it is interesting to note that our calculated VDEs, especially for the larger (HF)_n⁻ cavity isomers, are substantially greater than those reported in older calculations.^2,3 One possible explanation for the discrepancy is the fact that previous calculations focused on high-symmetry geometries, e.g., O_h symmetry for the hexamer anion.² Although we do obtain fully-relaxed D_∞h, D_3h, and T_d stationary points for the dimer, trimer, and tetramer anions, respectively, we failed in repeated attempts to locate a D_3h stationary point for (HF)₅⁻ or an O_h stationary point for (HF)₆⁻, both of which have been reported elsewhere.^2,3 At the B3LYP/6-31(1+,3+)G* level, both the pentamer and the hexamer anions adopt structures in which the excess electron is tetrahedrally coordinated, with the additional HF molecule(s) forming an incipient second solvation shell. A stationary point of (HF)₆⁻ with O_h symmetry can be located if point-group symmetry is constrained, and the resulting O_h structure has a VDE of 2.76 eV, compared to 3.07 eV for the fully-relaxed structure in Fig. 6. [Both VDEs are CCSD(T)/6-31(1+,3+)G* values.] In comparison, Jordan and Wang² report a VDE of 2.69 eV for their O_h structure, also at the CCSD(T) level. On the other hand, our D_3h trimer anion has a predicted VDE of 0.93 eV, much larger than the values of ≈0.6 eV reported by Gutowski and co-workers^3,42 for comparable D_3h structures. Further calculations—in particular, geometry optimizations at higher levels of theory, and a more thorough exploration of basis set effects—are necessary in order to resolve the true structures of these clusters, but for the purpose of benchmarking VDE calculations, the structures presented in Fig. 6 will suffice.

In addition to these cavity isomers of (HF)_n⁻, we also consider HF⋯HF⋯HF⋯ chains, artificially constrained to linear geometries but otherwise optimized at the B3LYP/6-31(1+,3+)G* level. These isomers bind an electron very weakly at the H-terminus and, as compared to the cavity isomers, are more analogous to the surface-bound anions obtained from small water clusters. Fig. 7 bolsters this analogy, as it shows that the fractional error in the MP2 detachment energy behaves in much the same way for these linear (HF)_n⁻ isomers as it does for small (H₂O)_n⁻ isomers. (Numerical data corresponding to this figure are given in Table 2.) In contrast, for cavity isomers of (HF)_n⁻, MP2 predicts a larger VDE than does CCSD(T). Given their very different electron binding motifs, there is no reason why the MP2 fractional errors should behave the same way for linear versus globular (HF)_n⁻; the important observation is that, in both cases, the MP2 fractional error appears to approach an asymptotic limit as the VDE increases.

Fig. 6 Optimized B3LYP/6-31(1+,3+)G* geometries of (HF)_n⁻ “cavity” isomers, along with VDEs [CCSD(T)/6-31(1+,3+)G* level] and selected δq_i values [Hartree–Fock/6-31(1+,3+)G* level].

Table 2 Hartree–Fock VDEs and CCSD(T) corrections to the VDE, Δ_CCSD(T), for isomers of (HF)_n⁻

Isomer	Hartree–Fock VDE/eV	Δ CCSD(T)/eV
n = 2 (linear)	0.004	0.023
n = 3 (linear)	0.106	0.041
n = 4 (linear)	0.183	0.053
n = 5 (linear)	0.240	0.061
n = 6 (linear)	0.280	0.065
n = 7 (linear)	0.310	0.068
n = 8 (linear)	0.332	0.069
n = 2 (cavity)	−0.009	0.123
n = 3 (cavity)	0.721	0.213
n = 4 (cavity)	1.595	0.196
n = 5 (cavity)	2.314	0.168
n = 6 (cavity)	2.917	0.150
n = 7 (cavity)	3.406	0.144
n = 8 (cavity)	3.868	0.137

---

Tables 1 and 2 list Δ_CCSD(T) for each (H₂O)_n⁻ and (HF)_n⁻ isomer examined so far. In no case does this quantity exceed 0.23 eV, which is substantially smaller than the standard a priori estimate of ∼1 eV of correlation energy per valence electron pair. Not surprisingly, Δ_CCSD(T) is somewhat larger for the cavity isomers of (HF)_n⁻ than it is for the linear isomers, since the excess electron is bound more tightly and interacts more strongly with the cluster in the former case, but while Δ_CCSD(T) (and, similarly, Δ_MP2) demonstrates a clear surface state/internal state correlation, this quantity does not correlate with the number of H₂O or HF monomers.

As a final set of small-cluster benchmarks, in Fig. 8 we compare absolute errors obtained from intermediate-level treatments of electron correlation, including CCSD, full MP4, and MP4 sans triple excitations, MP4(SDQ). Notably, the CCSD, MP4, and MP4(SDQ) methods exhibit essentially constant absolute errors for the (HF)_n⁻ cavity isomers, where the VDEs are large. The same does not hold for the more weakly-binding (H₂O)_n⁻ isomers, although these methods remain more accurate than MP2. In future work, we shall attempt to quantify the importance of various individual correlations beyond second order in perturbation theory.

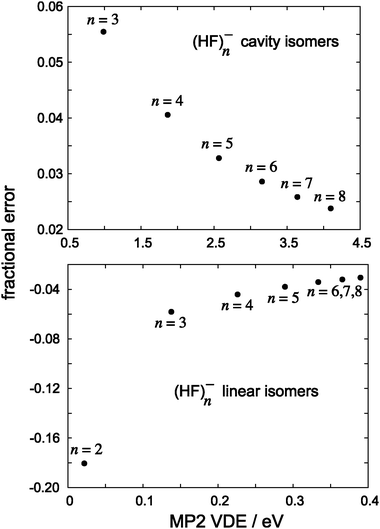Fig. 7 Fractional errors in MP2 detachment energies, with respect to CCSD(T) values, for isomers of (HF)_n⁻.

3.2. Comparison to large (H₂O)_n⁻ clusters

The results of the previous section provide strong evidence that MP2/6-31(1+,3+)G* detachment energies for (H₂O)_n⁻ lie within about 7% of CCDS(T) values for isomers with VDEs greater than 0.4 eV. For the dominant features in the photoelectron spectra, this régime is broached starting with n = 6, while larger clusters have even greater VDEs: 0.7 eV for (H₂O)₁₁⁻, and 1.0–1.2 eV for (H₂O)₂₀⁻ and (H₂O)₂₄⁻, for example.^15,23 In this section we attempt to address the accuracy of MP2 detachment energies for larger clusters, taking (H₂O)₂₀⁻ and (H₂O)₂₄⁻ as representative examples.

Fig. 9 presents the results of natural population analysis for several isomers of (H₂O)₂₀⁻ and (H₂O)₂₄⁻. These isomers were first studied in ref. 5, and the isomeric labels introduced in that work, which indicate the number of four-, five-, and six-member rings that comprise the cluster, are retained here. In order to make a fair comparison with the calculations in the previous section, we have re-optimized the geometries obtained in ref. 5 at the B3LYP/6-31(1+,3+)G* level, though this has no qualitative impact on the structures.

The three structures shown in the upper part of Fig. 9 are pentagonal dodecahedral or “5¹²” isomers of (H₂O)₂₀⁻ that bind the extra electron on the surface of the cluster, but via quite different morphologies, depending upon how the ten dangling hydrogen atoms are distributed. In 5¹² isomers A and B, the dangling hydrogens are asymmetrically distributed and the corresponding neutral clusters have enormous dipole moments (28.9 D and 21.9 D, respectively, at the Hartree–Fock level). As a result, the SOMO in each of these isomers is localized at one end of the cluster, which is clearly reflected in the δq_i values. Significant polarization is found only on two surface hydrogen atoms, and none of the hydrogen atoms involved in hydrogen bonding is significantly polarized by electron attachment. Charge penetration into these (H₂O)₂₀⁻ isomers does not appear to be any more significant than in the smaller water cluster anions depicted in Fig. 1, implying similar electronic structure in both cases.

Isomer 5¹²F of (H₂O)₂₀⁻ is markedly different from A and B. In this isomer, the ten dangling hydrogen atoms are located symmetrically around the equator of the cluster, so that μ₀ ≈ 0 and the SOMO is a torus that is completely delocalized over these hydrogens [see Fig. 13(c) of ref. 5]. None of these hydrogens has a |δq_i| value exceeding 0.050 but a large number of atomic charges lie in the range 0.025 ≤ |δq_i| < 0.050. For this particular isomer, the electron binding mechanism appears to differ significantly from any that we observed in small cluster anions. On the other hand, the predicted VDE for this isomer (see Table 3) is far too small to be consistent with the experimental estimates of 1.0–1.2 eV.^15,23

Table 3 Estimated VDEs for various isomers of (H₂O)₂₀⁻ (upper data set) and (H₂O)₂₄⁻ (lower data set), at X3LYP/6-31++G* optimized geometries (geometry I, from ref. 5); B3LYP/6-31(1+,3+)G* optimized geometries (geometry II); and B3LYP/6-31G* optimized geometries (geometry III)

		VDE/eV
Isomer		Hartree–Fock	MP2	Corrected MP2^a		BHLYP	MBPT2(BHLYP)
							Raw	Scaled^b
a Corrections to the MP2 VDE obtained by scaling the MP2 correlation energies by 1.053 (left column), or by scaling the MP2 VDE by 1.070 (right column). b VDE scaled by 0.8715.
4^45^46^2	I	0.026	0.074	0.077	0.079	0.181	0.219	0.191
5^12A	I	0.883	1.083	1.094	1.159	1.286	1.245	1.085
	II	0.903	1.101	1.111	1.178	1.291	1.254	1.093
5^12B	I	0.723	0.908	0.918	0.972	1.084	1.062	0.925
	II	0.704	0.883	0.892	0.945	1.050	1.030	0.898
5^12C	I	0.497	0.657	0.666	0.703	0.818	0.810	0.706
5^12D	I	0.379	0.515	0.522	0.551	0.668	0.672	0.586
5^12E	I	−0.051	−0.022	−0.021	—	0.111	0.135	0.118
5^12F	II	0.053	0.150	0.155	0.160	0.438	0.375	0.327
	III	0.093	0.227	0.234	0.243	0.559	0.483	0.421
4^66^8A	I	−0.086	−0.066	−0.065	—	0.010	0.084	0.073
4^66^8B	I	0.080	0.575	0.601	0.615	0.863	0.726	0.632
	II	0.177	0.583	0.605	0.624	0.838	0.716	0.624
4^146^4A	I	−0.035	0.003	0.004	0.004	0.171	0.201	0.175
4^146^4B	I	−0.035	0.004	0.004	0.004	0.421	0.346	0.302
5^126^2A	I	−0.076	−0.051	−0.050	—	0.079	0.118	0.103
5^126^2B	I	0.254	0.793	0.821	0.849	1.100	0.927	0.808
	II	0.337	0.782	0.807	0.837	1.068	0.901	0.785
5^126^2C	I	0.049	0.136	0.192	0.146	0.430	0.362	0.316
4^14	I	−0.077	−0.055	−0.055	—	0.048	0.141	0.123

---

Cavity isomers of large water cluster anions have different characteristics altogether, and Fig. 9 depicts two such isomers of (H₂O)₂₄⁻. The electron binding mechanism is again apparent from the natural population analysis: δq_i is quite large for each of the four hydrogen atoms that directly solvates the extra electron, but charge rearrangement is not limited to these atoms and is observed throughout the cluster. The SOMOs for these isomers (see Fig. 13 of ref. 5) corroborate this picture: the unpaired electron density has spherical symmetry and originates at the center of the cluster, but a non-negligible part of the SOMO extends beyond the cavity and into the water network. This same sort of through-cluster polarization was observed in cavity states of (HF)_n⁻, however, and did not affect the conclusion that MP2 calculations recover a constant fraction of the CCSD(T) correlation energy.

Hartree–Fock, MP2, and BHLYP detachment energies for these and several other (H₂O)₂₀⁻ and (H₂O)₂₄⁻ isomers studied in our previous work⁵ are listed in Table 3. For certain of these clusters, we have experimented with different density functionals (B3LYP and X3LYP⁴³) and different basis sets for performing the geometry optimizations, in order to evaluate how much this aspect affects the VDE. Note also that Δ_MP2 is given by the difference between the Hartree–Fock and MP2 detachment energies. In most cases Δ_MP2 ≲ 0.02 eV, just as we found in the small cluster examples of Section 3.1. The exceptions, (H₂O)₂₄⁻ isomers 4⁸6⁸B and 5¹²6²B, are cases where the extra electron is bound inside of the cluster. For these isomers, Δ_MP2 ≈ 0.5 eV, still considerably smaller than the correlation energy associated with valence electron pairs.

Several of the isomers listed in Table 3 possess VDEs that are slightly negative at the Hartree–Fock level. This represents a basis set artifact; a complete basis would correctly describe continuum states and therefore any unbound anion would have a VDE of exactly zero. In the present cases, a higher-quality basis set might bind some of the anions at the Hartree–Fock level, but even without further calculations we can say with confidence that the resulting VDEs would be quite small, since our previous work⁵ suggests that basis set effects beyond 6-31(1+,3+)G* are typically on the order of 0.05 eV or less. As an example, we performed a Hartree–Fock VDE calculation for (H₂O)₂₄⁻ isomer 4¹⁴6⁴B using the much larger TZVPP + 3s2p basis introduced in Section 2, which ought to be close to basis-set saturation at the SCF level. The resulting VDE, −0.027 eV, is nearly equal to the value of −0.035 eV obtained at the Hartree–Fock/6-31(1+,3+)G* level. On the one hand, this demonstrates that it is essentially impossible, in practice, to obtain a correct description of continuum states using atom-centered Gaussian basis functions. More importantly, however, this calculation offers additional evidence that improvements upon the 6-31(1+,3+)G* basis set are not likely to alter the conclusions reached in this study.

MP2 corrections to the negative Hartree–Fock VDEs in question are also quite small, affording VDEs that mostly remain negative, and in no case are greater than +0.004 eV. Clearly, the anions in question are either very weakly bound or else not bound at all, though a treatment of electron correlation beyond the MP2 level is required in order to make a definitive case for one of these possibilities over the other.

Table 3 also presents two corrected values of each MP2 detachment energy. The first is obtained by scaling the correlation energies of both the neutral and the anionic cluster by a factor of 1.053, the average ratio of the CCSD(T) to MP2 correlation energies for all of the data listed in Table 1. (Δ_MP2 is an extensive quantity, so in order to preserve the size-consistency of the MP2 method, the neutral and anionic correlation energies must be scaled by the same factor.) This correction amounts to less than 0.03 eV in every case except isomer 5¹²6²C of (H₂O)₂₄⁻, where it is almost 0.06 eV. In light of the consistent results obtained for small clusters in Section 3.1, and given that several other empirical scaling procedures for MP2 correlation energies have been shown to improve calculated properties significantly,^44–48 we consider these scaled MP2 values to be our most accurate estimates of the VDEs for these clusters. An alternative correction provided in Table 3 is obtained by scaling the VDE itself by a factor of 1.070, obtained by a fit of the fractional error data (Fig. 2) for the nine isomers of (H₂O)_n⁻ whose MP2 detachment energies exceed 0.4 eV. This procedure results in a somewhat larger correction to the MP2 detachment energy, increasing the largest VDEs by 0.05–0.06 eV.

BHLYP detachment energies for our (H₂O)₂₀⁻ and (H₂O)₂₄⁻ isomers are also listed in Table 3, and, consistent with the results for smaller clusters, are significantly larger than the corresponding (raw) MP2 values. The MBPT2(BHLYP) detachment energy can be larger or smaller than the BHLYP value, with the two results generally falling within 0.1–0.2 eV of one another. Upon scaling the MBPT2(BHLYP) detachment energies by a factor of 0.8715, equal to the average ratio of MBPT2(BHLYP) and CCSD(T) detachment energies for the small (H₂O)_n⁻ isomers in our test set, all but one of the resulting VDEs are within 0.18 eV of the scaled MP2 values. We regard the electronic structure of these isomers to be a solved problem, and consider the adjusted MP2 results (using scaled correlation energies) to be the most accurate existing estimates of their VDEs.

The lone outlier is (H₂O)₂₄⁻ isomer 4¹⁴6⁴B, which has a VDE of essentially zero at the MP2 level (corrected or uncorrected), but has an MBPT2(BHLYP) detachment energy of 0.302 eV after downward scaling. While even the BHLYP detachment energy for this isomer is far too small to account for the experimental photoelectron spectrum, the discrepancy between MP2 and MBPT2(BHLYP) is nevertheless worrisome insofar as it may portend a breakdown in the accuracy of second-order perturbation theory.

Examination of the Hartree–Fock and BHLYP SOMOs (Fig. 10) reveals that each is qualitatively consistent with the VDE obtained by subsequent second-order perturbation theory. In particular, the Hartree–Fock SOMO exhibits two diffuse lobes on the surface of the cluster, indicative of a weakly-bound anion. By changing the SCF initial guess (from a superposition of atomic densities to diagonalization of the core Hamiltonian), one can locate a second Hartree–Fock solution in which the SOMO consists of only one of these lobes, but which is only 2 × 10⁻⁵ au above the two-lobe solution shown in Fig. 10(a), and only 5 × 10⁻⁵ au higher in energy at the MP2 level. These energy differences are small but clearly distinct, given the thresholds discussed in Section 2, and indicate that this cluster exhibits a form of “electronic tautomerism”, at least at the Hartree–Fock and post-Hartree–Fock levels of theory. This tautomerism may be similar to the “bi-dipole-bound anion” effect, a symmetry artifact first discovered by Gutowski and co-workers⁴⁹ in linear (HCN)_n⋯HCCH⋯(NCH)_n chains. In those systems, the SOMOs have σ_g symmetry with lobes located on either end of the chain, but in each case the SOMO is nearly degenerate with a corresponding σ_u virtual orbital. As such, there exist low-lying Hartree–Fock solutions, corresponding to excitation of the unpaired electron into σ_g ± σ_u, that localize the unpaired electron on one end of the molecule.

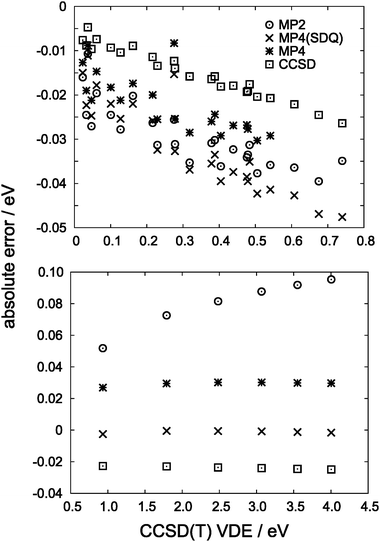Fig. 8 Errors in VDEs at different levels of theory, for (H₂O)_n⁻ isomers (upper panel) and (HF)_n⁻cavity isomers (lower panel). For (H₂O)_n⁻ isomers, full MP4 calculations were performed only for n ≤ 6.

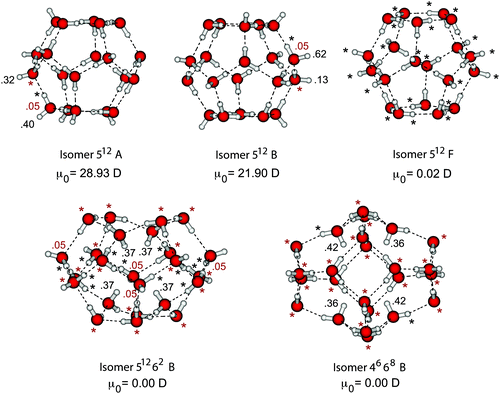Fig. 9 Isomers of (H₂O)₂₀⁻ (top row) and of (H₂O)₂₄⁻ (bottom row), along with Hartree–Fock μ₀ and δq_i values. The δq_i values in black correspond to hydrogen atoms while those in gray are for oxygen atoms.

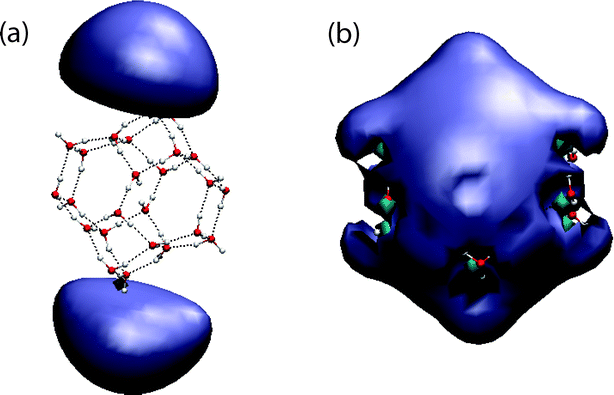Fig. 10 SOMOs for (H₂O)₂₄⁻ isomer 4¹⁴6⁴B, calculated at (a) the Hartree–Fock/6-31(1+,3+)G* level and (b) the BHLYP/6-31(1+,3+)G* level. Both plots use a contour value of 0.005 au.

In contrast to these Hartree–Fock solutions, the BHLYP SOMO contains significant density in the center of the cluster and penetrates throughout the water network, consistent with a nontrivial VDE. Starting with BHLYP orbitals and using an SCF algorithm based on direct minimization,⁵⁰ we attempted to locate a Hartree–Fock solution whose SOMO resembles the BHLYP one, but this calculation merely relaxed to the previously-obtained Hartree–Fock solution. It remains unclear whether the Hartree–Fock or the BHLYP orbitals are a better model of physical reality in this cluster isomer. In such cases of electronic tautomerism, where different SCF procedures (e.g., Hartree–Fock versus DFT) result in qualitatively different molecular orbitals, finite-order perturbation theory predictions are probably not sufficient to determine the electronic structure. Such examples appear to be rare, as this is the only one we have found despite extensive calculations for this and previous work.⁵

4. Summary

We have examined whether the accuracy of MP2 detachment energy predictions for (H₂O)_n⁻ and (HF)_n⁻ clusters degrades as a function of cluster size. In fact, the accuracy correlates not with n but with the VDE itself, a behavior that we attribute to the fact that, for (H₂O)_n⁻ isomers, the electron correlation energy Δ associated with the unpaired electron grows linearly as a function of the VDE. Even in cavity states of (H₂O)₂₄⁻, which ought to be relatively strongly correlated, Δ ≲ 0.5 eV, only half as large as the correlation energy associated with typical valence electron pairs. This weak electron correlation explains the success of MP2 theory for VDE predictions.

Because the total correlation energy of a cluster is dominated by the sum of monomer contributions, MP2 theory recovers an essentially constant fraction of the CCSD(T) correlation energy in (H₂O)_n, (HF)_n, and their anions, and as such the MP2 results can be easily adjusted in order to achieve better accuracy. An independent estimate of the VDE can be obtained by applying second-order many-body perturbation theory to DFT orbitals (obtained with the BHLYP functional), and in the small cluster isomers studied here, this procedure always affords an upper bound to the CCSD(T) detachment energy. For a wide variety of (H₂O)₂₀⁻ and (H₂O)₂₄⁻ isomers, these two estimates agree to within 0.15 eV, thus providing an error bar for MP2 detachment energies. The combination of MP2 and MBPT2(BHLYP) provides reasonably accurate VDE predictions, at low enough cost to be applied to fairly large clusters.

We have thus far discovered only one example in which MP2 and MBPT2(BHLYP) detachment energies differ by significantly more than 0.15 eV. In this case, Hartree–Fock theory exhibits a form of electronic tautomerism (which may be a symmetry artifact) and, more importantly, the SOMO is qualitatively different at the Hartree–Fock and BHLYP levels of theory. In this case, the error bar established by MP2 and MBPT2(BHLYP) is about 0.4 eV.

5. Note added in proof

We have recently calculated the VDE of isomer 4¹⁴6⁴B from section 3.2 at the RI-MP2/TZVPP+3s2p level, where RI indicates the resolution of identity approximation to MP2. (Our own tests and those in ref. 28 indicate that the RI approximation introduces errors of < 0.001 eV in VDEs.) The RI-MP2/TZVPP+3s2p result is 0.002 eV, as compared to 0.004 eV at the MP2/6-31(1+,3+)G* level.

Acknowledgements

This work was primarily supported by NSF grant CHE-9981997 (to M.H.-G.) and by an NSF postdoctoral fellowship (to J.M.H.). Additional support came from the Director, Office of Energy Research, Office of Basic Energy Sciences, Chemical Sciences Division of the US Department of Energy under Contract DE-AC03-76SF00098, and from supercomputer time from NERSC.

References

1. M. Gutowski, K. D. Jordan and P. Skurski, J. Phys. Chem. A, 1998, 102, 2624.
2. K. D. Jordan and F. Wang, Annu. Rev. Phys. Chem., 2003, 54, 367.
3. M. Gutowski and P. Skurski, J. Phys. Chem. B, 1997, 101, 9143.
4. F. Wang and K. D. Jordan, J. Chem. Phys., 2001, 114, 10717.
5. J. M. Herbert and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 5217.
6. M. Gutowski, P. Skurski, A. I. Boldyrev, J. Simons and K. D. Jordan, Phys. Rev. A, 1996, 54, 1906.
7. M. Gutowski, P. Skurski, K. D. Jordan and J. Simons, Int. J. Quantum Chem., 1997, 107, 2968.
8. P. Skurski and M. Gutowski, J. Chem. Phys., 1999, 111, 3004.
9. P. Skurski, M. Gutowski and J. Simons, J. Chem. Phys., 2001, 114, 7443.
10. Consult ref. 5 for a bibliography of electronic structure calculations for (H₂O)_n⁻ clusters.
11. H. Haberland, C. Ludewigt, H.-G. Schindler and D. R. Worsnop, J. Chem. Phys., 1984, 81, 3742.
12. H. Haberland, H. Langosch, H.-G. Schindler and D. R. Worsnop, J. Phys. Chem., 1984, 88, 3903.
13. J. Kim, I. Becker, O. Cheshnovsky and M. A. Johnson, Chem. Phys. Lett., 1998, 297, 90.
14. N. I. Hammer, J. R. Roscioli and M. A. Johnson, J. Phys. Chem. A, 2005, 109, 7896.
15. J. R. R. Verlet, A. E. Bragg, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2005, 307, 93.
16. A. E. Bragg, J. R. R. Verlet, A. Kammrath, O. Cheshnovsky and D. M. Neumark, J. Am. Chem. Soc., 2005, 127, 15283.
17. J. V. Coe, G. H. Lee, J. G. Eaton, S. T. Arnold, H. W. Sarkas, K. H. Bowen, C. Ludewigt, H. Haberland and D. R. Worsnop, J. Chem. Phys., 1990, 92, 3980.
18. R. N. Barnett, U. Landman, C. L. Cleveland and J. Jortner, J. Chem. Phys., 1988, 88, 4429.
19. R. N. Barnett, U. Landman, C. L. Cleveland and J. Jortner, Chem. Phys. Lett., 1988, 145, 382.
20. R. N. Barnett, U. Landman, G. Rajagopal and A. Nitzan, Israel J. Chem., 1990, 30, 85.
21. P. Ayotte and M. A. Johnson, J. Chem. Phys., 1997, 106, 811.
22. D. M. Bartels, J. Chem. Phys., 2001, 115, 4404.
23. J. V. Coe, Int. Rev. Phys. Chem., 2001, 20, 33.
24. L. Turi, W.-S. Sheu and P. J. Rossky, Science, 2005, 309, 914.
25. J.-W. Shin, N. I. Hammer, J. M. Headrick and M. A. Johnson, Chem. Phys. Lett., 2004, 399, 349.
26. The exponents on these additional diffuse functions differ slightly from the 6-31(1+,3+)G* exponents defined in our previous work (ref. 5), which were decremented by factors of 3.00 rather than 3.32.
27. The TZVPP + 3s2p basis consists of Ahlrichs’ doubly-polarized, valence triple zeta (TZVPP) basis for the oxygen atoms, the singly-polarized TZVP basis for the hydrogen atoms and a 3s2p set of diffuse basis functions centered on each oxygen and each hydrogen atom, with exponents taken from ref. 28.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 1999, 1, 4537.
29. P. M. W. Gill, B. G. Johnson and J. A. Pople, Chem. Phys. Lett., 1993, 209, 506.
30. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
31. P. J. Stephens, J. F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
32. J. Kong, C. A. White, A. I. Krylov, C. D. Sherrill, R. D. Adamson, T. R. Furlani, M. S. Lee, A. M. Lee, S. R. Gwaltney, T. R. Adams, C. Ochsenfeld, A. T. B. Gilbert, G. S. Kedziora, V. A. Rassolov, D. R. Maurice, N. Nair, Y. Shao, N. A. Besley, P. E. Maslen, J. P. Dombroski, H. Daschel, W. Zhang, P. P. Korambath, J. Baker, E. F. C. Byrd, T. Van Voorhis, M. Oumi, S. Hirata, C. Hsu, N. Ishikawa, J. Florian, A. Warshel, B. G. Johnson, P. M. W. Gill, M. Head-Gordon and J. A. Pople, J. Comput. Chem., 2000, 21, 1532.
33. G. Schaftenaar and J. H. Noordik, J. Comput. Aided Mol. Des., 2000, 14, 123.
34. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
35. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
36. F. Weinhold, in Encyclopedia of Computational Chemistry, eds. P. v. R. Schleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer III and P. R. Schreiner, Wiley, Chichester, United Kingdom, 1999, Vol. 3, p. 1792.
37. N. I. Hammer, J.-W. Shin, J. M. Headrick, E. G. Diken, J. R. Roscioli, G. H. Weddle and M. A. Johnson, Science, 2004, 306, 675.
38. N. I. Hammer, J. R. Rosciolli, M. A. Johnson, E. M. Myshakin and K. D. Jordan, J. Phys. Chem. A DOI:10.1021/jp053769c.
39. J. C. Rienstra-Kiracofe, G. S. Tschumper, H. F. Schaefer III, N. Sreela and G. B. Ellison, Chem. Rev., 2002, 102, 231.
40. All of the MP2 calculations reported here employ frozen core orbitals, but in our MBPT2(BHLYP) calculations all orbitals are correlated.
41. K. S. Kim, I. Park, S. Lee, K. Cho, J. Y. Lee, J. Kim and J. D. Joannopoulos, Phys. Rev. Lett., 1996, 76, 956.
42. M. Gutowski, C. S. Hall, L. Adamowicz, J. H. Hendricks, H. L. de Clercq, S. A. Lyapustina, J. M. Nilles, S.-J. Xu and K. H. Bowen Jr, Phys. Rev. Lett., 2002, 88, 143001.
43. X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. USA, 2004, 101, 2673.
44. M. Gerenkamp and S. Grimme, Chem. Phys. Lett., 2004, 392, 229.
45. I. Hyla-Kryspin and S. Grimme, Organometallics, 2004, 23, 5581.
46. S. Grimme, J. Phys. Chem. A, 2005, 109, 3067.
47. Y. Jung, R. C. Lochan, A. D. Dutoi and M. Head-Gordon, J. Chem. Phys., 2004, 121, 9793.
48. R. C. Lochan, Y. Jung and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 7598.
49. M. Gutowski, P. Skurski and J. Simons, Int. J. Mass Spectrom., 2000, 201, 245.
50. T. Van Voorhis and M. Head-Gordon, Mol. Phys., 2002, 100, 1713.

---

Footnote

† Electronic supplementary information (ESI) available: Geometries and energies. See DOI: 10.1039/b513098k

---