Excited state hydrogen transfer in fluorophenol·ammonia clusters studied by two-color REMPI spectroscopy

Abstract

Two-color (1 + 1′) REMPI mass spectra of o-, m- and p-fluorophenol·ammonia (1 ∶ n) clusters were measured with a long delay time between excitation and ionization lasers. The appearance of NH₄(NH₃)_n−1⁺ with 100 ns delay after exciting the S₁ state is a strong indication of generation of long-lived species via S₁. In analogy with the phenol·ammonia clusters, we conclude that an excited state hydrogen transfer reaction occurs in o-, m- and p-fluorophenol·ammonia clusters. The S₁-S₀ transition of o-, m- and p-fluorophenol·ammonia (1 : 1) clusters were measured by the (1 + 1′) REMPI spectra, while larger (1 ∶ n) cluster (n = 2–4) were observed by monitoring the long-lived NH₄(NH₃)_n−1 clusters action spectra. The vibronic structures of m- and p-fluorophenol·ammonia clusters are assigned based on vibrational calculations in S₀. The o-fluorophenol·ammonia (1 : 1) cluster shows an anharmonic progression that is analyzed by a one-dimensional internal rotational motion of the ammonia molecule. The interaction between the ammonia molecule and the fluorine atom, and its change upon electronic excitation are suggested. The broad action spectra observed for the o-fluorophenol·ammonia (1 : n) cluster (n ≧ 2) suggest the excited state hydrogen transfer is faster than in m- and p-fluorophenol·ammonia clusters. The different reaction rates between o-, m- and p-fluorophenol·ammonia clusters are found from comparison between the REMPI and action spectra.

---

1. Introduction

Excited state hydrogen transfer (ESHT) has been attracting many researchers because it provides new possibilities for the interpretation of well known photochemical reactions. This reaction channel was discovered through the generation of long-lived species from the photo-excited phenol·(NH₃)_n cluster.^1–6 When the two-color (1 + 1′) resonant ionization via S₁ state is applied to the phenol·ammonia cluster, NH₄(NH₃)_n−1⁺ ions are generated in addition to the parent phenol·ammonia cluster cations. The parent cluster ions cannot be observed when a long delay (200 ns) is introduced between the excitation and ionization lasers, because of the short lifetime in S₁ (a few ns to 50 ps). Yet, the NH₄(NH₃)_n−1⁺ ions are still observed at such long delays. Besides, these NH₄(NH₃)_n−1⁺ ions are not detected when the clusters are directly ionized by vacuum UV light from the ground state, which indicates that they are due to a reaction occurring in the excited state. NH₄(NH₃)_n−1⁺ ions must then be produced by direct ionization of long-lived species generated in the S₁ state of the phenol·(NH₃)_n clusters. The electronic and vibrational transitions of the long-lived species have been measured by UV-near IR-UV and UV-IR-UV ion dip spectroscopy that allowed to identify the long-lived species to neutral NH₄(NH₃)_n−1 radicals.^3–6 The generation mechanism of neutral radicals was completely different from the excited state proton transfer that was expected for the photo-excited phenol and corresponds to a hydrogen atom transfer from the excited phenol to the ammonia cluster (ESHT). Several other examples of ESHT or excited state hydrogen loss reactions have been now reported in indole·ammonia clusters,⁷ pyrrole·ammonia clusters,⁸ and amino-acid cations.^9–11 In aromatic molecules containing OH or NH groups, ESHT seems to be a general reaction that needs to be further investigated and understood.

Theoretically, the mechanism of the ESHT reaction points to the importance of a πσ* state localized on the OH group and dissociative along this coordinate (SDDJ model).¹² In the free molecule the πσ* state lies higher in energy than the S₁ ππ* state and crosses both the excited and ground states, which results in a competition between H loss and fast internal conversion. In clusters, the πσ* state is stabilized by the hydrogen-bond formation and still crosses the S₁ ππ* state, inducing the transfer of the hydrogen atom to the solvent cluster but the crossing with the ground state is removed. This πσ* model that explains qualitatively many different photochemical processes in aromatic acids should be tested in a more systematic way. In that view, we have studied the ESHT reaction in fluorophenol·ammonia clusters. Fluorine substitution is one of the most benign perturbations for phenol because the number of vibrational modes remains the same after substitution and the electronic state is weakly perturbed. The fluorine substituent has an induction effect that attracts the electron in the σ orbital. Furthermore, the strength of the perturbation is expected to vary with the substituent position (ortho-, meta- and para-) according to the OH group. Therefore the o-, m- and p-fluorophenol·(NH₃)_n clusters provide important data to validate the πσ* model. In the present work, as a first step of a systematic study, we have measured the two-color resonant enhanced two-photon ionization (1 + 1′ REMPI) spectra and the action spectra obtained by monitoring the reaction products NH₄(NH₃)_n−1 for o-, m- and p-fluorophenol·(NH₃)_n clusters. The vibronic structures are discussed based on the quantum chemical calculation in the neutral ground state. The difference of reaction efficiency among the three fluorophenol isomers will be discussed.

2. Experimental

The molecular beam chamber combined with the linear time of flight (TOF) mass spectrometer used in this work has been previously reported.^3–6 Fluorophenol·(NH₃)_n (1 : n) clusters were generated in a supersonic-jet expansion of a gas mixture of fluorophenol vapor (at room temperature) and NH₃/Ne (0.5%) premixed gas through a pulsed valve (General Valve). The supersonic jet was skimmed (Beam Dynamics skimmer, 2-mm-diameter) before entering the detection chamber. The clusters were excited to the S₁ state by the first laser ν₁. After an appropriate delay (typically 100 ns), the remaining clusters and their reaction products were ionized by the ionization laser ν₂. The generated ions were accelerated and extracted into in the TOF mass spectrometer and detected by an Even-cup detector.¹³ The signal was integrated by a digital boxcar integrator after amplification by a preamplifier (NF BX-31A), and was recorded by a personal computer. The output of a dye laser (Lumonics: HD-500) pumped by the 355 nm radiation of a Nd³⁺:YAG laser (Spectra Physics: GCR-170) was frequency-doubled in a KDP crystal (Inrad: AUTO TRACKER III) and used as the first laser light ν₁ to excite the clusters to S₁. The ionization laser ν₂ was the third harmonic (355 nm) of a Nd³⁺:YAG laser (Spectra Physics: INDI-40) or the frequency-doubled output (310 nm) of a dye laser pumped by the second harmonics of the Nd³⁺:YAG laser (HOYA Continuum, PowerLite 8010). The samples were purchased from Tokyo Kasei and used after purification by vacuum sublimation (p-fluorophenol) or vacuum distillation (o- and m-fluorophenol).

3. Theoretical calculation

All calculations have been performed with the Turbomole program package.¹⁴ The starting geometries for the cluster isomers have been selected in analogy with previous calculations performed for phenol·(NH₃)_n clusters.⁶ For fluorophenol clusters with one and two ammonia molecules, ground state geometry optimization and frequency calculations were performed with the RIDFT method implemented in Turbomole (resolution-of-the-identity approximation with the BP86 functional) with the triple-zeta valence plus polarization (TZVP) basis sets, in order to estimate the low frequency intermolecular vibrations. For the o-fluorophenol·ammonia complex, the ground state frequencies have also been calculated with the B3LYP functional and at the SCF/MP2 level, still with the TZVP basis set. The frequencies calculated with the three different methods are compared in Table 1. Since the vibrational frequencies obtained with the different methods are in reasonable agreement, the frequency calculations for other 1 ∶ 1 and 1 ∶ 2 clusters have been performed with the fastest RIDFT/TZVP method.

Table 1 Ground state frequencies (in cm⁻¹) of the o-fluorophenol·ammonia (1 ∶ 1) cluster calculated with different methods

RIDFT (B-P86)/TZVP	DFT (B3-LYP)/TZVP	SCF/RI-MP2/TZVP
23	26	29	Out of plane bending
55	46	78	NH3 torsion around H⋯N axis
110	119	101	In plane bending
197	187	188	Stretching OH⋯N
289	274	274	Wagging
298	308	300	Rocking (in plane)

---

4. Results and discussion

4.1 Mass-spectrum

Fig. 1 shows the mass spectrum of p-fluorophenol·(NH₃)_n clusters obtained by delaying the ionization laser by 5 ns (Fig. 1a) and 100 ns (Fig. 1b) after the excitation to S₁, the exciting laser ν₁ and the ionization laser ν₂ are fixed to 285 nm and 310 nm, respectively. The mass spectrum at 5 ns delay shows the peaks of the p-fluorophenol·(NH₃)_n cations (1 : n) (n = 0–4) and NH₄(NH₃)_n−1⁺ (n = 2–5) clusters. At long delays (Fig. 1b), the p-fluorophenol·(NH₃)_n mass peaks become very weak while the NH₄(NH₃)_n−1 peaks remain as intense as for short delays. The decrease of the p-fluorophenol·(NH₃)_n clusters ion signal is expected since the typical lifetime of excited phenol and derivatives is no more than a few nanoseconds. Thus the decay of the signal can be understood as the decay of S₁. In contrast, the stable signal of NH₄(NH₃)_n−1⁺ at long delay suggests that these ions are not generated from the p-fluorophenol·(NH₃)_n cations, but from long-lived species originating from S₁. The same phenomenon, NH₄(NH₃)_n−1⁺ surviving for long delays between excitation and ionization, has been found in phenol·(NH₃)_n clusters where the long-lived species have been shown to be neutral NH₄(NH₃)_n−1 radicals generated by an excited state hydrogen transfer (ESHT) reaction in S₁. Likewise, we conclude that an ESHT reaction also occurs in p-fluorophenol·(NH₃)_n clusters, leading to long-lived NH₄(NH₃)_n−1 radicals ionized with laser ν₂ at 310 nm. The same NH₄(NH₃)_n−1⁺ are also observed when o- and m-fluorophenol·(NH₃)_n clusters are excited to S₁. Thus ESHT reactions occur in the excited state of o-, m- and p-fluorophenol clustered with ammonia.

Fig. 1 Mass-spectrum of p-fluorophenol·(NH₃)_n clusters obtained by introducing the ionization laser ν₂ with (a) 5 ns and (b) 100 ns delay after the excitation to S₁. The exciting laser ν₁ and the ionization laser ν₂ are fixed to 285 nm and 310 nm, respectively. NH₄(NH₃)_n−1 radicals are known to be much more stable than free NH₄²⁶ and their lifetimes have been measured by Fuke et al. to be 3 μs and 7 μs for n = 2 and 3, respectively whereas NH₄ is a very short-lived species (15 ps).^26–28 The ionization potentials for NH₄(NH₃)_n−1 clusters decrease from 3.88 eV for n = 2, 3.31 eV for n = 3, to 2.97 eV for n = 4,^27,28 so they can be ionized with 310 nm photons (4 eV).

4.2 Calculated geometry and vibrations

The fluorophenol·NH₃ (1 : 1) complexes all adopt a near planar geometry in the ground state, with the ammonia hydrogen bonded to the hydrogen of the hydroxyl group, like in the phenol-ammonia complex. The lowest ground state intermolecular vibrations (RIDFT/TZVP) in the (1 : 1) clusters are all very similar as can be seen in Table 2. The calculation gives the frequency of out-of-plane bending mode around 20–30 cm⁻¹. The torsional motion of the ammonia molecule is the second lowest vibration with a frequency around 50–60 cm⁻¹.

Table 2 Calculated frequency of low-frequency intermolecular vibrations in o-, m-cis-, m-trans- and p-fluorophenol·ammonia (1 : 1) clusters in the ground state

Species	Out of plane bending	Torsion of NH3 about the H⋯N axis	In plane bending	OH⋯N stretching
a cis-conformation.
o-fluorophenol/NH3^a	22	55	110	197
p-fluorophenol/NH3	26	58	64	191
m-cis-fluorophenol/NH3	36	59	66	195
m-trans-fluorophenol/NH3	28	49	67	186

---

For (1 : 2) clusters, as in phenol, two close geometries are found, a cyclic H⋯NH₃⋯NH₃⋯O structure and an open structure where the ammonia dimer is out of plane.^6,15 For p-fluorophenol·(NH₃)₂ clusters, the geometries are very similar to those found for phenol·(NH₃)₂, and the cyclic isomer is slightly lower in energy (170 cm⁻¹). The ground state vibrational frequencies are not very different for the two isomers and will not enable their discrimination.

The cyclic and open structures are shown in Fig. 2a in the case of the m-fluorophenol·(NH₃)₂ (1 : 2) clusters. Since for the bare m-fluorophenol molecule, the trans- and cis-isomers are present in the jet, four structures have been calculated for the 1 : 2 clusters and their energies are all within 150 cm⁻¹. The cyclic structures are very similar for the cis- and trans-isomers, but in the open structure the second ammonia molecule gets much closer to the fluorine atom in the cis-isomer. The calculated low frequencies vibrational modes are listed in Table 3. In any conformation, the butterfly motion is the lowest frequency, followed by the waging and in-plane bending. Stretching vibrations are found around 190 cm⁻¹ (between the two ammonia molecules) and 220 cm⁻¹ (between the hydroxyl and the closest NH₃ molecule).

Fig. 2 Calculated geometries for the different isomers of the (a) m-, (b) o- and p-fluorophenol·(NH₃)₂ (1 : 2) cluster.

Table 3 Low vibrational frequencies calculated in the meta and para-fluorophenol·ammonia (1 : 2) clusters ( cm⁻¹)

	m-Fluorophenol cis isomer		m-Fluorophenol trans isomer		p-Fluorophenol
Vibrational mode	Cyclic	Open	Cyclic	Open	Cyclic	Open
a Ammonia 1 is the ammonia molecule linked to the hydroxyl group, ammonia 2 is linked to ammonia 1.
Butterfly motion	9	17	8	24	6	22
Wagging	44	27	33	34	37	29
In plane bend for cyclic isomer/	46		47		46
bending for the open isomer		55		62		77
Stretching of the ammonia dimer versus ring/	83		89		89
wagging (NH3)2 and fluorophenol		82		83		60
Torsion of ammonia 2^a	132	70	131	100	124	89
Out of plane fluorophenol deformation	197	199	200	187	147	147
Stretching ammonia 1..and ammonia 2^a	196	192	195	195	193	194
Coupled torsion of the 2 ammonia molecules	206	212	202	216	215	212
Stretching of OH…ammonia 1	223	223	213	219	218	221

---

The geometries found for o-fluorophenol·(NH₃)₂ (1 : 2) clusters are slightly different: in the cyclic geometry, the H⋯NH₃⋯NH₃⋯O moiety is in a plane that makes a 50° angle with the fluorophenol plane, whereas the m and p-fluorophenol·(NH₃)₂ (1 : 2) clusters are quasiplanar; in the open geometry, the second ammonia molecule interacts with the fluorine atom and is thus farther from the aromatic ring (Fig. 2b).

4.3 REMPI and action spectra of p-fluorophenol·(NH₃)_n clusters

The two-color action spectra of o-, m- and p-fluorophenol·(NH₃)_n cluster have been measured by monitoring the NH₄(NH₃)_n−1⁺ ion signal which is the photoionization signature of the ESHT reaction product NH₄(NH₃)_n−1. The (1 + 1′) resonant enhanced multiphoton ionization (REMPI) spectra were also recorded by monitoring the p-fluorophenol·(NH₃)_n parent ion signal. Fig. 3a and b show mass-selected (1 + 1′) REMPI spectra of p-fluorophenol·ammonia (1 : 1) and (1 : 2) clusters. For convenience, the REMPI spectrum obtained by monitoring the p-fluorophenol·(NH₃)_n ion is indicated in the figure as para (1 : n), while the action spectrum obtained by monitoring NH₄(NH₃)_n−1 are indicated as para (0∶n). The (1 : 1) cluster shows well-resolved vibronic structures, while no signal was found for the (1 : 2) cluster. On the other hand, the action spectra of p-fluorophenol·(NH₃)_n obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 2–4) exhibit clear and well-resolved spectra (Fig. 3c–e). Each action spectrum obtained by monitoring NH₄(NH₃)_n−1⁺ shows different spectral features and reflects the vibronic structures of S₁ for the corresponding p-fluorophenol·(NH₃)_n (1 : n) cluster.

Fig. 3 Mass-selected (1 + 1′) REMPI spectra of p-fluorophenol·(NH₃)_n for (a) the (1 : 1) and (b) the (1 : 2) clusters. The ionization laser ν₂ was fixed to 310 nm for both measurements. The action spectra of p-fluorophenol·(NH₃)_n obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 2–4) are shown in c–e, respectively. For n = 2, ν₂ was fixed to 310 nm (4 eV), while for n = 3,4, it was 355 nm (3.5 eV) because of the NH₄(NH₃)_n−1 ionization potential.^27,28 The delay between the excitation laser ν₁ and the ionization laser ν₂ was 5 ns for the REMPI measurements and 100 ns for the action spectra.

For the p-fluorophenol·ammonia (1 : 1) cluster (Fig. 3a), the lowest-frequency peak at 34 382 cm⁻¹ is assigned to the S₁ origin. The band at 430 cm⁻¹ from the origin is assigned to the first quantum of the intramolecular vibrational mode 6a (6a¹) in S₁ from comparison with the free p-fluorophenol.¹⁶ These two bands are associated with a low frequency band of 186 cm⁻¹, assigned to the intermolecular stretching vibration σ between p-fluorophenol and ammonia, calculated at 191 cm⁻¹ in the ground state (Table 2). In the (0 : 2) action spectrum obtained by monitoring NH₄(NH₃)⁺ (Fig. 3c), low-frequency progressions with spacing of 18 ∼ 20 cm⁻¹ are observed all over the investigated spectral range. The calculations suggest that the low-frequency vibration is an out of plane motion of the ammonia molecules with respect to the fluorophenol ring (butterfly motion, Table 3). The lowest member of the most red progression at 34 189 cm⁻¹ is assigned to the S₁ origin. Similarly, the bands at 34 604 and 34 996 cm⁻¹, located 415 and 807 cm⁻¹ above the origin are assigned to 6a¹ and 1¹ intramolecular vibrations. The correspondence to the vibronic structure of the (1 ∶ 1) cluster are indicated by broken lines. The bands at 34 400 and 34 817 cm⁻¹, i.e. 210 cm⁻¹ above the origin and 6a¹ bands can be assigned to the intermolecular stretching σ¹ and its combination band with 6a¹ (6a¹σ¹), in analogy with the ground state stretching frequency between the OH group and the first ammonia calculated at 219 and 221 cm⁻¹ in the cyclic and open isomers, respectively.

The vibronic structure of the (0 ∶ 3) action spectrum obtained by monitoring the NH₄(NH₃)₂⁺ product ion also shows low-frequency progressions in the higher frequency side, though the structure is not clear in the lower region (see Fig. 3d). The progression with 15 cm⁻¹ spacing starting around 34 939 cm⁻¹ is assigned to the S₁(1¹) transition of the (1 : 3) cluster and the weak bands having 15 cm⁻¹ interval around 34 610 cm⁻¹ are assigned to a progression built on the 6a¹ in analogy to the (0 : 2) action spectrum. The (0 ∶ 4) action spectrum obtained by monitoring NH₄(NH₃)₃⁺ presents long harmonic progressions of 14 cm⁻¹ spacing at 34 160, 34 580 and 34 985 cm⁻¹ as shown in Fig. 3e. Those bands are assigned to the S₁ origin, 6a¹ and 1¹ transitions of the corresponding (1 ∶ 4) cluster. We tentatively assigned the low frequency vibrations in (0 ∶ 3) and (0 ∶ 4) action spectra to the butterfly motions (out of plane bending motions).

4.4 REMPI and action spectra of m-fluorophenol·(NH₃)_n clusters

It has been known that m-fluorophenol and its hydrogen-bonded clusters have cis- and trans-isomers according to the orientation of OH group.^17–19 The hydrogen-bonded clusters with ammonia can also be expected to have cis- and trans-isomers. Fig. 4a shows the mass-selected REMPI spectrum of m-fluorophenol·ammonia (1 : 1) cluster where the two sharp peaks at 36 045 and 36 277 cm⁻¹ are assigned to the origins of cis- and trans- isomers, respectively. The red-shifts from the origin of free cis- and trans-m-fluorophenol are 578 and 553 cm⁻¹, respectively. The larger red-shift of the cis-(1 : 1) cluster suggests an effect of the position of the fluorine substituent on the intermolecular interaction. The ground state calculations indicate that the complex with the cis-isomer has a slightly lower energy than the complex with the trans-isomer (50 cm⁻¹). This is an indication of a different stabilization interaction in the cis (1 : 1) and trans (1 : 1) isomers.

Fig. 4 Mass-selected (1 + 1′) REMPI spectra of m-fluorophenol·(NH₃)_n for (a) the (1 : 1) and (b) the (1 : 2) clusters. The ionization laser ν₂ was fixed to 310 nm for both measurements. The action spectra of m-fluorophenol·(NH₃)_n obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 2–4) are shown in c–e, respectively. ν₂ was fixed at 310 nm for n = 2, and at 355 nm for n = 3 and 4. The delay between the excitation laser ν₁ and the ionization laser ν₂ was 5 ns for the REMPI measurements and 100 ns for the action spectra.

The S₁–S₀ transition of the (1 : 2) cluster has been measured by both mass-selected REMPI spectrum (Fig. 4b, indicated as meta (1 : 2)) and action spectrum obtained by monitoring NH₄NH₃⁺ (Fig. 4c, meta (0 : 2)). The REMPI spectrum shows sharp peaks on a broad background signal in the low frequency region from 35 800 to 36 200 cm⁻¹, but no clear peak is found in the region above 36 400 cm⁻¹. In contrast, the action spectrum shows clear and sharp peaks up to 36 700 cm⁻¹. The peak positions in the low frequency region coincide in both spectra, thus this difference suggests that the ESHT reaction is accelerated when the excess energy in S₁ increases.

Two low-frequency progressions of 12 and 13 cm⁻¹ spacing start at 35 819 cm⁻¹. The band at 35 819 cm⁻¹ is assigned to the origin of the cis-(1 : 2) cluster. The calculated vibrations for the cis-isomer in the ground state (cyclic or open) indicate that the low frequencies correspond to the bending motions of the ammonia molecules out of the plane defined by the aromatic ring (9 and 44 cm⁻¹ for the cyclic isomer, 17 and 27 cm⁻¹ for the open isomer, respectively).

A progression of 17 cm⁻¹ interval is found at around 36 100 cm⁻¹, and the lowest member at 36 108 cm⁻¹ is assigned to the trans-(1 : 2) cluster. This low frequency vibration is assigned to out of plane bending of the ammonia molecules (24 cm⁻¹ calculated for the open isomer, 8 cm⁻¹ for the cyclic one in S₀).

The progressions around 36 600 cm⁻¹ have intervals similar to those of the cis-isomer and are assigned to the 1¹ vibronic band of the cis-isomer. The red-shifts of the cis- and trans-(1 : 2) clusters are 226 and 169 cm⁻¹ from the cis- and trans-(1 : 1) clusters. As in the (1 : 1) clusters, the red-shift is larger for the cis-(1 : 2) isomer than for the trans-isomer. It may be due to an ammonia-fluorine interaction in the excited state of the cis-isomer since in the case of an open structure, the second ammonia molecule is closer to the fluorine atom.

Fig. 4d and 4e shows the action spectra obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 3 and 4), which are denoted as meta (0 : 3) and meta (0 : 4). Sharp structures are found in the action spectrum of meta (0 : 3), and the lowest band at 35 892 cm⁻¹ is assigned to the S₁ origin of the cis-(1 : 3) cluster. As for the cis-(1 : 2) cluster, two low-frequency progressions are found around the origin, and will be assigned to similar vibrational modes, out of plane bendings of the ammonia molecules. A short progression with 10 cm⁻¹ interval is found at around 36 100 cm⁻¹, and the lowest member at 36 118 cm⁻¹ is assigned to the origin of the trans-(1 : 3) cluster. The progression at ∼36 600 cm⁻¹ is considered to be built on the 1¹ vibronic band of the cis-(1 : 3) cluster. The action spectrum of meta (0 : 4) is broad with a maximum at 36 060 cm⁻¹. No evidence is found for the co-existence of isomers. The large ammonia cluster of four molecules may cause a stronger steric hindrance, and one of the isomer may not be stable enough to exist under this experimental condition.

4.5 REMPI and action spectra of o-fluorophenol·(NH₃)_n clusters

Fig. 5a shows the mass-selected REMPI spectrum of the o-fluorophenol·NH₃ (1 : 1) cluster that presents well-resolved vibronic structure, and the lowest band at 36 192 cm⁻¹ is assigned to the S₁ origin. Two progressions arise from the origin. One is a short progression with 40 cm⁻¹ interval. The second is a long anharmonic progression with an interval increasing in higher vibrational state from 30 to 42 cm⁻¹. This increasing spacing suggests that this progression originates from an internal rotational motion, rather than simple low frequency vibration. The quantum chemical calculation for the o-fluorophenol·NH₃ cluster in S₀ gives two vibrational modes lower than 60 cm⁻¹ in the ground state. One is the out-of-plane bending vibration between ammonia and o-fluorophenol molecules (22 cm⁻¹, see Table 2) and the other is the torsion (or pseudo-rotation) of the ammonia molecule around the hydrogen-bonding, which is calculated as 55 cm⁻¹. We have assigned the long anharmonic progression to the pseudo-rotation and the short progression of 40 cm⁻¹ to the out-of-plane bending.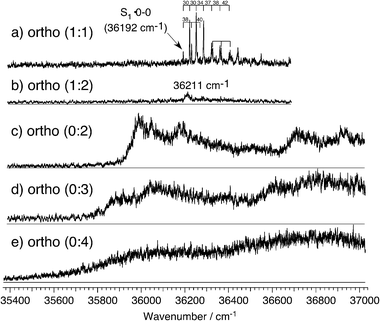

Fig. 5 Mass-selected (1 + 1′) REMPI spectra of o-fluorophenol·(NH₃)_n for (a) the (1 : 1) and (b) the (1 : 2) clusters. The ionization laser ν₂ was fixed to 310 nm for both measurements. The action spectra of o-fluorophenol·(NH₃)_n obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 2–4) are shown in c–e, respectively. ν₂ was fixed at 310 nm for n = 2, and at 355 nm for n = 3 and 4. The delay between the excitation laser ν₁ and the ionization laser ν₂ was 5 ns for the REMPI measurements and 100 ns for the action spectra.

To confirm the assignment of the anharmonic progression, the observed vibrational levels can be analyzed by a one-dimensional internal rotational motion. This model has been successfully applied to various internal rotational motions.^20–23 The potential curve for internal rotation is described by the following function,

where φ is the torsional angle between the ammonia molecule and the fluorophenol plane, and the higher terms n ≥ 3 are neglected. The Hamiltonian is expressed bywhere B is the reduced internal rotational constant of the ammonia rotor around the O–H⋯N top axis. The eigenvalues of the Hamiltonian can be obtained by a basis set of one dimensional free rotor wavefunctions, cos(mφ) and sin(mφ).²⁴ Two-hundred basis functions were used for the calculation, and three parameters, i.e. B, V₃, and V₆, are determined by least square fitting. The best fit was obtained when B = 5.06 ± 0.28 cm⁻¹, V₃ = 55 ± 12 cm⁻¹, and V₆ = −7 ± 3 cm⁻¹ when the two last levels (6a₁ and 7e) are left out of the least square fitting. The calculated energy level positions are compared to the observed frequencies in Table 4. The observed level frequencies are mostly reproduced by the calculation except for the higher 6a₁ and 7e levels. This disagreement for the 6a₁ and 7e levels may be due to level perturbations, in particular to levels associated with the short 40 cm⁻¹ progression starting repeated 134 cm⁻¹ above the origin (see Fig. 5a). The agreement between model and experiment leads to the conclusion that the anharmonic progression in the (1 : 1) cluster is due to the internal rotation of the ammonia molecule. The internal rotation of a hydrogen-bonded ammonia molecule has been reported for 1-naphthol·ammonia cluster.²⁵ The similar barrier height (46.5 cm⁻¹) also support the assignments.

Table 4 Observed and calculated frequencies of the internal rotational bands in o-fluorophenol·ammonia (1 : 1) cluster

Assignments	Observed	Calculated^a
a B = 5.06 cm^−1, V3 = 55 cm^−1, V6 = −7 cm^−1. b S1 origin observed at 36 192 cm^−1.
0a1	0^b	0
1e	0	2.3
2e	30	33
3a1	60	60
4e	94	90
5e	131	134
6a1	169	190
7e	211	255

---

The internal rotational motion has not been observed in m- and p-fluorophenol·ammonia (1 : 1) clusters, though the same internal rotation of ammonia is possible in these clusters. It suggests that the internal rotational potential curve is not changed much by the electronic excitation in m- and p-fluorophenol·ammonia (1 : 1) clusters. In both clusters, the ammonia molecule is located far from the fluorine atom, no strong interaction is expected, and the ammonia molecule should be a nearly free rotor, regardless of the electronic excitation. In contrast, in the o-fluorophenol·ammonia (1 : 1) cluster, the ammonia molecule is just beside the fluorine substituent and a cyclic hydrogen-bond among –OH⋯N–H⋯F– is expected in the quantum chemical calculation. Such interaction will prevent the ammonia rotation and this validates the one-dimensional rotor analysis with three- and six-fold barriers. This hindrance will be changed drastically by the electronic excitation thus the potential curve for the ammonia rotation can also be changed by the electronic excitation. Therefore the appearance of the ammonia rotational levels suggests the existence of a ammonia-fluorine interaction and its change upon electronic excitation.

The REMPI spectrum obtained by monitoring the ion signal of the o-fluorophenol·(NH₃)₂ (1 : 2) cluster shows no signal except for a small broad band at 36 211 cm⁻¹ (see Fig. 5b), lying slightly higher in energy than the origin of the (1 : 1) cluster. It is difficult to believe that the larger hydrogen-bonded cluster gives a blue-shift of the origin. At the present time, we have no good explanation for this peak but it should not be assigned to the o-fluorophenol·(NH₃)₂ cluster. On the other hand, the action spectrum obtained by monitoring NH₄(NH₃)⁺ (ortho (0 : 2)) presents broad features in the region lower than the origin of the (1 : 1) cluster (Fig. 5c). We assigned this spectrum to the o-fluorophenol·(NH₃)₂ cluster and the broad peak at 35 990 cm⁻¹ is assigned to the S₁ origin. Broadened peaks are observed at 55, 190, 730 and 920 cm⁻¹ above the origin, and are tentatively assigned to intermolecular bending, intermolecular stretching σ¹, intramolecular 1¹ and 1¹σ¹ combination band, respectively.

The action spectra obtained by monitoring NH₄(NH₃)_n−1⁺ (n = 3 and 4), denoted ortho (0 : 3) and ortho (0 : 4), are also broad, as shown in Fig. 5d and 5e. The onset of the broad signal is red-shifted in both spectra from the spectrum of the (1 : 2) cluster. In the p-fluorophenol·(NH₃)_n clusters, sharp vibronic structures are observed not only in the small clusters but also in the larger (1 : 3) and (1 : 4) clusters. For the m-fluorophenol·(NH₃)_n clusters, the (1 : 4) cluster presents a broadened spectrum but smaller clusters exhibit sharp vibronic structures. The spectral broadening may be related with the excited state hydrogen transfer reaction rate, suggesting that it is faster in o-fluorophenol·(NH₃)_n clusters.

4.6 Fluorination effect on ESHT and its dependence on the substituent position

We have shown that excited o-, m- and p-fluorophenol clustered with ammonia undergo an hydrogen transfer (ESHT) reaction from the fluorophenol to the ammonia cluster. The fluorine substituent has an induction effect on the σ orbital, that may perturb the ESHT reaction rate by changing the energy of the πσ* state, which promotes the ESHT through a conical intersection with the ππ* state. Here, we will discuss qualitative changes of the ESHT reaction by comparing the REMPI and action spectra in the three fluorophenol·(NH₃)₂ (1 : 2) clusters. The REMPI spectrum of m-fluorophenol·(NH₃)₂ shows the same peaks as those in the (0 : 2) action spectrum obtained by monitoring NH₄NH₃⁺. It means that the ESHT reaction rate is comparable to the ionization rate, which is determined by the ionization cross-section from S₁ and the photon density of the ionization laser. In contrast, the REMPI spectra monitoring the o- and p-fluorophenol·(NH₃)₂ cluster ions did not show the vibronic structures of the cluster, which can be interpreted as a faster rate for ESHT than for ionization. We used the same intensity for the ionization laser, so the photon density is roughly the same in all the measurements. Thus, if we assume that the ionization cross sections are the same for the three fluorophenol·(NH₃)_n clusters, ESHT in m-fluorophenol·(NH₃)_n is thought to be the slowest. The action spectra of m- and p-fluorophenol·(NH₃)_n show sharp vibronic structures, while that of o-fluorophenol·(NH₃)_n is broad. If the broadening is due to ESHT, the reaction rate in o-fluorophenol·(NH₃)_n is faster than that in p-fluorophenol·(NH₃)_n clusters. Therefore, we roughly estimate that the ESHT reaction between excited fluorophenol and ammonia clusters becomes faster in the order meta-, para- and ortho-.

5. Conclusion

Two-color (1 + 1′) REMPI mass spectra of o-, m- and p-fluorophenol·ammonia (1 : n) clusters were measured with a long delay time between the two lasers. The generation of a long-lived species via S₁ was assessed by the observation of NH₄(NH₃)_n−1⁺ with a 100 ns delay after exciting the S₁ state. As in the case of phenol·ammonia clusters, excitation to S₁ induces an excited state hydrogen transfer reaction from the o-, m- and p-fluorophenol molecule to the ammonia clusters. The S₁–S₀ transition of o-, m- and p-fluorophenol·ammonia (1 : 1) clusters were measured by the (1 + 1′) REMPI spectra, while larger (1 : n) cluster (n = 2–4) were observed by action spectra that monitor the ionized reaction products NH₄(NH₃)_n−1⁺. The vibronic spectra observed in m- and p-fluorophenol·ammonia (1 : 1) clusters are tentatively assigned on the basis of vibrational calculations in the ground state. The o-fluorophenol·NH₃ (1 : 1) cluster shows an anharmonic progression that is analyzed in terms of one-dimensional rotational motion of the ammonia molecule. The interaction between the ammonia and the fluorine atom, and its change upon electronic excitation are suggested. The broad action spectra of the o-fluorophenol·ammonia (1 ∶ n) clusters (n ≧ 2) suggest the excited state hydrogen transfer is faster than in m- and p-fluorophenol·ammonia clusters. To obtain more details on the changes in ESHT reaction rates, experiments using time-resolved spectroscopy are now in progress. The different reaction rates between o-, m-and p-fluorophenol·ammonia clusters could be due to an effect of the geometry on the electronic states, especially on the πσ* state. Preliminary calculations of the excited state geometries suggest a significant out of plane distortion of the o-fluorophenol·ammonia cluster, which can promote an efficient state mixing between ππ* and πσ* state. Higher level calculations are necessary to understand the different reaction rate of fluorophenols and are now in progress.

Acknowledgements

The authors thank Professor Kenro Hashimoto in Tokyo Metropolitan University, Dr Kota Daigoku in Aoyama University and Dr Pierre Carçabal for valuable discussions and helpful comments. This work has been supported in part by a joint Centre National de la Recherche Scientifique/Japan Society for Promotion of Science bilateral program.

References

1. G. A. Pino, C. Dedonder-Lardeux, G. Grégoire, C. Jouvet, S. Martrenchard and D. Solgadi, J. Chem. Phys., 1999, 111, 10747.
2. G. A. Pino, G. Grégoire, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard and D. Solgadi, Phys. Chem. Chem. Phys., 2000, 2, 893.
3. S. Ishiuchi, M. Saeki, M. Sakai and M. Fujii, Chem. Phys. Lett., 2000, 322, 27.
4. S. Ishiuchi, M. Sakai, K. Daigoku, T. Ueda, T. Yamanaka, K. Hashimoto and M. Fujii, Chem. Phys. Lett., 2001, 347, 87.
5. S. Ishiuchi, K. Daigoku, M. Saeki, M. Sakai, K. Hashimoto and M. Fujii, J. Chem. Phys., 2002, 117, 7077.
6. S. Ishiuchi, K. Daigoku, M. Saeki, M. Sakai, K. Hashimoto and M. Fujii, J. Chem. Phys., 2002, 117, 7083.
7. C. Dedonder-Lardeux, D. Grosswasser, C. Jouvet and S. Martrenchard, PhysChemComm, 2001, 1.
8. O. David, C. Dedonder-Lardeux, C. Jouvet, H. Kang, S. Martrenchard, T. Ebata and A. L. Sobolewski, J. Chem. Phys., 2004, 120, 10101.
9. H. Kang, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, G. Gregoire, C. Desfrancois, J. P. Schermann, M. Barat and J. A. Fayeton, Phys. Chem. Chem. Phys., 2004, 6, 2628.
10. H. Kang, C. Jouvet, C. Dedonder-Lardeux, S. Martrenchard, G. Gregoire, C. Desfrancois, J. P. Schermann, M. Barat and J. A. Fayeton, Phys. Chem. Chem. Phys., 2005, 7, 394.
11. H. Kang, C. Dedonder-Lardeux, C. Jouvet, G. Gregoire, C. Desfrancois, J. P. Schermann, M. Barat and J. A. Fayeton, J. Phys. Chem. A, 2005, 109, 2417.
12. A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093.
13. D. Bahat, O. Cheshnovsky, U. Even, N. Lavie and Y. Magen, J. Phys. Chem., 1987, 91, 2460.
14. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165.
15. M. Schmitt, C. Jacoby, M. Gerhards, C. Unterberg, W. Roth and K. Kleinermanns, J. Chem. Phys., 2000, 113, 2995.
16. C. Ratzer, M. Nispel and M. Schmitt, Phys. Chem. Chem. Phys., 2003, 5, 812.
17. A. Oikawa, H. Abe, N. Mikami and M. Ito, J. Phys. Chem., 1984, 88, 5180.
18. M. Ito and A. Oikawa, J. Mol. Struct., 1985, 126, 133.
19. A. Oikawa, H. Abe, N. Mikami and M. Ito, Chem. Phys. Lett., 1985, 116, 50.
20. H. Ikoma, K. Takazawa, Y. Emura, S. Ikeda, H. Abe, H. Hayashi and M. Fujii, J. Chem. Phys., 1996, 105, 10201.
21. K. Suzuki, Y. Emura, S. Ishiuchi and M. Fujii, J. Electron Spectrosc. Relat. Phenom., 2000, 108, 13.
22. K. Suzuki, S. Ishiuchi and M. Fujii, Faraday Discuss., 2000, 115, 229.
23. K. Suzuki, S. Ishiuchi, M. Sakai and M. Fujii, J. Electron Spectrosc. Relat. Phenom., 2005, 142, 215.
24. J. P. Lewis and J. Laane, J. Mol. Struct., 1972, 12, 427.
25. S. J. Humphrey and D. W. Pratt, J. Chem. Phys., 1996, 104, 8332.
26. G. I. Gellene and R. F. Porter, J. Phys. Chem., 1984, 88, 6680.
27. K. Fuke, R. Takasu and F. Misaizu, Chem. Phys. Lett., 1994, 229, 597.
28. K. Fuke and R. Takasu, Bull. Chem. Soc. Jpn., 1995, 68, 3309.

---