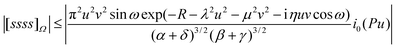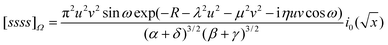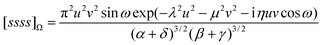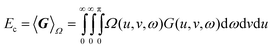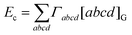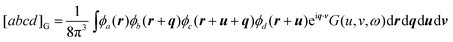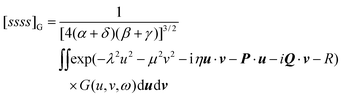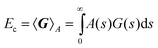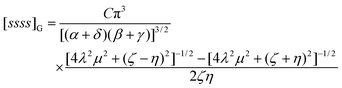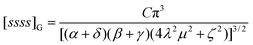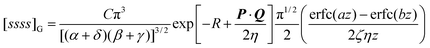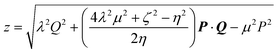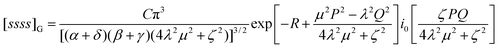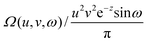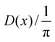DOI:
10.1039/B511472A
(Invited Article)
Phys. Chem. Chem. Phys., 2006,
8, 15-25
A family of intracules, a conjecture and the electron correlation problem
Received
11th August 2005
, Accepted 8th September 2005
First published on 22nd September 2005
Abstract
We present a radical approach to the calculation of electron correlation energies. Unlike conventional methods based on Hartree–Fock or density functional theory, it is based on the two-electron phase-space information in the Omega intracule, a three-dimensional function derived from the Wigner distribution. Our formula for the correlation energy is isomorphic to the Hartree–Fock energy expression but requires a new type of four-index integral. Preliminary results, obtained using a model that is based on the known correlation energies of small atoms, are encouraging.
1. Introduction
Coulomb’s Law seems straightforward: particles of the same charge repel; opposites attract. But the deceptive simplicity of inverse-square laws yields surprising complexity even in very small systems. The classical three-body problem defeated the brightest minds of the 19th century and the quantum analogue proved equally resistant in the 20th. In the helium atom, for example, the two electrons dodge and weave as they seek to remain close to the nucleus but far from each other and, despite 80 years of work, an exact mathematical description of their motion still remains undiscovered.
Although an exact solution to the electronic Schrödinger equation1 appears unlikely, the development of effective approximations brings rich rewards since the ability to calculate molecular energies accurately allows the ab initio determination of structure, bonding and reactivity and has ramifications within biochemistry, materials science and medicine.
In the early days of quantum theory, Hartree introduced the orbital approximation2 wherein each electron is assumed to move independently in the mean field of all others and this was subsequently modified by Fock3 to accommodate the requirements of the Pauli principle. Though the Hartree–Fock (HF) model is simpler than the Schrödinger formulation, the associated integro-differential equations are still difficult to solve in polyatomic systems. However, if the orbitals are expanded in a finite basis set, the more tractable Roothaan–Hall eigenvalue equations emerge4,5 and intensive efforts over the last thirty years have led to algorithms6 for these whose computational cost grows only linearly with the size of the molecular system. Using such methods and a standard PC, one can now perform a finite-basis HF calculation on a system with a few hundred atoms in a few hours.7
HF theory often yields fairly accurate predictions of molecular structure but it is less satisfactory for most other properties. In particular, its mean-field treatment of electron motion cannot account properly for the formation of an electron pair during bond formation and it is therefore usually necessary to go beyond the HF model and explicitly include the fact that the motions of the electrons are correlated. Allowing the electrons to avoid one another stabilizes the system and the difference between its exact many-body energy and its HF energy is known8 as the correlation energy Ec. The task of calculating it is known as “the correlation problem” and has been the single greatest challenge to the progress of quantum chemistry since the subject’s inception in 1927.
Models of electron correlation fall into two broad classes. Those in the first class, which include configuration interaction, Møller–Plesset perturbation theory and coupled cluster theory,9 are based on the mathematical observation that an improved wavefunction can be formed by linearly combining eigenfunctions of the HF Hamiltonian. Although in the limit these methods provide exact results, they are intrinsically inefficient because they have to approximate the derivative discontinuities in the exact wavefunction10 by sums of smooth functions. As a consequence, their computational costs become prohibitive even for quite small systems. This is the price that one pays for using a mathematically, rather than physically, motivated model.
The second class of models comprise the density-functional theories (DFT) and are based on the Hohenberg–Kohn theorem11 which states that the exact energy of the ground state of a system is a unique functional of the exact electron density ρ(r). Because ρ(r) is a much simpler object than the wavefunction, DFT calculations are relatively inexpensive and have become the most popular tools in quantum chemistry. However, although the existence of the unique Hohenberg–Kohn functional is proven, its form is unknown and the search for useful surrogates continues and has become increasingly empirical in recent years.12 Many functionals are now available, each with its own strengths and weaknesses, but none entirely satisfactory. Moreover, it appears unlikely that one-electron DFT models will ever be able to treat intrinsically two-electron phenomena such as dispersion energies.13
Although the pursuit of more accurate functionals is unlikely to cease for some time, it is worth pausing to ask whether ρ(r) is really the best starting point for calculations of electron correlation. After all, ρ(r) measures the probability of finding one electron at the point r and yet electron correlation is concerned with the stabilization achieved when two electrons manage to avoid each other. Isn’t it more natural, as Hylleraas emphasized when he used a wavefunction for the helium atom that explicitly includes the interelectronic distance,14 to base an electron correlation model on the two-electron density? The answer is that, although this is certainly an attractive idea, a mechanism must be found by which two-electron information can be included without significantly degrading the computational advantages enjoyed by DFT. This has proven to be a major challenge.
If it is agreed that information about pairs of electrons is useful for understanding electron correlation, one must then ask which property of the two electrons should be included and how this is best incorporated. The most obvious candidate is the interelectronic distance u
=
|r1
−
r2| for one instinctively expects electrons that are close together to be strongly correlated. However, the naïveté of this expectation becomes clear when one considers the sequence of ground-state helium-like ions H−, He, Li+, …, whose exact and HF energies are known15,16 to be
| | 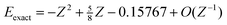 | (1.1) |
| | 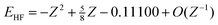 | (1.2) |
where
Z is the nuclear charge of the ion. It follows from these that
Ec
=
−0.04667 +
O(
Z−1) and the correlation energy therefore tends toward a constant as the nuclear charge increases. Thus, for example, although the two electrons in the U
90+ ion are generally much closer together than those in the Ne
8+ ion, the resulting correlation energies are almost equal. This counterintuitive discovery clearly reveals the insufficiency of
u as a correlation
indicator.
A few years ago, Rassolov argued17 that not only the separation u, but also the relative momentum v
=
|p1
−
p2|, of two electrons influence the extent of their correlation. Rassolov’s insight immediately explains the similarity in the correlation energies of the helium-like ions: as Z increases, the mean separation 〈u〉 decreases as 1/Z, but the mean relative momentum 〈v〉 grows as Z and, evidently, these two effects cancel rather precisely. On this basis, we speculate that the variable s
=
uv may be a useful correlation indicator and, more generally, we are led to consider models that make use of both position and momentum information.
However, although a simple Fourier transform allows us to interconvert the position-space wavefunction Ψ(r1,…,rn) and momentum-space wavefunction Φ(p1,…,pn) of an n-electron system, a basic tenet of quantum mechanics forbids the construction of a joint position–momentum wavefunction. This intrinsic limitation is intimately connected with the Heisenberg uncertainty principle and is one of the key features that distinguishes classical mechanics from its quantum successor. Likewise, the position-space probability density function |Ψ(r1,…,rn)|2 and its momentum-space analogue |Φ(p1,…,pn)|2 are unproblematic but there is no comparable joint probability density.
One might imagine, therefore, that an electron correlation model based simultaneously in both position and momentum space would be fraught with fundamental difficulties! Nonetheless, in this article, we develop Rassolov’s idea into an approach for estimating the correlation energy in any system. Our starting point is Wigner’s phase-space distribution, from which we derive a number of simpler functions called intracules, which we then use as the foundations for a variety of electron correlation models. We have implemented and tested the simplest of these and present results for a number of atoms and the H2 molecule. Except where otherwise noted, the 6-311G basis set and atomic units are used throughout.
2. Wigner distributions and intracules
2.1. Wigner distribution
Although a quantum mechanical joint position–momentum probability density does not exist, Szilard and Wigner were undeterred by this discouraging news and, in a triumph of mathematics over physics, managed to construct a function| | | Wn(r1,…,rn,p1,…,pn)
=
π−3n∫…∫ψ(r1
+
q1,…,rn
+
qn)*ψ(r1
−
q1, …, rn
−
qn)e2i(p1·q1+…+pn·qn) dq1…dqn | (2.3) |
that behaves, in many ways, as the notional joint probability density should.18 One of its chief weaknesses is that, although it is everywhere real, it is not everywhere positive. Nonetheless, as Wigner wrote, Wn(r1,…,rn,p1,…,pn)
“cannot be really interpreted as the simultaneous probability for coordinates and momenta [but] this must not hinder the use of it in calculations as an auxiliary function which obeys many relations we would expect from such a probability.” Such splendid optimism (in which physics trumps mathematics) will also be our unashamed policy throughout this article.
A distribution that possesses some, but not all, of the mathematical properties required of a probability density is often called a “quasi-probability” density. The Wigner distribution is such an object, and so are most of the intracules discussed below. However, for the sake of brevity, we will usually drop the prefix and use the term “probability” throughout this article. We hope that the reader will tolerate our laxity.
We note in passing that, although it is the oldest, the Wigner distribution is not the only possible phase-space distribution and several others have been developed over the years. We will not consider these alternatives in this article but it is worth pointing out that the Husimi distribution19–22 is everywhere positive and, in a sense, more Heisenberg-friendly. There are two reasons for preferring the Wigner distribution to the Husimi analogue. First, the Husimi distribution contains an adjustable parameter (called κ in ref. 40) but it is not clear how to assign a value to this. Second, the Husimi distribution is somewhat more mathematically complicated than the Wigner one.
2.2. Reduced Wigner distribution W2(r1,r2,p1,p2)
The n-electron Wigner distribution is a complicated function of 6n coordinates (excluding spin) and it is even less intelligible than the 3n-coordinate wavefunctions to which it is equivalent. However, since our interest lies primarily in the behaviour of pairs of electrons, it is sensible to ask whether a two-electron function can be distilled out of the Wigner distribution. The distillation turns out to be easy,23 requiring only an integration over all of the uninteresting variables, and yielding the second-order reduced Wigner distribution| | | W2(r1,r2,p1,p2)
=
∫…∫Wn(r1,…,rn,p1,…,pn) dr3…drn dp3…dpn | (2.4) |
which can be interpreted as the joint probability of the positions and momenta of two electrons in the n-electron system. Unfortunately, this distribution also has many negative regions and has received little attention but the first-order reduced Wigner distribution| | | W1(r, p)
=
∫∫W2(r, r′, p, p′) dr′ dp′ | (2.5) |
has been studied. Following pioneering work by Dahl and Springborg, W1(r,p) has been calculated for a variety of small atoms and molecules.24–30
2.3. Omega intracule Ω(u,v,ω)
The reduced Wigner distribution W2(r1,r2,p1,p2) is a much simpler object than the full Wigner distribution W(r1,…,rn,p1,…,pn) but is nonetheless a function of 12 variables and remains a conceptually formidable entity. Once again, we ask whether it is possible to effect another reduction without losing important information.
A key insight comes from the recognition that the physics of electron correlation depends less on the absolute positions and momenta of two electrons than on their relative position r12
=
r1
−
r2 and relative momentum p12
=
p1
−
p2. Further thought along these lines leads one to suspect that the absolute directions of the vectors r12 and p12 are less important than their magnitudes r12 and p12 but that the dynamical angle θuv between them may be significant. We argue therefore that most of the important information in W2(r1, r2, p1, p2) is captured by the three key variables, r12, p12 and θuv, whose joint probability density is
| | 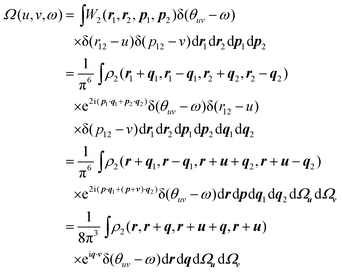 | (2.6) |
where
Ωu and
Ωv are the angular parts of
u and
v, respectively, and
ρ2 is the spinless second-order reduced density
matrix31 or 2-RDM. We call this the Omega intracule.
Choosing u to be the polar axis of v and integrating over Ωv yields
| | 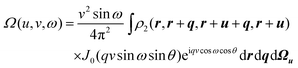 | (2.7) |
(where
J0(
x) is the usual Bessel function) from which it is trivial to prove that
Ω(
u,
v,
ω)
=
Ω(
u,
v,π
−
ω), as required by time-reversal symmetry.
32 Likewise, all of the intracules considered below also inherit this property.
Notwithstanding its questionable credentials, the Omega intracule is a versatile function that often behaves as if it were a proper probability density. For example, if it is constructed from a HF wavefunction, it yields the two-electron energy
| | 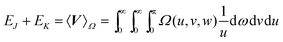 | (2.8) |
and the relative-motion component of the kinetic energy
| | 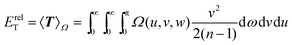 | (2.9) |
(but not the smaller centre-of-mass component
33) as expectation values of the traditional operators. Later in this article, we will speculate that the correlation energy can be written similarly, in terms of an analogous correlation operator
G.
In determinant-based quantum chemical calculations using one-electron basis functions ϕa(r), the spinless second-order density matrix can be written as
| | 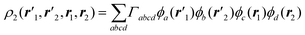 | (2.10) |
where
Γabcd is a two-particle density
matrix element. Thus, we have
| | 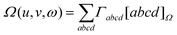 | (2.11) |
where we have introduced the ten-dimensional Omega integral
| | 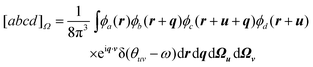 | (2.12) |
These are more difficult than the analogous [
ab|
cd] Coulomb integrals but the usual approach,
34 in which the fundamental [
ssss]
Ω integral is found and differentiated with respect to the coordinates of the Gaussians, remains applicable. We return to this later in this article.
As well as being an interesting function in its own right, Ω(u,v,ω) is the progenitor of a family (Fig. 1) of other intracules of which only two, the Position and Momentum intracules, had been discussed in the literature prior to 2003. The remainder of this section discusses several of the members of this family.
 |
| | Fig. 1 Hierarchical relationships between intracules. | |
2.4. Wigner intracule W(u,v)
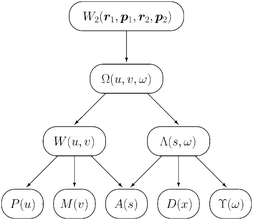
There are several ways in which the Omega intracule can be reduced further. The most obvious is simply to integrate over one of its three arguments. For example, integration over the dynamical angle yields a function| | 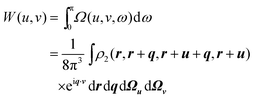 | (2.13) |
that we have previously called the Wigner intracule.35 This can be interpreted as the joint probability density of r12 and p12, without regard to ω. We have shown how W(u,v) can be calculated for Hartree–Fock wavefunctions employing Gaussian basis functions,36 and we have applied this to perform detailed studies of the helium and hookium atoms37,38 (in hookium the electron–electron interaction is Coulombic but the electron–nuclear interactions follow Hooke’s law) and to survey a range of atomic and molecular ground and excited states.36,39
The Wigner intracules of most systems are found to possess small negative regions. This reminds us that they are not bona fide probability densities and it also prompts us to ask whether such negative regions are an essential feature of phase-space distributions. One of us has recently shown40 how to condense the reduced Husimi distribution η2(r1,r2,p1,p2) to the Husimi intracule H(u,v) and has argued that the latter, which is everywhere non-negative, can be interpreted rigorously as a joint probability distribution.
2.5. Lambda intracule Λ(s,ω)
The Omega intracule can also be reduced by combining two of its variables. Since the product s
=
uv appears to be important in the context of electron correlation, it is of interest to combine the u and v coordinates in this way to yield a novel two-dimensional function| | 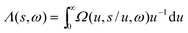 | (2.14) |
that gives the joint probability density of s and ω.
2.6. Position intracule P(u)
The two-dimensional Wigner and Lambda intracules are reduced forms of Ω(u,v,ω) but, as Fig. 1 shows, each can itself be further reduced to yield various one-dimensional intracules. For example, integrating the Wigner intracule over v yields the function| | 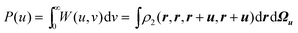 | (2.15) |
that gives the probability density of finding two electrons at a distance u. This was the original intracule and was discussed in the seminal paper by Coulson and Neilson.41 Unlike most of the others discussed in this article, it is a rigorous probability density and has been widely studied; see ref. 35 and 42 and references therein.
2.7. Momentum intracule M(v)
If, instead, the Wigner intracule is integrated over u, one obtains the function| | 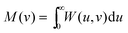 | (2.16) |
that gives the (rigorous) probability density of finding two electrons with relative momentum v. This intracule was introduced by Banyard and Reed43 and has been investigated by a number of researchers, especially Koga; see ref. 35 and 44 and references therein.
2.8. Action intracule A(s)
If the Lambda or Wigner intracule is appropriately integrated, it affords the function| | 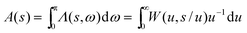 | (2.17) |
that gives the probability distribution of s and which we have called the Action intracule. We have calculated it for HF wavefunctions of the He, Li and Be atoms,35 the Kellner wavefunction of the He-like ions,38 and the exact wavefunctions of the lowest singlet and triplet states of hookium in the high-density limit.45 (The high-density limit is where the Hooke’s law force constant tends to infinity.) In each of these cases, A(s) turns out to be a disarmingly dull unimodal function.
2.9. Dot intracule D(x)
The Lambda intracule can also yield the probability density D(x) of the dot product| | 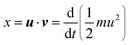 | (2.18) |
which, in a classical picture, gives the rate of change of r212. It is not difficult to show that D(x) is even and that| | 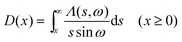 | (2.19) |
2.10. Angle intracule ϒ(ω)
If the Lambda intracule is integrated over s, one obtains the function| | 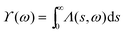 | (2.20) |
that gives the probability density of finding two electrons with dynamical angle ω.
2.11. Omega intracule for n particles in a harmonic well
The Omega intracule of the ground state of n non-interacting fermions in a harmonic well can be found in closed form and it is illuminating to construct it for a few values of n. If n
= 2, both particles occupy the ψ0(x)ψ0(y)ψ0(z) orbital and the wavefunction is| | 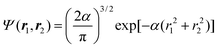 | (2.21) |
We therefore obtain| | 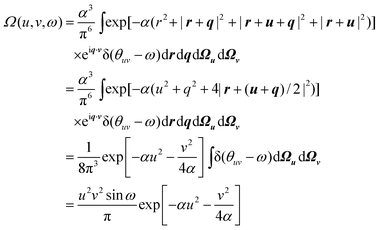 | (2.22) |
This intracule is atypical in two ways: first, it is non-negative everywhere; second, it is a product of a function of u, a function of v and a function of ω implying that, in this system, the three variables are statistically independent.
The Omega intracules for 3 ≤
n
≤ 8 can be found similarly. The ground state is usually degenerate but, in each case, we have chosen the spin multiplicity and configuration that most closely resemble the analogous ground-state atom. Each intracule turns out to be a linear combination of the six normalized integrals
| | 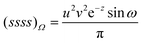 | (2.23) |
| | 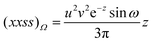 | (2.24) |
| | 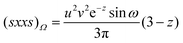 | (2.25) |
| | 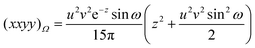 | (2.26) |
| | 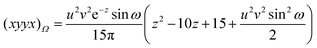 | (2.27) |
| | 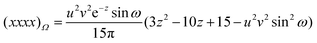 | (2.28) |
where
z
=
αu2
+
ν2/4
α, and the intracules, together with their multiplicities and configurations, are listed in
Table 1. One finds that all share the trivial
ω-dependence found in the
n
= 2 case but this simplicity is peculiar to uncoupled harmonic oscillators. They can be integrated to obtain the lower intracules in
Fig. 1 and some of these are also listed in the Table.
Table 1 Intracules for n fermions in a harmonic well
Such harmonic ensembles are sufficiently simple that all of their intracules and related properties can be found in closed form and yet their intracules are surprisingly similar to those of qualitatively analogous atoms. The n
= 8 case, for example, has an outer shell of six particles in three orbitals and can be viewed as a crude model of the Ne atom. Its Action and Dot intracules, which are plotted in Fig. 2 and 3, are
| | 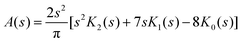 | (2.29) |
| | 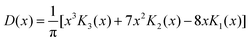 | (2.30) |
where the
Kn are modified Bessel functions of the third kind.
A(
s) is positive for most values of
s and decays exponentially for large
s but is slightly negative for
s
≲ 0.5, reminding us that Action intracules are not proper probability densities.
D(
x) is almost bell-shaped but has a small dip around
x
= 0. These descriptions also apply to the corresponding intracules of the Ne atom which are, of course, much more complicated to compute.
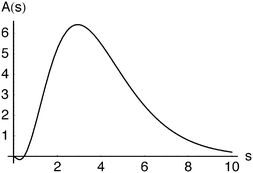 |
| | Fig. 2 Action intracule for eight fermions in a harmonic well. | |
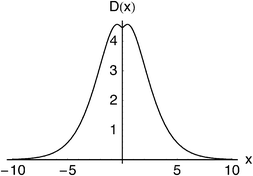 |
| | Fig. 3 Dot intracule for eight fermions in a harmonic well. | |
2.12. Fundamental Omega integral [ssss]Ω
The Omega integral over four s-type Gaussian functions is more difficult. If their centres are {A,B,C,D} and exponents are {α,β,γ,δ}, it is helpful to introduce the scalars| | 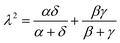 | (2.31) |
| | 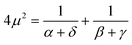 | (2.32) |
| | 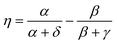 | (2.33) |
| | 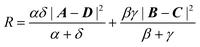 | (2.35) |
and the vectors| | 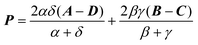 | (2.36) |
| | 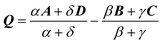 | (2.37) |
| | 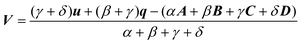 | (2.38) |
and to define χ to be the angle between P and Q. We can then write| | 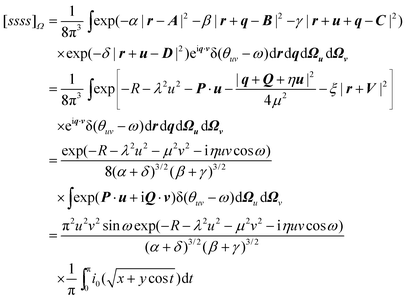 | (2.39) |
where| | | x
=
(Pu)2
+
(iQv)2
+ 2(Pu)(iQv) cos χ cos ω | (2.40) |
| | | y
= 2(Pu)(iQv) sin χ sin ω | (2.41) |
and i0(x)
=
x−1sinh x. We have not been able to evaluate the integral over t in closed form, but it seems to respond well to equal-weight n-point quadrature using 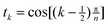 .
.
We note that, in general, [ssss]Ω is complex but its conjugate occurs elsewhere in the sum (2.11) and the total intracule Ω(u,v,ω) is therefore real.
Because the number of Omega integrals grows with the fourth power of the size of the basis set, it is essential to be able to determine quickly that an individual integral is negligible so that its computation can be avoided. To this end, one requires a simple but rigorous upper bound on the magnitude of [abcd]Ω and, for example, it is possible to show that
| | 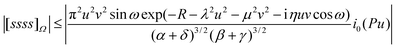 | (2.42) |
However, this bound is not uniformly tight and improved versions are being sought.
46
If A, B, C and D are collinear, we have y
= 0 and eqn (2.39) reduces to
| | 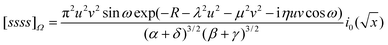 | (2.43) |
Integration of
eqn (2.43) over
ω yields the collinear fundamental Wigner integral and this can be reduced to a messy expression involving the complex error function.
36
If A, B, C and D are concentric, we have x
=
y
=
R
= 0 and eqn (2.39) reduces to
| | 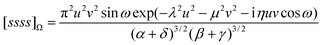 | (2.44) |
3. Intracule-based correlation models
If it was clear after Section 1 that it is desirable to improve our attack upon the electron correlation problem by admitting two-electron information, but unclear how precisely to do this, the foregoing Section reveals that we now suffer from an embarrassment of riches!
Suppose that we have derived the Omega intracule from the HF wavefunction of a system. Then—provided that we are willing to blur the distinction between a true probability density and a quasi-probability density—we have an impressively detailed picture of the dynamical behaviour of the electrons within the system. We know, for any given values of u, v and ω, the likelihood of finding two electrons at a distance u and moving with a relative speed v at a dynamical angle ω. But how can we exploit this to predict correlation energies?
Gilbert’s theorem47 is the reduced density matrix analogue of the Hohenberg–Kohn theorem, assuring us that the first-order reduced density matrix (1-RDM) contains sufficient information to reconstruct the Hamiltonian and, therefore, all other properties of the system. The corresponding theorem for the Omega intracule, which would guarantee that
for some universal functional
F, has not yet been proven but we hope that this deficiency will be rectified in the near future. In the meantime, we will proceed presumptively and see what can be achieved.
Inspired by second-order perturbation theory, we posit that the exact correlation energy is the sum of contributions from each of the n(n
− 1)/2 pairs of electrons in the system and, by analogy with eqns (2.8) and (2.9), we conjecture that it can be written
| | 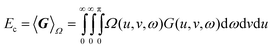 | (3.46) |
where the correlation kernel
G(
u,
v,
ω) is a universal function. Substituting
eqns (2.11) and
(2.12) into
eqn (3.46), one finds that the correlation energy is
| | 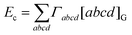 | (3.47) |
where we have introduced the correlation integrals
| | 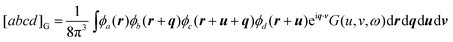 | (3.48) |
These last two equations embody one of the key ideas of this article.
If we assume that our conjecture is either correct or nearly so, the practical usefulness of this approach to the electron correlation problem depends simply on the degree to which the correlation integrals in eqn (3.48) can be computed both accurately and efficiently. It follows from the penultimate line of eqn (2.39) that the fundamental Gaussian correlation integral is
| | 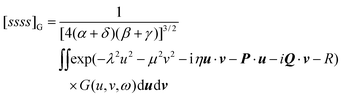 | (3.49) |
which has a very pleasing symmetry. Integrals of higher angular momenta can be constructed from this by differentiation with respect to the coordinates of the Gaussian centres.
34
We do not know how to construct the exact G(u,v,ω) but it is possible to derive properties that it must satisfy45 and we anticipate that, much as in DFT, these will be used to guide the construction of progressively more accurate approximations. One elementary property, that G(u,v,ω)
=
G(u,v,π
−
ω), is a consequence of time-reversal symmetry.
Special cases emerge for constrained approximations to the kernel. For example, if the correlation kernel depends on s
=
uv but is independent of ω, (2.46) becomes
| | 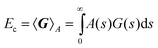 | (3.50) |
This particular simplification was originally motivated by the observations of Section 1 and we have explored it in depth. Accordingly, although Fondermann
et al. have deduced from numerical evidence that this form of
G may be insufficiently flexible to describe changes in
Ec during bond stretching,
48 we will focus on it for the remainder of this article.
Using thought-experiment as our guide, what can we say about the likely form of G(s)? Suppose that we were able to “switch off” the HF approximation so that the electrons in our system were suddenly able to avoid one another. It seems likely that the electrons most inclined to exploit this new freedom would be those that are close together and moving relatively slowly, that is, those for which s is small. In contrast, we anticipate the weakest correlation effects for electrons that are far apart and moving relatively quickly, that is, those for which s is large. Thus, we expect G(s) to be a decaying function of s.
4. Numerical results
4.1. Illustrative intracules
We have previously reported intracules for various atoms and molecules, in ground and excited states,35,37–39,45 but some illustrations at this point may nonetheless be helpful. Fig. 4 shows the HF/6-311G Wigner intracule for a ground-state beryllium atom whose 1s and 2s orbitals are each doubly occupied. Suppose that two of the electrons are observed. If both are in the 1s orbital, they will tend to be close together and moving rapidly, yielding the peak at (u,v)
≈
(0.55,3.3). If both are in the 2s orbital, they will usually be further apart and moving relatively slowly, yielding the peak at (u,v)
≈
(3.0,0.68). If one is in the 1s and the other is in the 2s orbital (which is four times as likely as either of the other possibilities), intermediate u and v values arise, giving the peak at (u,v)
≈
(2.1, 2.2).
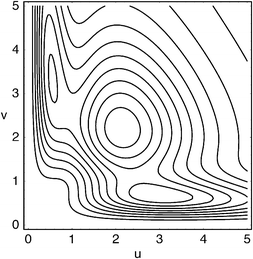 |
| | Fig. 4 Wigner intracule for the beryllium atom (u
=
|r1
−
r2| and v
=
|p1
−
p2|). | |
Fig. 5–7 show the Angle, Lambda and Dot intracules of the Be atom. Their symmetries about ω
=
π/2 and x
= 0 are obvious but these plots do not otherwise appear as immediately informative as Fig. 4. Nonetheless, the rather bland Angle intracule implies that the electrons in this atom spend most of their time “orbiting”
(ω
≈
π/2), rather than moving away from (ω
= 0) or towards (ω
=
π) each other and the Lambda intracule resolves this picture further, its asymmetric contours revealing that, although the angular momentum of this orbital motion is most often s
≈ 2.2ℏ, much larger values are not uncommon. The Dot intracule completes the story by showing that rapid changes in the interelectronic distance r12, though not very probable, do sometimes occur.
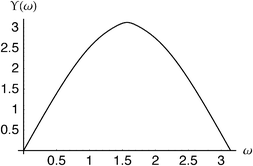 |
| | Fig. 5 Angle intracule for the beryllium atom. | |
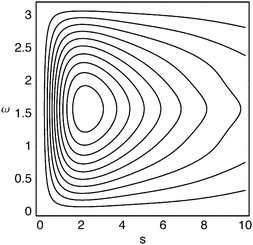 |
| | Fig. 6 Lambda intracule for the beryllium atom. | |
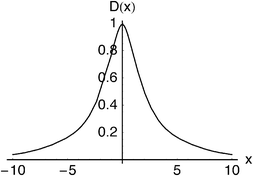 |
| | Fig. 7 Dot intracule for the beryllium atom. | |
Insofar as we can imagine the motion of electrons in an atom, all of these classical portraits seem intuitively reasonable.
4.2. Simple correlation kernels
The simple argument in Section 3 suggested that G(s) should be a decaying function of s and so we explored a number of plausible candidates, including exponentials and Gaussians. To our surprise, we found that the most successful elementary choice iswhere j0(x)
=
x−1 sin x. This kernel does decay, but very slowly, and it is highly oscillatory. We do not yet understand why it works as well as it does but we are fortunate because this choice of G(s) also leads to relatively simple [abcd]G integrals. Moreover, it is easy to show that the [ssss]G/C values that result are always positive.
There are, of course, many ways to assign precise values to C and ζ. An elegant approach is to require that they yield the correct correlation energies for the lowest singlet and triplet states of high-density hookium, for both the correlation energies and the Action intracules of these states are known exactly in closed form.45 This leads to
| | | G1(s)
=
−0.119106 j0(0.889244s) | (4.52) |
Alternatively, the parameters can be chosen to reproduce the correlation energies of the He and Ne atoms. This strategy is not as clean as the first, because neither the correlation energies nor the Action intracules of these atoms are known exactly. However, by basing the calculations on HF/6-311G wavefunctions, this approach yields
| | | G2(s)
=
−0.0992 j0(0.893s) | (4.53) |
A third scheme finds the parameters by a least-squares fit to the correlation energies of all the atoms from H to Ar. This is even more ambiguous than the second approach, because the energies and intracules of the second-row atoms are not known very accurately, but it is the most pragmatic way to proceed and might be expected to yield the best kernel for chemical purposes. Basing the construction on UHF/6-311G wavefunctions, one obtains
| | | G3(s)
=
−0.0925 j0(0.88s) | (4.54) |
It is interesting that the three methods yield very similar values for
ζ.
4.3. Atomic results
The correlation integral required for atomic calculations employing Gaussian s functions is found by letting P
=
Q
=
0, R
= 0 and G(u,v,ω)
=
Cj0(ζuv) in eqn (3.49). This yields| | 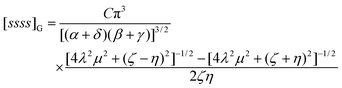 | (4.55) |
which reduces, in the special case where η
= 0, to| | 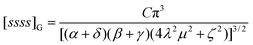 | (4.56) |
The higher integrals, e.g.
[pppp]G, are similar but contain a number of such terms.
We have used these formulae to compute the correlation energies for the ground states of each atom from H to Ar, basing all of our calculations on UHF/6-311G wavefunctions. Table 2 compares the exact unrestricted correlation energies49 with the estimates obtained using each of the three parameter choices described above. We emphasize that, although our calculations are based on Hartree–Fock wavefunctions using a modest basis set, they yield estimates of the exact
(full CI, infinite-basis) correlation energies. In this sense, they resemble traditional density-functional calculations, not wavefunction-based ones.
Table 2 Atomic correlation energies (in mEh) and errors of the Gn(s) models
| |
H |
He |
Li |
Be |
B |
C |
N |
O |
F |
Ne |
Na |
Mg |
Al |
Si |
P |
S |
Cl |
Ar |
MADa |
|
Mean absolute deviation.
|
| −Exact |
0 |
42 |
45 |
94 |
121 |
151 |
185 |
249 |
318 |
391 |
396 |
438 |
465 |
500 |
540 |
597 |
658 |
723 |
|
| ΔLYP |
0 |
2 |
9 |
1 |
5 |
9 |
7 |
9 |
4 |
−7 |
12 |
22 |
30 |
31 |
26 |
33 |
33 |
28 |
15 |
| ΔG1 |
0 |
9 |
11 |
14 |
25 |
38 |
54 |
64 |
74 |
86 |
93 |
108 |
120 |
121 |
127 |
140 |
155 |
170 |
78 |
| ΔG2 |
0 |
0 |
2 |
−5 |
−1 |
5 |
10 |
7 |
4 |
0 |
5 |
10 |
15 |
9 |
6 |
7 |
8 |
8 |
6 |
| ΔG3 |
0 |
−2 |
0 |
−9 |
−5 |
1 |
7 |
3 |
−2 |
−6 |
−2 |
2 |
7 |
1 |
−1 |
−1 |
−1 |
0 |
3 |
The G1(s) parameters are exact for the lowest singlet and triplet states of high-density hookium but they systematically overestimate atomic correlation energies by more than 20% and the C parameter is primarily responsible for this. The mean absolute deviation (MAD) is 78 mEh.
The G2(s) parameters are exact for He and Ne and yield satisfactory energies for other atoms (MAD = 6 mEh) but still overestimate in most cases. This is not entirely unexpected, because both He and Ne have completely filled shells and their electrons are therefore more strongly correlated than those of most other atoms.
The G3(s) parameters are tailored to give good overall performance for all of the atoms considered and they yield encouraging correlation energies (MAD < 3 mEh), particularly for the second-row atoms. This model is much more accurate than the popular LYP functional (MAD = 15 mEh) and it is remarkable that the simple correlation scheme defined by eqns (3.50) and (4.51) yields such an accurate account of correlation in these many-electron systems.
The chemistry of atoms is not very exciting but it is interesting to examine the effectiveness of the G3(s) model for the prediction of atomic ionization energies. Table 3 compares the exact (non-relativistic clamped-nucleus) ionization energies50,51
| | | I(A)
=
E(A+)
−
E(A) | (4.57) |
with the corresponding HF,
G3(
s), LSDA, BLYP and B3LYP estimates, all using the 6-311G basis set. The overall accuracy of the
G3(
s) model is comparable to that of the local density DFT model but is about 50% worse than the gradient-corrected and hybrid DFT methods. All of them are much more accurate than HF theory.
Table 3 Atomic ionization energies (mEh) and errors of various models
| |
H |
He |
Li |
Be |
B |
C |
N |
O |
F |
Ne |
Na |
Mg |
Al |
Si |
P |
S |
Cl |
Ar |
MAD |
| Exact |
500 |
904 |
198 |
343 |
305 |
414 |
535 |
500 |
641 |
794 |
189 |
281 |
220 |
300 |
387 |
381 |
477 |
582 |
|
| ΔHF |
0 |
−42 |
−2 |
−47 |
−13 |
−16 |
−20 |
−62 |
−64 |
−65 |
−7 |
−38 |
−18 |
−19 |
−18 |
−48 |
−42 |
−39 |
31 |
| ΔLSDA |
−22 |
−12 |
3 |
−11 |
11 |
15 |
16 |
10 |
15 |
17 |
8 |
3 |
1 |
3 |
4 |
5 |
10 |
9 |
10 |
| ΔBLYP |
−2 |
7 |
5 |
−13 |
10 |
4 |
−3 |
14 |
3 |
−5 |
8 |
−1 |
−5 |
−8 |
−11 |
−1 |
−1 |
−6 |
6 |
| ΔB3LYP |
2 |
12 |
8 |
−8 |
14 |
10 |
4 |
15 |
6 |
0 |
10 |
3 |
0 |
−2 |
−3 |
4 |
5 |
2 |
6 |
| ΔG3 |
0 |
−2 |
3 |
−9 |
16 |
18 |
19 |
−5 |
−3 |
0 |
−2 |
−1 |
9 |
7 |
17 |
8 |
19 |
26 |
9 |
In order to afford good ionization energies, a quantum chemical method must make the same correlation energy error when applied to the neutral and cationic species. This can be a harsh test, for the removal of an electron can sometimes lead to qualitative changes in the correlation behaviour in a system. For example, it is known52 that, whereas the correlation energies of some atoms (He, Li, N–Na) are “normal”, those of other atoms (Be, B, C, Mg–Ar) are “anomalous” in that they increase linearly, without bound, as the nuclear charge Z is increased. This is illustrated by the similar correlation energies of He and Li+
(42 and 43 mEh, respectively) and the very different correlation energies of Be and B+
(94 and 111 mEh, respectively). Careful inspection of Table 3 reveals that the G3(s) model performs well for the normal atoms but more poorly for the anomalous ones and suggests that an important topic of future research will be to devise a modified Hartree–Fock–Wigner scheme that does not suffer from this weakness. We note that Perdew pointed out long ago that this is also a major challenge for density functional theories.53
Finally, we turn to the subtle variations in correlation energies of the He-like ions discussed in the Introduction. Table 4 and Fig. 8 compare the LYP, G2(s) and G3(s) estimates (using HF-limit wavefunctions) with the exact values54 for nuclear charges 1 ≤
Z
≤ 10. It is clear that, whereas LYP is over-sensitive to Z, the Gn(s) models are almost independent of it, perhaps reflecting an intrinsic deficiency of the action-only ansatz(3.50).
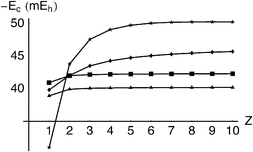 |
| | Fig. 8 Correlation energy Ec in the He-like ions as a function of nuclear charge Z. LYP (stars), exact (diamonds), G2(s)
(squares), G3(s)
(triangles). | |
Table 4 Correlation energies (in mEh) of He-like ions
| |
H− |
He |
Li+ |
Be2+ |
B3+ |
C4+ |
N5+ |
O6+ |
F7+ |
Ne8+ |
| −Exact |
39.82 |
42.04 |
43.50 |
44.27 |
44.74 |
45.05 |
45.28 |
45.45 |
45.59 |
45.69 |
| −LYP |
31.01 |
43.78 |
47.55 |
49.05 |
49.72 |
50.03 |
50.17 |
50.22 |
50.23 |
50.21 |
| −G2(s) |
40.94 |
42.00 |
42.15 |
42.21 |
42.24 |
42.25 |
42.27 |
42.28 |
42.48 |
42.49 |
| −G3(s) |
38.91 |
39.92 |
40.06 |
40.12 |
40.14 |
40.16 |
40.17 |
40.18 |
40.19 |
40.19 |
4.4. Molecular results
Although the choice G(u,v,ω)
=
Cj0(ζuv) leads to some simplifications, we have not yet been able to obtain the resulting general four-centre correlation integral (3.49) in closed form. However, in the case where the centers A, B, C and D are collinear, we have found| | 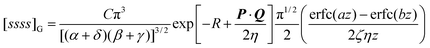 | (4.58) |
where| | 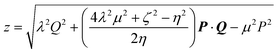 | (4.59) |
| | | a
=
[4λ2μ2
+
(ζ
+
η)2]−1/2 | (4.60) |
| | | b
=
[4λ2μ2
+
(ζ
−
η)2]−1/2 | (4.61) |
and erfc(x) is the complementary error function. As P, Q, R and z tend to zero, eqn (4.58) reduces to eqn (4.55). In the special case where η
= 0, it can be shown that eqn (4.58) reduces to| | 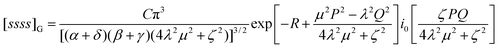 | (4.62) |
and, as P, Q and R tend to zero, this obviously yields eqn (4.56).
Eqns (4.58) and (4.62), and their derivatives, allow us to compute the correlation energy (3.47) with G(u,v,ω)
=
Cj0(ζuv) for linear molecules with nuclear-centred Gaussian basis functions. We have not yet performed a systematic study of a large set of such molecules and here we report only a few indicative results for the prototypical hydrogen molecule.
Near-exact energies of the clamped-nucleus, non-relativistic Schrödinger equation for H2 are available from the Hylleraas-type calculations of Kolos et al.55 and these reveal that, at the equilibrium bond length (1.4 a0), the exact correlation energy is 40.8 mEh. Using the HF/6-311G wavefunction, the G3(s) model yields Ec
= 39.4 mEh, which is encouraging. However, as Rassolov et al. have noted,56 this achievement is almost matched by the LYP density functional (for which Ec
= 38.3 mEh) and the more serious challenge is to reproduce the variation in the correlation energy as the bond length is varied. Table 5 and Fig. 9 compare the exact correlation energy with the G3(s) and LYP estimates over a range of bond lengths. Rassolov et al. noted that LYP fails to predict the growth in Ec as R increases and we see that G3(s) fails similarly, albeit less dramatically. As with the He-like ions, the misbehaviour can probably be traced48 to the action-only ansatz(3.50).
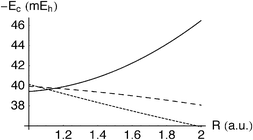 |
| | Fig. 9 Correlation energy Ec in the H2 molecule as a function of bond length R. Exact (solid), G3(s)
(dashed), LYP (dotted). | |
Table 5 Correlation energy (in mEh) of H2 at various bond lengths R
(in a0)
|
R
|
1.0 |
1.1 |
1.2 |
1.3 |
1.35 |
1.4 |
1.45 |
1.5 |
1.6 |
1.7 |
1.8 |
2.0 |
| −Exact |
39.40 |
39.61 |
39.91 |
40.33 |
40.57 |
40.85 |
41.15 |
41.49 |
42.24 |
43.11 |
44.11 |
46.52 |
| −LYP |
40.16 |
39.68 |
39.21 |
38.77 |
38.55 |
38.33 |
38.12 |
37.91 |
37.49 |
37.09 |
36.68 |
35.91 |
| −G3(s) |
39.95 |
39.83 |
39.70 |
39.55 |
39.46 |
39.38 |
39.29 |
39.20 |
39.00 |
38.79 |
38.56 |
38.07 |
5. Concluding remarks
The calculation of correlation energies at a low computational cost is one of the major goals of quantum chemistry. In this article, we have introduced a radical approach that is distinguished from conventional post-Hartree–Fock and density functional methods by its explicit dependence on two-electron phase-space information. In order to accomplish this, we have defined a number of two-electron probability densities (intracules), some of which may be of interest in their own right. The new correlation method requires the computation of four-index integrals of a novel type but, apart from this, can be easily appended to a HF calculation. Furthermore, the entire procedure can be performed self-consistently57 to yield a scheme that is reminiscent of Kohn–Sham density functional theory. The method is conceptually simple and provides a new perspective on the phenomenon of electron correlation. Preliminary results, using a simple two-parameter correlation kernel, are encouraging and we are confident that the accuracy of the method can be improved further by refinement of this kernel.
References
- E. Schrödinger, Ann. Phys., 1926, 79, 361 Search PubMed.
- D. R. Hartree, Proc. Cambridge Philos. Soc., 1928, 24, 89 Search PubMed.
- V. Fock, Z. Phys., 1930, 61, 126.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS.
- G. G. Hall, Proc. R. Soc. London, Ser. A, 1951, 205, 541–552 Search PubMed.
- E. Schwegler and M. Challacombe, J. Chem. Phys., 1999, 111, 6223–6229 CrossRef CAS.
- J. Kong, C. A. White, A. I. Krylov, D. Sherrill, R. D. Adamson, T. R. Furlani, M. S. Lee, A. M. Lee, S. R. Gwaltney, T. R. Adams, C. Ochsenfeld, A. T. B. Gilbert, G. S. Kedziora, V. A. Rassolov, D. R. Maurice, N. Nair, Y. Shao, N. A. Besley, P. E. Maslen, J. P. Dombroski, H. Dachsel, W. Zhang, P. P. Korambath, J. Baker, E. F. C. Byrd, T. V. Voorhis, M. Oumi, S. Hirata, C. Hsu, N. Ishikawa, J. Florian, A. Warshel, B. G. Johnson, P. M. W. Gill, M. Head-Gordon and J. A. Pople, J. Comput. Chem., 2000, 21, 1532–1548 CrossRef CAS.
- E. Wigner, Phys. Rev., 1934, 46, 1002–1011 CrossRef CAS.
-
A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, McGraw-Hill, New York, 1989 Search PubMed.
- T. Kato, Commun. Pure. Appl. Math, 1957, 10, 151–177 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., Sect. B, 1964, 136, 864–871 Search PubMed.
- P. M. W. Gill, Aust. J. Chem., 2001, 54, 661–662 CrossRef CAS.
- F. London, Z. Phys. Chem., Abt. B, 1930, 11, 222–251 CAS.
- E. A. Hylleraas, Z. Phys., 1930, 65, 209 CAS.
- E. A. Hylleraas and J. Midtdal, Phys. Rev., 1956, 103, 829–830 CrossRef CAS.
- J. Linderberg, Phys. Rev., 1961, 121, 816–819 CrossRef CAS.
- V. A. Rassolov, J. Chem. Phys., 1999, 110, 3672–3677 CrossRef CAS.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- K. Husimi, Proc. Phys. Math. Soc. Jpn, 1940, 22, 264 Search PubMed.
- J. E. Harriman, J. Chem. Phys., 1988, 88, 6399–6408 CrossRef CAS.
- H. Schmider, J. Chem. Phys., 1996, 105, 3627–3635 CrossRef CAS.
- M. Novaes, J. Opt. B, 2003, 5, S342–S348 Search PubMed.
- H. J. Groenewold, Physica, 1946, 12, 405–460 CrossRef.
- J. P. Dahl and M. Springborg, Mol. Phys., 1982, 47, 1001–1019 CAS.
- M. Springborg, Theor. Chim. Acta, 1983, 63, 349–356 CrossRef CAS.
- J. M. Gracia-Bondía, Phys. Rev. A, 1984, 30, 691–697 CrossRef CAS.
- M. Springborg and J. P. Dahl, Phys. Rev. A, 1987, 36, 1050–1062 CrossRef CAS.
- J. P. Dahl and M. Springborg, J. Chem. Phys., 1988, 88, 4535–4547 CrossRef CAS.
- H. Schmider and J. P. Dahl, Int. J. Quantum Chem., 1996, 60, 439–452 CrossRef CAS.
- S. Nouri, Phys. Rev. A, 1998, 57, 1526–1528 CrossRef CAS.
-
E. R. Davidson, Reduced Density Matrices in Quantum Chemistry, Academic, New York, 1976 Search PubMed.
-
L. D. Landau and E. M. Lifshitz, Quantum Mechanics, Pergamon, Oxford, 2nd edn., 1965 Search PubMed.
-
V. A. Rassolov, personal communication.
- S. F. Boys, Proc. R. Soc. London, Ser. A, 1950, 200, 542–554 Search PubMed.
- P. M. W. Gill, D. P. O’Neill and N. A. Besley, Theor. Chem. Acc., 2003, 109, 241–250 Search PubMed.
- N. A. Besley, D. P. O’Neill and P. M. W. Gill, J. Chem. Phys., 2003, 118, 2033–2038 CrossRef CAS.
- D. P. O’Neill and P. M. W. Gill, Phys. Rev. A, 2003, 68, 22505 CrossRef.
- P. M. W. Gill, N. A. Besley and D. P. O’Neill, Int. J. Quantum Chem., 2004, 100, 166–171 CrossRef CAS.
- N. A. Besley and P. M. W. Gill, J. Chem. Phys., 2004, 120, 7290–7297 CrossRef CAS.
- N. A. Besley, Chem. Phys. Lett., 2005, 409, 63–69 CrossRef CAS.
- C. A. Coulson and A. H. Neilson, Proc. Phys. Soc., London, 1961, 78, 831–837 CrossRef CAS.
- A. M. Lee and P. M. W. Gill, Chem. Phys. Lett., 1999, 313, 271–278 CrossRef CAS.
- K. E. Banyard and C. E. Reed, J. Phys. B, 1978, 11, 2957–2967 CrossRef CAS.
- N. A. Besley, A. M. Lee and P. M. W. Gill, Mol. Phys., 2002, 100, 1763–1770 CrossRef CAS.
- P. M. W. Gill and D. P. O’Neill, J. Chem. Phys., 2005, 122, 94110 CrossRef CAS.
-
D. L. Crittenden and P. M. W. Gill, in preparation.
- T. L. Gilbert, Phys. Rev. B, 1975, 12, 2111–2120.
- R. Fondermann, M. Hanrath, M. Dolg and D. P. O’Neill, Chem. Phys. Lett. Search PubMed , in press.
- D. P. O’Neill and P. M. W. Gill, Mol. Phys., 2005, 103, 763–766 CrossRef CAS.
- E. R. Davidson, S. A. Hagstrom, S. J. Chakravorty, V. Meiser Umar and C. Froese Fischer, Phys. Rev. A, 1991, 44, 7071–7083 CrossRef CAS.
- S. J. Chakravorty, S. R. Gwaltney, E. R. Davidson, F. A. Parpia and C. Froese Fischer, Phys. Rev. A, 1993, 47, 3649–3670 CrossRef CAS.
- J. Linderberg and H. Shull, J. Mol. Spectrosc., 1960, 5, 1–16 CAS.
- J. P. Perdew, E. R. McMullen and A. Zunger, Phys. Rev. A, 1981, 23, 2785–2789 CrossRef.
- C. C. J. Roothaan and A. W. Weiss, Rev. Mod. Phys., 1960, 32, 194–205 CrossRef CAS.
- W. Kolos, K. Szalewicz and H. J. Monkhorst, J. Chem. Phys., 1986, 84, 3278–3283 CrossRef CAS.
- V. A. Rassolov, M. A. Ratner and J. A. Pople, J. Chem. Phys., 2000, 112, 4014–4019 CrossRef CAS.
-
D. P. O’Neill and P. M. W. Gill, Recent Advances in Electron Correlation Methodology, ACS Press, Washington DC, 2005 Search PubMed.
Footnotes |
| † DLC gratefully acknowledges a postdoctoral fellowship from the ANU. |
| ‡ DPO is grateful for an ANU PhD scholarship. |
| § NAB thanks the EPSRC for an Advanced Research Fellowship. |
|
| This journal is © the Owner Societies 2006 |
Click here to see how this site uses Cookies. View our privacy policy here. 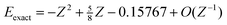
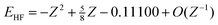
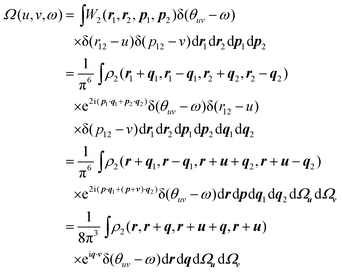
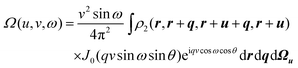
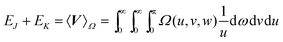
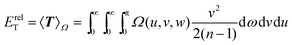
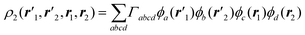
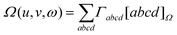
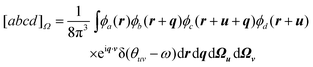

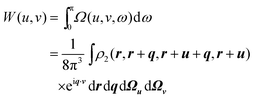
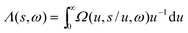
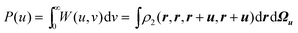
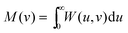
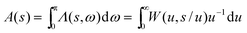
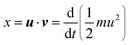
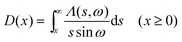
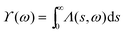
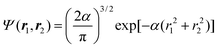
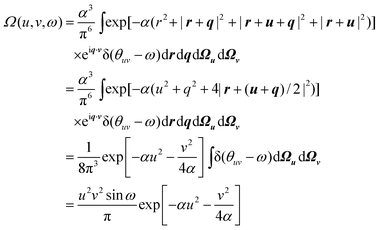
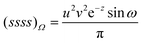
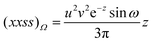
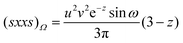
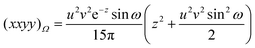
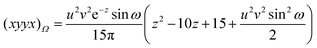
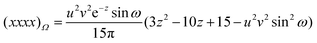
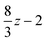

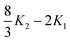


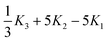
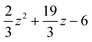
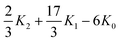
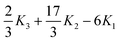
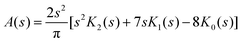
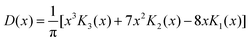


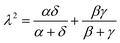
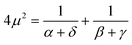
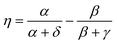
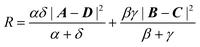
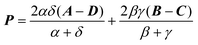
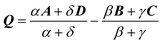
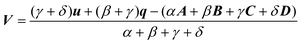
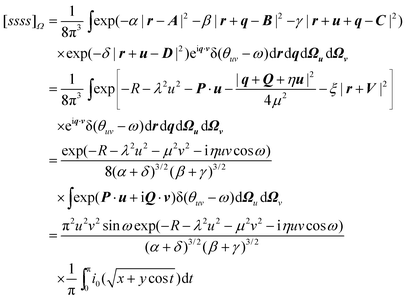
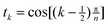 .
.