Vibrational spectroscopy of hydroxy-heterobiaryls. IR-active modes of [2,2′-bipyridyl]-3,3′-diol

Abstract

All observed IR-active vibrational modes of [2,2′-bipyridyl]-3,3′-diol (BP(OH)₂) and its two isotopomers, BP(OD)₂ and BP(OH)₂-d₆ have been assigned on the basis of the comparison of experimental results with predictions obtained from DFT (B3LYP/6-31G(d,p)) calculations. The sensitivity of the vibrational transitions to the environment has been studied by comparing the spectra recorded in vapour, different solutions, KBr pellets, and cryogenic argon matrices. The results may be useful for the quantum control of excited state single or double proton transfer in BP(OH)₂.

---

Introduction

[2,2′-bipyridyl]-3,3′-diol (BP(OH)₂), a molecule with two strong intramolecular N⋯HO hydrogen bonds, is one of the most intensely studied systems that exhibit excited state intramolecular proton transfer.^1–6 Upon electronic excitation, large increase of basicity of pyridine type nitrogen atoms, and concomitant acidity of the hydroxyl group is observed, which leads to ultrafast tautomerization of this system. The final photoproduct, identifiable by its strongly Stokes-shifted fluorescence, corresponds to the transfer of two protons in the original form of the compound. However, it was also found that the initially excited form may decay along two competing channels, one involving a synchronous transfer of two protons, while the other being a stepwise reaction shown in Fig. 1. A proof of the latter was the observation of a single-proton-transferred transient.²

Fig. 1 Single (SPT) and double (DPT) proton transfer paths in the excited state of BP(OH)₂.

In rapid phototautomerization processes, the proton transfer reaction path often contains contributions from vibrations that do not directly involve proton motion, but, instead, they modulate the distance between the hydrogen bonded atoms, and thus affect the reaction barrier for the proton transfer. BP(OH)₂, with its bimodal pattern of phototautomerization, is an ideal model system for studies of vibrations which can either promote or hinder a single or double proton transfer. Investigation of such vibrational modes may provide useful information for designing of quantum control experiments, in which an appropriately shaped sequence of laser pulses could drive the system into a selected reaction channel. Naturally, a prerequisite for such an experiment is the detailed understanding of the vibrational structure of the system.

Some time ago, we studied low frequency vibrations of BP(OH)₂ and its derivatives and we suggested which vibrational modes can be operative for each of the two proton transfer channels.^7–8 The present study aims at providing a complete picture of the IR-active vibrations of this molecule. For this purpose, IR spectra have been measured in various environments, as well as in the gas phase, at different temperatures. Besides the parent molecule (1), two BP(OH)₂ isotopomers have been studied: (1) BP(OD)₂ (2), with deuterated hydroxyl groups; (2) BP(OH)₂-d₆ (3), with all CH protons replaced by deuterons. The assignments made in this work are based on the comparison of the observed isotopic shifts with the results obtained by DFT calculations. Additional arguments are provided by the analysis of spectral bandwidths and the sensitivity of the location and intensity of a given band to the environment.

Experimental and computational details

The synthesis and purification of BP(OH)₂ have been described elsewhere.⁹ BP(OH)₂-d₆ was kindly provided to us by Professor Ł. Kaczmarek, Pharmaceutical Research Institute, Warsaw, Poland. Deuteration of hydroxylic protons was achieved by dissolving 1 in deuterated methanol and subsequent solvent evaporation.

The IR spectra have been measured on a NICOLET SX 170 FTIR spectrometer. Low-temperature spectra were obtained for samples isolated in argon matrices at 15 K. These were prepared by the deposition of the substance, heated to 350 K, into a stream of gas onto a cold window of a Displex 202 cryostat (APD Cryogenics). In order to record the spectra in the vapour phase, the sample was put in a gas cell, consisting of a 12 cm long glass tube with KBr windows on both ends. The cell was heated by placing it in a large chamber filled with hot air. In this way temperatures up to 450 K could be obtained.

The room temperature spectra in KBr were recorded in pellets containing 1–2% w/w of the investigated compound, prepared by the standard procedure. The solution spectra were obtained after subtracting the solvent contribution, measured in the same cell.

The calculations of the IR spectra were carried out at the B3LYP/6-31G(d,p) level of theory. RHF computations with the same basis set were also performed, yielding somewhat inferior results to the results obtained with the DFT method. Prior to computing the vibrational pattern, the geometry of the system was optimized, using either C_2h symmetry, or no symmetry restrictions whatsoever. Both approaches gave nearly identical results. The calculations were performed using the Gaussian 03 suite of programs.¹⁰

Results and discussion

Fig. 2 presents the infrared spectra obtained for the three isotopomers in KBr pellets. An outstanding feature in the spectra is a very broad band peaking at above 2500 cm⁻¹ in 1 and 3 and at around 2000 cm⁻¹ in 2. It is an indication of a strong intramolecular hydrogen bond in the system We previously showed⁷ by comparing BP(OH)₂ with its singly hydrogen bonded derivatives that the two hydrogen bonds in 1 reinforce each other due to larger rigidity of a doubly hydrogen bonded structure. This was manifested by similar band shapes and positions of the maximum in solution at 293 K and in Ar matrix at 17 K. In singly hydrogen bonded derivatives, a red shift was observed upon passing to the low temperature matrix.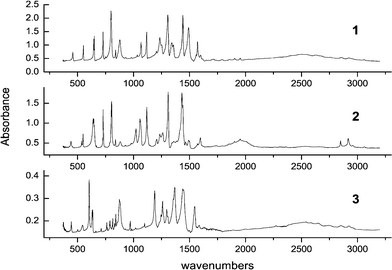

Fig. 2 IR spectra of 1–3 recorded in KBr pellets at 293 K.

Table 1 contains the peak positions along with the observed shifts in the deuterated forms. These are compared with the corresponding values obtained by calculations, which lead to the assignment of all the bands. For nearly all transitions the agreement between the observed and the calculated shifts is very good for both d₂ and d₆ species, which strongly supports the assignments. For example, the CH vibrations nicely show the expected isotope effect. An exception from the agreement is the 8b_u mode where the calculations predict for 2 a blue shift of 1 cm⁻¹, whereas the experiment in KBr yields a red shift of 9 cm⁻¹. However, this discrepancy disappears in the spectra recorded in argon matrices, where for both 1 and 2 this transition is observed at the same frequency of 1440 cm⁻¹. Interestingly, for the same mode in 3, the difference between the observed and the calculated values of the red shift equal to −73 and −42 cm⁻¹, respectively, is much larger than in all other cases.

Table 1 Experimental and calculated IR-active vibrations of BP(OH)₂ and its isotopomers

	BP(OH)2		BP(OD)2				BP(OH)2-d6
	[small nu, Greek, tilde]/cm^−1		[small nu, Greek, tilde]/cm^−1		Δ[small nu, Greek, tilde]/cm^−1^c		[small nu, Greek, tilde]/cm^−1		Δ[small nu, Greek, tilde]/cm^−1^c
	Exp.^a	Calc.^b	Exp.^a	Calc.^b	Exp.^a	Calc.^b	Exp.^a	Calc.^b	Exp.^a	Calc.^b	Approximate mode description^f
a KBr pellet, 293 K, unless indicated otherwise. b B3LYP/6-31G(d,p) calculations, correction factor 0.96. c Shift with respect to the parent, undeuterated molecule. d Solution in CH2Cl2. e Ref. 3. f s, stretch, b, bend, skel def, skeletal deformation, ip, in-plane, oop out-of-plane.
1bu	3078 w^d	3091(16.3)	3078 w	3091 (21.9)	0	0	2281 w	2292(16.1)	−797	−799	CH s
2bu	3061 m	3079(21.6)	3063 m	3078 (27.2)	2	−1	2272 m	2276(25.9)	−785	−803	CH s
3bu	3006 w	3063(11.5)	3012 w	3062 (14.0)	6	−1	2260 w	2260(5.97)	−746	−803	CH s
4bu	2540 vs	2943(1349.6)	1972 vs	2147 (710.7)	−568	−796	2540 vs	2943(1331.2)	0	0	OH s
5bu	1599 m	1607(13.5)	1597 m	1585 (45.0)	−2	−22	1586 m	1596 (24.3)	−13	−11	skel def, OH b
6bu	1571 m	1555(108.1)	1554 w	1537 (3.17)	−17	−18	1546 s	1528 (167.1)	−25	−27	skel def, OH b
7bu	1492 s	1482(252.7)	1091 w	1059 (29.0)	−401	−423	1440 s	1437 (263.2)	−52	−45	OH b
8bu	1441 s	1425(156.2)	1432 s	1426 (285.8)	−9	+1	1368 s	1381 (235.5)	−73	−42	CO s, CH b
9bu	1356 m	1360(57.6)	1414 m	1420 (36.0)	+58	+60	1296 s	1298 (10.7)	−60	−62	CH b, skel def
10bu	1306 s	1305 (144.8)	1309 s	1306 (126.1)	+3	+1	1259 s	1265 (152.1)	−47	−40	CO s, skel def
11bu	1252 m	1249 (231.0)	1262 m	1266 (101.6)	+10	+17	1188 s	1182 (126.6)	−64	−67	CH b, OH b, skel def
12bu	1204 w	1190 (2.79)	1208 w	1192 (8.50)	+4	+2	881 w	859 (6.1)	−323	−321	CH b
13bu	1117 m	1095 (32.5)	1118 m	1104 (124.7)	+1	+9	797 m	778 (8.46)	−320	−339	CH b
14bu	1067 m	1048 (15.4)	1058 m	1040 (77.1)	−9	−8	970 m	943 (8.32)	−97	−105	CH b
15bu	1033 w	1005 (5.5)	1023 m	1000 (15.7)	−10	−5	1018 w	994 (2.53)	−15	−11	skel def
16bu	840 m	828 (3.85)	839 m	827 (2.99)	−1	−1	831 m	815 (4.32)	−9	−13	skel def
17bu	650 m	630 (35.9)	645 m	628 (36.6)	−5	−2	636 m	614 (34.1)	−14	−16	CNC b
18bu	552 m	541 (9.58)	549 m	538 (8.78)	−3	−3	540 m	531 (8.09)	−12	−10	CCC b
19bu	458 m	451 (9.91)	441 m	436 (11.6)	−17	−15	444 m	437 (9.56)	−14	−14	CO b
20bu	203 w ^e	198 (9.3)	200 w ^e	194 (9.3)	−3	−4		189 (8.4)		−9	ring ip b
1au	982 w	939 (0.95)	982 w	938 (1.80)	0	−1	814 w	775 (4.39)	−168	−164	CH wag
2au	931 w	888 (2.04)	930 w	888 (1.69)	−1	0	767 w	731 (6.01)	−164	−157	CH wag
3au	878 s	879 (137.9)	640 s	644 (85.2)	−238	−237	874 s	878(155.7)	−4	−1	OH oop b
4au	804 s	782 (92.4)	804 s	784 (58.5)	0	+2	603 s	588 (39.4)	−201	−194	CH wag
5au	728 m	708 (11.6)	728 s	709 (25.3)	0	+1	711 w	692 (1.79)	−17	−16	CH wag
6au	566 vw	534 (0.07)		526 (2.08)		−8	498 w	488 (0.78)	−68	−46	skel oop def
7au	438 vw	430 (0.0001)		428 (0.25)		−2		393 (0.19)		−37	skel oop def
8au	246 vw ^e	239 (0.004)		238 (0.04)		−1		227(0.007)		−12	CO/CH wag
9au	111 w ^e	84 (2.75)	111 w ^e	84 (2.57)	0	0		79 (2.64)		−5	ring wag
10au	86 vw ^e	75 (0.82)	86 vw ^e	75 (0.90)	0	0		73 (0.60)		−2	NCCN torsion

---

Much help in the assignments also comes from the computed intensity patterns. For instance, the transition corresponding to the OH bending mode (7b_u) is predicted to have a strong intensity in 1 and 3, whereas in 2 the calculated intensity is an order of magnitude lower. This is indeed observed. Similar situation occurs for the 6b_u transition whose intensity sharply drops in 2, but increases in 3 with respect to 1, exactly as predicted by the calculations. Moreover, the calculations correctly predict the intensity increase in 2 for the 15b_u and 5a_u modes. All in all, the agreement between the observed and the calculated spectral patterns can be called very satisfactory. That also applies to the transition intensities.

Fig. 3 shows the correlation between the observed and the calculated spectra. All vibrations except the OH stretch have been taken into account. The values of the slope obtained for 1–3 are 0.960, 0.961, and 0.964, respectively; the corresponding root of mean square errors are 20.4, 21.6, and 17.2 cm⁻¹. The standard deviations for 1 and 2 are significantly reduced (to 14.6 and 15.7 cm⁻¹, respectively) if the three CH stretching modes are not taken into account; for 3, such a procedure does not change much the value of the standard deviation (it reduces only to 16.7 cm⁻¹). The above values have been obtained assuming that the intercept in the linear regression curve must be equal to zero. Without this constraint, the standard deviation values are much lower (14.9, 14.9, and 12.1 cm⁻¹for 1–3, respectively, taking into account all modes except 4b_u).

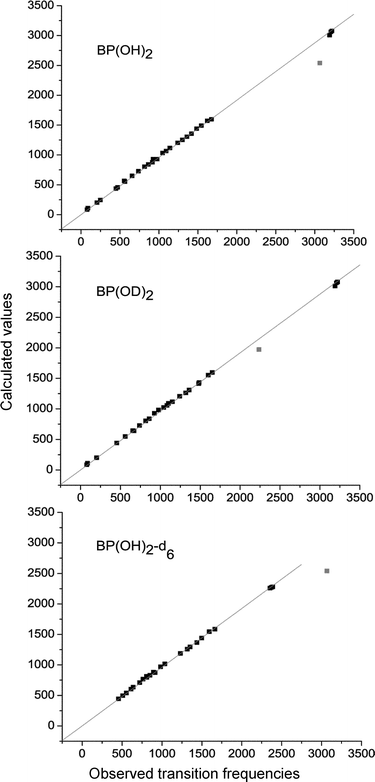Fig. 3 Correlation between the observed and calculated spectra.

One of the major goals of this study has been to characterize the OH vibrations involved in the intramolecular hydrogen bonds. The simple picture of three types of modes, corresponding to the isolated bond stretchings, the in-plane bendings, and the out-of-plane bendings may not be always correct. In particular, the in-plane OH bending could be expected to contribute significantly to several vibrations. However, the analysis of the spectral changes caused by OH→OD substitution shows that essentially only one band to which the in-plane OH bending can contribute is significantly affected. This is the transition observed at 1492 cm⁻¹ in 1 (and at 1440 cm⁻¹ in 3) which strongly shifts to the red (by 401 cm⁻¹) and loses its intensity, exactly as predicted by the calculations. Thus, this vibration, assigned to the 7b_u mode, can be safely characterized as the in-plane OH bending.

Similarly, the out-of-plane bending (3a_u mode) can be safely attributed to the transitions observed in KBr at 878 cm⁻¹ in 1 and at 874 cm⁻¹ in 3. In 2, this transition shifts to 644 cm⁻¹, in perfect agreement with the result of the calculations. However, while the nearly exact matching of the observed and computed shifts (238 and 237 cm⁻¹, respectively) is impressive, the good agreement of the absolute transition energies may be somewhat fortuitous. In vapour, this transition is observed at a much lower frequency, 844 cm⁻¹. The higher transition energy in condensed phases may be caused by two factors. The first is due to the fact that the vapour spectrum is recorded at a high temperature. Under these conditions, low frequency torsional modes may be excited, which effectively weakens the hydrogen bonds. The second factor involves the barrier imposed by the environment. In more rigid media, the frequencies of torsional modes are expected to be blue shifted, and thus the average structure should be more planar, resulting in a stronger hydrogen bond.

The band corresponding to the out-of-plane bending has very peculiar characteristics (Fig. 4). In addition to being strongly blue-shifted with respect to its position in vapour, it is extremely broad. The values of the bandwidth at half maximum strongly depend on the environment. In vapour, the bandwidth is as large as 65 cm⁻¹ (it should be remembered, though, that under these conditions all the bands are broadened). In condensed phase, the corresponding values are 20 cm⁻¹ in KBr (for all three compounds), 33 cm⁻¹ in CS₂, and 43 cm⁻¹ in CCl₄. We interpret this as an evidence of a strong coupling with low frequency torsions. Characteristically, in low-temperature argon matrices this band becomes so broad that its maximum is hard to determine. This may be due to the fact that the deposition from high temperature may result in freezing structures with various dihedral angles between the two rings.

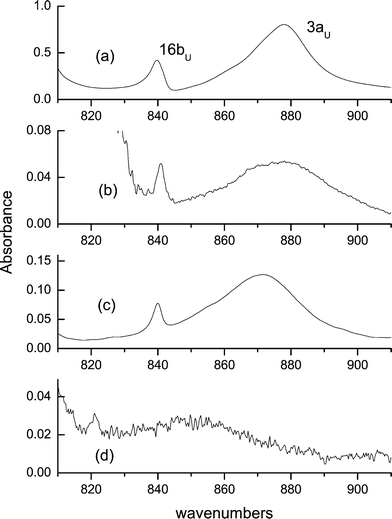Fig. 4 The out-of-plane OH bending vibration, measured in KBr (a), CCl₄ (b), CS₂ (c), and in vapour (d).

The very intense band corresponding to the OH stretching has a very large bandwidth of above 500 cm⁻¹, which drops to about 200 cm⁻¹ in 2. The position of the maximum is the same in the argon matrix at 15 K and in three different solvents at the room temperature (Table 2). In KBr, the maximum is red shifted by 140 cm⁻¹. This has been attributed to the polarizability of the hydrogen bond and to the large dielectric constant of KBr.³ In the vapour, this band is broadened and shifted to the blue, once again indicating the weakening of the hydrogen bond due to excitation of the low frequency torsional modes.

Table 2 Experimentally determined values of vibrations of BP(OH)₂ in various environments

	Ar matrix^a	Vapour^b	CCl4^c	CS2^c	CH2Cl2^c	KBr^c
a 15 K. b 400 K. c 293 K.
1bu		3074	3077	3075	3078
2bu		3059	3059	3056		3061
3bu			3009	3007	3010	3006
4bu	≈2680		2683	2681	2685	2540
5bu	1600		1598	1594	1600	1599
6bu	1570		1565		1565	1571
7bu	1489	1482	1482		1484	1492
8bu	1440	1441	1437		1437	1441
9bu	1358	1357	1354	1355	1355	1356
10bu	1309	1307	1304	1302	1303	1306
11bu	1254	1243	1250	1248	1247	1252
12bu	1204	1198	1201	1200	1202	1204
13bu	1118	1117	1114	1112	1115	1117
14bu	1072/1075	1069	1068	1067	1069	1067
15bu	1035		1034	1033	1034	1033
16bu	844		841	840	840	840
17bu	646/648	643	644	643	644	650
18bu	553			549	550	552
19bu	460			455	456	458
20bu
1au			967	965	971	982
2au			915	913	920	931
3au		844	877	872		878
4au	804	799		799	804	804
5au	733/738	728		728		728
6au						566
7au						435
8au
9au
10au

---

The behaviour of the in-plane OH bending mode, 7b_u, is the least perturbed among the three vibrations directly involving the hydrogen bonded protons, although its characteristics are also somewhat different from those of the other non-perturbed ‘normal’ transitions. Its bandwidth (22 cm⁻¹ in KBr, 9 cm⁻¹ in an Ar matrix) is definitively larger than those of other transitions (typical values for KBr and Ar are 5–8 cm⁻¹ and 3–4 cm⁻¹, respectively). The sensitivity of the band position to the environment is also large; its frequency changes from 1482 cm⁻¹ in vapour and CCl₄ to 1489 cm⁻¹ in argon and 1492 cm⁻¹ in KBr. As was the case for the OH stretching mode, the influence of rigid, polar KBr affects this mode the most.

The dependence of the band location on the environment is shown for all the modes in Table 2. Except for the weak band assigned to the 1a_u mode, the variations of the peak positions are not large, the average spread being about 4 cm⁻¹.

Several peaks observed in the spectra could not be assigned to the fundamental modes. These include peaks located around 1460, 1420, 1340, 1295, 1236, and 1133 cm⁻¹. Reliable assignments of these bands should become possible after analysing the pattern of Raman-active a_g and b_g modes.

Summary and conclusions

The results of the vibrational analysis based on the comparison of the experimental spectra with the DFT predictions led to reliable assignments of the bands observed in the IR spectra. We have observed and assigned all thirty IR-active vibrations of [2,2′-bipyridyl]-3,3′-diol. In most cases the assignments have been double-checked by analysing the spectral shifts observed and computed for two different deuterium-substituted derivatives.

As noted previously for the low frequency modes of BP(OH)₂ and its 5,5′-dimethyl derivative,⁸ the mutual exclusion principle is strictly obeyed. There is no clear indication of gerade symmetry modes in the IR spectra, whereas only such modes are detected in the Raman measurements.

The knowledge of the vibrational pattern of BP(OH)₂ allows us to make predictions regarding the importance of particular modes in the photoinduced tautomerization. Several vibrations may strongly affect structural parameters involved in the hydrogen bonds in this system (Fig. 5). Among them the 10a_u, 20b_u, 19b_u, 17b_u and 16 b_u modes alter the separation between the nitrogen and oxygen atoms, whereas the 3a_u, 9b_u, 7b_u, 5b_u and 4b_u modes change the distance between the nitrogen and the proton. For the in-plane vibrations of the b_u symmetry the nuclear motion should enhance the probability of a single proton transfer because it leads to simultaneous reduction of one N-O distance and enhancement of the other. On the contrary, the corresponding Raman-active in-plane vibrations of the a_g symmetry, with in-phase modulation of both distances, should promote the double proton transfer. For the out-of-plane vibration the situation is different, since both b_g and a_u modes simultaneously change the two distances. Thus, their influence on the tautomerization rate should be similar.

Fig. 5 Forms of normal modes that can contribute to single and double proton transfer reaction paths.

The development of femtosecond technology makes it now possible to experimentally verify such predictions. In a recent work, BP(OH)₂ has been studied by UV-visible pump–probe spectroscopy with 30 fs time resolution.⁶ The transient transmission curves showed strong oscillations, due to contribution from two modes, 196 and 295 cm⁻¹. The former, promoting a single proton transfer, was identified as an antisymmetric in-plane bending vibration. This is in good agreement with the vibration we assign to the 20 b_u mode. The former corresponds to a Raman-active vibration, previously assigned by us as 21a_g.⁸

With further enhancement in time resolution, it may also become possible to observe the contributions from higher frequency modes. Regarding the possibility of quantum-controlled proton transfer, BP(OH)₂ seems to be a very promising candidate. What remains to be done in order to completely understand its vibrational structure is the characterization of the Raman active modes and proper description of the anharmonic effects. These are among the subjects of our future works.

References

1. H. Bulska, Intramolecular cooperative double proton transfer in [2,2′-bipyridyl]-3,3′-diol, Chem. Phys. Lett., 1983, 98, 398–402.
2. H. Zhang, P. van der Meulen and M. Glasbeek, Ultrafast single and double proton transfer in photo-excited [2,2′-bipyridyl]-3,3′-diol, Chem. Phys. Lett., 1996, 253, 97–102.
3. D. Marks, H. Zhang, M. Glasbeek, P. Borowicz and A. Grabowska, Solvent dependence of (sub)picosecond proton transfer in photoexcited [2,2′-bipyridyl]-3,3′-diol, Chem. Phys. Lett., 1997, 275,, 370–376.
4. D. Marks, H. Zhang, P. Borowicz, A. Grabowska and M. Glasbeek, Femtosecond intramolecular proton transfer in photoexcited mono- and dienol derivatives of bipyridine, Chem. Phys. Lett., 1999, 309, 19–28.
5. M. Glasbeek, D. Marks and H. Zhang, Femtosecond studies of double proton transfer in [2,2′-bipyridyl]-3,3′-diol, J. Luminesc., 1997, 72-74, 832–834.
6. S. Lochbrunner, K. Stock, C. Schriever, E. Riedle, Symmetry breaking wavepacket motion and absence of isotope effect in ultrafast excited state proton transfer, Femtochemistry and Femtobiology, ed. M. M. Martin and J. T. Hynes, Elsevier, 2004, pp. 193–196.
7. P. Borowicz and J. Waluk, Electronic and vibrational spectroscopy of phototautomerizing heteroazaaromatics with intramolecular hydrogen bonds, J. Mol. Struct., 1995, 349, 277–280.
8. P. Borowicz, O. Faurskov-Nielsen, D. H. Christensen, L. Adamowicz, A. Leś and J. Waluk, Vibrational spectroscopy of hydroxy-heterobiaryls. I. Low frequency modes, Spectrochim. Acta, Part A, 1998, 54, 1291–1305.
9. A. Grabowska and Ł. Kaczmarek, Bipyridyl-diols, molecules undergoing an internal double proton transfer reaction in electronically excited states, Pol. J. Chem., 1992, 66, 715–731.
10. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.04, Gaussian, Inc., Pittsburgh, PA, 2003.

---

Footnote

† Dedicated to Professor Hiroshi Masuhara on the occasion of his 60th birthday.

---