Recent experimental and theoretical developments towards the observation of parity violation (PV) effects in molecules by spectroscopy

Abstract

Parity violation (PV) at the molecular level is known to be responsible for a tiny energy difference between the two enantiomers of a chiral molecule. This parity violation energy difference (PVED) has not yet been detected by experiment. In the last few years, the search for PV effects in molecules has made important steps ahead for several reasons. On one hand, very accurate infra-red spectroscopy measurements were performed by metrologists on bromochlorofluoromethane (CHFClBr) with a 10 Hz accuracy, which so far is the most precise. On the other hand, relativistic calculations were used for the evaluation of ΔE_PV allowing for a screening of favorable molecules for future measurements. The synthesis of such chiral molecules with high parity violation effects is currently being investigated. In memory of Professor Jean-Bernard Robert.

---

Jeanne Crassous

Jeanne Crassous was born in Jarny, France, in 1968. She studied chemistry at the École Normale Supérieure de Lyon, and received her PhD in 1996 under the guidance of Prof. André Collet (ENS Lyon), working on the absolute configuration of bromochlorofluoromethane. After a one-year post-doctoral period studying the chirality of fullerenes in Prof. François Diederich's group (ETH Zurich), she received a CNRS research position (CR1). She is currently interested in the preparation of enantioenriched molecules for their chirality related properties.

Christian Chardonnet

Christian Chardonnet is a former student of the École Normale Supérieure of Paris. He is now a research director at CNRS, team leader and former director of Laboratoire de Physique des Lasers-UMR CNRS Université Paris 13-Villetaneuse (France). His research interests are ultra-high resolution molecular spectroscopy and frequency metrology.

Trond Saue

Trond Saue was born in Harstad, Norway, in 1964. He received his PhD in theoretical chemistry at the University of Oslo, Norway, in 1996. After postdoctoral positions in Denmark and France as well as an assistant professorship at the university of Tromsø, Norway, he became CNRS assistant professor (CR1) at the Laboratoire de Chimie Quantique et de Modélisation Moléculaire at the Université Louis Pasteur in Strasbourg, France, in 2001. His research is centered on four-component molecular relativistic calculations, in later years with particular emphasis on density functional theory and molecular properties. He has published about 30 research papers and is a main author of the program system Dirac (http://dirac.chem.sdu.dk/).

Peter Schwerdtfeger

Peter Schwerdtfeger received his PhD from Stuttgart University in 1986. He became a Feodor-Lynen Alexander von Humboldt Fellow in 1987 at the University of Auckland, and a research fellow at the Australian National University in 1989. In 1991 he took up a lectureship at the University of Auckland, received his habilitation and venia legendi from the Philipps-University in Marburg in 1995, and in 1999 was awarded a personal chair at Auckland University. In 2001 he received a James Cook Fellowship. Since March 2004 he has held the chair in theoretical chemistry at Massey University in Auckland. His current research interests are in all aspects of electronic structure theory and relativistic quantum theory. He has been honoured with the Prince and Princess of Wales Science Award (1988), the SGS Prize (1994), the Hector Medal (2001), and is a Fellow of the Royal Society of New Zealand.

---

Introduction

Chirality is commonly regarded as the property of geometrical objects that cannot be brought to coincide with their mirror-image. From the stereochemical point of view, chirality is the property of those stereomers that are called enantiomers. Note that in this context space reflection and space inversion are equivalent since the two symmetry operations differ by a π rotation about an axis perpendicular to the mirror plane, which does not change the handedness of the molecule. Although the existence of stable enantiomers at first sight seems trivial, this is not so from a quantum mechanical point of view. The standard Hamiltonian which describes the electromagnetic interactions between the constituent particles of a molecule is invariant under space inversion, and enantiomers cannot therefore correspond to eigenstates of this Hamiltonian since they do not have well-defined parity. This problem was addressed by Hund as early as 1927¹ who concluded that once a particular enantiomer has been prepared the barrier to interconversion typically gives tunneling times of million of years, in other words, the enantiomer is kinetically stable. However, this argument does not rule out the possibility of preparing a superposition of single molecule enantiomers, something which has never been observed by experiment so far.² Interactions with the environment would subsequently lead to localization to a particular enantiomer and one would have to carry out experiments on the isolated molecule at very low temperatures. However, even under such conditions localization, or rather the oscillation of handedness, would occur with the introduction of parity non-conservation in the Hamiltonian. The total Hamiltonian H then consists of a parity even (H₀) and odd (H_PV) part,

H = H₀ + H_PV (1)

and therefore transforms as

P⁻¹HP = H₀ − H_PV = H − 2 H_PV ≠ H (2)

where P is the parity operator. Consequently, if one enantiomer (R) becomes stabilized by E_PV, its mirror image (L) then becomes destabilized by the same amount and we obtain an energy difference between two enantiomers

ΔE_PV = E_PV,L − E_PV,R = 2 E_PV (3)

commonly called parity violation energy difference (PVED). A fascinating aspect of PVED in chiral molecules is the possible link to the origin of biochirality,³ since the chemistry of life is based on L-amino acids and D-monosaccharides.

Among the four fundamental forces that rule the physical world, only the weak force⁴ does not conserve parity. Although parity violation has been observed in nuclear⁵ and atomic physics,⁶ it has never been unequivocally observed at the molecular level to date. Such a tiny energy difference (about 10⁻¹⁷kT at 300 K) should be measurable by any absorption spectroscopy provided a high resolution is reached.⁷ Several unsuccessful attempts have been made; for instance Mössbauer spectroscopy has been conducted on an iron complex,⁸ and circular dichroism was measured in recrystallized transition metal complexes.⁹ NMR has also been suggested as a possible technique to measure parity violation.¹⁰ Interestingly, infra-red (IR) spectroscopy has been the focus of several groups, following an original idea of Letokhov.¹¹ In 1977, Glorieux et al. tried to measure differences in absorption energies of camphor enantiomers.¹² The resolution reached (300 kHz) was too low to evidence PV effects (see below). Quack has proposed several types of spectroscopic experiments, among which are the measurement of time-dependent optical activity in molecules displaying tunneling splitting and PVED of the same magnitude and a direct measurement of ΔE_PV using an intermediate spectroscopic level such as an excited achiral electronic state.¹³

In this paper we will provide a case study in the form of our joint efforts to detect PVED by infra-red spectroscopy. To evidence such tiny effects as PV in molecules, much care has to be taken to control and to improve the sensitivity and the resolution of the spectroscopy technique used. An experiment reaching a resolution of 10⁻¹³ for the relative frequency difference (Δν_PV/ν) has been carried out on bromochlorofluoromethane (CHFClBr) in Chardonnet’s laboratory and is described below. Preparation of enantioenriched molecules which are particularly favorable for PV observation is also most challenging. Chiral synthesis is currently being carried out by Crassous’s team and is also described in this paper. Finally, concomitant theoretical calculations (conducted at the relativistic level by Saue and Schwerdtfeger) aim at a better understanding of the origin of PV in molecules and guide the choice of chiral molecules for future experiments.

Theoretical considerations

Any measurement of PV effects between enantiomers of a chiral molecule requires strict verification by theory. Hence, a direct measurement of PV energy differences between enantiomers offers the best chance of both experimental and theoretical verification. Other suggested experiments like direct polymerization, condensation and crystallization¹⁴ will suffer from the lack of theoretical justification for such complex processes. Let us therefore briefly summarize some important theoretical aspects of the electroweak interaction between charged particles important for chiral molecular systems. A more detailed theoretical description has been given recently by Berger.¹⁵

In quantum field theory electromagnetic interactions are viewed as an exchange of virtual photons. In molecular systems the weak interaction is dominated by the exchange of virtual Z⁰ bosons between electrons and nucleons. The corresponding Hamiltonian is expressed as^16,17

The summation is over all electrons i and nuclei n. r_in is the distance between electron i and nucleus n. G_F is the Fermi-coupling constant with a current value of G_F = (1.16637 ± 0.00002) × 10⁻¹¹ MeV⁻² or (2.22255 ± 0.00004) × 10⁻¹⁴ au, clearly indicating how weak the interaction really is. Q_W,n = −N_n + Z_n (1 − 4 sin²θ_W) is the weak nuclear charge of nucleus n where Z is the number of protons and N the number of neutrons. ρ_n (r_in) is the (normalized) weighted average over the proton and neutron distribution in the nucleus and this operator therefore only samples the electronic wave function in this very local region. θ_w is the Weinberg angle with sin²θ_w = 0.2259 ± 0.0046. K_n is a factor dependent on the nucleus also containing the Weinberg angle, and I is the nuclear spin operator. Finally, α and γ₅ are the well known Dirac matrices. This interaction Hamiltonian is accordingly expressed within a four-component relativistic framework, that is as an extension to the Dirac equation. It is possible to reduce it to a non-relativistic form, but a zero result is obtained with H⁽¹⁾_PV unless the spin–orbit interaction, which is a truly relativistic effect, is included. We refer to 19,20 and 22 for further details on the non-relativistic approach.

The nuclear spin dependent term H⁽²⁾_PV shown in eqn. (4) is the dominant operator for Mössbauer and nuclear magnetic resonance transitions.^18,10c The first term H⁽¹⁾_PV is the dominant operator for electronic or vibrational transitions and has been used in most theoretical investigations of PV effects. At the relativistic Hartree–Fock level the parity non-conserving energy shift E_PV is obtained to first order as an expectation value.¹⁹

At the four-component relativistic level, electron correlation has been introduced through finite-field coupled-cluster calculations as well as analytic density functional or second-order Møller–Plesset theory.²⁰

It is currently a nontrivial issue to find the right compound for molecular PV measurements.²¹ In Quack's influential review article from 1989 on structure and dynamics of chiral molecules²² a number of chiral species was suggested which deserve further experimental and theoretical study. Most of the current theoretical work concentrates on vibrational transitions, although we mention here theoretical work on Mössbauer,⁸ NMR,¹⁰ and electronic spectroscopy.²³ Molecular beam experiments using a high precision tuneable CO₂ laser currently offer the best resolution for PV measurements. In fact, one of the first attempts to find PV differences in transition frequencies was made by Arimondo et al. in 1977 using the 1083.4788 cm⁻¹ R(28) CO₂ laser line for D- and L-camphor,¹² which lies in the C–C*–CO bending mode range (C* denotes a chiral carbon). They concluded that PV effects in camphor must be below 300 kHz. A recent relativistic theoretical study shows that PV effects in camphor are probably below 10⁻⁵ Hz.²⁴ It is therefore of no surprise that Rein stated in 1975 that the direct observation of energy differences between optical isomers is beyond the scope of present experimental facilities²⁵ (and still it is). However, parity violation effects scale as Zⁿ (n ≈ 5 for H⁽¹⁾_PV and n ≈ 3 for H⁽²⁾_PV, Z is the nuclear charge),²⁶ as shown in Fig. 1 in the case of H₂X₂ molecules for E_PV (see eqn.(5)) and for the NMR frequency shift. This high Z-scaling behaviour implies that one has to introduce one or more heavy elements into the chiral molecular system, either as a central atom or as a ligand (or both because of the single-center theorem²⁷), in order to reach the current experimental limit of around 1 Hz. The CO₂ laser operates in the C–F vibrational frequency range and recent theoretical and experimental work therefore concentrated on chiral methane fluoride derivatives.

Fig. 1 Z ⁿ scaling behaviour for the Group 16 H₂X₂ systems for the PV energy contribution ΔE_PV (in kJ mol⁻¹) and for the PV line splitting Δν_PV (in Hz) where B₀ (in T) is the static magnetic flux density of the NMR spectrometer. Data were taken from refs. 10c–20.

Theoretical work on CHFClBr from three different research groups showed that the parity violation energy contribution E_PV is around 0.03 Hz³⁹ at the Hartree–Fock level of theory (1 au = 6.5797 × 10¹⁵ Hz = 2625.5 kJ mol⁻¹), while a simple one-dimensional approach along the C–F stretching normal mode gave a PV difference Δν_RL = v_PV,R − v_PV,L of −1.7 mHz²⁸ for the fundamental transitions (v_PV,R and v_PV,L defined in an analogous way to eqn. (3)). A few important facts should be mentioned however. First, anharmonicity effects in the C–F stretching mode cannot be neglected, including only harmonic effects gives the wrong sign for v_PV,R or v_PV,L.^39a,29 Second, coupling with other modes can substantially alter Δv_RL as demonstrated in Quack's group.³⁰ In fact, for CDFClBr a substantial enhancement in Δv_RL is predicted. This implies that future high precision theoretical work has to include possibly all nine normal modes in the vibrational analysis. Third, electron correlation is important for the determination of E_PV contrary to what has been believed so far, and various density functionals give quite different results leading even to a change of sign for E_PV.³¹ However, Δv_RL values seem to be typically an order or two in magnitude smaller than absolute energy differences and do not vary substantially between different methods.

Other potential candidates for vibrational PV measurements are CHFClI, CHFBrI and CFClBrI.¹⁹ Out of this series CHFBrI seems to be the most promising molecule with a calculated four-component relativistic Hartree–Fock value of Δv_RL = −50.8 mHz for the C–F stretching fundamental transition.²⁸ Future investigations will need to improve this value using a multi-mode analysis and E_PV calculated at the correlated level of theory for both CHFBrI and CDFBrI.

Faglioni and Lazzeretti recently considered BiHFBr and BiHFI.³² These systems are non-planar with a predicted high inversion barrier and are therefore chiral. The PV frequency shift Δv_RL is very high and possibly up to about 20 Hz, but these species are thermodynamically unstable and one needs to consider the first overtone of the H–Bi–X bending mode in order to reach the CO₂ laser frequency range. On a similar basis, E_PV values were reported for all Group 14 compounds EHFClBr (E = C, Si, Ge, Sn and Pb).^39a However, these compounds become less thermodynamically stable with increasing nuclear charge on the central atom, and the important fundamental modes lie outside the CO₂ laser frequency range.

A number of other compounds with relatively high parity violation energy differences were suggested in the past, namely Ge(CF₃)ClBrI, Os(η⁵-C₅H₅)(CHPh)Cl(PⁱPr₃), Re(η⁵-Cp*)(O)(CR₃)Cl (Cp* = C₅(CH₃)₅), (η⁵-C₅H₅)Re(CO)(NO)I, ClHgCHFBr, PR₃AuCHFClBr and BiCH₃I(κ²-CH₂(CH)₂NH₂),^33–34,35 some of them are known in the literature. The calculated Hartree–Fock E_PV reported were in the 100 Hz region, but it is not clear how electron correlation might change these values. Nevertheless, for two model compounds, Os(η⁵-C₅H₅)(=CCl₂)Cl(PH₃) and Re(η⁵-Cp*)(=O)(CH₃)Cl the vibrational spectra have been calculated (Fig. 2), with the Os=CCl₂ and the Re=O stretching modes both in the CO₂ laser frequency range, and a calculated Δv_RL value of around 1 Hz.³⁵ It is however questionable if these molecules are suitable for high precision vibrational spectroscopy.

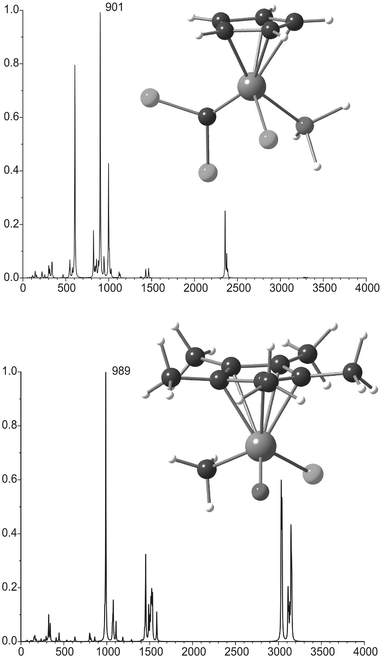Fig. 2 Predicted vibrational spectra for the model compounds Os(η⁵–C₅H₅)(=CCl₂)Cl(PH₃) and Re(η⁵–Cp*)(=O)(CH₃)Cl. The most intense lines indicated belong to the Os=C and Re=O stretching modes respectively. Data taken from ref. 35.

Accurate IR spectroscopy of bromochlorofluoromethane enantiomers: first set of experiments

In order to reach the best resolution to be able to observe parity violation in molecules, saturation spectroscopy (which suppresses the Doppler broadening, reducing the molecular linewidth from 50 MHz down to 10 kHz) together with a home-made ultrastable CO₂ laser were used. These experiments were first performed on S-(+) and R-(−)-CHFClBr (1) having enantiomeric excesses (ee's) of 56.5 and 22%, respectively.³⁶ Twin 3 m long Fabry-Perot cavities were each filled with one of the two enantiomers of CHFClBr and fed with the frequency-stabilized CO₂ laser. One hyperfine component of the ν₄ C–F stretching fundamental band of CHF³⁷Cl⁸¹Br was selected and differences in the frequency absorption of this transition for the two enantiomers placed in the two cavities were searched for. Note that it is essential to have the enantiomers available because we perform the spectroscopy on the two species separately and the sensitivity of the comparison is limited by the precision with which we measure the line center and not by the resolution of the experiment which would be the case with a racemic mixture, the typical gain in sensitivity is about four orders of magnitude. Over 580 measurements a mean difference of 9.4 Hz was obtained, with a statistical uncertainty of 5.1 Hz and residual systematic uncertainties due to the instrumentation of 12.7 Hz,³⁷ν_exp (R-(−)-1)–ν_exp (S-(+)-1) = 9.4 ± 5.1 ± 12.7 Hz. Consequently, no PV effect could be observed at a relative sensitivity of Δν/ν = 3.9 10⁻¹³, but an improvement of five orders of magnitude was achieved compared to the experiment done on camphor.¹²

In another improved experimental set up, a stronger and narrower CHFClBr test transition was selected,³⁸ and samples having higher ee's for (+) and (−)-1 (72% and 56%, respectively) were used. Over 771 measurements the final result obtained for the average frequency difference between the lines of the two samples of enantiomers was ν_exp (R-(−)-1)–ν_exp (S-(+)-1) = − 4.2 ± 0.6 ± 1.6 Hz (including statistical and systematic uncertainties due to the instrumentation), which corresponds to a relative sensitivity of Δν/ν = 4 × 10⁻¹⁴ for the frequency difference (the absolute frequency itself was also precisely measured: ν = 32 397 293 834.1 ± 3.0 kHz). The latter set of experiments also revealed that the significant frequency difference was proportional to pressure and cannot be a signature of a PV effect. This is probably due to uncontrollable residual gases present in the cells at a level below 5% for a typical pressure of 0.05–0.1 Pa. In parallel, quantum chemistry calculations on the expected vibrational frequency shift in the case of CHFClBr³⁹ have concluded that the PV effect is three orders of magnitude smaller than the experimentally reached sensitivity.

Synthesis of chiral molecules for the observation of PV

As mentioned above, the first candidates for the observation of PV by the use of ultrastable CO₂ were simple chiral molecules containing one asymmetric carbon and one C–F bond, displaying a C–F stretching mode around 1000 cm⁻¹, namely bromochlorofluoromethane (CHFClBr) 1 and chlorofluoroiodomethane (CHFClI) 2. The synthesis of enantioenriched forms of such compounds that are devoid of chemical function requires original synthetic methods. In these two cases a decarboxylation reaction in a protic solvent of an appropriate diastereomerically enriched strychninium salt⁴⁰ was used. In this way, it was possible to provide physicists with samples of (+)-1 and (−)-1 with respective ee's between 56–72% and 22–56% for PVED tests. Today it is possible to prepare (+) and (−)-1 with ee's up to 89% and 56% respectively by decarboxylation in ethyleneglycol at 120 °C of diastereomerically enriched salts {(+)-FClBrC–CO₂H, (−)-strychnine} and {(−)-FClBrC–CO₂H, (−)-strychnine}.⁴¹ Similarly (+)-2 and (−)-2 with ee's up to 63.3% and 23% respectively⁴² were prepared by decarboxylation of diastereomerically enriched salts {(+)-FClIC–CO₂H, (−)-strychnine} and {(−)-FClIC–CO₂H, (−)-strychnine}, in triethyleneglycol at 110 °C and under reduced pressure (see Scheme 1). Such reaction is known to take place with retention of configuration.⁴³ Future work will also consider the deuterated species of 1 and 2.

Scheme 1 Synthesis of enantioenriched samples of S-(+)-2 and R-(−)-2 by decarboxylation of diastereomerically resolved strychninium salts. The ee's were measured by gas chromatography on a chiral stationary phase and by NMR of a complexation process.

The enantiomeric purities of 1 and 2 could be obtained by two methods. A first method used low temperature analytical gas-chromatographic separation on an immobilized chiral stationary phase based on octakis(3-O-butanoyl-2,6-di-O-n-pentyl)-γ-cyclodextrin.^42,44 In a second method a host–guest complexation process with enantioenriched chiral cryptophane hosts was used. For instance, (−)-cryptophane-C ((−)-3) enabled measurement of the enantiomeric purities of (+)-1 and (−)-1 samples.^41,45 Indeed, diastereomeric host–guest complexes {(+)-1 @ (−)-cryptophane-C} and {(−)-1 @ (−)-cryptophane-C} could be visualized by ¹H NMR in CDCl₃ at 300 K. A thiomethylated cryptophane, namely (−)-cryptophane-E-(SCH₃)₆ ((−)-4),⁴⁶ was used in the case of (−)-2 and gave an ee of 23 ± 3%. In this case, the diastereomeric host–guest complexes {(+)-1 @ (−)-cryptophane-E-(SCH₃)₆} and {(−)-1 @ (−)-cryptophane-E-(SCH₃)₆} were visualized by ¹⁹F NMR in C₂D₂Cl₄ at 300 K (see Fig. 3). The question of the absolute configuration has been addressed by Raman optical activity (ROA) and molecular dynamics simulations for R-(−) and S-(+)-1⁴⁷, and more recently by optical rotation calculation⁴² and vibrational circular dichroism (VCD) for R-(−) and S-(+)-2.⁴⁸

Fig. 3 Ee determination of (−)-2 by ¹⁹F NMR in C₂D₂Cl₄ at 300 K using cryptophane (−)-4 as a chiral complexing agent. Two doublets corresponding to diastereomeric host–guest complexes {(+)-2 @ (−)-4} and {(−)-2 @ (−)-4}.

As explained above, organometallic complexes containing heavier atoms display much higher PV effects. For this reason, we are now focused on the synthesis of chiral–at–metal complexes. These are, for example, oxorhenium complexes bearing chiral ligands which transfer their chirality to the metal atom. As mentioned above, the presence of the Re=O bond is very important because its stretching mode at 900–1000 cm⁻¹ can be brought to coincidence with the CO₂ absorption lines. Compounds of this type have recently been described by Faller et al.⁴⁹ Several grams of oxorhenium complexes TpReO(ephedrine) and TpReO(proline) (Tp = hydrotrispyrazolylborate) can be obtained in a few steps.

A complete determination of spectroscopic (rotational and rovibrational) constants of the racemic molecule is necessary because it enables one to identify a few rovibrational bands which could be favorable for a PV test. In this context, a supersonic molecular beam could easily be obtained with CHFClI, and microwave⁵⁰ and rovibrational⁵¹ spectroscopy could be studied. In comparison, nothing is known about oxorhenium complexes and much effort will be made in the following months to investigate the rotational and vibrational spectroscopy of these chiral rhenium complexes for the purpose of a PV test based on the new experimental set-up described in the following section.

A new experimental set-up

Although more favorable molecules for the PV effect are very promising, the experimental set-up based on saturation spectroscopy in absorption cells already shows its limits. Molecular beam spectroscopy using a two-photon Ramsey fringe experiment, recently developed in Villetaneuse, seems to be very promising mainly because the collisional effects can be reduced by more than three orders of magnitude. The principle of this experiment is to generate a supersonic beam of chiral molecules which expands in a high-vacuum chamber (residual pressure below 10⁻⁴ Pa). This beam will interact with two standing waves generated in a four-mirror Fabry-Perot cavity. A Doppler-free two-photon transition between v = 0 and v = 2 vibrational levels occurs in each standing wave and an interference signal between the two excitation channels reveals Ramsey fringes with a resolution proportional to the inverse of the molecular time of flight between the two zones. With a supersonic beam of SF₆ and a distance between zones of 1 m, a resolution of 100 Hz was obtained⁵² (see Fig. 4) which is three orders of magnitude higher than with the PV experiment in cells. The absolute frequency was measured very precisely at 28 412 764 347 322.1 ± 2.7 Hz. In a differential experiment that we plan to do, the uncertainty should be much lower since a lot of the systematic effects cancel out. The idea is to adapt this set-up for a new PV experiment: we will use a unique beam machine and feed it alternatively with the two enantiomers with a cycling time of 1–10 s to record separately the two spectra and directly compare the line centers. One essential advantage will be that the laser–molecule interaction conditions will be exactly the same. We can expect a sensitivity of 0.01 Hz, which should be enough to detect unambiguously the PV effect with the new generation of molecules. However, one must say that this expectation will be highly dependent on the quality of the signal that we obtain. This is related to the capability of feeding the beam with molecules which are solid at room temperature. Heating or laser techniques exist to sublimate molecules but must be checked on each particular case.

Fig. 4 Simplified block diagram of the two photon Ramsey fringes experiment with a supersonic beam of SF₆. A first CO₂ laser locked to the saturation signal of OsO₄ is used as a local oscillator. A second laser is phase-locked to the first one and can be tuned with a RF synthesizer (not shown) through the Ramsey fringes. The detection of the population in the v = 2 level is performed by shifting the laser frequency on another optical path to reach the resonance with the transition v = 2→v = 1. The spectrum with a 100 Hz resolution and a signal to noise ratio of 45 over 1 s is displayed.

Conclusion

In this paper we have described our attempts to observe parity violation in molecular systems using very accurate infra-red spectroscopy based on a CO₂ laser. For this purpose, simple chiral molecules such as CHFClBr and CHFClI have been prepared in enantiomerically enriched forms and very accurate IR spectroscopy has been conducted on bromochlorofluoromethane enantiomers, improving the sensitivity by five orders of magnitude compared to a former test conducted on camphor. In parallel, highly accurate relativistic calculations have been done on the chiral halogenomethanes, but also on more favourable molecules such as transition metal complexes.

In summary, we have shown the interplay between theory and experiment. Quantum chemical calculations serve to guide and validate experiment and may provide a deeper understanding of the effect of the molecular environment. The synthesis of candidate molecules in enantiomerically enriched forms is a non-trivial task. The detection of PV effects in molecules pushes spectroscopic techniques to their limits. Similarly, high precision calculations are needed to confirm these experiments.

If successful, these experiments allow tests of the standard model of the universe in the low-energy regime. They may answer important questions regarding the stability and reactivity of chiral molecules. Although there are a number of papers proposing that biomolecular chirality is, or may be, a consequence of PV,^1,7b,53–60 there is currently, in our opinion, no proof that such a connection exists.^7,61–66 It may, furthermore, be difficult to establish such a connection.^67,68 For a nice recent review on the origin of homochirality in nature see Frank, Bonner and Zare.⁶⁹

Acknowledgements

Radovan Bast is warmly thanked for providing us with a cover picture.

References

1. F. Hund, Z. Phys., 1927, 43, 805–826.
2. J. A. Cina and R. A. Harris, J. Chem. Phys., 1994, 100, 2531–2536.
3. Y. Yamagata, J. Theor. Biol., 1966, 11, 495–498.
4. D. Lee and C. N. Yang, Phys. Rev., 1956, 104, 254–258.
5. C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes and R. P. Hudson, Phys. Rev., 1957, 105, 1413–1415.
6. (a) M. A. Bouchiat and C. C. Bouchiat, Phys. Lett. B, 1974, 48, 111–114; (b) L. M. Barkov and M. S. Zolotorev, JETP, 1980, 52, 360–376; (c) M. A. Bouchiat and C. C. Bouchiat, Rep. Prog. Phys., 1997, 60, 1351–1396; (d) C. S. Wood, S. C. Bennett, D. Cho, B. P. Masterson, J. L. Roberts, C. E. Tanner and C. E. Wieman, Science, 1997, 275(5307), 1759–1763.
7. Following the Salam hypothesis, calorimetry has also been used to attempt to detect PV in phase transitions in amino acid crystals. See: (a) A. Salam, in Chemical Evolution: Origin of Life, ed. C. Ponnamperuma and J. Chela-Flores, A Deepak Publishing, Hampton, VA, 1993, pp. 101–107; (b) W. Wang, F. Yi, Y. Ni, Z. Zhao, X. Jin and Y. Tang, J. Biol. Phys., 2000, 26, 51–65; (c) R. Sullivan, M. Pyda, J. Pak, B. Wunderlich, J. Thompson, R. Pagni, H. Pan, C. Barnes, P. Schwerdtfeger and R. Compton, J. Phys. Chem. A, 2003, 107, 6674–6680.
8. A. S. Lahamer, S. M. Mahurin, R. N. Compton, D. House, J. K. Laerdahl, M. Lein and P. Schwerdtfeger, Phys. Rev. Lett., 2000, 85, 4470–4473.
9. (a) A. Szabo-Nagy and L. Keszthelyi, Proc. Natl. Acad. Sci. USA, 1999, 96, 4252–4255; (b) A. Szabo-Nagy, and L. Keszthelyi, in Advances in Biochirality, ed. P. Gyula, C. Zucchi and L. Caglioti, Elsevier, Amsterdam, 2002, pp. 367–376.
10. (a) A. L. Barra, J. B. Robert and L. Wiesenfeld, Phys. Lett. A, 1986, 115, 443–447; (b) A. L. Barra and J. B. Robert, Mol. Phys., 1996, 88, 875–886; (c) G. Laubender and R. Berger, ChemPhysChem., 2003, 4, 395–399.
11. (a) V. S. Letokhov, Phys. Lett., 1975, 53A, 275–277; (b) O. N. Kompanets, A. R. Kukudzhanov, V. S. Letokhov and L. L. Gervits, Opt. Commun., 1976, 19, 414–416.
12. E. Arimondo, P. Glorieux and T. Oka, Opt. Commun., 1977, 23, 369–372.
13. M. Quack, Angew. Chem. Int. Ed., 2002, 41, 4618–4630 , and references therein.
14. (a) L. Keszthelyi, J. Biol. Phys., 1994, 20, 241–245; (b) L. Keszthelyi, Mendeleev Commun., 2003, 13, 129–130; (c) L. Keszthelyi, Orig. Life Evol. Biosphere, 2001, 31, 249–256.
15. R. Berger, in Relativistic Electronic Structure Theory. Part 2: Applications, ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2004, pp. 188-288.
16. S. A. Blundell, J. Sapirstein and W. R. Johnson, Phys. Rev. D, 1992, 45, 1602–1623.
17. J. Sapirstein, in Relativistic Electronic Structure Theory. Part 1: Fundamentals, ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2002, pp. 468-522.
18. A. Soncini, F. Faglioni and P. Lazzeretti, Phys. Rev. A, 2003, 68, 33402.
19. J. K. Laerdahl and P. Schwerdtfeger, Phys. Rev. A, 1999, 60, 4439–4453.
20. J. N. P. van Stralen, L. Visscher, C. V. Larsen and H. J. Aa. Jensen, Chem. Phys., 2005, 311, 81–95.
21. F. Faglioni and P. Lazzeretti, Phys. Rev. E, 2002, 65, 11904.
22. M. Quack, Angew. Chem. Int. Ed. Engl., 1989, 28, 571–586.
23. R. Berger, Phys. Chem. Chem. Phys., 2003, 5, 12–17.
24. P. Schwerdtfeger, A. Kühn, R. Bast, J. K. Laerdahl, F. Faglioni and P. Lazzeretti, Chem. Phys. Lett., 2004, 383, 496–501.
25. D. W. Rein, J. Mol. Evol., 1974, 4, 15–22.
26. M. A. Bouchiat and C. Bouchiat, J. Phys. (Paris), 1974, 35, 899; M. A. Bouchiat and C. Bouchiat, J. Phys. (Paris), 1974, 36, 493.
27. R. A. Hegstrom, D. W. Rein and P. G. H. Sandars, J. Chem. Phys., 1980, 73, 2329–2341.
28. P. Schwerdtfeger, J. K. Laerdahl and Ch. Chardonnet, Phys. Rev. A, 2002, 65, 42508.
29. M. Quack and J. Stohner, Chirality, 2001, 13, 745–753.
30. M. Quack and J. Stohner, J. Chem. Phys., 2003, 119, 11228–11240.
31. P. Schwerdtfeger, T. Saue, J. N. P. van Stralen and L. Visscher, Phys. Rev. A, 2005, 71, 12103.
32. F. Faglioni and P. Lazzeretti, Phys. Rev. A, 2003, 67, 32101.
33. P. Schwerdtfeger, J. Gierlich and T. Bollwein, Angew. Chem. Int. Ed., 2003, 42, 1293–1296.
34. R. Bast and P. Schwerdtfeger, Phys. Rev. Lett., 2003, 91, 23001.
35. P. Schwerdtfeger and R. Bast, J. Am. Chem. Soc., 2004, 126, 1652–1653.
36. J. Crassous and A. Collet, Enantiomer, 2000, 5, 429–438.
37. (a) C. Daussy, T. Marrel, A. Amy-Klein, C. T. Nguyen, C. J. Bordé and C. Chardonnet, Phys. Rev. Lett., 1999, 83, 1554–1557; (b) C. Chardonnet, C. Daussy, T. Marrel, A. Amy-Klein, C. T. Nguyen and C. J. Bordé, in Parity Violation in Atomic Physics and Electron Scattering, ed. B. Frois and M. A. Bouchiat, World Scientific, New-York, 1999, 325-355; (c) C. Chardonnet, T. Marrel, M. Ziskind, C. Daussy, A. Amy-Klein and C. J. Bordé, J. Phys. IV, 2000, 10-Pr8, 45–54.
38. M. Ziskind, T. Marrel, C. Daussy and C. Chardonnet, Eur. Phys. J. D, 2002, 20, 219–225.
39. (a) J. K. Laerdahl, P. Schwerdtfeger and H. M. Quiney, Phys. Rev. Lett., 2000, 84, 3811–3814; (b) M. Quack and J. Stohner, Zeit. Phys. Chem., 2000, 214, 675–703; (c) R. G. Viglione, R. Zanasi, P. Lazzeretti and A. Ligabue, Phys. Rev. A, 2000, 62, 52516-1-5.
40. Diastereomerically enriched strychninium salt {(+)-FClBrC–CO₂H, (−)-strychnine} and {(−)-FClBrC–CO₂H, (−)-strychnine} were obtained with respective diastereomeric excesses (de) of 81% and 48–51%. Indeed, these diastereomeric salts displayed in methanol a ternary solubility diagram corresponding to a solid solution. For more details see J. Costante, N. Ehlinger, M. Perrin and A. Collet, Enantiomer, 1996, 1, 377–386.
41. J. Crassous, F. Monier, J.-P. Dutasta, M. Ziskind, C. Daussy, C. Grain and C. Chardonnet, ChemPhysChem., 2003, 4, 541–548 and references therein.
42. J. Crassous, Z. Jiang, V. Schurig and P. Polavarapu, Tetrahedron: Asymmetry, 2004, 15, 1995–2001.
43. V. Schurig, M. Juza, B. J. Green, J. Horakh and A. Simon, Angew. Chem. Int. Ed. Engl., 1996, 35, 1680–1682.
44. H. Grosenick, V. Schurig, J. Costante and A. Collet, Tetrahedron: Asymmetry, 1995, 6, 87–88.
45. J. Canceill, L. Lacombe and A. Collet, J. Am. Chem. Soc., 1985, 107, 6993–6996.
46. C. Garcia, D. Humilière, N. Riva, A. Collet and J.-P. Dutasta, Org. Biomol. Chem., 2003, 1, 2207–2216.
47. (a) J. Costante, L. Hecht, P. L. Polavarapu, A. Collet and L. D. Barron, Angew. Chem. Int. Ed., 1997, 36, 885–887; (b) J. Costante-Crassous, T. J. Marrone, J. M. Briggs, J. A. McCammon and A. Collet, J. Am. Chem. Soc., 1997, 119, 3818–3823.
48. X. Cao, T. Freedman, L. Nafie and J. Crassous, to be published.
49. J. W. Faller and A. R. Lavoie, Organometallics, 2000, 19, 3957–3962.
50. A. Cuisset, J. R. Aviles Moreno, T. R. Huet, D. Petitprez, J. Demaison and J. Crassous, J. Phys. Chem. A, submitted.
51. P. Soulard, J. Crassous, P. Asselin, to be published.
52. A. Shelkovnikov, C. Grain, R. J. Butcher, A. Amy-Klein, A. Goncharov and C. Chardonnet, IEEE J. Quantum Electron., 2004, 40(8), 1023–1029.
53. A. Salam, J. Mol. Evol., 1991, 33, 105–113.
54. T. Kitayama, T. Ushikubo, K. Morihashi and O. Kikuchi, J. Mol. Struct., 2002, 586, 1–7.
55. R. Zanasi, P. Lazzeretti, A. Ligabue and A. Soncini, Phys. Rev. E, 1999, 59, 3382–3385.
56. A. J. Macdermott, Orig. Life Evol. Biosphere, 1995, 25, 191–199.
57. G. E. Tranter, Nature, 1985, 318, 172–173.
58. (a) S. F. Mason, Nature, 1984, 311, 19–23; (b) S. F. Mason, Chem. Soc. Rev., 1988, 17, 347–359; (c) S. F. Mason, Biosystems, 1987, 20, 27–35.
59. A. J. MacDermott, Orig. Life Evol. Biosphere, 1995, 25, 191–199.
60. R. Berger, M. Quack and G. S. Tschumper, Helv. Chim. Acta, 2000, 83, 1919–1950.
61. W. A. Bonner, Orig. Life Evol. Biosphere, 1996, 26, 27–45.
62. R. Berger and M. Quack, ChemPhysChem., 2000, 1, 57–60.
63. J. K. Laerdahl, R. Wesendrup and P. Schwerdtfeger, Chem. Phys. Chem., 2000, 1, 60–62.
64. R. Wesendrup, J. K. Laerdahl, R. N. Compton and P. Schwerdtfeger, J. Phys. Chem. A, 2003, 107, 6668–6673.
65. P. Schwerdtfeger and U. Müller-Herold, in Symmetry 2000, Part 1, ed. I. Hargittai and T. C. Laurent, Portland Press, London, 2002, pp. 317-328.
66. R. A. Hegstrom and D. K. Kondepudi, Sci. Am., 1990, 262, 108–115.
67. W. A. Bonner, Chirality, 2000, 12, 114–126.
68. R. N. Compton and R. M. Pagni, Adv. At. Mol. Opt. Phys., 2002, 48, 219–261.
69. P. Frank, W. A. Bonner and R. N. Zare, in Chemistry for the 21st Century, ed. E. Keinan and I. Schechter, Wiley-VCH, Weinheim, 2001, pp. 173-208.

---