Mechanistic studies of La³⁺- and Zn²⁺-catalyzed methanolysis of aryl phosphate and phosphorothioate triesters. Development of artificial phosphotriesterase systems

Abstract

The methanolyses of a series of O,O-diethyl O-aryl phosphates (2,5) and O,O-diethyl S-aryl phosphorothioates (6) promoted by methoxide and two metal ion systems, (La³⁺)₂(⁻OCH₃)₂ and 4:Zn²⁺:⁻OCH₃ (4 = 1,5,9-triazacyclododecane) has been studied in methanol at 25 °C. Brønsted plots of the log k₂ values vs.^s_spK_a for the phenol leaving groups give β_lg values of −0.70, −1.43 and −1.12 for the methanolysis of the phosphates and −0.63, −0.87 and −0.74 for the methanolysis of the phosphorothioates promoted by the methoxide, La³⁺ and Zn²⁺ systems respectively. The kinetic data for the metal-catalyzed reactions are analyzed in terms of a common mechanism where there is extensive cleavage of the P–XAr bond in the rate-limiting transition state. The relevance of these findings to the mechanism of action of the phosphotriesterase enzyme is discussed.

---

Introduction

Phosphorus triesters and phosphonate esters of general structure 1 (LG = leaving group, Z = alkyl, aryl, alkoxide or aryloxide) are widely used as insecticides, acaricides^1,2 and OP-based chemical warfare (CW) agents.³ Owing to their toxicity and lingering effects on the environment, considerable effort has been directed toward methods of facilitating the controlled decomposition of these materials, particularly through hydrolysis and oxidation.^3,4 Transition metal ions and lanthanides and certain mono- and di-nuclear complexes thereof are known to promote the hydrolysis of neutral phosphate and/or phosphonate esters,^5,6 and Pt and Pd metallocycles are remarkably efficacious for thiophosphate pesticide hydrolysis.⁷

By contrast, metal-catalyzed alcoholysis reactions of organophosphates have received scant attention, although our recent work indicates that this is an effective strategy for the destruction of neutral organophosphate esters.⁸ For example, a methanolic solution of 2 mmol dm⁻³ in each of La³⁺ and NaOCH₃ catalyzed the methanolysis of paraoxon (2, also a simulant for the phosphonofluoridate chemical weapon G-agents) by 10⁹-fold relative to the background reaction at near-neutral ^s_spH ^9,10 and ambient temperature. La³⁺, and other lanthanides, also promote the ethanolysis of paraoxon¹¹ and the 1,5,9-triazacyclododecane complexes of Zn²⁺ or Cu²⁺, as their monomethoxy forms (4:M²⁺:⁻OCH₃), give excellent catalysis of the methanolysis of 2 and of the P=S derivative, fenitrothion (3) for which La³⁺ is ineffective.¹² A preliminary analysis of the effects of structural variation in the phosphate¹³ on the rates of catalyzed methanolysis of 2, its phenyl counterpart 5a, and the two corresponding O,O-diethyl S-phenyl- and O,O-diethyl S-(p-nitrophenyl)-phosphorothioate derivatives, 6a and 6b, indicated that the La³⁺-catalyzed methanolysis of the phosphorus esters is very sensitive to the nature of the leaving group, contrasting the relative insensitivity for La³⁺-catalyzed methanolysis of the corresponding aryl acetate esters.^14,15 At the ^s_spH optimum of 9 the second-order rate constants for La³⁺-catalyzed methanolysis of p-nitrophenyl acetate and phenyl acetate are very similar at 38 and 29 dm³ mol⁻¹ s⁻¹,^14,15 while those for methanolysis of 2 and 5a vary by 1000-fold at ca. 2 dm³ mol⁻¹s⁻¹ and ca. 1.3 × 10⁻³ dm³ mol⁻¹s⁻¹ respectively.¹³

The large leaving group effect on the rate of the La³⁺-catalyzed methanolysis of these phosphate triesters prompted the present investigation of the La³⁺- and Zn³⁺-catalyzed methanolysis of a series of phosphate (2,5) and phosphorothioate (6) esters. As will be shown, the mechanism of this reaction proceeds through a rate-limiting transition state having a very large degree of cleavage of the P-leaving group bond and is thus very different from that determined for the metal-catalyzed methanolysis reactions of the corresponding phenoxy acetate esters. These findings have important implications for the mechanism of action of phosphotriesterase, a dinuclear Zn²⁺-containing enzyme isolated from a soil bacterium, that effectively catalyzes the hydrolysis of paraoxon.¹⁶

Experimental

(a) Materials

3-Nitrophenol (99%), pentafluorophenol (99+%), 4-chlorophenol (99+%), 4-chloro-2-nitrophenol (98%), 4-methoxyphenol (99%), 4-methoxythiophenol (97%), 4-fluorothiophenol, NaHSO₄, diazabicycloundecane (98%), and diethyl chlorophosphate (97%) were purchased from Aldrich and used as supplied. 4-Chlorothiophenol (98%, Acros Organics) and 3,5-dichlorothiophenol (98%, Matrix Scientific) were used as supplied.

Phosphates 2 and 5a as well as phosphorothioates 6a and 6b were available from a previous study.¹³ All the other esters were prepared according to the following general protocol. CAUTION: phosphorothioates 6, and the phosphate triesters 2 and 5 are all acetylcholinesterase inhibitors, and should be synthesized and used with due attention to safety protocols.

Phosphates: 10 mmol of the appropriate phenol was added slowly to a solution of 1.6 mL diazabicycloundacene (DBU) in 20 mL of dry THF under argon and the resulting mixture was cooled in an ice bath while slowly adding 10 mmol diethylphosphoryl chloride. The mixture was then allowed to stir at room temperature for 3 h. The products were extracted three times with 20 mL of diethyl ether and washed twice with 20 mL of saturated NaHSO₄, twice with 20 mL of 10% phosphate buffer and five times with 20 mL of water. The ether layer was dried with sodium sulfate and, following filtration, the volatiles were removed by rotary evaporation. Purification was achieved by flash chromatography over silica gel eluting with ethyl acetate–hexane (1 : 5 ratio) to produce the products in yields of around 60%.

The general method for the synthesis and purification of the phosphorothioate esters was the same as for the phosphotriesters except that the thiophenols, diethyl chlorophosphate and dry THF were mixed together before introducing DBU. The yields for the syntheses of phosphorothioate esters were around 55%.

All of the above esters had ¹H NMR, ³¹P NMR, and mass spectra consistent with the structure.

(b) General UV/vis kinetics

Materials used to prepare solutions for kinetic determinations: sodium methoxide (0.5 mol dm⁻³), 1,5,9-triazacyclododecane (97%), tetrabutylammonium hydroxide (1.0 mol dm⁻³), La(OTf)₃ (99.999%), anhydrous methanol (99.8%) and N-ethylmorpholine (99%) were all commercially available (Aldrich), while Zn(OTf)₂ (98%) was obtained from Strem Chemical. Stock solutions (5 mmol dm⁻³) of each of the phosphate and phosphorothioate substrates were prepared in 99.8% anhydrous acetonitrile (Aldrich). La(OTf)₃, sodium methoxide, and tetrabutylammonium hydroxide stock solutions were made in anhydrous methanol to 50 mmol dm⁻³. Zn(OTf)₂ stock solutions in anhydrous methanol were formulated between 50 and 70 mmol dm⁻³ while the 1,5,9-triazacyclododecane stock solution in methanol was made between 30 and 50 mmol dm⁻³.

For each kinetic run using Zn²⁺, the 4:Zn²⁺:⁻OCH₃ catalyst was made in situ by adding known amounts of the Zn(OTf)₃, 1,5,9-triazacyclododecane and tetrabutylammonium hydroxide stock solutions to anhydrous methanol such that the final volume was 2.5 ml with the final ratios of ligand, Zn²⁺ and ⁻OCH₃ being 1 : 1 : 0.5 to self-buffer the solution at ^s_spH 9.1. The kinetics were followed by monitoring the change in absorbance of (0.5 to 2) × 10⁻⁴ mol dm⁻³ of 5d, 5b, 5e, 5c and 6a, 6c, 6e, 6b, 6f and 6d at 344, 276, 290, 428, 260, 266, 290, 277, 265, and 270 nm respectively. The absorbance vs. time data were fit to a standard first-order exponential equation to obtain the pseudo-first-order rate constants, k_obs. The rates of reaction were monitored in duplicate at 4–7 different catalyst concentrations from 0.4 to 2.0 mmol dm⁻³. Second-order rate constants, k₂^obs, for the catalyzed reaction were obtained from plotting k_obsvs. [4:Zn²⁺:⁻OCH₃] and are presented in Tables 1 and 2.

Table 1 Second-order rate constants (k₂) for the methanolysis of phosphates 2 and 5 promoted by methoxide, La³⁺ and 4:Zn²⁺:⁻OCH₃ in methanol solvent, T = 25 °C

Aryloxy-phosphate	pKa ^a	^sspKa ^b	k 2 ^(OMe)/dm^3 mol^−1 s^−1	k 2 ^La ^c/dm^3 mol^−1 s^−1	k 2 ^4:Zn:OMe/dm^3 mol^−1 s^−1
a pKa values in water from ref. 18. b ^sspKa values in methanol from refs. 10, 15, and 17. c k 2 ^La determined in a 17 mmol dm^−3N-ethylmorpholine buffer at ^sspH 9.1. d k 2 values from ref. 13. e From duplicate initial rate measurements monitored by ^1H NMR in CD3OD as described in the Experimental section.
Pentafluoro (5b)	5.53	8.84	0.201 ± 0.002	1070 ± 40	23.0 ± 0.6
4-Chloro-2-nitro (5c)	6.32	10.64	(6.4 ± 0.1) × 10^−2	185 ± 7	11.4 ± 0.4
p-Nitro (2)	7.14	11.30	(1.02 ± 0.03) × 10^−2	23.2 ± 0.9 ^d	1.3
m-Nitro (5d)	8.39	12.41	(6.0 ± 0.1) × 10^−3	2.42 ± 0.07	0.58 ± 0.01
p-Chloro (5e)	9.38	13.59	(6.3 ± 0.1) × 10^−4	(1.98 ± 0.07) × 10^−2	(8.04 ± 0.04) × 10^−3
p-H (5a)	10.0	14.33	1.4 × 10^−4 ^d	1.97 × 10^−3 ^d
p-Methoxy (5f)	10.20	14.7	(6.50 ± 0.01) × 10^−5 ^e	(2.2 ± 0.1) × 10^−4 ^e	(2.25 ± 0.05) × 10^−4 ^e

---

Table 2 Second-order rate constants (k₂) for the methanolysis of phosphorothioates 6 promoted by methoxide, La³⁺ and 4:Zn²⁺:⁻OCH₃ in methanol solvent, T = 25 °C

ArylS-phosphorothioate	pKa ^a	^sspKa ^b	k 2 ^OMe/dm^3 mol^−1 s^−1	k 2 ^La/dm^3 mol^−1 s^−1	k 2 ^4:Zn:OMe/dm^3 mol^−1 s^−1
a Aqueous pKa values from ref. 16e. b ^sspKa values in methanol computed from two-point linear regression pKa^(MeOH) = 1.2 (pKa^(water)) + 2.83. c Experimental ^sspKa values from ref. 19. d Kinetic k2^La values from ref. 13.
p-Nitro (6b)	4.61	8.4 ^c	0.12 ^d	12.4 ^d	0.84 ± 0.01
3,5-Dichloro (6d)	5.07	8.9	0.152 ± 0.001	14.0 ± 0.5	0.97 ± 0.01
p-Chloro (6c)	5.97	10.1	(1.88 ± 0.03) × 10^−2	1.23 ± 0.05	(11.6 ± 0.01) × 10^−2
p-Fluoro (6e)	6.54	10.7	(1.11 ± 0.02) × 10^−2	0.46 ± 0.01	(5.34 ± 0.06) × 10^−2
p-H (6a)	6.68	10.9 ^c	4.8 × 10^−3 ^d	0.48 ^d	(4.2 ± 0.1) × 10^−2
p-Methoxy (6f)	6.95	11.2	(2.22 ± 0.03) × 10^−3	(9.3 ± 0.2) × 10^−2	(1.46 ± 0.04) × 10^−2

---

The La³⁺-catalyzed reactions were monitored by UV/vis spectrophotometry under buffered (N-ethylmorpholine, 17 mmol dm⁻³) conditions at three ^s_spH values between 8.34 and 9.14 in the presence of (0.2 to 2.0) × 10⁻³ mol dm⁻³ La(OTf)₃. This was done to ensure that the optimum rate of the reaction for all substrates plateaued by ^s_spH 9.0. The rates of methanolysis of (0.5 to 2) × 10⁻⁴ mol dm⁻³ solutions of 5d, 5b, 5e, 5c and 6c, 6e, 6f, 6d were monitored at 348.6, 275, 286, 386.7, 235, 288, 239.6, and 281 nm respectively to obtain the pseudo-first-order rate constants (k_obs) at each [La³⁺], and the gradients for the k_obsvs. [La³⁺] plots were calculated to give the overall k₂^obs values for the La³⁺-catalyzed methanolysis at ^s_spH 9.1 which are given in Tables 1 and 2. Kinetic data for 2, 5a, 6a and 6b were obtained from ref. 13. Initial rate kinetic data for La³⁺-catalyzed methanolysis of 5f were obtained by ¹H NMR spectrometry by observing the rate of disappearance of starting material and the rate of formation of product for the first 10% of the reaction in CD₃OD. Into two separate NMR tubes were placed 10 mmol dm⁻³ of substrate 5f along with 1.5 mmol dm⁻³ of catalyst (1 : 1 ratio of La³⁺ : ⁻OCH₃) in 1 mL of CD₃OD. The tubes were immersed in a thermostated bath at 25 °C and the ¹H NMR spectra were monitored periodically over 155 h. The integrations of the signals corresponding to the aromatic protons in the starting material and product were used to determine the initial rates which were converted into the second-order rate constants given in Table 1.

Kinetic data for Zn²⁺-catalyzed methanolysis of 5f were determined similarly in duplicate using 10 mmol dm⁻³ of substrate, 5 mmol dm⁻³ each of Zn(OTf)₂ and 1,5,9-triazacyclododecane and 2.5 mmol dm⁻³ of Bu₄NOCH₃ in 1 mL of CD₃OD, periodically monitored by ¹H NMR over 45 h. The initial rate for the methoxide reaction with 5f was determined from duplicate reactions of 10 mmol dm⁻³ of substrate and 25 mmol dm⁻³ of sodium methoxide followed for 45 h to 23% completion.

The pseudo-first-order rate constants for methanolysis of the other phosphorus esters promoted by methoxide were determined by UV/vis (monitored at the same wavelength as for La³⁺-catalyzed methanolysis) in duplicate at four different [⁻OCH₃] ranging from 0.01 to 0.04 mol dm⁻³. The second-order rate constants for these (k₂^OMe) were computed as the gradients of the k_obsvs. [methoxide] plots and are given in Tables 1 and 2.

Results

Given in Tables 1 and 2 are the second-order rate constants for the methanolysis of the phosphates and phosphorothioates promoted by ⁻OCH₃, La³⁺ and 4:Zn²⁺:⁻OCH₃. In all cases, these were determined from the gradients of the plots of k_obsvs. [methoxide] or [metal^x+]_total. In the case of 4:Zn²⁺, the solutions were self-buffered at ^s_spH 9.1 through half neutralization of the catalyst ([4:Zn²⁺:⁻OCH₃]/[4:Zn²⁺:HOCH₃] = 1). Earlier work with 4:Zn²⁺ showed that the catalytic activity was entirely due to the methoxide form, 4:Zn²⁺:⁻OCH₃,^12b and the k₂^4:Zn:OMe values reported in Tables 1 and 2 were calculated based on the concentration of the catalytically active species. La³⁺catalysis for all substrates was determined by observing the k_obsvs. [La³⁺]_total at the ^s_spH value of 9.14 in a 17 mmol dm⁻³N-ethylmorpholine buffer system. Earlier work on the La³⁺-catalyzed methanolysis of paraoxon had shown that the catalytic rate constant plateaus between ^s_spH ca. 8.3 and ca. 9.2,⁸ so it was important to see that the same trend exists for all the other phosphate and phosphorothioate esters, which is confirmed in this work. Given in Tables 1 and 2 are the observed second-order rate constants determined at ^s_spK_a 9.1, where earlier analysis⁸ indicated that >90% of the catalysis occurs through a single form of the catalyst, namely La³⁺₂(⁻OCH₃)₂, vide infra.

Also given in Tables 1 and 2 are the ^s_spK_a values for the phenols and thiophenols in methanol. While experimental methanol ^s_spK_a values for most of the phenols are available^17,18 or can be calculated from their water values by the linear regressions given in refs. 10 and 17 (pK_a^MeOH = 1.12 pK_a^H₂O + 3.56), to our knowledge the only two available thiol ^s_spK_a values in methanol are thiophenol (10.9) and p-nitrothiophenol (8.4).¹⁹ Using these two values, a computed linear regression of ^s_spK_a^(MeOH) = 1.2 (pK_a^(water)) + 2.83 is proposed to relate the aqueous and methanolic pK_a values for the unknown aryl thiols.

In Figs. 1, 2 and 3, as aids to visualizing the data, are presented Brønsted plots of the second-order rate constants for methoxide-, La³⁺- and 4:Zn²⁺:⁻OCH₃-catalyzed methanolysis of the phosphate and phosphorothioate esters vs. the ^s_spK_a of the conjugate acids of the ArO⁻ or ArS⁻ leaving groups. Linear regressions for the methoxide reactions of the phosphates (except 5b which falls well under the Brønsted plot in Fig. 1) and phosphorothioates (except 6b) are given in eqns. (1) and (2) respectively.

log k₂^OMe_(phosphate) = (6.20 ± 0.70) − (0.70 ± 0.05) ^s_spK_a^HOAr (1)

log k₂^OMe_{(phosphorothioate)} = (6.00 ± 0.86) − (0.76 ± 0.08) ^s_spK_a^HSAr (2)

For the metal-catalyzed reactions, the Brønsted plots of which are given in Figs. 2 and 3, the appropriate linear regressions for the phosphates (excluding 5b) are given in eqns. (3)and (4) whereas those for the phosphorothioates (except 6b) are given in eqns. (5) and (6).

log k₂^La_(phosphate) = (17.60 ± 1.07) − (1.43 ± 0.05) ^s_spK_a^HOAr (3)

log k₂^4:Zn:OMe_(phosphate) = (13.05 ± 1.59) − (1.12 ± 0.13) ^s_spK_a^HOAr (4)

log k₂^La_{(phosphorothioate)} = (8.93 ± 1.01) − (0.87 ± 0.10) ^s_spK_a^HSAr (5)

log k₂^4:Zn:OMe_{(phosphorothioate)} = (6.64 ± 0.69) − (0.74 ± 0.06) ^s_spK_a^HSAr (6)

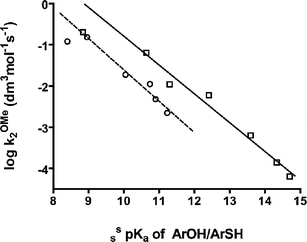Fig. 1 Brønsted plots of the log second-order rate constant for methoxide attack on phosphates 2 and 5 as well as on phosphorothioates 6 (except 6b) vs. ^s_spK_a values for the corresponding phenols or thiophenols; linear regressions for the phosphate (except 5b) and phosphorothioate (except 6b) data give slopes of −0.70 ± 0.05 (solid line, □) and −0.76 ± 0.08 (dashed line, ○) respectively.

Fig. 2 Brønsted plot of the log second-order rate constant for La³⁺- and 4:Zn²⁺:⁻OCH₃-catalyzed methanolysis of phosphates 2 and 5 vs. ^s_spK_a values for the corresponding phenols; linear regressions through the La³⁺ and 4:Zn²⁺:⁻OCH₃ data (except 5b) give gradients of −1.43 ± 0.08 (solid line, □) and −1.12 ± 0.13 (dashed line, ○) respectively. Note that the points on lower right for the p-methoxy derivative (5f) are coincident.

Fig. 3 Brønsted plot of the log second-order rate constant for La³⁺- and 4:Zn²⁺:⁻OCH₃-catalyzed methanolysis of phosphorothioates 6 vs. ^s_spK_a values for the corresponding thiophenols; linear regressions through the La³⁺ and 4:Zn²⁺:⁻OCH₃ data give gradients of −0.87 ± 0.10 (solid line, □) and −0.74 ± 0.06 (dashed line, ○) respectively.

Shown in Figs. 4 and 5 are alternative presentations of the data where the methoxide rate constants are plotted vs. the La³⁺ or 4:Zn²⁺:⁻OCH₃ rate constants for all the phosphate and phosphorothioate substrates. The linear regressions for these are given in eqns. (7) and (8), and (9) and (10) respectively.

log k₂^La_(phosphate) = (1.94 ± 0.10) log k₂^OMe_(phosphate) + (4.65 ± 0.26) (7)

log k₂^4:Zn:OMe_(phosphate) = (1.49 ± 0.11) log k₂^OMe_(phosphate) + (2.78 ± 0.27) (8)

log k₂^La_{(phosphorothioate)} = (1.15 ± 0.11) log k₂^OMe_{(phosphorothioate)} +(2.10 ± 0.18) (9)

log k₂^4:Zn:OMe_{(phosphorothioate)} = (0.99 ± 0.06) log k₂^OMe_{(phosphorothioate)} + (0.79 ± 0.11) (10)

Fig. 4 Plots of log k₂^OMe vs. log k₂^La (□) or log k₂^4:Zn:OMe (○) for the methanolysis of phosphate esters at 25 °C: slope for La³⁺ plot is 1.94 ± 0.10; slope for 4:Zn:OMe plot is 1.49 ± 0.11 all data included. Note that the data points for the p-methoxy derivative (5f) in lower left corner are coincident.

Fig. 5 Plots of log k₂^OMe vs. log k₂^La (□) or log k₂^4:Zn:OMe (○) for the methanolysis of phosphorothioate esters at 25 °C: slope for La³⁺ plot is 1.15 ± 0.10; slope for 4:Zn:OMe plot is 0.99 ± 0.06.

Discussion

The various second-order rate constants for the reactions of the phosphates and phosphorothioates are presented in Tables 1 and 2 along with the leaving group phenol ^s_spK_a values in methanol and water. For the aryloxy esters the HOAr ^s_spK_avalues are all known or can be computed from known linear regressions relating the methanol and aqueous pK_a values.^10,15,17,18 As far as we are aware, the HSAr ^s_spK_avalues in methanol for the arylthiols are only known for the thiophenol and for p-nitrothiophenol, and if we assume that there is also a linear dependence of these methanol and aqueous pK_a values one can compute a two-point linear regression of ^s_spK_a^(MeOH) = 1.2 (pK_a^(water)) + 2.83 from which the ^s_spK_avalues for the other thiols may be estimated. Although the gradient of this linear regression is quite similar to that reported for the phenols (1.12),¹⁷ these computed thiol ^s_spK_avalues are viewed as estimates only for the construction of various Brønsted plots for the phosphorothioate esters.

In constructing the various Brønsted plots for the La³⁺-catalyzed processes, we used the second-order rate constants obtained as the gradients of plots of Δk_obs/Δ[La³⁺] under buffered conditions at ^s_spK_a 9.1, so the k₂^La values are presented per La³⁺ ion even though we have determined that the actual catalytic species are dimers (La³⁺)₂(⁻OCH₃)_2,3,4 the relative importance of which depend on the ^s_spK_aand the [dimer].^8,13,20 For the La³⁺ catalytic study, the aryloxy phosphate esters encompass a range of 10⁶ in leaving group acidity and about 10⁷ in k₂^La but only about three orders of magnitude in k₂^OMe. The second-order rate constants for the 4:Zn²⁺:⁻OCH₃-catalyzed reactions were determined under self-buffered conditions at ^s_spK_a 9.1 through half neutralization of the catalyst, and the k₂^4:Zn:OMe values reported in Tables 1 and 2 are computed on the basis of the active form.

(a) Uncatalyzed reaction of methoxide

The Brønsted plots of log k₂^OMe data for methoxide reactions of the phosphate and phosphorothioate esters vs. the ^s_spK_a values shown in Fig. 1 provide reasonable linear correlations, the respective β_lg values being −0.70 ± 0.05 and −0.76 ± 0.08. In both series the derivatives having the lowest ^s_spK_avalues of the leaving phenol/thiophenol (5b and 6b) are less reactive than predicted on the basis of the equilibrium ^s_spK_a data, and cursory inspection reveals that the plots have some curvature, with the latter points lying below the indicated lines. Non-linear Hammett and Brønsted behaviours have been observed for the hydroxide reactions of substituted aryl benzoates²¹ and acetates²² and Schowen²³ reported that log k₂ values for methoxide reactions of aryl acetates and carbonates in methanol are not linearly related to the ^s_spK_a values for ionization of the corresponding phenols. Our previous study of the methanolysis of aryl acetates also showed some discontinuity in the Brønsted plot of log k^OMevs. phenol ^s_spK_a for the most acidic phenols such as pentafluoro- and 2,4-dinitro-phenol.¹⁵ Such curvature, if observed, does not result from a change in mechanism or rate-limiting step in the reaction but is related to a greater importance of the resonance and inductive interactions in the equilibrium acid dissociation constants (on which the Hammett and ^s_spK_a values are based) than in the kinetic processes where far less charge development generally occurs in the rate-limiting TS.^21–23 In the present study we have chosen to omit the data for the pentafluorophosphate and phosphorothioate derivatives, 5b and 6b, from calculation of the gradients of the Brønsted plots. The β_lg values of −0.70 and −0.76 respectively for the methoxide reaction of esters 2 and 5 (except 5b) and 6 (except 6b) can be compared with the corresponding hydroxide β_lg values of −0.41 to −0.35 for 2-aryloxy-2-oxo-1,3-dioxaphosphorinanes^24,25 −0.43 and −0.44 for hydroxide attack on diethyl aryl phosphate triesters,^16e,26 and −0.42 for hydroxide attack on diethyl S-aryl phosphorothiolates.^16e

Khan and Kirby,²⁴ and later Rowel and Gorenstein,²⁵ discussed the reaction of oxyanions with some 2-aryloxy-2-oxo-dioxaphosphorinanes concluding that, for strong nucleophiles such as hydroxide and methoxide, the mechanism was consistent with, although not uniquely so, a two-step process that proceeds via a five-coordinate intermediate as in eqn. (11).

The relatively low β_lg values of ca. 0.4 obtained with these nucleophiles is consistent with little cleavage of the P–OAr bond in the TS, and supports a process having a rate-limiting k₁ step with preferential breakdown of the intermediate to the product.

However, as the nucleophiles became weaker, the β_lg values increased, supporting either a two-step process where the breakdown became more rate limiting²⁴ or a change in mechanism to a concerted, S_N2 displacement at P.²⁵

More recently, Williams and co-workers provided convincing evidence for a single transition state for the transfer of the diphenylphosphoryl group between phenoxide anions in water.²⁷ In that case, a Brønsted plot of the second-order rate constants for reaction of the phenoxides with p-nitrophenyl diphenyl phosphate against the pK_a of the nucleophile's conjugate acids gave a straight line with β_nuc = 0.66 with no evidence of a break which would have been required if there was an intermediate produced. In the case of the HO⁻ nucleophile reacting with diethyl aryloxy phosphates, they judged, by analogy with the above reactions, that HO⁻ displacement of aryloxy leaving groups was probably concerted, although with little cleavage of the ArO–P bond.²⁶ This conclusion is supported by the ¹⁸O-phenoxy kinetic isotope effect of 1.006 for hydroxide-promoted cleavage of paraoxon 2 which was interpreted²⁸ as being consistent with a bond order of 0.75 for the P–OAr bond in the “S_N2-like transition state of an associative mechanism with concerted, asynchronous departure of the leaving group”.

Our data for methanolysis of the aryl phosphates 2 and 5 and diethyl S-aryl phosphorothioates 6 indicate that the β_lg values are more negative by ca. 0.3 units than is the case for the hydroxide reactions.^16e,24,25 Following the “effective charge treatment” described by Jencks²⁹ and Williams,³⁰ the Brønsted β_lg value for nucleophilic attack of methoxide on the aryloxyphosphates suggests a process where the rate-limiting transition state has appreciable changes in the P–OAr bond. This could be viewed as resulting from either a two-step process with the attack step largely rate limiting due to the fact that the methoxide nucleophile is a far poorer leaving group than any of the aryloxy anions,³¹ or more likely with a concerted process as shown in Scheme 1. The extent of breaking of the P–OAr bond in the TS can be measured by the Leffler parameter, α, which measures the change in the Brønsted β_lg for the TS relative to the β_eq for equilibrium transfers of acyl or phosphoryl groups between oxyanion nucleophiles. In the case of the transfer of the (EtO)₂P=O group, the β_eq value is −1.87 ²⁶ with the O–Ar oxygen in the starting material having a net effective charge of +0.87. When methoxide is the nucleophile, the Leffler parameter of β_lg/β_eq = 0.37 suggests that the P–OAr cleavage is 37% of the way from starting material to product.

Scheme 1

For phosphorothioates 6 reacting with methoxide, a similar sort of analysis for the reaction proceeding through a two- or one-step reaction can be invoked. In this case one has no exact measure of the effective charge on the S-atom in the ArS–P unit, but based on comparison of the known effective charges on the S and O atoms of ArS–C(=O)CH₃ and ArO–C(=O)CH₃ of 0.4 and 0.7 respectively,^30a one might expect that S is less positive than O in the case of the ArX–P unit. Assuming the effective charge on S is 0.5–0.6, the Leffler α for a concerted P–SAr cleavage can be computed as ca. 0.45–0.50.

(b) La³⁺- and 4:Zn²⁺:⁻OCH₃-catalyzed methanolysis

Given in Figs. 2 and 3 are the respective Brønsted plots for the metal-catalyzed methanolysis of the phosphate and phosphorothioates. For phosphates 2 and 5, the respective β_lg values for La³⁺ and 4:Zn²⁺:⁻OCH₃ are large and negative, being −1.43 ± 0.08 and −1.12 ± 0.13 respectively if we exclude the pentafluoro derivative 5b which deviates downward from both plots, probably due to the known difficulties in plotting kinetic data against ionization data of phenols.²³ The La³⁺ and 4:Zn²⁺:⁻OCH₃ Brønsted plots for the phosphorothioates given in Fig. 3 have β_lg values of −0.87 ± 0.10 and −0.74 ± 0.06 respectively.

The large negative β_lg values for the metal-ion-catalyzed methanolysis of the phosphate esters suggests a process where there is considerable cleavage of the leaving group in the transition state, far more than is the case for the methoxide reaction. In our previous study of the La³⁺ and 4:Zn²⁺:⁻OCH₃-promoted methanolysis of acetate esters having aryloxy and some alkoxy leaving groups,¹⁵ we determined that both metal systems exhibited Brønsted plots with a break at ca.^s_spK_a 14.7, consistent with a catalyzed process comprising a pre-equilibrium binding of the metal ion followed by kinetic steps proceeding through a reversibly-formed intermediate as shown in Scheme 2. With good leaving groups the internal attack of metal-coordinated methoxide on the transiently bound ester was rate limiting (β_lg ≈ 0), but with poor leaving groups the breakdown of the metal-coordinated anionic tetrahedral intermediate was rate limiting (β_lg = −0.71). In that case, it appeared that metal ion coordination actually stabilized the tetrahedral intermediate, but the situation with the present phosphate/phosphorothioate esters is clearly different because there is a large dependence of the rate on the leaving group in the ^s_spK_a region where β_lg is zero for the reaction of the carboxylate esters. Accordingly we suggest that, for the metal-catalyzed methanolysis of these phosphates/phosphorothioates, there is no evidence for a change in rate-limiting step for aryloxy or arylthio leaving groups and, by inference, no evidence for an intermediate.

Scheme 2 M^X+–⁻OCH₃ refers to (La³⁺)₂(⁻OCH₃)₂ or 4:Zn²⁺:⁻OCH₃.

Although we have never observed evidence of saturation kinetics, it is difficult to envision any mechanism for the metal-promoted reactions where the ion does not bind to the phosphate to provide Lewis activation toward attack. Indeed, phosphate complexation of lanthanides and actinides is well known³² and structures are known for Zn²⁺ complexes of phosphine oxides³³ and tritoluoyl phosphate.³⁴

We analyze the present Brønsted plots as being consistent with the mechanism in eqns. (12) and (13)

where there is a rapid pre-equilibrium binding followed by an intramolecular concerted displacement of the leaving group. Given in eqns. (14) and (15)

k₂^obs = K_bk₁ = C_bC₁ 10^{(β_b + β₁)pK_a} (14)

log k₂^obs = {log C_b + log C₁} + (β_b + β₁)pK_a (15)

are two forms of the kinetic expression for this process where β_b and β₁ refer to the Brønsted β_lg values for the binding and kinetic steps, and pK_a refers to the acid dissociation constant for the conjugate acid of the leaving groups. (Although these expressions are derived for the concerted pathway, which we favour on the basis of the large and negative β_lg values for the metal-catalyzed reaction, they have the identical form for a two-step process proceeding through an intermediate where the formation of the intermediate is rate limiting.) The experimental Brønsted β_lg values are thus (β_b + β₁), a composite measure of the influence of the leaving group on the pre-equilibrium binding step and the kinetic step. It is difficult to predict an exact value for β_b and what few data there are available in the literature³⁵ suggest that this should be (+), but probably not large. For example, Rackham reported that the europium shift reagent Eu³⁺(2,2,6,6-tetramethylheptane-3,5-dione⁻)₃ binds trimethyl phosphate and triphenyl phosphate with constants of 348 and 23.2 mol⁻¹ dm³ respectively, and suggested that the fall in the binding constant can be attributed to steric bulk and the inductive withdrawal of the phenoxy group relative to the methoxy group.³⁶ Du Preez and Preston have also reported that the extraction into toluene of Sc^III, Yt^III and the trivalent Ln^III ions from aqueous nitrate solutions by coordination to neutral organophosphorus (P=O) compounds correlates with the Taft σ* values of the substituents.^32d,e These considerations indicate that for the La³⁺- or 4:Zn²⁺:⁻OCH₃-promoted methanolysis of the phosphates, the observed β_lg may be a lower limit because it will be reduced by the positive β_b.

Presented in Scheme 3 is a proposed mechanism of reaction for the La³⁺-catalyzed reaction of the phosphate which earlier studies have shown is largely (>90%) attributable to the involvement of a bis-methoxy-bridged dimer, (La³⁺)₂(⁻OCH₃)₂, 7 in Scheme 3.⁸ In Scheme 3, for the sake of visual clarity, we have omitted the methanols of solvation on each La³⁺ as well as any possible associated triflates about which we have no information. It seems unlikely that a methoxy group bound between two La³⁺ ions will be sufficiently nucleophilic to attack the phosphate,³⁷ so we propose that the pre-equilibrium binding of phosphate to form 8 induces opening of one of the methoxy bridges to reveal a kinetically active form (9) with one of the La³⁺ ions acting as a Lewis base, the other serving to deliver the methoxide intramolecularly. Since the Leffler parameter, α, for the La³⁺-catalyzed reaction is β_lg/β_eq = −1.43/−1.87 = 0.76, the transition state for this reaction (10) has extensive cleavage of the P–OAr bond, and this large value is most consistent with a concerted reaction within the complex. Catalytic turnover requires a final dissociation of the diethyl methyl phosphate with the reformation of 7. In the case of the 4:Zn²⁺:⁻OCH₃-catalyzed reaction a similar mechanism is envisioned but this time the transition structure (shown below as structure 12)

will be four-coordinate with a Leffler α of β_lg/β_eq = −1.12/−1.87 = 0.60. This also signifies extensive dissociation of the P–OAr bond in the transition state, but less so than in the case of La³⁺ catalysis.

Scheme 3 When X = O, α = 0.76.

While one might expect that the positively charged metal ion might stabilize an anionic penta-coordinate intermediate, the far more negative β_lg values observed for the metal-ion-catalyzed reactions, compared to those for the methoxide reactions, suggest that the metal ions do not stabilize sufficiently any putative intermediate to direct the reaction through a stepwise pathway. The reason why the La³⁺ reaction exhibits a significantly more negative β_lg than does the Zn²⁺ reaction is not immediately obvious, but could result from better attack/departure angles in the 6-membered La³⁺ TS relative to the 4-membered Zn²⁺ TS or from a greater electrostatic stabilization of the transition structure in the case of the more highly charged La³⁺ system. Given the fact that the catalysis becomes better with the aryloxy anion leaving groups with lower ^s_spK_a values for their conjugate acids, it does not seem likely in either the La³⁺ or Zn²⁺ cases that direct coordination of the leaving group to the metal ion is a significant factor in the catalysis.

In the case of La³⁺- and Zn²⁺-catalyzed methanolysis of the phosphorothioate esters the observed β_lg values of −0.87 and −0.74 also signify an associative mechanism with some departure of the leaving group, but it is difficult to assign the extent of the bond cleavage since the β_eq value is not known for the phosphoryl transfer between thiol and oxygen nucleophiles. It is highly instructive to consider the graph shown in Fig. 6 which is a plot of the log k₂ constants for the La³⁺- and 4:Zn²⁺⁻OCH₃-catalyzed reactions for the entire series of phosphate and phosphorothioate esters. The fact that the slopes for each series of substrate are very similar and without breaks over some seven orders of magnitude for the La⁺³ reaction and five orders of magnitude for the Zn²⁺ reaction indicates that there is no change of mechanism throughout either series. Furthermore, the slopes of 1.30 ± 0.05 and 1.17 ± 0.04 for the phosphate and the phosphorothioate reactions are some measure of the greater efficacy of the La³⁺ reaction which may relate to the higher net positive charge or better geometry for the La³⁺-catalyzed processes. Finally, the fact that both the phosphate and phosphorothioate esters lie essentially on the same line indicates that there cannot be any special catalytic assistance to the departure of the leaving group since one would expect a different effect for assistance of departure of the softer SAr group by Zn²⁺ relative to the ‘hard’³⁸ La³⁺. This is drastically different to a situation we have previously reported where, for the methanolysis of P=S and P=O phosphates, La³⁺ and Zn²⁺ or Cu²⁺ show very different catalytic effects implying that in these materials coordination to the phosphoryl O and S are required components of catalysis.¹² Thus on the basis of the current evidence, it is reasonable that the phosphorothioate methanolysis promoted by both metal-containing systems is concerted and proceeds analogously to the process depicted in Scheme 3.

Fig. 6 Plots of log k₂^La vs. log k₂^4:Zn:OMe for the methanolysis of phosphate (■) and phosphorothioate (□) esters at 25 °C: the linear regression for the phosphate ester plot is log k₂^La = (1.30 ± 0.05) log k₂^4:Zn:(OMe) + (1.03 ± 0.10), r² = 0.9930; the linear regression for the phosphorothioate esters is log k₂^La = (1.17 ± 0.04) log k₂^4:Zn:(OMe) + (1.18 ± 0.05), r² = 0.9952.

(c) Comparision of k₂^OMe and k₂^4:Zn(OMe) or k₂^La

Comparison of the La³⁺ and 4:Zn²⁺:⁻OCH₃ kinetic data in Tables 1 and 2 with the corresponding k₂^OMe kinetic data indicates that the metal ion systems are more effective than methoxide for promoting the methanolysis of this series of phosphates and phosphorothioates. For the phosphates 2 and 5, the k₂^La/k₂^OMe ratio varies from 5000 for the pentafluorophenoxy derivative 5b to ca. 3 for the phenoxy derivative 5a. Over the same series, the k₂^4:Zn:OMe/k₂^OMe ratio varies only by 40-fold (115 to ca. 3). On the other hand, the phosphorothioates show very little variation of the k₂^La/k₂^OMe or k₂^4:Zn:OMe/k₂^OMe ratios with leaving groups, the values being 40–100 throughout the arylthio series for the former and 5–8 for the latter.

Shown in Figs. 4 and 5 are the plots of log k₂^OMevs. log k₂^La or log k₂^4:Zn:OMe for the phosphates and phosphorothioates. As was the case in our earlier study of the metal-catalyzed methanolysis of esters,¹⁵ we assume here that the mechanism of methoxide-promoted methanolysis is similar enough for all the phosphate esters with the nucleophilic addition being either rate limiting or concerted with leaving group departure that the rate constant, k₂^OMe, can be used as an empirical measure of the composite effects of structural changes that incorporate both electronic and steric effects. This approach has advantages over the Brønsted or Hammett plots since the latter rely on substituent-induced changes to equilibrium pK_a processes which may not be appropriate for how a substituent influences a particular reaction where the rate-limiting step(s) have less charge development on the leaving group. An additional benefit is that this treatment does not rely on experimental or estimated ^s_spK_a values for a given substituent which, if in error, may influence the conclusions based on the slopes of Brønsted plots.

The slopes of the lines in Fig. 4 for methanolysis of the phosphates are 1.94 and 1.49 for La³⁺ and the Zn²⁺ complex respectively, indicating that catalytic enhancement of the methanolysis reaction by the metal ion gets better as the leaving group gets better. The data also suggest that for leaving groups having ^s_spK_a values larger than 15, the second-order rate constant for the methoxide reaction will be larger than those for either metal-catalyzed reaction. The slopes of the lines in Fig. 5 for the phosphorothioates are, within experimental uncertainty, essentially unity for both the La³⁺- and Zn²⁺-catalyzed reactions. Importantly, the fact that all the plots in Figs. 4 and 5 are linear with no break over the range of substrates studied indicates that there is no change in mechanism or rate-limiting step for one of the reactions which is not manifested in the other.

(d) Relevance to the phosphotriesterase enzyme

The above study has a direct bearing on the mechanism of action of phosphotriesterase (PTE), a Zn²⁺-contaning enzyme found in the soil-dwelling bacterium Pseudomonas diminuta which has been shown to degrade pesticides such as paraoxon and parathion.¹⁵ X-Ray diffraction shows that the active site comprises two Zn²⁺ ions separated by 3.4 Å, one of which is coordinated to the protein by two His imidazoles and an aspartate, and the second by two histidines: both metal ions are bridged by the oxygens of N-carboxy lysine and an ⁻OH or water having a kinetic pK_a of 5.8–5.9 ^16c,39 which is thought to be the active nucleophile.^16a,39,40 X-Ray diffraction studies also showed that inhibitors such as triethyl phosphate and di-iso-propyl methylphosphonate bind to the more solvent-exposed Zn²⁺ion with P=O coordination.⁴¹ The metal ions can be removed from the wild-type enzyme and replaced by Cd²⁺, Ni²⁺, Co²⁺ and Mn²⁺, and all reconstituted enzymes show activity. The native enzyme has been shown to react with paraoxon in ¹⁸O-labelled water to produce the (EtO)₂P(=O)¹⁸OH product, and also to react with chiral O-ethyl phenylphosphonothioic acid to give a product that is inverted.⁴² Detailed kinetic studies of the hydrolysis of a series of diethyl aryl phosphates and phosphorthioates conducted on the (Zn²⁺)₂ wild-type enzyme by Hong and Raushel indicated that the respective Brønsted β_lg values of V_maxvs. pK_a of aryl phosphates and phosphorothioates in water were −2.2 and −1.0 respectively, the high value for the phosphates being interpreted as arising from a significantly dissociative mechanism with a quite product-like transition state.^16e

There is much in common between the reactivity of the enzyme for both phosphates and phosphorothioates and that which is operative for our very simple dinuclear (La³⁺)₂(⁻OCH₃)₂ and mono-nuclear 4:Zn²⁺:⁻OCH₃ systems. The most obvious similarity comes from comparison of the large Brønsted β_lg we see for both sets of substrates and those exhibited by the wild-type enzyme. However, very much higher β_lg values are reported for the Cd²⁺- and Mn²⁺-enzymes (−3.0 and −4.3 respectively) which clearly are far greater than one expects for simple P–OAr bond cleavage in water.^16e The latter β_lg values are obtained by plotting the rate data against the aqueous pK_a values which likely do not reflect faithfully the solvation and electrostatic stabilization of the leaving anion in the active site. In fact, if the pK_a values in the lower dielectric constant solvents MeOH or DMSO were used, which tends to expand the pK_a scales of phenols,¹⁹ this would lessen considerably the β_lg values. Nevertheless, the kinetic data do indicate a very large degree of cleavage of the P–OAr and P–SAr bond in the rate-liming step of the enzymatic phosphoryl transfer, similar to what we have observed in our simple catalytic system which we have interpreted in terms of a concerted mechanism. All the other data from the enzyme studies, for example the inversion of configuration in hydrolysis of an optically active starting material and ¹⁸O-incorporation of solvent water to the hydrolytic product⁴² are consistent with a concerted mechanism for the enzyme.

Conclusions

The above study indicates that metal-catalyzed methanolyses of these series of phosphate and phosphorothioate triesters proceed by a mechanism that involves considerable cleavage of the leaving group in the rate-limiting step, in fact more cleavage than in the analogous methoxide attack on the same esters. The data indicate that while the dinuclear (La³⁺)₂(⁻OCH₃)₂ system has a large and negative β_lg for phosphate methanolysis (−1.43), that of the mononuclear complex 4:Zn²⁺:⁻OCH₃ is slightly less at −1.15. These large negative values are best interpreted in terms of a concerted displacement mechanism with considerable departure of the leaving group bond in the rate-limiting step. The reason for the difference in β_lg of the La³⁺ and Zn²⁺ complexes may be a result of differences in total (+) in the vicinity of the transition structure, or geometric differences where the La³⁺-containing transition structure is more optimally aligned for internal methoxide displacement of the leaving group. It is interesting to note that, despite the fact that metal-catalyzed hydrolysis of phosphate triesters has been extensively investigated for many years,^5,6 in no case of which we are aware has such a significant catalytic effect over such a wide series of substrates been observed. A significant aspect of the efficacy of the La³⁺ and Zn²⁺ catalysts in methanol must arise from a medium or solvent effect since in general the metal hydroxo counterparts in water are significantly less reactive than our metal methoxide catalysts in methanol and even less reactive than hydroxide itself. Given that the phosphotriesterase enzyme contains a dinuclear Zn²⁺ active site, it would be interesting to compare the efficacy for alcoholysis promoted by an appropriate dinuclear Zn²⁺-containing catalyst with that of 4:Zn²⁺:⁻OCH₃, a study which is currently underway in these laboratories.

Acknowledgements

The authors gratefully acknowledge the financial assistance of the Natural Sciences and Engineering Research Council of Canada, Queen's University and the United States Department of the Army, Army Research Office, Grant No. W911NF-04-1-0057⁴³and the Defense Threat Reduction Agency, Joint Science and Technology Office (06012384BP). T. L. thanks the Summer Student Work Experience Program at Queen's University.

References and notes

1. A. Toy and E. N. Walsh, Phosphorus Chemistry in Everyday Living, American Chemical Society, Washington, DC, 2nd edn., 1987, ch. 18–20; L. D. Quin, A Guide to Organophosphorus Chemistry, Wiley, New York, 2000; M. A. Gallo and N. J. Lawryk, Organic Phosphorus Pesticides. The Handbook of Pesticide Toxicology, Academic Press, San Diego, CA, 1991; P. J. Chernier, Survey of Industrial Chemistry, VCH, New York, 2nd edn., 1992, pp. 389–417.
2. K. A. Hassall, The Biochemistry and Uses of Pesticides, VSH, Weiheim, 2nd edn., 1990, pp. 269–275.
3. Y.-C. Yang, J. A. Baker and J. R. Ward, Chem. Rev., 1992, 92, 1729; Y.-C. Yang, Acc. Chem. Res., 1999, 32, 109; Y.-C. Yang, Chem. Ind. (London), 1995, 334.
4. H. Morales-Rojas and R. S. Moss, Chem Rev., 2002, 102, 2497 and refs. cited therein.
5. S. H. Gellman, R. Petter and R. Breslow, J. Am. Chem. Soc., 1986, 108, 2388; R. S. Brown and M. Zamkanei, Inorg. Chim. Acta, 1985, 108, 201; R. S. Kenley, R. H. Flemming, R. M. Laine, D. S. Tse and J. S. Winterle, Inorg. Chem., 1984, 23, 1870; B. S. Cooperman, in Metal Ions in Biological Systems, H. Sigel, ed., Marcel Dekker, New York, 1976, vol. 5, p. 79 and refs. cited therein; F. M. Menger, L. H. Gan, E. Johnson and H. D. Durst, J. Am. Chem. Soc., 1987, 109, 2800; F. M. Menger and T. Tsuno, J. Am. Chem. Soc., 1989, 111, 4903; P. Scrimin, P. Tecilla and U. Tonellato, J. Org. Chem., 1991, 56, 161 and refs. cited therein; F. Tafesse, Inorg. Chim. Acta, 1998, 269, 287; P. Scrimmin, G. Ghinlanda, P. Tecilla and R. A. Moss, Langmuir, 1996, 12, 6235; C. A. Bunton, P. Scrimmin and P. Tecilla, J. Chem. Soc., Perkin Trans. 2, 1996, 419; Y. Fujii, T. Itoh and K. Onodera, Chem. Lett. Jpn., 1995, 305; S. J. Oh, C. W. Yoon and J. W. Park, J. Chem. Soc., Perkin Trans. 2, 1996, 329; T. Berg, A. Simeonov and K. Janda, J. Comb. Chem., 1999, 1, 96; J. R. Morrow and W. C. Trogler, Inorg. Chem., 1989, 28, 2330; R. W. Hay and N. Govan, J. Chem. Soc., Chem. Commun., 1990, 714; T. C. Bruice, A. Tsubouchi, R. O. Dempsy and L. P. Olson, J. Am. Chem. Soc., 1996, 118, 9867; J. A. A. Ketelar, H. R. Gersmann and M. M. Beck, Nature, 1956, 177, 392; D. Kong, A. E. Martell and J. Reibenspies, Inorg. Chim. Acta, 2002, 333, 7; R. W. Hay and N. Govan, Polyhedron, 1998, 17, 463; R. W. Hay and N. Govan, Polyhedron, 1998, 17, 2079; R. W. Hay, N. Govan and K. E. Parchment, Inorg. Chem. Commun., 1998, 1, 228; B. L. Tsao, R. J. Pieters and J. Rebek, Jr., J. Am. Chem. Soc., 1995, 177, 2210; M. Yamami, H. Furutachi, T. Yokoyama and H. Ōkawa, Inorg. Chem., 1998, 37, 6832; C. M. Hartshorn, A. Singh and E. L. Chang, J. Mater. Chem., 2002, 12, 602; V. Chandrasekhar, A. Athimoolan, S. G. Srivatsan, P. S. Sundaram, S. Verma, A. Steiner, S. Zacchini and R. Butcher, Inorg. Chem., 2002, 41, 5162; M. Rombach, C. Maurer, K. Weis, E. Keller and H. Vahrenkamp, Chem. Eur. J., 1999, 5, 1013.
6. L. Barr, C. J. Easton, K. Lee, S. F. Lincoln and J. S. Simpson, Tetrahedron Lett., 2002, 7797; W. H. Chapman and R. Breslow, J. Am. Chem. Soc., 1995, 117, 5462; T. Koike and E. Kimura, J. Am. Chem. Soc., 1991, 113, 8935; M. M. Ibrahim, K. Ichikawa and M. Shiro, Inorg. Chim. Acta, 2003, 353, 187; M. D. Santana, G. Garcia, A. A. Lozano, G. López, J. Tudela, J. Pérez, L. García, L. Lezama and T. Rojo, Chem. Eur. J., 2004, 10, 1738; F. Mancin, E. Rampazzo, P. Tecilla and U. Tonellato, Eur. J. Org. Chem., 2004, 281; K. Yamaguchi, F. Agaki, S. Fujinami, M. Suzuki, M. Shionoya and S. Suzuki, Chem. Commun., 2001, 375.
7. G. M. Kazankov, V. S. Sergeeva, L. A. Efremenko, S. D. Varfolomeev and A. D. Ryabov, Angew. Chem., Int. Ed., 2000, 39, 3117; G. M. Kazankov, V. S. Sergeva, A. A. Borisenko, A. L. Zatsman and A. D. Ryabov, Russ. Chem. Bull., Int. Ed., 2001, 50, 1844.
8. J. S. W. Tsang, A. A. Neverov and R. S. Brown, J. Am. Chem. Soc., 2003, 125, 7602.
9. For the designation of pH in non-aqueous solvents we use the forms described by Bosch and co-workers¹⁰ based on the recommendations of the IUPAC Compendium of Analytical Nomenclature. Definitive Rules 1997, Blackwell, Oxford, UK, 3rd edn., 1998. If one calibrates the measuring electrode with aqueous buffers and then measures the pH of an aqueous buffer solution, the term ^s_spK_a is used; if the electrode is calibrated in water and the ‘pH’ of the neat buffered methanol solution then measured, the term ^s_spK_a is used; and if a correction factor of −2.24 (in the case of methanol) is subtracted from the latter reading, then the term ^s_spK_ais used.
10. Given that the autoprotolysis constant of methanol is 10^−16.77 (mol dm⁻³)², the neutral ^s_spK_a in methanol is 8.4; see E. Bosch, F. Rived, M. Rosés and J. Sales, J. Chem. Soc., Perkin Trans. 2, 1999, 1953.
11. R. S. Brown, A. A. Neverov, J. S. W. Tsang, G. T. T. Gibson and P. J. Montoya-Pelaez, Can. J. Chem., 2005, 82, 1.
12. (a) A. A. Neverov and R. S. Brown, Org. Biomol. Chem., 2004, 2, 2245; (b) W. Desloges, A. A. Neverov and R. S. Brown, Inorg. Chem., 2004, 43, 6752.
13. J. A. W. Tsang, A. A. Neverov and R. S. Brown, Org. Biomol. Chem., 2004, 2, 3457.
14. A. A. Neverov, T. McDonald, G. Gibson and R. S. Brown, Can. J. Chem., 2001, 79, 1704.
15. A. A. Neverov, N. E. Sunderland and R. S. Brown, Org. Biomol. Chem., 2005, 3, 65.
16. (a) M. M. Benning, J. M. Kuo, F. M. Raushel and H. M. Holden, Biochemistry, 1995, 34, 7973; M. M. Benning, J. M. Kuo, F. M. Raushel and H. M. Holden, Biochemistry, 1994, 33, 15 001; (b) D. P. Dumas, S. R. Caldwell, J. R. Wild and F. M. Raushel, J. Biol. Chem., 1989, 264, 19 659; (c) G. A. Omburo, J. M. Kuo, L. S. Mullins and F. M. Raushel, J. Biol. Chem., 1992, 267, 13 278; (d) J. L. Vanhooke, M. M. Benning, F. M. Raushel and H. M. Holden, Biocehmistry, 1996, 35, 6020; (e) S.-B. Hong and F. M. Raushel, Biochemistry, 1996, 35, 10 904.
17. F. Rived, M. Rosés and E. Bosch, Anal. Chim. Acta, 1998, 374, 309.
18. V. A. Palm, Tables of Rate and Equilibrium Constants of Heterocyclic Reactions, Vol. 1 (1), Proizbodstvenno-Izdatelckii Kombinat Biniti, Moscow, 1975; V. A. Palm, Tables of Rate and Equilibrium Constants of Heterocyclic Reactions, Suppl. Vol. 1, issue 3, Tartuskii gosudarsvennii Universitet, Tartu, 1985.
19. B. W. Clare, D. Cook, E. C. F. Ko, Y. C. Mac and A. J. Parker, J. Am. Chem. Soc., 1966, 88, 1911.
20. G. T. T. Gibson, A. A. Neverov and R. S. Brown, Can. J. Chem., 2003, 81, 495 ; We have determined that the maximal activity for the La³⁺-catalyzed methanolysis of both carboxylate esters and phosphate triesters lies in the ^s_spK_aregion between 8.7 and 9.1, where 95% of the activity is attributed to La³⁺₂(⁻OCH₃)₂. Thus, the conditional observed k₂^La rate constants reported in Tables 1 and 2 are ca. half of the k₂ of the La³⁺₂(⁻OCH₃)₂ active form.
21. Z. S. Chaw, A. Fischer and D. A. R. Happer, J. Chem. Soc. B, 1971, 1818; J. Kirsch, A. Clewell and A. Simon, J. Org. Chem., 1968, 33, 127; A. A. Humffray and J. J. Ryan, J. Chem. Soc. B, 1967, 468.
22. J. J. Ryan and A. A. Humffray, J. Chem. Soc. B, 1966, 842; T. C. Bruice and M. Mayahi, J. Am. Chem. Soc., 1960, 82, 3067; J. F. Kirsch and W. P. Jencks, J. Am. Chem. Soc., 1964, 86, 837.
23. C. G. Mitton, R. L. Schowen, M. Gresser and J. Shapley, J. Am. Chem. Soc., 1969, 91, 2036.
24. S. A. Khan and A. J. Kirby, J. Chem. Soc. B, 1970, 1172.
25. R. Rowell and D. G. Gorenstein, J. Am. Chem. Soc., 1981, 103, 5894.
26. S. A. Ba-Saif and A. Williams, J. Org. Chem., 1988, 63, 2204.
27. S. A. Ba-Saif, M. A. Waring and A. Williams, J. Am. Chem. Soc., 1990, 112, 8115.
28. S. R. Caldwell, F. M. Raushel, P. M. Weiss and W W Cleland, Biochemistry, 1991, 30, 7444.
29. W. P. Jencks and M. Gilchrist, J. Am. Chem. Soc., 1968, 90, 2622; D. J. Hupe and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 451; J. M. Sayer and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 464; M. J. Gresser and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 6963.
30. (a) S. Thea and A. Williams, Chem. Soc. Rev., 1986, 15, 125; (b) A. Williams, Acc. Chem. Res., 1984, 17, 425; (c) A. Williams, Concerted Organic and Bio-organic Mechanisms, CRC Press, Boca Raton, FL, 2000.
31. Given that the autoprotolysis constant of methanol is 10^−16.77 (mol dm⁻³)² (ref. 10) one can compute an ^s_spK_a of methanol of 18.13 on the mol dm⁻³ scale.
32. (a) J. Petrova, S Momchilova, E. T. K. Haupt, J. Kopf and G. Eggers, Phosphorus, Sulfur, Silicon Relat. Elem., 2002, 177, 1337; (b) D. R. Peterman, R. V. Fox and H. W. Rollins, Abstract of papers, 223rd ACS National Meeting, Orlando, FL, April 7–11, 2002, NUCL-131; (c) J. R. Ferraro, A. W. Herlinger and R. Chiarizia, Solvent Extr. Ion Exch., 1998, 16, 775; (d) R. Du Preez and J. S. S. Preston, South Afr. J. Chem., 1986, 39, 89; (e) R. Du Preez and J. S. S. Preston, South Afr. J. Chem., 1986, 39, 137; (f) D. F. Peppard, G. W. Mason, W. J. Driscoll and S. J. McCarty, J. Inorg. Nucl. Chem., 1959, 12, 141; (g) E. N. Lebedeva, M. G. Zaitseva, O. V. Galaktionova, L. V. Bystrov and S. S. Korovin, Koord. Khim., 1981, 7, 870 ( Chem. Abstr. , 1981 , 95 , 87 058 ); (h) O. V. Galaktionova, E. N. Lebedeva, V. V. Yastrebov and S. S. Korovin, Zh. Neorgan. Khimii, 1980, 25, 2660 ( Chem. Abstr. , 1980 , 93 , 226 562 ); (i) A. K. Pyartman, A. A. Kopyrin, E. A. Puzikov and K. B. Bogatov, Zhu. Neorgan. Khimii, 1996, 41, 347 ( Chem. Abstr. , 1996 , 125 , 124 905 ); (j) A. K. Pyartman, A. A. Kopyrin, E. A. Puzikov and K. B. Bogatov, Zhu. Neorgan. Khimii, 1996, 41, 686 ( Chem. Abstr. , 1996 , 126 , 11 927 ); (k) A. K. Pyartman, V. A. Keskinov, S. V. Kovalev and A. A. Kopyrin, Radiochemistry (Moscow) (Translation of Radiokhimiya), 1997, 39, 142 ( Chem. Abstr. , 1997 , 127 , 210 889 ).
33. C. A. Kosky, J.-P. Gayda, J. F. Gibson, S F. Jones and D. J. Williams, Inorg. Chem., 1982, 21, 3173.
34. C. M. Mikulski, L. L. Pytlewski and N. M. Karagannis, Inorg. Chim. Acta, 1979, 32, 263.
35. R. Schurhammer, V. Erhart, L. Troxler and G. Wipf, J. Chem. Soc., Perkin Trans. 2, 1999, 2423 and refs. cited therein.
36. D. M. Rackham, Spectrosc. Lett., 1980, 13, 513.
37. N. H. Williams, W. Cheung and J. Chin, J. Am. Chem. Soc., 1998, 120, 8079; D. Wahnon, A.-M. Lebuis and J. Chin, Angew. Chem., Int. Ed. Engl., 1995, 34, 2412.
38. T. L. Ho, Hard and Soft Acids and Bases Principle in Organic Chemistry, Academic Press, New York, 1977.
39. S. D. Aubert, Y. Li and F. M. Raushel, Biochemistry, 2004, 43, 5707.
40. M. M. Benning, H. Shim, F. M. Raushel and H. M. Holden, Biochemistry, 2001, 40, 2712.
41. M. M. Benning, S.-B. Hong, F. M. Raushel and H. M. Holden, J. Biol. Chem., 2000, 275, 30 556.
42. V. E. Lewis, W. J. Donarski, J. R. Wild and F. M. Raushel, Biochemistry, 1988, 27, 1591.
43. The content of the information does not necessarily reflect the position or the policy of the federal government, and no official endorsement should be inferred.

---