A combined analysis to identify airborne PM10 sources
Darío R.
Gómez
a,
Silvia L.
Reich
*b,
Laura E.
Dawidowski
a and
Cristina
Vázquez
a
aUnidad de Actividad Química, Centro Atómico Constituyentes, Comisión Nacional de Energía Atómica, Avda. General Paz 1499, B1650KNA San Martín, Argentina
bEscuela de Ciencia y Tecnología, Universidad Nacional de General San Martín, Calle Alem 3901, B1653HIM Buenos Aires, Argentina. E-mail: silreich@cnea.gov.ar
First published on 19th November 2004
Abstract
A two step procedure that combines an air dispersion model with a receptor model was used to identify the key sources that contribute to air levels of suspended particulate matter. The contribution to PM10 concentrations measured at four monitoring sites in San Nicolás, Argentina, of the following sources, a thermal power plant, an integrated steel mill, motor vehicle exhaust fumes, and finally dust from paved and unpaved roads, have been analysed. Moreover, an air dispersion model was used to estimate the contribution of the thermal power plant, emissions of which have been described in depth by means of hourly fuel consumption and specific emission factors. The ratio “apportionment coefficient” was introduced to relate the contribution of this source to the measured 24 h PM10 concentrations by analysing the frequency of occurrence of connecting winds between the power plant and each monitoring site. In San Nicolás 70% of the PM10 sampled at three of the four monitoring sites could be attributed to the power plant in those scenarios where winds connected the facility’s tall point sources with the sampling locations. The contribution to the measured PM10 levels of the rest of the sources that are present in the analysed area was confirmed by way of receptor models. For this purpose, the multielemental composition of 41 samples was determined by Wavelength Dispersive X-ray Fluorescence analysis. In order to ascertain the underlying correlations between PM10 samples and potential sources, Principal Component Analysis was performed on the standard matrix of composition profiles, which comprises the measured PM10 samples being enlarged with the composition profiles of the potential contributing sources. The diagonalization of the covariance matrix was used as a screening procedure to differentiate the most likely contributing sources from those that were not significant.
Introduction
Air concentration of particulate matter (PM) is of concern worldwide because of its association with adverse health effects.1 Outdoor human exposure to PM results from various sources in different locations and its measurement is always constrained by the availability of resources.2 An effective air pollution control technique requires the identification of airborne pollutant emission sources, especially those located in areas where air quality standards are likely to be exceeded.Source oriented (air dispersion) models that associate emissions to air concentrations evaluate the contribution of several polluting sources to the deterioration of air quality at given receptor sites.3 Air dispersion models rely on an accurate, exhaustive description of the relevant source emissions, chemical reactions and physical processes that take place in the atmosphere in order to simulate the atmospheric transport of pollutants. This type of model has been applied throughout the world and its regulatory use has been prescribed for many countries. As a first measure, in Argentina, the National Electricity Regulatory Agency issued a regulation that named a series of air dispersion models that served the agents of the Argentinean Wholesale Electricity Market (WEM) as a guidance to select the appropriate model for assessing the environmental impact of their activities.4
In those cases where emissions cannot be adequately characterised, receptor models complement dispersion analysis by inferring the contributions of the other possible PM sources through measurements of the particles’ chemical and physical properties. Receptor models use air concentrations together with the presence and amount of chemical components in source emissions so as to quantify each source’s contribution. Different techniques, such as enrichment factor, chemical mass balance, multiple linear regression, principal components, edge detection, neural network, aerosol evolution, and aerosol equilibrium models, have been used to detect PM air quality problems.5
Source and receptor models are complementary rather than competitive. Each one of them has its advantages and shortcomings, yet in many cases they compensate for one another. Seigneur et al.3 firstly suggested that both types of models should be combined in a PM 24 h average concentration modelling. However, only one type of model is customarily used for air pollution impact assessment. Chow et al.6 used the chemical mass balance (CMB) receptor model7 and the ISCST-3 air dispersion model8 to estimate middle and neighbourhood scale variations of source contributions in Las Vegas, USA. More recently, Qin and Oduyemi9 employed a method that combines both types of model for the identification of aerosol sources and the estimation of the contribution of sources to air pollution in Dundee, UK. Five aerosol sources were identified using a positive matrix factorisation (PMF) receptor model10 while the ISCST-3 model was used to estimate the contribution of vehicle emissions, a source that was comprehensively characterised in the emission inventory but could not be identified by the receptor model.
In this work, a total of 288 PM10 samples were collected at four monitoring sites during a 3 month operational period in San Nicolás, Argentina. Gravimetric analysis was performed for all PM collected filters, which were stored after weighing. Subsequently, the obtained information on PM10 mass concentration was contrasted with the concentrations measured at the monitoring sites that resulted from the estimations of the ISC3-model of the thermal power plants’ emissions. This approach resulted in the inference of the contribution of the thermal power plant to PM air pollution. The content of eleven elements, namely Ba, Ce, Cr, Cu, Fe, K, Mn, Pb, Rb, Sr and Ti was later measured by Wavelength Dispersive X-ray Fluorescence spectrometry (WDXRF) in 41 out of the 288 employed filters. These multivariate measurements were input to a receptor model in an attempt to obtain information on the other contributing PM emission sources.
PM sources in San Nicolás
The city of San Nicolás, Argentina is located at about 250 km NW of Buenos Aires, the capital of the country. San Nicolás has a population of more than 100 000, is surrounded by a rather large area of countryside and has considerable industrial activity.The large stationary PM emission sources in San Nicolás belong to the only Argentinean power plant that burns coal and to an integrated steel mill that produces steel from iron ore and scrap. The main point and area PM emission sources within this facility are located at the sintering plant, the coke ovens, and the blast furnace. Furthermore, there are numerous fugitive dust sources originating from wind erosion of raw and intermediate material stockpiles, vehicle traffic on paved and unpaved roads, and outdoor handling of materials. The rest of the industrial activity in the zone is composed of a number of smaller facilities that include metal producing plants that employ steel produced at the integrated steel mill, a pesticide plant, and a textile plant. In addition, there are grain storage processes from nearby agricultural activities. Road vehicle emissions represent the largest PM emission from mobile sources in the area. An important portion of the particles present in the atmosphere also originate from fugitive emissions from paved and unpaved roads that are difficult to characterise.
During the last decade, the people of San Nicolás frequently complained about dust deposition on roofs and open spaces of their homes and although they were related to the outmoded term ‘nuisance dust’, used in industrial hygiene practices,11 the attention was centred on the adverse health effects of airborne PM. Under these circumstances, the Electricity Regulatory Agency of Argentina, responsible for the surveillance of the environmental impact of the wholesale electricity market, requested an air pollution monitoring campaign to elucidate the role of the thermal power plant in local air pollution. The campaign was carried out at four monitoring sites, where measurements of sulfur dioxide were also performed. Reich et al.12 analysed these series of sulfur dioxide concentrations and were able to demonstrate that the power plant and the steel mill were the main sources of this pollutant. The current work complements this previously reported information on the analysis of suspended particulate matter.
We were able to collect thorough information on the PM emission parameters of the power plant and as much data as were available for the rest of the sources. Activity information for the thermal power plant was obtained from the wholesale electricity market databases. It consisted of the daily dispatch carried out during the monitoring campaigns and the average fuel consumption as a function of the load factor for each generating unit. The emissions were characterised by measured gravimetric concentration, temperature, and velocity and particle size distribution of the flue gases.
Hence, this study was performed with detailed information regarding the thermal power plant and yet fragmentary information on the rest of the sources. As the electricity sector was one of the first to express concern and take responsibility for the environmental impact of its activities, the industrial and transport sectors have thus practically eluded air pollution surveillance from local environmental agencies. Therefore, the characteristics of their emissions are either poorly known or inaccessible to the public.
Experimental
Collection of PM samples
The Electricity Regulatory Agency requested that the monitoring strategy should focus on the contribution of the thermal power plant to PM10 air pollution. Consequently, monitoring sites were selected following two criteria, namely a series of complaints indicating the areas affected by dust deposition episodes, and the zones where air dispersion modelling results showed the thermal power plant’s highest contribution to PM air concentration. This contribution was evaluated using (1) measured thermal power plant emission parameters, (2) the ISCST-3 Gaussian dispersion model; and (3) corresponding climatologic statistics13 that considered the occurrence of the most probable combinations of atmospheric stability classes, wind velocities and directions. Four monitoring sites were distributed within an approximate radius of 1 km with the power plant located at its centre (Fig. 1). Site 1 was selected taking into account ‘nuisance dust’ complaints, while the location of sites 2, 3 and 4 was determined according to the modelling results. | ||
| Fig. 1 Layout of San Nicolás city showing the localization of the four monitoring sites, the thermal power plant, the steel mill and other facilities. | ||
High volume samplers (SIBATA HVC 100N, Japan) with a flow rate of 1200 l min−1 were used to collect 24 h samples of PM10 on glass-fibre filters (8 × 10 inch, ADVANTEC, GB100R, 0.6 μm nominal rating). Each filter was placed in a clean polyethylene bag for transport and storage and was heated in a vacuum drying oven at 110–120 °C for 120 min prior to being used. Six samples of fly ash emitted by the thermal power plant were also collected during this campaign. The samples were taken under isokinetic conditions by means of an Okano Works sampler (ESA 302 CT, Japan) using ceramic-fibre thimble filters. Glass-fibre and thimble filters were weighed (after moisture equilibration) before and after sampling to determine the net particulate mass gain. The required environment for filter conditioning for the 24 h equilibration period involved a controlled temperature with a variance of less than ±3 °C and a constant relative humidity within the range of ±5%. After being weighed, the filters were stored in clean containers for refrigeration.
The operation and maintenance of systems (including calibration), treatment and handling of samples and data validation were carried out according to QA/QC guidelines of the World Health Organization.14
Selection criteria for multielemental chemical analysis
A subset of 41 out of the 288 collected samples was selected for WDXRF analysis. The main selection criterion was based on the prevalence of wind directions that connected either the thermal power plant or the steel mill with the monitoring locations during the corresponding 24 h sampling periods. For this purpose, data on wind velocity and direction measured at monitoring site 1 were used. Additionally, one sample per site was taken for those periods in which the corresponding involvement of the thermal power plant was unlikely.The six fly ash samples were combined and carefully mixed, and the resulting mixture was measured with WDXRF so as to obtain an average source profile of the thermal power plant. The profiles for other potential contributing sources were not available and the possibility of sampling them is beyond the scope of this work. Under these circumstances, surrogate profiles for these sources were selected from the SPECIATE database by US EPA.15
The elements measured by WDXRF in the set of collected samples at the four monitoring sites were selected taking into consideration the average multielemental composition of PM emitted from the thermal power plant, the surrogate profiles of the other selected emission sources and the capability of the analytical technique. The following criteria were adopted for the selection of the final set of elements: (1) the element was to act as a marker for each source16 (2) the element concentration was to be the highest for a given profile; (3) the element was to be present at one source while its presence was null or negligible for the rest of the sources; and (4) the possibilities and limitations of the analytical instrument for the specific elements.
Experimental determination of chemical elements
Eleven elements, namely Ba, Ce, Cr, Cu, Fe, K, Mn, Pb, Rb, Sr and Ti were measured using a WDXRF spectrometer equipped with a tungsten X-ray target tube. Experimental conditions for measurements were selected according to the characteristics of each element. For those elements with atomic number lower than 20 (Ca) an ADP analyser crystal and a gas P10 flow detector were employed. For the rest of the elements, a LiF(2,0,0) diffraction crystal and scintillation counter were used. Furthermore, the use of standard reference materials provided by NIST, SRM 1648 (urban particulate matter) and 1633b (coal fly ash) was implemented. Due to the fact that the area explored by WDXRF (approx. 3 cm2) was a small fraction of the total filter (about 300 cm2), homogeneity controls were performed. In order to explore the variability of different portions of the filter, chromium concentrations were employed for 10 of the 41 analysed filters. The selection of this element is justified by the fact that it shows the lowest concentration value.17 In all tests, the homogeneity of the deposit for each filter was verified by measuring Cr concentrations within ±10% of the mean value.Analysis of the contribution of the thermal power plant
Measured PM10 mass concentrations
The outline of the measured PM10 concentrations is displayed in Fig. 2. Together with it, the current 24 h PM10 national standard, 150 μg m−3, is plotted as a reference. Moreover, boxes were placed around the median concentration for each monitoring site, representing the 25th and 75th percentile (lower and upper quartile, respectively). Outliers and extremes, which are defined as those values that are located at a distance greater than 1.5–3 times the height of the box, are also displayed. | ||
| Fig. 2 Summary of PM10 concentrations (μg m−3) measured in San Nicolás. | ||
There are a significant number of violations of this standard, i.e. 35% of the 288 measured concentrations surpassed the limit value in at least one monitoring site. Excesses per site are summarised as follows, site 1 (27%) > site 2 (12%) > sites 3 and 4, with only one sample each above 150 μg m−3.
Inputs to the air dispersion model
The emission parameters of the thermal power plant are required as inputs to the air dispersion model. The thermal power plant has five electricity generation units that discharge the flue gases through three stacks. Hourly PM emissions from these sources were characterized during the modeling period taking into consideration specific information about activity data and previous flue gas measurements. These measurements were carried out during six previous monitoring campaigns and stand for average operating conditions. They mainly consist of PM mass concentration, oxygen and water content, flue gas velocity, and temperature. Average emission factors were derived from this set of measurements for each electricity generation unit. A size distribution analysis was also available for the samples collected at the facility’s stacks.The activity data comprise three items: hourly dispatch of the electricity generation units, the type of fuel employed (either coal or natural gas), and finally the corresponding fuel consumption rate. With this information, combined with the average oxygen and water content, and from fuel combustion mass balances, the gas velocity for each stack was calculated. By means of the corresponding emission factor, the PM mass concentration in the flue gases was calculated for each stack. In order to have regard for particle deposition, size distribution was also input to the air dispersion model.
At monitoring site 1, surface meteorological variables, which include air temperature, wind speed and direction, were computed. Since San Nicolas is located on a flat terrain, the hourly cloudiness, which is employed for the calculation of stability classes, was retrieved from the closest National Weather Service Station located at an approximate distance of 40 km. Furthermore, mixing heights were estimated by way of the Zilintinkevich18 approximation.
Application of the air dispersion model
The contribution of the thermal power plant to air 24 h PM10 concentration at the four monitoring sites was calculated by means of the ISCST-3 model for plain terrain in accordance with the local topography. ISCST-3 is an appropriate Gaussian plume dispersion model of regulatory use in the USA that has been recently incorporated into the list of models to be used by the electricity sector in Argentina.4 The model has been widely employed worldwide to model air dispersion of plumes from point sources of industrial facilities,19–22 plus its uncertainties have been thoroughly assessed23–25. Moreover, it has been recently used for the modeling of 24 h PM10 air concentrations so as to analyze the role of source variations and the contribution of road vehicle emissions.9ISCST-3 assumes constant average meteorological and emission conditions during a characteristic time frame of one hour and is not suitable for calm conditions. In order to consider the persistence of air PM10 concentrations for the latter conditions in the vicinity of each monitoring site, hourly concentrations that were calculated with the model were modified by the following rule:
 | (1) |
For each sampling day (d), the average concentration at monitoring site k (C24 h,k(d)calculated) was defined as the corresponding 24 h arithmetic mean of the hourly concentrations calculated by the model. The contribution of the thermal power plant to the measured 24 h concentration depends on the daily occurrence of connecting winds between the source and a given monitoring site. By connecting wind, we considered those that blew from within a 45° sector centred on the bisecting line, defined as the segment connecting the power plant with the monitoring location.
Contribution of the thermal power plant
In order to point out the link between measured concentrations and emissions from the thermal power plant, we defined the following Apportionment Coefficient (ACd,k) for each site k and day d: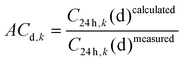 | (2) |
This ratio is an implicit function of the daily number of hours (p) of the occurrence of connecting winds. For each monitoring site and for each amount p, the mean values of ACd,k are plotted as a function of p in Fig. 3. The pattern of the thermal power plant contribution for sites 2, 3 and 4 shows a similar trend, with maximum apportionment of about 70% for full occurrence of connecting winds during the 24 h measuring period (Fig. 3a). On the other hand, the apportionment of the facility at site 1 is comparatively much lower (Fig. 3b). This fact is consistent with the location of this site relative to ‘nuisance dust’. The site is rather close to the power plant and relatively far from the locus of the statistically expected maximum airborne PM10 contribution. It has been noticeably impacted by deposited particles but much less by PM10.
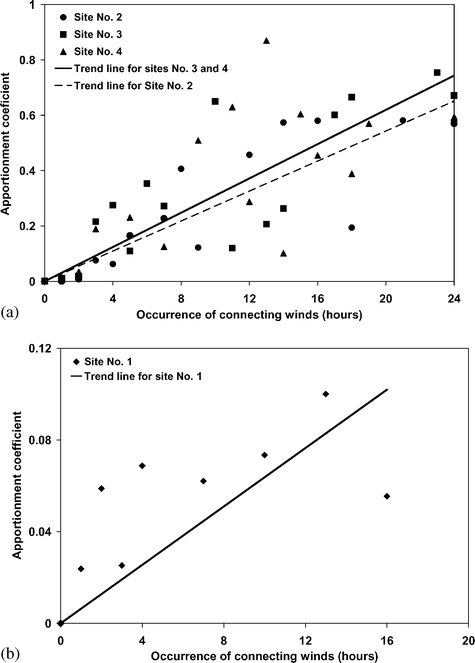 | ||
| Fig. 3 Apportionment coefficient defined in eqn. (2) as a function of occurrence of connecting winds between the power plant and the corresponding monitoring site. Trend lines are also shown in the figures (a) Sites No. 2–4, (b) Site No. 1. | ||
Analysis of other PM sources
As was previously mentioned, there are important PM10 sources in San Nicolás other than the thermal power plant, for which emission characteristics were not available. A receptor model provides a means of identifying these PM10 sources and thus estimating their contribution.Receptor models are helpful in elucidating the relative apportionment of different sources of PM10 through the information embedded in the set of multielemental composition profiles of environmental samples (receptors) and candidate sources.26,27 Currently, there are two basic approaches to the receptor model problem depending on the extent of available a priori knowledge about the number and nature of the sources. The Chemical Mass Balance (CMB) model is well established for those situations in which the polluting sources are known and the composition of the emissions has been analysed.28 This model provides a quantitative estimate of the contribution of each identified source. Eigenvector analysis,29 also named Principal Component Analysis (PCA) or Factor Analysis (FA), has been employed to confirm and sometimes identify unrecognised emission sources.
Factor analysis estimates the number and the chemical composition of the possible sources through the analysis of the eigenvectors of the correlation matrix of the measured airborne particulate matter concentrations. The underlying assumption of FA is that the eigenvectors adequately represent the real sources’ profiles.30 As the results of FA usually possess rotational ambiguity31 rotation is customarily performed so as to impose the expected characteristics for the factors.32 Although those results with negative source contributions may not be mathematically avoided, several new methods have been proposed to shortcut this inconvenience. The contributions of Paatero et al.33 with the formalism of the Positive Matrix Factorisation method (PMF) together with the Edge Detection Method by Henry34 are worth mentioning within this context.
It is possible to obtain the number of sources, their profiles and apportionments by performing factor analysis on the matrix of the measured chemical concentrations. Source profiles are not customarily incorporated to the data set employed when performing FA. Profiles of identified sources need to be compared with the real emission profiles so as to validate the results obtained by FA. In most cases, surrogate profiles from available databases rather than measured ones are employed. The SPECIATE database from the EPA is one of the most widely used to obtain these profiles.
Screening procedure based on PCA
In this part of the work, we have attempted to confirm the role of the thermal power plant as a relevant PM emission source and also identify, out of the list of PM sources that are present in the monitoring area, those with relevant contributions to the air PM10 measured levels. This cautious approach takes into account the use of stored filters from a monitoring network whose centre is the thermal power plant. Within this context we have considered the caveat by Watson et al.5 that multivariate composition profiles measured from the obtained filters can not account for quantitative source apportionment, yet they be may useful for a preliminary or first-level assessment. Bearing this in mind, we performed PCA based on the covariance matrix for the combined set of the multielemental composition profiles of (1) the 41 measured PM10 samples, (2) the measured PM emitted by the thermal power plant and (3) PM surrogates for the potential contributing sources that were not locally measured. This receptor matrix (PM10 samples) and source profiles is denominated RS matrix.In the case of PM10 multielemental composition profiles, the use of the covariance matrix implies that the concentrations of the different chemical species in the combined set are not normalised. These concentrations are measured in the same units and thus the use of the covariance matrix allows the relative importance of the profile elements to be taken into account together with their variability. On the other hand, the use of the correlation matrix, as the basis of factor analysis, would mask this fact by assigning the same weight to the concentrations of all the measured species. Principal components derived from the covariance matrix are thus different from those obtained from the correlation matrix suggesting that standardisation is not inconsequential.29 Furthermore, aside from the convenience of dimensional reduction, PCA is a powerful tool for revealing relationships that allow interpretations that would ordinarily be veiled within the complete set of variables.
When PCA is performed on the RS matrix, the multielemental profiles of the measured PM10 samples and those of the candidate sources are projected onto the same space and, by means of a screening procedure, the selection of the most likely contributors among the candidate sources is performed. In this work we put forward the consideration of geometric distance in this reduced space for the selection of the source profiles. Hence, very small source apportionments may firstly be discarded and also similar source profiles can be grouped as one contributor. The rationale for this screening is discussed below.
The combined set of PM10 profiles in the RS matrix belongs to an n-dimensional space where n is the number of measured elements. Fig. 4a illustrates a case where only four sources (A, B, C and D) contribute to the airborne concentrations of a set of PM10 samples. Mass conservation implies that samples are inside the tetrahedron defined by these sources in the n-dimensional space, where n = 3 for graphical representation in Fig 4a. The first two principal components define the score plane α of the zone of maximum variance. When the set of PM10 samples and sources is projected onto this plane, the triangle B′C′D′, whose vertices are the projections of the sources, is defined (Fig. 4b). All projected samples, being linear combinations of the sources, lie within this figure. The projection of source A belongs also to the triangle, although it is not a linear combination of the rest of the sources. Any PM10 concentration that lies outside the triangle B′C′D′ is exterior to the tetrahedron ABCD and therefore cannot be described by the contribution of the four candidate sources. Other source profiles can also be taken into account and projected onto the score plane α. Nothing can be said if the source lies within the triangle B′C′D′. Yet, if it lies outside the triangle and far from the locus of PM10 samples, it can be distinguished as an unlikely contributing source. Since the PCA has been derived from the covariance matrix, a big distance between two objects on the PC1-PC2 plane is a metric of dissimilarity in the composition. In effect, important distances on the PC1-PC2 imply big distances in the original n-dimensional space of profile compositions. Conversely, short distances on the PC1-PC2 plane do not necessarily imply short distances in the original n-dimensional space. This topological preserving PCA transformation is therefore not freed from ambiguity as it allows the removal of certain sources, but there may exist a non contributing source whose projection lies within the polygon defined by the most likely sources and cannot be discarded. In order to define this polygon, we used the confidence ellipse of the measured PM10 samples. This type of ellipse is useful for establishing confidence intervals for the prediction of candidate sources and other samples to the same measured data set. The probability that a new pair of values (PC1, PC2) will fall within the area marked by the ellipse is determined by the value of the coefficient that defines the ellipse.35 Sources belonging to the confidence ellipse or its vicinity are the most likely contributors to the airborne concentration of the measured samples.
 | ||
| Fig. 4 Rationale for the screening procedure based on PCA performed on the RS matrix of receptor and source profiles. (a) Receptors in a 3-dimensional space as linear combinations of the four sources A, B, C and D. Receptors are inside the convex tetrahedron ABCD. (b) Sources and receptors projected onto the score plane α of maximum variance. | ||
Application to San Nicolás
In addition to the thermal power plant, the following PM sources were taken into account: (1) several processes and operations related to the integrated steel mill; (2) transportation; (3) fugitive dust emissions from paved and unpaved roads; and (4) other chemical processing plants. Table 1 summarises the information on measured PM10 multielemental composition at the four monitoring sites. Mean Ba concentration is significantly lower in site 1 while the concentrations of the rest of the metals are higher in site 1 than those measured in the other three locations. This dissimilarity in concentration profile for site 1 is consistent with the distinct apportionment found for this spot using dispersion models. The average emission profile of the thermal power plant is also reported in Table 1. The selected profiles from the US EPA SPECIATE database15 that were used for the local sources are listed in Table 2.| Site no. 1 | Site no. 2 | Site no. 3 | Site no. 4 | San Nicolás power plant | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min. | Max. | Mean | Min. | Max. | Mean | Min. | Max. | Mean | Min. | Max. | Average | |
| Ba | 0.029 | 0.001 | 0.100 | 0.082 | 0.010 | 0.170 | 0.058 | 0.010 | 0.120 | 0.066 | 0.025 | 0.150 | 0.075 ± 0.025 |
| Cr | 0.005 | 0.001 | 0.038 | 0.001 | 0.001 | 0.001 | 0.003 | 0.001 | 0.013 | 0.001 | 0.001 | 0.001 | 0.002 ± 0.0002 |
| Cu | 0.463 | 0.190 | 1.750 | 0.228 | 0.040 | 0.450 | 0.219 | 0.097 | 0.470 | 0.074 | 0.020 | 0.170 | 0.012 ± 0.001 |
| Fe | 4.854 | 0.000 | 17.800 | 2.557 | 0.270 | 6.850 | 1.827 | 0.000 | 4.790 | 0.588 | 0.250 | 0.930 | 2.5 ± 0.229 |
| K | 0.686 | 0.070 | 3.050 | 0.090 | 0.010 | 0.450 | 0.348 | 0.030 | 0.990 | 0.018 | 0.006 | 0.032 | 1.296 ± 0.119 |
| Mn | 0.202 | 0.027 | 0.750 | 0.088 | 0.022 | 0.220 | 0.050 | 0.020 | 0.093 | 0.013 | 0.000 | 0.021 | 0.043 ± 0.004 |
| Ni | 0.002 | 0.001 | 0.005 | 0.003 | 0.001 | 0.013 | 0.001 | 0.001 | 0.003 | 0.001 | 0.001 | 0.001 | 0.013 ± 0.001 |
| Pb | 0.116 | 0.019 | 0.710 | 0.005 | 0.001 | 0.011 | 0.007 | 0.001 | 0.023 | 0.004 | 0.001 | 0.009 | 0.007 ± 0.0006 |
| Rb | 0.307 | 0.190 | 0.480 | 0.001 | 0.001 | 0.002 | 0.002 | 0.001 | 0.005 | 0.001 | 0.001 | 0.003 | 0.012 ± 0.004 |
| Sr | 0.006 | 0.001 | 0.027 | 0.002 | 0.001 | 0.018 | 0.002 | 0.001 | 0.016 | 0.002 | 0.000 | 0.018 | 0.16 ± 0.015 |
| Ti | 0.226 | 0.036 | 1.050 | 0.136 | 0.015 | 0.535 | 0.113 | 0.036 | 0.330 | 0.039 | 0.010 | 0.087 | 0.800 ± 0.074 |
| Description by main TSP sources | Profile number |
|---|---|
| Steel plant | |
| Sinter plant | 28301 |
| Open hearth furnace | 28302 |
| Basic oxygen furnace | 28303 |
| Baghouse catch dust | 26206 |
| Coke oven | 26101 |
| Coke dust | 21203 |
| Coal dust | 21204 |
| Average steel production | 90004 |
| Transportation | |
| Several profiles | 33004, 33005, 33009 |
| Fugitive dust emission from roads | |
| Paved roads | 41135, 41107 |
| Unpaved roads | 41220, 41205 |
| Other profiles for stationary sources | |
| Average chemical manufacturing | 90002 |
Firstly the PCA was performed on the RS matrix (11 metals × 58 composition profiles). These 58 composition profiles correspond to the 41 PM10 samples + the thermal power plant profile + the 16 surrogate profiles from the SPECIATE database. Results of the covariance PCA for the data matrix are shown in Table 3, which exhibits the variance percentage associated with the first 3 of the 12 components (PC1 to PC3). It is evident that the first two account for 99.5% of the information, indicating the efficiency of the transformation. Table 4 shows the eigenvectors of these Principal Components. Metal mass fraction, followed by Fe, K, Pb and Cr appeared as the main variables in PC1 to PC3. Due to the high cumulative percentage for the first two components, rotations of the whole PCA transformation give no further information.
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| Eigenvalue | 63.82 | 2.86 | 0.18 |
| Percentage of variance associated with each PCi | 0.95 | 0.04 | 0.003 |
| Cumulative percentage | 0.953 | 0.995 | 0.998 |
| Variable | PC1 | PC2 | PC3 |
|---|---|---|---|
| Concentration of Ba | < 0.001 | −0.004 | 0.091 |
| Concentration of Cr | 0.055 | 0.057 | −0.201 |
| Concentration of Cu | 0.030 | 0.057 | 0.049 |
| Concentration of Fe | 0.312 | −0.804 | 0.015 |
| Concentration of K | 0.310 | 0.484 | −0.523 |
| Concentration of Mn | 0.013 | −0.028 | −0.023 |
| Concentration of Ni | 0.003 | −0.010 | −0.082 |
| Concentration of Pb | 0.151 | 0.331 | 0.811 |
| Concentration of Rb | 0.009 | −0.010 | 0.012 |
| Concentration of Sr | 0.001 | −0.001 | −0.011 |
| Concentration of Ti | < 0.001 | −0.019 | −0.089 |
| Metallic mass fraction | 0.883 | 0.053 | 0.051 |
The plotting of filter samples and candidate sources on the PC1-PC2 plane (Fig. 5a) allows a rapid screening of sources’ contribution. A confidence ellipse for the measured filters is also plotted in Fig. 5a. For such a purpose, we employed the STATISCA software (Statsoft, Tulsa, USA). The sinter plant may be singled out as an unlikely contributing source because its distance to the centre of the confidence ellipse is greater than twice its semimajor axis. In the original 11-dimensional space of element concentrations (μg g−1), it is often convenient to employ the lever rule. In this case, the ratio of the contribution of two sources to a particular PM10 sample is the inverse of the ratio of the lengths of the lines connecting the PM10 sample concentration to the concentrations of each of the sources, in order. The big distance between the sinter plant and the confidence ellipse in the PC1-PC2 plane implies a greater or equal distance in the original concentration space. Consequently, the lever rule indicates a comparatively smaller contribution, if any, of the sinter plant to the PM10 samples within the confidence ellipse. It is possible to validate this result regarding the sinter plant’s PM emissions. Even when important emissions are seen coming from this plant, they are mainly composed of rather big particles that tend to deposit rapidly inside the steel mill and thus their chances of reaching the monitoring sites located outside the facility are extremely small.
 | ||
| Fig. 5 Receptors, thermal power plant and other potential sources on the PC1-PC2 plane. The confidence ellipse of the set of PM10 samples is indicated. (a) The long distance of the projected sinter plant profile allows its consideration as an unlikely contributing source. (b) Receptor and sites are further discriminated. | ||
A closer look at the distribution of receptors and potential sources, excluding the sinter plant is shown in Fig. 5b. The PM10 samples pertaining to each sampling site as well as the different type of sources have been represented in a distinctive manner. Practically all PM10 samples, except one collected at site 1 pertain to the confidence ellipse. In Fig. 5b, the farthest source from the ellipse is the steel mill furnace lying at a distance somewhat greater than the semimajor axis. As a conservative approach, this source was kept as a likely contributor. The thermal power plant and the remaining surrogate profiles were also kept as potentially contributing sources, as they either belong to the confidence ellipse or are located in its close vicinity. For all practical purposes, profiles of coal dust, coke dust and coke oven, nearly located at the same locus on the PC1-PC2 plane, can be considered as a unique average source named as carbonaceous dust. Finally, many PM10 samples were left outside the rather elongated convex polygon, whose vertices stand for possible sources. This is due partly because of the uncertainty regarding the adequate representation of the actual sources by the surrogate profiles. The existence of at least another potential unidentified source may be also a plausible explanation. The zone where the projection of such a potential source could be located is indicated in Fig. 5b. The contribution of this source could add up to the measured concentration of most PM10 samples. In fact, there are numerous agricultural activities in the area that could not be represented by the database’s available profiles.
The preceding analysis has confirmed the thermal power plant as a contributing source and has also indicated the adoption of a reduced set of profiles as the remaining most likely contributing sources, namely transportation, unpaved roads and the integrated steel mill, with its emission of carbonaceous dust, exhaust from furnaces and dust control equipment. It also suggested that the set of selected sources may be incomplete and thus further sources, probably from agricultural activities, should be taken into account. Apportionment of the detected sources was not attempted, not only because of the incompleteness of the set of candidate sources but also because the stored PM10 samples were collected with the thermal power plants as a focus. Thus, the sampling sites did not optimally represent the contribution of the detected possible sources.
Conclusions
This work shows the potential of combining dispersion and receptor analysis to elucidate the role of a known source within the framework of incomplete characterization of other sources. For the thermal power plant that was well-characterized, we have introduced an apportionment coefficient which allowed a rapid assessment of the relative contribution of this source to 24 h PM10 concentrations in a receptor site.For the rest of the sources, which were identified but not characterized, we have proposed a screening procedure based on principal component analysis that used the covariance matrix of the combined set of multielemental composition of measured filters, plus the profiles of all the possible candidate sources. This procedure, which to the best of our knowledge has been employed for the first time in this paper, is useful to discard non significant contributing sources. By means of this technique, it is possible to generate more reliable source information for the chemical mass balance problem. In this work, the original 16 candidate profiles were reduced to 4 distinct sources.
We also tried to highlight the value of fully exploiting the underlying information in stored filters prior to investing considerable time and expense in larger monitoring projects. In countries like Argentina, with few and fragmentary environmental databases, and with limited budget for environmental assessment, local regulators can take advantage of this type of study to estimate the order of magnitude of the different problems awaiting to be tackled.
The present study used air quality information collected during a monitoring campaign that constituted one of the few systematic studies of such nature that has been undertaken in Argentina. Although it was originally intended for the measurement of air quality at those locations where the role of the power plant was considered significant, our analysis was also useful in elucidating the significance of other sources. This convinced the local environmental authorities to undertake a more consistent air quality programme for the area.
Acknowledgements
This work was performed as part of the Project PICT 13-08772 of the Agencia Nacional de Promoción Científica y Tecnológica of Argentina. The support from the Electricity Regulatory Agency and the assistance from the National Weather Service of Argentina are greatly appreciated.References
- M. Sharpe, J. Environ. Monit., 2000, 2, 71N RSC.
- J. C. Chow, J. P. Engelbrecht, J. G. Watson, W. E. Wilson, N. H. Frank and T. Zhu, Chemosphere, 2002, 49, 961 CrossRef CAS.
- C. Seigneur, P. Pai, P. K. Kopke and D. Grosjean, Review of Air Quality Models for Particulate Matter, American Petroleum Institute, Washington, DC, 1998 Search PubMed.
- L. E. Dawidowski, D. R. Gómez and S. L. Reich, Guía Metodológica para la Evaluación del Impacto Ambiental Atmosférico, Imprenta del Congreso de la Nación, Buenos Aires, 1997 Search PubMed.
- J. G. Watson, T. Zhu, J. C. Chow, J. Engelbrecht, E. M. Fujita and W. E. Wilson, Chemosphere, 2002, 49, 1093 CrossRef CAS.
- J. C. Chow, J. G. Watson, M. C. Green, D. H. Lowenthal, D. W. DuBois, S. D. Kohl, R. T. Egami, J. Gillies, C. F. Rogers and C. A. Frazer, J. Air Waste Manage. Assoc., 1999, 49, 641 CAS.
- J. A. Cooper, J. G. Watson and J. J. Huntzicker, Atmos. Environ., 1984, 18, 347.
- User’s Guide for the Industrial Source Complex (ISC3) Dispersion Model, Vol. II-Description of Model Algorithms, US Environmental Protection Agency, EPA-454/B-95-003a., Research Triangle Park, NC, 1995 Search PubMed.
- Y. Qin and K. Oduyemi, Atmos. Environ., 2003, 37, 1799 CrossRef CAS.
- P. Paatero, User’s Guide for Positive Matrix Factorisation Programs PMF2 and PMF3, University of Helsinki, Helsinki, 1998 Search PubMed.
- R. O. McClellan, Toxicology, 2002, 181–182, 329 CrossRef CAS.
- S. L. Reich, D. R. Gómez and L. E. Dawidowski, Atmos. Environ., 1999, 33, 3045 CrossRef CAS.
- Estadísticas Climatológicas. Serie B – No. 37, Servicio Meteorológico Nacional, Buenos Aires, 1992 Search PubMed.
- Quality Assurance in Urban Air Quality Monitoring, in GEMS/AIR Methodology Review Handbook Series, UNEP, Nairobi, 1997, Vol. 1 Search PubMed.
- SPECIATE database, US Environmental Protection Agency, Research Triangle Park, NC, 2002.
- D. F. Gatz, Atmos. Environ., 1975, 9, 1 CrossRef CAS.
- R. Tertian and F. Claisse, Principles of Quantitative X-Ray Fluorescence Analysis, Heyden & Son, London, 1983, pp. 307–314 Search PubMed.
- S. S. Zilitinkevich, Boundary Layer Meteor., 1972, 3, 141 Search PubMed.
- D. B. Turner, L. W. Bender, T. E. Pierce and W. B. Petersen, Environ. Software, 1989, 4, 52 Search PubMed.
- C. F. Braga, R. C. M. Alves, E. C. Teixeira and M. Pires, J. Environ. Monit., 2002, 4, 897 RSC.
- S. A. Abdul-Wahab, S. M. Al-Alawi and A. El-Zawahry, Environ. Model. & Software, 2002, 17, 563 Search PubMed.
- M. Schuhmacher, J. L. Domingo and J. Garreta, Environ. Res., 2004, 95, 198 CrossRef CAS.
- T. Sax and V. Isakov, Atmos. Environ., 2003, 37, 3481 CrossRef CAS.
- M. Lorber, A. Eschenroeder and R. Robinson, Atmos. Environ., 2000, 34, 3995 CrossRef CAS.
- Yegnan, D. G. Williamson and A. J. Graettinger, Environ. Model. Software, 2002, 17, 639 Search PubMed.
- Receptor Modeling for Air Quality Management, ed. P. K. Hopke, Elsevier Science, Amsterdam, 1991 Search PubMed.
- R. C. Henry, Chemom. Intell. Lab. Syst., 1997, 37, 37 CrossRef CAS.
- J. A. Cooper, J. G. Watson and J. J. Huntzicker, Atmos. Environ., 1984, 18, 1347 CrossRef.
- R. A. Johnson and D. W. Wichern, Applied Multivariate Statistical Analysis, Prentice Hall, Upper Saddle River, NJ, 1998 Search PubMed.
- R. C. Henry, Chemom. Intell. Lab. Syst., 2002, 60, 43 CrossRef CAS.
- P. Paatero and U. Tapper, Chemom. Intell. Lab. Syst., 1993, 18, 183 CrossRef CAS.
- Y. Qin, K. Oduyemi and L. Y. Chan, Chemom. Intell. Lab. Syst., 2002, 61, 75 CrossRef CAS.
- P. Paatero, P. K. Hopke, X.-H. Song and Z. Ramadan, Chemom. Intell. Lab. Syst., 2002, 60, 253 CrossRef CAS.
- R. C. Henry, Chemom. Intell. Lab. Syst., 2003, 65, 179 CrossRef CAS.
- N. D. Tracey, J. C. Young and R. L. Mason, J. Qual. Technol., 1992, 2, 88 Search PubMed.
| This journal is © The Royal Society of Chemistry 2005 |
