Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr†
Received 30th September 2004, Accepted 26th October 2004
First published on 15th November 2004
Abstract
An implementation of analytic basis set gradients is reported for the optimization of auxiliary basis sets in resolution-of-the-identity second-order Møller–Plesset perturbation theory (RI-MP2) and approximate coupled-cluster singles-and-doubles (RI-CC2) calculations. The analytic basis set gradients are applied in the optimization of auxiliary basis sets for a number of large one-electron orbital basis sets which provide correlation energies close to the basis set limit: the core–valence basis sets cc-pwCVXZ (B–Ne, Al–Ar) with X
= D, T, Q, 5, the quintuple-ζ basis sets cc-pV5Z (H–Ar) and cc-pV(5 + d)Z (Al–Ar) and the doubly-polarized valence quadruple-ζ basis sets QZVPP for Li–Kr. The quality of the optimized auxiliary basis sets is evaluated for several test sets with small and medium sized molecules.
1. Introduction
In 1998 Weigend et al.1 demonstrated that with optimized auxiliary basis sets the resolution-of-the-identity (RI) approximation for four-index electron repulsion integrals2–4
(ERIs) leads to large savings in the computational costs for second order Møller–Plesset perturbation theory (MP2) calculations while the errors introduced by this approximation can be kept small compared to the one-electron basis set error. The RI approximation reduces the CPU time for MP2 calculations typically by about an order of magnitude or more and the scaling of the core memory and disk space requirements is decreased so that they are no longer bottlenecks for large scale MP2 calculations.5Since then the RI approximation for ERIs has been successfully applied to several correlated ab initio methods as e.g. the approximate coupled-cluster singles-and-doubles model CC2,6 multi-reference CI and perturbation theory,7,8 local MP2 9 and coupled-cluster methods10 and the explicitly correlated MP2-R12 11 approach. Today the RI approximation for ERIs is implemented in several programm packages and has become a standard tool for large scale calculations with correlated ab initio methods. (For the usage of the RI approximation in the framework of density functional and Hartree–Fock theory the reader is referred to refs. 4, 12–15)
As mentioned above, optimized auxiliary basis sets are a prerequisite for the efficiency and accuracy of the resolution-of-the-identity approximation for ERIs. The optimization of auxiliary basis sets is, however, usually considered to be a tedious task, in particular for correlated ab initio methods. For RI-MP2 and RI-CC2 (for which the same basis sets can be used) optimized auxiliary basis sets have been reported in refs. 1 and 16 for the basis sets SVP,17 TZVP18 and TZVPP1 and the correlation-consistent basis sets19–21 cc-pVXZ, cc-pV(X
+ d)Z, aug-cc-pVXZ, and aug-cc-pV(X
+ d)Z for X
= D, T and Q. These optimizations were carried out with a special version of the RI-MP2 program of Weigend and Häser,5 which was modified to calculate the weighted error functional for the approximated ERIs, eqn. (5) below. The derivatives of the functional with respect to the exponents and contraction coefficients were evaluated numerically by finite differences. Such an approach is limited in its applicability by an unfavourable scaling of the computational costs and the limited accuracy of the numerical gradients.
The aim of the present work is to resolve this bottleneck with an implementation of analytic gradients and to provide an efficient tool for the optimization of such auxiliary basis sets.
In Section II the weighted error functional which is used for the optimization of the auxiliary basis sets for RI-MP2 and RI-CC2 calculations is briefly reviewed and the expressions for the first derivatives with respect to parameters of the auxiliary basis are derived. By relating the result to the expressions for RI-MP2 energy gradients5,22,23 it is shown how these derivatives can be implemented by simple modifications of an RI-MP2 gradient program. In Section III the implementation of the analytic basis set gradient is applied for the optimization of auxiliary basis sets for a number of large one-electron basis sets, which in Section IV are assessed by comparing for several test sets with in total 193 molecules the error introduced by the resolution-of-the-identity approximation with the one-electron basis set error. In Section V a short summary and some conclusions are given.
II. Gradients for the optimization of auxiliary basis sets
In a spin orbital basis the MP2 correlation energy is| |  | (1) |
where 〈ab‖ij〉
=
(ai|bj)
−
(aj|bi). The indices i, j denote here occupied and a, b virtual (unoccupied) canonical SCF spin orbitals and εp are the SCF orbital energies. In the RI approximation the four-index ERIs are approximated as| | 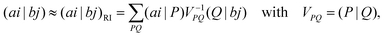 | (2) |
where P and Q are auxiliary basis functions and (ai|P) and (P|Q) are three- and two-index ERIs.The resolution-of-the-identity error in the MP2 correlation energy, which is defined as the difference between the result obtained in a RI-MP2 calculation and that of a conventional calculation, can be split into two contributions:
| |  | (4) |
The errors in the individual four-index electron repulsion integrals (ERIs) can be positive or negative, therefore the first term, which is linear in the error of the ERIs, can not be used as a functional for a variational optimization of the auxiliary basis sets. Only the second term, which is quadratic in the error of the ERIs, is negative semi-definite and suitable for a variational optimization. The negative of the latter term,
i.e. the functional
| |  | (5) |
is minimized to determine optimized auxiliary basis sets for the resolution-of-the-identity in RI-MP2 and RI-CC2 calculations.
1,16 In
δRI the SCF orbital energies appear as in the MP2 energy linear in the denominators. Compared to other choices for the denominators and in particular to a minimization of just the average squared errors in the ERIs, this leads to an optimal convergence for correlation energies with the size of the thereby optimized auxiliary basis sets.
Previous optimizations of auxiliary basis sets for RI-MP2 calculations1,16 employed for the minimization of δRI numerical gradients evaluated by finite differences. This technique required the evaluation of δRI at least once for each basis set parameter that had to be varied. This lead to a rapid increase in the computational costs with the basis set size for fully optimized auxiliary basis sets. Futhermore, the numerical errors of the finite difference procedure hinder a tight convergence of the optimization procedure. For the optimization accurate auxiliary basis sets for large one-electron orbital basis sets analytic basis set gradients are thus an important prerequisite.
The gradient of δRI with respect to a parameter λ of the auxiliary basis set {P} can be expressed in a form which is very similar to that of some contributions to the gradient for the RI-MP2 correlation energy:
| |  | (6) |
| |  | (7) |
The intermediates
![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) aoμνP
aoμνP and
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) aoPQ
aoPQ are three- and two-index two-electron densities which differ from corresponding intermediates in the calculation of RI-MP2 energy gradients
5,22 only in that the amplitudes calculated in the RI approximation,
| |  | (8) |
are replaced by the difference amplitudes
| |  | (9) |
The three-index two-electron density matrix ![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) ao is defined as:5,22
ao is defined as:5,22
| |  | (10) |
and the two-index two-electron density density matrix
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ao
ao is obtained as:
5,22| |  | (11) |
Based on the above equations, the derivatives of δRI with respect to the exponents and contraction coefficients of the auxiliary basis can be obtained by relatively simple modifications of an RI-MP2 energy gradient code. This has been exploited to implement these basis set gradients in the RICC2 module6,22 of the TURBOMOLE package.24 In combination with the optimization module RELAX and a small script which controls the iterative optimization this results in an efficient (almost) black box procedure for the optimization of auxiliary basis sets, which is made available with the current version25 of the TURBOMOLE package. Since the canonical orbitals and the non-approximated four-index ERIs do not depend on the auxiliary basis, these need to be evaluated only once. This reduces the costs for a gradient calculation for δRI to about 2–3 times the costs of a RI-MP2 energy calculation. For atoms a single gradient calculation for δRI lasts even for large one-electron basis sets on modern PCs typically some seconds, so that these optimization can easily be carried out interactively.
III. Optimization of auxiliary basis sets
In ref. 16 optimized auxiliary basis sets were reported for the correlation consistent basis set series cc-pVXZ and aug-cc-pVXZ (X
= D, T, Q) for the elements H, He, B–Ne, Al–Ar and Ga–Kr as well as for the cc-pV(X
+ d)Z and aug-cc-pV(X
+ d)Z basis set series for the atoms Al–Ar. As pointed out above, these and the auxiliary basis sets reported in ref. 1 for the basis sets SVP, TZVP and TZVPP were obtained using numerical gradients obtained by a finite difference technique.In the present work the analytic gradient implementation described in Section II has been employed to complement these auxiliary basis sets by those for the highly accurate one-electron basis sets cc-pV5Z19 and aug-cc-pV5Z20 for the atoms H, He and B–Ne and cc-pV(5 + d)Z and aug-cc-pV(5 + d)Z21,20 for the atoms Al–Ar as well as by those for the weighted core–valence basis set series26 cc-pwCVXZ for the atoms B–Ne and Al–Ar with cardinal numbers X = D, T, Q, 5.
In the course of optimizing the wCX auxiliary sets it was found that a few of the valence auxiliary basis sets (cc-pVDZ for C–F, cc-pVTZ and cc-pVQZ for Ne, and the diffuse functions for the respective aug-cc-pVXZ basis sets) reported in ref. 16 were not completly converged. Since this caused problems for the optimization of the core–valence wCX auxiliary functions, these basis sets have been reoptimized. The new auxiliary cc-pVDZ (C–F), cc-pVTZ (Ne) and cc-pVQZ (Ne) basis sets lead only to slight improvements for the RI approximation, but are more consistent (in the range of exponents covered) with the other cc-pVXZ auxiliary basis sets and are now made available via ftp27 as default auxiliary basis sets.
In ref. 16 no auxiliary basis sets were reported for the cc-pVXZ sets28 for the (earth) alkali atoms Li, Be, Na and Mg. These have now been included in the present work. Furthermore, optimized auxiliary basis set are reported for the doubly-polarized valence quadruple-ζ basis QZVPP published recently by Weigend et al.29 for the atoms H–Kr. The latter basis is a valuable alternative to the cc-pVQZ basis, in particular for the third-row elements Ga–Kr, since in difference to the latter basis it allows to correlate the 3d shell. Since in the work described in ref. 1 no auxiliary basis sets were optimized for the rare gas atoms He, Ne, Ar and Kr, for these atoms also auxiliary SVP, TZVP and TZVPP basis sets have been constructed in the course of the present work. All auxiliary basis sets reported here are available together with those from refs. 1 and 16 by ftp27
(see below).
A. Auxiliary quintuple-ζ basis sets
To keep the auxiliary quintuple-ζ basis sets consistent with those for the lower cardinal numbers (X = D, T, Q), these basis sets were constructed using a similar scheme as that described in ref. 16. For He–Ar the optimizations of the cc-pV5Z (cc-pV(5 + d)Z) auxiliary sets were carried out for the atoms in there electronic ground state based on a spin-unrestricted Hartree–Fock (UHF-SCF) wavefunction, while for hydrogen the optimization was done for the H2 molecule (RHH
= 1.39 a0). Even though the cc-pV5Z basis sets have only been designed to correlate the valence electrons, they are often used without applying a frozen core approximation. Therefore all occupied (and virtual) orbitals have been included in the calculation of the error functional δRI. This is done to guarantee a high accuracy for the RI approximation irrespective of the use of the frozen core approximation. For the second-row atoms Al–Ar the same auxiliary sets are used for cc-pV5Z and cc-pV(5 + d)Z and the optimizations have been carried with the slightly larger cc-pV(5 + d)Z orbital basis.As is apparent for the atoms, the auxiliary basis sets should include at least functions with angular momenta up to locc
+
lbas, where locc is the highest angular momentum occupied in the SCF wavefunction and lbas the highest angular momentum included in the orbital basis, to obtain an accurate resolution of the identity for products of one occupied and one virtual orbital. For the hydrogen atom, which in covalent bonds is often strongly polarized, it turned however out that also functions with laux
=
locc
+
lbas
+ 1 should be included.1,16 For consistency and to use the same number of auxiliary basis functions for atoms of the same row and orbital basis sets of the same size, also for He, Li and Be functions with laux up to locc
+
lbas
+ 1 are included. As for the lower cardinal numbers, the auxiliary basis sets are not contracted and the same number of primitive functions is used for atoms in the same row of the periodic table and same orbital basis set size. The number of GTOs included for each angular momentum are given in Table 1.
Table 1 Number of primitive GTOs for the auxiliary basis sets cc-pVXZ and cc-pwCVXZ. For the atoms Al–Ar the same auxiliary basis sets are used for the cc-pVXZ and the cc-pV(X
+ d)Z orbital basis sets. In parentheses are the ratios of the number of basis functions in the auxiliary and the orbital basis given
| | cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z |
|---|
| | cc-pV(D + d)Z | cc-pV(T + d)Z | cc-pV(Q + d)Z | cc-pV(5 + d)Z |
|---|
| H, He | 3s2p1d (2.8) | 4s3p2d1f (2.1) | 5s4p3d2f1g (1.8) | 6s5p4d3f2g1h (1.7) |
| Li–Ne | 7s5p4d2f (4.0) | 8s6p5d3f1g (2.7) | 8s7p6d5f3g1h (2.4) | 10s8p7d6f4g3h1i (2.1) |
| Na–Ar | 9s7p5d3f (3.3) | 10s8p7d5f2g (3.1) | 11s9p8d6f3g1h (2.5) | 12s11p9d7f5g3h1i (2.3) |
| | cc-pwCVDZ | cc-pwCVTZ | cc-pwCVQZ | cc-pwCV5Z |
|---|
| B–Ne | +3s2p1d (3.9) | +4s3p2d1f (2.6) | +4s4p3d2f1g (2.2) | +4s4p4d3f2g1h (1.9) |
| Al–Ar | +3s3p3d2f (4.3) | +4s4p3d2f1g (3.0) | +4s4p3d3f3g2h (2.4) | +4s4p4d3f3g2h2i (2.0) |
For the atoms He, Li and Be the auxiliary functions with the highest angular momentum (h for He and i for Li and Be) could not be optimized at the atoms, since they do not contribute to the correlation energy of the (unpolarized) atoms. These functions were determined as follows: the exponent for the h function for He was interpolated as 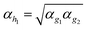 and for Li and Be the exponents of the i functions were taken from the second h function, because for B–Ne the (optimized) exponents for i where close to those of the second h function.
and for Li and Be the exponents of the i functions were taken from the second h function, because for B–Ne the (optimized) exponents for i where close to those of the second h function.
The additional diffuse functions for the aug-cc-pV5Z (aug-cc-pV(5 + d)Z) auxiliary sets were optimized for the respective anions. As for the lower cardinal numbers, it was found that the addition of one diffuse auxiliary function for each angular momentum is sufficient to obtain for the aug-cc-pV5Z (aug-cc-pV(5 + d)Z) basis sets a similar accuracy as for the non-augmented sets. For He the exponent of the diffuse h function was again interpolated from the g functions as  .
.
B. Auxiliary core–valence basis sets
In analogy to the cc-pwCVXZ and cc-pwCV(X
+ d)Z orbital basis sets the respective auxiliary basis sets are build up in a modular way by adding to the cc-pVXZ auxiliary basis a set of functions (“wCX”) with tight exponents to expand the additional four-index integrals 〈ai‖bj〉 which are obtained when the core–valence correlation functions are included in the orbital basis. Their role is to expand orbital products ϕα(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )ϕi(
)ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) where either ϕi is a core orbital or ϕα one of the additional correlation and polarization functions of the (orbital) core–valence set. Thus, for the atoms B–Ne, for which the core consists of the 1s orbital and the orbital core–valence set includes functions with angular momenta up to lwC
=
lbas
− 1 =
X
− 1, it is sufficient to include in the wCX auxiliary set functions with angular momenta up to locc
+
lbas
− 1. For the second-row atoms Al–Ar, however, the most important core orbitals are those of the 2s2p shell and therefore the wCX auxiliary sets include, as the orbital core–valence set, functions with the same maximum angular momentum as the cc-pVXZ sets. Table 1 lists the number of GTOs added in each angular momentum for the cc-pwCVXZ auxiliary basis sets.
) where either ϕi is a core orbital or ϕα one of the additional correlation and polarization functions of the (orbital) core–valence set. Thus, for the atoms B–Ne, for which the core consists of the 1s orbital and the orbital core–valence set includes functions with angular momenta up to lwC
=
lbas
− 1 =
X
− 1, it is sufficient to include in the wCX auxiliary set functions with angular momenta up to locc
+
lbas
− 1. For the second-row atoms Al–Ar, however, the most important core orbitals are those of the 2s2p shell and therefore the wCX auxiliary sets include, as the orbital core–valence set, functions with the same maximum angular momentum as the cc-pVXZ sets. Table 1 lists the number of GTOs added in each angular momentum for the cc-pwCVXZ auxiliary basis sets.The exponents of the auxiliary core–valence functions were mostly optimized as described above for the cc-pVXZ auxliary basis sets. For some functions, however, minimization of δRI led to exponents which were close to an exponent of one of the tight functions already contained in the cc-pVXZ auxiliary set. In these cases the respective exponents were replaced by the geometric mean of the two closest exponents in the cc-pVXZ auxiliary basis. For the optimization of the wCX auxiliary sets all occupied orbitals have been included in the calculation of δRI and its gradients; only for the cc-pwCVDZ and cc-pwCVTZ sets for Al–Ar the 1s orbitals have been excluded (frozen).
C. Auxiliary QZVPP basis sets for Li to Kr
For the doubly-polarized valence quadruple-ζ basis sets from Weigend et al.29 several groups of atoms have to be distinguished which differ in how the orbital basis sets have been constructed. The optimization schemes for the orbital basis sets are reflected and, for some of the atoms, are also exploited in the construction of the auxiliary basis sets. The size of the resulting auxiliary basis sets are given in Table 2 together with the size of the QZVPP orbital basis sets and the ratios of the number of functions in the two basis sets Naux/Norb.
Table 2 Number of GTOs in the orbital and auxiliary QZVPP basis sets
| | Orbital basis | Auxiliary basis | Naux/Norb |
|---|
| H, He | [4s3p2d1f] | (5s4p3d2f1g) | 1.8 |
| Li | [6s4p2d1f] | (9s6p3d2f) | 1.6 |
| Be | [7s4p2d1f] | (9s7p4d2f) | 1.8 |
| B–Ne | [7s4p3d2f1g] | (8s7p6d5f3g1h) | 2.3 |
| Na | [9s5p4d2f] | (12s11p9d7f3g) | 2.9 |
| Mg | [9s5p5d2f] | (12s11p8d6f3g) | 2.4 |
| Al–Ar | [9s6p4d2f1g] | (11s9p8d6f3g1h) | 2.3 |
| K | [11s6p4d3f] | (14s13p9d8f5g) | 2.8 |
| Ca | [11s6p4d3f] | (14s12p9d8f5g) | 2.8 |
| Sc–Ni | [11s6p5d3f2g] | (15s13p11d8f7g5h2i) | 3.3 |
| Cu–Zn | [11s6p5d3f2g] | (15s13p11d9f7g5h2i) | 3.4 |
| Ga–Kr | [11s7p4d4f1g] | (13s12p11d9f7g5h1i) | 3.3 |
a. H, He, B–Ne and Al–Ar. For these atoms the QZVPP (orbital) basis is made up of the segmented contracted QZV kernel of s and p functions (for H and He only s functions) and a primitive set of polarization functions taken for H, He and B–Ne from the cc-pVQZ and for Al–Ar from the cc-pV(Q + d)Z basis. One could thus expect that the auxiliary basis sets for the cc-pVQZ basis would provide an accurate resolution of the identity also for the QZVPP orbital basis. Test calculations with the molecules used for evaluating the performance of the auxiliary basis sets (see below) showed, however, that this gives RI errors which are larger than what one would like to have for a quadruple-ζ basis set. Therefore, an QZVPP auxiliary basis has been constructed for these atoms from the f, g and h (for H and He the p, d and f) functions of the cc-pVQZ (cc-pV(Q + d)Z) auxiliary basis and a new spd set (for H and He an s set) which has been optimized by minimizing δRI for the atoms. Only for hydrogen the optimization was done at the H2 molecule. For Al–Ar the 1s orbital was through this optimization excluded from the calculation of the δRI functional and its gradient.
b. Ga–Kr. The QZVPP orbital basis for the third row atoms Ga–Kr is constructed in a similar way as those for B–Ne and Al–Ar, but since Ga–Kr have an occupied 3d shell the QZV kernel includes also d functions and only the f and g polarization functions of the cc-pVQZ sets are included in the QZVPP basis. The most important difference, however, is that in addition Weigend et al. added two tight f functions to account for the polarization and correlation of the 3d shell. Since the correlation of the 3d shell has a strong effect on the optimized auxiliary functions of all included angular momenta, all functions of the QZVPP auxiliary basis were determined by minimizing for the neutral atoms (in their electronic ground state)
δRI for the occupied orbitals of the shells 3s3p3d and 4s4p.
c. Li, Be, Na, Mg, K and Ca. For the (earth) alkali atoms Weigend et al. determined the polarization functions for the QZVPP basis by maximization of the MP2 correlation energy. They differ in the number of functions and in the maximum angular momentum by those for the respective cc-pVQZ basis sets and, most importantly, account to a much larger extent for core and core–valence correlation effects to ensure a balanced treatment of neutral atoms and cations. To carry these features over to the auxiliary basis, first a set of relatively tight functions was optimized for the cations which has then been augmented by some more diffuse functions optimized for Li, Na and K for the metal dimers and for Be, Mg and Ca for the tetramers. The calculation of δRI included for all six atoms the occupied orbitals of the valence and the next lower shell.
d. Sc–Zn. A similar procedure was applied for the optimization of the auxiliary basis sets for the transition metal atoms. The innermost tight functions were optimized for the cations with the highest oxidation number usually found in chemical compounds, while the outermost diffuse functions were optimized for the neutral atoms. For Ti–Co also cations with intermediate oxidation numbers (Ti2+, V3+, Cr3+, Mn2+, Mn4+, Fe2+, Co2+) were included in the optimization to determine auxiliary functions with intermediate exponents. As for Ga–Ar, the occupied orbitals from the 1s2s2p core shells were for the optimization excluded from the calculation of the error functional δRI.
IV. Evaluation of the auxiliary basis sets
The auxiliary basis sets described above have mostly been optimized for atoms (or atomic cations and anions). To evaluate the accuracy obtained with these basis sets in calculations on molecules, we investigated the RI error, eqn. (3), for a set of 193 small and medium sized compounds. Depending on the availability of the basis sets this test set is divided into five subsets as shown in Table 3.
Table 3 The test sets used to evaluate the performance of the optimized auxiliary basis sets. The first set consists of 42 molecules that contain only H, He and the elements B–Ne, while the second set comprises of 30 molecules which contain also at least one of the second row elements Al–Ar. Since the aug-cc-pVXZ and cc-pwCVXZ basis set series are not available for the (earth) alkali atoms Li, Be, Na and Mg, the molecules containing these atoms are grouped into two separate sets (19 molecules containing Li or Be and 12 molecules with Na or Mg) and the last set comprises 90 molecules containg the third row elements K–Kr
| Row 1 (B–Ne) | Row 2 (Al–Ar) |
|---|
| B2H6, B4H4, BF3, BH3, BH3CO, BH3NH3, B3N3H6 | H2S, H2S2, P2, CS2, S2, S5, SF2 |
| C2H2, C2H3N, C2H4, C2H6, C4H4, C6H6, CF4, CO | SF4, Cl2, ClF, ClF3, Al2O3, Al2S3 |
| CH2O, CH2O2, CH3N, CH3OH, CH4,CO2, F2, H2, Ne2 | AlCl3, AlF3, AlH3, HCl, PF3, PF5 |
| H2CO3, H2O, H2O2, HCN, HF, HNC, HNO, NH3, NH4F | PH3, Ar2, H2SO4, H3PO4, HCP |
| HNO2, HNO3, He2, N2, N2H2, N2H4, N4, NF3, OF2 | SF6, SiCl4, SiF4, SiH4, SiO2, SiS2 |
| Row 1 (Li, Be) | Row 2 (Na, Mg) |
|---|
| Li2, Li2O, Li4(CH3)4, Li4Cl4, Li4H4, Li8, LiBH4, LiCl | Na2O, Na2S, Na3N, Na3P |
| LiF, LiH, Li2S, PLi3, Be2F4, Be2H4 | NaCl, NaF, NaH, Na2 |
| Be4, Be(CH3)2, BeF2(OH2)2, BeH2, BeS | MgCl2, MgF2, MgH2, Mg4 |
| Row 3 (K–Kr) |
|---|
| K2, K2S, K3P, KBr, KCl, KF, KH, Ca4, CaCl2, CaF2, CaH2, ScCl3, ScF, ScF3, ScH3, ScO |
| TiCl4, Ti(CO)4, TiF3,TiF4, TiH4, TiO, TiO2, TiS2, VH5, VO, VOF3, CrCl3, Cr(CO)6, CrF3, CrH, CrO3 |
| MnF2, MnO, MnO2, MnO3F, MnO4−, MnS, Fe(CO)5, FeF2, FeF3, FeO, Fe(C5H5)2, CoCl2, CoCl3, CoF2, CoF3, CoO |
| NiCl2, Ni(CO)4, NiF2, NiF3, NiO, NiS, Cu2O, Cu2S, CuCl, CuCl2, CuCN, CuF, CuH, ZnCl2, ZnF2, ZnH2, Zn(CH3)2 |
| GaCl, GaCl3, GaF, GaH3, GeCl4, GeF4, GeH4, GeO, GeO2, As4, AsCl3, AsCl6−, AsH3, Se8, SeH2, SeO2 |
| Br2, BrCl, BrO−, BrO2−, BrO3−, BrO4−, HBr, HCBr3, Kr2 |
All basis sets included in the present work are available for the atoms H, He, B–Ne and Al–Ar and for these the most comprehensive comparison is possible. The hierarchical structure of the correlation consistent basis sets from Dunning and coworkers for these atoms allows to obtain accurate estimates for the basis set limit of the MP2 correlation energy. In the present work the limits have been extrapolated with the formula
from the results for
X
= 5 and 6 or 4 and 5 (see
Tables 4 and 5 and
Fig. 1). The results for the valence basis sets (shown in
Table 4) reflect the well-known convergence behaviour of the correlation consistent basis sets cc-pVXZ (cc-pV(
X
+ d)Z). The results for the SVP, TZVPP and QZVPP basis sets, which are shown for comparison, are quite similar to those for the cc-pVXZ (cc-pV(
X
+ d)Z) basis sets with, respectively,
X
= D, T and Q. This is not surprising since for these atoms the TZVPP and QZVPP basis sets include the polarization functions from the basis sets of Dunning and coworkers. The diffuse functions included in the aug-cc-pV
XZ and aug-cc-pV(
X
+ d)Z sets have only a minor effect on the convergence of the correlation energy, as is seen from the results in
Table 5, and also for the core–valence basis sets the relative errors in the (core plus valence) correlation energy are very similar to those of the valence correlation energy in the standard basis sets.
 |
| | Fig. 1 One-electron basis set errors in the MP2 valence correlation energy (in % of the estimated limiting value) shown as normalized Gaussian distributions determined from ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms. and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms. | |
Table 4 Relative errors in the MP2 valence correlation energies obtained with the cc-pVXZ (H, He, B–Ne) and cc-pV(X
+ d)Z (Al–Ar) series and for the basis sets SVP, TZVPP and QZVPP. Listed are the mean error ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = (1/n)∑ni=1Δi, the standard deviation
= (1/n)∑ni=1Δi, the standard deviation  , and the maximum absolute error, |Δ|max
= maxi
|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. For the row 2 (Al–Ar) test set the results for the cc-pVXZ basis sets are given in parentheses. The basis set limits Ecorrlim have been extrapolated from the results for cc-pV5Z (cc-pV(5 + d)Z) and cc-pV6Z (cc-pV(6 + d)Z)
, and the maximum absolute error, |Δ|max
= maxi
|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. For the row 2 (Al–Ar) test set the results for the cc-pVXZ basis sets are given in parentheses. The basis set limits Ecorrlim have been extrapolated from the results for cc-pV5Z (cc-pV(5 + d)Z) and cc-pV6Z (cc-pV(6 + d)Z)
| Row 1 (B–Ne) | cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z | cc-pV6Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −29.66 | −11.66 | −5.28 | −2.72 | −1.57 | −29.76 | −11.98 | −5.52 |
| Δstd | 3.93 | 1.93 | 0.99 | 0.50 | 0.29 | 4.18 | 2.06 | 1.11 |
| |Δ|max | 41.95 | 17.28 | 8.13 | 4.19 | 2.42 | 42.56 | 18.13 | 9.39 |
| Row 2 (Al–Ar) | cc-pV(D + d)Z | cc-pV(T + d)Z | cc-pV(Q + d)Z | cc-pV(5 + d)Z | cc-pV(6 + d)Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −34.18 | −14.30 | −6.83 | −3.65 | −2.11 | −35.28 | −14.59 | −6.83 |
| | (−34.67) | (−14.42) | (−6.97) | (−3.78) | (−2.19) | | | |
| Δstd | 4.19 | 1.93 | 1.03 | 0.64 | 0.37 | 4.36 | 2.08 | 1.05 |
| | (4.52) | (2.06) | (1.12) | (0.72) | (0.42) | | | |
| |Δ|max | 43.13 (44.90) | 18.61 (19.10) | 9.24 (9.70) | 5.44 (5.83) | 3.15 (3.37) | 44.61 | 19.02 | 9.08 |
Table 5 Relative errors in the MP2 valence correlation energies obtained with the aug-cc-pVXZ (aug-cc-pV(X + d)Z) basis sets and the MP2 core plus valence correlation energies calculated with the cc-pwCVXZ basis sets. Listed are the mean error ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = (1/n)∑ni=1Δi, the standard deviation Δstd
=
= (1/n)∑ni=1Δi, the standard deviation Δstd
=
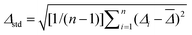 , and the maximum absolute error, |Δ|max
= maxi|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. The values for Ecorrlim have been estimated from the results for X
= Q and 5. Note that for the cc-pwCVXZ basis sets a frozen core approximation was applied to the 1s inner core orbitals of the second row elements Al–Ar
, and the maximum absolute error, |Δ|max
= maxi|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. The values for Ecorrlim have been estimated from the results for X
= Q and 5. Note that for the cc-pwCVXZ basis sets a frozen core approximation was applied to the 1s inner core orbitals of the second row elements Al–Ar
| Row 1 (B–Ne) | aug-cc-pVDZ | aug-cc-pVTZ | aug-cc-pVQZ | aug-cc-pV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −25.89 | −10.01 | −4.48 | −2.29 |
| Δstd | 2.86 | 1.55 | 0.80 | 0.41 |
| |Δ|max | 35.19 | 14.63 | 6.88 | 3.52 |
| Row 2 (Al–Ar) | aug-cc-pV(D + d)Z | aug-cc-pV(T + d)Z | aug-cc-pV(Q + d)Z | aug-cc-pV(5 + d)Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −29.24 | −12.19 | −5.72 | −2.93 |
| Δstd | 3.21 | 1.59 | 0.79 | 0.41 |
| |Δ|max | 36.48 | 15.63 | 7.20 | 3.69 |
| Row 1 (B–Ne) | cc-pwCVDZ | cc-pwCVTZ | cc-pwCVQZ | cc-pwCV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −32.42 | −11.57 | −4.98 | −2.55 |
| Δstd | 2.55 | 1.00 | 0.52 | 0.27 |
| |Δ|max | 41.03 | 14.76 | 6.57 | 3.37 |
| Row 2 (Al–Ar) | cc-pwCVDZ | cc-pwCVTZ | cc-pwCVQZ | cc-pwCV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −46.07 | −18.53 | −8.39 | −4.29 |
| Δstd | 4.99 | 2.62 | 1.24 | 0.63 |
| Δmax | 54.19 | 21.96 | 10.02 | 5.13 |
The estimates for the one-electron basis set errors given in Tables 4 and 5 can be compared with the auxiliary basis set error (i.e. the RI error). The latter should be smaller by at least an order of magnitude to ensure that the overall accuracy of a quantum chemical calculation is not affected by the RI approximation. In ref. 16 it was demonstrated for the cc-pVXZ (cc-pV(X
+ d)Z) basis sets with X
= D, T, Q that with the optimization strategy and the number of GTOs chosen for the auxiliary basis sets, the RI errors are more than two orders of magnitude smaller than the one-electron basis set errors. The present results for the elements H, He, B–Ne and Al–Ar, which are based on improved estimates for the basis set limit of the MP2 valence correlation energy and now include the new auxiliary basis sets for X
= 5 and for the QZVPP basis are shown in Table 6 and Fig. 2. The results for the aug-cc-pVXZ (aug-cc-pV(X
+ d)Z) and the core–valence basis sets cc-pwCVXZ are collected in Table 7. These numbers show that with the new optimized auxiliary basis sets for the QZVPP, cc-pV5Z (cc-pV(5 + d)Z), aug-cc-pV5Z (aug-cc-pV(5 + d)Z) and the core–valence basis sets cc-pwCVXZ similar relative accuracies (i.e. ratios of the RI and the one-electron basis set errors) are obtained as for the basis sets reported in refs. 1 and 16. For all these basis sets the RI errors are more than two orders of magnitude smaller than the one-electron basis set errors.
 |
| | Fig. 2 RI auxiliary basis set errors in the MP2 valence correlation energy (in % of the estimated one-electron basis limit for the latter) shown as normalized Gaussian distributions determined from ![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms. and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms. | |
Table 6 Relative RI error in the MP2 valence correlation energy obtained with the cc-pVXZ (cc-pV(X + d)Z), SVP, TZVPP and QZVPP basis sets for molecules with the main group elements B–Ne and Al–Ar. The relative RI error was calculated as ΔiRI
=
(Ecorr
−
Ecorr,RI)/Ecorrlim
× 100% with Ecorrlim extrapolated from the correlation energies in the cc-pV5Z (cc-pV(5 + d)Z) and cc-pV6Z (cc-pV(6 + d)Z) basis sets
| Row 1 (B–Ne) | cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | 0.0013 | 0.0078 | 0.0058 | 0.0026 | 0.0202 | 0.0076 | 0.0046 |
| Δstd | 0.0164 | 0.0067 | 0.0034 | 0.0015 | 0.0219 | 0.0074 | 0.0033 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0132 | 0.0081 | 0.0058 | 0.0026 | 0.0232 | 0.0084 | 0.0046 |
| |Δ|max | 0.0339 | 0.0268 | 0.0134 | 0.0069 | 0.0781 | 0.0247 | 0.0125 |
| Row 2 (Al–Ar) | cc-pV(D + d)Z | cc-pV(T + d)Z | cc-pV(Q + d)Z | cc-pV(5 + d)Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −0.0061 | −0.0011 | 0.0033 | 0.0021 | 0.0014 | 0.0003 | 0.0032 |
| Δstd | 0.0353 | 0.0124 | 0.0070 | 0.0028 | 0.0436 | 0.0181 | 0.0068 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0256 | 0.0087 | 0.0041 | 0.0023 | 0.0270 | 0.0118 | 0.0042 |
| Δmax | 0.1202 | 0.0419 | 0.0254 | 0.0095 | 0.1496 | 0.0620 | 0.0239 |
Table 7 Relative RI error in the MP2 valence correlation energy obtained with the aug-cc-pVXZ (aug-cc-pV(X
+ d)Z) basis sets and the MP2 all electron correlation energies calculated with the cc-pwCVXZ basis sets for X
= D, T, Q, 5. The relative RI error was calculated as ΔiRI
=
(Ecorr
−
Ecorr,RI)/Ecorrlim
× 100% where Ecorrlim was obtained as described in the caption of Table 5
| Row 1 (B–Ne) | aug-cc-pVDZ | aug-cc-pVTZ | aug-cc-pVQZ | aug-cc-pV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −0.0013 | 0.0063 | 0.0047 | 0.0022 |
| Δstd | 0.0143 | 0.0047 | 0.0022 | 0.0009 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0118 | 0.0064 | 0.0047 | 0.0022 |
| Δmax | 0.0293 | 0.0205 | 0.0101 | 0.0051 |
| Row 2 (Al–Ar) | aug-cc-pV(D + d)Z | aug-cc-pV(T + d)Z | aug-cc-pV(Q + d)Z | aug-cc-pV(5 + d)Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −0.0150 | −0.0009 | 0.0034 | 0.0023 |
| Δstd | 0.0260 | 0.0137 | 0.0040 | 0.0015 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0242 | 0.0078 | 0.0035 | 0.0023 |
| Δmax | 0.0691 | 0.0539 | 0.0154 | 0.0056 |
| Row 1 (B–Ne) | cc-pwCVDZ | cc-pwCVTZ | cc-pwCVQZ | cc-pwCV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | 0.0001 | 0.0038 | 0.0035 | 0.0020 |
| Δstd | 0.0122 | 0.0053 | 0.0024 | 0.0010 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0099 | 0.0049 | 0.0035 | 0.0020 |
| Δmax | 0.0274 | 0.0182 | 0.0092 | 0.0046 |
| Row 2 (Al–Ar) | cc-pwCVDZ | cc-pwCVTZ | cc-pwCVQZ | cc-pwCV5Z |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | −0.0048 | −0.0009 | 0.0017 | 0.0011 |
| Δstd | 0.0112 | 0.0054 | 0.0024 | 0.0009 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0101 | 0.0045 | 0.0020 | 0.0011 |
| Δmax | 0.0271 | 0.0142 | 0.0082 | 0.0034 |
For alkali and alkali earth atoms and, in particular, for transition metal atoms the basis set convergence is less regular than for elements of the main groups III–VIII and it depends much more on the oxidation state. Therefore, it has not been tried to extrapolate the basis set limit of the MP2 correlation energies for the molecules that contain the elements Li, Be, Na, Mg and K–Kr. The results for the RI errors are listed in Tables 8 and 9. Since the basis set convergence for these compounds is slower than for the molecules which contain only the atoms H, He, B–Ne and Al–Ar, it is expected that for the (earth) alkali and transition metal atoms the RI errors are in most cases also more than two orders of magnitude smaller than the one-electron basis set errors. Somewhat larger RI errors are only observed for the small SVP and cc-pVDZ basis sets for the alkali and earth alkali dimers and tetramers (Li2, Li8, Be4, Na2, Mg4, K2, Ca4) and to a smaller extend for their hydrids. If these molecules are taken out of the test sets the average and in particular the maximum RI errors are considerably smaller (e.g. for the SVP basis set the maximum RI errors decrease to 0.0632% for Li and Be, 0.1778% for Na and Mg and 0.0733% for K–Kr). However, for these cases also the convergence with respect to the one-electron basis set is rather poor since the small standard basis sets do not contain the diffuse polarization functions required for an accurate description of these compounds.
Table 8 Relative RI error in the MP2 valence correlation energy for molecules containing Li, Be, Na or Mg. The relative RI error was calculated as ΔiRI
=
(Ecorr
−
Ecorr,RI)/Ecorr
× 100%. The following orbitals have not been considered in the calculation of the correlation energy: 1s for B–F, 1s2s2p for P, S, Cl and 1s for Na, Mg
| Row 1 (Li, Be) | cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | 0.0473 | 0.0120 | 0.0097 | 0.0046 | 0.0556 | 0.0353 | 0.0062 |
| Δstd | 0.1101 | 0.0155 | 0.0111 | 0.0038 | 0.0816 | 0.0536 | 0.0059 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0701 | 0.0143 | 0.0097 | 0.0046 | 0.0665 | 0.0365 | 0.0062 |
| Δmax | 0.3478 | 0.0392 | 0.0479 | 0.0134 | 0.2211 | 0.2224 | 0.0212 |
| Row 2 (Na, Mg) | cc-pVDZ | cc-pVTZ | cc-pVQZ | cc-pV5Z | SVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | 0.0565 | 0.0188 | 0.0159 | 0.0026 | 0.1934 | 0.0096 | 0.0008 |
| Δstd | 0.1531 | 0.0457 | 0.0284 | 0.0027 | 0.6396 | 0.0388 | 0.0025 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0889 | 0.0280 | 0.0175 | 0.0027 | 0.2906 | 0.0259 | 0.0018 |
| Δmax | 0.4722 | 0.1311 | 0.0913 | 0.0091 | 2.1438 | 0.0795 | 0.0056 |
Table 9 Relative RI error in the MP2 valence correlation energy for molecules containing the atoms K–Kr. The relative RI error was calculated as ΔRIi
=
(Ecorr
−
Ecorr,RI)/Ecorr
× 100%. The following orbitals have not been considered in the calculation of the correlation energy: 1s for C–F, 1s2s2p for P, S, Cl and K–Zn and 1s2s2p3s3p for Ga–Kr
| | SVP | TZVP | TZVPP | QZVPP |
|---|
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | 0.0181 | −0.0049 | −0.0018 | 0.0000 |
| Δstd | 0.2619 | 0.0590 | 0.0177 | 0.0015 |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) | | | 0.0593 | 0.0227 | 0.0087 | 0.0011 |
| Δmax | 2.1917 | 0.3632 | 0.1034 | 0.0042 |
V. Summary and conclusions
The present communication reports an implementation of analytic gradients for the weighted error functional used in the optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations. Combined with standard optimization techniques the analytic (auxiliary) basis set gradients provide an efficient tool for the optimization of auxiliary basis sets.This has been applied in Section III to construct auxiliary basis sets for the correlation-consistent quintuple-ζ basis sets cc-pV5Z (cc-pV(5 + d)Z) and aug-cc-pV5Z (aug-cc-pV(5 + d)Z), and for the core–valence basis sets cc-pwCVXZ with X
= D, T, Q, 5 from Dunning and coworkers19,20,26,30 as well as for the QZVPP basis sets from Weigend et al.29 In the course of this work a few auxiliary basis sets reported in ref. 16
(cc-pVDZ for C–F, cc-pVTZ and cc-pVQZ for Ne, and the diffuse functions for the respective aug-cc-pVXZ basis sets) have been reoptimized and new auxiliary basis sets have been constructed for the cc-pVXZ series with X
= D, T, Q, 5 for the (earth) alkali atoms Li, Be, Na, and Mg and for the SVP, TZVP and TZVPP basis sets for Ne, Ar and Kr.
The accuracy of the auxiliary basis sets has been tested for MP2 correlation energies for several test sets with in total 193 molecules. Similar as for the auxiliary basis sets for SVP, TZVP, TZVPP and the correlation consistent basis sets with X
= D, T, Q also for the new auxiliary basis sets developed in the present work, the errors introduced by the resolution-of-the-identity approximation are about two orders of magnitude smaller then the one-electron basis set errors. Thus, the RI errors do not affect the accuracy of the final results of RI-MP2 and RI-CC2 calculations compared to experiment or to other correlation methods or calculations performed with other one-electron basis sets. In particular for the correlation consistent basis set series the RI errors will therefore also not affect the results of basis set extrapolations e.g. using eqn. (12) above.
Somewhat larger RI errors, for the small SVP and cc-pVDZ basis sets in the order of a few percent of the correlation energy, are found for metal dimers and small clusters and for metal hydrids, i.e. for unusual oxidation states and/or binding situations. However, in all those cases also the one-electron basis set errors are larger than usual. This is a consequence of the strategy used for the construction of the auxiliary basis sets in the present and in previous work. It followed as much as possible the schemes used for the construction of the respective one-electron basis sets. In particular, the optimization of the exponents of the auxiliary basis has (apart from a few exceptions) been done for the (isolated) atoms or atomic ions. The auxiliary basis sets should thus provide an accurate approximation for the resolution of the identity basically in about the same cases in which the corresponding one-electron basis sets are able to describe accurately the correlated wavefunction.
References
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- J. L. Whitten, J. Chem. Phys., 1973, 58, 4496–4501 CrossRef CAS.
- B. I. Dunlap, J. W. D. Connolly and J. R. Sabin, J. Chem. Phys., 1979, 71, 3396–3402 CrossRef CAS.
- O. Vahtras, J. E. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- F. Weigend and M. Häser, Theor. Chim. Acta, 1997, 97, 331–340 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5162 CrossRef CAS.
- S. Grimme and M. Waletzke, Phys. Chem. Chem. Phys., 2000, 2, 2075–2081 RSC.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- H.-J. Werner, F. R. Manby and P. J. Knowles, J. Chem. Phys., 2003, 118, 8149 CrossRef CAS.
- M. Schütz and F. R. Manby, Phys. Chem. Chem. Phys., 2003, 5, 3349–3358 RSC.
- A. J. May and F. R. Manby, J. Chem. Phys., 2004, 121, 4479–4485 CrossRef CAS.
- C. van Alsenoy, J. Comput. Chem., 1988, 9, 620 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–289 CrossRef CAS.
- M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136–9148 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- T. H. Dunning, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef CAS.
- C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef CAS.
- M. Schütz, H.-J. Werner, R. Lindh and F. R. Manby, J. Chem. Phys., 2004, 121, 737–750 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
- TURBOMOLE V5.7, http://www.turbomole.com.
- K. A. Peterson and T. H. Dunning, J. Chem. Phys., 2002, 117, 10548–10560 CrossRef CAS.
- The Turbomole basis set library is available by FTP from ftp://ftp.chemie.uni-karlsruhe.de/pub/basen auxiliary basis sets for RI-MP2 and RI-CC2 calculations are available from ftp://ftp.chemie.uni-karlsruhe.de/pub/cbasen.
- The basis sets were obtained from: Extensible Computational Chemistry Environment Basis Set Database, Version 02/25/04, as developed and distributed by the Molecular Science Computing Facility, Environmental and Molecular Sciences Laboratory which is part of the Pacific Northwest Laboratory, P.O. Box 999, Richland, Washington 99352, USA, and funded by the US Department of Energy. PNL is a multiprogram laboratory operated by Batelle Memorial Institute for the US Department of Energy under contract DE-AC06-76RLO 1830.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
Footnote |
| † The optimized auxiliary basis sets reported in the present work are available together with those of refs. 1 and 16 by ftp27 or on request from the author. The implemented analytic basis set gradient for the functional δRI is available as part of the TURBOMOLE program package. For details the reader is refered to the TURBOMOLE web page.25 |
|
| This journal is © the Owner Societies 2005 |
Click here to see how this site uses Cookies. View our privacy policy here. 
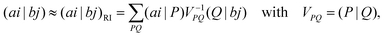




![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) aoμνP and
aoμνP and ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) aoPQ are three- and two-index two-electron densities which differ from corresponding intermediates in the calculation of RI-MP2 energy gradients5,22 only in that the amplitudes calculated in the RI approximation,
aoPQ are three- and two-index two-electron densities which differ from corresponding intermediates in the calculation of RI-MP2 energy gradients5,22 only in that the amplitudes calculated in the RI approximation,

![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) ao is defined as:5,22
ao is defined as:5,22
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ao is obtained as:5,22
ao is obtained as:5,22
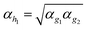 and for Li and Be the exponents of the i functions were taken from the second h function, because for B–Ne the (optimized) exponents for i where close to those of the second h function.
and for Li and Be the exponents of the i functions were taken from the second h function, because for B–Ne the (optimized) exponents for i where close to those of the second h function. .
.![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )ϕi(
)ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) where either ϕi is a core orbital or ϕα one of the additional correlation and polarization functions of the (orbital) core–valence set. Thus, for the atoms B–Ne, for which the core consists of the 1s orbital and the orbital core–valence set includes functions with angular momenta up to lwC
=
lbas
− 1 =
X
− 1, it is sufficient to include in the wCX auxiliary set functions with angular momenta up to locc
+
lbas
− 1. For the second-row atoms Al–Ar, however, the most important core orbitals are those of the 2s2p shell and therefore the wCX auxiliary sets include, as the orbital core–valence set, functions with the same maximum angular momentum as the cc-pVXZ sets. Table 1 lists the number of GTOs added in each angular momentum for the cc-pwCVXZ auxiliary basis sets.
) where either ϕi is a core orbital or ϕα one of the additional correlation and polarization functions of the (orbital) core–valence set. Thus, for the atoms B–Ne, for which the core consists of the 1s orbital and the orbital core–valence set includes functions with angular momenta up to lwC
=
lbas
− 1 =
X
− 1, it is sufficient to include in the wCX auxiliary set functions with angular momenta up to locc
+
lbas
− 1. For the second-row atoms Al–Ar, however, the most important core orbitals are those of the 2s2p shell and therefore the wCX auxiliary sets include, as the orbital core–valence set, functions with the same maximum angular momentum as the cc-pVXZ sets. Table 1 lists the number of GTOs added in each angular momentum for the cc-pwCVXZ auxiliary basis sets.
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms.
and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms.![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = (1/n)∑ni=1Δi, the standard deviation
= (1/n)∑ni=1Δi, the standard deviation  , and the maximum absolute error, |Δ|max
= maxi
|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. For the row 2 (Al–Ar) test set the results for the cc-pVXZ basis sets are given in parentheses. The basis set limits Ecorrlim have been extrapolated from the results for cc-pV5Z (cc-pV(5 + d)Z) and cc-pV6Z (cc-pV(6 + d)Z)
, and the maximum absolute error, |Δ|max
= maxi
|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. For the row 2 (Al–Ar) test set the results for the cc-pVXZ basis sets are given in parentheses. The basis set limits Ecorrlim have been extrapolated from the results for cc-pV5Z (cc-pV(5 + d)Z) and cc-pV6Z (cc-pV(6 + d)Z)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) = (1/n)∑ni=1Δi, the standard deviation Δstd
=
= (1/n)∑ni=1Δi, the standard deviation Δstd
=
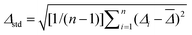 , and the maximum absolute error, |Δ|max
= maxi|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. The values for Ecorrlim have been estimated from the results for X
= Q and 5. Note that for the cc-pwCVXZ basis sets a frozen core approximation was applied to the 1s inner core orbitals of the second row elements Al–Ar
, and the maximum absolute error, |Δ|max
= maxi|Δi| with Δi
=
(EXcorr
−
Ecorrlim)/Ecorrlim
× 100%. The values for Ecorrlim have been estimated from the results for X
= Q and 5. Note that for the cc-pwCVXZ basis sets a frozen core approximation was applied to the 1s inner core orbitals of the second row elements Al–Ar
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)

![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms.
and Δstd for the tests with row 1 (B–Ne) and row 2 (Al–Ar) atoms.![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif)
![[capital Delta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e135.gif) |
|