Methane clustering in explicit water: effect of urea on hydrophobic interactions
Chris
Oostenbrink
and
Wilfred F.
van Gunsteren
*
Laboratory of Physical Chemistry, Swiss Federal Institute of Technology, ETH-Hönggerberg, 8093, Zurich, Switzerland. E-mail: wfvgn@igc.phys.chem.ethz.ch; Fax: +41-1-632 1039; Tel: +41-1-632 5501
First published on 17th November 2004
Abstract
Methane aggregation in water has been studied by simulation for thirteen systems of different sizes and compositions. It was found that favourable cluster formation only occurs after a certain critical cluster size has been reached. The effect of urea on hydrophobic clustering was studied for two urea concentrations. High urea concentrations result in slightly enhanced methane cluster formation, rather than a reduction of the hydrophobic effect. Structural analysis of the Kirkwood–Buff excess coordination and preferential solvation points at a mechanism in which urea pushes the methane into the water, locally increasing methane concentration and hence promoting cluster formation.
Introduction
Chemical protein denaturation due to high urea concentrations is a well-known, but poorly understood phenomenon. It is still unclear whether the urea-denaturation mechanism functions mostly through direct interaction of urea with amino acid side chains,1 or rather through a weakening of hydrophobic interactions within the protein. It is not unlikely that both effects play a role.2 The hydrophobic effect has been studied extensively for small nonpolar molecules such as methanes.3–5 Some computational investigations are concerned with pairs,6,7 triplets8 or quadruplets9 of methane molecules. Others are based on simulations of a larger number of nonpolar solutes10–12 and aggregation of such solutes.13 The effect of urea on the hydrophobic effect in such model systems has also been studied for single nonpolar solutes,14,15 pairs of solutes16–18 and the ‘folding’ of hydrocarbon chains.1From a brute-force simulation of two methane molecules which included hundreds of association and dissociation events, the standard free energy of pairing for two methanes was estimated to be about +3 kJ mol−1.7 Similar results were obtained by Raschke et al.13 who calculated the free energy associated with the growth of a cluster of i methanes by addition of another methane,
| mi + m1 ⇄ mi+1 | (1) |
 | (2) |
Structural information on solutions of small hydrophobic molecules in water and aqueous urea solutions can be obtained from the radial distribution function, gms(r), where s can be either another methane (m), urea (u) or water (w). Zhang and McCammon7 make use of the nearest neighbour distance distribution gmm(1,r) which is the distribution of the distance at which the closest particle can be found. From the radial distribution, the Kirkwood–Buff integrals can be calculated as
 | (3) |
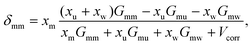 | (4) |
 | (5) |
 | (6) |
In this work we investigate the hydrophobic aggregation of methane at different concentrations in pure water and in urea–water mixtures. For single methane molecules the experimental transfer free energy from pure water to a 6.9 M aqueous urea solution is +0.8 kJ mol−1,21,22 which was reproduced in a recent computational study.14,15
The formation of methane clusters will be studied and through the Kirkwood–Buff integrals we will try to give a structural interpretation of the observed methane aggregation.
Methods
Thirteen molecular dynamics simulations have been performed on systems with varying concentrations of methane and urea in explicit water. The GROMOS simulation package23,24 was used in conjunction with the SPC water model25 and the urea model described in ref. 26. Methane is represented in a united atom manner by a single Lennard-Jones particle, with parameters taken from the GROMOS force field 45A3.27 System sizes and compositions are summarized in Table 1. Subscripts in system names are a rough indication of the concentration of methane (in 10−1 M) and the urea concentration (in M). Seven simulations involved methane–water systems with methane concentrations ranging from 0.53 to 2.53 M. Another six simulations were performed in the presence of urea at concentrations of ca. 6.5 M and 10 M.| Code | 〈V〉 (nm3) | N tot | N m | N u | x m | x u | [m] (M) | [u] (M) |
|---|---|---|---|---|---|---|---|---|
| a Subscripts in system names are a rough indication of the concentration of methane (in 10−1 M) and the urea concentration (in M). Names beginning with 2 are roughly twice the size as the corresponding simulation without 2. For every simulation, the average volume 〈V〉, the total number of molecules Ntot, the number of methanes Nm, and the number of urea molecules Nu in the box are given. From these numbers one can calculate the mole fractions for methane and urea xm and xu and the concentrations, [m] and [u]. | ||||||||
| S5,0 | 31.09 | 1000 | 10 | 0.01 | 0.53 | |||
| S10,0 | 31.41 | 1000 | 20 | 0.02 | 1.06 | |||
| S15,0 | 31.75 | 1000 | 30 | 0.03 | 1.57 | |||
| S20,0 | 32.11 | 1000 | 40 | 0.04 | 2.07 | |||
| S25,0 | 32.8 | 1000 | 50 | 0.05 | 2.53 | |||
| 2S10,0 | 68.97 | 2197 | 43 | 0.02 | 1.04 | |||
| 2S25,0 | 73.38 | 2197 | 109 | 0.05 | 2.47 | |||
| S20,6 | 38.54 | 1000 | 50 | 150 | 0.05 | 0.15 | 2.16 | 6.47 |
| 2S20,6 | 80.63 | 2197 | 109 | 329 | 0.05 | 0.15 | 2.25 | 6.78 |
| 2S10,10 | 90.48 | 2197 | 43 | 549 | 0.02 | 0.25 | 0.79 | 10.08 |
| S20,10 | 42.61 | 1000 | 50 | 250 | 0.05 | 0.25 | 1.95 | 9.75 |
| 2S20,10 | 94.43 | 1000 | 109 | 549 | 0.05 | 0.25 | 1.92 | 9.66 |
| S25,10 | 43.62 | 1000 | 64 | 250 | 0.064 | 0.25 | 2.44 | 9.52 |
Initial coordinates were obtained by placing molecules randomly on a cubic grid at the experimental density of water or the corresponding water–urea mixture. Periodic boundary conditions were applied. Initial velocities were assigned randomly from a Maxwell–Boltzmann distribution, corresponding to a temperature of 298 K. After equilibration the simulations were performed for at least 10 ns at a constant temperature of 298 K and a constant pressure of 1 atm using the weak coupling algorithm28 with relaxation times τT = 0.1 ps and τp = 0.5 ps, respectively, and an estimated isothermal compressibility of 4.575 × 10−4 (kJ mol−1 nm−3)−1 for the simulations in water and 8.494 × 10−4 (kJ mol−1 nm−3)−1 for the water–urea mixtures. Nonbonded interactions were calculated using a triple-range cutoff scheme. Interactions within a short cutoff of 0.8 nm were calculated at every time step from a pairlist that was updated every 5 steps. At these times interactions between molecules at distances shorter than 1.4 nm were also calculated and kept constant between updates. A reaction field contribution29 was added to the energies and forces to account for a homogeneous medium outside the cutoff of 1.4 nm with a relative dielectric permittivity of 61.30
Coordinates were stored every 0.5 ps for later analysis. First neighbour distribution functions and radial distribution functions were calculated over the trajectories. Molecular centers were chosen to be the particle position for methane, the oxygen atom for water and the central carbon for urea. From the radial distribution functions, Kirkwood–Buff integrals (3) were calculated. Because of the poor convergence of these integrals at longer distances, the average value over the distance 1.0 to 1.5 nm of Gss′(r) was taken as an estimate of Gss′. An analysis of methane clustering was performed using a distance criterion of 0.55 nm for bound methane molecules. All methane molecules within this distance to another methane molecule were considered to be part of the same cluster.
Macroscopically, systems at the chosen methane concentrations are not expected to be stable, methane is expected to evaporate from the solution at the mentioned thermodynamic state point. However, microscopically these systems can be studied as a model to investigate the hydrophobic clustering and the effect of urea on such clustering. The stability of a system can be investigated from the derivative of the molar activity of methane, am, with respect to the composition. In particular, for a binary system of methanes in water, the quantity
 | (7) |
Results
Radial distribution functions for selected simulations are displayed in Fig. 1. For simulation S20,10, the methane–urea and methane–water radial distribution functions are given in Fig. 2, as well as the development of the Kirkwood–Buff integrals as a function of r. The horizontal lines in this figure indicate the average over the distance 1.0 to 1.5 nm. These approximations of Gmx are given in Table 2 where the local excess mole fractions according to eqns. (4)–(6) are presented as well. As can be seen from Fig. 2, the value of Gmx is fairly well converged at these distances. Care should be taken however, when evaluating the Kirkwood–Buff integrals for simulations that show a stronger clustering. As can be seen from Fig. 1, the gmm(r) for simulations S25,0 and S25,10 is not close to 1 at the averaging distance yet and consequently the value of Gmm is not converged as well as the examples in Fig. 2. Still, it is obvious that Gmm is significantly larger than in the other cases.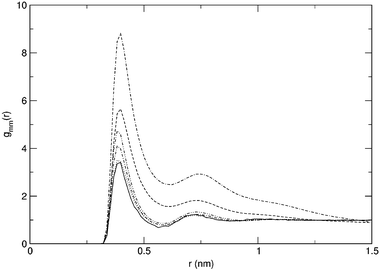 | ||
| Fig. 1 Methane–methane radial distribution functions for simulations S5,0 (solid), S20,0 (dotted), S25,0 (dashed), S20,6 (dot–dash), S20,10 (dot–dot–dash) and S25,10 (dash–dash–dot). | ||
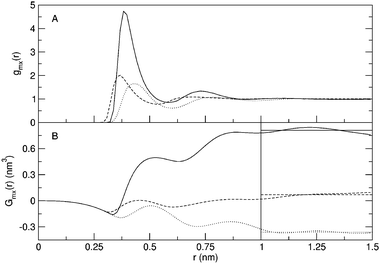 | ||
| Fig. 2 Molecular radial distribution functions (A) and Kirkwood–Buff integrals (B) for simulation S20,10. Solid curves: methane–methane correlation; dotted curves: methane–urea correlation; dashed curves: methane–water correlation. Horizontal lines in panel B indicate values averaged over the distances 1.0 to 1.5 nm. | ||
| System |
G
mm
(nm3) |
G
mu
(nm3) |
G
mw
(nm3) |
δ
mm
(×100) |
δ
mu
(×100) |
δ
mw
(×100) |
|---|---|---|---|---|---|---|
| a Kirkwood–Buff integrals for methane in the various simulations. The Kirkwood–Buff integrals Gss′ are an average of the function Gss′(r), equation, from 1.0 to 1.5 nm. Using eqns. (4)–(6), the excess mole fractions δss′ were calculated for a correlation volume Vcorr = 14.14 nm3. | ||||||
| S5,0 | 0.266 | −0.0495 | 0.022 | −0.022 | ||
| S10,0 | −0.025 | −0.0439 | 0.003 | −0.003 | ||
| S15,0 | 0.201 | −0.0613 | 0.054 | −0.054 | ||
| S20,0 | 0.281 | −0.0777 | 0.098 | −0.098 | ||
| S25,0 | 3.079 | −0.485 | 1.224 | −1.224 | ||
| 2S10,0 | 0.165 | −0.0621 | 0.031 | −0.031 | ||
| 2S25,0 | 13.846 | −2.169 | 5.915 | −5.915 | ||
| S20,6 | 0.459 | −0.258 | −0.0316 | 0.177 | −0.231 | 0.054 |
| 2S20,6 | 0.212 | −0.246 | 0.0042 | 0.083 | −0.237 | 0.154 |
| 2S10,10 | 0.225 | −0.317 | 0.141 | 0.027 | −0.609 | 0.581 |
| S20,10 | 0.810 | −0.361 | 0.0687 | 0.287 | −0.635 | 0.348 |
| 2S20,10 | 15.653 | −2.509 | −0.910 | 5.866 | −3.700 | −2.166 |
| S25,10 | 8.840 | −1.786 | −0.523 | 4.180 | −2.781 | −1.399 |
In order to assess the stability of the systems, the quantity ∂ ln am/∂ ln xm was calculated from eqn. (7) for the binary systems and presented in Table 3. For all systems, the requirement of a positive derivative does hold, although for systems S25,0 and 2S25,0, it does approach zero. The positive values indicate that even though macroscopically high concentrations of methane are not expected to be stable, the microscopic systems under investigation here do yield stable systems within these time and length scales. A high concentration of methane can be used as a model system to investigate hydrophobic effects.
| System | G ww (nm3) | ∂ ln am/∂ ln xm |
|---|---|---|
| a Stability of the binary systems under investigation. From the Kirkwood–Buff integrals Gmm, Gww and Gmw, the value of ∂ ln am/∂ ln xm has been calculated using eqn. (7). For a thermodynamically stable system, this value is required to be positive. | ||
| S5,0 | −0.0197 | 0.901 |
| S10,0 | −0.0199 | 0.974 |
| S15,0 | −0.0177 | 0.781 |
| S20,0 | −0.0165 | 0.666 |
| S25,0 | 0.0336 | 0.145 |
| 2S10,0 | −0.0227 | 0.860 |
| 2S25,0 | 0.236 | 0.037 |
Fig. 3 displays the nearest-neighbour distance distribution for simulations S5,0, S15,0 and S25,0. Even for simulations with the highest methane concentration or the largest amount of clustering, a minimum could always be determined after the first solvation shell. The average distance to this minimum lies at 0.55 nm, which was taken as the criterion to determine methane molecules that are bound together. The same distance was found by Zhang and McCammon.7 Using this criterion, the clustering of methane molecules was determined. Fig. 4 shows for the simulation with the highest methane concentration (S25,0) that clusters of all sizes are being formed and broken reversibly throughout the simulation. This indicates that the simulation of a microscopically stable system is sampling an equilibrium state and that many events of cluster growth and shrinkage are being observed. Throughout this simulation which has a total of 50 methane molecules, an average of 14 methanes are not bound to any other. The total number of methane molecules at any given time point adds up to 50 methane molecules, which is not discernible due to the resolution of Fig. 4.
 | ||
| Fig. 3 Methane–methane nearest neighbour distribution, gmm(1,r) for three simulations. The vertical dashed line indicates the cutoff distance of 0.55 nm taken as the bound–unbound boundary. | ||
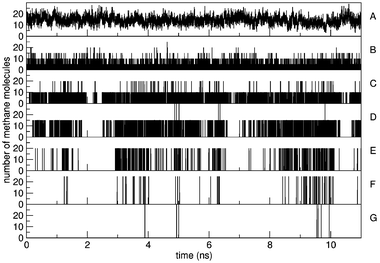 | ||
| Fig. 4 The number of methane molecules that are found in clusters of size 1 (A), 5 (B), 10 (C), 15 (D), 20 (E), 25 (F), 30 (G) is displayed as a function of simulation time for simulation S25,0. | ||
From the average occurrences of clusters, the free energies of cluster growth were calculated according to eqn. (2). These are displayed for some simulations in Fig. 5. Large fluctuations are due to insufficient sampling of the larger clusters. Consider, for example, simulation S25,0 (dashed curve in Fig. 5). From Fig. 4 it can be seen that clusters of size 30 are too rare for an accurate calculation of the free energy of cluster growth around this size. The distribution of methane molecules over the clusters is given in Table 4. Starting from the methane molecules that are not bound to any other methane, the total number of methanes is calculated by taking larger clusters into account. Table 4 lists the cluster sizes that need to be considered to obtain 50, 75, 95 or 99% of all methanes. Consider, for example, S5,0 where 78% of the methanes are on average not bound to any other methane molecule, hence the 1 for columns labeled with 50% and 75%. 18% of the methane molecules are involved in bimolecular clusters resulting in a 2 for the column labeled with 95% (78 + 18 > 95). In order to capture 99% of the methane molecules, clusters of size 3 also need to be taken into account. These numbers are being compared to a theoretical distribution for a system with the same volume and methane concentration, in which only reactions of the type (1) are taken into account and in which the free energy of cluster growth is equal to zero for all clusters.
 | ||
| Fig. 5 Free energy of methane cluster growth as a function of the cluster size, for simulations S5,0 (solid), S20,0 (dotted), S25,0 (dashed), S20,6 (dot–dash), S20,10 (dot–dot–dash) and S25,10 (dash–dash–dot). Large fluctuations at the end of the curves stem from poor statistics for large cluster sizes. | ||
| Theoretical with ΔGgrowth = 0 | Simulation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| System | x single | 50% | 75% | 95% | 99% | x single | 50% | 75% | 95% | 99% |
| a Comparison of the distribution of methane clusters in the theoretical case where the free energy of cluster growth is equal to zero, and from the simulations. Starting from the fraction of singly solvated methanes, xsingle, increasing cluster sizes are considered. Listed are the cluster sizes at which 50, 75, 95 or 99% of the methanes are included. | ||||||||||
| S5,0 | 0.52 | 1 | 2 | 4 | 5 | 0.78 | 1 | 1 | 2 | 3 |
| S10,0 | 0.37 | 2 | 3 | 5 | 7 | 0.63 | 1 | 2 | 3 | 4 |
| S15,0 | 0.29 | 2 | 4 | 6 | 9 | 0.49 | 2 | 3 | 5 | 7 |
| S20,0 | 0.24 | 3 | 4 | 7 | 10 | 0.40 | 2 | 3 | 6 | 9 |
| S25,0 | 0.21 | 3 | 4 | 8 | 11 | 0.29 | 3 | 8 | 18 | 23 |
| 2S10,0 | 0.37 | 2 | 3 | 5 | 7 | 0.61 | 1 | 2 | 3 | 5 |
| 2S25,0 | 0.22 | 3 | 4 | 8 | 11 | 0.21 | 7 | 18 | 35 | 45 |
| S20,6 | 0.24 | 3 | 4 | 7 | 10 | 0.36 | 2 | 3 | 7 | 12 |
| 2S20,6 | 0.23 | 3 | 4 | 7 | 10 | 0.38 | 2 | 3 | 6 | 9 |
| 2S10,10 | 0.43 | 2 | 3 | 4 | 6 | 0.67 | 1 | 2 | 3 | 4 |
| S20,10 | 0.25 | 2 | 4 | 7 | 9 | 0.38 | 2 | 3 | 8 | 12 |
| 2S20,10 | 0.27 | 2 | 4 | 7 | 9 | 0.27 | 4 | 17 | 36 | 46 |
| S25,10 | 0.22 | 3 | 4 | 8 | 11 | 0.23 | 5 | 17 | 29 | 34 |
Discussion
From Table 4 it can be seen that strongly enhanced clustering is observed for simulations S25,0, 2S25,0, 2S20,10 and S25,10. The methane molecules are distributed over clusters of a larger size in these simulations than would be expected for a system in which the free energy of cluster growth is equal to zero. Slightly larger cluster sizes can also be observed for systems S20,6 and S20,10, while for the systems that correspond to lower methane densities, the clustering seems to be slightly unfavoured. This can also be seen from Fig. 5. For all systems, the free energy of cluster growth is positive for small cluster sizes. Only in the simulations where large enough clusters are formed, does it become negative. Even though the simulations do seem to sample equilibrium states (Fig. 4), one can argue that the direct calculation of ΔGgrowth is not a good measure to observe cluster formation. After all, the formation of a cluster of a specific size can be the result of many other reactions than reaction (1). Especially at larger cluster sizes, it is unlikely that we sample this specific reaction often enough to estimate the equilibrium constant. Moreover, the shape of the curves in Fig. 5 is critically dependent on the concentration of single methanes (xsingle in Table 4) throughout the simulation. However, the distribution that was calculated for hypothetical systems in which ΔGgrowth = 0 would also be obtained if one were to take more reactions into account. Because free energy is a state function, the balance between clusters of sizes A and B should be the same when calculated over different paths. Going from size A to size B through an intermediate cluster size A′ will still lead to the same free energy difference between A and B of 0 kJ mol−1 and hence to the same distribution. Kinetic barriers are not taken into account in the calculation of this hypothetical distribution.The strong clustering in systems S25,0, 2S25,0, 2S20,10 and S25,10 is also easily observed through the methane–methane radial distribution function gmm(r). This is exemplified in Fig. 1 where it is obvious that the excess radial structure around the methane molecules continues over distances even beyond 1.0 nm. The resulting Kirkwood–Buff excess coordination numbers in Table 2 do not leave any doubt as to the clustering of methanes that was observed. As mentioned in the previous section, the bigger numbers in this table do indeed indicate strong clustering, but should not be considered accurate due to the remaining structure in the corresponding radial distribution function at the distance over which the Kirkwood–Buff integrals are averaged.
By comparing the different systems at similar concentrations, one can explore the finite size effects in the simulations. From the data that is presented and additionally from the radial distribution functions that were not drawn in Fig. 1, it can be seen that the system pairs (S10,0; 2S10,0), (S25,0; 2S25,0) and (S20,6, 2S20,6) do indeed behave similarly in the formation of methane clusters. For system pair (S20,10, 2S20,10) this is not the case. The methanes in simulation S20,10 are distributed over only slightly larger clusters than the theoretical zero energy system, whereas system 2S20,10 does show a strong clustering of the methane molecules. It is possible that due to the larger absolute number of methane molecules, a critical cluster size could be obtained more easily in this system than in system S20,10, just reaching the regime where ΔGgrowth < 0.
Based on the mole fraction of methanes in the different systems, one would be tempted to conclude that urea reduces the strength of the hydrophobic interactions. Systems S25,0, 2S25,0, S20,6, 2S20,6, S20,10 and 2S20,10 have the same mole fraction of methane (0.05) at increasing mole fractions of urea. Strong methane clustering is observed for systems with no urea, which seems to disappear for most similar simulations including urea. However, if one compares the methane concentrations in terms of concentration in M, it becomes clear that simulations S20,6, 2S20,6, S20,10 and 2S20,10 should rather be compared to simulation S20,0, which does not show significant methane clustering either. In fact, careful examination of the distribution of methanes over the clusters would indicate that the simulations in water–urea mixtures show an increased methane clustering. This is especially obvious for simulation 2S20,10, but also simulations S20,6 and S20,10 involve slightly larger clusters. Also the methane–methane Kirkwood–Buff excess coordination numbers are slightly larger for these simulations as compared to S20,0. Simulation S25,10 involves a higher absolute number of methane molecules, but at a concentration that is comparable to simulation S25,0. The clustering characteristics are also comparable, with relatively large clusters being formed. Overall, it seems that the presence of urea in the computational box does not greatly influence the formation of methane clusters. If an effect is observed it would rather seem that urea enhances the cluster formation than that it reduces the hydrophobic effect.
A possible explanation for this finding can be obtained by looking at the excess coordination numbers and the preferential solvation. In simulations that do not show strong cluster formation, methane molecules still seem to be slightly more often coordinated with other methanes than with water molecules, resulting in small preferential solvations of methane by methane. Once strong clustering sets in, the preferential solvation becomes more pronounced. Interestingly enough, methane molecules also seem to prefer other methanes over urea, and even to prefer water over urea, as can be seen from Fig. 2 and the smaller values of δmu than δmw for systems that do not show large scale clustering in Table 2. This was also observed for single methane molecules in urea–water mixtures.14,15 Once clustering has taken place, the preferred excess mole fraction of methane is so large that the difference between urea and water becomes less pronounced. A mechanism can be imagined in which the methane molecules are driven away from the urea into the water. The local concentration of methane in water is increased, leading to a larger likelihood of cluster formation. Urea shows a homogeneous distribution in water,26 which is also the case for these simulations (data not shown). In order to maintain this homogeneous distribution, and allow for the methanes to avoid contact with urea molecules, an enhanced clustering is preferred. Note that simulation 2S20,10 has an even lower number density of methane than S20,0, but still displays a stronger cluster formation. The enhanced clustering of methane in water upon addition of urea can also be understood from the fact that the work of cavity creation is larger in 6.9 M urea than in water.14
The results obtained here are in accordance with the experimental finding that the free energy of transfer for methane from water to a 6.9 M aqueous urea solution is slightly positive, at +0.8 kJ mol−1.21,22 This value has been reproduced computationally as well.14,15 In addition, direct simulations of protein denaturation by urea seem to indicate direct interactions of urea with the outer shell of the protein,2,32 after which the hydrophobic core swells. The hydrophobic core is then first solvated by water, and only later by urea.2
Conclusion
Molecular dynamics simulations of different methane concentrations have again shown that methane aggregation and cluster formation only become favourable at cluster sizes of at least 5 methane molecules.13 A direct investigation of the hydrophobic effect based on dimers6,7 or small clusters8,9 is therefore questionable. From 13 simulations of different sizes and composition, the influence of urea on methane aggregation was studied. It appears that high urea concentrations result in a slightly enhanced clustering of methane molecules, rather than a reduction of the hydrophobic interactions.From an evaluation of the Kirkwood–Buff excess coordination numbers and the preferential solvation of methane molecules, a possible mechanism could be envisioned, in which the urea repels methane molecules which are then driven into water solvation. This will easily lead to enhanced local concentrations of methane and thus to an increased cluster formation. Once the critical size of clusters has been formed, the free energy of cluster growth will be favourable and additional methane molecules are readily taken up. The implication of these results for the mechanism of chemical protein denaturation by urea is that no evidence was found for a direct effect on purely hydrophobic interactions, but that an effect is more likely to come from a direct interaction of urea with polar groups on the protein surface. This is supported by molecular dynamics simulations of proteins in urea.2,32
Acknowledgements
The authors would like to thank Nico van der Vegt for valuable suggestions. Financial support by the National Center of Competence in Research (NCCR) Structural Biology of the Swiss National Science Foundation (SNSF) is gratefully acknowledged.References
- R. D. Mountain and D. Thirumalai, J. Am. Chem. Soc., 2003, 125, 1950–1957 CrossRef CAS.
- B. J. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5142–5147 CrossRef CAS.
- N. T. Southall, K. A. Dill and A. D. J. Haymet, J. Phys. Chem. B, 2002, 106, 521–533 CrossRef CAS.
- L. R. Pratt, Ann. Rev. Phys. Chem., 2002, 53, 409–436 CAS.
- B. Widom, P. Bhimalapuram and K. Koga, Phys. Chem. Chem. Phys., 2003, 5, 3085–3093 RSC.
- N. T. Southall and K. A. Dill, Biophys. Chem., 2002, 101, 295–307 CrossRef.
- Y. Zhang and J. A. McCammon, J. Chem. Phys., 2003, 118, 1821–1827 CrossRef CAS.
- S. Shimizu and H. S. Chan, Proteins, 2002, 48, 15–30 CrossRef CAS.
- C. Czaplewski, S. Rodziewicz-Motowidlo, M. Dabal, A. Liwo, D. R. Ripoll and H. A. Scheraga, Biophys. Chem., 2003, 105, 339–359 CrossRef CAS.
- T. Ghosh, A. E. García and S. Garde, J. Am. Chem. Soc., 2001, 123, 10997–11003 CrossRef CAS.
- T. Ghosh, A. E. García and S. Garde, J. Chem. Phys., 2002, 116, 2480–2486 CrossRef CAS.
- T. Ghosh, A. E. García and S. Garde, J. Phys. Chem. B, 2003, 107, 612–617 CrossRef CAS.
- T. M. Raschke, J. Tsai and M. Levitt, Proc. Nat. Acad. Sci. U. S. A., 2001, 98, 5965–5969 CrossRef CAS.
- D. Trzesniak, N. F. A. van der Vegt and W. F. van Gunsteren, Phys. Chem. Chem. Phys., 2004, 6, 697–702 RSC.
- D. Trzesniak, N. F. A. van der Vegt and W. F. van Gunsteren, Phys. Chem. Chem. Phys., 2004 Search PubMed , in press.
- A. Wallqvist and D. G. Covell, J. Am. Chem. Soc., 1998, 120, 427–428 CrossRef CAS.
- M. Ikeguchi, S. Nakamura and K. Shimizu, J. Am. Chem. Soc., 2001, 123, 677–682 CrossRef CAS.
- S. Shimizu and H. S. Chan, Proteins, 2002, 49, 560–566 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774–777 CrossRef CAS.
- A. Ben-Naim, Statistical thermodynamics for chemists and biochemists, Plenum Press, New York, 1992 Search PubMed.
- D. B. Wetlaufer, S. K. Malik, L. Stoller and R. L. Coffin, J. Am. Chem. Soc., 1964, 86, 508–514 CrossRef CAS.
- G. Graziano, J. Phys. Chem. B, 2001, 105, 2632–2637 CrossRef CAS.
- W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular simulation: The GROMOS96 manual and user guide, Vdf Hochschulverlag AG an der ETH Zürich, Zürich, 1996 Search PubMed.
- W. R. P. Scott, P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, P. Huber, P. Krüger and W. F. van Gunsteren, J. Phys. Chem. A, 1999, 103, 3596–3607 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular Forces, ed. B. Pullman, Reidel, Dordrecht, The Netherlands, 1981, pp. 331–342 Search PubMed.
- L. J. Smith, H. J. C. Berendsen and W. F. van Gunsteren, J. Phys. Chem. A, 2004, 108, 1065–1071 CrossRef CAS.
- L. D. Schuler, X. Daura and W. F. van Gunsteren, J. Comput. Chem., 2001, 22, 1205–1218 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- T. N. Heinz, W. F. van Gunsteren and P. H. Hünenberger, J. Chem. Phys., 2001, 115, 1125–1136 CrossRef CAS.
- S. Weerasinghe and P. E. Smith, J. Chem. Phys., 2003, 118, 10663–10670 CrossRef CAS.
- L. J. Smith, R. M. Jones and W. F. van Gunsteren, Proteins, 2004 Search PubMed , in press.
| This journal is © the Owner Societies 2005 |
