Analysis of chloride, bromide and iodide using miniaturised isotachophoresis on a planar polymer chip

Abstract

A new method has been developed to allow the determination of the halide anions chloride, bromide and iodide using isotachophoresis. This method employs a new electrolyte system which incorporates the novel application of indium(III) as a complexing agent. This electrolyte system was devised based on the findings of an investigation into the potential for using indium(III) as a complexing counter ion to selectively manipulate the effective mobilities of halide ions. A leading electrolyte incorporating 3.5 mmol dm⁻³ of indium(III) allowed the simultaneous determination of chloride, bromide and iodide to be successfully achieved. The new procedure allows such separations to be made without interference from common inorganic anions such as sulfate and nitrate. Separations were performed using a miniaturised planar poly(methyl methacrylate) chip with integrated platinum wire conductivity detection electrodes. Using this instrumentation the limits of detection were calculated to be 0.7 mg dm⁻³, 1.7 mg dm⁻³ and 2.2 mg dm⁻³ for chloride, bromide and iodide respectively.

---

Introduction

Isotachophoresis (ITP) is an electrophoretic separation technique which is eminently suitable for the separation of small inorganic anions. The composition of the leading electrolyte governs many of the separation parameters such as the concentration of the sample zones and the velocity at which they migrate through the separation system. This control over sample zone concentration makes ITP a very robust analytical technique, which can be used for analysing both dilute and concentrated samples. Unfortunately separations of halides, an important group of ions, are difficult to achieve using ITP due to two main reasons. The problems in such analyses arise from the fact that bromide, iodide and chloride possess high and similar electrophoretic mobilities of 81.3 × 10⁻⁵ cm² V⁻¹ s⁻¹, 79.7 × 10⁻⁵ cm² V⁻¹ s⁻¹ and 79.1 × 10⁻⁵ cm² V⁻¹ s⁻¹ respectively.¹ The magnitude of these mobilities make determination problematic due to the difficulty in finding a suitable leading ion with a higher mobility. A number of possible strategies to overcome this problem have been investigated. The simplest method that has been tried to determine chloride is to simply employ this species as the leading ion.^2–5 Analysis can then be made due to the fact that if any chloride is present within the sample it will migrate with the leading ion. This will lengthen the leading ion zone and thus allow quantification to be made. Using such a method it is not possible to obtain qualitative information from the analysis and the minimum quantity which can be detected is restricted. Attempts have also been made to use the fastest anion, OH⁻, as a leading ion.^6,7 However, such an approach is less than ideal as it can only be used in unbuffered, high pH electrolyte systems. Other anions with high absolute mobilities, such as ferrocyanide and ferricyanide, only possess high effective mobilities with very low leading ion concentrations (≤2.0 mmol dm⁻³) and neutral or alkaline pH levels and thus are of little practical use. One suitable leading ion that was identified by Meissner et al. is dithionate.⁸ This ion can be used with a leading ion concentration of up to 5 mmol dm⁻³ and pH levels higher than 3.0. However, to use dithionate at acidic pH levels requires the user to produce dithionic acid as this substance is not commercially available. The use of dithionate can therefore be said to offer a useful method of performing halide analysis and thus has seen subsequent application.⁹

Unfortunately finding a suitable leading ion on its own does not solve the problem of enabling the halides to be separated from one another. To achieve this requires the use of some additional method for manipulating the effective mobilities of the ions. To date the only method that has allowed the analysis of chloride without interference from either iodide or bromide using aqueous based electrolytes is that developed by Boček et al. which involved the use of cadmium(II) as a complexing species.¹⁰ This group demonstrated that the simultaneous determination of chloride, bromide and iodide could be achieved using this method. However, to achieve a good separation required a reasonably high concentration of cadmium(II), 6 mmol dm⁻³. The use of cadmium(II) as a complexing agent has since been successfully employed in a number of other studies.^11–14 The major problem with using cadmium is that this species is highly toxic and a known carcinogen,¹⁵ and as such its use from a practical point of view is undesirable. Iodide can be separated from both bromide and chloride using α-cyclodextrin,^16–18 γ-cyclodextrin¹⁸ or poly(vinylpyrrolidone) (PVP).^19,20 The separation of bromide from chloride is more difficult but some success has been achieved in ITP using tetradecyldimethylbenzylammonium (Zeph)²¹ or PVP.¹⁹

An alternative method of performing halide separations using ITP is to employ non-aqueous electrolyte systems. Under such conditions the mobilities of the halide ions are sufficiently different to allow the separations to be made. The separation of chloride and bromide has been achieved in ITP using 99–100% methanol as the electrolyte solvent.^22–24 There has also been a limited application of cadmium(II) as a complexing agent to allow the isotachophoretic determination of chloride in electrolyte systems containing aqueous mixtures of acetone,⁷ ethanol⁷ and methanol.²⁵ The use of non-aqueous solvents does however limit the materials which can be used for producing separation devices and complicates procedures for producing and handling samples and electrolytes.

ITP can be performed with relatively simple instrumentation and has shown itself to be a method eminently suitable for application in a miniaturised format which offers benefits such as improved analytical performance and reduced analysis times. Thus, a variety of applications such as metal cations in industrial process streams,²⁶ organic anions in wines²⁷ and food additives,²⁸ have been carried out on chip based ITP separation devices. However, to date the method has not been applied to the separation of the halide species, chloride, bromide and iodide. The determination of chloride in water samples using dithionate as a leading ion has however, been achieved using miniaturised ITP on a poly(methyl methacrylate) (PMMA) device.⁹ Miniaturisation technology has also been applied to capillary zone electrophoresis (CZE), a related electroseparation technique that can be applied to the analysis of small inorganic anions. In CZE smaller differences in effective mobilities can be resolved than in ITP. However, the separation of the halide ions still generally requires the use of some mechanism, such as the use of ion-pairing with zwitterionic surfactants²⁹ or cationic polymers,³⁰ to enhance the mobility differences between chloride, bromide and iodide anions. There have been a number of studies using miniaturised CZE to allow the rapid analysis of chloride using PMMA devices.^31–35 No known applications of miniaturised CZE to determinations of bromide and iodide have yet been made.

This paper describes a new method which allows the simultaneous determination of chloride, bromide and iodide by ITP using indium(III) as a novel complexing counter ion. Examination of metal–anion stability constants revealed that indium(III) forms relatively stable halide complexes. The formation constants (log K₁) of the chloride, bromide and iodide complexes are 2.41, 2.01 and 1.64 respectively.³⁶ The hydrolysis of indium(III) occurs at a sufficiently high pH, pK_a1 = 3.54,³⁷ that it was thought that this species could be used to manipulate the effective mobility of halide anions during isotachophoretic analysis. The method has been employed for miniaturised isotachophoretic separations on a planar PMMA separation device fitted with integrated conductivity detectors. This new procedure was successfully used with model mixtures and allowed chloride concentrations to be determined in water samples.

Experimental

Instrumentation

The miniaturised PMMA separation device used in this work was produced in-house using a direct milling technique that has been detailed previously.³⁸Fig. 1 shows a schematic view of the device. The device comprises two separation channels; one linking the injection cross to the bifurcation point, which has a length of 57 mm, and the second running between the bifurcation point and well B. This latter channel is 200 µm wide and 300 µm deep whereas all other channels are 300 µm wide and 300 µm deep. The channel linking the bifurcation point to well B incorporates a conductivity detector 44 mm along its length. This conductivity detector consists of a pair of on-column 75 µm diameter platinum wire electrodes (Aldrich, Gillingham, Dorset, UK) arranged in an opposed configuration. Two similar detectors, which were not used in this work, are located 5 mm either side of the bifurcation point, as shown in Fig. 1.

Fig. 1 Schematic diagram of the miniaturised PMMA separation device. All channels are 300 µm wide and 300 µm deep except that linking well B to the bifurcation point which is 200 µm wide and 300 µm deep. Letters A, B, C, D and E refer to the wells into which the inlet/outlet connections to the device are made. Leading electrolyte enters through B, terminating electrolyte through C and sample through A. D and E exit to waste. Dimensions are shown in mm.

A PS350 high voltage, 5 kV power supply (Stanford Research Systems, Sunnyvale, CA, USA), configured to supply negative voltages, was used to provide the constant currents required to drive the separations. Conductivity detection was achieved using a system built in-house, which uses capacitive coupling to isolate the low voltage detection circuitry from the high separation voltages. This design is based on an oscillating circuit and leads to the output from the detector being in the form of a frequency. As the conductivity increases the frequency decreases, with a near linear relationship over the conductivity range encountered with isotachophoretic separations.

Electrolyte and sample movement was made using a gravity feed hydrodynamic fluid transport system. This system was controlled by means of a series of two-way solenoid actuated valves (LFAA1201718H, The Lee Company, Westbrook, CT, USA) positioned between the separation device and solution reservoirs/waste containers. With this arrangement pressure driven sample injection can be performed.

Control of the power supply, fluid transport system and data acquisition from the detector was carried out using a standard PC with LabVIEW software (version 7.1, National Instruments, Austin, TX, USA). The NIDAQ driver (National Instruments), programmed using LabVIEW, was used to control the hardware interfacing which was done using three National Instruments cards. The cards used were a PCI-GPIB board for the power supply, a PCI-6503 digital input/output card for the fluid transport system and a PCI-6601 timing and digital input/output card for the detector.

Separation conditions

A seven step control program, shown in Table 1, was used to perform all of the separations carried out during this investigation. Steps 1 and 2 flush out the system and fill the separation channel with leading electrolyte. Step 3 positions the terminating electrolyte in the correct position within the device. Steps 4 and 5 enable the insertion of the sample. The former step positions the sample at the injection cross whereas the latter fills the separation channel between the cross and bifurcation point, thus giving an injection volume of 5.1 µl. The actual isotachophoretic separation begins in step 6 with a current of 40 µA applied between wells B and C. The electrolyte system used in this work has quite a high conductivity hence a high separation current was used in this step to reduce the analysis times. In step 7 the applied current is reduced to 20 µA, to slow down the separated zones, improving the detection of dilute samples.

Table 1 Separation program used to carry out miniaturised isotachophoretic separations

Step	Time/s	Current/µA	Valve status					Fluid flow path
			A	B	C	D	E
● = closed ○ = open.a Step duration 270 s with leading electrolytes containing 0–2.0 mmol dm^−3 indium(III).b Step duration 320 s with leading electrolytes containing 2.0–4.0 mmol dm^−3 indium(III).
1	20	0	●	○	●	●	○	B → E
2	20	0	●	○	●	○	●	B → D
3	1	0	●	●	○	○	●	C → D
4	0.5	0	○	●	●	○	●	A → D
5	0.3	0	○	●	●	●	○	A → E
6	270^a/320^b	40	●	●	●	●	●	no flow
7	1000	20	●	●	●	●	●	no flow

---

Chemicals

The compositions of the electrolytes used in this work are given in Table 2. The following chemicals were used to produce these electrolytes: nitric acid (2 mol dm⁻³ volumetric standard, Riedel-de Haën, Gillingham, Dorset, UK); indium nitrate (99.9%, Aldrich, Gillingham, Dorset, UK); hydroxyethyl cellulose (HEC) (molecular weight ca. 250 000) (Aldrich); glycylglycine (99+%, Acros, Loughborough, UK) and cyanoacetic acid (99%, Aldrich). Chloride and fluoride samples were prepared using ion standard solutions (1000 mg dm⁻³) obtained from BDH (Poole, UK). Stock solutions (1000 mg dm⁻³) of other anions were produced using appropriate salts. Iodide (99.5%, BDH), carbonate (99.99%, Aldrich) and thiocyanate (99%, Aldrich) samples were produced using potassium salts. Sodium salts were used to produce bromide (99.99% Aldrich), bromate (99+%, Acros), chlorate (99+%, Acros), iodate (98+%, Aldrich), nitrite (99.99%, Aldrich) perchlorate (99+%, Acros), phosphate (99%, Aldrich), sulfate (99+%, Aldrich), sulfite (99.99%, Aldrich) and thiosulfate (99.5%, Aldrich) samples. All samples and electrolytes were prepared using >18 MΩ water (Elga Maxima Ultra Pure, Veolia Water Systems, High Wycombe, UK).

Table 2 Composition of the electrolytes investigated for analysing halide ions; HEC = hydroxyethyl cellulose

Parameter	Electrolyte
	Leading	Terminating
a Leading ion concentration was 13.5 mmol dm^−3 when the concentration of the complexing agent was 4.0 mmol dm^−3.
Ion	12^a mmol dm^−3 NO3^−	20 mmol dm^−3 cyanoacetate^−
Complexing agent	0–4.0 mmol dm^−3 In^3+	—
pH	3.0	ca. 2.2
pH buffer	Glycylglycine	—
Additive	1 g dm^−3 HEC	—

---

Results and discussion

Electrolyte system

The use of indium(III) as a complexing agent to assist the performance of electrophoretic separations has not previously been advocated. Therefore, initial work in this study concentrated on investigating the potential of using this species as a complexing counter ion to allow the isotachophoretic determination of the halide ions chloride, bromide and iodide. To achieve this aim a series of experiments were carried out using different concentrations of indium(III) in the leading electrolyte to study what influence the presence of this species had on the effective mobilities of these ions of interest. Thus separations were performed using the electrolyte systems detailed in Table 2, with indium(III) concentrations ranging from 0–4 mmol dm⁻³. These electrolyte systems are based on the use of nitrate as the leading ion as this species does not complex significantly with indium(III), log K₁ = 0.18.³⁶ Analyses of samples containing iodide, bromide and chloride were performed in triplicate with each electrolyte system and the resulting relative step heights (RSH) recorded. In ITP step heights are related to mobility, thus the RSH gives an indication of the effective mobilities of the species. Fig. 2 shows the results obtained with the different indium(III) concentrations. In this work the RSH was calculated using the following expression:
where f_LE = frequency of the response produced by the leading electrolyte (Hz); f_sample = frequency of the response produced by the sample (Hz); f_TE = frequency of the response produced by the terminating electrolyte (Hz). The frequency response obtained from the conductivity detector is a consequence of the electronic design, based on an oscillating circuit. The frequency decreases as the conductivity increases, with a near linear relationship over the frequency changes recorded.

Fig. 2 Effect of indium concentration on the relative step heights observed for chloride, bromide, iodide and sulfate. The results were produced using nitrate as the leading ion and cyanoacetate as the terminating ion. Error bars indicate two standard deviations based on three replicates.

The results obtained clearly indicate that indium(III) does complex with the halide species. In the absence of indium(III) all three species have similar effective mobilities, which are higher than that of the nitrate leading ion, and thus no sample zones were observed. The overall trend observed is that RSHs increase with increasing indium concentration. The pattern observed for the halides is consistent with the stability constants for indium–halide complexes which is chloride > bromide > iodide. Chloride forms the most stable complexes and is thus retarded to the highest degree and consequently displays the highest steps. The leading electrolyte containing 4 mmol dm⁻³ of indium has a higher leading ion concentration (13.5 mmol dm⁻³) than all of the other results (12 mmol dm⁻³). This change will alter the concentrations present in the zones and hence the complexation reactions. This is possibly the reason why the observed RSHs with this indium concentration are lower than might be expected.

Whilst investigating an appropriate indium(III) concentration to enable the separation of the halide ions of interest to be made, samples containing sulfate were also analysed. This was done because this species is a widely found, high mobility, anion and could therefore interfere with the attempted separations. Indeed, from the results obtained using cadmium(II) as a means of enabling halide separations,¹⁰ it is likely that in certain situations sulfate would impede the determination of chloride or bromide. However, as can be seen in Fig. 2, when indium(III) was used as a complexing agent sulfate always exhibited a lower effective mobility than chloride, bromide or iodide and thus will not cause any interference in the determination of these ions.

An illustration of the effect of indium(III) on the observed step heights of halide anions can be seen in Fig. 3. This figure shows the isotachopherograms obtained for samples containing bromide and chloride with leading electrolytes containing two different indium(III) concentrations. The difference in the RSHs can be clearly seen with bromide exhibiting only a very low step with the system (a) containing 2.0 mmol dm⁻³ compared to a much higher step with the system (b) containing 3.5 mmol dm⁻³. The observed step heights suggest that the greatest difference in effective mobilities, and hence best separation, between the three individual halide species and the leading ion could be obtained with a leading electrolyte containing 3.5 mmol dm⁻³ of indium(III). Thus, such an electrolyte was used for all subsequent analyses.

Fig. 3 Isotachopherograms illustrating the difference in step heights exhibited by bromide and chloride ions with different indium(III) concentrations in the leading electrolyte. (a) Leading electrolyte 1.5 mmol dm⁻³ HNO₃, 3.5 mmol dm⁻³ In(NO₃)₃, 1 g dm⁻³ HEC, pH 3.0 (glycylglycine). (b) Leading electrolyte 6.0 mmol dm⁻³ HNO₃, 2.0 mmol dm⁻³ In(NO₃)₃, 1 g dm⁻³ HEC, pH 3.0 (glycylglycine). Terminating electrolyte 20 mmol dm⁻³ cyanoacetic acid. 1 = Leading electrolyte; 2 = bromide; 3 = chloride; 4 = terminating electrolyte. The trace in figure (b) has been shifted to the right by 30 s to make the diagram clearer.

Separations

The electrolyte system containing 3.5 mmol dm⁻³ indium(III) was applied to the separation of mixtures of chloride, bromide and iodide. Using this electrolyte allowed successful separations of such mixtures to be achieved using miniaturised ITP. An example of such a separation, with a sample containing 10 mg dm⁻³ chloride, 10 mg dm⁻³ bromide and 40 mg dm⁻³ iodide, is shown in Fig. 4. The isotachopherogram obtained shows a good resolution between all of the sample species. Such a result indicates that separations should be possible over a wide range of sample concentrations.

Fig. 4 Isotachopherogram of a separation of a sample containing 10 mg dm⁻³ chloride, 10 mg dm⁻³ bromide and 40 mg dm⁻³ iodide. Leading electrolyte 1.5 mmol dm⁻³ HNO₃, 3.5 mmol dm⁻³ In(NO₃)₃, 1 g dm⁻³ HEC, pH 3.0 (glycylglycine). Terminating electrolyte 20 mmol dm⁻³ cyanoacetic acid. 1 = Leading electrolyte; 2 = iodide; 3 = bromide; 4 = chloride; 5 = terminating electrolyte.

Investigations were also made to test the stability of the method. In ITP, quantitation is made on the basis of the zone lengths observed. To test the reproducibility of this information a series of separations were performed with a sample containing an identical mixture to that shown in the example in Fig. 4. The results of this study are shown in Table 3. It was found that over a single day excellent reproducibility was observed for zone lengths with all three sample zones yielding results with relative standard deviations (RSD) of between 2.1–3.1% for 10 consecutive determinations. Over the course of four days a slight reduction in reproducibility was noted with RSDs of 6.1–7.0% observed over 37 runs. This still represents a good level of performance that is comparable to that noted with miniaturised ITP using an injection method incorporating syringe pumps.³⁹Table 3 also shows details of the reproducibility of the qualitative information contained in isotachopherograms, the step heights. With the same mixture used to test zone length stability, excellent short term reproducibility in the step heights was observed. The RSHs from 10 consecutive runs yielded RSDs of 1.0%, 1.9% and 5.1% for chloride, bromide and iodide respectively. Over a longer term lower levels of performance were observed with all three species, with the RSDs found to be 7.5%, 11.4% and 20.6% for chloride, bromide and iodide. These figures do however represent results for a wide variety of samples and concentrations analysed over a period of 24 days. The difference in step heights between the species are sufficiently large that such a level of performance should not cause any problems with identifying particular ions. Generally it can be seen that the standard deviations are similar for all three species suggesting a systematic error. This means that consequently the RSD for iodide appears significantly poorer than for the other two species. Comparable behaviour has previously been observed whilst analysing metal cations using similar instrumentation.²⁶

Table 3 Reproducibility of qualitative and quantitative information with the electrolyte system containing 3.5 mmol dm⁻³ indium(III)

Qualitative information				Quantitative information
Ion	RSH ± SD	RSD (%)	n	Zone Length ± SD/s	RSD (%)	n
n = number of runs; RSD = relative standard deviation; RSH = relative step height; SD = standard deviation.a Results with 1 sample over 1 day.b Results with multiple samples over 24 days.c Results with 1 sample over 4 days.
Short term reproducibility^a				Short term reproducibility^a
I^−	0.149 ± 0.008	5.3	10	13.18 ± 0.41	3.1	10
Br^−	0.304 ± 0.006	1.9	10	6.22 ± 0.13	2.1	10
Cl^−	0.538 ± 0.006	1.0	10	24.63 ± 0.62	2.5	10
Long term reproducibility^b				Long term reproducibility^c
I^−	0.155 ± 0.032	20.6	126	12.21 ± 0.86	7.0	37
Br^−	0.298 ± 0.034	11.4	134	6.30 ± 0.39	6.2	37
Cl^−	0.522 ± 0.041	7.8	168	23.25 ± 1.42	6.1	37

---

The experiments performed whilst developing the electrolyte system revealed that sulfate would not interfere with the determination of any of the halide ions of interest under any conditions investigated. With the leading electrolyte containing 3.5 mmol dm⁻³ indium(III), that is most suited to allowing the simultaneous determination of chloride, bromide and iodide, the effective mobility of sulfate is so low that the species is not observed at all, due to it possessing a lower effective mobility than the terminating ion. To check for possible interference from other species a series of experiments were performed using a wide range of inorganic anions as samples. The RSH values produced reveal that in most cases little interference is likely. No visible steps were produced by samples containing fluoride, phosphate, carbonate, nitrite, thiosulfate, sulfite or iodate. Under the electrolyte conditions used the effective mobilities of fluoride, phosphate and carbonate are all lower than that of the terminating electrolyte due to the species being only partially dissociated because of the pH level used. Partial dissociation is also part of the reason for the absence of a nitrite step although complexation between this species and indium(III) seems also to contribute to the low effective mobility observed. This was thought to be the case because under similar electrolyte conditions but without the indium(III), nitrite did produce a visible step with a RSH ± standard deviation (SD) of 0.827 ± 0.048 (n = 3). Thiosulfate and sulfite are retarded by the complexing agent to such an extent that they have too low an effective mobility to be observed whereas iodate, although essentially fully dissociated, simply has a low mobility. A small number of ions were however found to produce visible steps. The RSHs ± SDs for these species were found to be 0.031 ± 0.021 (n = 6) for perchlorate, 0.107 ± 0.028 (n = 17) for chlorate, 0.376 ± 0.025 (n = 7) for bromate and 0.775 ± 0.064 (n = 28) for thiocyanate. None of these species were found to interfere with chloride determination. No significant interference in bromide analysis was observed either. However, it was thought that excessive bromate concentrations could lead to co-migration between this species and bromide. For a particular application the indium(III) concentration could be manipulated if this situation was thought to be a problem. This change could be made as the presence of indium(III) does not significantly affect the mobility of bromate, as this species exhibits a RSH ± SD of 0.397 ± 0.044 (n = 3) in the absence of the complexing agent. The main interference was found to be co-migration of chlorate and iodide despite the apparently reasonable difference in RSHs of these species. It was noted that the step produced by thiocyanate shows that the effective mobility of this species is significantly retarded by interaction with the indium(III). When no indium(III) was present this species produced a step with a RSH ± SD of 0.301 ± 0.010 (n = 3). The low pH at which the separations are performed means that most organic anions will not be fully ionised and thus are unlikely to cause interference.

Calibration curves were produced for chloride, iodide and bromide. The chloride curve was produced using four replicates of eleven samples with concentrations ranging from 1 mg dm⁻³ to 200 mg dm⁻³ whereas those for bromide and iodide were based on four replicate runs of eight samples with concentrations in the range of 2.5 mg dm⁻³ to 150 mg dm⁻³. Full details of the equations of these curves, produced using weighted linear regression, are shown in Table 4. Good linearity in the curves was obtained with correlation coefficients of ≥0.990 achieved with all three species. Using the regression equations allowed limits of detection (LODs) to be calculated. This was done based on the method recommended by the Royal Society of Chemistry (UK) which defines the LOD as the blank signal plus three times the standard deviation of this value.⁴⁰ However, this procedure needs adapting for use with ITP as, in the absence of background contamination, blank signals are invariably zero. Therefore, it is more realistic to use an estimated blank, taken as the intercept, plus three times the standard deviation of this value, instead. Using this method LODs were calculated to be 1.7 mg dm⁻³ and 2.2 mg dm⁻³ for bromide and iodide respectively. However a chloride step was found to be present in the blank runs, which explains the high value of the intercept in the regression equation shown for this species in Table 4. The origin of this contamination was thought to be from the electrolyte solutions. Thus, as these solutions are replenished for each separation the size of the contamination zone was found to be fairly consistent. Based on 77 runs the length of the chloride zone in blank samples was found to be 6.14 ± 0.45 s, with the error shown representing the standard deviation. The LOD for chloride could therefore be calculated using the actual blank value. Using such a procedure the LOD for this species was determined to be 0.7 mg dm⁻³. Comparison of the performance of the method with other methods for analysing chloride using ITP is restricted by the lack of previously obtained LODs for this species. For other halide species the values obtained in this work represent an improvement on those obtained using conventional capillary scale equipment for bromide and iodide when using Zeph,²¹ and a similar level to that achieved for iodide using α-cyclodextrin.¹⁷ The use of PVP has however allowed the detection of lower concentrations of iodide to be made when UV absorbance detection was employed on a capillary scale system.¹⁹ The calculated LOD for chloride is of a similar magnitude to those achieved using miniaturised CZE.^31,32,35 The linear range of 28 µmol dm⁻³ to 5.6 mmol dm⁻³ (1–200 mg dm⁻³) observed for chloride with the miniaturised ITP method developed offers at least an order of magnitude improvement to that reported using miniaturised CZE.³⁴

Table 4 Weighted linear regression equations for chloride, bromide and iodide calibration curves

	LOD/mg dm^−3	a ± SD/s	b ± SD/s dm^3 mg^−1	r	n	Concentration range/mg dm^−3
Where a = intercept; b = slope; n = number of data points (4 replications performed at each); r = correlation coefficient.
Cl^−	0.7	6.41 ± 0.40	1.59 ± 0.04	0.994	11	1–200
Br^−	1.7	0.58 ± 0.35	0.61 ± 0.01	0.997	8	2.5–150
I^−	2.2	0.94 ± 0.17	0.23 ± 0.01	0.990	8	2.5–150

---

The good resolution between the steps produced by the different halide anions means that the method is robust enough to allow the determination of a particular species even when other ions are present in an excess. Given the abundances of the different species it is likely that chloride in particular may be present in amounts significantly in excess of either bromide or iodide. Fig. 5 shows an example of an isotachopherogram produced by such a separation with a sample containing 10 mg dm⁻³ bromide and 20 mg dm⁻³ iodide in the presence of 100 mg dm⁻³ chloride. It can be seen that despite the presence of a very long (184 s) chloride zone that clear steps are still exhibited for the bromide and iodide. No interference was noted even with larger disparities in concentration. For example in a sample containing 175 mg dm⁻³ chloride, 7.5 mg dm⁻³ of bromide was found to produce a step of 5.29 ± 0.31 s with a RSH of 0.313 ± 0.020, the errors shown represent SDs based on four replicate runs. Using the calibration equation for bromide this equates to a concentration of 7.8 mg dm⁻³ which represents a recovery of 104%.

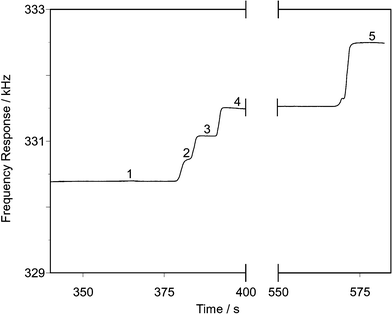Fig. 5 Isotachopherogram of a separation of a sample containing 10 mg dm⁻³ bromide, 20 mg dm⁻³ iodide and 100 mg dm⁻³ chloride. Leading electrolyte 1.5 mmol dm⁻³ HNO₃, 3.5 mmol dm⁻³ In(NO₃)₃, 1 g dm⁻³ HEC, pH 3.0 (glycylglycine). Terminating electrolyte 20 mmol dm⁻³ cyanoacetic acid. 1 = Leading electrolyte; 2 = iodide; 3 = bromide; 4 = chloride; 5 = terminating electrolyte.

As an example of an application of the method it was used to analyse the chloride content of some commercially available natural mineral waters. The determined chloride concentrations together with the quoted anionic components of the analysed waters are shown in Table 5. An example of such an analysis, for a sample of Highland Spring water, is shown in Fig. 6. It can be seen that only chloride produces a zone with the electrolyte system used, the other anions in the sample, nitrate, sulfate and carbonate, have either a too high or too low effective mobility and are therefore not seen. Good agreement of the chloride content compared to the quoted concentrations were observed with Volvic and Highland Spring waters. However, a high recovery was observed for Brecon Carreg water. This may be due to differences in the actual composition of the water as the quoted composition is for a typical sample. Variations in the compositions of different components by up to 25% are permitted within regulatory requirements.⁴¹ Other potential applications include the analysis of process streams, a task to which miniaturised ITP has proved to be amenable.^26,42 In particular the method could be suitable for the analysis of solutions associated with the photographic industry. For example the determination of halides in developer solutions could be made with no expected interference from other matrix components, such as sulfite or carbonate, which are likely to be present.⁴³

Fig. 6 Isotachopherogram produced by the analysis of Highland Spring mineral water. Leading electrolyte 1.5 mmol dm⁻³ HNO₃, 3.5 mmol dm⁻³ In(NO₃)₃, 1 g dm⁻³ HEC, pH 3.0 (glycylglycine). Terminating electrolyte 20 mmol dm⁻³ cyanoacetic acid. 1 = Leading electrolyte; 2 = chloride; 3 = terminating electrolyte.

Table 5 Concentrations of chloride in mineral waters as determined using miniaturised isotachophoresis together with stated compositions

Sample	Quoted concentration/mg dm^−3				Determined concentration/mg dm^−3 ± SD
	Cl^−	NO3^−	SO4^2−	HCO3^−	Cl^−
Volvic	13.5	6.3	8.1	71	12.2 ± 0.4
Highland Spring	5.0	<2.0	7.0	133	4.6 ± 0.3
Brecon Carreg	9	2.2	9	206	11.3 ± 0.4

---

Conclusions

The use of indium(III) as a complexing counter ion has been shown to offer a means of manipulating the effective mobilities of halide anions. This species complexes with chloride, bromide and iodide to differing amounts and thus allows these species to be readily separated using miniaturised ITP. Without the presence of this species such a separation is difficult to achieve given the similar mobilities of the species. The method has been shown to give a reproducible performance, be applicable over a wide range of sample concentrations, 1–200 mg dm⁻³ in the case of chloride, and be robust enough to allow the determination of a particular halide anion when an excess of one or both the other species is present. Little interference towards performing the analyses was observed from other ions. The method is particularly suited to the analysis of chloride as using the conditions developed in this work, a leading electrolyte at pH 3.0, containing 3.5 mmol dm⁻³ of indium(III), no interference in the determination of this species is likely.

Acknowledgements

The authors would like to thank the United Kingdom Home Office for funding this research programme and the Forensic Explosives Laboratory, of the Defence Science and Technology Laboratory, Fort Halstead, for their support.

References

1. D. Kaniansky, M. Masár, J. Marák and R. Bodor, J. Chromatogr., A, 1999, 834, 133–178.
2. I. Zelenský, V. Zelenská, D. Kaniansky, P. Havaši and V. Lednárová, J. Chromatogr., 1984, 294, 317–327.
3. D. Kaniansky, I. Zelenský, A. Hybenová and F. I. Onuska, Anal. Chem., 1994, 66, 4258–4264.
4. J. Ježek and M. Suhaj, J. Chromatogr., A, 2001, 916, 185–189.
5. P. Sázelová, V. Kašička, D. Koval, F. Kilár, D. Knopp and G. Peltre, J. Chromatogr., A, 2003, 990, 303–309.
6. J. Vacík and I. Muselasová, J. Chromatogr., 1985, 320, 199–203.
7. S. Murai, T. Ozawa and Y. Maki, Bunseki Kagaku, 1984, 33, 229–233.
8. T. Meissner, F. Eisenbeiss and B. Jastorff, J. Chromatogr., A, 1999, 838, 81–88.
9. R. Bodor, V. Madajová, D. Kaniansky, M. Masár, M. Jöhnck and B. Stanislawski, J. Chromatogr., A, 2001, 916, 155–165.
10. P. Boček, I. Miedziak, M. Deml and J. Janák, J. Chromatogr., 1977, 137, 83–91.
11. Z. Ryšlavý, P. Boček, M. Deml and J. Janák, J. Chromatogr., 1978, 147, 369–373.
12. P. S. L. Janssen and J. W. van Nispen, J. Chromatogr., 1984, 287, 166–175.
13. P. Pei and D. J. Vonderschmitt, J. Clin. Chem. Clin. Biochem., 1987, 25, 253–259.
14. T. Takaoka, I. Ikeuchi and T. Amano, Bunseki Kagaku, 1990, 39, 103–108.
15. The Dictionary of Substances and Their Effects, ed. S. Gangolli, Royal Society of Chemistry, Cambridge, UK, 2nd electronic edn, 1999.
16. M. Tazaki, M. Takagi and K. Ueno, Chem. Lett., 1982, 639–640.
17. K. Fukushi and K. Hiiro, J. Chromatogr., 1990, 518, 189–198.
18. K. Fukushi and K. Hiiro, J. Chromatogr., A, 1994, 684, 343–349.
19. V. Madajová, E. Turcelová and D. Kaniansky, J. Chromatogr., 1992, 589, 329–332.
20. J. Sádecká and J. Polonský, Talanta, 2003, 59, 643–649.
21. K. Fukushi and K. Hiiro, J. Chromatogr., A, 1997, 760, 253–258.
22. J. L. Beckers and F. M. Everaerts, J. Chromatogr., 1970, 51, 339–342.
23. T. Hirokawa, T. Tsuyoshi and Y. Kiso, J. Chromatogr., 1987, 408, 27–41.
24. D. Kaniansky, M. Koval and S. Stankoviansky, J. Chromatogr., 1983, 267, 67–73.
25. A. Yamada, K. Hodouchi, H. Q. Ma, K. Kobayashi and H. Matsubara, Bunseki Kagaku, 1993, 42, 867–872.
26. J. E. Prest, S. J. Baldock, P. R. Fielden, N. J. Goddard, K. Kalimeri, B. J. Treves Brown and M. Zgraggen, J. Chromatogr., A, 2004, 1047, 289–298.
27. M. Masár, D. Kaniansky, R. Bodor, M. Jöhnck and B. Stanislawski, J. Chromatogr., A, 2001, 916, 167–174.
28. R. Bodor, M. Žúborová, E. Ölvecká, V. Madajová, M. Masár, D. Kaniansky and B. Stanislawski, J. Sep. Sci., 2001, 24, 802–809.
29. M. A. Woodland and C. A. Lucy, Analyst, 2001, 128, 28–32.
30. C. Stathakis and R. M. Cassidy, Anal. Chem., 1994, 66, 2110–2115.
31. M. Pumera, J. Wang, F. Opekar, I. Jelínek, J. Feldman, H. Löwe and S. Hardt, Anal. Chem., 2002, 74, 1968–1971.
32. J. Wang, M. Pumera, G. Collins, F. Opekar and I. Jelínek, Analyst, 2002, 127, 719–723.
33. J. Wang, G. Chen and A. Muck, Anal. Chem., 2003, 75, 4475–4479.
34. J. Wang, G. Chen, A. Muck and G. E. Collins, Electrophoresis, 2003, 24, 3728–3734.
35. J. Tanyanyiwa, E. M. Abad-Villar, M. T. Fernández-Abedul, A. Costa-García, W. Hoffmann, A. E. Guber, D. Herrmann, A. Gerlach, N. Gottschlich and P. C. Hauser, Analyst, 2003, 128, 1019–1022.
36. D. G. Tuck, Pure Appl. Chem., 1983, 55, 1477–1528.
37. Lange's Handbook of Chemistry, ed. J. A. Dean, McGraw-Hill, London, 15th edn, 1999.
38. J. E. Prest, S. J. Baldock, P. R. Fielden, N. J. Goddard and B. J. Treves Brown, Analyst, 2002, 127, 1413–1419.
39. M. Masár, M. Žúborová, J. Bielčíková, D. Kaniansky, M. Jöhnck and B. Stanislawski, J. Chromatogr., A, 2001, 916, 101–111.
40. Analytical Methods Committee, Analyst, 1987, 112, 199–204.
41. The Natural Mineral Water, Spring Water and Bottled Drinking Water (Amendment) (England) (No. 2) Regulations, 2003.
42. J. E. Prest, S. J. Baldock, P. R. Fielden, N. J. Goddard and B. J. Treves Brown, Analyst, 2003, 128, 1131–1136.
43. T. Masadome, R. Sonoda and Y. Asano, Talanta, 2000, 52, 1123–1130.

---