Molecular tectonics: geometry and energy based analysis of coordination networks

Abstract

The combination of the bis-monodentate tecton 1 based on the fluorene skeleton and bearing two pyridine units as coordinating sites with HgCl₂ acting as a metallatecton leads to a 1-D coordination network in the crystalline phase as demonstrated by single crystal X-ray diffraction. When considering only geometrical features of the organic and metallic tectons, the generation of the network may be described as resulting from interconnection through Cl–Hg interactions of consecutive metallamacrocycles formed between two tectons 1 and two HgCl₂ complexes. However, the analysis of the solid by energy criteria evaluated using the PACHA algorithm reveals that the bridging (Hg–Cl–Hg) process participates for only 19% of the overall energy whereas the π–π interaction between fluorene units contributes up to 60%. Thus, when taking into account both μ-bridging process and π–π interactions, the overall system may be described as a 2-D hybrid metallo-organic network.

---

A crystal is by essence a compact and periodic system for which all the components are in close contact. The periodic nature of the crystalline system implies translations into all three directions of space. Thus, a crystal is by definition a 3-D network. However, when interested in the design of molecular networks in the crystalline phase, by considering the crystal as a supramolecular architecture,^1,2 one may design, within the 3-D assembly, specific intermolecular interactions between components composing the solid. These interaction motifs may be regarded as recognition patterns or assembling cores appearing through the self-assembly processes taking place during the crystallisation event. Thus, by considering the assembling cores as structural nodes of the architecture, one may describe the formation of molecular networks as resulting from translations of the nodes into one (1-D), two (2-D) or three directions (3-D) of space. The approach dealing with the design and generation of molecular networks followed by us is called molecular tectonics.^3,4 The strategy applied by this approach is based on tectons⁵ which are active building units bearing recognition information and thus capable of recognising each other. The recognition event may be set-up through a variety of reversible attractive intermolecular interactions such as van der Waals, electrostatic, π–π, H-bonding and coordination bonding. Many examples of inclusion-⁶, H-bonded-⁷ and coordination-⁸ networks have been generated over the last 15 years.

Let us focus here on coordination networks which are infinite metallo-organic architectures resulting from mutual bridging between organic (T_O) and metallic (T_M) tectons. The design of this type of molecular networks with predefined dimension (1-, 2- or 3-D) is based on the interplay between both electronic and geometric requirements of the organic and the metallic tectons. We have initiated a systematic investigation dealing with different possibilities of combining organic and metallic tectons possessing a variety of shapes.⁹ In particular we have prepared the tectons 1 (Scheme) which is a “V” shape neutral bis monodentate coordinating unit based on the fluorene skeleton bearing two pyridine derivatives.¹⁰ Few other related fluorene based ligands have been reported.¹¹

Scheme 1

Here we report on the formation and structural analysis by single crystal X-ray diffraction of a coordination network obtained in the presence of HgCl₂ complex as well as an energy analysis of all types of interactions between different components in the crystalline phase.

The combination of the neutral organic tecton (TO) 1 adopting a “V” shape geometry with HgCl₂ which should behave as a neutral metallatecton (T_M) offering two available coordination sites located at the extremities of a “V” appeared as an interesting case since, when only considering the formation of coordination bonds, in principle one would expect either the formation of a discrete metallamacrocycle (Fig. 1a) or the generation of three different infinite 1-D coordination networks (Fig. 1b, c and d). Whereas for the first two cases, (Fig. 1b and c), the cationic mercury(II) centre adopts a pseudo tetrahedral coordination geometry, for the third possibility (Fig. 1d), an extension of the coordination sphere of mercury from four to five is required. This would occur through bridging of two adjacent metallic centres by two chloride anions implying a square based pyramidal coordination geometry. This last type of 1-D network may be also described as resulting from the interconnection of discrete metallamacrocycles (Fig. 1a) by Cl–Hg bonds.

Fig. 1 Schematic representation of the formation of either discrete neutral metallamacrocycle (a) or infinite 1-D neutral coordination networks (b–d) based on the mutual bridging between the bis monodentate tecton 1 possessing a “V” shape geometry and HgCl₂ metallatecton offering two available coordination sites occupying the extremities of a V.

At room temperature, upon slow diffusion of a CHCl₃ solution of 1 into a EtOH solution of HgCl₂, colourless single crystals were obtained after ca. 48 hours (see experimental section).

Geometry based analysis of the crystal structure

The structural analysis of the crystal by X-ray diffraction revealed the following features. The crystal (triclinic system, P1̄ as the space group, Z = 2) is composed of tecton 1, HgCl₂ and H₂O solvent molecules. The latter appeared to be disordered. For the organic tecton 1, the plane of the ester group (C–O distance varying between 1.336 Å and 1.348 Å and C=O 1.192 Å and 1.200 Å, OCO angle of ca. 123.7°) is tilted with respect to the pyridine ring (CCCO dihedral angles of −7.4° and −16.8°).

In a first analysis, one observes the formation of a discrete [2,2] metallamacrocycle (Fig. 2). The coordination sphere around Hg²⁺ cations is composed of two Cl⁻ anions with Hg–Cl distances of 2.355 and 2.376 Å and two N atoms (Hg–N distances of 2.390 and 2.497 Å) belonging to two different tectons 1. The coordination geometry around the metal is a distorted tetrahedron (Cl–Hg–Cl and N–Hg–N angles of 160.0° and 100.7° respectively). The distance between two endocyclic mercury centres is 16.68 Å.

Fig. 2 A portion of the crystal structure showing the formation of a neutral [2,2]metallamacrocycle obtained upon self-assembly of the tecton 1 with HgCl₂. H atoms are not represented for clarity. For bond distances and angles see text.

A second level of analysis reveals that in fact the metallamacrocycles are interconnected through di-μ₂-chloro bridges (Hg–Cl distance of 3.190 Å, Hg–Cl⋯Hg angle of 92.5°) leading thus to a 1-D coordination network schematically represented in Fig. 1d. When considering this rather long Hg–Cl bond, the coordination sphere around is then composed of three chloride anions and two N atoms with a distorted square based pyramidal geometry (Fig. 3). The parallel packing of the above mentioned 1-D networks generates sheets and, due to stacking interactions between the aromatic moieties of 1, the packing of sheets leads to channels in which disordered water molecules are located (Fig. 3). Thus, when considering both types of interactions, i.e. μ₂-chloro bridging between metallatectons HgCl₂ and π–π stacking interactions between the aromatic moieties of the organic tecton 1, the structure may be described as a 2-D molecular network. It may be generated using two perpendicular translations one dealing with the coordination assembling core (Hg–Cl–Hg) and other with the assembling core generated by π–π stacking.

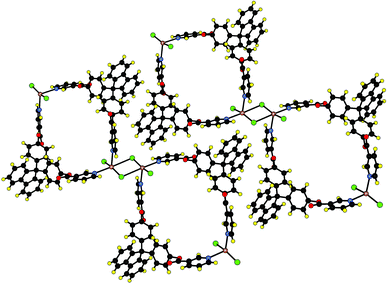Fig. 3 A portion of the crystal structure showing the formation of the neutral 1-D coordination network formed by bridging by chloride centres of consecutive metallamacrocycles and the lateral packing of 1-D networks The channels generated are filled with water clusters (not represented). H atoms are not represented for clarity. For bond distances and angles see text.

Often, in this type of contribution, once arrived at that level of description, the report would be ended by drawing some conclusions and mentioning the work in progress. However, having in hand a reliable approach and a computational methodology permitting a detailed energy based analysis of molecular crystalline solids, we analysed the above mentioned crystalline system in terms of the energetic contributions of different intermolecular interactions to the formation of the crystal and the description of the latter as a molecular network.

Energy based analysis of the crystal structure

A further step in describing the crystal mentioned above may be based on an energy analysis of all possible interactions between the components in the crystalline material which may be described as a ternary system based on 3 interacting molecules: the organic tectons 1, HgCl₂ as the metallatecton and H₂O molecules. The central point is to find the best description in terms of intermolecular interactions of molecular components composing the crystal. Assuming that the shorter is better, commonly, one relies on careful bond length analysis to describe the structure in terms of molecular network formation. However, although this approach is perfectly suited for covalent bonds that are ruled by overlap integrals vanishing very rapidly with distance, one may wonder if this still holds for weaker bonds based on electrostatic interactions that decrease only very slowly with distance. The answer to this fundamental question is by no means obvious and should be carefully checked using energetic criteria instead of geometric arguments.¹² Concerning the computation of interaction energies from molecular or crystalline data, two broad classes of methods are generally used:

i) Methods relying on empirical force fields that have the very well understood shortcoming of limited transferability resulting from parameterisation on specific systems.¹³

ii) Ab initio methods that are free from empirical input but that suffer from the basis set superposition error.¹⁴

As our interest lies in building molecular networks involving metallatectons of variable nature (M = Hg, Co, Ni, Zn, Mn…), the empirical force field approach was ruled out as this would require parameterisation of M⋯X (M = M, H, C, O, N, Cl) pair potentials for each kind of metal, a very tedious task. For the same reason, ab initio methods were not very attractive owing to the need to solve the Dirac equation (relativistic effects cannot be neglected for heavy elements such as mercury) and to quite different basis sets for treating light atoms (C, H, O, N, Cl) and mercury atoms. Finally, the quite large number of atoms (several hundreds) in the unit cells of our networks and the need to perform periodic calculations was another reason for using the many simpler but nevertheless non-empirical PACHA algorithms.¹⁵ This powerful approach of chemical bonding is based on a spherical charge approximation of density functional equations and the only input required from the user is a CIF file describing the molecular (theoretical models) or crystalline (X-ray or neutron diffraction data) structure. In the following, we will recall the basic assumptions and approximations lying behind the PACHA algorithm. For further technical details the reader should consult the already published literature.

The first important point is that PACHA was not designed for treating small systems, as usually done in most true ab initio approaches. It was rather designed at its very beginning for treating very large systems such as supramolecular assemblies or crystalline networks in the most rigorous and non-empirical way. But rigorous does not mean that there are no approximations. In fact, three main assumptions are the very heart of the PACHA formalism:

i) Spherical charge approximation of equations deriving from density functional theory (DFT).¹⁶ This is obviously the most drastic approximation and at first sight one may wonder how such a crude approach could give meaningful and accurate results. In fact, we have no other possible choice because it is the only way to reduce the estimation of electronic densities from atomic structure to the resolution of a linear system of equations involving only electronegativity and chemical hardness as atomic data. Obviously, the drawback is that we are not in a position to get all the exquisite details provided by a full quantum mechanical treatment such as distribution of electronic density among available atomic or molecular orbitals. At this stage it must be realised that the originality of the PACHA approach does not lie in this purely mathematical treatment of DFT equations but rather in a clever choice of the atomic parameterisation.

ii) Accordingly, most previous approaches based on electronegativity equalization deals with empirical sets of atomic electronegativity and chemical hardness that are adjusted to reproduce ab initio sets of atomic charges. Recalling that there is no quantum mechanical operator that can be bracketed by a wave function yielding an atomic charge expectation value, it should be obvious that proceeding this way would just lead to completely arbitrary sets of electronegativity and chemical hardness data. This is very bad for two reasons. First, the fundamental impossibility of assigning a single and unique atomic charge to an atom in a molecule is transferred to the electronegativity and chemical hardness themselves, adding still more confusion to these already loosely defined quantities. Second, this prevents obtaining a unique splitting between purely electronic terms (F-contribution hereafter) and purely electrostatic ones (EB-contribution hereafter) as required by the Hellman–Feynman theorem.¹⁷ It is at this point that the PACHA clears up all these problems. Relying on the fully rigorous quantum mechanical proofs that electronegativity is indeed a measure of the electronic chemical potential¹⁸ and that chemical hardness is a measure of atomic size,¹⁹ singles and unique non-empirical values may be assigned to each atomic element of the periodic table. The choice of the Allen scale for electronegativity and of atomic radii derived after resolution of the Dirac equation was made because these values are fixed by Nature herself and not by tedious calibration procedures based on experimental quantities that may contain measurement errors. This is really a crucial advantage of the PACHA formalism over all other electronegativity-based methods, because when computing a charge distribution from an experimental X-ray structure we are sure that only errors coming from the diffraction experiment itself are introduced in the resulting charge distribution. The other advantage of proceeding this way is that we have now a single and unique partition of the molecular or crystalline energy E_tot = EB + F into two terms, a purely electrostatic one EB that may be straightforwardly evaluated from the partial charge distribution and the other one F including all terms depending on electron-electron interactions that remain completely unknown.

iii) The last assumption is then that this F-term including all the problematic quantum mechanical contributions could be treated as a mere integration constant (this idea was directly suggested by R. P. Feynman himself in his 1939 paper) when evaluating interaction energies. From a theoretical viewpoint this constancy of the F-term may be justified by noticing that these quantum mechanical contribution drops very rapidly with interatomic distance and that energy differences among interacting fragments are evaluated at frozen geometry. From a practical point of view, if two sub-systems characterised by their respective electrostatic balances EB₁ and EB₂ are in interaction through non-covalent bonds to form a new system characterised by its electrostatic balance EB₁₂ one may expect that F-terms encapsulating all quantum-mechanical electron-electron interactions should be approximately additive (F₁₂ ∼ F₁ + F₂). This means that the overall interaction energy (E_int = E₁₂ − E₁ − E₂) should be well approximated by the difference of three easily accessible electrostatic balances (E_int ∼ EB₁₂ − EB₁ − EB₂). The drawback of this approach is that it is impossible to get decomposition of the interaction energy into its various contributions. For instance in the particular case of hydrogen bonding, PACHA cannot give you the usual partition of the total bonding energy into electrostatic, polarisation, exchange repulsion, charge-transfer and coupling.²⁰ It gives you only the total interaction energy, i.e. what should be the result of all the summed interactions. In one sense, this is fortunate because only this sum can be experimentally measured allowing checking the validity of the formalism.

Concerning the validity of the proposed formalism we refer interested readers to a previous work¹⁵ and thus give below only a summary of experimental checks that demonstrate that PACHA is able to deal with many different experimental aspects of physical chemistry in a smooth and perfectly reproducible way. A first check was then to verify that if H-atoms coordinates of ice polymorphs were unknown, PACHA would have correctly and easily predicted their values knowing only the O-atom positions.²¹ Such a one-to-one correlation between theory and experiment for so widely different ice structures would not have been possible with an inaccurate method unable to account for all polarization effects that are so important in hydrogen bonding. This success obviously comes from the fact that the whole charge distribution in a molecule or in a lattice may be recomputed within a negligible computation time after any alteration of atomic coordinates. Consequently, most of this time is spent for looking at the best geometry on electrostatic grounds and not for evaluating the electronic density as other software do. It is just because the charge distribution is constantly evolving reflecting each move in atomic coordinates into an energy value that polarisation is correctly handled. If quantum-mechanical methods are also currently able to compute a new wave function and thus a new charge distribution for any alteration in geometry, this could be done only for quite small chemical systems at the present time. Concerning interaction energies, it was shown that PACHA was also able to reproduce the H-bond energy measured in the water dimer using microwave spectroscopy or the sublimation energy of hexagonal ice measured by calorimetric techniques.²¹ Quite recently it was also shown that it was possible to compute with no further approximations surface energies in good agreement with experimental values for a wide range of wide range of chemical compounds^22,23 Consequently, even if the presented computational method is by no means “standard” (it is impossible to get atomic orbital populations or to break an interaction energy into several contributions), PACHA nevertheless does a quite good job as far as H-atomic coordinates, H-bond energies or surface enthalpies are concerned. Obviously, one may argue that any new computational method should not only be validated against experimental data but also judged by its ability to reproduce results obtained by other theoretical models. On this ground also it was shown, at least in the case of the water molecule, that PACHA predicted a small charge transfer Δq = +0.014 on going from the gas phase to the solid state in perfect coherence with rigorous ab initio methods that lead to values between +0.009 and +0.017 depending on the quality of the basis set. Again, it is important to stress that owing to the fact that atomic charge is not an observable in the quantum mechanical sense, agreement can be expected only on charge differentials and not on absolute values.

At the present time the PACHA algorithm is the only non-empirical theoretical tool able to study large water assemblies trapped in supramolecular cavities²⁴ and may also be used in the case of non H-bonded systems.²³ Its application in molecular tectonics was already explored in the case of 0D-systems²⁵ and it is applied here for the first time to molecular networks of higher dimensionality. The home-made graphical interface used for all the computations is freely available.²⁶

Disorder treatment

For the case studied here, the first step is to locate hydrogen atoms on disordered water molecules before calculating realistic interaction energies. The X-ray diffraction study reveals the presence four independent water molecules (atoms labelled O5, O6, O7 and O8 in the CIF file) in the asymmetric unit cell, each displaying a 1/2-occupation factor.

Fig. 4 (left) shows that these water molecules are located inside cavities formed by two tectons 1 and two HgCl₂ molecules. The analysis of interatomic distances shows clearly that the oxygen atom O7 displays two very short distances with atoms O5 (205 pm) and O8 (223 pm). Fig. 4 (right) demonstrates the result of applying a 1/2-occupation factor on all O-atoms belonging to water molecules. Although this operation avoids the presence of short contacts, it nevertheless generates voids leading to a non-realistic situation. In fact, these arguments may be made more quantitative by evaluating molecular volumes²⁷ using standard van der Waals radii²⁸ for C (170 pm), H (120 pm), N (155 pm), O (152 pm), Cl (175 pm) and Hg (155 pm). Using these data it is found that the radius of the sphere that may be inscribed into the dimeric ring shown in Fig. 4 is 3.66 Å (first van der Waals contact with atom H2 in α-position from the carboxylate group), corresponding to a minimum free volume of 205 ų. Considering a volume of ca. 19.4 ų for a water molecule, the cavity formed in the crystal may be occupied by no more than 10 water molecules These observations suggest employing a model where full occupancy factors are used, but where atomic coordinates of atom O7 are slightly modified (−0.203, 0.385, 0.039) instead of (−0.091, 0.367, 0.066) in order to restore more realistic O⋯O contacts: d(O7⋯O5) = d(O7⋯O6) = d(O7⋯O8) = 280 pm. With this single minor and satisfying adjustment, all H-atoms may be located using the PACHA algorithm (CIF file for atomic coordinates is given as supplementary material‡). The final stoichiometry of the crystal used hereafter is then [HgCl₂·1·(H₂O)₄]₂, corresponding to a 75% filling factor of the central cavity.

Fig. 4 Filling of the central cavity defined by a {HgCl₂·1}₂ metallamacrocycle by water molecules. Left: the filling with full space-group symmetry. Right: The filling taking into account the 1/2-occupation factor assigned by X-ray diffraction. See text for further details.

This treatment of water disorder was made as simple as possible in order to get H-bond energies that may be easily compared with other non-disordered situations (such as the water dimer for instance). More sophisticated treatments of crystallographic disorder validated by solid-state NMR spectroscopy have been published elsewhere.^24,29 In this respect PACHA follows the same common practice in theoretical calculations to work on suitably adjusted models rather than on crude experimental data in order to get meaningful results. Obviously, one may then wonder what would have been the effect on the computed energies of using the original X-ray atomic coordinates for O7 instead of the adjusted value. In this case PACHA would have led to a H-bond energy of about −140 kJ·mol⁻¹. On one hand, this value is in perfect coherence with the extremely short (205 pm) distance between atoms O5 and O7, as it is known from experiments, that the shorter the O⋯O distance the stronger the hydrogen bond.²⁰ On the other hand, we know that this value cannot be correct, as it is obviously much too strong for an interaction between two neutral molecules. But this wrong value also gives us an idea of the sensitivity of the model to bond length variation. In this particular case, the error was quite large just because it is very difficult to locate the best model for water atoms owing to the large scattering power of HgCl₂. But of course these large errors apply only to atoms belonging to water molecules and not to other atoms in the structure. For all these atoms, errors coming from the refinement procedure are usually encapsulated into esd-values associated to each optimised coordinate. In fact this last kind of information may also be used by PACHA to probe the effect of small coordinate variations upon the final reported EB-value. The procedure is very simple and straightforward. First a confidence level is fixed, typically 3σ variations around reported mean values (corresponding to a 99.7% confidence interval). Then a large number (at least 100) of slightly different crystal structures are generated at random leading to a set of slightly different PACHA parameters simulating the situation of a real crystal where small random variations may occur owing to the recording at a finite temperature. The last step is then to perform a standard statistical analysis on this set of data leading for each PACHA variable to mean values with their associated standard deviations. Applying this rigorous procedure to the present crystal structure, it was found that the relative error affecting the EB parameter was less than 2%. Derived interactions energies being around 50 kJ·mol⁻¹, the accuracy of the reported values may be estimated at about 1 kJ·mol⁻¹.

Treatment of the isolated dimer [HgCl₂·1·(H₂O)₄]₂

Fig. 5 shows the application of the PACHA formalism to the formation of the hydrated neutral [2,2] metallamacrocycle [HgCl₂·1·(H₂O)₄]₂, leading to an overall interaction energy E_int = −388 kJ·mol⁻¹. If this clearly shows that the dimer should be a stable object relative to the separated tectons, it implies nothing about how this energy is distributed with respect to the various interactions responsible for the cohesion of this supramolecular object. In order to reach this type of information, one should dive more deeply into this structure by considering the existence of two interacting water tetramers encapsulated into the neutral metallamacrocycle. At first sight we may expect that formation of four Hg–N coordination bonds should account for a large part of this interaction energy.

Fig. 5 Electrostatic balances (EB_H, EB₁, EB_W and EB_d) for the tectons involved in the formation of the hydrated neutral [2,2] metallamacrocycle {HgCl₂·1·(H₂O)₄}₂. From these values the overall energy of interaction E_int may be approximated by E_int = EB_d − 2 × (EB_H + EB₁ + 4 × EB_W).

This may be checked in Fig. 6 (right) where it is found that formation of the Hg–N coordination is characterised by an energy E_HgN = −42 kJ·mol⁻¹. As expected this value is high enough to distinguish it from a mere van der Waals or H-bond interaction, but nevertheless low enough to make a clear difference with a strong covalent bond arising from the equal sharing of two electrons. Now using the left part of Fig. 6, we are in position to compute in another way the cohesive energy of the metallamacrocycle. Here ring closure leads to a [HgCl₂·1]₂ entity characterised by the existence of four Hg–N bonds with an interaction energy evaluated as E_cav = −162 kJ·mol⁻¹, i.e. about −41 kJ·mol⁻¹ per Hg⋯N bond. This value is perfectly consistent with the previously derived one and shows that ring closure has a slight destabilising effect on the Hg⋯N interaction. After this satisfying treatment of the metallamacrocycle, we may now turn our attention towards the encapsulated water assemblies.

Fig. 6 Analysis of the formation of the neutral metallamacrocycle from isolated metallatecton and organic tecton. The interaction energy associated to the formation of one Hg–N coordination bond (right) is given by E_HgN = EB_coord − EB_H − EB₁. The interaction energy associated to the formation of the cavity (left) is evaluated as by E_cav = EB_mac − 2 × (EB_H + EB₁) and should correspond to the formation of four Hg–N coordination bonds.

Fig. 7 allows quantifying the contributions arising from the existence of these hydrogen-bonded water molecules. First, the mean H-bond strength for a four-member ring is E_HB = EB_tetra/4 = −26 kJ·mol⁻¹ and corresponds to the typical value found in the water dimer or in hexagonal ice for instance.²¹ One may also deduce that both rings are non-interacting or even weakly repulsing each other since E_2tetra = +2 kJ·mol⁻¹. With these data in hand, it may easily be checked that E_int = −388 ○ 4 × E_HgN + 8 × E_HB + E_2tetra = −365 kJ·mol⁻¹, the difference corresponding to the favourable energy of encapsulation E_incl = −23 kJ·mol⁻¹ of the two water tetramers inside the central cavity. Accordingly, another independent way of evaluating this encapsulation energy is given in Fig. 8 and leads to a very similar value E_incl = −22 kJ·mol⁻¹.

Fig. 7 Resolution using the PACHA algorithm of the water structure trapped inside the central cavity defined by a [HgCl₂·1]₂ metallamacrocycle. The total H-bond energy within a single tetramer is given by E_tetra = EB_W4 − 4 × EB_W, whereas the interaction energy between the two water tetramer is evaluated as E_2tetra = EB_W8 − 2 × EB_W4.

Fig. 8 Evaluation of the encapsulation energy for the two water tetramers inside the metallamacrocycle E_incl = EB_d − EB_W8 − EB_mac.

It should be obvious from the above analysis that this last value gathers all attractive interactions that are neither H-bonds between water molecules nor Hg–N coordination bonds and should thus correspond to what is generally named “van der Waals” interactions. At first sight, it may seems that this a quite large value, but when we take into account that this energy was derived from a molecular species containing exactly one hundred non-hydrogen atoms we get an average per atom contribution of about −0.2 kJ·mol⁻¹ well in line with the recognised weakness of van der Waals bonds. But one may also argue that treating C, N, O and Hg atoms on the same ground cannot be correct and that most of this polarisation energy should come from the presence of heavy mercury atoms. The obvious question is then: can we prove that just by looking at the molecular structure?

Fig. 9 shows the molecular fragments that could help us obtain a satisfactory answer to this question. For instance it should be clear that polarisation of water tetramers by HgCl₂ metallatectons corresponds to an overall repulsive interaction as E_rep = EB_HgW4 − EB_H − EB_W4 = +17 kJ·mol⁻¹. On the other hand, polarisation of the water tetramer by the organic tecton 1 is as expected weakly favourable E_pol = EB_(1)W4 − EB₁ − EB_W4 = −3 kJ·mol⁻¹, but clearly too low (pure van der Waals interactions) to overcome the repulsion between HgCl₂ and the water tetramer. As expected, when we consider interaction between the van der Waals {1·(H₂O)₄} complex and the metallatecton HgCl₂ leading to half of the metallamacrocycle [HgCl₂·1·(H₂O)₄]₂, we recover the Hg–N coordination bond: EB_m − EB_H − EB_(1)W4 = −41 kJ·mol⁻¹. But when we consider encapsulation of the hydrated {HgCl₂·(H₂O)₄} complex by the organic tecton 1, we get a large negative value: EB_m − EB₁ − EB_HgW4 = −60 kJ·mol⁻¹. Taking into account that this value includes the formation of one Hg–N bond leaves about −18 kJ·mol⁻¹ for the mutual polarisation energy between 1 and the hydrated metallatecton. There should be no doubts that we are here quantifying (may be for the first time) an interesting illustration of the templating effect concept, so important in materials chemistry.

Fig. 9 Electrostatic balances of some molecular fragments involved in the encapsulation of water tetramers into [2,2] metallamacrocycles. See text for details.

The energy-based study mentioned above has thus led to a fine description of the formation of the [HgCl₂·1·(H₂O)₄]₂ metallamacrocycle. As expected (and rigorously proved), the formation of this supramolecular entity is first driven by the formation of coordination bonds between N atoms located on the pyridine moieties belonging to the organic tecton 1 and mercury cations. With four Hg⋯N bonds, the energy associated with this coordination interaction (−4 × 40.6 = −162 kJ·mol⁻¹) represents ca. 42% of the total interaction energy E_int. The other large contribution comes from the formation through hydrogen bonding of two independent four-member rings of water molecules (−8 × 25.6 = −205 kJ·mol⁻¹) which represents ca. 53% of the total interaction energy. Finally, the encapsulation of the two water clusters inside the central cavity of the metallamacrocycle through van der Waals interactions involving mainly mercury atoms (−22 kJ·mol⁻¹), accounts for the remaining 5%. Although this hierarchy in weak interactions is by no means not very surprising it was, nevertheless, derived in a quite general way after a rigorous ab initio energy analysis based solely on experimental X-ray diffraction data.

Treatment of the full network [{HgCl₂·(1)·(H₂O)₄}₂]

The above mentioned analysis was restricted to the description of the discrete hydrated {HgCl₂·1·(H₂O)₄}₂ metallamacrocycle. It is worth noting that the same theoretical tool may be used on the same experimental data for the evaluation of interactions existing only in the solid state and thus allows the description of the crystal in terms of molecular networks formation. Here we rely on lattice sums techniques that allow dealing in a perfectly converged way with electrostatic interactions (Madelung summation). In our case, the total 3D-packing energy EB_pack may be readily evaluated from the knowledge of EB_mad = −2888 kJ·mol⁻¹ computed by applying 3D-Madelung techniques to our crystalline data. Comparison with the value found for the isolated hydrated metallamacrocycle (Fig. 5) leads to the desired value EB_pack = EB_mad − EB_d = −111 kJ·mol⁻¹. As in the above treated molecular case, this value is not very informative as it only shows that the crystal is more stable than the gaseous metallamacrocycles. Again, a much more valuable information would be to identify the type of molecular interactions responsible for the cohesion of the crystalline solid. A first widely used approach would to extract from the crystalline 3D-data a molecular fragment representative of the kind of interaction that must be characterised and hope that the total number of atoms is large enough to get a reliable and yet converged value for the interaction energy. In our case, this approach means that we have to isolate two interacting metallamacrocycles characterised by a value EB_dim(mac) and compare it with twice the value EB_d characterising the isolated metallamacrocycle: E_dim(mac) = EB_dim(mac) − 2 × EB_d. A possible way to check if convergence has been reached would be to generate a trimer, get its EB_trim(mac) value and get a new interaction energy: E_trim(mac) = [EB_trim(mac) − 3 × EB_d]/2 and check that E_dim(mac) ≈ E_trim(mac) and so on until a converged value is obtained. But there also exists a cleverer and quite general procedure allowing a fully converged value to be obtained. It consists in generating from the available crystalline data a n×n×n supercell (that would hold n³ metallamacrocycles in our case). By keeping in this supercell the atomic coordinates of one metallamacrocycle, one isolates this molecular unit from its closest neighbours. Applying standard 3D-lattice sum techniques to this supercell displaying a 1/n³ filling factor should lead to a new value EB_free just equal to the value EB_mol computed without the presence of the lattice. For instance, in our case we got for a 2 × 2 × 2 supercell displaying a 1/8 filling factor the value EB_∞(mac) = −2777 kJ·mol⁻¹ (the subscript ∞ reminds us that this value was obtained after a full 3D-Madelung summation). Comparing this value to the one EB_d previously derived for an isolated metallamacrocycle shows that the selected volume is large enough to assume that all possible neighbours are located at infinity in all directions. Then, all we have to do is to add to this nearly empty supercell the atomic data necessary to generate a second metallamacrocycle displaying a particular interaction with the first one and compute the new associated EB_∞(int) electrostatic balance. As before, the difference E_∞(int) = EB_∞(int) − EB_∞(mac) then gives the fully converged interaction energy taking into account any possible formation of chains or layers coming from the existence of lattice periodicity.

Fig. 10 (top) shows the first type of association that may be identified in our crystal structure. It describes the “polymerisation” of [HgCl₂·1·(H₂O)₄]₂ metallamacrocycles through the formation of di-μ-chloro bridges between mercury atoms leading to E_∞(μ-Cl) = [EB_∞(μ-Cl) − EB_∞(mac)] = −24 kJ·mol⁻¹. By comparison considering only a dimer {[HgCl₂·1·(H₂O)₄]₂}₂ would have lead to EB_dd(μ-Cl) = −5578 kJ·mol⁻¹ and to E_dim(μ-Cl) = EB_dd(μ-Cl) − 2 × EB_d = −24 kJ·mol⁻¹ = E_∞(μ-Cl). In this case there is a perfect match between the molecular and solid state value, meaning that this bridging interaction is purely molecular. It may be interesting to compare this interaction energy corresponding to the formation of a long Hg–Cl bond (319 pm) to EB_H/2 = −75 kJ·mol⁻¹, characterising the electrostatic energy associated to the formation of a much shorter (236 pm) Hg–Cl covalent bond. The large observed difference between these two values shows that it is perfectly possible to discriminate between a true covalent bond and a mere acid–base interaction within the PACHA formalism, even if it deals only with the electrostatic part of any chemical bond. Referring to the above-derived value of EB_pack we see that such a bridging interaction accounts for only 21% of the total packing energy indicating the existence of other types of interaction. Fig. 10 (bottom) shows how metallamacrocycles are packed along the a-axis through π–π interactions between fluorene moieties. For this new kind of interaction involving a face-to-face stacking of 20 aromatic rings we get E_∞(π–π) = [EB_∞(π–π) − EB_∞(mac)] = −66 kJ·mol⁻¹ accounting for about 60% of the total packing energy. As before considering only a dimer {[HgCl₂·1·(H₂O)₄]₂}₂ would have led to EB_dd(π–π) = −5620 kJ·mol⁻¹ and to E_dim(π–π) = EB_dd(π–π) − 2 × EB_d = −66 kJ·mol⁻¹ ≈ E_∞(π–π). At this stage we have identified and quantified the two “obvious” networking interactions and are left with about 19% of interactions of unidentified origin. Even if this value is quite small relative to the other two, it is however not zero and one may then dive more deeply into the structure in order to look more closely at these very weak interactions. A good way to identify these weak interactions is to sit on a mercury atom and look at all possible Hg⋯Hg contacts within a sphere of radius 1.5 nm. 11 such contacts are then found, eight of them being already accounted for by the formation of either μ-Cl bridges (406 pm, 1429 pm and 1453 pm) or by the existence of π–π stacking (2 × 692 pm, 2 × 1383 pm and 1462 pm). The three last remaining Hg⋯Hg contacts (791 pm, 812 pm and 1487 pm) should then correspond to yet unconsidered interactions between our metallamacrocycles.

Fig. 10 The two strongest interactions identified in the molecular network {[HgCl₂·1·(H₂O)₄]₂}_∞ and leading to the formation of molecular chains. Top: association through di-μ₂-chloro bridges of [HgCl₂·1·(H₂O)₄]₂ hydrated metallamacrocycles characterised by a fully converged electrostatic balance EB_∞(μ-Cl). Bottom: association by π–π stacking between fluorene moieties of [HgCl₂·1·(H₂O)₄]₂ hydrated metallamacrocycles characterised by a fully converged electrostatic balance EB_∞(π–π).

Fig. 11 (top) shows the first kind of interaction responsible for the 1487 pm Hg⋯Hg contact. It involves a parallel stacking of fluorene moieties associated to a perpendicular stacking of phenyl and nicotinate moieties. The corresponding energy of interaction is given by E_∞(VdW) = [EB_∞(VdW) − EB_∞(mac)] = −14 kJ·mol⁻¹ accounting for about 12% of the total packing energy. Considering only a dimer {[HgCl₂·1·(H₂O)₄]₂}₂ would have led to EB_dd(VdW) = −5568 kJ·mol⁻¹ and to E_dim(VdW) = EB_dd(VdW) − 2 × EB_d = −14 kJ·mol⁻¹ ≈ E_∞(VdW). At last Fig. 11 (bottom) shows the interaction responsible for the last two Hg⋯Hg contacts involving long Hg⋯Cl bonds (515 pm) and characterised by E_∞(Hg⋯Cl) = [EB_∞(Hg⋯Cl) − EB_∞(mac)] = −7 kJ·mol⁻¹. Again, considering only a dimer {HgCl₂·1·(H₂O)₄}₄ would have led to EB_dd(Hg⋯Cl) = −5561 kJ·mol⁻¹ and to E_dim(Hg⋯Cl) = EB_dd(Hg⋯Cl) − 2 × EB_d = −7 kJ·mol⁻¹ ≈ E_∞(Hg⋯Cl). This last interaction accounting for the remaining 7% of the total packing energy we can be sure that nothing has been missed as far as packing considerations are concerned.

Fig. 11 The two weakest interactions identified in the molecular network {[HgCl₂·1·(H₂O)₄]₂}_∞ also leading to the formation of molecular chains. Top: Perpendicular association between phenyl and nicotinate rings of [HgCl₂·1·(H₂O)₄]₂ hydrated metallamacrocycles characterised by a fully converged electrostatic balance EB_∞(VdW). Bottom: Association through long Hg⋯Cl contacts of [HgCl₂·1·(H₂O)₄]₂ hydrated metallamacrocycles characterised by a fully converged electrostatic balance EB_∞(Hg⋯Cl).

Discussion

Fig. 12 shows the final energetic partition that was deduced from the available crystalline data for both the metallamacrocycle (top) and the molecular network obtained after further association of these supramolecular objects in the solid state. The first important point to note is that only a crystallographic CIF file is required as input from the user to get this kind of information. All the physics needed to transform a set of atomic coordinates and atomic labels into realistic electronic densities are hard coded in the software and no special calibration procedure is needed. This means that, organic molecules, organometallic complexes, minerals and even alloys will be treated with a universal atomic parameterisation. Consequently, most of the time is spent in handling atomic disorder and isolating suitable fragments for energy evaluation. A second important point is to realise that each computed energetic partition is a real fingerprint for a given a supramolecular object (that may be as here either a molecule or a whole network). Consequently, the observed hierarchy between all the interactions responsible for the formation of the object reflected by these pie-graphs does not refer to the intrinsic strength of these interactions.

Fig. 12 Detailed energetic partitions according to the PACHA formalism between all the molecular interactions identified in the crystal structure of the molecular network {[HgCl₂·1·(H₂O)₄]₂}_∞. Top: partition within the isolated hydrated metallamacrocycle between hydrogen bonding (HB), acid–base coordination (Hg–N) and van der Waals polarisation (VdW). Middle: partition within the 3D crystal between π–π stacking (π–π), acid–base bridging (μ-Cl), van der Waals polarisation (VdW) and Hg⋯Cl polarisation (Hg⋯Cl). Bottom: resolution of the 60% π–π stacking contribution into three homomolecular interactions involving the organic tecton 1, the metallatecton (HgCl₂) or the water tetramer (H₂O) and a heteromolecular interaction (cross) gathering all cross-polarisation possibilities between these three molecules.

For instance, referring to Fig. 12 (top) we see that our metallamacrocycle is held by three kinds of interactions: hydrogen bonding, acid–base coordination and van der Waals polarisation. One should not then deduce from the relative size of the three sectors that the strongest interaction is hydrogen bonding and the weakest one van der Waals polarisation. One should rather take into account that the metallamacrocycle formation involves creation of 8 hydrogen bonds and 4 Hg–N bonds showing that the strongest interaction is as expected acid–base coordination (42/4 = 10.5%) and not hydrogen bonding (53/8 = 6.6%). The intrinsic strength of van der Waals polarisation is obviously more difficult to define owing to its multicentric nature. But as it was demonstrated that it was the encapsulation of the hydrated metallatecton that was responsible for the remaining 5%, one may safely assume that van der Waals polarisation within the metallamacrocycle involves 14 non-hydrogen atoms (2 mercury atoms, 4 chlorine atoms and 8 oxygen atoms) leading to an average per atom strength of 5/14 = 0.4%. One then recovers the well-known fact that a hydrogen bond is about 20 times stronger than a van der Waals interaction.

The same remarks apply to Fig. 12 (middle) showing that formation of our molecular network involves 4 kinds of interactions: π–π stacking, acid–base bridging, van der Waals polarisation and Hg⋯Cl polarisation. In order to decide which is the strongest interaction, we must first normalise the data by noticing that network formation involves the creation of 2 μ-Cl bridges (Fig. 10, top) and 2 Hg⋯Cl weak bonds (Fig. 11, bottom). Concerning van der Waals polarisation, Fig. 11 (top) shows that it involves mainly two phenyl groups and two nicotinate rings, i.e. 15 non-hydrogen atoms. One may also notice that the π–π stacking process between aromatic moieties leads also to a columnar stacking of water tetramers and metallatectons (Fig. 11). Fig. 12 (bottom) shows how this overall 60% may be further decomposed into separate contributions. The water contribution was evaluated by comparing a water nanotube characterised by EB_∞(W8⋯W8) = −1576 kJ·mol⁻¹ to a system of isolated water nanopools characterised by EB_∞(W8) = −1573 kJ·mol⁻¹, leading to E_∞(W8⋯W8) = [EB_∞(W8⋯W8) − EB_∞(W8)] = −3 kJ·mol⁻¹. Similarly, the metallatecton contribution was obtained by comparing two columnar association of HgCl₂ metallatectons characterised by EB_∞(M⋯M) = −311 kJ·mol⁻¹ to a system of isolated dimeric metallatectons characterised by EB_∞(Hg₂Cl₄) = −299 kJ·mol⁻¹, leading to E_∞(M⋯M) = [EB_∞(M⋯M) − EB_∞(Hg₂Cl₄)] = −12 kJ·mol⁻¹. At last, the purely organic contribution was evaluated by comparing two columns of the organic tecton 1 characterised by EB_∞(1⋯1) = −762 kJ·mol⁻¹ to a system of isolated (1)-dimers characterised by EB_∞(1-dim) = −717 kJ·mol⁻¹, leading to E_∞(1⋯1) = [EB_∞(1⋯1) − EB_∞(1-dim)] = −45 kJ·mol⁻¹. Obviously, this kind of separation is a little bit artificial because the water nanopools are also polarised by 1 or by the metallatecton and similarly there is a cross contribution between 1 and HgCl₂. The order of magnitude of these cross contributions is nevertheless readily evaluated after a comparison between E_∞(π–π) = −66 kJ·mol⁻¹ and the sum E_∞(W8⋯W8) + E_∞(M⋯M) + E_∞(1⋯1) = −61 kJ·mol⁻¹, leading to E_∞(cross) = −5 kJ·mol⁻¹. This last partition clearly shows why the E_∞(π–π) contribution may be labelled “π–π” as we really know by the above analysis that the largest contribution to E_∞(π–π) comes from the stacking of the organic tecton 1 and not from the unavoidable concomitant formation of a water nanotube or of a columnar association of mercury atoms. Obviously, this kind of conclusion would also have been reached by invoking the quite large Hg⋯Hg or water⋯water distances (691.5 pm), but as wave-functions really goes up to infinity this kind of arguments could always be criticised invoking special resonance or yet unknown relativistic effects. Here such arguments cannot be invoked because we are already dealing with infinite objects (“∞” subscripts reminding that lattice sums have been performed to get the energy) and that the set of orbital radii used was obtained by solving the Dirac equation instead of the Schrödinger one.

Now that we have reached the pure organic contribution E_∞(1⋯1) = −45 kJ·mol⁻¹ free from other polarisation effects, we are in position to speculate upon the intrinsic order of magnitude of a single π–π interaction in order to compare it with the strength of a μ-Cl bridge for instance. The organic tecton having 7 aromatic rings, we anticipate that the E_∞(1⋯1) value corresponds to 14 π–π interactions leading to an average value E(π–π) = −3 kJ·mol⁻¹. As expected this is significantly larger than a mere van der Waals interaction and nevertheless much lower than a typical hydrogen bond or a Hg–Cl⋯Hg bridge characterised by E(μ-Cl) = E_∞(μ-Cl)/2 = −12 kJ·mol⁻¹.

In terms of network description of the crystal, the energy based analysis leads to the conclusion that the structure may be considered as a 2-D network based on both coordination bonding (Hg–Cl) occurring between the metallatectons HgCl₂ and π–π stacking interactions between the aromatic moieties of the organic tecton 1. Fortunately, this conclusion was also drawn from the geometry-based analysis of the crystal structure with however no information on the hierarchy of interactions in terms of energy. The clear advantage of the energy analysis is that we are allowed to make much more precise statements by saying that this network is best described by the interconnection through di-μ₂-chloro bridges of nanopools of water molecules confined inside metallo-organic π–π-nanotubes. The detailed energy analysis also clearly indicates that in terms of energy hierarchy, the contribution of the π–π stacking interactions is roughly three times larger than the contribution of the coordination bonding through μ-Cl bridging of mercury centres. Just because aromatic rings are more numerous than chlorine atoms in the metallamacrocycle, this is true even when it is realised that the μ-Cl bridge is intrinsically much stronger than a single π–π stacking.

Experimental section

Crystallisation conditions

In a crystallising tube, upon slow liquid–liquid diffusion at room temperature of a solution of the tecton 1 (5 mg) in chloroform (1 ml) into a solution of HgCl₂ (1.5 mg) in EtOH (1.5 ml) colourless single crystals were obtained after ca. 48 hours.

Crystal structure determination

X-ray diffraction data collection was carried out on a Kappa CCD diffractometer equipped with an Oxford Cryosystem liquid N₂ device, using graphite-monochromated Mo-Kα radiation. For all structures, diffraction data were corrected for absorption and analysed using OpenMolen package.³¹ All non-H atoms were refined anisotropically.

Crystal data for : (1·HgCl₂) (colourless crystals, 173 K): C₃₇H₂₄Cl₂HgN₂O₄·2H₂O, M = 868.14, triclinic, space group P1̄, a = 6.9151(1), b = 17.3434(3), c = 17.8375(3) Å, α = 116.613(5)°, β = 94.225(5)°, γ = 90.319(5)°, V = 1905.64(10) ų, Z = 2, D_c = 1.51 g cm⁻³, μ = 4.223 mm⁻¹, 8749 data with I > 3σ(I), R = 0.043, Rw = 0.067. CCDC 228260. See http://www.rsc.org/suppdata/nj/b4/b402213k/ for crystallographic data in .cif or other electronic format.

Conclusions

Although the complete prediction of crystal structures is currently out of reach,^13,30 nevertheless, based on intuitive knowledge acquired by chemists, the design of molecular networks in the crystalline phase with some degree of precision may be attempted by the molecular tectonics strategy. This approach, empirical in nature, may some time lead to the generation of molecular networks with predicted connectivity if the information governing the formation of the network which is based on molecular recognition events is accurately incorporated with the structure of tectons.

Beside the debate on whether molecular networks in the crystalline phase may or not be designed, once the crystal is obtained, it is pertinent to analyse the collected data using energy criteria. The energy based analysis of the reported crystal structure performed here using the PACHA algorithm gives a detailed description of the structure in terms of energetic contributions of different intermolecular interactions. Based on the hierarchy of interactions, the analysis permits a fine description of the structure in terms of networks formation. It is worth noting that the results derived from this type of analysis is of ab initio quality since no pre-acquired knowledge of what is an hydrogen bond, a π–π interaction, a coordination bond or a van der Waals interaction is required. It was also shown that in any cases the molecular approximation so widely used in ab initio methods is dramatically good and perfectly justified for this kind of network. Furthermore, the methodology described here is general and may be applied to any type of network or interaction in the solid state.

Acknowledgements

Thanks to A. Jouaiti and N. Kardouh for the synthesis of 1 and for making the crystal and to N. Kyritsakas for the structural analysis. The Université Louis Pasteur and the Ministry of Research and Technology are acknowledged for financial support.

References

1. J. D. Dunitz, Pure Appl. Chem., 1991, 63, 177.
2. J.-M. Lehn, Supramolecular Chemistry, Concepts and Perspectives, VCH, Weinheim, 1995.
3. S. Mann, Nature, 1993, 365, 499.
4. G. Brand, M. W. Hosseini, O. Félix, P. Schaeffer and R. Ruppert, in NATO ASI Series, ed. O. Kahn, Serie C, Kluwer, Dordrecht, 1995, 484, 129–142; M. W. Hosseini, in NATO ASI Series, ed. G. Tsoucaris, Serie C, Kluwer, Dordrecht, 1998, 519, 209–219; M. W. Hosseini, in NATO ASI Series, eds. D. Braga, F. Grepioni and G. Orpen, Series C, Kluwer, Dordrecht, Netherlands, 1999, 538, 181–208.
5. M. Simard, D. Su and J. D. Wuest, J. Am. Chem. Soc., 1991, 113, 4696.
6. M. W. Hosseini and A. De Cian, Chem. Commun., 1998, 727; J. Martz, E. Graf, A. De Cian and M. W. Hosseini, in Perspectives in Supramolecular Chemistry, ed. G. Desiraju, Wiley, 2003, 177–209.
7. M. C. Etter, Acc. Chem. Res., 1990, 23, 120; G. D. Desiraju, Crystal Engineering: The Design of Organic Solids, Elsevier, New York, 1989; G. M. Whitesides, J. P. Mathias and T. Seto, Science, 1991, 254, 1312; C. B. Aakeröy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397; S. Subramanian and M. J. Zaworotko, Coord. Chem. Rev., 1994, 137, 357; D. S. Lawrence, T. Jiang and M. Levett, Chem. Rev., 1995, 95, 2229; J. F. Stoddart and D. Philip, Angew. Chem., Int. Ed. Engl., 1996, 35, 1155; M. W. Hosseini, Coord. Chem. Rev., 2003, 240, 157.
8. S. R. Batten and R. Robson, Angew. Chem. Int. Ed., 1998, 37, 1460; A. J. Blake, N. R. Champness, P. Hubberstey, W.-S. Li, M. A. Withersby and M. Schröder, Coord. Chem. Rev., 1999, 183, 117; M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319; B. Moulton and M. J. Zaworotko, Chem. Rev., 2001, 101, 1629.
9. C. Kaes, M. W. Hosseini, C. E. F. Rickard, B. W. Skelton and A. White, Angew. Chem. Int. Ed., 1998, 37, 920; G. Mislin, E. Graf, M. W. Hosseini, A. De Cian, N. Kyritsakas and J. Fischer, Chem. Commun., 1998, 2545; M. Loï, M. W. Hosseini, A. Jouaiti, A. De Cian and J. Fischer, Eur. J. Inorg. Chem., 1999, 1981; M. Loï, E. Graf, M. W. Hosseini, A. De Cian and J. Fischer, Chem. Commun., 1999, 603; C. Klein, E. Graf, M. W. Hosseini, A. De Cian and J. Fischer, Chem. Commun., 2000, 239; H. Akdas, E. Graf, M. W. Hosseini, A. De Cian and J. McB. Harrowfield, Chem. Commun., 2000, 2219; A. Jouaiti, M. W. Hosseini and A. De Cian, Chem. Commun., 2000, 1863; B. Schmaltz, A. Jouaiti, M. W. Hosseini and A. De Cian, Chem. Commun., 2001, 1242; A. Jouaiti, V. Jullien, M. W. Hosseini, J.-M. Planeix and A. De Cian, Chem. Commun., 2001, 1114; C. Klein, E. Graf, M. W. Hosseini, A. De Cian and J. Fischer, New J. Chem., 2001, 25, 207; S. Ferlay, S. Koenig, M. W. Hosseini, J. Pansanel, A. De Cian and N. Kyritsakas, Chem. Commun., 2002, 218; B. Zimmer, M. Hutin, V. Bulach, M. W. Hosseini, A. De Cian and N. Kyritsakas, New. J. Chem., 2002, 26, 1532; A. Jouaiti, M. W. Hosseini and N. Kyritsakas, Eur. J. Inorg. Chem., 2002, 57; A. Jouaiti, M. W. Hosseini and N. Kyritsakas, Chem. Commun., 2002, 1898; B. Zimmer, V. Bulach, M. W. Hosseini, A. De Cian and N. Kyritsakas, Eur. J. Inorg. Chem., 2002, 3079; A. Jouaiti, M. W. Hosseini and N. Kyritsakas, Chem. Commun., 2003, 472; P. Grosshans, A. Jouaiti, M. W. Hosseini and N. Kyritsakas, New. J. Chem., 2003, 27, 793; P. Grosshans, A. Jouaiti, V. Bulach, J.-M. Planeix, M. W. Hosseini and J.-F. Nicoud, Chem. Commun., 2003, 1336.
10. P. Grosshans, A. Jouaiti, N. Kardouh, M. W. Hosseini and N. Kyritsakas, New J. Chem., 2003, 27, 1806.
11. D. M. Ciurtin, N. G. Pshirer, M. D. Smith, U. H. F. Bunz and H.-C. zur Loye, Chem. Mater., 2001, 13, 2743; Y.-B. Dong, M. D. Smith and H.-C. zur Loye, Inorg. Chem., 2000, 39, 4927; N. G. Pshirer, D. M. Ciurtin, M. D. Smith, U. H. F. Bunz and H.-C. zur Loye, Angew. Chem. Int. Ed., 2002, 41, 583; K. R. J. Thomas, J. T. Lin, Y.-Y. Lin, C. Tsai and S.-S. Sun, Organometallics, 2001, 20, 2262.
12. J. D. Dunitz and A. Gavezzotti, Acc. Chem. Res., 1999, 32, 677.
13. A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309; B. A. Grzybowski, A. V. Ishchenko, R. S. DeWitte, G. M. Whitesides and Eugene I. Shakhnovich, J. Phys. Chem. B, 2000, 104, 7293.
14. S. L. Price, A. J. Stone, J. Lucas, R. S. Rowland and A. E. Thornley, J. Am. Chem. Soc., 1994, 116, 4910.
15. M. Henry, Chem. Phys. Chem., 2002, 3, 561.
16. W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315.
17. R. P. Feynman, Phys. Rev., 1939, 56, 340.
18. R. G. Parr, R. A. Donnely, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801.
19. L. Komorowsky, Chem. Phys. Lett., 1987, 134, 526.
20. G. A. Jeffrey, An introduction to hydrogen bonding, Oxford University Press, New-York, 1997.
21. M. Henry, Chem. Phys. Chem., 2002, 3, 601.
22. J. M. Douillard and M. Henry, J. Colloid Interface Sci., 2003, 263, 554.
23. M. Henry, Solid State Sci., 2003, 5, 1201.
24. M. Henry, J. Cluster Sci., 2002, 13, 437; L. Beitone, J. Marrot, T. Loiseau, G. Ferey, M. Henry, C. Huguenard, A. Gansmuller and F. Taulelle, J. Am. Chem. Soc., 2003, 125, 1912; L. Beitone, C. Huguenard, A. Gansmuller, M. Henry, F. Taulelle, T. Loiseau and G. Ferey, J. Am. Chem. Soc., 2003, 125, 9102; A. Müller and M. Henry, C. R. Chim., 2003, 6, 1201; M. Henry, J. Cluster Sci., 2003, 14, 267; M. Henry, F. Taulelle, T. Loiseau, L. Beitone and G. Férey, Chem. Eur. J., 2004, 10, 1366.
25. A. Rammal, F. Brisach and M. Henry, J. Am. Chem. Soc., 2001, 123, 5612; K. Gigant, A. Rammal and M. Henry, J. Am. Chem. Soc., 2001, 123, 11 632; M. Henry, in Handbook of organic-inorganic hybrid materials and nanocomposites, ed. H. S. Nalwa, American Scientific Publishers, Stevenson Ranch, 2003, pp. 1–82.
26. M. Henry, WinPacha V2.5 software, 1993–2004, http://www-chimie.u-strasbg.fr/∼lcmes/chimist (click on link Pacha). A tutorial (French only!) is also available (Windows only!) as well as a very limited help file in English. Further help may obtained by sending an e-mail to henry@chimie.u-strasbg.fr.
27. A. Gavezotti, J. Am. Chem. Soc., 1983, 105, 5220.
28. A. Bondi, J. Phys. Chem., 1964, 68, 441.
29. T. Loiseau, C. Serre, C. Huguenard, G. Finkh, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem. Eur. J., 2004, 10, 1373.
30. J. D. Dunitz, Chem. Commun., 2003, 545.
31. OpenMolenN, Interactive Structure Solution, Nonius B. V., Delft, The Netherlands, 1997.

---

Footnotes

† Dedicated to the memory of J.-M. Kern.

‡ CCDC 228260. See http://www.rsc.org/suppdata/nj/b4/b402213k/ for crystallographic data in .cif or other electronic format.

---