Scaled polar surface area descriptors: development and application to three sets of partition coefficients†
Robert A. Saunders and James A. Platts*
Department of Chemistry, Cardiff University, P.O Box 912, Cardiff CF10 3TB, UK. E-mail: platts@cf.ac.uk; Fax: +44 (0)29 2087 4030; Tel: +44 (0)29 2087 4950
First published on 31st October 2003
Abstract
Modifications to the standard definition of polar surface area (PSA) are reported and tested against the octanol–water, chloroform–water and cyclohexane–water partition coefficients of 110 organic and drug-like molecules. It is shown that increasing the flexibility of PSA-based models can lead to some improvements in accuracy, but that these still fall well short of previously published methods. To compete with such methods, PSA-based descriptors must be scaled according to the known hydrogen bonding characteristics of common functional groups. Introducing this scaling markedly improves accuracy, with predictive errors typically around one-half of a log P unit, confirmed by splitting the data into training and test sets. All models developed follow known characteristics of the partition coefficients considered and are statistically and chemically valid.
Introduction
The ability to predict a priori the solvation properties of molecules, especially drugs and other bio-active molecules, has led to a great deal of research activity,1 especially within the pharmaceutical and agrochemical industries. Prediction of a molecule's solvation properties at the beginning of the product design process allows early identification and removal of candidate molecules with unsuitable characteristics. This is particularly important with the growing popularity of high throughput screening and combinatorial methods where libraries of thousands of compounds are used.Perhaps the most popular approach to this has been to estimate the solvation property directly, for example as the sum of atom or fragment contributions. Unfortunately, this method has been limited to those solvation properties where sufficient data are available to assign the necessary fragment contributions, such as the octanol–water partition log Poct,2 the aqueous solubility log Sw,3 and solubility in polymers4 and supercritical CO2.5 Unfortunately, other properties of much interest, particularly those related to biological transport, remain inaccessible to such methods, since a minimum requirement is a data set numbering at least several hundred compounds.
An alternative is to relate the solvation property of interest to a set of fundamental molecular properties, or descriptors; this typically requires far fewer variables than the fragment approach and can hence be applied to smaller sets of data. A well-known example of this is Abraham's linear solvation energy relation (LSER) method,6,7 which reduces the property to a set of solute–solvent interactions, such as hydrogen bonding, polar and cavity effects. This approach has been successfully applied to an enormous range of chemical, biological and environmental solvation processes, such as octanol–water partition,8 the partitioning between air and the plant cuticular matrix9 and the blood-brain barrier partition.10
It is worth noting that the descriptors used in this method are carefully chosen to model specific interactions, such that just five descriptors have proved to be very general across a wide variety of solvents. An alternative approach is found in QSPR methods, which select an appropriate subset from larger pools of up to several hundred possible descriptors, choosing a new subset for each property of interest.11–13 In this way, one may find correlations that could otherwise have been missed, but can also forgo the clarity and interpretability of LSER-type models.
Molecular polar surface area (PSA) is a descriptor that has gained in popularity since its introduction in 1990.14 At its simplest, it is defined as the surface area of a molecule that arises from N, O, N–H and O–H atoms and is simply calculated from the 3D molecular structure. PSA has been used, either alone or in combination with other descriptors such as log Poct, to model a wide range of biological properties such as blood-brain distribution,15,16 intestinal absorption17–19 and oral bio-availability.20
The results of these studies have revealed much about the role of PSA, and hence of H-bonding and polarity, within biological systems. For instance, Palm et al.’s study21 of intestinal absorption revealed that molecules with a PSA ≤ 60 Å will exhibit high and almost complete intestinal absorbance, while molecules with a PSA ≥ 140 Å exhibit poor intestinal absorbance. An important result for the present study is that the PSA calculated from a single minimum energy conformation makes an equally good descriptor for intestinal absorption as that averaged over all accessible conformations.21
Other descriptors based on molecular surface areas have been proposed. Amidon et al.22 developed a new set of descriptors by splitting the total surface area into functional group and hydrocarbon surface areas, which were then used to successfully predict aqueous solubility. Winiwarter et al.23 used molecular surface areas scaled by partial atomic charges in their studies of human intestinal permeability. Stenberg et al.24 deconvoluted PSA and molecular surface area into seperate descriptors to create a model of intestinal absorbance of drugs. This model, denoted the partitioned total surface area (PTSA), was a marked improvement over traditonal PSA methods, giving results comparable to those obtained from more computationally demanding methods such as quantum mechanical calculations.
Despite many successes, the use of PSA is not without problems. Chief amongst these, as noted by Clark,17 is that the simple definition of PSA takes no account of the relative polarity or interaction strength of the atoms or groups that contribute. For instance, it has been shown25 that the hydrogen bond donor strength of N–H groups can vary by an order of magnitude (for instance, on Abraham's free energy scale from zero to one, dimethylamine is found at 0.08, while tetrazole is at 0.79). Another difficulty in using PSA is that it reduces the various ways a molecule can interact with its surroundings (i.e., hydrogen bonding, electrostatic, inductive/dispersive effects) to a single descriptor, whereas it is well-established4,8,9 that such interactions can have very different effects in different solvation environments. This can be accounted for by inclusion of such properties as log Poct, but this can raise further problems associated with errors or the outright failure of methods such as ClogP.
In this paper, we aim to set out ways in which these problems might be avoided by developing new descriptors based around the original definition of PSA. The principal method we use is the assignment of scaling factors to the surface areas of atoms contributing to PSA according to their known hydrogen bonding characteristics. We also investigate whether there is any advantage in splitting PSA into its component H-bond acid and base surface areas, which should give greater flexibility to describe solvation. In addition, the surface areas of other groups known to contribute to intermolecular interactions (e.g. halogens, aromatics) are explored as possible descriptors. Throughout, partition coefficients between water and three different solvents are used to test these descriptors.
Computational methods
A data set of 110 molecules with experimentally determined values of the water–octanol, water–chloroform and water–cyclohexane partition coefficients (denoted log Poct, log Pchl and log Pcyc throughout) was compiled. The data was collated from two sources, namely Zissimos et al.'s recent LSER study of partition coefficients26 and the MedChem02 database27 (see Table 1). The molecules fall into two broad classes, being either simple organic molecules or more complex ‘drug-like’ molecules.| Name | log Poct | log Pchl | log Pcyc | Name | log Poct | log Pchl | log Pcyc |
|---|---|---|---|---|---|---|---|
| 1-Butanol | 0.84 | 0.42 | −0.87 | Butanone | 0.29 | 1.15 | −0.25 |
| 1-Heptanol | 2.72 | 2.41 | 1.12 | Butyl acetate | 1.82 | 3.05 | 1.75 |
| 1-Hexanol | 2.03 | 1.69 | 0.45 | Butylamine | 0.97 | 0.78 | −0.29 |
| 1-Naphthol | 2.84 | 1.50 | 0.58 | Chlorobenzene | 2.89 | 3.37 | 3.13 |
| 1-Naphthylamine | 2.25 | 2.60 | 1.26 | Chlorpromazine | 5.40 | 6.21 | 5.24 |
| 1-Pentanol | 1.56 | 1.05 | −0.26 | Deprenyl | 2.90 | 4.29 | 2.81 |
| 1-Propanol | 0.25 | −0.30 | −1.49 | Desipramine | 4.21 | 5.33 | 3.38 |
| 2,4-Dimethylphenol | 2.30 | 1.50 | 0.59 | Diclofenac | 4.51 | 2.97 | 1.88 |
| 2,5-Dimethylphenol | 2.33 | 1.59 | 0.57 | Diethyl ether | 0.89 | 1.88 | 0.93 |
| 2-Bromophenol | 2.33 | 1.64 | 1.16 | Diethylamine | 0.58 | 0.76 | −0.34 |
| 2-Butanol | 0.76 | 0.30 | −0.96 | Ephedrine | 1.13 | 1.10 | −0.44 |
| 2-Chlorophenol | 2.15 | 1.36 | 0.87 | Ethanol | −0.31 | −0.87 | −1.89 |
| 2-Fluorophenol | 1.71 | 0.57 | −0.30 | Ethyl acetate | 0.73 | 1.82 | 0.34 |
| 2-Hydroxybenzaldehyde | 1.81 | 2.43 | 1.37 | Ethylamine | −0.13 | −0.35 | −1.80 |
| 2-Hydroxybenzoic acid | 2.26 | 0.58 | −0.46 | Fluoxetine | 3.75 | 5.48 | 3.62 |
| 2-Iodophenol | 2.65 | 1.97 | 1.26 | Ibuprofen | 3.97 | 3.03 | 1.88 |
| 2-Methoxyphenol | 1.32 | 1.70 | 0.47 | Imidazole | −0.08 | −0.83 | −3.70 |
| 2-Methylphenol | 1.98 | 1.23 | −0.04 | Indole | 2.14 | 2.95 | 0.79 |
| 2-Methylpyridine | 1.11 | 1.79 | 0.23 | Iodobenzene | 3.25 | 3.70 | 3.54 |
| 2-Naphthol | 2.70 | 1.74 | 0.29 | Isoquinoline | 2.08 | 3.07 | 1.11 |
| 2-Nitroaniline | 1.85 | 1.83 | 0.36 | Lidocaine | 2.44 | 4.08 | 1.23 |
| 2-Nitrophenol | 1.85 | 2.53 | 1.45 | Methanol | −0.77 | −1.33 | −2.49 |
| 3,5-Dimethylphenol | 2.35 | 1.60 | 0.38 | Methyl acetate | 0.18 | 1.16 | −0.19 |
| 3-Chlorophenol | 2.50 | 1.02 | −0.12 | Methyl benzoate | 2.12 | 3.01 | 2.08 |
| 3-Ethylphenol | 2.50 | 1.41 | 0.36 | Methyl hexanoate | 2.42 | 3.48 | 2.39 |
| 3-Methylphenol | 1.98 | 0.89 | −0.34 | Methyl pentanoate | 1.87 | 3.01 | 1.81 |
| 3-Methylpyridine | 1.20 | 1.89 | 0.27 | Methyl propanoate | 0.76 | 1.87 | 0.57 |
| 3-Nitroaniline | 1.37 | 1.60 | −0.42 | Miconazole | 5.34 | 5.42 | 4.69 |
| 3-Nitrophenol | 2.00 | 0.50 | −0.51 | Naphthalene | 3.30 | 4.18 | 3.50 |
| 4-Bromophenol | 2.59 | 1.07 | −0.09 | Nicotine | 1.17 | 1.89 | 0.36 |
| 4-Chlorophenol | 2.39 | 1.07 | −0.35 | Nitrobenzene | 1.85 | 2.93 | 1.69 |
| 4-Ethylphenol | 2.47 | 1.47 | 0.37 | Nitromethane | −0.35 | 0.44 | −0.93 |
| 4-Hydroxyacetophenone | 1.45 | 0.08 | −2.16 | Nitropropane | 0.87 | 1.91 | 0.53 |
| 4-Hydroxybenzoic acid | 1.58 | −2.00 | −1.77 | o-Toluidine | 1.32 | 1.96 | 0.61 |
| 4-Iodophenol | 2.91 | 1.56 | 0.57 | Papaverine | 2.95 | 4.28 | 2.56 |
| 4-Methylphenol | 1.97 | 1.06 | −0.35 | Pentanoic acid | 1.39 | 0.32 | −1.10 |
| 4-Methylpyridine | 1.22 | 1.77 | 0.21 | Phenol | 1.47 | 0.32 | −0.93 |
| 4-Nitroaniline | 1.39 | 1.26 | −1.00 | Phenylacetic acid | 1.00 | 0.57 | −1.23 |
| 4-Nitrophenol | 1.91 | 0.20 | −2.05 | Procaine | 2.14 | 2.13 | −0.13 |
| Acetamide | −1.09 | −2.00 | −4.88 | Propanone | −0.24 | 0.50 | −0.96 |
| Acetanilide | 1.16 | 0.78 | −1.51 | Propranolol | 3.48 | 1.03 | −0.64 |
| Acetic acid | −0.17 | −1.60 | −3.05 | Propylamine | 0.47 | 0.25 | −0.98 |
| Acetonitrile | −0.34 | 0.40 | −1.46 | p-Toluidine | 1.39 | 1.95 | 0.56 |
| Acetophenone | 1.58 | 2.78 | 1.27 | Pyridine | 0.65 | 1.29 | −0.31 |
| Aniline | 0.90 | 1.35 | 0.05 | Pyrrole | 0.75 | 0.91 | −0.36 |
| Aspirin | 0.90 | 0.63 | −2.00 | Quinine | 3.47 | 2.29 | 0.04 |
| Atropine | 1.83 | 2.44 | −1.02 | Resorcinol | 0.80 | −1.34 | −3.79 |
| Benzaldehyde | 1.47 | 2.25 | 1.13 | t-Butanol | 0.35 | −0.04 | −1.15 |
| Benzamide | 0.64 | 0.11 | −1.92 | Tetracaine | 3.51 | 2.90 | 2.05 |
| Benzene | 2.13 | 2.76 | 2.35 | Toluene | 2.73 | 3.41 | 2.99 |
| Benzoic acid | 1.87 | 0.60 | −0.85 | Triethyl phosphate | 0.80 | 2.28 | −0.14 |
| Benzonitrile | 1.56 | 2.71 | 1.11 | Triethylamine | 1.44 | 1.86 | 1.10 |
| Benzylamine | 1.09 | 1.18 | −0.12 | Trimethyl phosphate | −0.52 | 0.76 | −2.22 |
| Biphenyl | 4.01 | 4.67 | 4.16 | Tripropyl phosphate | 1.87 | 3.67 | 1.18 |
| Butanoic acid | 0.79 | −0.27 | −1.76 | Tryptamine | 2.15 | 1.53 | −0.60 |
The solvent systems used were chosen as they cover a range of interaction types: both octanol and water are H-bond acids and bases, albeit of different strengths, while chloroform is an acid but not a base, and cyclohexane is neither. Further, they form three-quarters of the ‘critical quartet’ of partitions proposed by Leahy et al.,28 designed to encode all important interactions for solvation (insufficient data were available for the final solvent of the quartet, propylene glycol dipelargonate, to be included here). This is therefore a stringent test of descriptors and models. Molecules were chosen to represent a range of both chemical and numerical diversity, with maximum and minimum values for log Poct of 5.40 and −1.09, for log Pchl of 6.21 and −2.00, and for log Pcyc of 5.24 and −4.88.
Initial 3D molecular structures were generated using CORINA,29 and were subsequently optimised using AM1, as implemented in HyperChem 6,30 with an optimisation criterion of <0.01 kcal Å−1 mol−1. No further conformational freedom was explored in this work, following the conclusions of Palm et al.21 All surface area properties were calculated from this AM1 geometry using a locally modified version of the Fortran77 program MOLVOL of Dodd and Theorodou.31 The program was modified to read MDL's MOL file format and automatically assign the atomic radii recommended by Clark.17 This program was used without any further modification to calculate molecular total and polar surface areas (TSA and PSA, respectively) and to summarise the surface areas of H-bond acid and base groups (ASA and BSA) (See ESI† Table S3 for a full set of calculated descriptors).
The connectivity defined in the MOL file was then used to define a total of 46 simple functional groups with known H-bonding characteristics: these are defined in Table 2. These functional groups were assigned scaling factors according to their position on Abraham's ΣαH2 and ΣβH2 scales,6 which experimentally define H-bond donor and acceptor strengths, respectively. This scale was chosen as the values reflect the hydrogen bonding properties of many functional groups as determined by many years of careful experiment. PSA, ASA and BSA were modified simply by multiplying the exposed surface area of each atom by the relevant scaling factor from Table 2. Throughout this work, total surface area (TSA) is used without modification.
| Description | Scaling factor | Description | Scaling factor |
|---|---|---|---|
| N bases | Other bases | ||
| 1y amine | 0.60 | Thiol, sulfide | 0.30 |
| 2y amine | 1.20 | Phosphine, phosphate | 0.55 |
| 3y amine | 3.00 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond C double bond | 0.06 |
| Amide | 0.25 | C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C triple bond C triple bond | 0.13 |
| Aniline | 0.40 | ||
| Cyano | 0.37 | N–H acids | |
| Nitro | 0.00 | Amine | 0.08 |
| Pyridine | 0.52 | Aniline | 0.12 |
| Pyrrole | 0.21 | Pyrrole | 0.21 |
| Sulfonamide | 0.08 | Amide | 0.25 |
| O bases | Anilide | 0.50 | |
| Carbonyl | 0.45 | Sulfonamide | 0.45 |
| Alcohol | 0.48 | Thioamide | 0.50 |
| Phenol | 0.36 | ||
| Ether | 0.55 | O–H acids | |
| Acid, ester –O– | 0.00 | Alcohol | 0.38 |
| Furan | 0.15 | Phenol | 0.54 |
| Nitro | 0.15 | Carboxylic acid | 0.60 |
Sulfoxide S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.93 | ||
Sulfonamide S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.36 | Other acids | |
Sulfone S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.36 | Alkyne | 0.09 |
Phosphate P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.55 | ||
| Intramolecular Bases | Intramolecular acids | ||
O in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ortho-substituted to phenol O ortho-substituted to phenol | 0.25 | Phenol ortho to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.05 |
O in N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ortho-substituted to phenol O ortho-substituted to phenol | 0.05 | Phenol ortho to N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.05 |
| O ortho-substituted to phenol | 0.20 | Phenol ortho to O | 0.25 |
| O ortho-substituted to aniline | 0.10 | Aniline ortho to O | 0.20 |
O in N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ortho-substituted to aniline O ortho-substituted to aniline | 0.05 | Aniline ortho to N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O | 0.10 |
To test the quality of the modified PSA models, comparisons were made against models derived from Abraham's LSER descriptors, as calculated by the recently published group contribution approach.32 All models, whether based on PSA or LSER, were found with multivariate linear regression analysis (MLRA) using JMP Discovery software.33 Statistics used were: R2, the fraction of variance explained by the model; RMS, the root mean square error in the model; F, Fischer's test of significance and R2CV, the cross-validated R2 found via the leave-one-out method. The significance of descriptors was measured by their t-ratios, with the 95% significance criteria applied.
Results and discussion
Table 3 contains the results of our initial attempts to model partition coefficients using PSA-type descriptors. Single parameter fits, using TSA, PSA, etc., are very poor indeed, with typical R2 values of 0.05–0.15, and hence are not considered further. The simplest model in Table 3, employing just total and unscaled polar surface areas, is clearly unsatisfactory for all three solvents, typically accounting for only 50–60% of the variance in the data and giving RMS errors almost twice those from LSER models. Thus, it seems that simple PSA-type descriptors are incapable of forming accurate models of these partition processes. The ‘completeness’ of the dataset, at least in terms of physical properties spanned, is confirmed by the fact that the LSER model of log Poct is not significantly different from that recently published for 8200 compounds in the log P* list of the MedChem97 database.34| Model | log Poct | log Pchl | log Pcyc | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMS | F | R2 | RMS | F | R2 | RMS | F | |
| a Calculated in the manner of ref. 33 | |||||||||
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSA PSA | 0.577 | 0.792 | 75.7 | 0.614 | 0.941 | 88.1 | 0.542 | 1.160 | 65.7 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ASA ASA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSA BSA | 0.578 | 0.794 | 50.2 | 0.714 | 0.836 | 88.2 | 0.618 | 1.065 | 59.2 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSA PSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HalSA HalSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BenSA BenSA | 0.750 | 0.613 | 82.0 | 0.642 | 0.940 | 47.1 | 0.583 | 1.117 | 38.1 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ASA ASA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSA BSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HalSA HalSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BenSA BenSA | 0.751 | 0.616 | 65.1 | 0.758 | 0.776 | 65.1 | 0.675 | 0.991 | 44.9 |
| LSERa | 0.906 | 0.378 | 208.1 | 0.874 | 0.544 | 150.4 | 0.854 | 0.663 | 126.9 |
Breaking down PSA into acid and base surface areas yields slightly improved statistics in two cases, log Pchl and log Pcyc, but no significant change for log Poct. Closer inspection reveals that PSA is dominated by H-bond base atoms (PSA and BSA are correlated with R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.99) such that PSA and BSA are effectively interchangeable. It is well-known7 that log Poct has no dependence on H-bond acidity, so either descriptor can be used equally well here and ASA is not significant in the model. On the other hand, both log Pchl and log Pcyc are strongly affected by H-bond acidity, since water is a stronger H-bond base than either solvent, such that the extra flexibility afforded by this model is significant.
0.99) such that PSA and BSA are effectively interchangeable. It is well-known7 that log Poct has no dependence on H-bond acidity, so either descriptor can be used equally well here and ASA is not significant in the model. On the other hand, both log Pchl and log Pcyc are strongly affected by H-bond acidity, since water is a stronger H-bond base than either solvent, such that the extra flexibility afforded by this model is significant.
Table 3 demonstrates that including the surface areas of halogen atoms and aromatic carbons (HalSA and BenSA) improves the quality of fit substantially, due mainly to the ability of the two descriptors to encode important polar and polarisability properties of a molecule that are neglected by PSA-type descriptors. In each case, the most flexible model explains around 15% more of the data than models produced using only TSA and PSA, which highlights the importance of polarity/polarisability as well as size and H-bonding. Once again, decomposing PSA gives no improvement for log Poct, but results in markedly better statistics for the other two solvents. These results demonstrate that it is possible to improve upon ‘standard’ PSA simply by summing the surface areas of different atom types, rather than just those expected to be involved in hydrogen bonding.
Despite these improvements, it is still evident that the models do not take into account all the factors that determine partition coefficients, since even the best results are 12–15% less accurate than the equivalent LSER models. Our postulate is that this difference arises out of the simple definition of PSA and related descriptors, wherein the relative H-bonding abilities of the N, O, N–H and O–H atoms are effectively ignored.
The values shown in Table 2 reflect the hydrogen bonding properties of functional groups as determined by many years of careful experiment. As such, there are some useful insights into why the simple definition of PSA is insufficient for our purposes. As well as the above example of N–H groups varying in acidity, it is also evident that O–H groups are generally stronger acids than are N–H groups. Nitrogen bases are usually stronger than their oxygen counterparts; other atoms such as sulfur can also act as bases. Even within these broad groupings substantial variation exists; for example, the weak basicity of amide N’s compared to their amine analogues, or the weakness of sp3 O in esters compared to ethers. Intramolecular H-bonding, which ‘ties-up’ both acid and base atoms, also has a large effect. In the current study, we have defined this simply as a H-bond donor sited ortho to an acceptor on an aromatic ring. Work is ongoing to identify important classes of intramolecular H-bonds and their effects on ΣαH2 or ΣβH2.35 The scaling factors also take into consideration that certain functional group have relatively large hydrogen bonding acid and base properties but small surface areas. For example, tertiary amines are known to have a higher ΣβH2 than primary amines, yet the exposed surface area of N in a tertiary amine is approximately 15 Å2 smaller than that of the N in a primary amine.
Applying these weights to the calculation of PSA, ASA, and BSA results in remarkable improvements in modelling all three partitions, as reported in Table 4. Considering log Poct first, Table 4 shows that even the simplest model, employing just molecular size and scaled PSA, is a great improvement over the unscaled equivalent, explaining 17% more of the variance in log Poct and reducing the RMS error by 0.18 log units. The form of this model is also encouraging, showing that molecular size increases log Poct while polarity/H-bonding reduces it. Increasing the flexibility of the model by breaking down scaled PSA into its component parts yields an improvement of around 0.03 in R2, unlike in the unscaled models above. Adding in the halogen and aromatic surface areas improves statistics still further, such that the final 5-parameter model has R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.85 and RMS
0.85 and RMS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.48 for log Poct, improvements of 0.28 and 0.31 over the original model. To highlight this improvement, Fig. 1 shows observed vs. calculated values of log Poct for both original and final models, along with the analogous comparisons for log Pchl and log Pcyc.
0.48 for log Poct, improvements of 0.28 and 0.31 over the original model. To highlight this improvement, Fig. 1 shows observed vs. calculated values of log Poct for both original and final models, along with the analogous comparisons for log Pchl and log Pcyc.
 | ||
Fig. 1 Observed vs. calculated values of log Poct, log Pchl and log Pcyc, using TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSA (in a, c, e) and full scaling (in b, d, f). PSA (in a, c, e) and full scaling (in b, d, f). | ||
| Model | log Poct | log Pchl | log Pcyc | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMS | F | R2 | RMS | F | R2 | RMS | F | |
| a Calculated in the manner of ref. 33 | |||||||||
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSA PSA | 0.750 | 0.610 | 163.6 | 0.749 | 0.744 | 159.6 | 0.750 | 0.875 | 160.6 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ASA ASA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSA BSA | 0.784 | 0.570 | 128.9 | 0.899 | 0.495 | 316.5 | 0.857 | 0.665 | 211.5 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PSA PSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HalSA HalSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BenSA BenSA | 0.833 | 0.505 | 131.7 | 0.753 | 0.780 | 79.8 | 0.751 | 0.880 | 79.1 |
TSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ASA ASA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BSA BSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HalSA HalSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BenSA BenSA | 0.847 | 0.480 | 115.7 | 0.909 | 0.474 | 208.9 | 0.867 | 0.649 | 134.9 |
| LSERa | 0.906 | 0.378 | 208.1 | 0.874 | 0.544 | 150.4 | 0.854 | 0.663 | 126.9 |
Fig. 2 shows how the surface of 3-chloropenol is partitioned by our descriptors. Values for each descriptor are given, along with the residuals for each solvent system. It is clear that PSA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TSA cannot account for the solvation properties of even this simple molecule and that while extra flexibility improves prediction a little, scaling is required for accurate results.
TSA cannot account for the solvation properties of even this simple molecule and that while extra flexibility improves prediction a little, scaling is required for accurate results.
 | ||
| Fig. 2 Descriptors calculated for 3-chlorophenol: (a) traditional PSA, (b) unscaled and (c) scaled equations. | ||
Table 4 also shows that our best surface area model is not as accurate as the LSER model and therefore not as accurate as many of the dedicated algorithms for calculation of log Poct, such as ClogP. However, we emphasise that our purpose here is not to generate yet another log Poct calculator, but to use this and other water–solvent partition data as a test of PSA and related descriptors. In this context, the accuracy attained and improvements made here are, we believe, sufficient to justify the modifications made.
A similar pattern of improvements is obtained for log Pchl, though here the improvement in statistics due to scaling PSA is even greater: the simplest scaled model is slightly better than unscaled ones in Table 3, with R2 increased by 0.13 and RMS reduced by 0.20 log units. In this case splitting up PSA gives substantially better accuracy, but including more descriptors is barely significant [see the Electronic supplementary information (ESI) Table S1]. Nonetheless, the 5-parameter model is the most accurate found in this study and is actually better than the LSER model, with almost 90% of variance explained and an RMS error of just 6% of the total spread of data.
The final partition coefficient, log Pcyc, is probably the most difficult to model of the three, since the two solvents are possibly the most dissimilar imaginable; log Pcyc hence covers the largest range of values (over 10 log units) considered here. This is reflected in Table 3, in which the statistics for log Pcyc are the poorest. It is encouraging, therefore, that the results in Table 4 represent a substantial increase in accuracy; here, the scaled 2-parameter model is 0.19 better in R2 and 0.29 log units better in RMS error. As with log Pchl, splitting up PSA improves results still further but inclusion of HalSA and BenSA is less useful, and again the 5-parameter surface area model is slightly more accurate than its LSER equivalent. In contrast with log Poct, very few methods for the rapid prediction of these, or indeed many other partition coefficients directly from structure, have been reported and the results in Table 4 indicate that these models are among the most accurate yet developed.
Details of the models (shown in ESI Table S1) reveal that size (TSA) is generally the most important term, followed closely by base and acid surface areas. The largest cross-correlation between descriptors is just R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.47 for this data set, such that MLRA is appropriate and direct interpretation of coefficients is meaningful. The models broadly follow expected trends, with the size term always increasing log P and H-bonding decreasing it. Further, ASA is less significant for log Poct than the other partitions due to the similar basicity of water and n-octanol. Halogen and benzene surface areas play a lesser role, typically acting to increase log P, although perhaps surprisingly HalSA is not statistically significant in a model of log Pchl. Thus, not only are the models developed statistically valid, but they also reflect known physicochemical properties of the solvent systems.
0.47 for this data set, such that MLRA is appropriate and direct interpretation of coefficients is meaningful. The models broadly follow expected trends, with the size term always increasing log P and H-bonding decreasing it. Further, ASA is less significant for log Poct than the other partitions due to the similar basicity of water and n-octanol. Halogen and benzene surface areas play a lesser role, typically acting to increase log P, although perhaps surprisingly HalSA is not statistically significant in a model of log Pchl. Thus, not only are the models developed statistically valid, but they also reflect known physicochemical properties of the solvent systems.
R2CV values of 0.806, 0.88, and 0.82, respectively, indicate that the models reported here are capable of making reliable predictions. However, a more realistic test of predictive ability lies in the construction of training and test sets. Five randomly selected test sets of 22 data points (20% of the full data set) were removed from the data set, then models were built on the remaining data and used to predict log P for the omitted molecules (RMS errors and R2 values for these test sets are shown in ESI Table S2). Considerable variation is found, but when averaged over all test sets the accuracy is comparable to that for the complete data set. We therefore have some confidence in the predictive power of our models.
Fig. 1 graphically demonstrates the improvements made by scaling PSA-type descriptors, but also reveals that each regression contains several compounds that are rather poorly treated. It is instructive to examine these in more detail: a breakdown of compounds giving large errors for more than one solvent is presented in Table 5. Only two molecules give consistently large errors for all three log P values, namely chlorpromazine and miconazole. The constant under estimation of chlorpromazine is likely to be due to a combination of resonance and ortho effects around an aromatic ring, which are probably not well represented in our simple scaling factors.
| Compound | Residual log Poct | Residual log Pchl | Residual log Pcyc |
|---|---|---|---|
| Chlorpromazine | 1.57 | 1.60 | 2.53 |
| Miconazole | −1.02 | −1.29 | −1.58 |
| Propranolol | 0.18 | −1.77 | −1.36 |
| Quinine | 1.42 | 0.58 | 1.32 |
The error in miconazole is due largely to miconazole having a HalSA of more than double that of any other molecule in the data set. This large value of HalSA is beyond the limits of the models generated from the data sets. Creation of a model using only the descriptors TSA, ASA, BSA and BenSA showed a marked improvement in the residuals of miconazole for log Poctand log Pcyc.
Propranolol shows errors for log Pchl and log Pcyc but not for log Poct, suggesting problems with ASA. Propranolol contains several possible intramolecular H-bonds, proper description of which is beyond the simple definition used here. Thus far, we have been unable to come up with a general definition that includes molecules with intramolecular H-bonds but excludes those without—again, work is ongoing in this area. Finally, quinine is poorly predicted for log Poct and log Pcyc, but is surprisingly well predicted for log Pchl. The reasons for this are unclear, but we note that atropine may also contain an intramolecular H-bond.
As well as these troublesome molecules, it is interesting to consider those molecules that are better predicted with scaled descriptors than with unscaled. Several individual classes of molecules are identifiable here, for example those containing several unusually strong (or weak) H-bond donors or acceptors. Resorcinol, or 3-hydroxyphenol, is a case in point, as the increase in scaling of ASA for phenols reduces the average error from −1.425 to −0.03. Other examples of this include imidazole (−0.8 cf.−1.54), nicotine (−0.19 cf.–1.29) and 4-hydroxy acetophenone (–0.24 cf.–1.09). Tryptamine, on the other hand, contains relatively weak pyrrole and amine H-bond donors; scaling down the contribution of these improves the average error from 0.70 to 0.45 due to better prediction of log Pchl.
Another class of molecule showing markedly better prediction are those containing NO2 groups, which have a large exposed polar surface area but are known to be poor H-bond acceptors.23 Scaling down their contribution to PSA gives smaller errors for nitropropane (−0.1 cf. 0.98), nitrobenzene (0.22 cf. 1.04) and 3-nitroaniline (0.08 cf. 1.16). The related molecules 2-nitroaniline (0.22 cf. 1.48) and 2-nitrophenol (0.47 cf. 1.18) should also benefit from this scaling, but the intramolecular H-bond term also contributes, as evidenced by the improvements in 2-hydroxybenzaldehyde (0.13 cf. 0.55).
It has been suggested that PSA can be estimated with some confidence from 2D group contributions, that is by summation of a set of pre-defined fragments with associated surface areas.36 This prompted us to look in more detail at the surface areas calculated for the molecules currently under consideration. We find that many fragments do indeed have fairly constant surface areas, such as the polar hydrogens in carboxylic acids, pyrroles and amines, and that a 2D method could predict surface area for these atoms. However, other fragments show greater variation in surface area; for example, the ether oxygen in miconazole has a surface area of 2.73 Å2 while that in quinine has one of 11.31 Å2. Carbonyls are another example: of the 27 occurrences of carbonyls within the data set, values range from 15.46 to 22.43 Å2, for atropine and diclofenac, respectively (see Fig. 3). Phenols provide further evidence that true 3D information is encoded within PSA descriptors: the surface area of the phenolic hydrogen is calculated to be 4.08 Å2 for phenol itself, 3.00 Å2 for 2-methylphenol, 2.61 Å2 2-iodophenol but increases to 4.10 Å2 for 4-iodophenol.
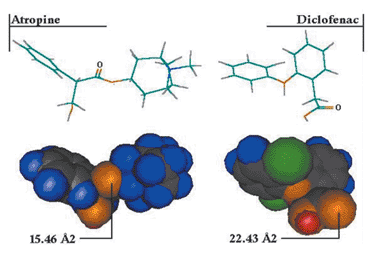 | ||
| Fig. 3 Variation in the carbonyl surface area for atropine and diclofenac. | ||
Conclusions
We have set out a variety of models of the water–octanol, water–chloroform and water–cyclohexane partition coefficients of over 100 organic and drug molecules. These show that simple polar surface area and related molecular properties are unable to properly describe solvation, with only 50 to 60% of total variance accounted for. Stepwise introduction of flexibility into such models gives rise to small increases in accuracy, but even the best of these falls short of Abraham's LSER results. Satisfactory models can only be developed if polar surface area descriptors are scaled, or weighted, according to the known hydrogen bonding properties of the atoms and groups involved. Assigning weights to 46 simple classes of hydrogen bond acids and bases gives a substantial increase in accuracy across the board, the best example of this being for log Pchl, which has R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.91 and and RMS error of 0.47 compared with the original values of 0.61 and 0.94. Given the promising results reported here, we hope now to extend our studies to biological systems that are of much current interest, such as blood-brain distribution, intestinal absorption and oral bio-availability.
0.91 and and RMS error of 0.47 compared with the original values of 0.61 and 0.94. Given the promising results reported here, we hope now to extend our studies to biological systems that are of much current interest, such as blood-brain distribution, intestinal absorption and oral bio-availability.Acknowledgements
The authors are grateful to EPSRC for support of this research under grant ref. GR/N20638.References
- S. D. Pickett, I. M. McLay and D. E. Clark, J. Chem. Inf. Comput. Sci., 2000, 40, 263 CrossRef CAS.
- P. Buchwald and N. Bodor, Curr. Med. Chem., 1998, 5, 353 Search PubMed.
- G. Klopman, S. Wang and D. M. Balthasar, J. Chem. Inf. Comput. Sci., 1992, 32, 474 CrossRef CAS.
- A. L. Baner, ACS Symp. Ser., 2000, 753, 37 CAS.
- R. Gerszt, F. L. P. Pessoa and M. F. Mendes, Braz. J. Chem. Eng., 2000, 17, 261 Search PubMed.
- M. H. Abraham, Chem. Soc. Rev., 1993, 22, 73 RSC.
- M. H. Abraham, H. S. Chadha, F. Martins, R. C. Mitchell, M. W. Bradbury and J. A Gratton, Pestic. Sci., 1999, 55, 78 Search PubMed.
- M. H. Abraham, H. S. Chadha, G. S. Whiting and R. C. Mitchell, J. Pharm. Sci., 1994, 83, 1085 CAS.
- J. A. Platts and M. H. Abraham, Environ. Sci. Technol., 2000, 34, 318 CrossRef CAS.
- J. A. Platts, M. H. Abraham, Y. H. Zhoa, A. Hersey, L. Ijaz and D. Butina, Eur. J. Med. Chem., 2001, 36, 719 CrossRef CAS.
- A. R. Katritzky, V. S. Lobanov and M. Karelson, Chem. Soc. Rev., 1995, 24, 279 RSC.
- P. D. T. Huibers, V. S. Lobanov, A. R. Katritzky, D. O. Shah and M. Karelson, Langmuir, 1993, 12, 1462 CrossRef.
- P. D. T. Huibers, V. S. Lobanov, A. R. Katritzky, D. O. Shah and M. Karelson, J. Colloid Interface Sci., 1997, 187, 113 CrossRef CAS.
- R. O. McCracken and K. B. Lipkowitz, J. Parasitol., 1990, 76, 180 Search PubMed.
- D. E. Clark, J. Pharm. Sci., 1999, 88, 815 CrossRef CAS.
- J. Kelder, P. D. J. Grootenhuis, D. M. Bayada, L. P. C. Delbressine and J. P. Ploemen, Pharm. Res., 1999, 16, 1514 CrossRef CAS.
- D. E. Clark, J. Pharm. Sci., 1999, 88, 807 CrossRef CAS.
- K. Palm, P. Stenburg, K. Luthman and P. Artursson, Pharm. Res., 1997, 14, 568 CrossRef CAS.
- H. van de Waterbeemd, G. Camenisch, G. Folkers and O. A. Raevsky, Quant. Struct.-Act.Relat., 1996, 15, 480 Search PubMed.
- D. F. Veber, S. R. Johnson, H. Cheng, B. R. Smith, K. W. Ward and K. D. Kopple, J. Med. Chem., 2002, 45, 2615 CrossRef CAS.
- K. Palm, K. Luthman, A. L. Ungell, G. Strandlund and P Artursson, J. Pharm. Sci., 1996, 85, 32 CrossRef CAS.
- G. L. Amidon, S. H. Yalkowsky, S. T. Anik and S. C. Valvani, J. Phys. Chem., 1975, 21, 2239 CrossRef.
- S. Winiwarter, F. Ax, H. Lennernas, A. Hallberg, C. Pettersson and A. Karlen, J. Mol. Graphics Modell., 2003, 21, 273 CrossRef CAS.
- P. Stenberg, U. Norinder, K. Luthman and P. Artursson, J. Med. Chem., 2001, 44, 1927 CrossRef CAS.
- M. H. Abraham, M. Berthelot, C. Laurence and P. J. Taylor, J. Chem. Soc., Perkin Trans. 2, 1998, 187 RSC.
- A. M. Zissimos, M. H. Abraham, M. C. Barker, K. J. Box and K. Y. J. Tam, Chem. Soc., Perkin Trans. 2, 2002, 470 Search PubMed.
- A. J. Leo, Masterfile 2002, MedChem software, Med. Chem. Biobyte Corp., Claremont, CA, 2002 Search PubMed.
- D. E. Leahy, J. J. Morris, P. J. Taylor and A. R. Wait, J. Chem. Soc., Perkin Trans. 2, 1992, 723 RSC.
- J. Gasteiger, J. Sadowski, J. Schuur, P. Selzer, L. Steinhauer and V. Steinhauer, J. Chem. Inf. Comput. Sci., 1996, 36, 1030 CrossRef CAS.
- HyperChem 6, Hypercube, Inc., 2000, Gainesville, FL Search PubMed.
- L. R. Dodd and D. N. Theodorou, Mol. Phys., 1991, 72, 1313 CAS.
- J. A. Platts, D. Butina, M. A. Abraham and A. Hersey, J. Chem. Inf. Comput. Sci., 1999, 39, 835 CrossRef CAS.
- JMP, SAS Software, 2000, Cary, NC Search PubMed.
- J. A. Platts, M. H. Abraham, D. Butina and A. Hersey, J. Chem. Inf. Comput. Sci., 2000, 40, 71 CrossRef CAS.
- F. T. T. Huque and J. A. Platts, Org. Biomol. Chem., 2003, 1, 1419 RSC.
- P. Ertl, B. Rohde and P. Selzer, J. Med. Chem., 2000, 43, 3714 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: tables giving the coefficients and t-ratios of the models, the statistics for the test sets and the full data set and descriptors employed. See http://www.rsc.org/suppdata/nj/b3/b307023a/ |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2004 |
