Microfluidic flow transducer based on the measurement of electrical admittance

Abstract

A new flow transducer for measuring the flow rate of a conducting fluid in a microchannel is reported. In this paper, the measure of flow of such fluid under laminar flow conditions based on the change of electrical admittance is established with the aid of a pair of electrodes parallel to the line of flow in a glass–PDMS microfluidic device. This flow sensor is simple in design and can be integrated to most of the microfluidic platforms. The effect of flow rate of the electrolyte, the frequency of the applied ac voltage, the voltage applied across the detector electrodes, and the conductivity of the electrolyte are varied to optimize for high sensitivity. The optimized values are then used to demonstrate the measurements of very low flow rates (<1 nL s⁻¹). This flow sensor can be extended towards the measurement of chemical and biochemical buffers and reagents.

---

Introduction

The development of multifunctional, high throughput lab-on-a-chip devices depends heavily on the ability to measure flow rate and perform quantitative analysis of fluids in minute volumes. Traditionally, there have been many MEMS-based (MEMS = microelectromechanical system) flow sensors for gaseous flows.¹ In recent times, there has been some advancement in measuring micro-flows of liquids. Examples of sensing principles explored in the measurement of microfluidic flow are heat transfer detection,^2–4 molecular sensing,⁵ atomic emission detection,⁶ streaming potential measurements,⁷ electrical impedance tomography,⁸ ion-selective field-effect transitors⁹ and periodic flapping motion detection.¹⁰ Flow sensors form the integral part of micrototal analysis systems¹¹ with multisensors. Conversely, a measure of electric current is used for pumping a measurable flow rate of fluids in electro-osmotic flow (EOF).¹²

Flow sensors based on sensing the temperature difference between two points in the microchannel^2–4 can sense very low flows. However, such flow sensors require a complicated design and the integration of the heater, temperature sensors and membrane shielding is difficult to implement. Moreover, the sensitivity and accuracy of the flow sensors depend on the environment associated in the heat transfer. Most other methods are not capable of measuring very low flow rates. We consider flow sensing by directly measuring the electrical admittance of the fluid using two surface electrodes.

In electrolytes flowing in a microchannel under laminar flow conditions, a parabolic velocity profile exists and so the ions in the middle of the channels travel faster than those near the walls. This results in the redistribution of ions within the electric double layer (EDL) formed in the channel.¹³ The ac voltage across the channel electrodes (Fig. 3) drives the ions back and forth across the electrodes. The ionic redistribution develops electrokinetic effects and contributes to change in electric admittance. Thus the flow of fluid is very sensitive to the admittance across microelectrodes^14,15 in the flow channels, and measuring the increase in admittance precisely accounts for the flow rate. Our flow sensor operating with optimized electric parameters can be efficient and accurate for precise values of flows. This method is relatively simple and suitable for most of the chemical and biochemical microfluidic applications since most of the reagents used are electrolytes. In this paper, we present such a flow sensor based on the measurement of electrical admittance.

Principle

In hydrodynamic conditions, forced convection dominates the transport of ions to the electrodes within the flow channels. When the width of the microfluidic channel is very small compared to the length of the channel, the lateral diffusion of the ions is significant under laminar flow. Under an ac electrical signal applied across the channel, the equivalent circuit¹⁶ of the microsystem is shown in Fig. 1. The electrical double layer¹⁷ formed across the channel is formed from two capacitances namely diffuse layer capacitance (C_s) and the outer Helmholtz plane capacitance (C_e). The former is due to ion excess or depletion in the channel, and the latter is due to the free electrons at the electrodes and is independent of the electrolyte concentration. The smaller of these capacitances dominates the admittance since these two capacitances are in series. The frequency of the applied ac voltage, flow rate and conductivity of the fluid are the factors affecting the admittance of the fluidic system and our flow sensing principle is based on the optimization of these parameters.

Fig. 1 The equivalent circuit for the channel and electrodes flow sensor cell. The solution in the channel offers a parallel resistive (R_s) and capacitive (C_s) impedance while the electrodes by themselves offer serial capacitive (C_e) impedance with the solution.

For an electrochemical oxidation of a species A to A⁺ in a microchannel, the convective–diffusive equation for mass transport under steady state conditions is given by eqn. (1):

where [A] is the concentration of the species, D_A is the diffusion coefficient and v_x is the velocity in the direction of flow. The first term is the lateral diffusion in the microchannel and the second term is the transport along the length of the channel. Under steady state flow conditions the boundary condition is given by eqn. (2). The solution of this equation predicts the mass transport limited current (i_L)¹⁸ as a function of flow rate, Q as given by eqn. (3):where n is the number of electrons transferred, F, the Faraday constant, x_e is the electrode length, h, the cell half-height, d, the width of the cell and w, the electrode width. It is to be noted that the current due to flow of electrolyte is directly proportional to the cube root of volume flow rate of the fluid. The ac voltage signal is considered rather than dc voltage since the application of an ac voltage in the flow sensor does not promote any electrode reaction. Optimization of the electrical parameters like voltage and frequency of the ac signal are considered as an operating condition for measuring low flow rates. This optimizes the distance of movement of ions and their relaxation behavior across the channel electrodes so that the current admittance suffered is maximum.

Experiment

Fabrication

The flow sensor is fabricated¹⁹ on a glass substrate with gold surface electrodes (Fig. 2a) and the microfluidic channel is made on PDMS. Gold metal of thickness 100 nm is deposited on an adhesion layer of titanium with thickness 20 nm using e-beam deposition. A spinned layer of Shipley photoresist (1827) is used for patterning (Fig. 2b) the metal. The electrodes are patterned by etching gold and titanium with potassium iodide solution (KI + I₂ + H₂O = 4:1:40) and 2% HF respectively. The Shipley photoresist is removed with acetone. The distance between the electrodes is 100 µm and the length of the electrodes is 5 mm. Gold electrical lines are patterned on the glass as shown in Fig. 2a for the electrical measurement. Measurement is performed across one of the three electrodes. PDMS channels of width 500 µm are made from an SU8 mold.²⁰ Glass and PDMS are bonded together after treatment with oxygen plasma for 1 min. The fluidic channel is aligned with the parallel electrodes using a stereo microscope.

Fig. 2 (a) Layout design of fabricated electrodes and the wiring for measuring the current flow. (b) Cross-section of fabricated flow sensor along the electrodes at AA′ in (a).

Measurements

The measuring instrumentation is similar to that used in strain gauge or thermocouple interfaces. An ac voltage is applied across the channel electrodes in series with a standard resistor. The voltage across the resistor is fed to a National Instrument's data acquisition card (NI DAQ PCI 6024E) through the signal conditioner (SCXI 1100) as shown in Fig. 3. The rms values of voltage across the standard resistor are measured in Labview with a scanning rate of 20 000 samples per s and averaging every 10 000 samples.

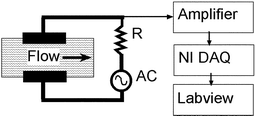Fig. 3 Experimental setup for measuring current increase due to flow of electrolytes (standard resistance R = 1 kΩ, AC is the ac signal source, NI DAQ is PCI 6024E).

Sodium hydroxide (NaOH) solutions with conductivities ranging from 5 to 200 mS cm⁻¹ (corresponding to 0.01 M to 1 M) are prepared with NaOH pellets bought from Fisher Scientific. The concentration of the NaOH solution is chosen at 0.8 M and experiments are carried out for frequency and current response. Microfluidic flow is maintained at a constant flow rate using a Harvard Picoplus Syringe pump. An ac signal of rms voltage 0.05 V is applied in the circuit by a signal generator. The rms voltage across the parallel microelectrodes increases to 0.04 V after wetting the channel (with no flow of electrolyte through it). With some trials of experiments it was found that the current values grow and decay exponentially and stay constant after 1 min. In order to keep the uniformity in all the experiments, the fluid is allowed to flow in the channel for 1 min and the flow is switched off for 1 min before any other measurement. The current flowing across the pair of electrodes is calculated from the measured voltage across the standard resistor of 1 kΩ. The current exponentially grows when the flow is switched on and then stays constant. After switching off the flow, the current again decays exponentially until it reaches a constant value. The difference between two constant values of current gives the current increase due to flow and is measured in all the experiments.

Results and discussion

Flow of fluid is quantitatively analyzed for the flow sensor characteristics in steps of 5 µL min⁻¹, and an almost linear response was shown (as in Fig. 4) for the currents measured with flow rates. The ac frequency used in this case is 500 Hz at 0.05 V. As pointed out earlier, the current increase, which is a measure of admittance is proportional to the cube root of volume flow rate. NaOH is used in this paper as a convenient test solution to demonstrate the flow sensor. The problem with higher concentration NaOH is that it tends to absorb the atmospheric CO₂ and form carbonic acid. This is reflected in the drift of the baseline in Fig 4a. The drift in the baseline can be calibrated with respect to time. However this drift in baseline is not seen for biochemical solutions that are buffered.

Fig. 4 Flow sensor response with flow rate. (a) Instantaneous value of RMS current which depends on flow rate. Every 1 min the flow is turned on in steps of 5 µL min⁻¹ starting from 10 µL min⁻¹ with no flow for every 1 min. The numbers above the plateaus represent the flow rates in µL min⁻¹. (b) RMS current increase due to flow is plotted for the flow rates.

In another experiment, the frequency of the ac signal is swept from 10 Hz to 5 kHz in steps of 10 Hz in the 10–100 Hz range, 100 Hz in the 100–1000 range and 1 kHz in the 1–5 kHz range. Since the equivalent circuit of the microchannel is capacitive dominant, the base current (with no flow) increases with frequency. At each frequency, the measurement of current before and after flow is brought to a constant value by waiting for 1 min. The redistribution of ions in the channel causes an increase or decrease of current. It is observed that the admittance is maximized at 500 Hz as shown in Fig. 5. This is due to the competitive capacitive effects of the Ce and Cs as described earlier. It is to be understood that the efficiency of the flow sensor is found to be high at this frequency.

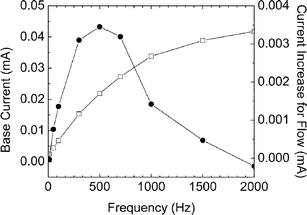Fig. 5 Frequency response of the flow sensor for different applied frequency. The squares are the static (no flow) response in the frequency sweep and the circles are the increase in RMS current due to a flow of 10 µL min⁻¹.

The ac voltage applied has a great influence on the flow driven current. Higher voltage increases the diffusive region in the channel which in turn decreases the diffusive capacitance (Cs). But the contribution of the capacitance at outer Helmholtz plane becomes more prominent and the admittance increases. Furthermore, at voltages more than 400 mV, partial electrolysis takes place and the effective current decreases with voltage. Fig. 6 shows the optimization of voltage of the ac signal used in the flow sensor. The V–I characteristic of the flow sensor (with no flow) shows a parabolic response similar to the conductivity measurement of electrolytes. Thus the flow sensor is tuned for the ac voltage of 400 mV.

Fig. 6 V–I characteristics of the flow sensor. The squares are the RMS current for no flow and the circles are for a flow of 10 µL min⁻¹. The optimization is to find the RMS voltage for which the sensor is more sensitive for the flow of fluid.

NaOH solution of different concentrations were studied in the flow sensor. It is found that there is an optimum value of the concentration of the electrolyte for the flow sensor to be at its maximum efficiency. Fig. 7 shows that the concentration of the flow sensor is optimized at 0.2 M. At lower concentrations the admittance increases with more numbers of ions in the fluid system. When the ionic concentration is too large the flow of fluid does not further increase the admittance because of inter-ionic interactions. However generally the buffers or electrolytes used in microfluidic application are in mM concentration and the optimization of concentration is not necessary.

Fig. 7 Dependence of concentration of the electrolyte to the flow. The square, circle and triangles are for 300, 500 and 700 Hz respectively of the ac voltage applied.

Using the optimized electrical parameters (f = 500 Hz, V = 0.4 V and concentration = 0.2 M), the flow sensor is designed for measuring very low values of flow rate starting at 0.05 µL min⁻¹ (<1 nL s⁻¹). The response shows a cube root behavior even at very low flow rates as shown in Fig. 8. The sensitivity at these optimizations is 5.2 × 10⁻⁴ mA/(µL/min). In another experiment, fluorescent beads of diameter 2.5 µm are mixed with NaOH and sent through the channel. The motion of the beads at the flow rates .05, 0.1, 0.2, 0.4, and 0.6 µL min⁻¹ are recorded using optical video microscopy at 30, 60, 120, 250, 250 frames per s respectively, and the beads at a particular stream are analyzed and averaged to predict the velocity response at very low flow rates. The sensor results are compared with the velocity of beads (the symbol * in Fig. 8) and shows similar response. Thus the calibration of the flow sensor is accomplished using the velocity measurements with beads.

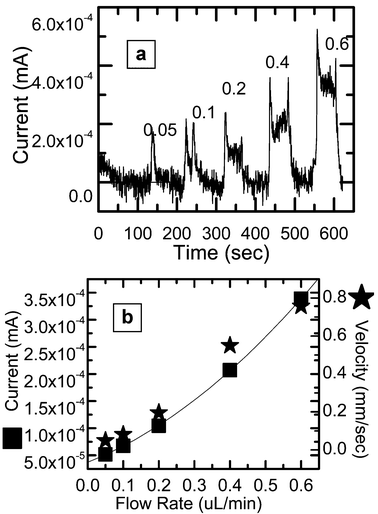Fig. 8 Flow sensor response at very low flow rates. (a) The instantaneous current values with the variation and switching of flows. The results of (a) are re-plotted in (b). Also shown the right axis of (b) is the velocity of beads at different flow rates of the fluid. (The peaks in (a) correspond to the flow rate values labelled.)

Though this paper presents NaOH as the fluid used for demonstration of this flow sensor, different electrolytes and biochemical buffers have been tested for the sensitivity. CaCl₂, KCl and KOH (from Fisher Scientific) and a concentration of 0.8 M is used. Dulbecco's Phosphate Buffered Saline (D-PBS) solution and Modified Eagle Medium (D-MEM) (high glucose) buffer are bought from GIBCO and are used in the same concentration. Optimization of frequency of the ac signal alone is done for the fluids at 50 mV rms applied voltage. The typical increase of currents is measured for the flow rate of 10 µL min⁻¹ and the sensitivity values are tabulated in Table 1. These buffers and reagents are used in chemical and biochemical experiments. When these fluids are used in lab-on-chips, the flow rates of the fluids can be determined using the flow sensor we described in this paper. It is to be noted that though we optimized the conductivity of the electrolyte for this study, it is not required and therefore the sensor can be used with arbitrary concentrations. Conductivity depends on the constituent materials and changing the conductivity of certain buffers/reagents will alter the biochemical reaction.

Table 1 Sensitivity of various electrolytes and biochemical buffers tested using the flow sensor

No.	Electrolytes/buffers	Sensitivity (mA/(µL/min))
1	CaCl2	1.2E-4
2	KCl	1.5E-4
3	KOH	2.8E-4
4	D-PBS	1.0E-4
5	D-MEM	3.2E-4

---

The principle of measuring electrical admittance laid out in this paper can be used to decipher parameters other than flow. There have been several reports^21,22 on the detection of biomelecules and cells in lab-on-chip devices based on impedance spectroscopy of the solution. In these methods, the measurements are done with static fluids. By measuring impedance change due to different conditions of flow it is possible to investigate the constituents of the solution. In the future, impedance spectroscopy based on differential flow can thus be used to characterize electrolytes including biomolecules, cells or microbes under laminar flow.

Conclusions

A novel microfluidic flow sensor based on electrical admittance measurement is designed, fabricated and characterized. The efficiency of the flow sensor is maximized by the optimization of electrical parameters such as frequency and voltage of the applied ac signal. These optimized values are then used to measure flow rates as low as 1 nL s⁻¹. The response of the flow sensor is compared with the velocity of microbeads in the same channel using video microscopy and image processing. Some of the advantages of the flow sensor include simplicity in design, integration to most microfluidic platforms, high signal-to-noise ratio, measurements of a wide range of liquids including biochemical buffers and compatibility with micromachining processes. This flow sensor has the potential to measure a broad range of liquid properties, including the characterization of biomolecules and microbes in microfluidic channels.

Acknowledgements

We acknowledge Mr. Lisen Wang for his assistance in the fabrication and Prof. William C. Tang, Daphne Collins, Gisela Lin, Jeff Fisher and Szu-Wen Wang for their comments in editing the paper. This work is supported by UCI.

References

1. S. Tung, J. Sheppard and E. Chiu, A MEMS flowmeter for measuring very small flow rates, Int. J. Nonlinear Sci. Numerical Simulation, 2002, 3(3–4), 273–276.
2. N. Okulan, H. T. Henderson, and H. A. Chong, A new pulsed-mode micromachined flow sensor for an integrated microfluidic system, in Solid-state Sensor and Actuator, Hilton Head Island, SC, 1998.
3. E. Meng, S. Gassmann, and Y. C. Tai, A MEMS Body Fluid Flow Sensor, in Micro Total Analysis System (uTAS '01), 2001, Monterey, USA.
4. H. Ernst, A. Jachimowicz and G. A. Urban, High resolution flow characterization in Bio-MEMS, Sens. Actuators, A., 2002, 100(1), 54.
5. J. A. Wu and W. Sansen, Electrochemical time of flight flow sensor, Sens. Actuators, A., 2002, 97–98, 68–74.
6. T. Nakagama, T. Maeda, K. Uchiyama and T. Hobo, Monitoring nano-flow rate of water by atomic emission detection using helium radio-frequency plasma, Analyst, 2003, 128(6), 543–546.
7. K. D. Caldwell and M. N. Myers, Flowmeter Based on Measurement of Streaming Potential, Anal. Chem., 1986, 58, 1583–1585.
8. M. Wang, W. Yin and N. Holliday, A highly adaptive electrical impedance sensing system for flow measurement, Meas. Sci. Technol., 2002, 13, 1884–1889.
9. A. Poghossian, H. Lüth, J. W. Schultze and M. J. Schöning, (Bio-)chemical and physical microsensor arrays using an identical transducer principle, Electrochim. Acta, 2001, 47, 243–249.
10. G. B. Lee, T. Y. Kuo and W. Y. Wu, A novel micromachined flow sensor using periodic flapping motion of a planar jet impinging on a V-shaped plate, Exp. Thermal Fluid Sci., 2002, 26(5), 435–444.
11. P. Norlin, O. Ohman, B. Ekstrom and L. Forssen, A chemical micro analysis system for the measurement of pressure, flow rate, temperature, conductivity, UV-absorption and fluorescence, Sens. Actuators, B., 1998, 49(1–2), 34–39.
12. P. D. I. Fletcher, S. J. Haswell and X. Zhang, Electrical currents and liquid flow rates in micro-reactors, Lab Chip, 2001, 1(2), 115–121.
13. R. F. Probstein, Physicochemical Hydrodynamics, John Wiley & Sons, Inc., New York, 1994, ch. 6.
14. R. G. Compton and J. Winkler, Hydrodynamic Voltammetry with Channel Microband Electrodes: Alternating Current Impedance Measurements, J. Phys. Chem., 1995, 99, 5029–5034.
15. J. A. Cooper and R. G. Compton, Channel Electrodes – A Review, Electroanalysis, 1998, 10, 141–155.
16. K. Y. Tam, J. P. Larsen, B. A. Coles and R. G. Compton, A channel flow cell with downstream impedance spectroscopy detection: theory and applications, J. Electroanal. Chem., 1996, 407, 23–35.
17. A. C. Fisher, Electrode Dynamics, Oxford Chemistry Primers, Oxford University Press, Oxford, 1996.
18. V. G. Levich, Physicochemical Hydrodynamics, Prentice Hall, Englewood Cliffs, NJ, 1962.
19. Y. Xia, E. Kim and G. M. Whitesides, Micromolding in Capillaries: Applications in Microfabrication, Chem. Mater, 1996, 8, 1558–1567.
20. D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, Rapid Prototyping of Microfluidic Systems in Poly(dimethylsiloxane), Anal. Chem., 1998, 70, 4974–4984.
21. O. A. Sadik, H. Xu, E. Gheorghiu, D. Andreescu, C. Balut, M. Gheorghiu and D. Bratu, Differential Impedance Spectroscopy for Monitoring Protein Immobilization and Antibody-Antigen Reactions, Anal. Chem., 2002, 74, 3142–3150.
22. C. Xiao, B. Lachance, G. Sunahara and J. H. T. Luong, An in-depth Analysis of electric cell-substrate impedance sensing to study the attachment and spreading of mammalian cells, Anal. Chem., 2002, 74, 1333–1339.

---