Ultrafast temporary charge transfer in pyrrolidinyl–benzonitrile and pyrrolyl–benzonitrile in the gas phase

Abstract

4-(N-pyrrolidinyl)benzonitrile and 4-(N-pyrrolyl)benzonitrile were excited by an ultrashort pulse at 270 nm to their L_a (S₂) states and then probed by ionization at long wavelengths. Parent and fragment ion signals show components with time constants <100 fs which we attribute to ultrafast relaxation to the L_b (S₁) state. From this short time we infer a conical intersection between the L_b and L_a surfaces. The wave packet can branch there, one part going temporarily to a strongly displaced state. Its shift was concluded from an anisotropy observed only there. The only excited state known to have a large displacement is the charge-transfer (CT) state. The positive anisotropy indicates that the CT state belongs to the 2A species for both molecules. For pyrrolylbenzonitrile, this is in contrast to previous assignments. The anisotropy, and a coherent oscillation observed in pyrrolidinylbenzonitrile, support the idea that the amino-group twist is an important component of the CT reaction coordinate.

---

1. Introduction

On UV excitation in solvents of suitable polarity, many donor–acceptor substituted aromatics such as 4-dimethylaminobenzonitrile (DMABN) show dual fluorescence, originating from an L_b-like and a charge-transfer (CT) state (reviews^1–4). The pathway for charge transfer is still controversial (see e.g.refs. 5–7.), although the amino-group twist is most popular as the reaction coordinate. Gas-phase investigations with femtosecond time resolution have resulted in new insights, revealing the key role of a conical intersection (CI),^8–10 a feature only beginning to be considered in CT reactions. Furthermore, coherent oscillations observed with this method gave evidence of the relaxation direction and thus also provides information about components of the reaction coordinate.^9,10 The method involves exciting such a molecule by a weak femtosecond UV pump pulse (in our case at 270 nm) and then probing it by ionization by an intense IR pulse, measuring the ion yields mass-selectively as a function of pump–probe delay. Using various probe wavelengths (810, 1300 and 2100 nm), we investigated in this work 4-(N-pyrrolidinyl)–benzonitrile (PYRBN) and 4-(N-pyrrolyl)–benzonitrile (PBN). The donor group in the former is a saturated amino group, whereas in the latter it is the aromatic pyrrole.

According to spectroscopy in cold molecular beams (PYRBN,^11–13 PBN;¹⁴ see also the work on pyrrolylbenzene¹⁵), the longest-wavelength absorption leads to the L_b state (1B₂ in the idealized symmetry C_2v). The transition is weak and polarized perpendicularly to the long molecular axis. This band is insensitive to para-substituents (since the latter are in a node of the L_b wavefunction) and the medium (due to the small transition moment and little change of dipole moment). A much stronger absorption, parallel-polarized and partially covering the weaker one in solution (solution spectra of PYRBN:,¹⁶ of PBN:^17–19) leads to the L_a state (symmetry 2A₁). The excitation wavelength is near the absorption maximum of this band.

As will be further discussed in sec. 4, in the compounds with a saturated amino group the L_a state involves promotion of an electron from the HOMO to the LUMO, the former being π-antibonding and the latter weakly π-bonding between the amino group and the benzene ring (see e.g.refs. 20 and 21). As to conclude from the fluorescence polarization, the CT state also belongs to the A species in these cases;²² the L_a and CT states are thus just two locations on the same 2A surface.^{1,4,8,21,23,24} This surface is lowered from L_a to CT by interaction with a higher π-antibonding nA state on excursion along certain coordinates, a candidate for which is the amino-group twist.^8,21 Along the same coordinates, the lower L_b state rises and crosses the 2A surface in a symmetry-allowed conical intersection (CI). After initial excitation to L_a, a wave packet can thus rapidly reach the CI and branch there to the CT and L_b states. The temporary population in CT is then depleted towards L_bvia a path leading around the lower cone of the CI (see sec. 4). We found this scheme to apply for DMABN and PIPBN^8–10 and present evidence that it is also suitable for PYRBN. Surprisingly, it seems also to apply for PBN. This was not expected, because quantum chemical calculations predicted a 2B symmetry for the CT state, involving excitation from another pyrrole orbital to the LUMO.^20,25 On the other hand, another calculation²⁶ only reported on a CT state of 2A type. In pyrrolylbenzene two CT states, one with B and the other with A symmetry, were found very close-by.²⁷

The pyrrole ring is slightly twisted versus the benzene ring in S₀ and L_b of pyrrolylbenzene¹⁵ and probably similarly in PBN (symmetry group C₂). Both rings are expected to be planar. In PYRBN, however, the amino N is slightly pyramidal, and the two rings are not twisted against each other (symmetry group C_s) according to a DFT calculation.²⁸ This was also inferred from photoelectron spectra.¹⁶ (Such spectra were reported for PBN, too.^17,29) A previous prediction of a slight twist and puckering of the pyrrolidino ring by molecular mechanics¹² is probably less reliable than the DFT calculation.²⁸ The kinetics and fluorescence of PYRBN^30–36 and PBN^17,18,29,37 were previously investigated in solution. It was found that the L_b → CT charge-transfer reaction required a solvent of at least medium polarity (to lower the CT state) for PYRBN, whereas PBN shows this reaction already in alkanes.

2. Experimental

The preparation of PYRBN and PBN is described in refs. 17, 29 and 33. The two species were investigated in the gas phase in the set-up (details described in ref. 38) heated to 130 °C to avoid adsorption; the substances themselves were at 20 °C. The molecules were pumped by a frequency-tripled pulse of a Ti:sapphire laser system (270 nm, 75 fs, 10⁹ W cm⁻²) and then probed by nonresonant dissociative ionization at the fundamental wavelength (810 nm, 50 fs, 10¹³ W cm⁻²); in further experiments, probing was done by the output of a parametric generator (Topas) at 1300 and 2100 nm (40 fs, 10¹³ W cm⁻²). The two beams had linear polarizations with an angle of 55° (“magic angle”) between each other in order to avoid time dependences induced by molecular rotation. In some experiments at 810 nm we also compared the signals at parallel and perpendicular polarizations. More experimental details are described in refs. 8 and 10.

The shape of the signals did not depend on the pump intensity (varied by a factor of about three). This proves that they are produced by a single pump photon. Varying the probe intensity by a similar factor did not change the time constants, although the later parts of the signals (coming from lower molecular states) were raised at higher probe intensities.

3. Results

The UV spectra of PYRBN and PBN (not shown), measured in the gas phase at 80 °C, look very similar to that of DMABN.³⁹ The strong structureless L_a band has a maximum at 273 (PYRBN) and 270 nm (PBN) (4.54 and 4.59 eV). A weak precursor at longer wavelengths is certainly the L_b band for both molecules; according to the supersonic-beam spectra, their 00 bands are at 32 018^11–13 and 34 424 cm⁻¹¹⁴ (3.97 and 4.26 eV), respectively. Hence the initial excitation at 270 nm places the molecules at an energy of 0.57 and 0.33 eV above the L_b minimum.

The ion signals investigated with time resolution were the parent ion (M⁺) and the most intense fragment (about 10% of M⁺), which was M⁺ − 1 for PYRBN and M⁺ − 28 for PBN. Time dependent signals at different probe wavelengths are shown for the first few picoseconds in Figs. 1 and 2 for PYRBN and 3 for PBN. Similarly as found in PIPBN^10,40 and DMABN,⁹ PYRBN exhibits a periodic modulation of the signals between about 0.5 and 3 ps which is extracted (see below) and Fourier-transformed in Fig. 2 from the data for the parent ion with 1.3 μm probing. By contrast, although the PBN signals show some irregularities, an oscillation could not unambiguously be extracted from them. The time evolution was measured up to 600 ps (not shown); in this part, the signals simply decayed doubly exponentially.

Fig. 1 The time-dependent PYRBN parent (mass 172 u) and fragment (171 u) ion signals (normalized to the maxima), measured at the indicated probe wavelengths at the magic angle between pump and probe polarizations. The parent is actually about 10 times stronger than the fragment. The solid lines represent simulations of the nonperiodic parts (see text).

Fig. 2 Upper panel: The PYRBN parent ion signal with probing at 1310 nm. The thin solid lines show the simulated contributions ¹⁷²σ₁L₁ + ¹⁷²σ₂L₂,¹⁷²σ₃L₃ and ¹⁷²σ₄L₄ (see text) from locations L₁–L₄ to the nonperiodic part of the signal. Subtracting their sum (the sums are shown in Fig. 1) from the data leaves the oscillatory residue at the bottom of the panel, which is simulated by function (1). The bold solid line is the sum of nonperiodic and periodic parts of the simulation. Lower panel: Fourier transform of the bottom trace of the upper panel.

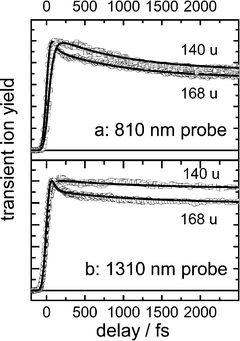Fig. 3 The time-dependent PBN parent (mass 168 u) and fragment (140 u) ion signals (normalized to the maxima), measured at two probe wavelengths at the magic angle between pump and probe polarizations. The parent is actually about 10 times stronger than the fragment. The solid lines represent simulations of the nonperiodic parts (see text).

In a first step, we simulated the nonperiodic part of the signals by a sum of exponentials with time constants τ_i (Table 1), convoluted with pump and probe pulses. Subtracting this part from the PYRBN data left the oscillating part (Fig. 2), whose Fourier transformation (Fig. 2 bottom) gave the wavenumber and period τ_osc also reported in Table 1. This part could also be simulated by a damped oscillation of the type

exp(−t/τ_deph)cos(2πt/τ_osc + φ) (1)

Using τ_osc from the Fourier transform, we deduced the dephasing time and phase from this simulation. The simulation procedure is described in detail in refs. 10 and 38.

Table 1 Lifetimes τ_i of the locations (observation windows, indicated by the arrows in Fig. 5) i on the potential energy surfaces and cross-sections ^mσ_i for generating the ions of mass m for PYRBN. Nonzero values of ^mσ_i show from which signals (m) we deduced the lifetimes of the locations i. The error limits of τ₄ and τ₅ are the standard deviations of the values determined in 10 runs from the doubly exponential fits to the late-time signals. τ₃ is from the full fit with nonperiodic functions (sum of exponentials), and its error is again the standard deviation in ten runs. τ₁ and τ₂ are from the full simulation including convolution with pump and probe pulses, and the errors indicate the estimated limits where the simulation is still reasonable. The oscillation wavenumber ν is from Gaussian fits to the Fourier transforms, averaged over 10 scans with the standard deviation given

Exponential parts of PYRBN
i	1	2	3	4	5	Anisotropy r
τ i	5 ± 5 fs	40 ± 10 fs	540 ± 50 fs	160 ± 10 ps	1100 ± 100 ps
^172 σ i (810 nm)	1	0.243	0.235	0.262	0.157	0
^171 σ i (810 nm)	1	0.188	0.175	0.225	0.135	0.2
^172 σ i (1300 nm)	1	0.40	0.144	0.128
^171 σ i (1300 nm)	0	1	0.674	0.550
^172 σ i (2100 nm)	1	0.277	0.025	0.018

---

Exponential parts of PBN
i	1	2	3	4	5	Anisotropy r
τ i	5 ± 5 fs	48 ± 10 fs	910 ± 90 fs	104 ± 10 ps	352 ± 21 ps
^168 σ i (810 nm)	1	0.680	0.373	0.389	0.123	0
^140 σ i (810 nm)	0	0.890	1	0.940	0.205	0.3
^168 σ i (1300 nm)	1	0.488	0.447	0.335
^140 σ i (1300 nm)	0	1	0.673	0.496	0.162

---

Oscillation in PYRBN^a

a Half the ν values obtained from Fourier transform, see text.

ν = 31.9 ± 0.5 cm⁻¹, τ_osc = (2c ν)⁻¹ = 524 fs, τ_deph = 1.4 ps, φ = 0.82π

---

For a given molecule, the set of time constants is the same, independent of probe conditions. Only the coefficients of the exponentials depend on the probe wavelength and the ion mass observed. This is interpreted by population L_i flowing consecutively from one observation window L_i to the next. This flow is described by rate equations, whose solution is a sum of exponentials for each population (the same, independent of probe conditions). Each L_i has a mass spectrum of its own, and their dependence on the probing conditions help to distinguish the signals from the different L_i; the spectra are represented by the relative ionization cross sections ^mσ_i, i.e. the probabilities to produce an ion of mass m from window L_i. They are simulation parameters and are also given in the table. The data are redundant for deducing the τ_i and the populations L_i. Fig. 2 shows by the thin lines the simulation components (^mσ_i × L_i), whose sums for all i add up to the signals for mass m. The very short τ₁ is needed to reproduce the steep rise of the parent signals. τ₂ causes, for instance, the delayed rise of the fragment as compared to the parent, clearly visible at 1300 nm. τ₃ represents the decay of the initial spike, which is evident in particular at the longer probe wavelengths. The flat part of the signals extending from <1 ps to beyond the range shown is due to contributions from L₃ and L₄, the former decaying in the same time τ₃ as the latter rises. The decays in the range up to 600 ps (τ₄, τ₅) are not shown.

Fig. 4 shows the anisotropies r calculated for the two molecules from the signals at 810 nm (other wavelengths not investigated) with the probe polarization parallel and perpendicular to that of the pump:

r = (S_∥ − S_⊥)/(S_∥ + 2S_⊥). (2)

Obviously, for both molecules r ≈ 0 for the parent ion, whereas for the fragment r begins with positive values and decays in the picosecond range. The asymptotic value, which is difficult to determine, is set to 0 in the figure.

Fig. 4 Time dependence of the anisotropy r = (S_∥ − S_⊥)/(S_∥ + 2S_⊥) of parent and fragment signals. (a) PYRBN, (b) PBN. The probe laser was at 810 nm. For the parent, r is practically zero.

4. Discussion

4.1. Relaxation path for PYRBN

The PYRBN signals are very similar to those for DMABN and PIPBN.^8,10 Because also the molecules are very similar, we can directly take over the assignments. Consequently we also use the same scheme of potential surfaces and relaxation paths (Fig. 5). Similarly as in DMABN, an evidence for transient population of the CT state is based on the anisotropy. This can be seen as follows: The ionization itself is isotropic, which is confirmed by the zero-anisotropy observed for the parent ion. Photodissociation of the parent ion by absorption of an additional probe photon can, however, give rise to an anisotropy of the fragment ions, which will be positive if there is a resonant ionic transition at 810 nm (1.53 eV) polarized parallel to the pump laser, that is parallel to the long axis of the molecule. After vertical ionization from a state with near-equilibrium geometry, there is no such resonance, as to judge from the energy difference of photoelectron bands.¹⁶ Therefore a substantial distortion is necessary in the neutral molecule to reach a geometry with such a resonance in the ion; the only low-lying excited state with strong displacement is the CT state. This assignment implies that the anisotropy decay of Fig. 4 contains a contribution from this internal relaxation (time constant τ₃) and is not purely due to rotation; evidence for such a double origin was presented for DMABN in ref. 9. As already discussed previously,⁸ the temporary population of the CT state implies that low-quantum yield CT emission should be detectable from the gas phase and in nonpolar solvents; the latter has indeed been observed in DMABN.^41,42 It is interesting in this context that a recent work on spectroscopy of similar molecules in cold supersonic beams also suggested population of the CT state, if the excess energy is sufficient.⁴³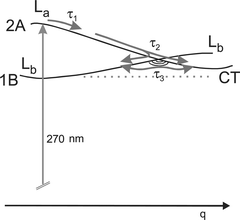

Fig. 5 Potential energy surfaces and relaxation paths. The reaction coordinate q changes direction along the path, but probably everywhere contains the amino-group twist as an important component. The second coordinate spanning the branching space of the conical intersection (CI) must have b symmetry and probably contains the amino-group pyramidalization as a component. The τ₃ equilibration follows a path around the lower cone. This diagram is used for both PYRBN and PIPBN.

It is instructive to have a closer look to the ionic resonance. Energy differences of ion states are just equal to orbital energy differences in the neutral molecules. Orbitals and their energies are easy to understand by the help of their nodal pattern. The HOMO of PYRBN has the symmetry species b₁ and is π-antibonding between donor and acceptor moieties (Fig. 6). The ground state of the parent ion (²B₁) has a hole in this orbital (single occupancy). The HOMO − 1 has a node containing the amino group; it has the species a₂. An ionic ²A₂ → ²B₁ transition would be perpendicularly polarized, which would disagree with our parallel anisotropy in observation window L₃ (or the strongly displaced state claimed to correspond to CT). HOMO − 2 provides the right symmetry (b₁), since an ionic ²B₁ → ²B₁ transition would be parallel; it is π-bonding between amino donor and the benzonitrile parts. A displacement coordinate drastically weakening this π interaction may approach the two b₁ orbitals sufficiently, so that a resonant transition in the ion will be possible, as indicated in Fig. 6. There are not many coordinates with this property. A twist of the amino group was predicted to do it,^16,20 and Figs. 5 and 6 were therefore drawn assuming that the twist is an important (but not the only, see below) component of the reaction coordinate. A strong pyramidalization of the amino group would probably be less effective, and planarization would do the opposite.

Fig. 6 Bottom: π orbitals and energies of neutral PYRBN (a) and PBN (b) versus twist angle θ as calculated by Parusel.²⁰ Top: Ionic states resulting from a hole in the corresponding orbitals; for instance, the ground state (²B₁) of the ion PYRBN⁺ has a hole in the HOMO (b₁ orbital). Ionic excitation energies are equal to orbital energy differences. The suggested resonance with the probe laser is indicated. Symmetry species in C_2v are only given for zero twist angle. For θ = 90°, see ref. 20. The indicated ionization energies (in eV) from the different occupied orbitals were taken from photoelectron spectra.¹⁶

So, as in PIPBN¹⁰ and DMABN,^8,9 we assign for PYRBN the times below 100 fs (τ₁, τ₂) to departure from the Franck–Condon region and further relaxation through a conical intersection (CI) to both the L_b and CT minima (Fig. 5). The conclusion that the path leads through a CI can again be obtained from the shortness of τ₂. The next time constant (τ₃) corresponds to L_b ↔ CT equilibration around the lower cone of the CI. As before, the much longer τ₄ is ascribed to intersystem crossing, probably to T_n, which then can rapidly equilibrate with T₁. From there, the molecule decays within τ₅ to the ground state, from which ionization was too weak to be detected. (Any excited state would be detectable.) This process may be accompanied by decomposition such as H elimination, as suggested in PIPBN.⁹

4.2. The oscillation in PYRBN

The observed oscillation period is 530 fs. Its damping (dephasing) time is 1.4 ps. The only excited state with sufficiently long lifetime is L_b (or the observation window L₄, representing the L_b-CT equilibrium. This equilibrium is expected to lie on the L_b side, because the CT state is higher in energy). So the oscillation must be a vibration in the L_b well. In fact, converting the period τ_osc to wavenumbers ν by ν = 1/cτ_osc, one receives 64 cm⁻¹, very close to a value (69 cm⁻¹) observed in supersonic-beam spectra of the L_b state of PYRBN.^11–13

There are not many vibrations with such a low wavenumber in this molecule. According to semiempirical PM3 calculations for S₀, there are only three below 100 cm⁻¹: (1) arching (42 cm⁻¹), where the CN and pyrrolidine groups bend in phase out of plane versus the benzene ring, (2) amino group twist (54 cm⁻¹) and (3) another arching (85 cm⁻¹), where the CN and pyrrolidino-N bend in phase out of plane, whereas the C₂H₄ end group moves out of phase. Because the electronic interaction of the benzene with its substituents is only minor in the L_b state, these wavenumbers are not expected to be very different in this excited state. Hence, the observed oscillation should be assigned to the lower-frequency arching or to the twist vibrations. Arching involves the inversion motion of the amino nitrogen.

However, both vibrations deserve a little more scrutiny, taking the symmetry of PYRBN into account: According to DFT calculations,²⁸ in the ground state, the twist angle θ = 0 and the wagging angle (angle between the benzene and pyrrolidine planes) is only ω = 8°. Any barrier at ω = 0 will be smaller than in DMABN (where ω = 15° in S₀⁴⁴), where it has recently been reevaluated and found to be <100 cm⁻¹ in S₀ and <50 cm⁻¹ in L_b.⁴⁵ (As mentioned in the Introduction, a molecular-mechanics calculation predicted θ = 15° in S₀.¹² This would imply also a minor barrier at θ = 0°. It would not much change the following considerations.) The L_b potential must be very similar, since the 00 transition is by far stronger than the adjacent bands in the vibrational structure.^11–13 Therefore both types of vibration will occur between two turning points that are symmetry-equivalent. Also the ion is expected, due to the partial double bond between the amino group and the benzene ring, to have its potential minimum at θ = 0 and ω ≈ 0, not displaced versus that of L_b. A vibration (belonging to an antisymmetric species) in such a symmetric potential will therefore give rise to signal maxima twice in each period. (This is the equivalent to the spectroscopic selection rule Δv = 2 for antisymmetric vibrations in electronic transitions. It will also apply for the 69-cm⁻¹ structure in the PYRBN supersonic beam spectrum,^11–13 if our assignment is correct.) Therefore we should divide by two to convert the observed period to wavenumbers:

ν = (2cτ_osc)⁻¹ (3)

We thus calculate ν = 32 cm⁻¹ for the vibration. At present we cannot decide between the two possible assignments to twist or arching. In DMABN we observed both types of oscillations,⁹ whereas in PIPBN we attributed a strong modulation to the arching vibration.⁹ Its assignment was based on a substituent mass effect observed for it. In PIPBN, the neutral and ion potentials are displaced against each other (due to the nonplanar piperidine ring), so that the factor of two in (3) does not apply, although it does apply in PYRBN for symmetry reasons: The potential is symmetric to ω = 0 in this molecule. (We assume that the vibration takes place above any barrier.). The wavenumber thus calculated for PIPBN was 31.4 cm⁻¹, very close to that calculated by (3) for PYRBN. Therefore we tend to the assignment as arching (involving amino group inversion). The other vibration might be excited, too, even if it is not observed because possibly the L_b and ion potentials are parallel in this direction, so that this vibration would not be Franck–Condon active and would not give rise to a signal modulation. The wavenumber observed by us (0.5 × 64 cm⁻¹) deviates from that in the cold supersonic jet (0.5 × 69 cm⁻¹) by much more than the experimental error (0.5 cm⁻¹, see Table 1). A plausible interpretation assumes that levels with v ≫ 1 are excited in our experiment, and the wavenumber difference is due to an anharmonic shift.

Also the L_a potential will be symmetric to θ = 0 and ω = 0, again due to the partial double bond. Therefore these vibrations will not (or nearly not) be Franck–Condon active in the pump transition. They are thus not expected to be excited by the pump laser. Instead, they will be stimulated by acceleration on the last slope on entering the L_b well from the CI. The direction of this slope therefore contains either θ or ω as an important component. Both can be justified (and would be supported by an assignment): It was argued above (see also Fig. 5) and previously^8–10 that a CI is probably displaced from the L_b minimum towards a direction with θ as a component. On the other hand, a b-type vibration such as the inversion (ω) could be stimulated by the 2A → 1B relaxation in the CI, which needs a symmetry-breaking distortion.⁹ It is remarkable that such oscillations can be understood as described, by considering a pathway with intermediate excursion of the wave packet via a conical intersection (as also recommended in ref. 46). A previous model⁴⁷ would only consider electronic matrix elements and Franck–Condon factors between L_a and L_b; the latter factors are ≈ 0, because the potentials are not shifted against each other in the θ and ω directions.

4.3. Relaxation path for pyrrolylbenzonitrile

The kinetic behavior of PBN is very similar to that of PYRBN: There seems to be the same number of steps or observation windows, and the time constants differ by not more than a factor of 2. This similarity is not expected, because PBN has 4 more π electrons than PYRBN, so that the level scheme could be different. In fact, the lowest-energy CT state was predicted to belong to the 1B species^20,25 (in contrast to the 2A CT state of DMABN or PYRBN; see also the reviews.^2,4Ref. 17 found evidence that two different CT states play a role in PBN, depending on the solvent). This state involves a transition from the HOMO of a₂ symmetry (localized on the carbons of pyrrole, node containing the nitrogen) to the b₁ LUMO of the benzonitrile moiety. The orbital energies thus calculated²⁰ are shown as functions of the twist angle θ in Fig. 6.

In this scheme, ionization from the CT state would leave a hole in the a₂ orbital, giving an ion ground state ²A₂. The positive anisotropy found (Fig. 4) indicates a resonance in the ion parallel to the molecular axis. We thus would need a ²A₂ → ²A₂ transition in the ion or the corresponding transition between a pair of a₂ orbitals. It is obvious from Fig. 6 that the available orbital pair does not approach each other along the twist, and it seems hard to imagine any other coordinate, relevant to a charge transfer reaction, that could do so: Both orbitals have a node containing the substituents. On the other hand, the pair of b₁ orbitals just does the required energy approach along the twist coordinate. If we postulate that the CT state observed by us involves excitation of a b₁ electron (HOMO − 1 in Fig. 6b), certainly to the LUMO (b₁) so that a 2A state would result, then the positive anisotropy would be understood by an ionic ²B₁ → ²B₁ transition in much the same way as for PYRBN (Fig. 6a). This postulate is very much encouraged by a CASPT2 calculation which predicts practically degenerate CT states of 2B and 2A symmetry in pyrrolylbenzene at perpendicular geometry.²⁷ We suppose that attaching a para-cyano substituent (resulting in PBN) will lower the 2A state more than the 2B state. In fact, another CASPT2 calculation reports for PBN at low energy only a 2A state with CT character.²⁶ We therefore interpret our anisotropy data as a support that the lowest CT state of PBN belongs to the 2A species and is thus on the same potential energy surface as the initially excited L_a state. This implies that the same scheme for the surfaces and relaxation paths can be used as for PYRBN (Fig. 5).

In contrast to PYRBN, no oscillations were observed in PBN (although some irregularities in the signals might indicate that there are some). It may be that the L_b potential and that of the ion are better parallel in PBN than in PYRBN, so an existing vibration would cause less signal modulation in PBN, because it would not be Franck–Condon active in ionization.

5. Concluding remarks

It was surprising that the same potential energy scheme and relaxation paths (Fig. 5) could be used for PYRBN and PBN. Apparently the states arising from the additional π electrons in PBN are higher in energy, including also a CT state of B symmetry. It is also remarkable how little the early times τ₁–τ₃ differ between the molecules DMABN,⁸ PIPBN,¹⁰ PYRBN and PBN investigated by our method. The largest variation was found in τ₃, which was 1.0, 1.9, 0.53 and 0.91 ps for the four compounds, respectively. τ₃⁻¹ is the sum of the forward (L_b → CT) and backward (CT → L_b) rates in the L_b/CT equilibration, with the rate for the exothermic backward reaction dominating. The CT → L_b reaction is less exothermic in the gas phase for PBN than for PYRBN. This can be concluded from the fact that CT fluorescence is already observed in nonpolar environments for PBN, whereas at least medium polar solvents are needed for PYRBN. Hence, the longer τ₃ for the former is not surprising. The same can be said about the pair PIPBN and DMABN. It seems also natural that reverse differences of rates were found in solution for the forward (L_b → CT) reactions, whose reaction enthalpy is the negative of that of the CT → L_b reaction.

It may be worth repeating^8–10 a comment on the amino-group twist as a component of the reaction coordinate. Whereas this twist gives rise to observable consequences such as the anisotropy (in this work) or a coherent oscillation (this work and refs. 9 and 10) and many others,^1–4 it will not be the only component: It seems natural that the electron transferred in the CT state to the benzonitrile moiety causes CC bond lengthening there. A CASPT2 calculation for PBN in fact found such effects.²⁶ Because bond stretching is energetically more effective than twisting, such components can give rise to steep slopes, which may explain our very fast initial relaxations (τ₁,τ₂).

Acknowledgements

T.Y. thanks the Alexander von Humboldt foundation for a research fellowship and S.A.T. thanks the VW Foundation for a financial support within project I/76 283.

References

1. E. Lippert, W. Rettig, V. Bonačić-Koutecký, F. Heisel and J. A. Miehé, Adv. Chem. Phys., 1987, 68, 1.
2. W. Rettig, Angew. Chem., Int. Ed. Engl., 1986, 25, 971.
3. W. Rettig, Top. Curr. Chem., 1994, 169, 254.
4. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899.
5. W. Rettig, B. Bliss and K. Dirnberger, Chem. Phys. Lett., 1999, 305, 8.
6. K. A. Zachariasse, Chem. Phys. Lett., 2000, 320, 8.
7. W. Rettig and B. Zietz, Chem. Phys. Lett., 2000, 317, 187.
8. W. Fuß, K. K. Pushpa, W. Rettig, W. E. Schmid and S. A. Trushin, Photochem. Photobiol. Sci., 2002, 1, 255.
9. S. A. Trushin, T. Yatsuhashi, W. Fuß and W. E. Schmid, Chem. Phys. Lett., 2003, 376, 282.
10. T. Yatsuhashi, S. A. Trushin, W. Fuß, W. Rettig, W. E. Schmid and S. Zilberg, Chem. Phys., 2004, 296, 1.
11. C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, D. Solgadi, J. McCombie, B. D. Howells, T. F. Palmer, A. Subaric-Leitis, C. Monte, W. Rettig and P. Zimmermann, Chem. Phys., 1995, 191, 271.
12. B. D. Howells, J. McCombie, T. F. Palmer, J. P. Simons and A. Walters, J. Chem. Soc., Faraday Trans., 1992, 88, 2587.
13. B. D. Howells, J. McCombie, T. F. Palmer, J. P. Simons and A. Walters, J. Chem. Soc., Faraday Trans., 1992, 88, 2595.
14. L. Belau, Y. Haas and W. Rettig, Chem. Phys. Lett., 2002, 364, 157.
15. K. Okuyama, Y. Numata, S. Odawara and I. Suzuka, J. Chem. Phys., 1998, 109, 7185.
16. W. Rettig and R. Gleiter, J. Phys. Chem., 1985, 89, 4676.
17. W. Rettig and F. Marschner, New J. Chem., 1990, 14, 819.
18. C. Cornelissen-Gude and W. Rettig, J. Phys. Chem. A, 1998, 102, 7754.
19. T. Yoshihara, V. A. Galievsky, S. I. Druzhinin, S. Saha and K. A. Zachariasse, Photochem. Photobiol. Sci., 2003, 2, 342.
20. A. B. J. Parusel, Phys. Chem. Chem. Phys., 2000, 2, 5545.
21. L. Serrano-Andrés, M. Merchán, B. O. Roos and R. Lindh, J. Am. Chem. Soc., 1995, 117, 3189.
22. W. Rettig and S. Lutze, Chem. Phys. Lett., 2001, 341, 263.
23. A. L. Sobolewski, W. Sudholt and W. Domcke, J. Phys. Chem. A, 1998, 102, 2716.
24. W. Sudholt, A. L. Sobolewski and W. Domcke, Chem. Phys., 1999, 240, 9.
25. W. Rettig, J. Mol. Struct., 1982, 84, 303.
26. S. Zilberg and Y. Haas, J. Phys. Chem. A, 2002, 106, 1.
27. B. Proppe, M. Merchán and L. Serrano-Andrés, J. Phys. Chem. A, 2000, 104, 1608.
28. A. B. J. Parusel, Chem. Phys. Lett., 2001, 340, 531.
29. W. Rettig and F. Marschner, Nouv. J. Chim., 1983, 7, 425.
30. W. Rettig and G. Wermuth, J. Photochem., 1985, 28, 351.
31. R. Günther and D. Oelkrug, J. Phys. Chem., 1993, 97, 8512.
32. D. Braun and W. Rettig, Chem. Phys. Lett., 1997, 268, 110.
33. W. Rettig, J. Lumin., 1980, 26, 21.
34. K. A. Zachariasse, M. Grobys, T. von der Haar, A. Hebecker, Y. V. Il'ichev, O. Morawski, I. Rückert and W. Kühnle, J. Photochem. Photobiol. A, 1997, 105, 373.
35. K. A. Zachariasse, M. Grobys, T. von der Haar, A. Hebecker, Y. V. Il'ichev, Y.-B. Jiang, O. Morawski and W. Kühnle, J. Photochem. Photobiol. A, 1996, 102, 59.
36. T. von der Haar, A. Hebecker, Y. V. Il'ichev, Y.-B. Jiang, W. Kühnle and K. A. Zachariasse, Recl. Trav. Chim. Pays-Bas, 1995, 114, 430.
37. M. Van der Auweraer, Z. R. Grabowski and W. Rettig, J. Phys.Chem., 1991, 95, 2083.
38. W. Fuß, W. E. Schmid and S. A. Trushin, J. Chem. Phys., 2000, 112, 8347.
39. R. Daum, S. Druzhinin, D. Ernst, L. Rupp, J. Schroeder and K. A. Zachariasse, Chem. Phys. Lett., 2001, 341, 272.
40. S. A. Trushin, W. Fuß, W. E. Schmid, T. Yatsuhashi, presentation at Conference on Femtochemistry 6, Paris, 2003.
41. W. M. Kwok, C. Ma, D. Phillips, P. Matousek, A. W. Parker and M. Towrie, J. Phys. Chem. A, 2000, 104, 4188.
42. G. Wermuth, Z. Naturforsch., A, 1983, 38, 641.
43. S. Jiang and D. H. Levy, J. Phys. Chem. A, 2002, 106, 8590.
44. O. Kajimoto, H. Yokoyama, Y. Ooshima and Y. Endo, Chem. Phys. Lett., 1991, 179, 455.
45. H. Saigusa, N. Miyakoshi, C. Mukai, T. Fukagawa, S. Kohtani and R. Nakagaki, J. Chem. Phys., 2003, 119, 5414.
46. W. Fuß, S. Lochbrunner, A. M. Müller, T. Schikarski, W. E. Schmid and S. A. Trushin, Chem. Phys., 1998, 232, 161.
47. M. Bixon and J. Jortner, J. Chem. Phys., 1997, 107, 1470.

---