Properties of WAu₁₂

Abstract

The icosahedral cluster-compound WAu₁₂ was recently predicted by Pyykkö and Runeberg and experimentally prepared in the gas phase by the group of Lai-Sheng Wang. The photoelectron spectra and electron affinity were reported; the other physical properties remain unknown. Anticipating further experimental studies on it, we report here predicted vibrational spectra, NMR chemical shifts, spin–spin coupling constants and quadrupole coupling constants as well as optical spectra at the level of single and double excitations. The population analysis is non-trivial. By direct numerical integration, a charge of roughly +1 is obtained for the central tungsten atom. The charge distribution is strongly delocalised but bonding regions are clearly seen. A considerable electric field gradient exists at the gold nuclei. Although the radial bonds are strong, the system is quite elastic. The DFT activation energy for rotating one hemisphere against the other one, at a D_5h transition state, is only about 20 kJ mol⁻¹. The corresponding h_u vibrational frequency is predicted to be slightly below 30 cm⁻¹.

---

1 Introduction

Metal clusters are of great current interest, not least due to their possible application in nanotechnology or catalysis. Pyykkö and Runeberg¹ recently predicted the existence of the closed-shell cluster WAu₁₂. They suggested that it was unusually stable due to three complementary reasons, namely relativistic effects, the aurophilic attraction and the perfect 18-electron bonding to the tungsten 6s, 6p and 5d shell, in the sense that all these shells do participate in the bonding. The system was experimentally prepared by Li et al.² shortly afterwards. It formed spontaneously from the metal vapours, injected to a helium carrier gas. Its photoelectron spectrum, yielding an estimate for the HOMO–LUMO gap, and electron affinity were measured. Further theoretical calculations and the experimental data supported the originally suggested icosahedral (I_h) structure.

Apart from these data, and the first, fairly rough calculated vibrational frequencies,¹ little is yet known about the properties of this system. Anticipating the preparation of macroscopic amounts of WAu₁₂, we here provide spectroscopical data for interpretation of IR, Raman, UV/VIS, Mössbauer and NMR measurements. A faithful characterization of the electronic charge distribution turned out to be non-trivial. The simplest population analysis methods failed abysmally. Finally we emphasize the fluxionality of WAu₁₂; the lower vibrational modes and hindered rotations can be easily thermally activated.

2 Quantum chemical methodology

2.1 Density-functional theory and ab initio methods

In this study, we have used the TURBOMOLE^3,4 and Amsterdam Density Functional^5–7 (ADF) program suites. In the TURBOMOLE calculations, we employed the effective core potentials (ECP) from the Stuttgart group.⁸ The small-core ECP replaces 60 of the core electrons and thus 19 electrons per gold atom and 14 electrons per tungsten atom are considered in the calculations.

Two different types of density functionals were employed in the study. The Becke–Perdew functional, BP86,^9,10 is a pure GGA functional, whereas Becke's three-parameter functional for exchange in combination with the LYP correlation functional,^11–14 B3LYP, is a hybrid functional, containing a portion of exact exchange. In connection with the BP86 functional we used the resolution-of-the-identity (RI) technique^15,16 to speed up the calculations where possible.

Apart from the core electrons substituted by the effective core potential, no additional electrons were frozen in the second-order Møller-Plesset (MP2) calculations. The coupled-cluster calculations and coupled-cluster response calculations at the CC2 level^17,18 were performed with the TURBOMOLE program package; CC2 is a second-order approximate, coupled-cluster singles and doubles (CCSD) model. In these calculations, the 12 lowest lying electron pairs were kept uncorrelated. The density fitting RI approach was also used in connection with the Møller–Plesset (MP2) and coupled cluster (CC) calculations.^19–22

Ahlrichs' Gaussian TZVP and TZVPP basis sets,²³ featuring a valence triple-zeta basis set with polarisation functions on all atoms, were used throughout in the Turbomole calculations. The replacement of the single Au f function with exponent 1.056 by two primitive f functions with exponents 1.19 and 0.2 follows Pyykkö et al.²⁴ In the case of the RIMP2/TZVPP(2f) calculations, the def-TZVPP auxiliary basis set^25,4 was used for the resolution of the identity. A VQZPP basis set was obtained by augmenting the TZVPP basis set with the additional functions given in Table 1.

Table 1 Additional primitive basis functions in the Gaussian VQZPP basis sets for W and Au (compared to the TZVPP basis). The primitive f function of the TZVPP basis set for gold was replaced by the three f functions given

Type	W	Au
s	0.01508098701	0.01721719738
p	0.00673701583	0.00900421289
d	0.03752146174	0.05643075118
f	2.06784897500	1.19000000000
	0.33085583600	0.43652508514
		0.16012953778

---

Further calculations were done with the Amsterdam Density Functional (ADF) package. Mainly the BP86 functional was used, but for control calculations, also other functionals were employed. Relativistic effects were included by means of the zeroth-order regular approximation (ZORA).²⁶ The Pauli approximation, which is also included in ADF, was found to give very unreliable results. The core electrons were treated as frozen in the population analyses and electron-localisation-function (ELF) calculations. A large core, 60 electrons for gold and tungsten, was used, except for the oxidation-state calculations (see section 3.5), where a smaller core with 46 electrons was used. The 60-electron core includes the 4f electrons of gold and tungsten. The Slater basis set used was the ‘ZORA-TZP’ one.²⁷ In the ADF calculations, the importance of f-type polarisation functions was found to be small. The bond lengths obtained using the standard TZV2P basis set²⁷ which includes f-type polarisation functions is less than 1 pm shorter than the bond distances obtained with the TZP basis set.

2.2 Vibrational spectra

For the vibrational analyses in a harmonic force field we computed the second derivatives of the total electronic energy as numerical first derivatives²⁸ of analytic energy gradients obtained from TURBOMOLE. Theoretically determined Raman intensities are often given in terms of intrinsic Raman scattering factors S_k for mode k,

S_k = 45a′²_k + 7γ^′2_k, (2.1)

where a^′_k and γ^′_k contain the derivatives ([small alpha, Greek, macron]^′_ij)_k of polarisability tensor components (cf.^28,29), However, for comparison with experimental data it is more suitable to state relative intensities in terms of differential cross sections, since these are proportional to the relative intensities. The Q-branch differential cross section for a scattering angle of 90° and an incident light beam which is plane-polarised perpendicular to the scattering plane is^28,29

2.3 Population analysis

In order to arrive at a detailed description of the electronic structure of WAu₁₂, we employed various methods of population analysis. The electron localisation function (ELF) is a useful tool developed by Becke and Edgecombe in 1989.^30,31 The ELF was calculated from the ADF molecular orbitals using the program dgrid.³² Plots of the ELF reveal regions of highly localised electrons, as in covalent bonds and lone pairs.

The charge-density distribution was also studied by explicit numerical integration. The spherical integration of the electron density was done as described in refs. 33 and 34. For the non-spherical integration the program basin³⁵ was used.

Three different methods for partitioning of the electrons between the atoms were employed: generalized atomic polar tensor (GAPT), shared electron number (SEN) and Voronoi charges. The GAPT charges are based on atomic polar tensors³⁶ and are calculated from the gradients of the dipole moment components. In the SEN approach,^37,38 partial charges are calculated from modified atomic orbitals in such a way that the unassigned charge in the molecule is minimized. Finally, the Voronoi partitioning works by integrating the electron density over the Voronoi cell fragments of the molecule. The Voronoi cell of an atom is defined as the region of space that is closer to that atom than to any other atom.³⁹

2.4 Optical spectrum

The electronic excitation energies of the dipole allowed transitions from the totally symmetric ground state to excited states of I_h symmetry were calculated at DFT level using the time-dependent density functional theory (TDDFT) approach implemented in TURBOMOLE.^40,41 The excitation spectrum was calculated using the BP86 and B3LYP functionals with the TZVPP and VQZPP basis sets. Excitation energies were also obtained by performing coupled-cluster response calculations with TURBOMOLE at the coupled-cluster singles (CCS) level as well as at an approximative coupled-cluster singles and doubles (CC2) level^17,18 using the TZVPP basis sets. The molecular structures optimized at the same level of theory were used in these calculations, except in the case of CCS, where the CC2 structure was used instead.

2.5 Magnetic properties

Nuclear magnetic shieldings σ and chemical shifts δ, nuclear spin–spin coupling constants (J-couplings) and nuclear quadrupole coupling constants (NQCC) for WAu₁₂ have been calculated with the codes described in refs. 42–45. These programs are part of the ADF package. The code for nuclear magnetic shieldings has been modified in order to achieve a better scaling with increasing system size.⁴⁶ We have employed the ‘ZORA-TZP’ Slater type basis sets from the ADF database⁵ for the computations. It offers a similar flexibility as the TZVP basis set that has been used in the TURBOMOLE computations and has been previously found to yield reasonably accurate shieldings and spin–spin coupling constants for tungsten complexes.^43,47 All ADF computations were done at the RIMP2/TZVPP(2f) geometry of R = 268 pm (see Table 2) using the BP86 functional. The relativistic treatment has been based on the ZORA Hamiltonian.²⁶ Due to the expense of the computation of nuclear spin–spin coupling constants with two-component spin–orbit coupled ZORA Kohn–Sham orbitals, a scalar relativistic (one-component) treatment has been chosen in this case. Nuclear magnetic shieldings and quadrupole coupling constants could be evaluated using a spin–orbit ZORA treatment. In order to obtain reliable spin–spin coupling constants, the Slater-type all-electron ZORA-TZP basis sets for W and Au were augmented with steep 1s basis functions as described in refs. 43 and 44. We will denote this basis set by “ZORA-TZP+s” in the following. For comparison, we have also evaluated the W nuclear magnetic shielding with both basis sets. In order to investigate the magnitudes of the relativistic corrections to the magnetic properties we have further performed nonrelativistic computations. In particular when using the all-electron ZORA basis sets on the Au atoms the SCF convergence and the quality of the density fit were not favorable. Therefore, for the nonrelativistic computations the triple-zeta all-electron nonrelativistic “AE” basis sets for Au and W from the ADF basis set database have been augmented with the polarisation functions from the nonrelativistic TZP frozen-core basis, and a density fit basis has been created for each atom. This nonrelativistic all-electron TZP basis did not cause the aforementioned problems and was thus used for the nonrelativistic estimates of the magnetic properties of WAu₁₂. For those gold atoms for which no nuclear magnetic property was evaluated, the core shells up to 4f have been kept frozen, both in the relativistic and the nonrelativistic computations. It has been confirmed, by comparison of a relativistic all-electron calculation of σ(W) with the respective computation employing frozen Au cores, that this restriction has only a minor influence on the shielding (about 200 ppm). For the determination of chemical shifts we have chosen WO₄²⁻ as reference, with a W–O distance of 179 pm.⁴⁷ Finally we note that the separation of the W shieldings to dia- and paramagnetic parts within the ZORA-GIAO approximation follows the partitioning originally devised by Wolff et al.⁴²

Table 2 Calculated distances R (in pm) for W–Au and Au–Au contacts for icosahedral WAu₁₂. TZVP and TZVPP are Ahlrichs' basis sets from the TURBOMOLE library

Method	R(W–Au)	R(Au–Au)
a Agrees with the RIMP2/TZVPP + f(Au) result in ref. 1.
RIMP2/TZVP	279.8	294.2
RIMP2/TZVPP	270.6	284.5
RIMP2/TZVPP(2f)	268.0^a	281.8
RICC2/TZVPP	269.9	283.8
BP86/RI/TZVP	279.8	294.2
BP86/TZVPP	278.6	292.9
BP86/TZVPP(2f)	276.1	290.3
BP86/VQZPP	273.9	288.0
B3LYP/TZVP	283.0	297.6
B3LYP/TZVPP	282.0	296.5
B3LYP/TZVPP(2f)	279.8	294.2
B3LYP/VQZPP	278.0	292.3

---

3 Results

3.1 Structure

The calculated distances for the icosahedral WAu₁₂ are shown in Table 2. The results agree with the previous ones.¹ Perhaps the ‘best’ W–Au bond length is the RIMP2 value with the largest basis, 268.0 pm. Due to the difficulties of DFT methods in describing the metallophilic part, both BP86 and B3LYP bond lengths are slightly longer. The CC2 bond distances agree well with the MP2 ones.

The distances for WAg₁₂ are shown in Table 3. They actually are closely similar to the corresponding values for WAu₁₂. Further test calculations also show similar bond distances for diatomic Ag and Au systems, which are presented in Table 4. The MP2 results are seen to be closer to experiment for these diatomics.

Table 3 Calculated distances R (in pm) for W–Ag and Ag–Ag contacts for icosahedral WAg₁₂. The TZVP and TZVPP basis sets are from the TURBOMOLE library

Method	R(W–Ag)	R(Ag–Ag)
RIMP2/TZVPP	271.1	285.0
BP86/RI/TZVP	277.6	291.9
BP86/TZVPP	277.2	291.5
B3LYP/TZVPP	281.4	295.9

---

Table 4 Calculated distances R_e (in pm) and vibrational wavenumbers [small nu, Greek, tilde] (in cm⁻¹) for diatomic molecules Ag₂, Au₂, and AgAu. The TZVPP basis set from the TURBOMOLE library was used

	R e			[small nu, Greek, tilde]
Species	BP86	RIMP2	Exp.	BP86	RIMP2	Exp.
a Ref. 68. b Ref. 69. c Ref. 70. d CCSD(T) value, ref. 71. e Ref. 72.
Ag2	257.0	252.9	253.03^a	183.9	200.6	192.0^b
Au2	254.7	248.2	247.15^c	168.3	191.5	190.9^c
AgAu	255.6	251.2	254.2^d	182.6	201.7	198.2^e

---

3.2 Vibrational spectra

The calculated vibrational frequencies are shown in Tables 5 and 6. By analogy with the bond-length trend, the RIMP2 frequencies are invariably larger than the two DFT sets. For the coinage-metal diatomics in Table 4, the RIMP2 frequencies are better than the BP86 ones. On the other hand, for a number of main-group polyatomics, the wavenumbers from BP86 calculations are known to be in good agreement with experimental wavenumbers due to an error cancellation.^28,48,49 Hence the difference between BP86 and RIMP2 frequencies may give an approximate error range of these methods.

Table 5 Vibrational wave numbers [small nu, Greek, tilde] (in cm⁻¹), infrared absorption coefficients A (in km mol⁻¹), and Raman scattering cross sections ^⊥σ_u for incident laser light, polarised perpendicular to the scattering plane, and a scattering angle of 90 deg. (in 10⁻³⁶ m² sr⁻¹), calculated at the RIMP2, BP86, and B3LYP levels. Raman intensities could not be obtained at the RIMP2 level. ‘—’ denotes IR- and/or Raman-silent vibrations

Basis set	No.	Irrep	[small nu, Greek, tilde] RIMP2	[small nu, Greek, tilde] BP86	[small nu, Greek, tilde] B3LYP	A RIMP2	A BP86	A B3LYP	^⊥ σ u,BP86	^⊥ σ u,B3LYP
TZVP	1	hu	36.6	28.9	28.0	—	—	—	—	—
	2	fg	78.8	45.9	43.7	—	—	—	—	—
	3	hg	73.9	68.1	65.4	—	—	—	7674	8054
	4	t1u	77.5	72.2	72.5	0.116	0.480	1.719	—	—
	5	t2u	83.5	81.4	77.1	—	—	—	—	—
	6	fu	89.0	88.3	84.7	—	—	—	—	—
	7	hg	131.8	110.6	104.0	—	—	—	2307	2706
	8	ag	125.8	131.1	124.5	—	—	—	2784	3165
	9	t1u	186.3	177.0	170.0	1.070	2.788	0.197	—	—
TZVPP	1	hu	51.4	29.5	26.4	—	—	—	—	—
	2	fg	81.6	46.8	42.0	—	—	—	—	—
	3	hg	86.1	68.7	64.5	—	—	—	7505	7909
	4	t1u	90.3	72.9	71.5	0.005	0.431	1.695	—	—
	5	t2u	92.6	81.0	75.8	—	—	—	—	—
	6	fu	118.9	89.7	83.2	—	—	—	—	—
	7	hg	141.8	111.4	102.7	—	—	—	2109	2655
	8	ag	150.7	131.7	123.5	—	—	—	2552	2943
	9	t1u	201.7	175.3	168.0	0.118	2.900	0.219	—	—

---

Table 6 Vibrational wave numbers [small nu, Greek, tilde] (in cm⁻¹), infrared absorption coefficients A (in km mol⁻¹), and Raman scattering cross sections ^⊥σ_u for incident laser light, polarised perpendicular to the scattering plane, and a scattering angle of 90° (in 10⁻³⁶ m² sr⁻¹), calculated at the BP86 and B3LYP levels. ‘—’ denotes IR- and/or Raman-silent vibrations

Basis set	No.	Irrep	[small nu, Greek, tilde] BP86	[small nu, Greek, tilde] B3LYP	A BP86	A B3LYP	^⊥ σ u,BP86	^⊥ σ u,B3LYP
TZVPP(2f)	1	hu	31.9	28.0	—	—	—	—
	2	fg	48.8	43.2	—	—	—	—
	3	hg	71.0	65.9	—	—	6728	7218
	4	t1u	73.7	71.6	0.541	1.803	—	—
	5	t2u	83.9	77.5	—	—	—	—
	6	fu	91.3	84.3	—	—	—	—
	7	hg	113.1	104.0	—	—	2374	2897
	8	ag	133.7	125.3	—	—	2397	2702
	9	t1u	176.7	167.9	4.693	0.959	—	—
VQZPP(2f)	1	hu	28.2	29.3	—	—	—	—
	2	fg	45.6	45.9	—	—	—	—
	3	hg	70.9	67.7	—	—	5202	6058
	4	t1u	72.2	73.1	0.677	1.809	—	—
	5	t2u	87.1	79.5	—	—	—	—
	6	fu	88.2	87.3	—	—	—	—
	7	hg	113.8	107.5	—	—	2971	2997
	8	ag	133.7	128.9	—	—	2290	2493
	9	t1u	181.8	170.9	4.623	0.967	—	—

---

The character of certain vibrations of WAu₁₂ is shown in Fig. 1. Only the two t_1u modes are IR active. Of them the highest, 9t_1u, looks like a particle inside a box, vibrating against it. Both the single, breathing a_g, and the two h_g vibrations are Raman active.

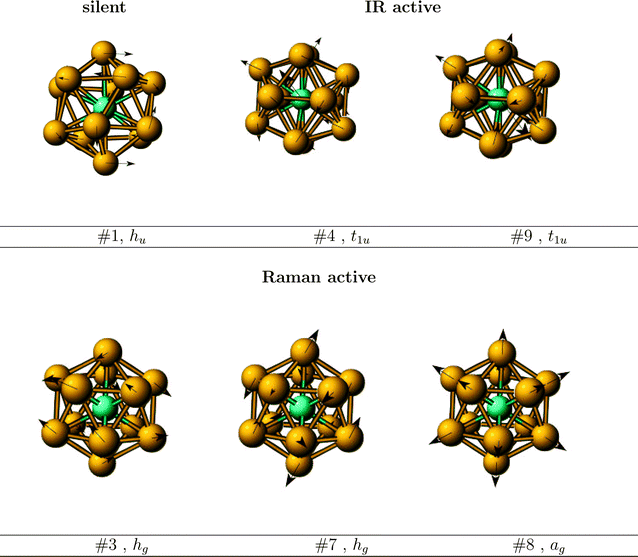Fig. 1 Normal modes of the IR and Raman active vibrations and of the (silent) lowest frequency mode.

The main character of the lowest, h_u vibration is having the two hemispheres rotating against each other. Note that there are six five-fold axes while h_u is five-dimensional. The D_5h transition state from I_h back to I_h will be discussed below.

As can be understood from Tables 5 and 6, the Raman intensities show a small dependence on the size of the basis set, which is, for instance, discussed in ref. 28. This is not the case for IR intensities, which suffer a larger change, in particular, for MP2 calculations. In general, the reason for this is the strong basis set dependence of the small dipole moment generated upon distortion of the equilibrium structure, which has no dipole moment due to inversion symmetry. In particular, the results from ab initio MP2 calculations depend much more strongly on the size of the basis set than DFT results do.

3.3 Intrasphere motions of the Au atoms

In order to analyse possible intrasphere motions of the Au atoms in WAu₁₂, we determined the relative energies for the transitions from the icosahedral to the D_5h and O_h structures of this compound. The latter structures are shown in Fig. 2.

Fig. 2 The D_5h transition state (left) and the O_h (right) stationary point of WAu₁₂.

Frequency analyses using density functional methods suggest that the O_h structure is a minimum (see Table 7), whereas RIMP2 predicts a fourth-order saddle point. The accuracy of the numerical procedure was tested for the critical mode and found to be much higher than the size of imaginary frequency. The D_5h structure is a transition state between two equivalent I_h structures (Table 8) and roughly 20 kJ mol⁻¹ above them at DFT level (Table 9). The RIMP2 value is higher, over 70 kJ mol⁻¹.

Table 7 The vibrational frequencies for the O_h structure of WAu₁₂ in cm⁻¹

No.	Irrep	[small nu, Greek, tilde] BP86/RI/TZVP	[small nu, Greek, tilde] RIMP2/TZVPP	[small nu, Greek, tilde] BP86/TZVPP	[small nu, Greek, tilde] B3LYP/TZVPP
1	a2g	14.50	i 51.89	13.02	12.25
2	t2u	23.13	i 32.35	22.30	22.25
3	eg	47.28	55.45	46.88	45.49
4	eu	50.83	63.32	50.94	46.37
5	t2g	75.64	87.85	75.52	70.99
6	t2u	77.10	78.44	76.56	71.71
7	t1u	80.56	97.21	80.38	78.70
8	t1g	82.54	99.53	82.93	75.84
9	eg	100.02	130.54	100.06	92.50
10	t1u	102.99	120.81	103.09	96.26
11	t2g	127.33	145.00	127.47	119.14
12	a1g	129.97	158.29	130.43	122.19
13	a2u	135.02	155.16	135.30	126.85
14	t1u	162.49	192.11	161.28	153.71

---

Table 8 The vibrational frequencies for the D_5h transition state structure of WAu₁₂ in cm⁻¹

No.	Irrep	[small nu, Greek, tilde] BP86/RI/TZVP	[small nu, Greek, tilde] RIMP2/TZVPP	[small nu, Greek, tilde] BP86/TZVPP	[small nu, Greek, tilde] B3LYP/TZVPP
1	a^″1	8.66i	23.59i	8.48i	8.09i
2	e^″2	25.81	35.80	25.16	25.00
3	e^″1	28.91	38.82	29.10	28.10
4	e^′1	46.44	67.82	46.67	43.47
5	e^″2	60.10	65.69	60.21	56.84
6	e^′2	66.00	77.91	66.04	63.01
7	e^″1	66.57	75.42	66.76	62.91
8	a^′1	74.53	84.72	74.23	69.96
9	a^″2	75.05	76.22	74.94	70.45
10	a^″2	83.76	92.05	82.22	80.63
11	e^′1	83.89	94.12	83.79	83.05
12	e^″2	84.70	109.34	85.50	78.63
13	e^′2	89.43	101.18	90.21	84.38
14	e^″1	112.99	129.75	113.25	106.30
15	e^′2	115.73	138.19	114.29	108.19
16	e^′1	119.13	137.07	118.51	112.30
17	a^′1	124.29	137.11	123.31	116.40
18	a^′1	129.18	149.09	128.44	121.59
19	e^′1	162.25	185.67	160.41	154.22
20	a^″2	165.23	185.89	163.82	157.52

---

Table 9 Relative energies in kJ mol⁻¹ for the reactions (A) T_d-Au₄²⁺ → D_4h-Au₄²⁺, (B) I_h-WAu₁₂ → D_5h-WAu₁₂, (C) I_h-WAu₁₂ → O_h-WAu₁₂, (D) I_h-Au₁₃⁵⁺ → D_5h-Au₁₃⁵⁺, and (E) I_h-Au₁₃⁵⁺ → O_h-Au₁₃⁵⁺. B3LYP(0.30/0.50) denotes the B3LYP functional with an exact exchange contribution of 30% or 50% instead the original value of 20%

Method	(A)	(B)	(C)	(D)	(E)
RIMP2/TZVPP	97.2	70.8	160.8	54.1	58.9
BP86/RI/TZVP	49.5	20.9	10.6	−5.6	−10.3
BP86/TZVPP	48.3	20.6	10.1	−6.1	−10.6
B3LYP/TZVPP	55.1	19.3	9.8	2.7	−3.8
B3LYP(0.30)/TZVPP	60.4	23.2	12.8	9.3	2.4
B3LYP(0.50)/TZVPP	69.5	31.0	14.2	20.0	13.1

---

According to transition state theory, an approximation for the rate constant for the rotation of the icosahedral structure to another icosahedral structure via the D_5h symmetric transition state is given by

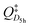where and Q_Ih are the partition functions (with respect to the lowest vibrational levels, v = 0) for the D_5h symmetric saddle point and the I_h symmetric reactant (and product) structure. In case of the D_5h structure, the 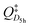is a reduced partition function without the degree of freedom which corresponds to the reaction coordinate. ΔV^‡ is the difference in (molar) potential energies for the two structures, including the zero-point kinetic energy (ZPE) contributions. The partition functions can also be included in the exponential function to yield where ΔG^‡ is the difference in Gibbs free energies. The temperature dependence of this rate constant is shown in Fig. 3 using the DFT data. It is seen that at 300 K a jump occurs about 10⁸ times per second, while at 50 K the rate is about 10⁻¹⁰. The results are summarized in Table 10. If the RIMP2 barrier were chosen, the jump frequencies are lower.

Fig. 3 Rate constant k (given as log₁₀(k)) as a function of the inverse temperature for the transition I_h-WAu₁₂ → D_5h-WAu₁₂.

Table 10 Gibbs free energy differences ΔG^‡ (in kJ mol⁻¹), and rate constants k (in s⁻¹) for the intramolecular, five-fold rotation of the I_h symmetric WAu₁₂ molecule evaluated for T = 298.15 K

Method	ΔG^‡	k
BP86/RI/TZVP	−28.09	7.45 × 10^7
BP86/TZVPP	−26.84	12.32 × 10^7
B3LYP/TZVPP	−27.74	8.60 × 10^7
RIMP2/TZVPP	−65.90	1.77 × 10^1

---

Searching for a simpler model for fluxional motions of small gold clusters, we calculated the barrier for the distortion of tetrahedral⁵⁰ Au₄²⁺ towards a D_4h-symmetric transition structure. The data are included in Table 9. No low barriers are found in this particular case. For the Au₁₃⁵⁺, the D_5h and O_h structures actually lie within a few kJ mol⁻¹ from the I_h.

We furthermore investigated the influence of the exact exchange contribution to all relative energies by setting the exact exchange in the B3LYP functional to 30% and 50%, since, for certain reactions,^51,52 the hybrid density functionals with a higher amount of exact exchange lead to improved descriptions of reaction barriers. In our case, the effect is 3 to 4 kJ mol⁻¹ for 30% exact exchange and 4 to 12 kJ mol⁻¹ for 50% exact exchange in case of the WAu₁₂ barriers, while the changes are larger for the highly charged Au₁₃⁵⁺ system (6 to 7 kJ mol⁻¹ for 30% exact exchange; about 17 kJ mol⁻¹ for 50% exact exchange). However, the results obtained with an increased percentage of exact exchange are still more in the range of the other DFT data than to those from RIMP2.

The fluxionality of these icosahedral clusters may enhance their eventual catalytical activity. Such an increase was recently noticed for the adsorption and activation of O₂ on gold clusters.⁵³ Similarly, Oviedo and Palmer⁵⁴ found a large number of isomers for Au₁₃. The group of Kappes⁵⁵ observed experimentally for Au₉⁺ two isomers below 140 K, corresponding to an activation energy of 10–20 kJ mol⁻¹.

A further, intriguing phenomenon that may or may not have a qualitative connection with the present fluxionality is the non-existence of frozen interstitial atoms in gold, down to 0.3 K.⁵⁶ For copper and silver they exist, and are activated at 38 and 28 K, respectively.⁵⁷ Sakai et al.⁵⁸ measured for the grain-boundary activation energy of nanocrystalline gold a value of 0.2 eV or 19 kJ mol⁻¹. Furthermore, a surface reorganization takes place for metallic gold. For all these aspects related to the general ‘softness’ of gold, see a review by Pyykkö.⁵⁹

We note that all ¹⁹⁷Au species with closed electron shells are identical heavy fermions. How low would the barriers have to be, for appreciable tunneling to take place, a process unlikely for a particle as heavy as the gold atom? Consider a one-dimensional potential step of height V and width 2a and let the gold atom, of mass m, vibrate against it with a frequency ν, near the bottom of the barrier. Then the average tunneling frequency becomes

Letting m be 3.2713 × 10⁻²⁵ kg, a be a fourth of a typical Au–Au distance or 75 pm and ν be 9.0 × 10¹¹ Hz, corresponding to 30 cm⁻¹, we obtain

f = 9.0 × 10¹¹exp[−93.766√V], (3.8)

with V expressed here in kJ mol⁻¹.

We conclude from the corresponding Fig. 4 that the barriers would have to be below 0.2 kJ mol⁻¹ for appreciable tunneling of a single gold atom to take place.

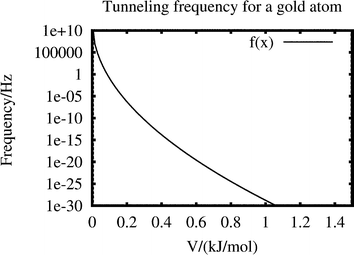Fig. 4 Average tunneling frequency of a gold atom, hitting a barrier of height V and width 2a = 150 pm 9.0 × 10¹¹ times per second. From eqn. (3.8).

3.4 Comparison to WAg₁₂

The frequency analysis of WAg₁₂ in Table 11 shows that the lowest frequencies are higher than those of WAu₁₂. For instance, the frequency for the h_u mode is increased by about 70% in the BP86/TZVPP calculation. The relative frequency shift in the higher-frequency modes is smaller. To analyze the differences in the force constants, we start from the quantities ϕ_i which are related to the square of the vibrational frequencies (Table 12) by . These force constants give a direct information of the electronic energy change ΔE along the vibrational normal coordinate Q_i, Since the normal coordinates Q_i are mass-weighted, we present the (non-mass-weighted) force constants k_i = ϕ_iμ_i, which are obtained by multiplying ϕ_i by the corresponding reduced mass μ_i. Note that the reduced mass for a polyatomic molecule was obtained using the definition where the summation is over all 3N entries (N is the number of atoms) in the matrix L, which diagonalizes the mass-weighted Hessian matrix, and m_j is the mass of the atom corresponding to entry j. The most notable difference in the force constants is again the increase of about 57% from Au to Ag for the lowest frequency, while most force constants for the higher-frequency modes are smaller for Ag. The former trend can qualitatively be related to the stronger s–d hybridization of gold and the latter trend to the relativistic increase of the stretching force constants. In simple terms, gold is softer, despite having stronger bonds, than silver. As a particular consequence, WAu₁₂ behaves like a ‘Rubik icosahedron’, in the sense of facile rotations of the two opposite hemispheres about the six five-fold axes.

Table 11 WAg₁₂: Vibrational wave numbers [small nu, Greek, tilde] (in cm⁻¹), infrared absorption coefficients A (in km mol⁻¹), and Raman scattering cross sections ^⊥σ_u for incident laser light, polarised perpendicular to the scattering plane, and a scattering angle of 90° (in 10⁻³⁶ m² sr⁻¹), from RIMP2, BP86, and B3LYP calculations. As an analytical method to calculate polarisabilities has not yet been implemented, Raman intensities cannot easily be obtained at the RIMP2 level. ‘—’ denotes IR and/or Raman silent vibrations. All results were obtained using Ahlrichs' TZVPP basis set

No.	Irrep	[small nu, Greek, tilde] RIMP2	[small nu, Greek, tilde] BP86	[small nu, Greek, tilde] B3LYP	A RIMP2	A BP86	A B3LYP	^⊥ σ u,BP86	^⊥ σ u,B3LYP
1	hu	57.88	50.26	47.00	—	—	—	—	—
2	fg	87.61	68.62	63.43	—	—	—	—	—
3	hg	99.10	86.73	82.02	—	—	—	5113	5840
4	t1u	89.86	91.49	89.52	0.033	2.525	4.107	—	—
5	fu	111.72	105.56	99.24	—	—	—	—	—
6	t2u	118.19	111.42	104.35	—	—	—	—	—
7	hg	158.62	133.29	123.48	—	—	—	3853	4397
8	ag	165.78	155.86	145.67	—	—	—	4334	5546
9	t1u	219.26	197.30	186.18	21.103	2.599	6.401	—	—

---

Table 12 Force constants (k in 10⁻³E_ha₀²) and reduced masses (μ in u) for WAu₁₂ and WAg₁₂ calculated at the BP86/TZVPP level

No.	Irrep	k BP86(WAu12)	k BP86(WAg12)	μ BP86(WAu12)	μ BP86(WAg12)
1	hu	6.5	10.2	196.97	106.91
2	fg	16.3	19.1	196.97	106.91
3	hg	35.2	30.4	196.97	106.91
4	t1u	38.7	39.5	192.37	124.64
5	t2u	48.9	50.2	196.97	106.91
6	fu	60.0	45.1	196.97	106.91
7	hg	92.4	71.9	196.97	106.91
8	ag	129.3	98.3	196.97	106.91
9	t1u	219.8	203.0	189.08	137.77

---

3.5 Bonding and population analysis

No definition of partial charges for non-identical atoms in molecules can be considered perfect. However, even if the definition of atomic charges can never be physically totally satisfactory, chemically they are very useful. One of the simplest population analyses available is the Mulliken method. However, it is known to be unstable with respect to basis set selection. For WAu₁₂, it completely fails; the Mulliken charge for W at the B3LYP/SVP level is −15 and the larger VQZPP basis set yields −78. Therefore, we considered alternative approaches to characterize the charge distribution of WAu₁₂. The partial charges for Au obtained with the GAPT³⁶ and SEN^37,38 methods given in Table 13 are zero or slightly positive.

Table 13 GAPT and SEN charges for W and Au in WAu₁₂ calculated with different methods

	GAPT^36		SEN^37,38
Method	W	Au	W	Au
RIMP2/TZVPP	0.06	0.00	—	—
BP86/TZVPP	0.23	−0.02	−4.10	0.34
BP86/VQZPP			−1.10	0.09
B3LYP/TZVPP	−0.09	0.01	−3.54	0.29
B3LYP/VQZPP			−1.01	0.08

---

To complete the picture, Voronoi charges were calculated. The Voronoi partitioning is based on integration of the electron density over the Voronoi cell fragments that define the molecule.³⁹ This method gives a charge of +0.91 for tungsten, using the BP86 functional with the TZVP basis. It has been suggested, that one should not use the Voronoi charges as such, but rather the change in charge from the atomic fragments to the molecule.⁶⁰ By using this so called Voronoi deformation density, a charge of +0.075 is obtained for tungsten.

All the population analyses above give, however, only an indirect picture of the charge distribution in WAu₁₂, and molecules in general. Their value comes more from giving trends in changes to atomic charges upon various perturbations of the system, not in providing absolute values as such.

For a highly symmetrical, nearly spherical species as WAu₁₂, there is a more direct alternative to population analyses, for extracting the charge of the central atom. By doing a direct integration of the electron density around W, and assuming a spherical atom, a good picture of the charge localisation can be obtained.^33,34 A somewhat arbitrary parameter in this case will be the radius of the tungsten atom. As seen from the integration curve in Fig. 5, any reasonable choice for the radius will yield a positive charge for tungsten. Two different radii have been selected for each method: The inflection point of the density accumulation, and half of the bond length. The inflection point, where the increase in electron density goes through a minimum, occurs for all electronic-structure methods at approximately 125 pm. The charges for W, obtained with these radii, are tabulated in Table 14. The tungsten is clearly positive.

Fig. 5 The charge of the tungsten atom as a function of its radius. Optimized structures for the respective methods have been used.

Table 14 Explicitly integrated charges for W in WAu₁₂ calculated with different methods. Values at the inflection point, 125 pm, and the midpoint of the W–Au distance are presented

Method	125 pm	Midpoint
RI-CC2/TZVPP	2.28	1.59 (135 pm)
BP86/TZVPP	2.71	1.80 (139 pm)
B3LYP/TZVPP	2.76	1.79 (141 pm)
B3LYP/VQZPP	2.76	1.87 (139 pm)

---

Both BP86 and B3LYP give very similar results. The most positive charge at a given radius is given by the B3LYP/TZVPP combination, which also has the longest W–Au distance. The closer to tungsten the gold atoms are, the more electron density they donate to the inner regions. The result for the coupled cluster RI-CC2 method is slightly different, implying a clearly less positive charge for the tungsten. For all quantum-chemical methods, to get even a neutral tungsten, the radius would have to be very large.

The assumption of a spherical central atom is naturally only an approximation. The electron cloud of tungsten is deformed by the gold atoms. This leads to a dodecahedral charge distribution and thereby to too small a number of electrons for tungsten. To correct for this, one can calculate the volume difference between a sphere and its inscribed dodecahedron. Then one can integrate over a thin shell to get the electron density in this region. Doing this at the point of inflection (125 pm) shows that approximately 0.5 electrons exist between the sphere and the polyhedron (BP86/TZVP). This gives a charge for tungsten of about +1.4 compared to +1.9 for the spherical integration. A direct integration of the dodecahedron was also performed. For this we determined the minimum of the gradient of the electron density. This defines a basin for tungsten that has the shape of a dodecahedron. Integrating the electron density in this basin also gives a charge of +1.4 for tungsten (BP86/TZVP).

Another chemically useful, but somewhat fluid, concept is the oxidation state of atoms in molecules. For gold, these have been determined using electron spectroscopy for chemical analysis (ESCA).⁶¹ The energy of the 4f_7/2 orbital plotted against the oxidation state of gold in different compounds gives approximately a straight line. The oxidation state of a new compound can be obtained from measured 4f_7/2 orbital energies. Here we applied this method in a computational way. By calculating the energy of the 4f_7/2 orbital for a few gold and tungsten compounds, whose oxidation states are known, we constructed straight lines representing the 4f_7/2 energies of gold and tungsten as a function of the oxidation state of the metal. The uncertainty in the fit is unfortunately a bit higher than desired, as can be seen in Figs. 6 and 7. Even so, the results suggest an oxidation state of about +1.5 for W and +0.7 for Au. Also this analysis points to a more positive tungsten. Positive oxidation states for all atoms in the system might seem somewhat contradictory for a chemist, while in metal physics it is common to regard for instance all atoms of metallic Eu or La as divalent and trivalent, respectively. Such a positive oxidation state of both tungsten and gold atoms can be given an explanation. The electron density difference between the WAu₁₂ molecule, and its constituent atoms shows how the electrons move upon formation of the cluster. The integrated electron density differences spheres around the tungsten and gold atoms are shown in Fig. 8. Near the atoms, the electron density difference between WAu₁₂ and the free atoms is negative, i.e., both W and Au in WAu₁₂ are more positively charged than the neutral atoms. The electron density close to the nucleus probably affects the 4f_7/2 orbital energy most, as these orbitals are quite close to the nuclei themselves. The fact that the ESCA analysis gives positive oxidation states for all atoms is not, after all, contradictory.

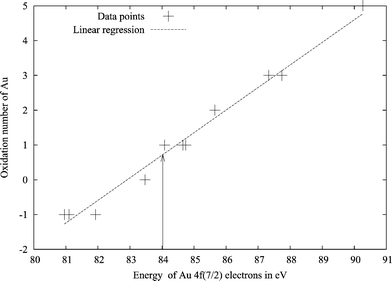Fig. 6 Plot of the 4f_7/2 electron energy versus the oxidation state of gold in different compounds. Calculated with BP86/TZVP using ADF. The arrow marks the value for gold in WAu₁₂.

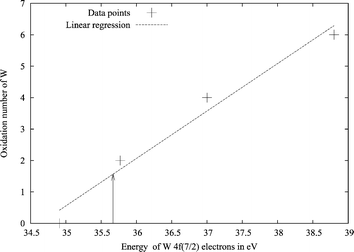Fig. 7 Plot of the 4f_7/2 electron energy versus the oxidation state of tungsten in different compounds. Calculated with BP86/TZVP using ADF. The arrow marks the value for tungsten in WAu₁₂.

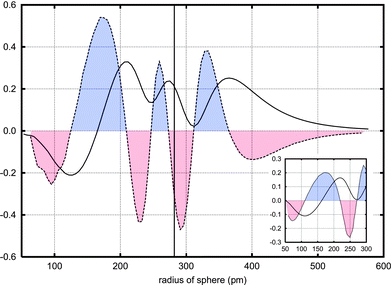Fig. 8 The integrated electron density difference between the WAu₁₂ molecule and the free atoms it is built from. Curves based on spheres around tungsten (big picture) and gold (inset) are shown. The density difference in it self is indicated by the whole line, its derivative as a dashed line. For clarity, the areas with a negative derivative are painted red (lower part), whereas areas with a positive derivate are blue (upper part). Thus, upon formation of the molecule, electrons move from the “red” areas to the “blue”. The vertical line at 282 pm shows the position of the gold atoms. Curve based on B3LYP/TZVPP-level calculations.

Fig. 8 also shows the differentiated changes in electron density (dashed lines). Areas with a negative derivative (shown in red) suffer a loss of electron density upon formation of the molecule, whereas areas with a positive derivative (in blue) gain electrons. A very large electron gathering between the tungsten and the gold atoms can be seen: A bond is formed.

Other features of the electron distribution also deserve commenting. As seen in Fig. 8, the derivative function has a long negative tail outside the WAu₁₂ molecule; at large distances, the electron cloud around the gold atoms is less diffuse compared to the electron density of the free atoms. In WAu₁₂, electrons are pulled inwards towards the centre. However, just outside the gold atoms, there is a sphere of electron gain. This reveals presence of a delocalised electron cloud, and might be an indication of molecular aromaticity. In fact, the nuclear magnetic shielding calculations show a quite strong long-range magnetic shielding effect where no electron density is present. The long-range magnetic shielding function has been used for estimating the strength of the magnetically induced currents which can be used as a measure of the degree of molecular aromaticity.⁶² Thus the magnetic shielding calculations also suggest that WAu₁₂ is aromatic.

Another method for looking at the bonding situation in WAu₁₂, is to calculate the electron-localisation function (ELF).³⁰ An isosurface of the ELF for the whole system is shown in Fig. 9. As seen in that figure, the gold atoms are far from spherical and there is an area of increased localised electrons between the tungsten and gold atoms. Fig. 10 shows a cut plane of the ELF curves for WAu₁₂. In this plane, the gold ligands look nearly triangular and between the gold and tungsten atoms one sees an area with high ELF values showing the covalent part of the gold–tungsten bond. The W–Au bond could be thought to lead to a local electron maximum between the atoms. Actually such a maximum rather seems to be pushed to the outer part of the cluster, leading to the peculiar shape of the gold atoms. This increase of electron density outside the cluster is also seen in Fig. 8. A comparison of the ELF plots in Fig. 10 with a corresponding ELF plot (not shown) for a neutral tungsten atom reveals the large size of the free tungsten atom and explains some of the difficulties of the electron partitioning schemes in assigning partial charges to tungsten and gold. Because the aurophilic attraction is predominantly of the dispersion type, it will not necessarily give any strong density deformations.

Fig. 9 Plot of an isosurface of the ELF of WAu₁₂.

Fig. 10 Cut plane through the ELF of WAu₁₂.

The proposed 18-electron bonding¹ was confirmed by different analyses. Table 15 shows contributions of the 5d, 6s and 6p orbitals of tungsten to the molecular orbitals. Also, looking at the radial distributions of orbitals of a_g, t_1u, and h_g symmetry, corresponding to the s, p, and d symmetries of W, shows their participation in bonding. Fig. 11 shows the normalised orbital density accumulation for selected, especially strong bonding orbitals.

Fig. 11 The radial integration of the norm for various molecular orbitals of WAu₁₂.

Table 15 The most important contributions to the molecular orbitals (MO) of WAu₁₂ from the 5d, 6s and 6p atomic orbitals of tungsten (AO(W)) calculated at the BP86/TZVP level. The MO energies (in eV) are given in the first column. The second and the third columns contain the MO number and its symmetry label. The percentage in the fourth column is the relative contribution from the AO in the fifth column to the given MO. The orbital energies (in eV) of the AOs and their occupation in spherically averaged atomic W are given in the two last columns

E/eV	MO No.	MO	%	AO (W)	E/eV	Occ
−12.975	88	12a1g	25.25%	6s	−6.549	2.0
−11.127	89	14e2g	28.53%	5dx^2−y^2,xy	−5.495	0.8
−11.127	90	13a1g	28.53%	5dz^2	−5.495	0.8
−11.126	91	14e1g	28.53%	5dyz,xz	−5.495	0.8
−10.892	92	16e1u	9.34%	6px,y	−1.288	0.0
−10.891	93	13a2u	9.34%	6pz	−1.288	0.0
−10.288	94	14a1g	14.86%	7s	0.736	0.0
−9.254	103	16e2g	2.84%	5dx^2−y^2,xy	−5.495	0.8
−9.254	104	15a1g	2.84%	5dz^2	−5.495	0.8
−9.253	105	16e1g	2.83%	5dyz,xz	−5.495	0.8
−8.704	109	17e1g	2.66%	5dyz,xz	−5.495	0.8
−8.704	110	17e2g	2.66%	5dx^2−y^2,xy	−5.495	0.8
−8.704	111	16a1g	2.65%	5dz^2	−5.495	0.8
−7.449	123	22e1u	2.69%	6px, y	−1.288	0.0
−7.448	124	17a2u	2.68%	6pz	−1.288	0.0
−6.252	127	17a1g	21.02%	5dz^2	−5.495	0.8
−6.252	128	20e2g	21.03%	5dx^2−y^2,xy	−5.495	0.8
−6.251	129	20e1g	21.04%	5dyz, xz	−5.495	0.8
HOMO
LUMO
−4.464	130	18a1g	46.74%	5dz^2	−5.495	0.8
−4.464	131	21e2g	46.74%	5dx^2−y^2,xy	−5.495	0.8
−4.464	132	21e1g	46.71%	5dyz,xz	−5.495	0.8
−4.205	133	19a1g	18.49%	6s	−6.549	2.0
−4.205	133	19a1g	10.01%	7s	0.736	0.0
−2.140	136	19a2u	22.68%	6pz	−1.288	0.0
−2.140	137	23e1u	22.66%	6px,y	−1.288	0.0

---

Finally, the shared electron number (SEN) analysis shows a very pronounced multicentre bonding in the molecule. At B3LYP/VQZPP-level, the W–Au pairs share as many as 4.1 electrons. The SEN between two adjacent golds is also high, 2.2. Furthermore, the three-centre analysis for the triangles W–Au–Au and Au–Au–Au gives SEN's of 1.8 and 1.3, respectively. Even for the four-centre trigonal pyramid, W–Au₃, the SEN is 1.2. The SEN analysis also further corroborates the 18-electron binding; the only positive contributors to the shared 4.1 electrons between W and the Au's are the a_g, t_1u, and h_g orbitals.

The presented bonding analyses allow us to comment on the way of writing the molecular formula as W@Au₁₂.² This notation implies a tungsten atom trapped inside an Au₁₂ cage. As clear bonding between the tungsten and gold atoms is found to exist, the W@Au₁₂ mental picture for the WAu₁₂ cluster is not really correct. The Au₁₂ cage does not exist as such but gets heavily distorted if the tungsten is removed. Hence the tungsten is not an addition to an otherwise stable molecule, in the same sense as in a M@C₆₀ system, which does have a strongly bound cage.

3.6 Optical properties

The excitation spectra of WAu₁₂ were calculated with both the BP86 and the B3LYP density functionals. In addition, RI-CC2, a coupled cluster method with single and approximate double excitations, was used. All methods give an excitation in the visible region between 380 and 460 nm, depending on the method and the basis set. This would give the compound a pale yellow or greenish-yellow color.

Much stronger absorption lines are found in the ultraviolet region. Both B3LYP and BP86 show a high intensity peak at about 250 nm. The overall correspondence between B3LYP and BP86 is, however, not very high. B3LYP gives quite similar spectra with both the TZVPP and VQZPP basis sets. BP86, on the other hand, seems to still be far from the basis set limit at TZVPP level; the VQZPP results differ significantly in the higher energy region of the spectra. Fig. 12 shows the spectra as calculated with various methods. Two of the lowest energy excitations calculated with various methods are compared in Table 16.

Fig. 12 Calculated UV/VIS spectra for WAu₁₂. The spectra from CC2/TZVPP (full line), B3LYP/VQZPP (dashed line) and BP86/VQZPP (dotted line) are compared. For RI-CC2, only excitations above 272 nm were obtained. All calculations used optimized structures.

Table 16 Calculated wavelengths (in nm) for the two energetically lowest-lying excitations for WAu₁₂, obtained with various methods. All calculations used optimized structures, except the CCS calculation, which used the RI-CC2/TZVPP structure. The oscillator strengths are given within parentheses. Only transitions with oscillator strengths stronger than 0.001 are considered

Method	exc 1	exc 2
CCS/TZVPP	284 (0.01)	267 (0.12)
CC2/TZVPP	442 (0.02)	381 (0.18)
BP86/TZVPP	466 (0.05)	408 (0.10)
BP86/VQZPP	455 (0.06)	401 (0.09)
B3LYP/TZVPP	420 (0.11)	346 (0.05)
B3LYP/VQZPP	418 (0.11)	345 (0.03)

---

It is worth noting that the CCS calculation gives much too energetic excitations; the double excitation character accounted for by CC2 lowers the energy considerably. For both CC2 peaks, the doubles contribution is over 18%. Such a high doubles contribution indicates that the uncertainties in the CC2 excitation energies can be significant.

Finally we have verified that the vertical excitation energy from the singlet ground state to a triplet excited state is 1.68 eV at B3LYP/VQZPP level. The triplet excited states were also considered by Li et al.²

3.7 Rotational spectra

The rotational constant, B, corresponding to the best calculated WAu₁₂ structure of R = 268.0 pm is 0.001490 cm⁻¹ (44.67 MHz or 2.14 mK). The high-resolution infrared and Raman spectra will show the corresponding rotational fine structure. Although the pure rotational levels are spectroscopically invisible, they will contribute to the partition function.

3.8 Hyperfine properties

Natural gold has only one stable isotope, ¹⁹⁷Au, I = [/]. The nuclear magnetic moment is very low, 0.1457 μ_N, and the nuclear quadrupole moment is +54.7 fm², see ref. 63. Consequently there will be 4¹² = 16 777 216 nuclear spin states of the twelve gold atoms, coupled to the rotational and vibrational wave functions of a freely moving molecule.

¹⁸³W has a natural abundance of 14.31%, I = ½ and a nuclear magnetic moment of 0.11778 μ_N. It is a frequently utilized NMR nucleus. The results of the NMR computations are listed in Table 17.

Table 17 Nuclear magnetic shieldings (σ in ppm), reduced spin–spin coupling constants (K in 10¹⁹ T² J⁻¹), and nuclear quadrupole coupling constants (NQCCs in MHz) calculated at the BP86/TZP level. Chemical shifts (δ in ppm) with respect to WO₄²⁻ as the reference

Property	rel.^a	nrel.^b
a Relativistic ZORA calculation with ZORA-TZP basis, including spin–orbit coupling unless otherwise noted. b Nonrelativistic calculation with nonrelativistic TZP basis. c ZORA-TZP+s basis for W (shieldings), or W and Au (coupling constants). See Sec. 2.5 for details d Scalar relativistic ZORA computation. e Corresponding to (5 ^1K + 5 ^2K + ^3K)/11.
σ(^183)W	15 741	13 191
	16 302^c
δ(^183)W	−13 279	−12 693
	−13 520^c
K(WAu)	7350^c^d	3322
^1 K(AuAu)	11 501^c^d	6000
^2 K(AuAu)	15 564^c^d	329
^3 K(AuAu)	693^c^d	−4596
K av(AuAu)	12 365^e	2459^e
NQCC (^197Au)	549^c	275
	482^c^d

---

Tungsten chemical shifts have previously been calculated with the ADF ZORA NMR method and the TZP basis by Ziegler et al.⁴⁷ They have obtained a good overall agreement with experimental data, with a mean absolute deviation of approximately 3% of the investigated ¹⁸³W chemical shift range of 7200 ppm. Spin–orbit contributions were found to be of minor importance for ¹⁸³W chemical shifts in ref. 47.

As to the chemical shifts, compared to the reference system WO₄²⁻, the ¹⁸³W nucleus in WAu₁₂ is very strongly shielded. The computations thus predict an extraordinarily large chemical shift for W in WAu₁₂ of more than −13 000 ppm. For comparison, the largest chemical shifts that have been calculated by Ziegler et al. in ref. 47 and compared to experiment were 3638 ppm for WS₄²⁻ and −3876 ppm for W(CO)₆, respectively, with respect to WO₄²⁻. A comparison with the nonrelativistic results demonstrates that the chemical shift in WAu₁₂ is only to a comparatively small extent due to relativistic effects. It results from a large positive paramagnetic shielding contribution of 3243 ppm as compared to the reference (WO₄²⁻: −8088 ppm). In addition, the spin–orbit coupling contributions of 3850 ppm to the ¹⁸³W shielding in WAu₁₂ are also significantly larger than for the reference (1937 ppm). Thus the spin–orbit contributions to the chemical shift here exceed the ones reported by Ziegler et al.⁴⁷ by a large margin. The diamagnetic shielding contributions for WAu₁₂ and the reference are very similar (8649 ppm for WAu₁₂ as compared to 8613 ppm for WO₄²⁻). It appears that the Au cage quite effectively shields the external magnetic field.

When converted to frequency units, the spin–spin coupling constants are quite small, reflecting the smallness of the W and Au nuclear magnetic moments, and the small s character of the bonds, compared with Hg–Hg bonds, see for the latter for instance ref. 64. The calculated J(WAu) is 65 Hz and the averaged J(AuAu) over all gold positions, corresponding to a rapid intramolecular hindered rotation, is 45 Hz. A comparison with the nonrelativistic data shows that the magnitudes of the W–Au as well as the Au–Au reduced coupling constants exhibit large positive contributions due to relativistic effects, in particular for ²K(AuAu). However, already at the nonrelativistic level large magnitudes for K(WAu) and ¹K(AuAu) and ³K(AuAu) are found. The relativistic increase of the coupling constants is comparatively small for a coupling constant between two heavy nuclei. The case of WAu₁₂ here appears to be similar to Pt–Pt and Pt–ligand coupling constants previously investigated in refs. 43,65,66. For these coupling constants typically a sizeable, but not huge, relativistic increase is obtained. Its magnitude depends sensitively on the chemical environment of the coupled nuclei and is balanced by relativistic effects on the hyperfine integrals, on the chemical bond between the coupled atoms, and on their interaction with other neighboring atoms. Interestingly, the two-bond Au–Au coupling constant is predicted to be larger than the one-bond coupling constant. They both exceed the three-bond coupling by an order of magnitude in the relativistic case.

The calculated NQCC values for the ¹⁹⁷Au nuclear ground state are of the order of 0.5 GHz. This is a typical order of magnitude for gold compounds. Note that the quadrupole splittings will then exceed the Zeeman splittings in typical laboratory fields. More specifically, in pure gold clusters, the Mössbauer quadrupole splittings of unbound surface atoms and surface atoms bound to trimethyl phosphines are observed to be⁶⁷ 1.40 and 3.5 mm/s, which translates to 87 and 218 MHz of splitting, respectively.

At most temperatures the spin–lattice relaxation, characterized by the time T₁, of the Au spin system is expected to be faster than the calculated J(WAu). Due to these fast spin flips, it is expected that the corresponding splitting of the W line will be averaged out. A single, narrow ¹⁸³W signal is expected, about 13 500 ppm upfield from the WO₄²⁻ standard. In the unlikely case of long T₁(Au) but fast molecular rotation, averaging out the quadrupole and direct spin–spin couplings, the W signal would be a 37-component weighted trisdekaheptuplet, with predicted intervals of 65 Hz, due to the coupling of the ¹⁸³W nucleus to the total nuclear spin of the twelve gold atoms, with a total spin I = 18.

The Mössbauer spectrum of every ¹⁹⁷Au nucleus will be dominated by its quadrupole splitting. If the inner and outer hindered rotations are both slower than about 100 MHz, it will be observed, otherwise not. In gas-phase magnetic resonance the predominant quantization will come from the twelve weakly coupled quadrupolar systems, altogether coupled to the molecular rotation states. The solid-state nuclear quadrupole resonance should show a single signal corresponding to the splitting between m_I = ±½ and ±[/]. For spin [/] that resonance will occur at NQCC/2, or 275 MHz.

Acknowledgements

This work was carried out during the tenure of a Humboldt Research Prize by P. Pyykkö at Erlangen. It occurred within WG 9 (‘HAMEC’) of the COST Action D26. The Helsinki group was supported by The Academy of Finland and by EU RTN “Molecular Properties and Molecular Materials (MOLPROP)”, contract No. HPRN-2000-00013. M.P.J. acknowledges an Acta Chemica Scandinavica travel grant. CSC–Scientific Computing Ltd. provided ample computer time. We thank Juha Vaara for help with some magnetic properties calculations, and Kai Nordlund and Jaak Suurpere for stimulating discussions. The Erlangen group was supported by the Fonds der Chemischen Industrie and by the collaborative research project SFB 583. J. N. gratefully acknowledges funding by a Kekulé-Stipendium of the Fonds der Chemischen Industrie. J.A. is grateful for financial support by the Deutsche Forschungsgemeinschaft in form of an “Emmy Noether” grant.

References

1. P. Pyykkö and N. Runeberg, Angew. Chem., Int. Ed. Engl., 2002, 41, 2174–2176.
2. X. Li, B. Kiran, J. Li, H.-J. Zhai and L.-S. Wang, Angew. Chem., Int. Ed. Engl., 2002, 41, 4786–4789.
3. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
4. TURBOMOLE, University of Karlsruhe, http://www.turbomole.com/.
5. Amsterdam Density Functional Program, Vrije Universiteit, Amsterdam, http://www.scm.com/.
6. C. Fonseca Guerra, O. Visser, J. G. Snijders, G. te Velde and E. J. Baerends, in Methods and Techniques for Computational Chemistry, STEF, Cagliari, 1995.
7. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, S. J. A. van Gisbergen, C. Fonseca Guerra, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
8. D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123.
9. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
10. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
11. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
12. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
13. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
14. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11 623–11 627.
15. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290.
16. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
17. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
18. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161.
19. D. Feller, E. D. Glendening, D. E. Woon and M. W. Feyereisen, J. Chem. Phys., 1995, 103, 3526–3542.
20. M. W. Feyereisen, D. Feller and D. A. Dixon, J. Phys. Chem., 1996, 100, 2993–2997.
21. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
22. C. Hättig and A. Kohn, J. Chem. Phys., 2002, 117, 6939–6951.
23. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
24. P. Pyykkö, N. Runeberg and F. Mendizabal, Chem. Eur. J., 1997, 3, 1451–1457.
25. F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152.
26. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
27. E. van Lenthe and E. J. Baerends, J. Comp. Chem., 2003, 24, 1142–1156.
28. J. Neugebauer, M. Reiher, C. Kind and B. A. Hess, J. Comput. Chem., 2002, 23, 895–910.
29. D. A. Long, Raman Spectroscopy, McGraw-Hill, New York, 1977.
30. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
31. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
32. M. Kohout, dgrid, Max-Planck-Institut für Chemische Physik fester Stoffe, Dresden, 2001.
33. M. P. Johansson, M. R. A. Blomberg, D. Sundholm and M. Wikström, Biochim. Biophys. Acta – Bioenergetics, 2002, 1553, 183–187.
34. M. P. Johansson, D. Sundholm, G. Gerfen and M. Wikström, J. Am. Chem. Soc., 2002, 124, 11 771–11 780.
35. M. Kohout, basin, Max-Planck-Institut für Chemische Physik fester Stoffe, Dresden, 2001.
36. J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333–8336.
37. E. R. Davidson, J. Chem. Phys., 1967, 46, 3320–3324.
38. R. Heinzmann and R. Ahlrichs, Theor. Chim. Acta, 1976, 42, 33–45.
39. G. te Velde, Numerical Integration and Other Methodological Aspects of Bandstructure Calculations in Chemistry, Vrije Universiteit, Amsterdam, 1990.
40. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
41. R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Chem. Phys. Lett., 1997, 264, 573–578.
42. S. K. Wolff, T. Ziegler, E. van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689–7698.
43. J. Autschbach and T. Ziegler, J. Chem. Phys., 2000, 113, 936–947.
44. J. Autschbach and T. Ziegler, J. Chem. Phys., 2000, 113, 9410–9418.
45. E. van Lenthe and E. J. Baerends, J. Chem. Phys., 2000, 112, 8279–8292.
46. J. Autschbach and E. Zurek, J. Phys. Chem. A, 2003, 107, 4967–4972.
47. A. Rodriguez-Fortea, P. Alemany and T. Ziegler, J. Phys. Chem. A, 1999, 103, 8288–8294.
48. M. Reiher, J. Neugebauer and B. A. Hess, Z. Phys. Chem., 2003, 217, 91–103.
49. J. Neugebauer and B. A. Hess, J. Chem. Phys., 2003, 118, 7215–7225.
50. P. Pyykkö and N. Runeberg, J. Chem. Soc., Chem. Commun., 1993, 1812–1813.
51. B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem., 2000, 104, 4811–4815.
52. B. J. Lynch and D. G. Truhlar, J. Phys. Chem., 2001, 105, 2936–2941.
53. H. Häkkinen, S. Abbet, A. Sanchez, U. Heiz and U. Landman, Angew. Chem., Int. Ed. Engl., 2003, 42, 1297–1300.
54. J. Oviedo and R. E. Palmer, J. Chem. Phys., 2002, 117, 9548–9551.
55. P. Weis, T. Bierweiler, E. Vollmer and M. M. Kappes, J. Chem. Phys., 2002, 117, 9293–9297.
56. H. Schroeder and B. Stritzker, Radiat. Eff., 1977, 33, 125–126.
57. P. Ehrhart, in Properties and interactions of atomic defects in metals and alloys, ed. H. Ullmaier, Springer, Berlin, 1991, vol. 25.
58. S. Sakai, H. Tanimoto, E. Kita and H. Mizubayashi, Phys. Rev. B, 2002, 66, 214 106.
59. P. Pyykkö, Angew. Chem., 2004, 116 , accepted.
60. F. M. Bickelhaupt, unpublished results.
61. J. Knecht, R. Fischer, H. Overhof and F. Hensel, J. Chem. Soc., Chem. Commun., 1978, 905–906.
62. J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435.
63. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 83rd edn., 2002.
64. J. Autschbach, C. D. Igna and T. Ziegler, J. Am. Chem. Soc., 2003, 125, 4937–4942.
65. J. Autschbach, C. D. Igna and T. Ziegler, J. Am. Chem. Soc., 2003, 125, 1028–1032.
66. J. Autschbach and T. Ziegler, J. Am. Chem. Soc., 2001, 123, 3341–3349.
67. L. Stievano, S. Santucci, L. Lozzi, S. Calogero and F. E. Wagner, J. Non-Cryst. Solids, 1998, 232–234, 644–649.
68. B. Simard, P. A. Hackett, A. M. James and P. R. R. Langridge-Smith, Chem. Phys. Lett., 1991, 186, 415–422.
69. V. Beutel, H.-G. Krämer, G. L. Bhale, M. Kuhn, K. Weyers and W. Demtröder, J. Chem. Phys., 1993, 98, 2699–2708.
70. G. A. Bishea and M. D. Morse, J. Chem. Phys., 1991, 95, 5646–5659.
71. V. Kellö and A. J. Sadlej, J. Chem. Phys., 1995, 103, 2991–2999.
72. J. C. Fabbi, J. D. Langenberg, Q. D. Costello, M. D. Morse and L. Karlsson, J. Chem. Phys., 2001, 115, 7543–7549.

---