Sorption and transport of water vapor in thin polymer films at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) °C
°C
Alberto
Arce†
,
Francesco
Fornasiero
,
Oscar
Rodríguez†
,
Clayton J.
Radke
and
John M.
Prausnitz
*
Chemical Engineering Department, University of California, Berkeley, and Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720. E-mail: prausnit@cchem.berkeley.edu; Fax: +1 510 642 4778; Tel: +1 510 642 3592
First published on 27th November 2003
Abstract
Using a gravimetric technique, experimental data at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C are reported for isothermal sorption equilibria and sorption kinetics of water vapor in poly(N,N-dimethyl methacrylamide)
(PDMAA), poly(2-dimethyl aminoethyl methacrylate)
(PDMAEMA), poly(acrylic acid)
(PAA), and in a typical membrane of a commercial soft-contact lens made of poly(2-hydroxyethyl methacrylate)
(PHEMA). The highest sorption of water vapor is in PDMAA. The Flory–Huggins model and the Zimm–Lundberg clustering theory are used to interpret the equilibrium data. Over the entire range of water activity, the four materials show clustering functions larger than −1 indicating that water molecules cluster together in the polymers. The least hydrophilic polymer, PDMAEMA, and the most hydrophilic one, PDMAA, show respectively, the highest and the lowest tendency of water molecules to form clusters. Water diffusion into the polymer matrix is faster in PDMAEMA (diffusion coefficient, D
°C are reported for isothermal sorption equilibria and sorption kinetics of water vapor in poly(N,N-dimethyl methacrylamide)
(PDMAA), poly(2-dimethyl aminoethyl methacrylate)
(PDMAEMA), poly(acrylic acid)
(PAA), and in a typical membrane of a commercial soft-contact lens made of poly(2-hydroxyethyl methacrylate)
(PHEMA). The highest sorption of water vapor is in PDMAA. The Flory–Huggins model and the Zimm–Lundberg clustering theory are used to interpret the equilibrium data. Over the entire range of water activity, the four materials show clustering functions larger than −1 indicating that water molecules cluster together in the polymers. The least hydrophilic polymer, PDMAEMA, and the most hydrophilic one, PDMAA, show respectively, the highest and the lowest tendency of water molecules to form clusters. Water diffusion into the polymer matrix is faster in PDMAEMA (diffusion coefficient, D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10–20
10–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1) and in PDMAA (D
10−8 cm2 s−1) and in PDMAA (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.9–8.7
4.9–8.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1) than in PHEMA-lens material (D
10−8 cm2 s−1) than in PHEMA-lens material (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.55–3.4
0.55–3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1) and PAA (D
10−8 cm2 s−1) and PAA (D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.98–3.5
0.98–3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1). The measured diffusion coefficients increase with water activity in the PHEMA-lens, decrease with activity in PDMAEMA, and show a more complex concentration dependence in PDMAA and PAA. By writing the diffusion coefficient as a product of an intrinsic mobility, Đ, and a non-ideality thermodynamic factor, Γ, the concentration dependence of D is explained by the interplay of two factors: rising plasticization with water activity, which causes an increase in Đ, and the effect of composition on Γ, decreasing with water activity.
10−8 cm2 s−1). The measured diffusion coefficients increase with water activity in the PHEMA-lens, decrease with activity in PDMAEMA, and show a more complex concentration dependence in PDMAA and PAA. By writing the diffusion coefficient as a product of an intrinsic mobility, Đ, and a non-ideality thermodynamic factor, Γ, the concentration dependence of D is explained by the interplay of two factors: rising plasticization with water activity, which causes an increase in Đ, and the effect of composition on Γ, decreasing with water activity.
Introduction
Sorption and diffusion of ordinary fluids in polymers is of interest in various technologies including packaging, membrane separations, drug-delivery systems and contact lenses.1–4 Sorption and diffusion of water in polymers that are used in a contact lens are of prime interest for achieving a contact lens that is suitable for extended or continuous wear.3This work reports experimental, isothermal vapor-sorption equilibria and diffusion coefficients of water in three homopolymer films whose monomers may be included in the formulation of continuous-wear contact lenses, and in a typical membrane used in commercial soft contact lenses made of poly(2-hydroxyethyl methacrylate)
(PHEMA). The homopolymers are poly(N,N-dimethyl methacrylamide)
(PDMAA), poly(2-dimethyl aminoethyl methacrylate)
(PDMAEMA), and poly(acrylic acid)
(PAA). Hydrophilic polymers are used in contact-lens technology because adequate water content in a contact lens is essential for eye comfort.5 Experiments are carried out at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, the average temperature of a contact lens on the eye, in a quartz-spring gravimetric apparatus.6 We use a well-defined, thin-film polymer-sample geometry and measure spring elongation as a function of time for different water-vapor activities. For each solvent-polymer system, the equilibrium data are used to calculate the binary Flory parameter.7 Toward obtaining some information on the molecular state of dissolved water, we use the clustering theory of Zimm and Lundberg.8,9 Water vapor diffusion coefficients are calculated from a diffusion model derived from Fick's second law. Although similar data have been reported for PAA at different temperatures,10 to our knowledge, no previous data have been reported for PDMAA and PDMAEMA.
°C, the average temperature of a contact lens on the eye, in a quartz-spring gravimetric apparatus.6 We use a well-defined, thin-film polymer-sample geometry and measure spring elongation as a function of time for different water-vapor activities. For each solvent-polymer system, the equilibrium data are used to calculate the binary Flory parameter.7 Toward obtaining some information on the molecular state of dissolved water, we use the clustering theory of Zimm and Lundberg.8,9 Water vapor diffusion coefficients are calculated from a diffusion model derived from Fick's second law. Although similar data have been reported for PAA at different temperatures,10 to our knowledge, no previous data have been reported for PDMAA and PDMAEMA.
Experimental
1. Materials and sample preparation
Water is obtained from a Barnstead NANOpure® system and degassed with a standard freeze/thaw procedure. Polymers used are PDMAA, PDMAEMA, PAA, and PHEMA-lens material. Table 1 gives characteristics of these polymers: supplier, molecular weight, density, and glass-transition temperature measured by modulated scanning calorimetry (DSC 2920, Modulated DSC, TA Instruments). Polymer films are prepared by solvent casting. The solvent used for casting PDMAEMA film is toluene (Fisher Scientific, 99.9%), whereas distilled water is used for PDMAA and PAA. Because PHEMA-lens material was kindly provided by Bausch & Lomb (serial number 2248-SH-140A) as a thin film stored in distilled water, it is used without further solvent treatment. Each film is dried at a temperature higher than its glass-transition temperature for 24 h to remove the solvent completely. The film is then cooled slowly (0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C min−1) in a vacuum oven (Napco E Series Model 5851) fluxed with dry nitrogen. PDMAEMA film is pre-equilibrated with liquid water for 24 h and then dried again following the same procedure. However, no similar treatment is made for PDMAA and PAA because they are water-soluble. The thickness of each film is measured using a micrometer (Mitutoyo MDC 0–1″ PF, accuracy ±3 µm) at different locations; the average is used for subsequent calculations.
°C min−1) in a vacuum oven (Napco E Series Model 5851) fluxed with dry nitrogen. PDMAEMA film is pre-equilibrated with liquid water for 24 h and then dried again following the same procedure. However, no similar treatment is made for PDMAA and PAA because they are water-soluble. The thickness of each film is measured using a micrometer (Mitutoyo MDC 0–1″ PF, accuracy ±3 µm) at different locations; the average is used for subsequent calculations.
| Polymer | Supplier | CAS No./Serial number | MW | ρ/g cm−3 | T g/°C |
|---|---|---|---|---|---|
| a Estimated. b SP2: Scientific Polymer Products, Inc. c Reported by supplier. d Equilibrium water content in pure water of 38 weight % (reported by Bausch & Lomb). | |||||
| PDMAA | Polymer Source | 26793-34-0 | 4000 | 1.15a | 105 |
| PDMAEMA | SP2b | 25154-86-3 | 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.10a | 18 |
| PAA | Aldrich | 9003-01-4 | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.15c | 108 |
| PHEMA-lens materiald | Bausch & Lomb | 2248-SH-140A | — | 1.15c | 118 |
2. Apparatus
A gravimetric technique is used for both sorption and diffusion experiments.6Fig. 1 shows a schematic of the apparatus. The elongation of a quartz spring (Ruska Instruments) determines the polymer's water uptake. The springs are calibrated using known masses previously weighed with a Mettler M3 microbalance with a precision of ±1 μg. The springs have a sensitivity of about 5 mm/mg, and the calibration curves are linear in all cases. The elongation measurements are corrected for the temperature-dilation effect as suggested by Ruska:LC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LM[1 LM[1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.35 1.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4(T 10−4(T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tcal)] Tcal)] | (1) |
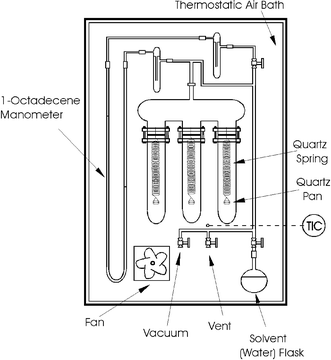 | ||
| Fig. 1 Schematic of the apparatus for water-vapor sorption and diffusion measurements. | ||
A U-tube manometer is used to measure the pressure. The manometer liquid is 1-octadecene, selected because of its low vapor pressure, immiscibility with water, suitable density for the pressure range of interest here, and for a suitable U-tube length. Its density is calculated with an equation given by Daubert and Danner.11
The spring elongation and the manometer-liquid-height difference are measured with a cathetometer (Wild, model KM274) with a precision of ±0.1 mm. The equipment is enclosed in an air bath with an Omega CN9000 PID controller (accuracy ±0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) to keep the experimental temperature very close to 35
°C) to keep the experimental temperature very close to 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
3. Vapor-sorption equilibria
A polymer sample (∼10–25 mg) is attached to a spring. Water-soluble polymers are loaded into a quartz pan (∼10 mg) (Ruska Instruments); non-water-soluble polymers are directly hung to the spring hook. After closing the glass chambers, using vacuum grease to seal the joints, the apparatus is evacuated with a vacuum pump, and both 1-octadecene and water are degassed by a standard freeze/thaw procedure.12 The polymer sample is dried at 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for at least 24 h to constant weight. Then the temperature is set to 35
°C for at least 24 h to constant weight. Then the temperature is set to 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, and a vacuum test is carried out to ensure that the apparatus can maintain the desired vacuum with changes of less than 0.2 torr day−1. The working-pressure range is between 4 and 40 torr.
°C, and a vacuum test is carried out to ensure that the apparatus can maintain the desired vacuum with changes of less than 0.2 torr day−1. The working-pressure range is between 4 and 40 torr.
After vacuum testing is satisfied, water vapor is injected by opening the solvent-flask valve. Spring elongation and pressure are measured at several time steps until equilibrium is reached, i.e. when several successive measurements agree within experimental error. Then a new injection is made. The experiments correspond to a range of vapor activities, aw, from 15 to 85%. Water activity is calculated assuming an ideal gas phase of pure water vapor, neglecting the tiny vapor pressure of 1-octadecene:
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C taken from Daubert and Danner.11 The constant-temperature bath contains three quartz springs to reduce the time for data acquisition.
°C taken from Daubert and Danner.11 The constant-temperature bath contains three quartz springs to reduce the time for data acquisition.
4. Diffusion measurements
The preparation procedure for sorption-kinetics measurements is identical to that for equilibrium measurements. Following vapor injection, water uptake and time are measured simultaneously. Time is obtained from a stopwatch (Fisher Scientific, uncertainty =0.13 s), started as soon as the manometer liquid moves. After equilibrium is reached, a new run is performed at a higher water activity. For PDMAA and PDMAEMA diffusion experiments, we use a new polymer film, different from that used in the equilibrium experiments. For PDMAA and PDMAEMA, the diffusion experiments are performed in steps of 20% in activity starting at zero up to 80%. Because the rate of sorption is very slow in PAA at low activity, the diffusion experiments are carried out in steps of 10% activity in the interval from 60 to 80%. For the PHEMA-lens material, diffusion measurements are made at 20, 40, 80 and 85% water activity.Results and discussion
1. Vapor-sorption equilibria
For each polymer, the equilibrium water content is obtained from the weight gain of the sample at long sorption time, when the weight reaches a stable value for a fixed water activity. Table 2 reports water-vapor activity and water weight fraction at equilibrium in these four polymers at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. For PAA, the results agree quantitatively with the isotherms measured by Chang et al.,10 identical at 30 and 40
°C. For PAA, the results agree quantitatively with the isotherms measured by Chang et al.,10 identical at 30 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. For PDMAA and PDMAEMA, no previous data have been reported. For PHEMA-lens material, our results are in very good agreement with similar data reported for PHEMA homopolymer.13
°C. For PDMAA and PDMAEMA, no previous data have been reported. For PHEMA-lens material, our results are in very good agreement with similar data reported for PHEMA homopolymer.13
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
°C
| PDMAA | PDMAEMA | PAA | PHEMA-lens material | ||||
|---|---|---|---|---|---|---|---|
| a w | w w | a w | w w | a w | w w | a w | w w |
| 0.14 | 0.025 | 0.14 | 0.004 | 0.29 | 0.037 | 0.19 | 0.015 |
| 0.24 | 0.053 | 0.24 | 0.008 | 0.48 | 0.086 | 0.40 | 0.038 |
| 0.38 | 0.095 | 0.38 | 0.019 | 0.59 | 0.138 | 0.66 | 0.083 |
| 0.49 | 0.136 | 0.49 | 0.032 | 0.69 | 0.200 | 0.72 | 0.102 |
| 0.58 | 0.178 | 0.58 | 0.048 | 0.80 | 0.292 | 0.78 | 0.126 |
| 0.68 | 0.235 | 0.68 | 0.076 | 0.86 | 0.395 | 0.84 | 0.154 |
| 0.76 | 0.293 | 0.76 | 0.112 | ||||
| 0.83 | 0.372 | 0.83 | 0.174 | ||||
The equilibrium isotherms show a large degree of upturn at high activities (Fig. 2). Two phenomena are suggested to interpret the equilibrium isotherm upturn: (1) plasticization of the polymer by water, and/or (2) clustering of water molecules. These phenomena provide opposite effects for the concentration dependence of the diffusion coefficient.14–16
The Flory–Huggins theory7 is widely used to correlate experimental phase equilibria for solvent-polymer systems:
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.44 correlates the sorption isotherm well. This value is less than 0.5, the upper limit for complete miscibility when χ is independent of composition, indicating that water is a good solvent for this polymer.17 In PAA, χ decreases from approximately 1 at low activities to 0.4 at high activities as activity increases. Chang et al.10 report similar values in the range of water activity between 0.7 and 0.9 at 40
0.44 correlates the sorption isotherm well. This value is less than 0.5, the upper limit for complete miscibility when χ is independent of composition, indicating that water is a good solvent for this polymer.17 In PAA, χ decreases from approximately 1 at low activities to 0.4 at high activities as activity increases. Chang et al.10 report similar values in the range of water activity between 0.7 and 0.9 at 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. In less hydrophilic PDMAEMA and PHEMA-lens material, χ is higher than 1.
°C. In less hydrophilic PDMAEMA and PHEMA-lens material, χ is higher than 1.
 | ||
Fig. 3 Flory interaction parameter χversus water-vapor activity for PDMAA, PDMAEMA, PAA, and PHEMA-lens material at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
Water molecules have a tendency to form clusters when absorbed in a polymer.18 To provide a measure for clustering, Zimm and Lundberg8,9 defined the clustering integral Gww. The ratio of the clustering integral to the partial molecular volume Gww/vw, called the clustering function, is obtained from equilibrium data:
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1, the solution is ideal, and the solvent molecules exclude only their own volume to other solvent molecules, not affecting their distribution. When Gww/vw is greater than −1, increasing values of the clustering function correspond to a stronger tendency of solvent molecules to cluster together. Clustering functions less than −1 denote the tendency of like molecules to remain isolated and increasingly so as Gww/vw becomes more negative. To calculate the derivative in eqn. (4) we plot aw/Φwversusaw and fit the plot to a second-order polynomial function.19–21 However, for PDMAA a linear fit is sufficient. Fig. 4 shows clustering functions larger than −1, indicating that water molecules tend to cluster together in these four materials. The least hydrophilic polymer, PDMAEMA, shows the largest clustering tendency, decreasing significantly with increasing water activity. Because the Flory interaction parameter for PDMAEMA/water is also a strong decreasing function of water activity, the lower tendency to cluster may be explained by more favorable polymer-water interaction at higher activities. Similar trends are observed in PAA and PDMAA. In the latter, water has the smallest tendency to cluster and the smallest Flory interaction parameter. However, PHEMA-lens material reveals a rising tendency for clustering with increasing water activity, despite the decreasing Flory interaction parameter.
−1, the solution is ideal, and the solvent molecules exclude only their own volume to other solvent molecules, not affecting their distribution. When Gww/vw is greater than −1, increasing values of the clustering function correspond to a stronger tendency of solvent molecules to cluster together. Clustering functions less than −1 denote the tendency of like molecules to remain isolated and increasingly so as Gww/vw becomes more negative. To calculate the derivative in eqn. (4) we plot aw/Φwversusaw and fit the plot to a second-order polynomial function.19–21 However, for PDMAA a linear fit is sufficient. Fig. 4 shows clustering functions larger than −1, indicating that water molecules tend to cluster together in these four materials. The least hydrophilic polymer, PDMAEMA, shows the largest clustering tendency, decreasing significantly with increasing water activity. Because the Flory interaction parameter for PDMAEMA/water is also a strong decreasing function of water activity, the lower tendency to cluster may be explained by more favorable polymer-water interaction at higher activities. Similar trends are observed in PAA and PDMAA. In the latter, water has the smallest tendency to cluster and the smallest Flory interaction parameter. However, PHEMA-lens material reveals a rising tendency for clustering with increasing water activity, despite the decreasing Flory interaction parameter.
 | ||
Fig. 4 Clustering function Gww/vw at various water-vapor activities for PDMAA, PDMAEMA, PAA, and PHEMA-lens material at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
The quantity ΦwGww/vw has been interpreted as the mean number of solvent molecules in the neighborhood of a given solvent molecule in excess of those provided by the mean solvent concentration.8,9 The sum (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΦwGww/vw), therefore, is the mean cluster size.22Fig. 5 shows ΦwGww/vw as a function of water vapor activity for four polymers. PDMAEMA shows the highest value of ΦwGww/vw that increases rapidly with water activity, reaching values in excess of 2 at high activities. In PDMAA, the mean cluster size is smaller with ΦwGww/vw always below 0.5. For PAA, ΦwGww/vw reaches a maximum near 1 at aw
ΦwGww/vw), therefore, is the mean cluster size.22Fig. 5 shows ΦwGww/vw as a function of water vapor activity for four polymers. PDMAEMA shows the highest value of ΦwGww/vw that increases rapidly with water activity, reaching values in excess of 2 at high activities. In PDMAA, the mean cluster size is smaller with ΦwGww/vw always below 0.5. For PAA, ΦwGww/vw reaches a maximum near 1 at aw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∼
∼![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70% and is larger than ΦwGww/vw for PHEMA-lens material until near 80% activity. Then, ΦwGww/vw for PHEMA-lens material increases to 1.2 at the highest activity. These results for PHEMA-lens material are similar to those reported elsewhere13 for water in PHEMA homopolymer.
70% and is larger than ΦwGww/vw for PHEMA-lens material until near 80% activity. Then, ΦwGww/vw for PHEMA-lens material increases to 1.2 at the highest activity. These results for PHEMA-lens material are similar to those reported elsewhere13 for water in PHEMA homopolymer.
 | ||
Fig. 5 Mean excess of water molecules around a central one, ΦwGww/vw, at various water-vapor activities for PDMAA, PDMAEMA, PAA, and PHEMA-lens material at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
2. Diffusion coefficients
Water diffusion in these polymers shows Fickian behavior. We define ΔMt and ΔM∞ as the weight gain of water sorbed at time t and at equilibrium, respectively. Plotting ΔMt/ΔM∞against the ratio of the square root of time to the thickness of the polymer (L) gives typical Fickian curves,23 as shown in Fig. 6. The plots are linear for at least the first half of the curve. However, these plots produce a non-zero intercept with the time axis. This suggests that the diffusion process follows Fickian kinetics, after a short initial time lag. The time lag in our data probably follows from an unavoidable experimental artifact: it is not possible to raise instantaneously water activity and surface concentration to the equilibrium values. We collect the time data starting from the instant when the manometer liquid begins to move. However, a small time (1–2 min) is needed before the system attains the desired water activity and achieves equilibrium with the polymer surface. As a consequence, a sigmoidal shape of the sorption curve is expected at the very early stage of sorption;23 this sigmoidal shape appears as a time lag in the uptake kinetics. | ||
Fig. 6 Sorption kinetics of water in polymers at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C at similar water-vapor activities: (a) PDMAA; (b) PAA; (c) PDMAEMA; (d) PHEMA-lens material. Symbols are experimental data, lines the fitting curves using eqn. (9). °C at similar water-vapor activities: (a) PDMAA; (b) PAA; (c) PDMAEMA; (d) PHEMA-lens material. Symbols are experimental data, lines the fitting curves using eqn. (9). | ||
Diffusion coefficients, D, are calculated using a model suggested by Crank23 to interpret kinetic absorption data “when the surface concentration changes rapidly but not instantaneously, a situation which usually arises when an instantaneous change is attempted in an experiment.”
We assume that at a fixed water activity, at the start, the water surface concentration approaches the equilibrium water concentration, C0, as an exponential function of time:
C(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±l,t) ±l,t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C0[1 C0[1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βt)] exp(−βt)] | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L/2 is the half thickness of the film; x
L/2 is the half thickness of the film; x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±l indicates the position of the interfaces polymer/water-vapor in a coordinate system with the origin in the middle of the film, and β is the inverse of the characteristic time for attaining saturation at the polymer/water-vapor interface. Subsequent diffusion is assumed to be Fickian. With the boundary condition given by eqn. (5) and with a constant diffusion coefficient D, integration of Fick's second law for slab geometry with fixed boundaries is:23
±l indicates the position of the interfaces polymer/water-vapor in a coordinate system with the origin in the middle of the film, and β is the inverse of the characteristic time for attaining saturation at the polymer/water-vapor interface. Subsequent diffusion is assumed to be Fickian. With the boundary condition given by eqn. (5) and with a constant diffusion coefficient D, integration of Fick's second law for slab geometry with fixed boundaries is:23 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞, i.e. when the water surface concentration does not change with time, we recover the typical isothermal Fickian curve for constant diffusion coefficient.
∞, i.e. when the water surface concentration does not change with time, we recover the typical isothermal Fickian curve for constant diffusion coefficient.
A sigmoidal shape in experimental diffusion data can also indicate anomalous kinetics. We cannot exclude completely this possibility. However, for our systems, only the very beginning would be eventually affected. Moreover, eqn. (6) can be considered a simplified version of the model proposed by Long and Richman24 to interpret anomalous sorption kinetics. When the instantaneous surface concentration C0 in eqn. (2) of ref. 24 is set equal to zero, the Long and Richman model reduces to eqn. (6).
Therefore, whether this sigmoidal shape is due to some non-Fickian effect or to the impossibility to raise the pressure instantaneously (as we believe in absence of stronger evidence of anomalous kinetics), the adopted model captures the essential features of both phenomena.
Fig. 6 shows water-sorption kinetics in the four polymers for a similar water activity. Points show experimental data whereas lines represent fitting curves obtained with eqn. (6). Table 3 reports the fitted coefficients D and β at each water activity together with the film thickness for each polymer. We use the Sigmaplot© program with a least-squares method to calculate D and β with eqn. (6). In general, the diffusion coefficient is concentration dependent; thus, the diffusion coefficient reported here are averages for a concentration range of each sorption step, from an initial water concentration to the equilibrium concentration at the corresponding water activity.
| Polymer | a w | 108D/cm2 s−1 | 108Đ/cm2 s−1 | β −1/s |
|---|---|---|---|---|
| PDMAA | 0.17 | 7.1 | 8.0 | 0 |
L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0329 0.0329 |
0.39 | 4.9 | 6.5 | 0 |
| 0.58 | 8.7 | 14 | 5 | |
| 0.77 | 8.1 | 17 | 122 | |
| PDMAEMA | 0.21 | 20 | 35 | 80 |
L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0417 0.0417 |
0.40 | 14 | 29 | 81 |
| 0.61 | 13 | 36 | 1 | |
| 0.76 | 10 | 29 | 9 | |
| PAA | 0.58 | 0.98 | 2.3 | 27 |
L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0206 0.0206 |
0.70 | 3.5 | 9.0 | 196 |
| 0.80 | 2.9 | 8.2 | 167 | |
| PHEMA-lens material | 0.19 | 0.62 | 0.72 | 127 |
L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0149 0.0149 |
0.40 | 0.55 | 0.78 | 8 |
| 0.78 | 3.2 | 7.6 | 8 | |
| 0.84 | 3.4 | 8.9 | 208 |
The inverse of β measures the characteristic time required to reach the equilibrium water content at the polymer/water-vapor interface. In all cases, 1/β is less than 3.5 min, much smaller than the diffusion time scale, L2/4D, and consistent with the time required for increasing the pressure at the desired level during the experiment. Therefore, the water concentration on the film surface reaches equilibrium after at most the first few measurements of water uptake in the diffusion experiments and, except for a few initial points (2–3), the experimental sorption curves have Fickian characteristics.
In general, the water diffusion coefficient in these four materials is concentration dependent. D in PAA reaches a maximum of 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at 69% water activity. Chang et al.10 report diffusion coefficients for water in PAA at 40
10−8 cm2 s−1 at 69% water activity. Chang et al.10 report diffusion coefficients for water in PAA at 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C reaching a maximum of 1
°C reaching a maximum of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at 60% activity. For PDMAA, D tends to increase at high activities. However, it has a minimum of 4.9
10−8 cm2 s−1 at 60% activity. For PDMAA, D tends to increase at high activities. However, it has a minimum of 4.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at 58% activity. Diffusion coefficients in PDMAA are larger than reported by Ichikawa et al.25
(0.98
10−8 cm2 s−1 at 58% activity. Diffusion coefficients in PDMAA are larger than reported by Ichikawa et al.25
(0.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1) at aw
10−8 cm2 s−1) at aw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50%. The calculated diffusion coefficient for water in the PHEMA-lens material increases with water activity from a constant 0.6
50%. The calculated diffusion coefficient for water in the PHEMA-lens material increases with water activity from a constant 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at lower activities to 3.4
10−8 cm2 s−1 at lower activities to 3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at higher activities. These values are similar to those obtained for PAA. They are in good agreement with those reported previously for PHEMA homopolymers.13,25 The water diffusion rate is faster in PDMAEMA than in the other three materials. D decreases with water activity from 20
10−8 cm2 s−1 at higher activities. These values are similar to those obtained for PAA. They are in good agreement with those reported previously for PHEMA homopolymers.13,25 The water diffusion rate is faster in PDMAEMA than in the other three materials. D decreases with water activity from 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 to 10
10−8 cm2 s−1 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 within the measured activity range.
10−8 cm2 s−1 within the measured activity range.
For binary systems, the Fickian diffusion coefficient can be written as the product of two terms, D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΓĐ;26 the first one is a thermodynamic non-ideality factor, Γ, defined by
ΓĐ;26 the first one is a thermodynamic non-ideality factor, Γ, defined by
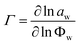 | (7) |
The non-ideality factor can be calculated from the clustering function:
 | (8) |
Fig. 7 shows that the thermodynamic factor is a decreasing function of water activity for our four systems. The same trend is observed for the diffusion coefficient in PDMAEMA. Therefore, the concentration dependence of the water diffusion coefficient reflects the concentration dependence of the thermodynamic factor for PDMAEMA.
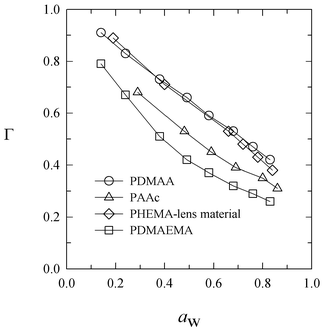 | ||
Fig. 7 Thermodynamic factor Γversus water-vapor activity for PDMAA, PDMAEMA, PAA, and PHEMA-lens material at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
D has the opposite trend in PHEMA-lens material, increasing at larger water activity, whereas the concentration dependence of the diffusion coefficient is more complex for PDMAA and PAA. An increasing diffusion coefficient is often associated with polymer plasticization because it augments the intrinsic mobility Đ. Therefore, while plasticization appears to dominate the concentration dependence of D in PHEMA-lens, the complex behavior observed in PAA and PDMAA is probably a result of the competing concentration dependence of Đ and Γ.
3. Mobilities
The ratio of the measured diffusion coefficients to the thermodynamic correction Γ gives the mobility Đ. The calculated Đ (Table 3) may have low accuracy because they are obtained from two experimental quantities, both subject to uncertainties. Moreover, error is introduced by differentiation (eqn. (7)) and by the interpolation procedure, necessary to evaluate Γ at the activity used in the diffusion experiments. Uncertainties in Đ of 20% or more are to be expected; a similar estimate has been reported elsewhere.27The mobility Đ increases from 6.5–8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 at low water activity to 14–17
10−8 at low water activity to 14–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 at high water activity for PDMAA, and from 0.55–0.62
10−8 cm2 s−1 at high water activity for PDMAA, and from 0.55–0.62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 to 3.2–3.4
10−8 to 3.2–3.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 for PHEMA-lens material. Despite some scatter in the reported values (easily accounted for by the possible source of error in the calculation), the mobility is nearly constant (29–36
10−8 cm2 s−1 for PHEMA-lens material. Despite some scatter in the reported values (easily accounted for by the possible source of error in the calculation), the mobility is nearly constant (29–36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1) with water activity in PDMAEMA, whereas for PAA, it rises sharply from 2.3 to 9.0
10−8 cm2 s−1) with water activity in PDMAEMA, whereas for PAA, it rises sharply from 2.3 to 9.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm2 s−1 in a relatively narrow activity range.
10−8 cm2 s−1 in a relatively narrow activity range.
The observed mobility trends are probably due to polymer plasticization. To support this conclusion, we have estimated the water uptake required for lowering the glass-transition temperature below 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for PDMAA and PAA. We used the Flory–Fox28 equation with a glass-transition temperature of water Tgw equal to −135
°C for PDMAA and PAA. We used the Flory–Fox28 equation with a glass-transition temperature of water Tgw equal to −135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C:
°C:
 | (9) |
The required water content is, respectively, 13.1 and 13.5 weight %. For PHEMA-lens material, we expect that the glassy-to-rubbery transition occurs at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for a water content similar to that measured for HEMA homopolymers, i.e. around 8 weight %.29 Therefore, all three polymers undergo a glassy-to-rubbery transition during equilibrium sorption experiments, roughly at water activity equal to 50%, 60% and 65% respectively. Also, some of the kinetic water-uptake experiments are performed in the glassy region (the first and second activity for PDMAA; the first and second activity for PHEMA-lens) some other experiments span a water-content range embedding the glassy-to-rubbery transition (most likely, the third diffusion step for PDMAA, the first one for PAA and the third one for PHEMA-lens material), whereas the remaining measurements are in the rubbery region.
°C for a water content similar to that measured for HEMA homopolymers, i.e. around 8 weight %.29 Therefore, all three polymers undergo a glassy-to-rubbery transition during equilibrium sorption experiments, roughly at water activity equal to 50%, 60% and 65% respectively. Also, some of the kinetic water-uptake experiments are performed in the glassy region (the first and second activity for PDMAA; the first and second activity for PHEMA-lens) some other experiments span a water-content range embedding the glassy-to-rubbery transition (most likely, the third diffusion step for PDMAA, the first one for PAA and the third one for PHEMA-lens material), whereas the remaining measurements are in the rubbery region.
While the equilibrium isotherms do not present noticeable features related to the glassy-to-rubbery transition (for example, inversion of curvature as reported for sorption of gases in polymers), there is a clear correlation between the activity region where the kinetic sorption experiment is performed and the mobilities. In particular, the calculated mobilities for PDMAA, PAA and PHEMA-lens material are much larger in the rubbery region than those in the glassy region; mobilities increase with water content in the polymer probably because of plasticization induced by water sorption.
By contrast, PDMAEMA mobility is roughly constant with water content. PDMAEMA has a glass-transition temperature well below 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C; the polymer is rubbery in the entire composition range at the experimental temperature and, therefore, there is no significant plasticization accompanying water sorption.
°C; the polymer is rubbery in the entire composition range at the experimental temperature and, therefore, there is no significant plasticization accompanying water sorption.
Conclusions
Experimental isothermal vapor-sorption equilibria and diffusion coefficients at 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C have been obtained for water in three homopolymers PDMAA, PDMAEMA, PAA, and in a PHEMA soft contact-lens material. Water sorption is higher in the water-soluble polymers PDMAA and PAA. PDMAA shows low water clustering; however, clustering is appreciable in non-water-soluble PDMAEMA. Water diffusion is Fickian after a short initial time-lag. Diffusion coefficients are concentration-dependent for all polymers. In PHEMA-lens material, the diffusion coefficient rises with water concentration suggesting plasticization by water. In PDMAEMA, the water diffusion coefficient is the largest. However, it decreases with water concentration, consistently with the concentration dependence of the thermodynamic correction. In PAA and PDMAA, the diffusion coefficient has a more complex dependence on water content. Water mobility increases significantly with water content for those polymers undergoing a glassy-to-rubbery transition induced by water sorption, while it is roughly constant for rubbery PDMAEMA.
°C have been obtained for water in three homopolymers PDMAA, PDMAEMA, PAA, and in a PHEMA soft contact-lens material. Water sorption is higher in the water-soluble polymers PDMAA and PAA. PDMAA shows low water clustering; however, clustering is appreciable in non-water-soluble PDMAEMA. Water diffusion is Fickian after a short initial time-lag. Diffusion coefficients are concentration-dependent for all polymers. In PHEMA-lens material, the diffusion coefficient rises with water concentration suggesting plasticization by water. In PDMAEMA, the water diffusion coefficient is the largest. However, it decreases with water concentration, consistently with the concentration dependence of the thermodynamic correction. In PAA and PDMAA, the diffusion coefficient has a more complex dependence on water content. Water mobility increases significantly with water content for those polymers undergoing a glassy-to-rubbery transition induced by water sorption, while it is roughly constant for rubbery PDMAEMA.
Acknowledgements
For financial support, the authors are grateful to the Office for Basic Sciences of the US Department of Energy and to the Donors of the Petroleum Research Fund administered by the American Chemical Society. A. Arce and O. Rodríguez thank the Ministerio de Ciencia y Tecnología (Spain) for fellowships FP2000-5251 and PN98-44807316, respectively. The authors also thank D. Flaherty for assistance with the experimental work, and G. Grobe of Bausch and Lomb Inc., Rochester, New York, for kindly providing thin films of PHEMA-lens material.References
- W. J. Koros and G. K. Fleming, J. Membrane Sci., 1993, 83, 1–80 Search PubMed.
- A. J. Kelkar and D. R. Paul, J. Membrane Sci., 2001, 181, 199–212 Search PubMed.
- B. Tighe, in Silicone Hydrogels, ed. D. Sweeney, Butterworth-Heinemann, Oxford, 2000, vol. 1, p. 1 Search PubMed.
- G. Hoch, A. Chauhan and C. J. Radke, J. Membrane Sci., 2003, 214, 199–209 Search PubMed.
- D. Fonn, P. Situ and T. Simpson, Optom. Vision Sci., 1999, 76, 700–704 Search PubMed.
- J. Crank and G. S. Park, in Diffusion in Polymers, ed. J. Crank and G. S. Park, Academic Press, London, 1968, vol. 1, p. 1–39 Search PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, London, 1953 Search PubMed.
- B. H. Zimm and J. L. Lundberg, J. Phys. Chem., 1956, 60, 425–428 CrossRef CAS.
- J. L. Lundberg, Pure Appl. Chem., 1972, 31, 261–281 CAS.
- M. J. Chang, A. S. Myerson and T. K. Kwei, J. Appl. Polym. Sci., 1997, 66, 279–291 CrossRef CAS.
- T. E. Daubert and R. P. Danner, Physical and Thermodynamics Properties of Pure Chemicals: Data Compilation, Hemisphere Publishing Corp., New York, 1989 Search PubMed.
- C. Panayiotou and J. H. Vera, Polym. J., 1984, 16, 89–102 Search PubMed.
- O. Rodriguez, F. Fornasiero, A. Arce, C. J. Radke and J. M. Prausnitz, Polymer, 2003, 44, 6323–6333 CrossRef CAS.
- J. A. Barrier, in Diffusion in Polymers, ed. J. Crank and G. S. Park, Academic Press, London, 1968, vol. 8, pp. 259–313 Search PubMed.
- K. A. Schult and D. R. Paul, J. Polym. Sci. Part B, 1996, 34, 2805–2817 CrossRef CAS.
- Y. M. Sun and J. Chen, J. Appl. Polym. Sci., 1994, 51, 1797–1804 CAS.
- M. H. V. Mulder, in Pervaporation Membrane Separation Processes, ed. H. R. Y. M., Elsevier Science Publishers B.V., Amsterdam, 1991, vol. 4, pp. 225–252 Search PubMed.
- K. A. Schult and D. R. Paul, J. Appl. Polym. Sci., 1996, 61, 1865–1876 CrossRef CAS.
- G. Skirrow and K. R. Young, Polymer, 1974, 15, 771–776 CrossRef CAS.
- R. J. Hernandez, J. R. Giacin and E. A. Grulke, J. Membrane Sci., 1992, 65, 187–199 Search PubMed.
- J. L. G. Ribelles, M. M. Pradas, G. G. Ferrer, N. P. Torres, V. P. Gimenez, P. Pissis and A. Kyritsis, J. Polym. Sci. Part B, 1999, 37, 1587–1599 CrossRef.
- S. Petrik, M. Bohdanecky, F. Hadobas and L. Simek, J. Appl. Polym. Sci., 1991, 42, 1759–1765 CrossRef CAS.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 1975 Search PubMed.
- F. A. Long and D. Richman, J. Am. Chem. Soc., 1960, 82, 513–519 CrossRef CAS.
- K. Ichikawa, T. Mori, H. Kitano, M. Fukuda, A. Mochizuki and M. Tanaka, J. Polym. Sci. Part B, 2001, 39, 2175–2182 CrossRef CAS.
- R. Taylor and R. Krishna, Multicomponent Mass Transfer, John Wiley & Sons Inc., New York, 1993 Search PubMed.
- J. L. Duda, Y. C. Ni and J. S. Vrentas, Macromolecules, 1979, 12, 459–462 CrossRef CAS.
- T. G. Fox, Bull. Am. Phys. Soc., 1956, 1, 123 Search PubMed.
- Y. M. Sun and H. L. Lee, Polymer, 1996, 37, 3915–3919 CrossRef CAS.
Footnote |
| † Permanent address: Department of Chemical Engineering, University of Santiago de Compostela, 15782 Santiago de Compostela, Spain. |
| This journal is © the Owner Societies 2004 |

