View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B207339K (Paper) New J. Chem., 2003, 27, 80-87

Ion pairing effects in intramolecular heterolytic H2 activation in an Ir(III) complex: a combined theoretical/experimental study

Karin Grueta, Eric Clot*b, Odile Eisenstein*b, Dong Heon Leead, Ben Patela, Alceo Macchioni*c and Robert H. Crabtree*a
aDepartment of Chemistry, Yale University, New Haven, CT 06520-8107, USA. E-mail: robert.crabtree@yale.edu
bLSDSMS (UMR 5636), Case courrier 14, Université Montpellier 2, 34095, Montpellier cedex 5, France. E-mail: odile.eisenstein@univ-montp2.fr; clot@univ-montp2.fr
cDipartimento di Chimica, Università di Perugia, Via Elce di Sotto 8, 06123, Perugia, Italy. E-mail: alceo@unipg.it
dDepartment of Chemistry, Chonbuk National University, Chonju, 561-756, Korea

Received (in Montpellier, France) 25th July 2002, Accepted 10th September 2002

First published on 31st October 2002

Abstract

A free pendant 2-amino group in a benzoquinolinate ligand bound to Ir(III) can cause heterolytic dissociation of an adjacent Ir–H2, depending on the nature of the phosphine, L. For L[thin space (1/6-em)]=[thin space (1/6-em)]PMePh2, heterolysis does not occur and an H2 complex, [IrH(H2)(bq-NH2)L2]BF4, is seen, but if L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3 or PCy3, heterolysis does occur and a hydride product, [IrH2(bq-NH3)L2]BF4, is formed by proton transfer from the bound H2 to the pendant NH2 group. The electronic effect of L is not dominant. Theoretical studies (DFT calculations) show that the H2 complex is predicted to be more stable for all the phosphines used, if the anion is ignored. We propose that the hydride isomer, formed when L is bulky, depends on ion pairing effects for its stability. The calculated electrostatic potentials for the two isomers suggest that the counter anion has to be located much closer to the metal in the H2 complex than in the hydride where the anion is much farther from the metal. The bulky phosphines PPh3 and PCy3 favor remote ion pairing and therefore favor the hydride isomer because steric effects disfavor close ion pairing as confirmed by ONIOM (B3PW91/UFF) calculations of the ion pair geometry. An improved synthesis of [IrH5(PCy3)2] is reported.

Introduction

Heterolytic H2 activation1 (eqn. 1), currently attracting increasing attention, may often go via an acidic H2 complex.2 For example, an all-Fe hydrogenase has recently been proposed to contain a basic amino group immediately adjacent to the H2 binding site capable of acting as a base for deprotonating coordinated H2.3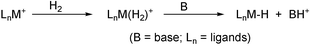
 
ugraphic, filename = b207339k-u1.gif(1)

We have briefly reported4 on a 2-aminobenzoquinolinate (bq-NH2) Ir(III) complex, designed to favor heterolysis of H2. The free –NH2, located on the bq framework near the H2 binding site, can act as an intramolecular base causing proton abstraction from H2. The rigidity of the bq framework prevents the amino group from directly binding to the metal, which would block the H2 binding site. Broadly similar complexes with an H2 binding site and a basic group on a ligand have been reported by Morris, Sabo-Etienne and Chaudret.5,6 We reported4 that moving from PPh3 to more basic ligands such as PMePh2 led to the formation of an H2 complex without heterolysis, so we ascribed the difference to an electronic effect. The work described here shows that this proposal is invalid since the very basic PCy3 also gives heterolysis. We have now looked for the origin of this effect by a combined experimental/theoretical study on this system. This leads us to propose that ion pairing is the key factor that favors heterolysis for bulky phosphines because the anion binding site for the hydride heterolysis product is more remote from the metal. Ion pairing has been implicated in a few other organometallic systems.7

Results and discussion

Choice of system

In order to separate out the effect of the pendant amino group, we needed to compare the 2-aminobenzoquinolinate (bq-NH2) system with the benzoquinolinate system, studied previously,8 lacking a pendant amino group (bq-H). In this early work with bq-H (eqn. 2), we showed that H2 replaces a labile ligand such as water or acetone in the starting material, 1, to give the H2 complex, 2. Bases such as excess NEt3 cause deprotonation and H2 heterolysis to give the hydride, 3.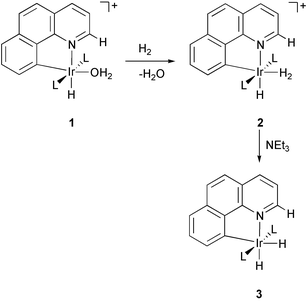
 
ugraphic, filename = b207339k-u2.gif(2)

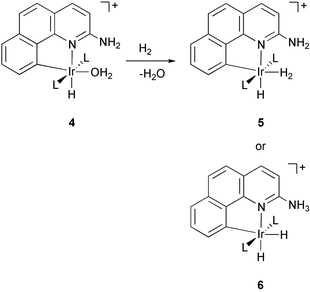
In the prior communication4 we reported that, depending on the phosphine, the aqua complex [IrH(bq-NH2)(OH2)(L)2]BF4, 4, reacts with H2 to afford either the dihydrogen compound [IrH(H2)(bq-NH2)(L)2]BF4, 5, or the hydride [IrH2(bq-NH3)(L)2]BF4, 6 (eqn. 3). Only dihydrogen compounds 5 were obtained upon hydrogenation of the parent system [IrH(bq-H)(OH2)(PPh3)2]BF4, 1, bearing no adjacent pendant group.8 Since the dihydrogen compounds of type 5 were originally4 obtained only with the more basic alkyl phosphines and the hydride 6 with the less basic PPh3, we ascribed this behavior to the electronic effect of the phosphines. We now report the hydride 6 also forms with the very basic PCy3 which has now led us to carry out a combined theoretical/experimental study that identifies a steric effect acting in the alternate ion pairs formed from 5 and 6 as the proposed origin of the effect.

 
ugraphic, filename = b207339k-u3.gif(3)

Synthesis

The required ligand precursor, 2-amino-7,8-benzoquinoline, was readily prepared from 7,8-benzoquinoline and NaNH2.9,10 Most of the required starting aqua complexes [IrH(bq-NH2)(OH2)L2]BF4 (4: a, L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3; b, L[thin space (1/6-em)]=[thin space (1/6-em)]P(p-C6H4CH3)3; c, L[thin space (1/6-em)]=[thin space (1/6-em)]P(p-C6H4OCH3)3; d, L[thin space (1/6-em)]=[thin space (1/6-em)]PMePh2) are known (4a)10 or could be synthesized by the known route10 or variants described in the experimental section. All were fully characterized as detailed in the experimental section or in prior papers. These syntheses (Scheme 1) involve cyclometalation of 2-aminobenzoquinoline with [(cod)IrL2]X/H210 or using preformed [IrH2(OH2)2L2]X in moist CH2Cl2 at room temperature to give the aqua complex [IrH(bq-NH2)(OH2)L2]X (4, bq-NH2[thin space (1/6-em)]=[thin space (1/6-em)]2-benzoquinolinato; X[thin space (1/6-em)]=[thin space (1/6-em)]BF4 or PF6) or using preformed [IrH2(Me2CO)2L2]X in acetone at room temperature to give the acetone complex [IrH(bq-NH2)(Me2CO)L2]BF4 (4′, the prime means acetone is the labile ligand).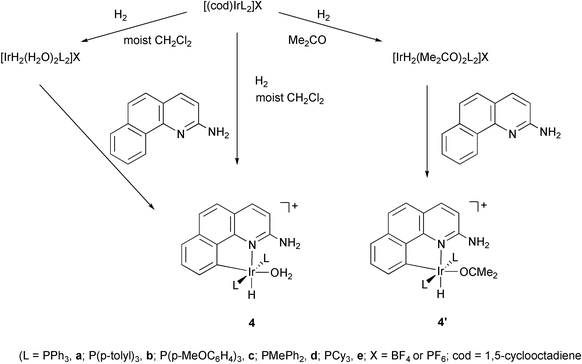
scheme, filename = b207339k-s1.gif
Scheme 1

The required PCy3 acetone complex [IrH(bq-NH2)(OCMe2)(PCy3)2]BF4 (4′e) had not previously been reported and some synthetic effort proved to be necessary to obtain it because the standard route10 from [(cod)Ir(PR3)2]BF4/H2, used above, was not available as [(cod)Ir(PCy3)2]X is unknown. Instead we have prepared it from the known11 [IrH5(PCy3)2] by protonation in acetone with HBF4 to give [Ir(PCy3)2(OCMe2)2(H)2]BF4in situ, followed by reaction with 2-aminobenzoquinoline to give the desired 4′e. Surprisingly, it was not possible to synthesize the aqua species for L[thin space (1/6-em)]=[thin space (1/6-em)]PCy3 but the acetone complex proved well behaved. Otherwise, the results were not dependent on the nature of the leaving group, acetone or water, or on the nature of the anion, BF4− or PF6−.

We also report an improved synthesis of [IrH5(PCy3)2] by a one step route from commercial [Ir(cod)Cl]2, treatment of which in CH2Cl2 with NaOMe and PCy3 under H2 gives the product in 59% yield. The isolation of the analytically pure pentahydride only requires filtration and washing. The spectroscopic characterization, 1H NMR: −11.27 ppm (t, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.21 Hz), 31P NMR: 33.42 ppm (s), IR: ν(Ir–H)[thin space (1/6-em)]=[thin space (1/6-em)]1929.1 cm−1, is in full agreement with the published data.11

Reaction of 4a–d with H2: experiment

At −70[thin space (1/6-em)]°C in CD2Cl2, the aqua complex, [IrH(bq-NH2)(OH2)(PPh3)2]BF4, 4a, reacts with H2 to give the hydride, [IrH2(bq-NH3)(PPh3)2]BF4, 6a, via H2 heterolysis. The 1H NMR spectrum shows two sharp hydride resonances in the terminal Ir–H region at −23.24 ppm and −25.63 ppm that are coupled to the cis-phosphines and to each other (dt, 2JHH′[thin space (1/6-em)]=[thin space (1/6-em)]8.50 Hz; 2JPH[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz). These are clearly normal hydrides with the normal 2JHH′ and 2JPH values usually seen10 in these systems. A broad resonance at 4.56 ppm of intensity 3H is assigned to the bq-NH3+ protons for compound 6a. The triplet hydride resonance at −16.22 ppm (2JPH[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz) and the amino resonance at 6.23 ppm characteristic of the starting material 4a reappears on passing a stream of N2, showing this conversion is reversible. The presence of anhydrous MgSO4 in the NMR tube is helpful to remove water and drive the equilibrium over to 6.

In an effort to see if an electronic effect operates in the PAr3 system, we looked at the phosphines, P(p-C6H4CH3)3 and P(p-C6H4OCH3)3. Hydride complexes were also obtained both with P(p-C6H4CH3)3, 6b, and P(p-C6H4OCH3)3, 6c. Warming the samples to room temperature led to loss of H2 below −20[thin space (1/6-em)]°C, with regeneration of the starting aqua complex, so none of 6a–c could be isolated as solids.

Changing the phosphine to PMePh2 gave a very different result. The appropriate aqua complex, [IrH(bq-NH2)(OH2)(PMePh2)2]BF4, 4d, also reacts with H2 at −70[thin space (1/6-em)]°C but to give the H2 complex [IrH(H2)(bq-NH2)(PMePh2)2]BF4, 5d. This assignment follows from the very different 1H NMR spectrum. The NH2 and hydride peaks characteristic of compound 4d disappear and are replaced by three new signals: an Ir–H triplet at −15.90 ppm (2JPH[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz) of intensity 1H, a characteristic broad Ir(H2) resonance of intensity 2H at −3.75 ppm, and a broad NH2 resonance of intensity 2H at 6.15 ppm appropriate for compound 5d. As noted previously, an H2 complex was also seen with PEt2Ph and P(n-Bu)3, but we report only the PMePh2 case in full here because unlike the oily PEt2Ph and P(n-Bu)3 species, complex 4d crystallized well and its characterization was completely convincing. Like 6, 5 also loses H2 on warming above −20[thin space (1/6-em)]°C, and so cannot be isolated as a solid.

The nature of the leaving group was not important: upon exposure to hydrogen, the acetone complexes (4′a–d) also afford the same compounds, H2 complex 5 or hydride 6, with exactly the same dependence on the phosphines as is obtained from the analogous aqua complex. However, the hydrogenation is complete only for 4′a and 4′e, not for 4′b–d, no doubt because the acetone is slightly more strongly bound than water.

An electronic effect?

Because less basic phosphines led to the hydride complexes, whereas more basic phosphines led to the dihydrogen complexes, we proposed in the prior communication4 that the change in the heterolytic H2 activation equilibrium was due to the electronic effects of the phosphines. We expected the basicity of the phosphine to influence the pKa of coordinated H2. In free H2, the pKa is ca. 35, but upon binding to the metal, it becomes very much more acidic (15 to −5).5,6 This acidification may be due to the metal fragment stabilizing the H− product of the heterolytic dissociation while binding H2 relatively weakly. A basic phosphine should enhance the back bonding to the empty σ* orbital of H2, causing tighter H2 binding and lowered acidity. To check this electronic interpretation, we decided to examine the case of PCy3, the most basic, but also one of the most bulky phosphines in common use. If electronic factors dominate, an H2 complex should be formed.

Reaction of the PCy3 complex, 4′e, with H2: experiment

In complete disaccord with the electronic effect model, hydrogenation of the PCy3 acetone complex 4′e, at −80[thin space (1/6-em)]°C in CD2Cl2, led to the hydride compound 6e with heterolytic H2 activation. This follows from the disappearance of the triplet Ir–H signal at −14.23 ppm (2JHP[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, 1H), and of the broad NH2 signal at 5.83 ppm (2H) of the amino group, with the appearance of two broad signals for the cis-hydrides at −25.06 (1H) and −21.04 ppm (1H), as well as a broad signal at 4.29 ppm (3H) assigned to the ammonium protons. Had the electronic effect been dominant, the basic PCy3 ligand should have afforded the H2 complex, but NMR resonances for this species were completely absent and the spectra of the two forms are so different that no doubt is possible.

To eliminate the very remote possibility that the ligands L in this series do not exert their usual electronic effects, we made the carbonyl derivatives of 4a–d and 4′e by reaction with CO at 1 atm in CH2Cl2 (eqn. 4). As expected, these showed ν(CO) IR frequencies entirely consistent with the usual increasing Tolman12 basicity order (values in parentheses): PPh3, 2026 (2068.9); P(p-C6H4CH3)3, 2024 (2066.7); P(p-C6H4OCH3)3, 2023 (2066.1); PMePh2, 2021 (2067.0); PCy3, 1995 (2056.4) cm−1. Our system is more sensitive to variation in the phosphine than is Tolman's classic LNi(CO)3, because we have a PR3/CO ratio of 2∶1 versus 1∶3 for Tolman. The increase in basicity on moving to PCy3 was very large, as expected, and so we can rule out an unexpected inversion of basicity in this case.

 
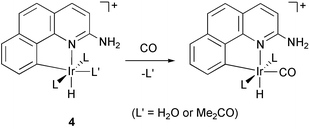ugraphic, filename = b207339k-u4.gif(4)

Initial theoretical analysis

The first model systems studied (DFT, B3PW91)13 were dihydrogen complex [Ir(bq-NH2)(PH3)2(H2)(H)]+ (7) and hydride [Ir(bq-NH3)(PH3)2(H)2]+ (8), where the only differences versus the experimental compounds 5 and 6 are the phosphine ligand (PH3vs. PPh3) and the absence of anion. The optimized geometries are shown in Fig. 1 and selected geometrical parameters are given in Table 1. The key finding is that dihydrogen complex 7 is strongly favored theoretically with a convincingly large energy preference of 14.4 kcal mol−1 while the hydride 6 (L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3) is favored experimentally. The H–H distance of the dihydrogen complex, 0.87 Å, is normal. Also notable is the dihydrogen bonded14 N–H⋯H–Ir group of the hydride form 8 with its short H⋯H distance of 1.379 Å.
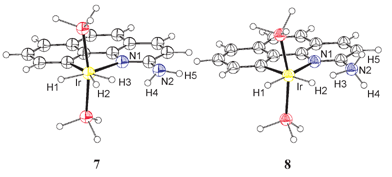Optimized geometry (B3PW91) for the dihydrogen complex IrH(H2)(bq-NH2)(PH3)2+, 7, and the hydride complex Ir(H)2(bq-NH3)(PH3)2+, 8.
Fig. 1 Optimized geometry (B3PW91) for the dihydrogen complex IrH(H2)(bq-NH2)(PH3)2+, 7, and the hydride complex Ir(H)2(bq-NH3)(PH3)2+, 8.
Table 1 Geometrical parameters (distances in Å, angles in degrees) for the dihydrogen complexes IrH(H2)(bq-NH2)(PHxF3−x)2+, 7, and the hydride complexes Ir(H)2(bq-NH3)(PHxF3−x)2+, 8, for x[thin space (1/6-em)]=[thin space (1/6-em)]0–3. The relative electronic energy (ΔE/kcal mol−1) and relative free enthalpy (ΔG/kcal mol−1) correspond to the transformation 8[thin space (1/6-em)]→[thin space (1/6-em)]7. The numbering of the hydrogen atoms is shown in Fig. 1 for the PH3 case
  PH3PH2FPHF2PF3
Complex 7H2–H30.8700.8660.8580.850
 H3⋯H41.9121.9632.0552.126
 N2–H41.0081.0091.0101.012
Complex 8Ir–H21.6981.6741.6731.682
 H2⋯H31.3791.4791.4941.613
 N2–H31.1501.1111.0951.074
 ∠Ir–H2⋯H394.294.797.095.7
 ∠H2⋯H3–N2176.5178.7178.5176.9
8[thin space (1/6-em)]→[thin space (1/6-em)]7ΔE−14.4−6.6−2.1+1.0
 ΔG−15.6−9.4−4.0+0.8

A problem with 7 and 8 is the use of PH3 as model ligand, since this is neither electronically or sterically comparable with the experimental ligands. To probe the electronic issue, we calculated the situation for the series PH3−xFx (x[thin space (1/6-em)]=[thin space (1/6-em)]0–3) to look at the sensitivity of the equilibrium 7/8 as a function of change of the phosphine electronic effect. The Tolman12 electronic parameters (TEPs) for these ligands are: PH3, 2083.2; PH2F, 2090.9; PHF2, 2100.9; PF3, 2110.8 cm−1, so they cover a broad range of values going from the range typical for phosphites to that of CO.15 PH3 is a significantly less strong donor than PPh3 or P(alkyl)3, however, so we felt the need to look at the trend for PH3−xFx and extrapolate it into a region more appropriate to the experimental phosphines. The resulting trend in calculated ΔG for 7/8, plotted against the TEP (Fig. 2), shows that the dihydrogen complex 7 is still favored for all L more basic than PHF2; only for the extremely electron-withdrawing ligand PF3, does the system favor hydride 8. This implies that within the assumptions made in the calculation, the experimental systems would have been expected to strongly favor the dihydrogen complex 7 for all the experimental phosphines, since these are all much more strongly electron-donating than PHF2.


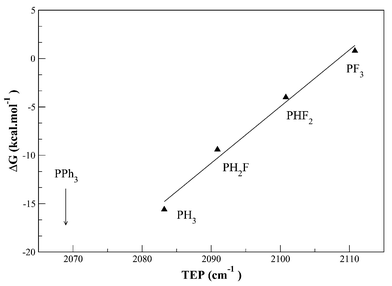Evolution of the free enthalpy ΔG (kcal mol−1) for the transformation 8 → 7 as a function of the Tolman Electronic Parameter (TEP)12,15 for the different PHxF3−x considered.
Fig. 2 Evolution of the free enthalpy ΔG (kcal mol−1) for the transformation 8[thin space (1/6-em)]→[thin space (1/6-em)]7 as a function of the Tolman Electronic Parameter (TEP)12,15 for the different PHxF3−x considered.

Dihydrogen bonding

Also of interest in these calculations is the change of the N–H and H⋯H bond lengths as the phosphine is varied (Table 1). This indicates that the dihydrogen bonding14 is strongly enhanced by the more donor ligands. Increasing donor power of the phosphine is expected to enhance the basic character of the metal–hydride bond and therefore enhance dihydrogen bonding. As shown in Fig. 3, the N–H bond elongates significantly and the H⋯H distance dramatically shortens on moving to more donor phosphines. The H⋯H distance of 1.379 Å for PH3 is far shorter than any experimentally observed value; these are usually14 in the range 1.7–2.0 Å.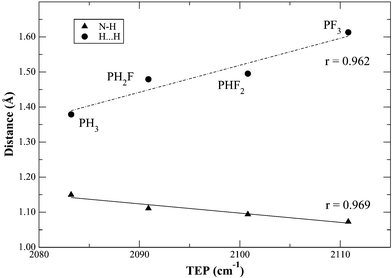
Change in the H2⋯H3 and N2–H3 bond distances (Å) in 8 as a function of TEP12,15 for the different PHxF3−x considered. See Fig. 1 for the atom numbering in 8.
Fig. 3 Change in the H2⋯H3 and N2–H3 bond distances (Å) in 8 as a function of TEP12,15 for the different PHxF3−x considered. See Fig. 1 for the atom numbering in 8.

Ion pairing effects

The theoretical analysis above indicates that all the phosphines in the series chosen would be expected to give the dihydrogen form and heterolysis should never be observed except with ligands like PF3 that are far less donating than any used experimentally. In searching for possible explanations, we noted that both of the anomalous cases where heterolysis was observed involve bulky (PPh3) or very bulky (PCy3) phosphines. It seemed very unlikely that this bulk could have a direct influence on the M(H2)(bq-NH2)/MH(bq-NH3) interconversion because both H2 and H ligands are sterically small and the energy deficit to be compensated is so large.

Large energies are known to arise by ion pairing: in CH2Cl2; these are typically in the range of 20–30 kcal mol−1 for organic cases.16 Very similar complexes to the present ones such as [Ir(PRPh2)2(dipy)(H)2]X (R[thin space (1/6-em)]=[thin space (1/6-em)]Ph, Me, X[thin space (1/6-em)]=[thin space (1/6-em)]BF4, PF6, CF3SO3, BPh4) have been unambiguously shown in our prior NMR work to give rise to tight ion pairing in CH2Cl2.17 In these stable complexes, the location of the anion, identified by NOE studies, was near the dipy ligand, on the side remote from the metal. Our prior theoretical analysis17 using the calculated electrostatic potential of the molecule reproduced the experimental location of the counterion, lending credence to this approach. The present bq system, with its extra benzene ring in the heterocyclic ligand blocking the binding site found for the dipy complex, is expected to strongly disfavor such binding. Instead, we thought ion pairing might occur near the H2 of the H2 complex and the bq-NH3 group of the hydride complex. In this case, the electronically expected H2 isomer could only be favored in practice if the ion pairing could occur unhindered by bulky L. If L is bulky, we thought that remote ion pairing at the bq-NH3 site might be the only allowed configuration thus favoring the hydride isomer.

The calculated electrostatic potential contour plots in the bq plane of the two isomers are very different, consistent with our picture of ion pairing at close versus remote sites. Fig. 4 illustrates the situation. The M(H2)(bq-NH2) isomer has a preferred anion binding region between the (H2) ligand and the (–NH2) group, close to the metal. In contrast, the MH(bq-NH3) isomer strongly prefers anion binding in the vicinity of the (–NH3) group, far from the metal (Scheme 2). This difference may be the factor that for bulky L favors the MH(bq-NH3) isomer, with its remote anion binding site, over the M(H2)(bq-NH2) isomer, with its anion binding site close to the metal and also to the bulky PR3 ligands.


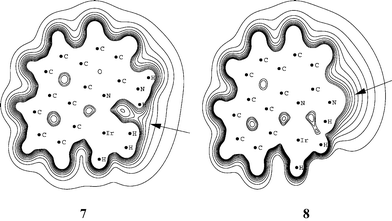Contour plot of the electrostatic potential in the plane of the bq ligand for 7 and 8. Contour lines are shown from 0.1 a.u. to 0.3 a.u. in 0.02 increments.
Fig. 4 Contour plot of the electrostatic potential in the plane of the bq ligand for 7 and 8. Contour lines are shown from 0.1 a.u. to 0.3 a.u. in 0.02 increments.

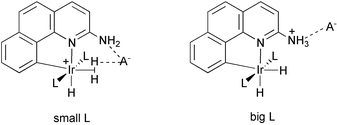scheme, filename = b207339k-s2.gif
Scheme 2

To confirm this analysis, combined quantum mechanical/molecular mechanics calculations, with the ONIOM (B3PW91/UFF) method, have been carried out on the full systems [IrH(H2)(bq-NH2)(PPh3)2][BF4], 9, and [Ir(H)2(bq-NH3)(PPh3)2][BF4], 10. Only the phenyl groups of the PPh3 ligands have been treated at the MM level, all the remaining atoms, and particularly the counter anion BF4−, were treated within the DFT framework.

For both systems, the position of the anion was in agreement with the analysis based on the electrostatic potential and the optimized geometries are shown in Fig. 5. BF4− is closer to the metal in 9 than in 10 (as illustrated by the Ir⋯B distances: 4.208 Å, 9; 5.241 Å, 10). In 9 there are two short H⋯F contacts between cation and anion, one with the H2 ligand (H⋯F[thin space (1/6-em)]=[thin space (1/6-em)]2.068 Å) and the other with the NH2 group (H⋯F[thin space (1/6-em)]=[thin space (1/6-em)]1.781Å). In 10, three short contacts are present, but only with the NH3+ group (H⋯F[thin space (1/6-em)]=[thin space (1/6-em)]1.668, 1.687, and 2.434 Å). As a consequence of the ion pair formation, the dihydrogen bond is longer in 10 than in 8 (H⋯H[thin space (1/6-em)]=[thin space (1/6-em)]1.379 Å, 8; H⋯H[thin space (1/6-em)]=[thin space (1/6-em)]1.517 Å, 10) and the N–H bond is shorter (N–H[thin space (1/6-em)]=[thin space (1/6-em)]1.150 Å, 8; N–H[thin space (1/6-em)]=[thin space (1/6-em)]1.067 Å, 10).


Optimized geometry (ONIOM(B3PW91/UFF)) for the ion pair dihydrogen complex [IrH(H2)(bq-NH2)(PPh3)2][BF4], 9, and the ion pair hydride complex [Ir(H)2(bq-NH3)(PPh3)2][BF4], 10. Atoms included in the QM part are shown in ball-and-stick format and atoms included in the MM part are shown in black.
Fig. 5 Optimized geometry (ONIOM(B3PW91/UFF)) for the ion pair dihydrogen complex [IrH(H2)(bq-NH2)(PPh3)2][BF4], 9, and the ion pair hydride complex [Ir(H)2(bq-NH3)(PPh3)2][BF4], 10. Atoms included in the QM part are shown in ball-and-stick format and atoms included in the MM part are shown in black.

The inclusion of the counter anion reduces the relative energy between the two isomers with 9 (dihydrogen complex) now being only 3 kcal mol−1 more stable than 10 (hydride complex). When both components of the ONIOM energy are considered individually, the assumption of increased steric repulsion within 9 is confirmed. The energy difference between the QM parts of 9versus10 is 6 kcal mol−1 in favor of dihydrogen complex 9, illustrating the stabilizing electronic contribution of ion pairing in 10. This value should be compared with the 14.4 kcal mol−1 energy difference found between dihydrogen 7 and hydride 8, implying that the anion stabilizes the hydride form by ca. 8 kcal mol−1. For the MM parts, 9 is 3 kcal mol−1less stable than 10, confirming that ion pair formation close to the H2 ligand introduces larger steric repulsions.

In our attempt to model ion pairing with NH3+ we expected to see H⋯F contacts with all the NH3+ protons as in 10. However, the electrostatic potential for 8 (Fig. 4) reveals that ion pair formation is not restricted to the NH3+ group. In particular, H3 of bq is a viable candidate for such H⋯F short contacts. Indeed we optimized another minimum (Fig. 6), 11, also with three short H⋯F contacts: two are with NH3+ (H⋯F[thin space (1/6-em)]=[thin space (1/6-em)]1.652 and 1.661 Å) and one is with the H3 (H⋯F[thin space (1/6-em)]=[thin space (1/6-em)]2.219 Å). The dihydrogen bond parameters in 11 differ from those in 10 (H⋯H[thin space (1/6-em)]=[thin space (1/6-em)]1.517 Å, N–H[thin space (1/6-em)]=[thin space (1/6-em)]1.067 Å, 10; H⋯H[thin space (1/6-em)]=[thin space (1/6-em)]1.539 Å, N–H[thin space (1/6-em)]=[thin space (1/6-em)]1.060 Å, 11) as the N–H proton is not directly involved in the interaction with BF4−.


Alternate ion pair geometry for the hydride complex [Ir(H)2(bq-NH3)(PPh3)2][BF4], 11. The H3 proton bq is explicitly shown to illustrate the close contact with BF4−. Atoms included in the QM part are shown in ball-and-stick format and atoms included in the MM part are shown in black.
Fig. 6 Alternate ion pair geometry for the hydride complex [Ir(H)2(bq-NH3)(PPh3)2][BF4], 11. The H3 proton bq is explicitly shown to illustrate the close contact with BF4−. Atoms included in the QM part are shown in ball-and-stick format and atoms included in the MM part are shown in black.

Complex 11 is marginally less stable than 9 but by only 0.4 kcal mol−1; the QM parts differ by only 1.9 kcal mol−1 as a result of an optimal arrangement for anion–cation specific interactions in 11.

In conclusion the ONIOM calculations strongly suggest that ion pairing is responsible for the unexpected experimental observation of 6 in the case of L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3. With close contacts between acidic protons and BF4−, strong electronic preference for the dihydrogen complex may be strongly reduced as illustrated by 9 and 11. Electronic and steric components of the ion pairing energy contribute to the effect with a more efficient interaction and a weaker steric repulsion in the hydride isomers.

Experimental probes of ion pairing

Unfortunately, experimental attempts to exchange the BF4− counter-anion of 6a and 6e in a CD2Cl2 solution at −80[thin space (1/6-em)]°C with a smaller one, like F−, with the goal of switching the isomer to the unobserved dihydrogen complex 5a,e, all failed. Instead, we always obtained the neutral dihydride [Ir(bq-NH2)(PR3)2)(H)2] formed by deprotonation of the NH3+ group by F−, acting as a base. Even using the weaker base, Cl−, led to the same deprotonation. This deprotonation product was known because it had been already synthesized by another route, the action of NaBH4 on the aqua or acetone complexes.

Polar solvents can separate tight ion pairs, but all attempts in our system led to displacement of the coordinated H2 and formation of the solvent complex where the labile site is occupied by the solvent.

19F,1H-HOESY NMR spectra have previously7 given invaluable information on ion pair structure by revealing contacts between the BF4− or PF6− anions and the complex cation. Some of the hydride complexes 5 and 6 studied here proved unsuitable, however, because of thermal instability and solubility problems. Two related stable and soluble complexes, [Ir(bq-H)(PPh3)2H(CO)]PF6,18 and [Ir(bq-NH2)(PPh3)2H(CO)]PF6, did give good data. The anion–cation contacts observed in the NMR spectrum (CD2Cl2, 208 K, 376.63 MHz)19 showed the anions in the expected locations, next to the bq-H 2- and 3-positions in the former and next to the amino group in the latter. Contacts with ortho and meta PPh3 protons were also detected. For the key case of [Ir(bq-NH3)(PPh3)2(H)2]PF6, 6a, formed in equilibrium from 4′a and H2, data were obtained showing strong contacts for the bq-NH3+ proton, as predicted by the theoretical study. Contacts with the ortho and meta PPh3 protons as well as the 3-protons of bq were seen but no contacts with the Ir–H protons. The theoretical prediction was therefore in excellent agreement with the subsequent experimental confirmation by NMR spectroscopy.

Conclusion

The equilibrium between the M(H2)(bq-NH2) and MH(bq-NH3) isomers seems to be decided by ion pairing effects. Theoretical studies in which no anion is included show that the M(H2)(bq-NH2) form is predicted to be more stable for all the phosphines used. The observation of the MH(bq-NH3) isomer for bulky phosphines is therefore anomalous. The calculated electrostatic potentials for the two isomers suggest that the counter anion should be paired much closer to the metal in the M(H2)(bq-NH2) case but that in the MH(bq-NH3) isomer it can be much farther from the metal. Bulky phosphines seem to favor remote ion pairing and therefore the MH(bq-NH3) isomer where steric effects disfavor close ion pairing.

Experimental section

All operations were carried out under argon atmosphere using standard Schlenk techniques. Solvents were dried over calcium hydride (CH2Cl2) or sodium/benzophenone (Et2O). Solvents were degassed prior use. IR spectra were recorded on a Midac M1200 FT-IR spectrometer. Microanalyses were carried out by Robertson Microlit Laboratories. 1H NMR and 31P{1H} NMR spectra were either recorded on GE Omega 300 or GE Omega 500 spectrometers, chemical shifts were measured with reference to the residual solvent resonance. The starting [Ir(cod)L2]X (X[thin space (1/6-em)]=[thin space (1/6-em)]BF4 or PF6) complexes were made as previously reported.11a,b

(2-Amino-7,8-benzoquinolinato)(solvento)bis(tri(p-tolyl)phosphine)iridium(III) salts (4, solvent[thin space (1/6-em)]=[thin space (1/6-em)]water; 4′ solvent[thin space (1/6-em)]=[thin space (1/6-em)]acetone)

These compounds can be prepared by one of three related methods. In method A (for 4), reported previously,10 [Ir(cod)L2]X (X[thin space (1/6-em)]=[thin space (1/6-em)]BF4 or PF6; 0.25 mmol) and 2-aminobenzoquinoline (0.25 mmol) in CH2Cl2 (10 ml) are treated with H2 (1 atm) for 30 min at 0[thin space (1/6-em)]°C (ice bath). The solvent volume is reduced by 50% on the vacuum line and the product is precipitated with hexanes–Et2O (1∶1, 10 ml) and recrystallized from CH2Cl2/Et2O. Method B (for 4′) goes through an intermediate acetone complex [IrH2(Me2CO)2L2]X.20 [Ir(cod)L2]X (0.25 mmol) in acetone (10 ml) is first treated with H2 (1 atm) for 30 min at 0[thin space (1/6-em)]°C (ice bath). The intermediate is then precipitated with Et2O then redissolved in acetone (10 ml) to which is added 2-aminobenzoquinoline (0.25 mmol) in acetone (10 ml). The mixture is stirred for 30 min and the final product precipitated with hexanes and recrystallized from CH2Cl2/Et2O. Method C (for 4), goes through an intermediate aqua complex [IrH2(H2O)2L2]X.20 [Ir(cod)L2]X (0.25 mmol) in moist CH2Cl2 (10 ml) is first treated with H2 (1 atm) for 30 min at 0[thin space (1/6-em)]°C (ice bath). The intermediate is then precipitated with hexanes and redissolved in moist CH2Cl2 (10 ml). Aminobenzoquinoline (0.25 mmol) is then added and the mixture stirred for 30 min. The final product is precipitated with hexanes and recrystallized from CH2Cl2/Et2O.
4a (BF4 salt). The complex was previously prepared by method A.10
4b (PF6 salt). The complex was best prepared by method C. 1H NMR (CD2Cl2, 500 MHz, 293K, ppm) δ −16.61 (br. s, Ir–H), 1.60 (br. s, 2H, H2O), 2.22 (s, 18H, Me), 6.00–8.10 (m, 39H, bq[thin space (1/6-em)]+[thin space (1/6-em)]NH2[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 1H NMR (CD2Cl2, 500 MHz, 183 K, ppm) δ −16.61 (br. s, Ir–H), 1.60 (br. s, 2H, H2O), 2.22 (s, 18H, Me), 6.00–8.10 (m, 39H, bq[thin space (1/6-em)]+[thin space (1/6-em)]NH2[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 18.83 (s). IR (thin film, cm−1): ν 2186.7 (IrH), 3361.1 (NH), 3464.2 (NH). Anal. Calcd. for C55H54F6IrN2OP3: C, 57.04, H, 4.70, N, 2.42%. Found: C, 56.89, H, 4.66, N, 2.28%. Yield: 80%.
4c (PF6 salt). The complex was best prepared by method C. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −16.76 (br. s, 1H, Ir–H), 1.89 (br. s, 2H, H2O), 3.72 (s, 18H, OMe), 6.20–8.00 (m, 33H, bq[thin space (1/6-em)]+[thin space (1/6-em)]NH2[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 1H NMR (CD2Cl2, 500 MHz, 183 K, ppm) δ −16.61 (br. s, Ir–H), 1.60 (br. s, 2H, H2O), 2.22 (s, 18H, Me), 6.00–8.10 (m, 39H, bq[thin space (1/6-em)]+[thin space (1/6-em)]NH2[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 16.69 (s). IR (thin film, cm−1): ν 2212.3 (IrH), 3361.1 (NH), 3469.2 (NH). Anal. Calcd. for C55H54F6IrN2O7P3: C, 52.57, H, 4.34, N, 2.23%. Found: C, 52.48, H, 4.22, N, 2.25%. Yield: 81%.
4d (BF4 salt). The complex was best prepared by method C. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −16.77 (t, 1H, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 1.50 (br. s, 2H, H2O), 1.60 (s, 6H, Me), 6.24 (br. s, 2H, NH2), 6.41–7.63 (m, 27H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 1H NMR (CD2Cl2, 500 MHz, 183 K, ppm) δ −16.34 (t, 1H, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 1.70 (s, 2H, Me), 6.10 (s, 1H, NHa) 6.39–7.89 (m, 28H, bq[thin space (1/6-em)]+[thin space (1/6-em)]NHb[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 5.08 (s). IR (thin film, cm−1): ν 2186.7 (IrH), 3319.8 (NH), 3412.7 (NH). Anal. Calcd. for C39H38F4IrN2OP2B: C, 52.53, H, 4.29, N, 3.14%. Found: C, 52.42, H, 4.19, N, 2.94%. Yield: 42%.

(2-Amino-7,8-benzoquinolinato)(acetone)bis(tricyclohexylphosphine)iridium(III) hexafluorophosphate (4′e)

The complex was best prepared by a variant of method B. [IrH5(PCy3)2] (0.25 mmol) was dissolved in acetone (10 ml) to which 1.5 equiv. HPF6 was added. The pale yellow intermediate, [IrH2(OCMe2)2(PCy3)2]PF6, was precipitated with Et2O, dried in vacuo (240 mg, 0.22 mmol) and immediately carried forward by redissolving in acetone (10 ml). Addition of 2-amino-7,8-benzoquinoline (43.6 mg, 0.22 mmol) in acetone (10 ml) is carried out with stirring, followed by precipitation of the product after 15 min with hexane (100 ml). Recryst: CH2Cl2/Et2O. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −14.34 (t, 1H, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 0.60–2.00 (m, 72H, Cy[thin space (1/6-em)]+[thin space (1/6-em)]CH3COCH3), 5.83 (s, 2H, NH2), 6.55–8.30 (m, 7H, bq). 1H NMR (CD2Cl2, 500 MHz, 183 K, ppm) δ −14.23 (t, 1H, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 0.60–2.00 (m, 72H, Cy[thin space (1/6-em)]+[thin space (1/6-em)]CH3COCH3), 6.05 (s, 1H, NHa) 6.70–8.50 (m, 7H, bq), 7.55 (s, 1H, NHb). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 14.86 (s). IR (thin film, cm−1): ν 1564 (C[double bond, length as m-dash]O), 2176 (IrH), 3364 (NH), 3427 (NH). Anal. Calcd. for C58H58F6IrN2O7P3: C, 53.83, H, 4.52, N, 2.16%. Found: C, 53.60, H, 4.43, N, 2.27%. Yield: 82%.

Observation of reaction with H2

The appropriate salt, 4, (10 μmol) was dissolved in CD2Cl2 (0.5 ml) in an NMR tube with anhydrous MgSO4 (5 mg) also present, cooled to −70[thin space (1/6-em)]°C (EtOH bath cooled with liq. N2) and H2 passed for 30 min. The NMR tube was transferred to a precooled probe (−80[thin space (1/6-em)]°C) and the spectrum observed.
Spectrum of 6a. 1H NMR (CD2Cl2, 500 MHz, 203 K, ppm) δ −25.63 (dt, 1H, 2JH–H′[thin space (1/6-em)]=[thin space (1/6-em)]8.50 Hz, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), −23.24 (dt, 1H, 2JH–H′[thin space (1/6-em)]=[thin space (1/6-em)]8.50 Hz, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 4.56 (br. s, 3H, NH3+), 6.80–8.00 (m, 37H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −25.83 (dt, 1H, 2JH–H′[thin space (1/6-em)]=[thin space (1/6-em)]8.50 Hz, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), −23.19 (dt, 1H, 2JH–H′[thin space (1/6-em)]=[thin space (1/6-em)]8.50 Hz, 2JH–P[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 1.70 (br. s, 2H, free H2O), 4.69 (br. s, 3H, NH3+), 6.80–8.00 (m, 37H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph).
6b. 1H NMR (CD2Cl2, 500 MHz, 203 K, ppm) δ −25.91 (br. s, 1H, Ir–H), −23.38 (br. s, 1H, Ir–H), 2.14 (s, 3H, Me), 4.15 (br. s, 3H, NH3+), 6.56–8.14 (m, 31H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph).
6c. 1H NMR (CD2Cl2, 500 MHz, 203 K, ppm) δ −26.10 (br. s, 1H, Ir–H), −23.44 (br. s, 1H, Ir–H), 3.66 (s, 3H, OMe), 4.29 (br. s, 3H, NH3+), 6.42–8.24 (m, 31H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph).
6e. 1H NMR (CD2Cl2, 500 MHz, 203 K, ppm) δ −25.03 (br. s, 1H, Ir–H), −21.06 (br. s, 1H, Ir–H), 0.60–2.40 (m, 60H, Cy), 4.29 (br. s, 3H, NH3+), 6.28–8.62 (m, 7H, bq).
5d. 1H NMR (CD2Cl2, 500 MHz, 208 K, ppm) δ −15.90 (br. s, 1H, Ir–H), −3.75 (br. s, 2H, Ir–H2), 1.70 (s, Me), 5.52 (s, NH2) 6.3–7.8 (m, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph).

(2-Amino-7,8-benzoquinolinato)(carbonyl)bis(tricyclohexylphosphine)iridium(III) hexafluorophosphate

For the case of the benzoquinolinate with L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3, the complex has been reported and structurally characterized.17 For the present complexes, the same method, treating 4 or 4′ (0.15 mmol) in CH2Cl2 (10 ml) with CO (1 atm) for 30 min, isolating with hexanes, then recrystallizing from CH2Cl2/hexanes, was used.
L[thin space (1/6-em)]=[thin space (1/6-em)]PPh3. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −14.98 (t, 1H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.21 Hz, Ir–H), 5.66 (s, 2H, NH2), 6.87–7.60 (m, 37H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 7.16 (s). IR (thin film, cm−1): ν 2026.0 (C[double bond, length as m-dash]O), 2222.6 (Ir–H), 3397.1 (N–H), 3510.5 (N–H). Anal. Calcd. for C50H40F6IrN2OP3: C, 55.40, H, 3.72, N, 2.58%. Found: C, 55.07, H, 3.72, N, 2.48%. Yield: 83%. Yellow solid.
L[thin space (1/6-em)]=[thin space (1/6-em)]P(p-C6H4CH3)3. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −15.07 (t, 1H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.21 Hz, Ir–H), 2.24 (s, 18H, Me), 5.61 (s, 2H, NH2), 6.87–7.62 (m, 31H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 5.36 (s). IR (thin film, cm−1): ν 2024.5 (C[double bond, length as m-dash]O), 2227.7 (Ir–H), 3392.0 (N–H), 3510.5 (N–H). Anal. Calcd. for C56H52F6IrN2OP3–CH2Cl2: C, 54.63, H, 4.34, N, 2.23%. Found: C, 54.94, H, 4.39, N, 2.09%. Yield: 83%. Pale pink solid.
L[thin space (1/6-em)]=[thin space (1/6-em)]P(p-C6H4OCH3)3. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −15.14 (t, 1H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.21 Hz, Ir–H), 3.74 (s, 18H, OMe), 5.79 (s, 2H, NH2), 6.57–7.66 (m, 31H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 2.85 (s). IR (thin film, cm−1): ν 2023.4 (C[double bond, length as m-dash]O), 2226.9 (Ir–H), 3397.4 (N–H), 3505.8 (N–H). Anal. Calcd. for C56H52F6IrN2O7P3–CH2Cl2: C, 50.75, H, 4.03, N, 2.08%. Found: C, 50.31, H, 4.09, N, 1.81%. Yield: 82%. Pale pink solid.
L[thin space (1/6-em)]=[thin space (1/6-em)]PMePh2. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −15.52 (t, 1H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.48 Hz, Ir–H), 1.72 (s, 6H, Me), 5.96 (s, 2H, NH2), 6.80–8.84 (m, 27H, bq[thin space (1/6-em)]+[thin space (1/6-em)]Ph). IR (thin film, cm−1): ν 2021.7 (C[double bond, length as m-dash]O), 2197.0 (Ir–H), 3391.9 (N–H), 3479.5 (N–H). Not obtained analytically pure.
L[thin space (1/6-em)]=[thin space (1/6-em)]PCy3. 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −16.63 (t, 1H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]14.65 Hz, Ir–H), 1.00–2.00 (m, 60H, Cy), 6.06 (s, 2H, NH2), 7.0–8.3 (m, 7H, bq). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 2.26 (s). IR (thin film, cm−1): ν 1994.5 (C[double bond, length as m-dash]O), 2121.5 (Ir–H), 3353.0 (N–H), 3508.2 (N–H). Not obtained analytically pure.

Improved synthesis of pentahydridobis(tricyclohexylphosphine)iridium(V)

Hydrogen gas was bubbled overnight at room temperature in an orange suspension of [Ir(cod)Cl]2 (1 eq, 685 mg, 0.98 mmol), PCy3 (4 eq, 1100 mg, 3.92 mmol) and NaOMe (2 eq, 106 mg, 1.96 mmol) in degassed dichloromethane (40 mL), under stirring. A white solid was obtained by filtration in vacuo, washed with H2O, then Et2O, and dried in vacuo (877 mg, 59%). 1H NMR (CD2Cl2, 500 MHz, 293 K, ppm) δ −11.27 (t, 5H, 2JHP[thin space (1/6-em)]=[thin space (1/6-em)]12.21 Hz, Ir–H), 1.10–2.25 (m, 66H, Cy). 31P{1H} NMR (CD2Cl2, 125 MHz, 293 K, ppm) δ 33.42 (s). IR (thin film, cm−1): ν(Ir–H) 1929.1. Anal. Calcd. for C36H68IrP2Cl.0.33CH2Cl2: C, 55.51, H, 9.19%. Found: C, 55.65, H, 8.69%. Yield: 59%.

19F,1H-HOESY NMR spectra

These were obtained following the procedure of ref. 17.

Computational details

All calculations were performed with the Gaussian 98 set of programs21 within the framework of hybrid DFT (B3PW91)22 for complexes 7 and 8 and with the ONIOM method23 for complexes 9, 10, and 11. These three complexes were optimized at the ONIOM(B3PW91/UFF) level, where the QM part was treated within the framework of density functional theory at the B3PW91 level22 and the UFF force field24 was used for the molecular mechanics calculations. In all calculations (QM and QM/MM) the iridium atom was represented by the relativistic effective core potential (RECP) from the Stuttgart group (17 valence electrons) and its associated (8s7p5d)/[6s5p3d] basis set,25 augmented by an f polarization function (α[thin space (1/6-em)]=[thin space (1/6-em)]0.95). The phosphorus atoms were also treated with Stuttgart's RECPs and the associated basis set,26 augmented by a polarization d function (α[thin space (1/6-em)]=[thin space (1/6-em)]0.387). A 6-31G(d,p) basis set was used for the atoms directly bound to Ir (N,C, and H) and the atoms of the NH2 (or NH3) group. The remaining atoms were treated by a 6-31G basis set. Full optimizations of geometry without any constraint were performed for both types of calculations (B3PW91 and ONIOM(B3PW91/UFF)), followed by analytical computation of the Hessian matrix to confirm the nature of the located extrema as minima on the potential energy surface. ΔG values were calculated at 298 K within the harmonic frequency approximation.

Acknowledgements

This work was supported by grants from the Ministero dell'Universitá e della Ricerca Scientifica e Tecnologica (MURST, Rome, Italy), Programma di Rilevante Interesse Nazionale, Cofinanziamento 2000-1 (A. M.), the CNRS and the Université Montpellier II (E. C. and O. E.), and the DOE (R. H. C., K. G.). R. H. C. thanks the Université Montpellier II for a position of invited professor.

References

  1. P. J. Brothers, Prog. Inorg. Chem., 1981, 28, 1 Search PubMed.
  2. D. M. Heinekey and W. J. Oldham Jr, Chem. Rev., 1993, 93, 913 CrossRef CAS.
  3. Y. Nicolet, A. Y. de Lacey, X. Vernede, V. M. Fernandez, E. C. Hatchikian and J. C. Fontecilla-Camps, J. Am. Chem. Soc., 2001, 123, 1596 CrossRef CAS.
  4. D.-H. Lee, B. Patel, E. Clot, O. Eisenstein and R. H. Crabtree, Chem Commun., 1999, 297 RSC.
  5. R. H. Morris, Can. J. Chem., 1996, 74, 1907 CAS.
  6. J. A. Ayllon, S. F. Sayers, S. Sabo-Etienne, B. Donnadieu, B. Chaudret and E. Clot, Organometallics, 1999, 18, 3981 CrossRef CAS.
  7. (a) C. Zuccaccia, G. Bellachioma, G. Cardaci and A. Macchioni, J. Am. Chem. Soc., 2001, 123, 11[thin space (1/6-em)]020 CrossRef CAS and refs. cited; (b) G. Lanza, I. L. Fragala and T. J. Marks, J. Am. Chem. Soc., 2000, 122, 12[thin space (1/6-em)]764 CrossRef CAS.
  8. R. H. Crabtree, M. Lavin and L. Bonneviot, J. Am. Chem. Soc., 1986, 108, 4032 CrossRef CAS.
  9. H. Vorbrüggen, Adv. Heterocycl. Chem., 1990, 49, 117.
  10. (a) B. Patel, D.-H. Lee, A. L. Rheingold and R. H. Crabtree, Organometallics, 1999, 18, 1615 CrossRef CAS; (b) K. Gruet, R. H. Crabtree, D.-H. Lee, L. Liable-Sands and A. L. Rheinold, Organometallics, 2000, 19, 2228 CrossRef CAS.
  11. (a) R. H. Crabtree and G. E. Morris, J. Organomet. Chem., 1977, 135, 395 CrossRef CAS; (b) R. H. Crabtree, H. Felkin and G. E. Morris, J. Organomet. Chem., 1977, 141, 205 CrossRef CAS; (c) S. Brinkmann, R. H. Morris, R. Ramachandran and S.-H. Park, Inorg. Synth., 1998, 32, 303 CAS.
  12. A. Tolman, Chem Rev., 1977, 77, 313 CrossRef CAS.
  13. see Computational Details.
  14. R. H. Crabtree, P. E. M. Siegbahn, O. Eisenstein, A. L. Rheingold and T. F. Koetzle, Acc. Chem. Res., 1996, 29, 348 CrossRef CAS.
  15. L. Perrin, E. Clot, O. Eisenstein, J. Loch and R. H. Crabtree, Inorg. Chem., 2001, 40, 5806 CrossRef CAS.
  16. K. Miyabe, S. Taguchi, I. Kasahara and K. J. Goto, J. Phys. Chem. B, 2000, 104, 8481 CrossRef CAS and refs cited.
  17. A. Macchioni, C. Zuccaccia, E. Clot, K. Gruet and R. H. Crabtree, Organometallics, 2001, 20, 2367 CrossRef CAS.
  18. (a) F. Neve, M. Ghedini, A. Tiripicchio and F. Ugozzoli, Inorg. Chem., 1989, 28, 3084 CrossRef CAS; (b) T. Dubé, J. W. Faller and R. H. Crabtree, Inorg. Chem., 2002, 41, 5561 CrossRef CAS.
  19. A potentially relevant issue in this chemistry is that the ε of the solvent is known to increase very greatly with decreasing temperature over the range used here, going from 9 at 298 K to 16 at 208 K.27 This is expected to counteract somewhat the normal entropy-based tendency for increasing ion pairing at low temperature.
  20. R. H. Crabtree, P. C. Demou, D. Eden, J. M. Mihelcic, C. Parnell, J. M. Quirk and G. E. Morris, J. Am. Chem. Soc., 1982, 104, 6994 CrossRef CAS.
  21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, P. I. Komaromi, G. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98 (Rev A7), Gaussian, Inc., Pittsburgh, PA, 1998.
  22. (a) A. D. J. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 82, 284.
  23. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. J. Morokuma, J. Phys. Chem., 1996, 100, 19[thin space (1/6-em)]357 CrossRef CAS.
  24. A. K. Rappé, C. J. Casewitt, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10[thin space (1/6-em)]024 CAS.
  25. D. Andrae, U. Häussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123 CAS.
  26. A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuss, Mol. Phys., 1990, 30, 1431.
  27. S. O. Morgan and H. H. Lowry, J. Phys. Chem., 1930, 34, 2385 CrossRef CAS.
This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2003