Distance criteria for crystal packing analysis of supramolecular motifs

Abstract

Supramolecular phenomena are determined by energies, but a different property, geometry, is commonly measured, and abundant data are available. The sum of van der Waals radii, the conventional distance criterion in assessing geometrical data, needs to be related to the relevant intermolecular potential, with cognisance of the chemistry of the molecular surface. The relationship between distance distributions in crystals and the distance scale of the intermolecular potential is evaluated, and the relevant concepts (and mis-concepts) are elaborated. The position of the minimum in the intermolecular potential, that is the most stabilising distance, is ca. 0.4 Å larger than the van der Waals distance. In crystals a small number of destabilising contacts less than the van der Waals distance can be enforced by a much larger number of longer stabilising distances. Crystal packing analyses with cut-offs at the van der Waals distance are likely to miss key supramolecular features.

---

Intermolecular interactions and their influences in supramolecular phenomena are determined by energies, but a different property, geometry, is commonly measured. Analyses of the packing of molecules in crystals are a principal source of information, mainly geometrical, about intermolecular interactions. This arises because the molecular crystal is a supramolecular entity par excellence,¹ and also because crystal structure data are so abundantly available.^2,3 These analyses of intermolecular interactions and crystal supramolecular motifs encompass all chemical types,⁴ including organic molecules, inorganic molecules, coordination complexes, organometallic molecules, biomolecules, and the interactions between polymer molecules.⁵

Here I comment on some concepts and procedures used in this research, and start with emphasis of two fundamental points.

First, energy properties determine crystallisation processes and the molecular packing in crystals, but intermolecular geometry is measured in the crystal structure. Therefore, a conceptual and operational relationship between distance and energy is essential, and interpretations of intermolecular interactions should embody this relationship. There are dangers of misconception: for example, the notion of ‘shorter is stronger’ that is commonly implicit and sometimes explicit in discussion of intermolecular interactions is questionable, and often erroneous.

Second, conventional practice is to assess the significance of intermolecular distance with reference to sums of atomic van der Waals radii. Then it is appropriate to ask: what intermolecular energy is associated with molecular surfaces at the vdW contact distance? or shorter distances? or longer distances? Again, the intermolecular potential—the energy–distance curve—is essential.

Intermolecular potential

A representative intermolecular energy-distance curve⁶ is shown in Fig. 1. The energy axis is labelled as stabilising for negative energies of the assembly relative to its components, and destabilising for positive energies. The terms stabilising and destabilising are used, rather than the usual ‘attractive’ and ‘repulsive’ which describe forces rather than energies: this distinction between the energetic and virial aspects of an intermolecuar interaction is expounded by Dunitz and Gavezzotti.⁷

Fig. 1 A representative intermolecular potential. Positive energies are destabilising, negative energies stabilising. The curve drawn is the experimentally determined potential for a pair of xenon atoms,⁹ and the major units on the distance axis are Å. The energy e^a and distance d^a describe the minimum, and d⁰ is the distance for zero energy.

At shorter distances the interaction between molecules is destabilising (due to Pauli exclusion) and rises steeply as distance decreases.⁸ At longer distances the interaction energy is negative and stabilising, an influence that extends to very long distances. The bottom of the energy well is described by energy e^a at distance d^a. The potential illustrated in Fig. 1 was measured experimentally for a pair of xenon atoms,⁹ and the distance axis is correctly calibrated in Å units: it is evident that the stabilising region (shaded) extends over several Å. Further properties of intermolecular potentials for representative chemical systems are described below, but first I discuss the observed distances in crystals.

Distribution of immediate intermolecular distances

Valuable information comes from the distributions of observed interatomic distances in crystals. The abundant experimental data provide opportunities for evaluation of intermolecular distances and angles (and other metrical properties) with statistical confidence, and such analyses are common in the current literature. A straightforward representation of these results is as a distribution of observed intermolecular distances in crystals for a defined atom pair, as illustrated by the upper black line in Fig. 2. The characteristics of distance distributions are quite dependent on the selection of the compounds, the crystals, the surface functionalities, and the atom types, but in well-formulated interrogations of known crystal structures there is a broad peak of immediate contacts superimposed on a rising background with increasing distance. The background is due to the approximately cubic increase in distances for a general array of atoms, as occurs in crystals. In Fig. 2 the observed distribution (—) has been separated into the general background (- - -) and the peaked distribution of immediate contacts (–■–) across the intermolecular domain. Alternative mathematical procedures are sometimes used to factor out this background increase and to include angular distributions,¹⁰ but for the present purpose of focussing on basic concepts the simplified distribution of Fig. 2 is valuable.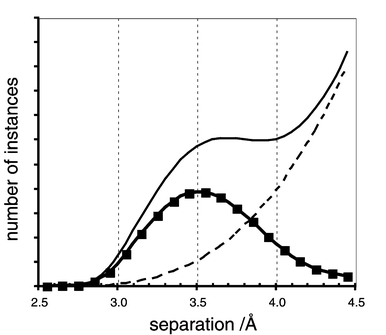

Fig. 2 A generalised and idealised representation of a distribution of interatomic distances (for defined atom types) between molecules in crystals. The solid curve represents the observed distribution comprised of the general background (- - -) for the general three-dimensional array of atoms in any crystal, and the distribution of immediate contacts (–■–) across an intermolecular domain.

A fundamental concept is that the histogram of immediate contacts between molecules is a reflection of the intermolecular potential. This relationship is shown in Fig. 3. Fewer contacts are expected as the destabilisation increases, while more contacts are likely to occur at the distances where stabilisation is strong. The peak in the distribution could be expected to be near the distance of the potential well. The rarity of empty space in crystals requires that the distribution of immediate contacts across the intermolecular space falls to low values at large distances. The distance axis in Fig. 3 is calibrated (Å) for representative distributions and potentials, to show that the dimensional widths of the distribution peak and the potential well are similar.

Fig. 3 A superimposition of the intermolecular potential (–●–) and the distribution of immediate contacts (–■–) in crystals, showing their complementary character. The distance scale is calibrated, but the correlation of the two plots along the distance axis is questionable.

But, this relationship still has an uncertainty, namely the registry of the distance scales for the intermolecular potential and the distance distribution. Do the distribution maximum and the potential minimum occur at the same separation, or is one plot displaced relative to the other along the distance axis?

Before answering this question, I introduce another relevant concept. As drawn in Fig. 3, the shortest contacts occur with substantial destabilisation. In this connection there is a key concept that a stable crystal containing polyatomic molecules will in general contain both stabilising and destabilising local interactions. A small number of shorter destabilising local interactions can (and usually will) be enforced by a much larger number of longer stabilising distances, with net energy advantage. The shape-complementarity or shape-awkwardness of molecules is a factor here, influencing details of the destabilising contacts, but this does not alter the general concept of a crystal at equilibrium tolerating some destabilising interactions in order to enable a larger number of stabilising interactions. This point, elaborated by Dunitz and Gavezzotti,⁷ is rarely explicit in the literature.

The van der Waals surface

The van der Waals surface is imagined as the impenetrable surface of the molecule, with some arbitrariness because no chemical system is considered to be completely hard. The well-known Bondi analysis¹¹ of van der Waals volumes and atom radii that define the van der Waals surface was “guided by the principle that one should adopt the smallest observed intermolecular distances as source of van der Waals radius data”. Additional data from the liquid phase and from real gas properties have been used in the assessment of the size of the van der Waals surface.

There can be complications, associated with the chemical nature of the molecular surface. Surface domains of molecules can be broadly classified as (a) hydrogenic, (b) Lewis basic, or (c) Lewis acidic. Uncomplicated intermolecular potentials and van der Waals surfaces occur where the contacts are hydrogenic⋯hydrogenic, Lewis basic⋯Lewis basic or (rarely) Lewis acidic⋯Lewis acidic. However, where a hydrogenic surface domain contacts a Lewis basic surface domain there are opportunities for hydrogen bonding extending from very weak¹² to very strong, and chemically-specific potentials need to be used. Similarly, intermolecular contacts between Lewis basic domains and Lewis acidic domains allow energetically enhanced interactions, which are sometimes described as secondary bonding¹³ particularly where the Lewis acid site is a metal atom. Larger softer atoms in exposed positions, such as terminal halogens, are often quite non-spherical in their intermolecular interactions,^10,14,15 an effect that can be considered in terms of Lewis basic and Lewis acidic domains of the one atom type. Further complications arise for ‘charge-transfer’ associations, and for charged molecules and strongly multipolar molecules in crystals. However, for the present purposes these complications are recognised but disregarded, because the objective is exposition of the underlying basic principles.

Distances and intermolecular potentials

Information about intermolecular potentials is limited. Most of the experimental data relevant to intermolecular energies are for chemically simple systems (detailed experimental potentials are available for pairs of the group 18 elements^9,16), and there is a shortage of experimental data on intermolecular energies for most of the real chemical systems involved in crystal packing analysis.¹⁷ There is a larger amount of computational and theoretical information, in the form of parametrised ‘non-bonded’ potentials,¹⁸ and quantum chemical calculations for small molecules. Table 1 provides information on the distance scales of some intermolecular potentials, expressed in terms of the distances d⁰ for zero energy and d^a for the energy well (see Fig. 1). These distances are compared with the conventional Pauling¹⁹ and Bondi¹¹ values for the van der Waals distance.

Table 1 Distances for intermolecular potentials, and van der Waals distances. d^w is the van der Waals distance, d⁰ is the distance at which the energy is zero, and d^a is the distance of the energy at which the intermolecular potential is most stabilising

Atom types	d ^w	d ^0	d ^a	Interaction, source, comments
a From ref. 7, originating in ref. 26. Additional values for d^a are contained in ref. 17. b These anomalous values quoted in ref. 7 may be a reflection of the anisometric character of Cl and S.
H⋯H	2.4 (Pauling, Bondi)	2.98	3.36	Empirical force field for organic crystals^a
H⋯H	2.4 (Pauling, Bondi)	2.7–2.9	3.1–3.4	CH4⋯CH4, DFT p91 functional^20
H⋯C	2.9 (Bondi)	2.92	3.29	Empirical force field for organic crystals^a
H⋯C	2.9 (Bondi)	3.1	3.4	T shaped C2H4·C2H4, ab initio MP2, MP3, MP4(SDQT) theory, adapted from ref. 21
C⋯C	3.4 (Bondi)		4.0–4.1	Offset-face-to-face C6H6··C6H6, ab initio CCSD(T), from ref. 22
C⋯C	3.4 (Bondi)	3.45	3.89	Empirical force field for organic crystals^a
N⋯N	3.0 (Pauling) 3.10 (Bondi)	3.28	3.70	Empirical force field for organic crystals^a
N⋯N	3.0 (Pauling) 3.10 (Bondi)		3.6–3.9	(N2)2 high level ab initio, from ref. 23
O⋯O	2.8 (Pauling) 3.04 (Bondi)	3.20	3.61	Empirical force field for organic crystals^a
F⋯F	2.7 (Pauling) 2.94 (Bondi)	2.84	3.20	Empirical force field for organic crystals^a
F⋯F	2.7 (Pauling) 2.94 (Bondi)	2.8–2.9	3.1–3.3	SnF4⋯SnF4, DFT p91+pwc functionals^20
S⋯S	3.7 (Pauling) 3.6 (Bondi)	3.39^b	3.83	Empirical force field for organic crystals^a
S⋯S, two-coordinate S	3.7 (Pauling) 3.6 (Bondi)	3.8–3.85	4.25–4.3	H2S⋯SH2, various geometries, ab initio MP2^24
Cl⋯Cl	3.6 (Pauling) 3.5 (Bondi)	3.39^b	3.83	Empirical force field for organic crystals^a
Au⋯Au	3.32 (Bondi)	2.95	3.4	References 15, 25

---

The pattern in Table 1 is that d^w is slightly less than d⁰, and d^a is 0.3 to 0.4 Å larger than d⁰. The significant point is that the conventional van der Waals surface occurs at a distance that is slightly destabilising, in the region marked with crosses on the potential in Fig. 1. It is sometimes posited that the van der Waals distance corresponds to a small destabilising energy of order kT, i.e. <1 kcal mol⁻¹.^4,27

Therefore it appears that the van der Waals distances that are often quoted in crystal packing analyses are the destabilising distances: they are the exceptional, shorter, unfavourable contacts that are ‘sacrificed’ in order that the crystal cohesion can be established elsewhere, at distances ca. 0.4 Å longer.

The validity of this relationship between d^w and d^a can be checked using the analyses of Roland and Taylor (R&T),²⁸ who constructed histograms (cf.Fig. 2) from the data in the Cambridge Structural Database for many combinations of the atom types H, C, N, O, F, S, Cl, Br and I. Charged molecules were excluded, and interactions with hydrogen bonding possibilities were separated. The objective was to characterise the component of the histogram that represented the immediate contact, with emphasis on its location along the distance axis. Because the actual histograms can be less regular than the idealisation in Fig. 2, R&T developed numerical algorithms that established the distance at which the number of observations is half that of the maximum. This position is effectively that of maximum slope on the leading edge of the distribution, and was selected because its derivation was numerically more robust than alternatives. R&T then compared these distances and the atom component radii derived from them with the van der Waals radii of Pauling and Bondi, finding better correlation with the Bondi radii. Overall the R&T radii were 0.987 of the Bondi radii. It is significant that the R&T procedure used vastly more data than Bondi (and Pauling), with higher precision.

The R&T procedure was not based on any physical model or concept of intermolecular potential, but only on the need for numerical stability. However, the result that the conventional van der Waals distances occur half way up the leading edge of the distribution of contact distances is valuable because it allows connection with the distance scale of the intermolecular potential. This calibration connection is made via the van der Waals distance, which has been located on both the potential and the distribution. This is shown in Fig. 4 where the broken line is the van der Waals distance common to the distribution and potential.

Fig. 4 Correlation along the distance axis of the distribution of observed distances (–■–) and the intermolecular potential (–●–), via registry of the van der Waals distance (broken line) that occurs half way up the leading edge of the distribution and just less than the zero energy point of the potential.

A key conclusion from Fig. 4 is that the majority (probably ca. 80%) of the observed distances between contiguous molecules are greater than the van der Waals distance, and in the region of energetic stabilisation, as would be expected intuitively. Crystal packing analysis that considers only distances at or below the van der Waals distance sees only the small minority of distances between the molecules, and misses the majority of influential distances.

It is worth mentioning here that parametrised potentials for intermolecular van der Waals energies, included in molecular mechanics and force-field computer programs, are based on d^a and e^a (Fig. 1). Thus the ‘van der Waals’ radii listed with the atom-type parameters in these programs sum to d^a, not d^w.

Molecules in contact

Contiguous molecules necessarily have a distribution of interatomic distances that extends beyond the shortest distance between the molecules, and details of these distributions depend on the shapes of the molecules. This aspect, and the other pitfalls mentioned above, can be demonstrated with the embrace motifs formed by metal complexes with 1,10-phenanthroline (phen) ligands.²⁹ One such embrace is the parallel fourfold phenyl embrace (P4AE) illustrated in Fig. 5(a) for a centrosymmetric pair of [Zn(phen)₂(OH₂)₂]²⁺ complexes in crystalline [Zn(phen)₂(OH₂)₂]SO₄·(H₂O)₆ [CSD refcode KOFCUD]. This embrace is comprised of an offset-face-to-face (OFF) pair of phen ligands in the centre, and two edge-to-face (EF) interactions. The planes of the central phen ligands are separated by 3.41 Å. A histogram of all distances between the C and N atoms of one ligand and those of the other is shown in Fig. 5(b). There is a continuing range of distances above 3.4 Å and those up to about 5 Å are responsible for the stabilising dispersion energy, and the existence of the motif. If this crystal structure had been searched for C/N⋯C/N distances ≤ 3.4 Å, the van der Waals distance, the motif would not have been detected. The crystal packing in KOFCUD is dominated by motifs like that shown in Fig. 5(a).²⁹

Fig. 5 (a) The parallel fourfold aryl embrace of two [Zn(phen)₂(OH₂)₂]²⁺ complexes in crystalline [Zn(phen)₂(OH₂)₂]SO₄·(H₂O)₆ [CSD refcode KOFCUD]: C green, N blue, H cyan, O red, Zn black; the atoms surfaces are drawn with the Bondi van der Waals radii. (b) The histogram of all C/N⋯C/N distances between the two central phen ligands engaged in the standard offset-face-to-face (OFF) motif.

Many known crystals containing metal–phen complexes manifest the offset-face-to-face relationship between pairs of phen ligands: this is analogous to the offset-face-to-face pairing of phenyl rings and other aromatic groups. In a previous analysis it was estimated that this OFF motif occurs in 70% of crystals with M(phen) complexes, 84% of crystals containing M(phen)₂ complexes, and 61% of crystals containing M(phen)₃ complexes.²⁹ What is the distribution of C/N⋯C/N distances in these? A new search of the CSD (May 2002) yields the C/N⋯C/N distance distribution shown in Fig. 6(a), for 742 good OFF motifs in 334 good crystal structures. Note several features: (i) the general shape reflects the intermolecular potential for C⋯C; (ii) the distance halfway up the leading edge is 3.45–3.5, slightly more than the van der Waals distance. It appears that a naive search of the CSD for M–phen complexes with intermolecular distances C/N⋯C/N ≤ 3.4 (the van der Waals distance for C⋯C) would reveal but a small fraction of the occurrences of a common supramolecular motif. Data-miners would consider that a more reliable search datum would be the minimum C/N⋯C/N distance between phen groups. Fig. 6(b) provides the histogram of these minimum distances for the 742 good OFF motifs. The conclusion is that only 38% of the good motifs would be detected if the distance cut-off was the van der Waals distance of 3.4 Å. These histograms demonstrate clearly that distance criteria must add at least 0.3 Å to the van der Waals distance.

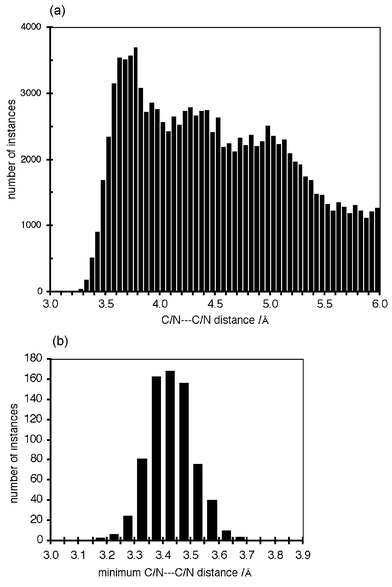Fig. 6 Distance statistics for 742 good offset-face-to-face M(phen)⋯(phen)M motifs in 334 crystals in the Cambridge Structural Database. In all motifs the planes of the phen ligands are within 10° of being parallel. (a) The histogram of all C/N⋯C/N distance distances (Å) up to 6 Å. (b) Histogram of the minimum C/N⋯C/N distance (Å) in each motif.

Conclusions

I consider the following to be important concepts for the understanding and analysis of the packing of molecules in crystals:

1. Interatomic distances between molecules at d^w, the sum of the van der Waals radii,³⁰ are distances of ‘neutral’ contact, where the contribution to intermolecular energy is close to zero, or slightly destabilising.

2. Exceptions may occur where the molecular surfaces contain non-innocent functions, such as Lewis acidic and Lewis basic sites, charges, strong multipoles, or strongly hydrogen bonding functions.³¹

3. The cohesive energy of a molecular crystal, and the determinators of molecular packing, derive from the stabilisation energy that comes from contacts longer than the van der Waals distance.

4. The key distance concept is d^a, the distance to the bottom of the intermolecular energy well: d^a is approximately d^w + 0.4 Å.

5. In a typical crystal a small proportion of distances less than d^w can occur because their destabilisation is compensated by the stabilisations permitted elsewhere in the intermolecular domain of the crystal.³²

6. The notion that ‘shorter is stronger’ is generally fallacious. It may be correct only where d > d^a or there are non-innocent intermolecular interactions.

In my view, any use of distance criteria for intermolecular interactions needs to be cognisant of the relevant chemistry of the molecular surface, and of the intramolecular bonding of surface atoms. Further, the selection of distance criteria is influenced by the question being asked in the investigation. For the purpose of exploring crystal packing for significant intermolecular interactions, distances up to d^a should be included. This applies to single investigations of one crystal structure, and to data-mining, involving general explorations, without expected outcomes, and also to targetted explorations for defined intermolecular motifs. When defining motifs as the targets of searches of the CSD the intermolecular dimensions should extend to at least d^a. Searches that cut off at d^w rather than d^a are likely to miss key features, and I know of such instances in the literature. A quite different objective is to detect anomalies in crystal structure or packing, and for these the sum of the van der Waals radii can be used as a distance cut-off.

Research in the molecular sciences tends to be restricted by the conceptual frame of the investigators, and my objective here is to focus reconsideration of some fundamental aspects of intermolecular interactions. The burgeoning (and valuable) topic of crystal supramolecularity possesses an abundance of numerical data, but these are data about a property (geometry) that is not the determinative property (energy). In such circumstances, valid concepts about the relationships between distance and energy are necessary.

Acknowledgements

My research is supported by the Australian Research Council and the University of New South Wales. Dr Marcia Scudder provided the information in Fig. 6.

References

1. J. D. Dunitz, Pure Appl. Chem., 1991, 63, 177–185; J. D. Dunitz, in The Crystal as a Supramolecular Entity, ed. G. R. Desiraju, Wiley, Chichester, 1996, pp. 1–30.
2. F. H. Allen, Acta Crystallogr., Sect. B, 2002, 58, 380–388; F. H. Allen and W. D. S. Motherwell, Acta Crystallogr., Sect. B, 2002, 58, 407–422.
3. The contemporary explosion of publications with ‘supramolecular’ in the title, and crystal structures as the data, is obvious.
4. I. G. Dance, in The Crystal as a Supramolecular Entity, ed. G. R. Desiraju, John Wiley, Chichester, 1996, pp. 137–233.
5. The adjective ‘supramolecular’ had origins in the description of interactions between polymer molecules: R. Hosemann and P. H. Lindenmeyer, J. Polym. Sci.: Part C, Polym. Symp., 1966, 20, 1–17; G. C. Oppenlander, Science, 1968, 159, 1311–1319.
6. The intermolecular potential is often calculated as the sum of interatomic potentials, because this simplification allows a smaller number of parameterised interatomic potentials to be used for a larger number and range of intermolecular interactions. Potentials between full molecules can be obtained by quantum chemical calculations.
7. J. D. Dunitz and A. Gavezzotti, Acc. Chem. Res., 1999, 32, 677–684.
8. The intermolecular potential, involving interactions between ‘closed valence shell’ atoms, is very different from the intramolecular bonding potentials with much deeper energy wells at standard bond distances that are roughly half the intermolecular distances.
9. J. F. Ogilvie and F. Y. H. Wang, J. Mol. Struct., 1992, 273, 277–290.
10. J. P. M. Lommerse, A. J. Stone, R. Taylor and F. H. Allen, J. Am. Chem. Soc., 1996, 118, 3108–3116.
11. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
12. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, 1999.
13. N. W. Alcock, Adv. Inorg. Chem. Radiochem., 1972, 15, 1–58; J. Starbuck, N. C. Norman and A. G. Orpen, New J. Chem., 1999, 23, 969–972; A. G. Orpen, Acta Crystallogr., Sect. B, 2002, 58, 398–406.
14. S. C. Nyburg and C. H. Faerman, Acta Crystallogr., Sect. B, 1985, 41, 274–279; G. A. Landrum, N. Goldberg and R. Hoffman, J. Chem. Soc., Dalton Trans., 1997, 3605–3613; P. Metrangolo and G. Resnati, Chem. Eur. J., 2001, 7, 2511–2519.
15. P. Pyykko, Chem. Rev., 1997, 97, 597–636.
16. J. F. Ogilvie and F. Y. H. Wang, J. Mol. Struct., 1993, 291, 313–322.
17. A. Gavezzotti and G. Filippini, in Theoretical Aspects and Computer Modelling of the Molecular Solid State, ed. A. Gavezzotti, John Wiley and Sons, Chichester, UK, 1997, pp. 61–97.
18. A. Gavezzotti, Theoretical Aspects and Computer Modelling of the Molecular Solid State, Molecular Solid State Series, John Wiley, Chichester, 1997.
19. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, New York, 1948, pp. 187–193.
20. I. Dance, unpublished results.
21. S. Tsuzuki, T. Uchimaru, M. Mikami and K. Tanabe, Chem. Phys. Lett., 1996, 252, 206–210.
22. P. Hobza, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1996, 100, 18 790–18 794.
23. A. Wada, H. Kanamori and S. Iwata, J. Chem. Phys., 1998, 109, 9434–9438; O. Couronne and Y. Ellinger, Chem. Phys. Lett., 1999, 306, 71–77.
24. C. Rovira and J. J. Novoa, Chem. Eur. J., 1999, 5, 3689–3697.
25. P. Pyykko, J. Li and N. Runeberg, Chem. Phys. Lett., 1994, 218, 133–138; P. Pyykko and F. Mendizabal, Chem. Eur. J., 1997, 3, 1458–1465.
26. G. Filippini and A. Gavezzotti, Acta Crystallogr., Sect. B, 1993, 49, 868–880.
27. A. Gavezzotti, J. Am. Chem. Soc., 1991, 95, 8948–8955; J. K. Badenhoop and F. Weinhold, J. Chem. Phys., 1997, 107, 5406–5421.
28. R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391.
29. V. M. Russell, M. L. Scudder and I. G. Dance, J. Chem. Soc., Dalton Trans., 2001, 789–799.
30. Following the more precise evaluations of Rowland and Taylor, the Bondi radii are unchanged, except for revision of the radius for H, from 1.2 to 1.1 Å.
31. Generalised correlations of distance distributions and intermolecular potentials for hydrogen bonds of different strengths are presented by Steiner: T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
32. A recent paper that explicitly recognises the forced character of short distances is I. S. Neretin, K. A. Lyssenko, M. Y. Antipin, Y. L. Slovokhotov, O. V. Boltalina, P. A. Troshin, A. Y. Lukonin, L. N. Sidorov and R. Taylor, Angew. Chem., Int. Ed., 2000, 39, 3273–3276.

---