Spin forbidden chemical reactions of transition metal compounds. New ideas and new computational challenges

Abstract

Many reactions of transition metal compounds involve a change in spin. These reactions may proceed faster, slower—or at the same rate as—otherwise equivalent processes in which spin is conserved. For example, ligand substitution in [CpMo(Cl)₂(PR₃)₂] is faster than expected, whereas addition of dinitrogen to [Cp*Mo(Cl)(PMe₃)₂] is slow. Spin-forbidden oxidative addition of ethylene to [Cp*Ir(PMe₃)] occurs competitively with ligand association. To explain these observations, we discuss the shape of the different potential energy surfaces (PESs) involved, and the energy of the minimum energy crossing points (MECPs) between them. This computational approach is of great help in understanding the mechanisms of spin-forbidden reactions, provided that accurate calculations can be used to predict the relevant PESs. Density functional theory, especially using gradient-corrected and hybrid functionals, performs reasonably well for the difficult problem of predicting the energy splitting between different spin states of transition metal complexes, although careful calibration is needed.

---

Rinaldo Poli

Rinaldo Poli obtained his PhD in 1985 from the Scuola Normale Superiore in Pisa under the supervision of Fausto Calderazzo. He spent one year with Geoffrey Wilkinson (exchange student, 1983–84) and two years with Al Cotton (research associate, 1985–87). He started his career at the University of Maryland, College Park, where he rose in the ranks to Full Professor, and moved to his current Professorial position in 1996. He has held Visiting Professor positions at the Technische Universität München (1993–94), Tokyo Metropolitan University (1995), the Inorganic Chemistry Laboratory at Oxford (1998), and Los Alamos National Laboratory (2001 and 2002).

Jeremy N. Harvey

Jeremy Harvey was born in Britain in 1969 but moved to Belgium aged five. He studied Chemistry and Philosophy at the Université Catholique de Louvain, completing his PhD on organic reaction mechanisms with Heinz Viehe in 1995. He spent two years as a Humboldt fellow with Helmut Schwarz at the Technische Universität Berlin, carrying out experimental and computational studies of gas-phase ion-molecule reactions, then one year with Benny Gerber at the Hebrew University, Jerusalem. In 1999, he took up a temporary lectureship in Bristol; his research interests are in computational chemistry and reaction mechanisms, particularly in transition metal chemistry.

---

1 Introduction

In chemical reactions, bonding electrons get redistributed so that chemical bonds are broken and formed. When some of the electrons in the reactants or the products are unpaired, this may lead to a change of the total electronic spin during the reaction. Such a change is often referred to as ‘forbidden’, but in fact, it is more appropriate to say that it is associated with a certain degree of spin-forbiddenness, which is determined by the magnitude of the spin-orbit coupling term (SOC) of the system’s Hamiltonian. Thus, spin changes tend to be more strictly forbidden when the affected electrons are localised on light atoms such as carbon, less so when they are on transition metals. The well-known phenomenon of spin equilibria in crossover compounds¹ highlights that spin changes are in fact common in transition metal chemistry. When it comes to chemical reactions, however, most people are either biased by the forbidden character of such changes and overemphasise their difficulty, or instead dismiss spin as being unimportant. Both misconceptions are common and make this field unusually devoid of clarity. In recent years, a more careful level of attention to the potential energy surfaces involved and the regions where they cross, as well as new computational techniques, are helping to clarify the situation.

In parallel with the work of one of us in this area,² an important factor over the last few years in making practicing transition metal chemists aware of the importance of spin-forbidden reactions has been the work of Schröder, Schwarz and Shaik on ‘Two-State Reactivity’ (TSR).³ This concept was first introduced to rationalize unexpected reactivity trends in gas-phase reactions such as the oxidation of hydrogen by the iron oxide cation, FeO⁺. Spin changes between sextet and quartet states at different points along the reaction coordinate were needed to account for the observed reactivity: these ‘spin-forbidden’ events actually led to an enhanced reactivity over what would have occurred if spin changes had been impossible. The TSR paradigm has also been applied fruitfully by its authors to areas such as bioinorganic oxidation by the P450 enzymes.⁴

With the huge progress in computing power and of software, and in particular the advent of density functional theory (DFT) as a practical method in molecular electronic structure,⁵ computational methods have become one of the standard tools used by experimental organometallic chemists to assist in understanding experimental observations.⁶ However, the problem of assessing reactivity in spin-forbidden reactions has been considerably more challenging than for the more common adiabatic reactions. Fig. 1 helps to explain how such reactions occur, using the paradigm of the potential energy surface, which gives the potential energy as a function of the positions of all the atomic nuclei in the molecule. The surfaces corresponding to the two spin states are shown as light and bold lines, respectively. A spin change can be thought of as occurring when the motion of the atoms of the molecule brings the system into the region where the two surfaces cross, and spin-orbit coupling then enables a ‘hop’ from one surface to the other. This is shown in part (a) of Fig. 1, which also shows that this hopping is associated with a probability p. This first description is appropriate when spin-orbit coupling is small, so that the electronic structure is best described in terms of the two pure (or diabatic) spin states. However, spin-orbit coupling can be very strong in transition metal compounds, so that a better—or at least equally good—description of the electronic structure in the ‘crossing’ region involves electronic states and potential energy surfaces (shown as dashed lines in Fig. 1(b)) of a mixed spin character, arising from an avoided crossing of the pure spin states. The system then simply moves towards the crossing region, and traverses it smoothly on the lowest mixed-spin (or ‘adiabatic’) surface, with the overall spin undergoing a similarly smooth transition from one limiting value to the other. In this description, a spin-forbidden reaction is not very different from normal, spin-allowed, reactions. This is because the barriers forming the transition states in such reactions can be thought of as arising following the (strongly) avoided crossing of two diabatic surfaces. Except in extreme cases, spin-orbit coupling in spin-forbidden reactions is rarely so strong that the adiabatic states differ significantly in energy from the diabatic ones, except within a fairly small region around the crossing point of the latter. For this reason, finding the crossing point gives very valuable information as to the relative energy of the regions a spin-forbidden reaction must necessarily pass through.

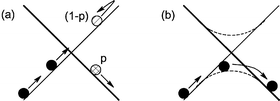Fig. 1 Schematic description of spin changes, in the (a) low and (b) high spin-orbit coupling limits.

Modern computational chemistry packages are typically very good at locating stationary points, such as minima or saddle points, on single potential energy surfaces.^5,6 Here, one wishes to locate the region where two such surfaces cross. More specifically, because the potential energy surfaces are multidimensional and therefore cross in many different points, one wishes to find the Minimum Energy Crossing Point or MECP between them. The MECP is not a stationary point on either of the individual spin surfaces and the common programs cannot find this point in a practical way for organometallic systems. However, the algorithm required to locate an MECP is quite simple, involving an energy minimisation on one surface under the constraint that the two surfaces have the same energy. Lagrange multiplier or other techniques have been developed to optimise MECPs.^7,8 All that is needed is to be able to compute the energy and its gradient on both of the surfaces, and this can readily be done with the available programs. The particular implementation developed by one of the authors can be readily used in conjunction with many of the popular computational packages, is freely available upon request, and has already been distributed to several groups working in this area.⁸ This and other developments are expected to lead to an increasing number of computational studies of spin-forbidden transition-metal reactions. This review will survey the progress made in this area.⁹ The common theme of the article will be the application of the MECP methodology to transition metal reactivity.

2 Spin change as a reaction acceleration phenomenon

Recently, one of us introduced the concept of ‘spin acceleration’,² whereby far from being slower than expected, a spin-forbidden reaction can proceed faster, because a spin change allows access to a lower energy pathway, proceeding through intermediates having a different number of unpaired electrons (e.g. see Fig. 2). In low-valent (e.g. organometallic) chemistry, the most typical case involves reagents and products having the lowest possible spin state (0 for 18-electron complexes; ½ for 17-electron complexes) and intermediates having a higher spin state, but the inverse can also be true in principle. This phenomenon was first proposed for a ligand exchange process on 17-electron (S = ½) [CpMoCl₂(PR₃)₂], proven by kinetic investigations to be fast and dissociative. The reconciliation of this apparent contradiction was based on the hypothesis that, upon ligand dissociation, the resulting 15-electron [CpMoCl₂(PR₃)] is energetically stabilized by flipping an electron to yield a spin quartet state, like known stable Cr(III) congeners.¹⁰ Proving this proposition would require measurement of the spin state for the reaction intermediate(s), a great challenge when the intermediate lies in a shallow energy minimum. Indeed, experimental studies aimed at this goal have not been successful.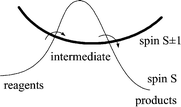

Fig. 2 Qualitative energy profile for a spin-accelerated reaction.

The strongest evidence in favour of this hypothesis came from computational chemistry. In this first study of an MECP for a large, realistic organometallic compound, we found the MECP between the doublet and quartet states of this system to lie only slightly higher in energy than the quartet dissociation asymptote, and significantly lower than the spin-allowed doublet dissociation products. We also found spin-orbit coupling between the doublet and quartet manifolds to be large, so that facile spin flipping should occur at the MECP. This gave strong support to the spin acceleration hypothesis.¹¹

In the same paper, we also examined the same reaction using a much more popular technique for studying spin-forbidden reactions, which we have called the partial optimisation method. This involves selecting a reaction coordinate (here, the breaking Mo–P bond length), and optimising the energy of both spin states at fixed values of this coordinate. This gives two one-dimensional curves, whose crossing gives an estimate to the MECP geometry and energy, as shown in Fig. 3. However, this technique is less accurate because it only gives a lower bound to the energy of the MECP, as the two partially optimised geometries for a given value of the reaction coordinate are typically quite different. Indeed, only one of the 3N-6 internal coordinates is kept the same for the independent surfaces, while the Franck-Condon principle requires that both energies and geometries be the same in order for the spin hopping to take place. Also, the partial optimisation method is significantly more expensive computationally, in that many partial optimisations need to be carried out, instead of a single MECP optimisation.

Fig. 3 Energies of the partially optimised doublet and quartet states of [CpMo(Cl)₂(PH₃)₂], relative to the doublet minimum. The dashed lines show the relative energies of the dissociated doublet and quartet states. Reproduced from ref. 11, by permission of the Royal Society of Chemistry (RSC) and the Centre National de la Recherche Scientifique (CNRS).

3 Spin-change induced reaction barriers

The example in the previous section shows that a reaction with an endothermic, rate-determining, step (such as a ligand dissociation) can feature spin acceleration provided a change in spin opens up a lower-lying dissociation asymptote. In contrast, exothermic reactions such as ligand association steps may involve an enthalpic barrier whose existence is solely due to the need to change the spin state. This principle is illustrated by Fig. 4. The MECP has a greater energy than the reagent energy if the reaction follows path (a) and a lower energy if it follows pathway (b). Therefore, a spin-change related enthalpic barrier (ΔH^‡) exists only in case (a). It is important to underline that this barrier has nothing to do with the spin ‘forbiddenness’ concept. Its presence is simply related to the need to achieve the same energy for the same geometry on both spin surfaces in order to allow the spin hopping process.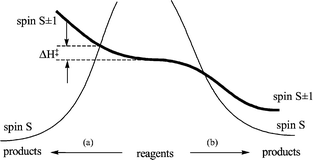

Fig. 4 Qualitative energy profiles for exothermic reactions involving a spin change.

An example of this phenomenon is provided by another ligand dissociation/association reaction that one of us has studied in detail.¹² Complex [Cp*MoCl(PMe₃)₂] is an example of a spin-stabilized open-shell organometallic compound, featuring a spin triplet ground state for 16 valence electrons. This compound was shown to react with either CO or N₂ to achieve the saturated and diamagnetic, 18-electron ligand addition product, [Cp*MoCl(PMe₃)₂(L)] (L = CO or N₂). The reaction with CO was found to be ca. three orders of magnitude faster than the reaction with N₂, even though the two ligands are isoelectronic and isosteric. This situation did not appear ‘normal’, because in all previous comparative kinetic studies of CO and N₂ addition to a given formally unsaturated fragment, the rates were found to be identical or at least very similar to each other. The question was therefore asked as to whether the spin change might be responsible for this unusual behaviour. Ab initio calculations, which were initially carried out at the MP2 level, confirmed this hypothesis and provided a greater insight into this phenomenon (see Fig. 5).

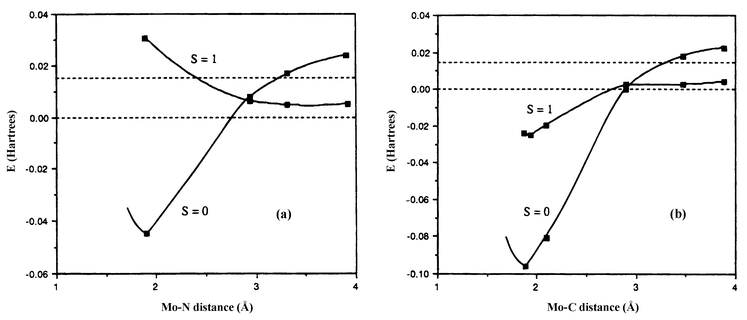Fig. 5 MP2 reaction co-ordinates (partial optimisation method) for the reaction of CpMoCl(PH₃)₂ with N₂ (a) and CO (b). Reproduced with permission from ref. 12, copyright 1997 American Chemical Society.

The crucial difference between the two reactions lies in the relative bonding strength of CO, N₂, and the other ligands already present on the metal fragment, and its effect on the shape of the triplet potential energy surface. When the new ligand is included, the electron count around the metal is formally 18, which, in a triplet state, means that one at least of the ligands must have weaker or no bonding at all. In the N₂ case, because dinitrogen is the weakest ligand involved, it cannot bond at all to the metal, and the triplet potential energy curve upon approaching this ligand is fairly strongly repulsive, excepting a shallow van der Waals well at larger bond lengths. Crossing with the attractive singlet surface leads to a spin-change induced barrier. Carbon monoxide, in contrast, establishes a stronger bond than, e.g. the chloride. As a consequence, as CO approaches, it bonds partly to the metal, with the Mo–Cl bonding undergoing simultaneous weakening. The combined effect of these stabilising and destabilising contributions is weakly repulsive at longer Mo–C distances, but becomes favourable as the ligand approaches closer. The (purely attractive) singlet curve crosses the triplet curve in the region where the latter is repulsive, but as the repulsion is much less than in the case of N₂, the crossing is consequently occurring at a much lower relative energy. This difference in the spin change-induced barriers, shown in Fig. 5, explains why the dinitrogen reaction is so much slower.

Although this initial computational study¹² was carried out using the less accurate partial optimisation method, using the small [CpMo(Cl)(PH₃)₂(L)] model system, and at the MP2 level of theory (which sometimes yields incorrect results for transition metal systems), it gave results which were in excellent qualitative agreement with experimental observations. In a more recent study,¹³ the relevant MECPs have been optimised for the small model and a larger one, [CpMo(Cl)(PMe₃)₂(L)], using DFT. The computed enthalpic barriers, for the large model, to recombination for N₂ (14.4 kcal mol⁻¹) and for CO (6.7 kcal mol⁻¹) are in near-quantitative agreement with the experimental values of (14.0 ± 1.0) and (5.0 ± 0.3) kcal mol⁻¹, respectively.

This newer study also highlighted some of the difficulties involved in computations on open-shell organometallic species. When the study was started, it became apparent that both the singlet and triplet [CpMo(Cl)(PH₃)₂] fragments, which have three-legged piano stool geometries, actually have two distinct energy minima characterised by a different (PMoP) angle, and different occupations of the metal-based a′ and a″ orbitals. Four interaction curves between the ligand and the organometallic moiety are therefore conceivable, leading to several possible crossing points, a point which had not been appreciated in the previous study. The ‘partial optimisation’ curves for the approach of N₂ to the metal are summarised in Fig. 6.

Fig. 6 B3LYP linear transit curves for the co-ordination of N₂ to the four lowest electronic states of [CpMoCl(PH₃)₂]. [See ref 13] Key optimised structures are viewed along the Mo–Cp centroid axis.

The most interesting point is that the ground state of the addition product, CpMoCl(PH₃)₂N₂, is actually derived from the fourth lowest state of the educt, CpMoCl(PH₃)₂ (2¹A′, d-occupancy (1a′)²(a″)²). In the most stable singlet state of the educt (1¹A′, d-occupancy (1a′)²(2a′)²), the potential 2a′ acceptor orbital is already occupied. This point was missed in the original investigation. Nevertheless, the newest study reproduces the previously determined significant surfaces (³A″ and 2¹A′) as well as the essential conclusion that the nitrogen addition reaction has a spin barrier. The CO addition process affords a qualitatively identical picture. As already mentioned, the accurate determination of the key MECP, occurring between the ³A″ and 2 ¹A′ states, gives results in good quantitative agreement with experiment for both ligand addition processes. Despite these extra details, the physical interpretation of the experiments remains the same: CO adds faster than N₂ to [Cp*Mo(Cl)(PMe₃)₂] because the spin change induced barrier is smaller. The correct interpretation of the experimental data in the earlier study, however, turns out to have been partly fortuitous, given the extra electronic states found to play a role in this chemistry. This serves as a reminder that in computational studies of open-shell, unsaturated species, one should make sure that all the relevant electronic states have been carefully identified!

Clearly, the spin-forbidden nature of a ligand association reaction can have a highly variable effect on its rate, depending on the presence (and height) or absence of a spin change induced barrier. In turn, the nature of this barrier will usually be correlated with the attractive or repulsive nature of the high-spin potential energy surface. It is not possible to reach meaningful conclusions about rates without taking into account these details of the surfaces involved. In this context, it is interesting to compare the reactions just mentioned with two other ligand association reactions which have been the subject of considerable discussion in the literature. Detrich et al. found the CO addition to spin triplet [TpCo(CO)] (Tp = hydrotris(3-isopropyl-5-methylpyrazolyl)borate), yielding spin singlet [TpCo(CO)₂], to be very fast and therefore proposed that spin changes will not usually have an effect on reaction rates.¹⁴ On the other hand, gas phase studies on the spin-forbidden CO addition to triplet [Fe(CO)₄] to give singlet [Fe(CO)₅] have shown it to be three orders of magnitude slower than the spin-allowed but otherwise comparable addition of CO to triplet [Fe(CO)₃].¹⁵ The authors attributed this to the spin-forbidden nature of the first reaction.

These two sets of results are not at all inconsistent: they merely reflect the fact that the spin change barriers are of different magnitude in the two reactions. This is because in the [Fe(CO)₅] case, the ³[Fe(CO)₄] – CO potential energy surface is largely repulsive, whereas the ³[TpCo(CO)] – CO curve is somewhat attractive. This can be readily understood on the basis of our previous discussion: because all the ligands are the same in the [Fe(CO)₅] system, no net gain is to be expected from weakening one of the existing Fe–C bonds in [Fe(CO)₄] so as to accommodate the incoming CO. Indeed, explicit location of the singlet/triplet MECP in [Fe(CO)₅] found it to lie higher in energy than the CO + ³[Fe(CO)₄] asymptote at the B3LYP level of theory.^9b Another such example, in which spin change leads to a net barrier to ligand association, is the reaction, studied by one of us, between quintet haem and carbon monoxide.¹⁶ In contrast, in the [TpCo(CO)] case, the bonding between cobalt and the pyrazolyl groups of Tp is probably weaker than the bonds to carbonyl, so that an attractive interaction can result from a redistribution of bonding character from the Co–N to Co–C bond. Although we have not yet located MECPs in this system, we have some computational evidence for this supposition. Thus, as in the [Cp*Mo(Cl)(PMe₃)₂(CO)] case,¹² [TpCo(CO)₂] is found to have a bound triplet state, lying higher in energy than the experimentally observed singlet species, but lower in energy than the ³[TpCo(CO)] + CO asymptote.¹⁷ All ligand–Co bond lengths at this triplet minimum are 0.1–0.2 Å longer than in ³[TpCo(CO)] and ¹[TpCo(CO)₂], consistent with a picture whereby all bonds have some anti-bonding character. The stability of this species suggests that the spin change barrier, if there is one, is likely to be small.

4 C–H Bond activation and reaction selectivities

Like the ligand association reactions we have just considered, oxidative addition to a metal centre, for example C–H bond activation, is often spin-forbidden. In both cases, the starting product is an unsaturated, typically 16-electron species, and these often have high-spin ground states. In contrast, the ligand addition product or C–H inserted species are usually closed-shell, 18-electron singlets. Unlike ligand association reactions, where the low-spin surface is most often uniformly attractive, oxidative addition frequently involves adiabatic barriers on the low-spin surface, separating the inserted species either from the fragments or from a non-inserted adduct. Whereas slow rates in spin-forbidden ligand association can only be due to the existence of a spin-change induced barrier, oxidative addition can be due either to the adiabatic barrier or to the spin-change barrier. Energy profiles corresponding to typical examples of the two reactions are shown in Fig. 7. In the specific example of Fig. 7(b), the surface includes a fairly strongly bound singlet alkane adduct, ¹[M·(RH)], and the spin change barrier precedes the formation of this adduct. The ordering and the relative energy of the barriers and intermediates will of course depend on the system. The triplet surfaces are shown as being repulsive in both cases. As discussed above, this may not always be so for ligand association reactions, but usually will be for C–H addition reactions of alkanes, because the latter are such weak ligands.

Fig. 7 Generic singlet and triplet potential energy surfaces for (a) ligand association and (b) C–H oxidative addition to a triplet unsaturated metal fragment, ³[M].

Because the spin change barrier or MECP has traditionally been difficult to find, computational studies in this area have mostly focused on the adiabatic barriers. This can be misleading. For example, we showed in a comparative study¹⁸ of methane oxidative addition to the spin triplet complexes [Cp₂W], [CH₂(C₅H₄)₂W], and [Cp*₂W], that the experimental trends in this and the reverse, reductive elimination reaction, could only be understood by considering both the adiabatic insertion barrier and the spin-change induced barrier. In some cases, of course, the spin-change barrier may be unimportant, but this should be shown, e.g. by computation, rather than simply assumed.

The [Cp*Ir(PR₃)] fragment is a prominent example of a species which can activate alkane C–H bonds. This system has been the object of a large amount of experimental¹⁹ and more recently computational work. Computations agree in predicting that this 16-electron fragment has a triplet ground state. Because the inserted compounds are singlets, these reactions are spin-forbidden. Spin-orbit coupling should be strong (third-row transition metal), so reasoning in terms of pure singlet and triplet states is not entirely appropriate, as discussed in the context of Fig. 1. However, such an approach should give a reasonable first approximation to the potential energy surfaces involved. Most computational studies of C–H bond activation in these systems have focussed only on the adiabatic insertion barriers.

Our subject here is a slightly different variation on the same theme, in which the insertion partner is no longer an alkane, but an alkene: the reaction of C₂H₄ with [Cp*Ir(PMe₃)(H)(c-C₆H₁₁)].²⁰ The experimental work on this reaction, including careful studies of the inter- and intramolecular isotope effects upon reaction with various deuterio ethylenes, led to the proposal of an empirical mechanism,²⁰ as shown in Fig. 8.

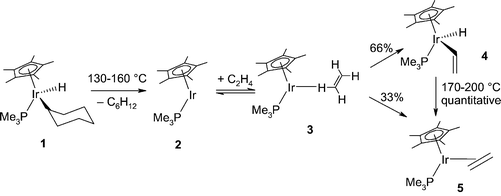Fig. 8 Empirical reaction mechanism for the competitive coordinative addition and C–H oxidative addition of ethylene to Cp*Ir(PMe₃).

The reaction starts with 1, which undergoes the reverse of an oxidative addition, reductive elimination, to give the key intermediate 2 upon heating. In turn, this fragment reacts with ethylene to give a mixture of the C–H bond activation product 4, and of the addition product 5. The isotope effects in this step were best explained on the basis of the initial reversible formation of a weak σ-complex 3 between the alkene and the unsaturated intermediate 2, which then partitions into the two products. The ethylene π-complex is the most stable species in this system, and the inserted species 4, although inert under the reaction conditions, rearranges quantitatively upon further heating. An initial theoretical study²¹ of this remarkable reaction focussed on the singlet potential energy surface, which is at first sight reasonable given that the reactant and the products are closed-shell, 18-electron species. However, the calculations were unable to explain the selectivity, because association of ethylene to the singlet fragment 2 to give 5 was found to be barrierless, and the authors speculated—correctly, as it turned out—that triplet states might be involved.

This reaction represents a still more challenging computational problem than the alkane activation reactions. The aim of our study of this reaction²² was to understand the origin of selectivity, in terms of the competition between two spin-forbidden pathways: one leading to oxidative addition, and one to ligand association. Our computed potential energy surfaces, showing the key MECPs, are presented in Fig. 9. Most of our computations were carried out on the simplified model system, [CpIr(PH₃)] + (C₂H₄). The left-hand part of the Figure shows the profile for loss of methane, which was chosen to model the experimental cyclohexane moiety involved. It should be noted that in this case, the MECP between the singlet and triplet surfaces lies slightly higher than the singlet separated products. This is because the triplet potential energy surface for interaction of methane with [CpIr(PH₃)] is largely repulsive. The adiabatic insertion/elimination barrier on the singlet surface (not shown on the Figure), in contrast, lies low in energy. This confirms our previous statement: reactivity in C–H bond activation of alkanes is in this case determined more by the spin-change induced barrier than by the adiabatic insertion barrier. Dissociation should lead in the first instance to the singlet fragment. Unimolecular relaxation to the triplet state should then be faster than any subsequent bimolecular step, for entropic reasons.

Fig. 9 Potential energy surfaces relevant to the two-state ligand association and C–H oxidative addition reactions for the model [CpIr(PH₃)] – C₂H₄ reaction. Relative energies in kcal mol⁻¹. Reproduced with permission from ref. 22, copyright 2001 Wiley-VCH.

Turning to the more interesting right-hand part of the Figure, and following it all the way to the right-hand side, the ligand association of ethylene can be seen to lie somewhere between the two extremes discussed above: whilst addition of ethylene on the triplet surface is exothermic by 10.8 kcal mol⁻¹, because partial binding of ethylene is more stabilising than the concomitant partial loss of bonding to the Cp ring, this bonding/unbonding pathway does not occur smoothly, so that the triplet surface is not uniformly attractive. There are in fact two small barriers which must be crossed on the way to the triplet local minimum. Although the MECP with the singlet state lies well below the triplet reactants (at −10.4 kcal mol⁻¹), it should therefore be expected that ligand association will not be diffusion controlled. In fact, the overall barrier to ethylene association is somewhat larger than would appear from Fig. 9, because our more limited calculations on the real [Cp*Ir(PMe₃)] system indicate that steric hindrance by the Cp* and PMe₃ ligands leads to this portion of the triplet potential energy surface lying somewhat higher in energy than shown on Fig. 9.²²

What, then, of the C–H oxidative addition process? As in the case of the methane reductive elimination profile at the left of Fig. 9, the adiabatic insertion barrier is low-lying. This barrier, lying at −7.7 kcal mol⁻¹, is a bit unusual in this case, because instead of connecting the C–H insertion product to a relatively weakly bound van der Waals-type adduct of the R–H moiety with the metal, as in the case of methane, it connects the C–H insertion product to a very strongly bound π-complex. Nevertheless, as for the methane addition reaction, it is in fact the spin change barrier which limits the rate of addition, rather than this adiabatic barrier. As already mentioned, the triplet ethylene – [CpIr(PH₃)] potential is much less repulsive than the corresponding methane surface, and the spin-change barrier is much lower, lying only 2.3 kcal mol⁻¹ above the fragments. This is comparable in height to the effective barrier to spin-forbidden ligand association, caused by the triplet surface barriers to association of ethylene. The similarity in the two barriers explains the experimental observation that both products are formed in roughly equal amounts. The uncertainties due to the choice of method (see below), the use of model compounds, and the neglect of spin-orbit coupling and dynamical effects, mean that quantitative predictions are impossible for what is after all a very complicated problem. Nevertheless, the ability to characterise the spin-change induced barriers, in the form of MECPs between singlet and triplet surfaces, enabled us to propose a computational model of this complex reaction which accounts for the key experimental observations.

5 Spin-states and computational accuracy

To locate meaningful MECPs, accurate computation of spin state relative energies is necessary. This rather obvious principle is schematically illustrated by Fig. 10, in which the first spin state is assumed to be well described by both levels of theory used, whereas the relative stability of the second state is underestimated at the unspecified ‘incorrect’ level. This leads to an apparent MECP which is different both in terms of geometry and of relative energy from the ‘true’ MECP. An extreme example of such behaviour was given for the test case of the phenyl cation, in ref. 8. The Hartree-Fock level of theory predicted a completely wrong geometry and relative energy for the MECP between the singlet and triplet states of this cation, as a consequence of its underlying poor description of the energy difference between these states.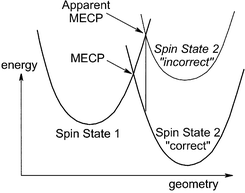

Fig. 10 Incorrect position of the MECP between two spin states when the relative energy of the two states is poorly described.

This problem has an analogue in single-surface computational chemistry. Reactants and products, even when they lie on the same potential energy surface, often have different correlation energies, and lower levels of theory may provide a poor description of their relative energy. One can think of the reactants and products as being described by diabatic valence-bond wavefunctions which undergo strong mixing in the region of the transition state. A poor description of one of the valence-bond states will distort the geometry and relative energy of the transition state, as shown in Fig. 11. However, unless the relative energy error is enormous, the ‘smoothing’ effect of the avoided crossing means that geometries and even energies of computed TSs can be fairly reliable, and in any case, single-point higher-level energies can be calculated at the lower-level optimised geometry of the TS, to yield much more accurate energetics. With no ‘smoothing’, and the fact that single-point energies are not meaningful (although an alternative dual high-level/low-level approach has been suggested⁸), the problem is probably worse for MECPs.

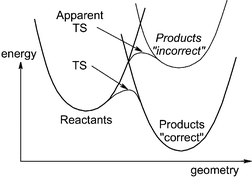Fig. 11 Incorrect description of an adiabatic TS due to an imbalanced treatment of the diabatic states (of same electronic spin!) corresponding to the reactants and products.

An accuracy of the order of 2 kcal mol⁻¹ on relative spin state energetics is needed when looking for MECPs, and this is one of the first things which should be checked when a study is undertaken. The whole MECP approach, based on the use of zeroth-order, spin-orbit free, surfaces, is an approximation in itself, and ultimately can only yield semi-quantitative results (see Fig. 1), so higher accuracy is not really necessary.

How can one get energies that are this accurate? Let us first consider this question in relation to a very simple compound. Methylene (CH₂) has a triplet ground state and a low-lying singlet excited state. The Hartree-Fock level⁵ significantly overestimates the excitation energy, due to the neglect of correlation energy, which is larger for singlet states. Due to a partial multi-reference character of the singlet state, the simple single-reference methods⁵ (which mix a large number of excited configurations with the Hartree-Fock wavefunction) such as MP2 (second order perturbation theory) only recover part of the correlation energy difference.²³ More advanced single-reference methods, such as the CCSD(T) coupled-cluster theory, are needed for good results. Multi-reference methods, in which a small number of configurations are included in the wavefunction from the very start, give good results, and the very accurate multi-reference configuration interaction techniques can be used to approach the exact result. Large basis sets are also needed to converge the energy difference.

Such methods are however expensive, so that it is still extremely difficult to carry out traditional ab initio computations of a sufficient quality, both in terms of correlation and basis sets, for realistic multi-ligand metal complexes. For this reason, even ‘benchmark’ computations on medium sized systems need to be treated with caution, especially when a single method is used, as the convergence (or lack of it) to the correlation and basis set limits can usually only be judged based on a series of computations at increasingly high levels. Whilst convergence can be achieved for smaller systems (roughly 5 atoms or less), peculiarities in the electronic structure of such systems make extrapolation difficult.

DFT⁵ has become a popular approach throughout computational chemistry because it offers results that are in principle exact, at a cost similar to that of the Hartree-Fock method, and is thereby readily applicable to the field of transition metal chemistry.⁶ The problem is that the exact functional is unknown, and the many different approximate functionals tend to give different results. For example, the state-splitting in methylene can vary from ca. 10 kcal mol⁻¹, with the B3LYP functional, to as much as 17.5 kcal mol⁻¹ with the B3PW91 method.²⁴ Given that the experimental value is 9.4 kcal mol⁻¹, B3LYP is in this case well within our desired accuracy bracket, whereas the other functional is not. For a system where the exact result is unknown, how should one choose? Is there a general rule (e.g. ‘BP86 is best’), or will the ‘best’ functional vary on a case by case basis?

Benchmarking of DFT by ab initio calculations leads to uncertain results, because it is often not clear how accurate the benchmarks themselves are. Such work (see for example ref. 25) is expected to become more important as computers and programs improve. Comparing with experiment is easier, with lots of information available on the ground state multiplicity, and sometimes the state splittings, of complexes. Unfortunately, there are as yet few systematic studies of functional performance, and direct comparison with experiment can be difficult due to the need to assess the importance of basis set limitations, solvent effects and free energy contributions. Also, the many new density functionals which are being constantly developed are rarely tested on any transition metal systems, let alone on state splittings, so that their performance is even harder to gauge.

Nevertheless, it can be observed that the nature of the exchange part of the functional has a strong influence on computed spin-state splittings. In particular, the proportion of ‘exact’, Hartree-Fock, exchange present, plays an important role. As already mentioned, pure Hartree-Fock calculations overestimate the stability of high-spin states because they describe electron exchange, but not electron correlation. At the other extreme, the simple, local spin density functional tends to exaggerate the stability of low-spin states. Gradient-corrected (‘non-local’) functionals such as the popular BP86 and BLYP functionals give an intermediate behaviour, which is often close to the experimental values. Hybrid functionals, such as B3LYP, BHalf-and-HalfLYP or B1LYP, also often closely approximate the experimental behaviour, with a tendency for the relative stability of the high-spin states to increase as the proportion of Hartree-Fock exchange is increased.

The dependence is particularly strong for compounds of the elements in the first transition row (Sc–Cu), which presumably is related to the large exchange interactions between the compact 3d orbitals. For this reason, different functionals frequently predict different ground states. For example, Paulsen et al. calculated the state splitting between singlet and quintet states of some Fe(II) spin-crossover compounds, using a variety of density functionals.²⁶ From experimental results, the temperature at which the two states have the same free energy in solution or in the solid state is well known. The authors computed this free energy difference in the gas phase, and found that the B3LYP method gave a negative ΔG (favouring the quintet), whereas the BLYP and PW91 functionals favoured the singlet. The different predictions varied by as much as 20 kcal mol⁻¹, with the B3LYP value, whilst incorrect, closest to the experimental value.

Reiher et al. made a related observation concerning computed singlet–quintet gaps in a family of Fe(II)-thiolato complexes.²⁷ They showed that the state splitting was linearly proportional to, and highly dependent on, the percentage of ‘exact’ exchange included in the functional, with pure functionals favouring the singlet, and hybrid functionals favouring the quintet. They found the best agreement with experiment, for the compounds they were considering, to occur with a modified form of the B3LYP functional, in which the proportion of exact exchange was reduced from 20 to 15%. It cannot however be expected that this ad hoc parameterisation will apply to all compound types. Khoroshun et al. also found hybrid functionals to favour high-spin states for a range of intermediates involved in a reaction profile relevant to polymerisation catalysis by a set of bis(imino)pyridyl Fe(II) complexes.²⁸ Here too, the suggestion was that the B3LYP functional was in better agreement with experiment than the pure functionals.

The dependence on exchange functional tends to be much smaller with the second- and third-row transition metals, with variations of 1–10 kcal mol⁻¹, for example, found between BLYP and B3LYP for the singlet–triplet splitting in a set of technetium compounds,²⁹ as compared to the differences of 20–30 kcal mol⁻¹ mentioned above for iron compounds.^26,27 We have carried out some calculations¹⁷ on a very interesting complex, [Cp′Nb(Cl)₂(PEt₃)₂] (Cp′ = C₅H₄Me), which is known from experiment to have a singlet ground state with a triplet lying 2.3 kcal mol⁻¹ higher in energy.³⁰ In this case, B3LYP predicts instead a triplet ground state (by 2.1 kcal mol⁻¹), but BP86 reproduces the experimental splitting fairly well.

To summarise, DFT does give qualitatively useful predictions of state-splittings, but needs to be used with caution, as the current functionals tend to disagree and there is no general rule as to which functional or class of functionals performs best. The need for caution is particularly true for first-row elements. A useful rule of thumb is that ‘pure’ functionals such as BP86 tend to exaggerate the stability of low-spin forms, whereas hybrid functionals such as B3LYP somewhat overestimate the stability of high-spin species. In the long term, it is to be hoped that a combination of experimentally-based calibration studies, high-level ab initio benchmarks, and the development and improvement of functionals will lead to a better level of predictability in the computation of spin state splittings. Because of their large dependence on exchange, it would in fact be valuable to use spin state splittings, especially of first transition row elements, in the early evaluation of new functionals.

How should one proceed in the meantime? In the first place, it is necessary to recognise that calibration is a large part of any multi-spin state study of transition metal chemistry. As a first step, one should check that the chosen method reproduces the multiplicity of the ground state of any species for which this is known. Any known experimental data on relative energies of spin states—even for species only partly comparable to those of interest—can also provide a very helpful assessment of the likely accuracy of the calculations. Computed bond energies can give indirect insight into relative spin states. Where bonding of a ligand is accompanied by a change in spin state, many methods can give quite accurate ‘prepared state’ bond energies, calculated with respect to the excited-state fragment, with the same spin as the whole molecule. This is because the change in electronic structure upon forming such a bond is smaller than when considering the true bond formation step. If the computed bond energy matches experiment, and the prepared state bond energy is felt to be reliable, then the excitation energy should also be well described. Finally, it is always useful to compare predictions from several very different functionals, such as BP86, B3LYP, and BHandHLYP, so as to check whether there is a large dependence on the treatment of exchange.

6 Conclusions

In this review, we have tried to show how reactions involving changes in electronic spin are fairly common in transition metal chemistry. Understanding the effect this can have on reactivity requires a careful consideration of the relevant potential energy surfaces, and the regions where they cross, in the vicinity of MECPs. It is simply not enough to decide that all these processes are forbidden, or equally that ‘forbiddenness’ is a useless concept! To gain the detailed knowledge needed to unravel reactivity in some of these systems, the insight available from computational chemistry is particularly valuable, and this explains the importance of such studies in this area.

Two important types of reaction have been discussed in more detail: ligand association, and oxidative addition of C–H bonds, to unsaturated, high-spin intermediates. These can be seen to have many common aspects, which can be traced back to the existence of spin change-induced barriers in the entrance channels of many of these reactions. However, some ligand association processes involve very small barriers only, due to the presence of attractive interactions on the high-spin surface, so that the MECP lies lower in energy than the reactants.

A particular focus has been placed on the reaction of [Cp*Ir(PMe₃)] with ethylene. The complexities of this process, in which spin-forbidden ligand association competes with oxidative addition, led to it being dubbed ‘mysterious’ by the experimental group investigating it.²⁰ Our identification of the MECPs between singlet and triplet potential energy surfaces in this system²² enabled us to propose a satisfactory qualitative explanation of the observed reactivity pattern for the first time.

We believe that the spreading awareness of the role and importance of spin changes in transition metal chemistry, as well as the availability of robust computational techniques for characterising the appropriate MECPs, will help to deepen the level of understanding in this area of mechanistic chemistry.

7 Acknowledgements

RP is grateful to the Conseil Régional de Bourgogne for funding the purchase of computing equipment, the Université de Bourgogne through their Computing Resources Centre, and CINES for a grant of free CPU time. JNH thanks the EPSRC for support. The authors also thank Dr Vidar Jensen for communicating unpublished results and for helpful conversations.

8 References

1. P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419.
2. R. Poli, Acc. Chem. Res., 1997, 30, 494.
3. D. Schröder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139 and references therein.
4. M. Filatov, N. Harris and S. Shaik, Angew. Chem., Int. Ed., 1999, 38, 3510.
5. Details of DFT and other electronic structure methods can be found in F. Jensen, An Introduction to Computational Chemistry, John Wiley, 1998.
6. E. R. Davidson (Guest Editor), Computational Transition Metal Chemistry, in Chem. Rev., 2000, 100, issue 2.
7. N. Koga and K. Morokuma, Chem. Phys. Lett., 1985, 119, 371.
8. J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95 and references therein.
9. (a) For previous reviews, see : J. N. Harvey, R. Poli and K. M. Smith, Coord. Chem. Rev., 2002 , in press; (b) J. N. Harvey, in Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker, New York, Basel, 2001.
10. A. Cole, J. C. Fettinger, D. W. Keogh and R. Poli, Inorg. Chim. Acta, 1995, 240, 355.
11. K. M. Smith, R. Poli and J. N. Harvey, New J. Chem., 2000, 24, 77.
12. D. W. Keogh and R. Poli, J. Am. Chem. Soc., 1997, 119, 2516.
13. V. Jensen and R. Poli, to be published.
14. J. L. Detrich, O. M. Reinaud, A. L. Rheingold and K. H. Theopold, J. Am. Chem. Soc., 1995, 117, 11745.
15. (a) R. J. Ryther and E. Weitz, J. Phys. Chem., 1991, 95, 9841; (b) D. L. Cedeno, E. Weitz and A. Berces, J. Phys. Chem. A, 2001, 105, 3773.
16. J. N. Harvey, J. Am. Chem. Soc., 2000, 122, 12401.
17. J. N. Harvey , to be published.
18. J. C. Green, J. N. Harvey and R. Poli, J. Chem. Soc., Dalton Trans., 2002, 1861.
19. B. A. Arndtsen, R. G. Bergman, T. A. Mobely and T. H. Peterson, Acc. Chem. Res., 1995, 28, 154.
20. P. O. Stoutland and R. G. Bergman, J. Am. Chem. Soc., 1988, 110, 5732.
21. J. Silvestre, M. J. Calhorda, R. Hoffmann, P. O. Stoutland and R. G. Bergman, Organometallics, 1986, 5, 1841.
22. K. M. Smith, R. Poli and J. N. Harvey, Chem. Eur. J., 2001, 7, 1679.
23. For a discussion of ab initio studies of methylene, see : C. D. Sherrill, M. L. Leininger, T. J. Van Huis and H. F. Schaefer, J. Chem. Phys., 1998, 108, 1040.
24. D. Das and S. L. Whittenburg, J. Mol. Struct. (Theochem), 1999, 492, 175.
25. V. R. Jensen and W. Thiel, Organometallics, 2001, 21, 4852.
26. H. Paulsen, L. Duelund, H. Winkler, H. Toftlund and H. X. Trautwein, Inorg. Chem., 2001, 40, 2201.
27. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48.
28. D. V. Khoroshun, D. G. Musaev, T. Vreven and K. Morokuma, Organometallics, 2001, 20, 2007.
29. D. M. Ball, C. Buda, A. M. Gillespie, D. P. White and T. R. Cundari, Inorg. Chem., 2002, 41, 152.
30. J. C. Fettinger, D. W. Keogh, H.-B. Kraatz and R. Poli, Organometallics, 1996, 15, 5489.

---