Influence of phosphorus and vanadium additives in the development of surface acid catalytic properties of mesoporous alumina

Abstract

Alumino-phosphoro-vanadate catalysts of the general formula Al₁₀₀P_xV_y, where x,y = 0, 5, 10 and 20, have been prepared by co-precipitation of calculated amounts of Al(NO₃)₃·9H₂O, H₃PO₄ and V₂O₅ dissolved in NH₄OH, with ammonia solution at pH = 9.5. The resulting solids, after characterization by N₂-porosimetry and XRD measurements, were checked for their surface acidity by ammonia–TPD and were also tested for their catalytic activity towards isopropanol decomposition. It was found that the addition of phosphorus increases the acid sites per square metre of the Al₁₀₀P_xV_y solids and the same effect is also observed by the addition of vanadium. The catalytic activity of the solids with y < 20, expressed as molecules decomposed per surface acid site per second, shows maxima for catalysts with higher cumulative addition of phosphorus and vanadium, at those P plus V concentrations that result in amorphous solids while the onset of crystallization results in reducing the activity. The opposite behaviour is observed for catalysts with 20% V where the crystal phase of V₂O₅ is apparent in XRD right from the beginning but becomes gradually amorphous at high phosphorus addition at x = 20.

---

Introduction

The development of well characterized metallophosphate solids possessing tailor-made surface characteristics, like porosity and acidity, is of interest for technological as well as for biochemical reasons. The technology-orientated possibilities include the use of such solids as acid dehydration/hydration catalysts¹ as selective adsorbents² as well as in separation technologies.³

On the other hand, the biochemically orientated interest stems from the participation of phosphorus in a very extended range of bio-solids like bones, teeth, scales and shells.⁴ For reasons which are related to minimization of diffusion limitations of reactants towards the surface of such solids and the maximization of the consequent surface reaction rates, such solids are often developed, both in technology and in nature, in porous forms which often possess a kind of hierarchy, either in their solid structure or in their porosity.⁵

Another property of such solids which affects their performance in technical applications like catalysis, as well as their behavior in biological processes like biomineralization, is their surface acidity.^6,7 Therefore, the existence of controlled surface acidity in confined spaces of such porous metallophosphate solids offers the possibility to monitor such effects. We should mention that in the recent years various research groups have developed mesoporous oxo-metallo-phosphates,^8–11 but these studies usually referred to the preparation and characterization of these solids.

In the context of an extended study program which has started some years ago, we have prepared and characterized from a structural,¹² textural,¹³ surface,^12(a),13(a) fractal¹⁴ and catalytic^12(a),15 point of view various aluminophosphate solids, containing also added cations like iron^12,14,15 chromium,^12(a),14,15 vanadium^13(b),16 and the first row transition elements.^13(a)

The present study is an extension of some previous works^13(b),16,17 referring to such phosphoro-vanado-aluminate solids and deals with the effect of the incorporation of phosphorus and vanadium into γ-Al₂O₃, as well as on the surface acidity and the catalytic dehydration activity of the obtained solids, using the iso-propanol decomposition as a probe reaction. Furthermore, another point is the scrutinization of the effect of amorphous or crystalline phases, of similar composition, on the catalytic activity.

Experimental and results

Preparation and characterization of specimens

The samples examined have the abbreviated formula Al₁₀₀P_xV_y where x,y = 0, 5, 10, 20. The whole formula involves substantial amounts of oxygen to balance the cations, but a precise oxide-based formula is not fully established so the abbreviated version is the most relevant in use.^13(b),16,17 The preparation procedure was as follows: calculated amounts of Al(NO₃)₃·9H₂O (Merck p.a.) and H₃PO₄ (Ferak p.a.) were dissolved in 250 ml of distilled water and V₂O₅ dissolved in 10 ml NH₄OH, was finally added. Then, an ammonia solution (Ferak p.a.) was added dropwise under stirring up to pH = 9.5 for 30 min. The gel formed was dried at 110 °C for 24 h. Since previous thermogravimetric studies¹⁷ had shown that such gels lose mass at around 300–350 °C but stabilize their mass above this temperature, heating in this region was carried out very slowly (1 °C min⁻¹) in a tubular furnace under atmospheric conditions. The final firing temperature was set to 600 °C for a 6 h period. The samples prepared and some of their properties are listed in Table 2. For convenience, the samples will be referred to as P_xV_y throughout the rest of the article.

Table 2 Surface areas, pore volumes, pore sizes, surface acidity and activation energies of the Al₁₀₀P_xV_y solids

Sample	Surface area (BJH)/m^2 g^−1	Pore volume (BJH)/cc g^−1	Mean pore diameter/nm	Peak of PSD^a/nm	FWHM/nm	Acid sites/10^17 m^−2	E app/kJ mol^−1
							Low temperature	High temperature
a PSD, pore size distribution.
Al100P0V0	201.3	0.43	8.5	6.54	2.5	6.54	107.7	—
Al100P5V0	245.3	0.52	8.4	6.34	2.4	9.53	120.0	—
Al100P10V0	319.8	1.19	14.0	9.14	4.4	10.35	116.4	—
Al100P20V0	239.5	0.93	15.5	10.74	6.3	11.68	128.5	—
Al100P0V5	270.5	0.45	6.6	5.44	2.1	10.98	65.3	135.8
Al100P5V5	352.6	0.70	8.0	6.24	2.9	12.06	65.2	122.7
Al100P10V5	386.1	1.15	11.9	9.24	4.6	21.37	93.8	—
Al100P20V5	336.0	0.48	5.7	10.34	5.9	14.10	95.8	—
Al100P0V10	301.9	0.50	6.6	5.24	2.1	12.19	23.6	141.6
Al100P5V10	359.0	0.83	9.3	6.94	3.4	6.92	41.1	107.9
Al100P10V10	321.5	1.11	13.8	10.24	5.4	17.76	47.2	101.3
Al100P20V10	257.9	0.36	5.6	12.44	10.2	17.49	77.2	—
Al100P0V20	176.7	0.46	10.3	8.14	5.2	24.05	83.4	27.6
Al100P5V20	286.3	0.74	10.4	7.34	4.1	20.92	90.9	37.5
Al100P10V20	305.2	1.02	13.4	9.24	6.0	18.99	60.5	86.7
Al100P20V20	199.9	0.24	4.9	12.64	10.3	25.08	62.9	110.4

---

The characterization of these samples by several techniques has already been reported^13(b),16,17 elsewhere and is therefore only briefly mentioned here. X-ray diffraction (XRD) has shown that the parent solid (P₀V₀) has the typical crystal structure of γ-Al₂O₃ (Table 1 and ref. 13(b)). An addition of phosphorus into the synthesis mixture results in the gradual formation of increased amounts of amorphous material. According to the XRD data the formation of crystalline AlPO₄ takes place in P₂₀V_y samples. Gradual incorporation of vanadium into the synthesis mixture decreases the crystallinity of the γ-Al₂O₃ phase, but this influence is much more weaker compared to that of phosphorus. For solids with 20% vanadium content, the V₂O₅ crystal phase is apparent.

Table 1 Detected crystal phases from the XRD technique for the Al₁₀₀P_xV_y solids

Sample	Detected crystal phases from XRD
Al100P0V0	γ-Al2O3
Al100P5V0	Amorphous
Al100P10V0	Amorphous
Al100P20V0	AlPO4
Al100P0V5	Amorphous
Al100P5V5	Amorphous
Al100P10V5	Amorphous
Al100P20V5	AlPO4
Al100P0V10	Amorphous
Al100P5V10	Amorphous
Al100P10V10	Amorphous
Al100P20V10	AlPO4
Al100P0V20	γ-Al2O3, V2O5
Al100P5V20	V2O5
Al100P10V20	V2O5
Al100P20V20	AlPO4, V2O5

---

The pore size distribution measurements were carried using a Fisons Sorptomatic 1900 instrument. The characterization techniques included the determination of nitrogen adsorption–desorption isotherms from which the pore size distributions were also found. Each sample was degassed before measurement for 12 h at T = 200 °C and P = 5 × 10⁻³ Torr. The surface areas and porosity measurements (BJH method)¹⁸ (Fig. 1 and Table 2) showed that the addition of P at a constant concentration of V, and/or the addition of V at a constant concentration of P, increases the specific surface area and the pore volume. The maximum surface area and pore volume is obtained for a 15% cumulative addition of the two elements.

Fig. 1 N₂ adsorption–desorption isotherms at 77 K (right side) and the corresponding pore size distributions (left side). D is the pore diameter.

Surface acidity measurements

The temperature-programmed desorption (TPD) of ammonia was used to evaluate the total (Lewis + Brönsted) surface acidity of the materials.¹⁰ Briefly, the procedure was as follows. The sample weighing about 0.5 g was put on the perforated bed of a silica tube with a diameter of 1 cm. The tube was connected to a gas chromatograph (Shimadzu GC-8A) with a thermal conductivity (TC) detector. Each sample was initially heated at 500 °C in a flow of helium for 2 h, whereupon the temperature was reduced to the working level of 100 °C. Then the sample was saturated with dried ammonia by replacing for 30 min the flow of helium through the sample by a flow of dried ammonia. The weakly adsorbed ammonia was flushed out with helium flow (20 ml min⁻¹) for 2 h at 110 °C. After stripping of the weakly adsorbed ammonia the sample was cooled to 100 °C and heating begun at a rate of 10 °C min⁻¹ till 500 °C where it remained for 2 h. The amount of ammonia eluted was trapped in a bubble bottle, which contained an excess of 0.01 N hydrochloric acid solution. The trapped ammonia was determined by volumetric titration of the excess HCl using 0.05 N NaOH. The results are summarised in Table 2, as surface acid sites per square metre of the sample.

Catalytic decomposition of isopropanol

The catalytic decomposition of isopropanol was performed in a bench-scale flow reactor, similar to that described previously.^3(b),13(a) The reactor consisted of a silica tube with a diameter of 1 cm with a sealed-in quartz bed onto which 0.25 g of catalyst was placed. The system was heated in a tubular furnace with a temperature accuracy within ±0.5 °C. Analyses of the reactants and products were carried out by sampling 1 cm³ of gases in a Shimadzu GC-15A gas chromatograph equipped with a thermal conductivity detector and connected to a Chromatopac C-R6A integrator. The column used for analysis was 2 m × 1/8″ stainless steel filled with 10% Carbowax 20M on Chromosorb W-HP (80–100 mesh). Helium was used as carrier gas in the GC. Another line drove helium through a saturator bottle (40 ± 1 cm³ min⁻¹) containing isopropanol. The partial pressure of isopropanol was 46 mbar. The experiments were carried out randomly in the temperature range 100–200 °C at 5 °C intervals. Before the catalytic experiments, all solids were heated at 200 °C for 2 h in a helium flow. No deactivation was observed during the scale of our experiments. The products detected were propene and di-isopropyl ether. The reaction rate at each temperature was calculated from the degree of conversion of isopropanol, and the selectivity for each main product at various degrees of conversion of isopropanol was also found.

The corresponding integral reaction rates per square metre of the catalyst are shown in Fig. 2 as a function of temperature. In Fig. 3 the selectivity towards propene (S_p) and di-isopropyl ether (S_e) is shown as a function of degree x of conversion.

Fig. 2 Temperature profiles of the catalytic activity (moles s⁻¹ m⁻²) for the isopropanol decomposition.

Fig. 3 Selectivity for the productions of propene (a) and of di-isopropyl-ether (b) as a function of conversion of isopropanol.

Discussion

The addition of phosphorus increases the acid sites per square metre of the P_xV_y solids and the same effect is also observed with the addition of vanadium. The maximum number of acid sites occurs for the P₂₀V₂₀ sample. Similar results referring to continuous increase of number of acid sites with the addition of phosphorus have also been reported elsewhere.^19,20 According to Morales et al.²⁰ the adsorption of phosphorus, in the form of PO₄³⁻, on the surface of γ-Al₂O₃, leads to duplication of the number of acid sites per atom Al for every P atom added. As reported in ref. 16, the incorporation of vanadium is not as straightforward as that of phosphorus and XRD measurements have shown that it induces loss of crystallinity of the γ-Al₂O₃ structure. Therefore vanadium interacts with the framework. Furthermore, MAS NMR experiments showed that a small percentage of vanadium (especially for the samples with 20% V) is heterogeneously spread over the surface in the form of small clusters of V₂O₅-like species, which may originate from the nature of the vanadium source, i.e. V₂O₅, not having reacted with the alumina.¹⁶ Al MAS spectra indicated the appearance of amorphous AlPO₄ for the lowest amount of phosphorus. Increasing the amount phosphorus causes the growth of this amorphous phase towards the inner part of the framework. The cumulative addition of phosphorus and vanadium led to the additional formation of crystalline AlPO₄. The amorphous AlPO₄ phase was composed of phosphoric species having at least three aluminium atoms in the second sphere of their coordination, near the surface of the pores. Both phosphorus and the rest of vanadium species are located near the surface of γ-Al₂O₃, probably forming Al–O–M bonds where M[double bond, length half m-dash]P, V.¹⁶ Therefore the synergistic action of the two elements in the formation of acid sites is the reason for the increment of the acidity with the cumulative addition of phosphorus and vanadium.

In Fig. 2 it is shown that for the solids without vanadium, the addition of 5% P decreases the reaction rate. However, addition of phosphorus up to 20% improves the catalytic activity. For a small addition of vanadium (5% V) an increase in the catalytic activity is observed. Further addition of vanadium leads to a plateau in the reaction rate at a reaction temperature of 140–160 °C, but at higher reaction temperatures, which results in an increment of the catalytic activity. For the samples with 20% vanadium content, the addition of phosphorus decreases the reaction rate. Moreover, it is clear that solids with 10% and 20% vanadium show higher activity at low reaction temperatures, as compared to the other solids.

In Fig. 3 it is shown that the selectivity to propene is decreased for solids without vanadium and for degrees of conversion up to 15%. However, at higher degrees of conversion the selectivity to propene is increased. The addition of phosphorus leads to increment of selectivity to propene and reduction on the selectivity to di-isopropyl ether. For the solids which contain vanadium, a steep and continuous increment of the propene selectivity is observed. In general, propene is the main product of the dehydration reaction with a selectivity of at least fifty percent. For samples with vanadium and at low degrees of isopropanol conversion, a very low production of acetone is observed. According to Bond et al.²¹ the production of acetone via dehydrogenation is due to the presence of vanadyl groups (V[double bond, length half m-dash]O) on the surface of the solids. The existence of such groups on our catalysts have been proved by solid state NMR measurements as presented above, and published in the past.¹⁶

The rate of dehydration, which is an acid catalysed reaction, should increase parallel to the surface density of sites. However, this was not observed for all the examined solids. Therefore, it is plausible that parameters other than the number of acid sites could be critical in determining their apparent activity. Indeed, in Fig. 4a we observe that the activity of the solids (molecules decomposed per surface acid site per second) shows maxima for the catalysts with higher cumulative addition of phosphorus and vanadium, exactly at those P plus V concentrations that result in amorphous solids (compare with XRD data in Table 1). The sample Al₁₀₀P₀V₀ is excluded. The opposite behaviour is observed for catalysts with 20% vanadium content. The differentiated behavior of the samples Al₁₀₀P_xV₂₀ as far as E_app, as well as the Selectivity concern, can be only due to the different crystal phases existing in the samples, which differentiate their surface acidity.

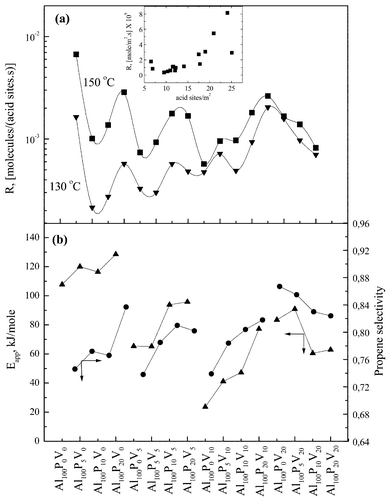Fig. 4 Variation of (a) catalytic activity at 130 and 150 °C expressed as molecules decomposed per surface acid site per second; in an including graph the rate of dehydration as a function of the number of acid sites is shown. (b) E_app values for low reaction temperatures (▲) and selectivity to propene (●).

As far as the kinetics of isopropanol decomposition is concerned, we consider 1^st order kinetics which is the simplest and most common treatment applied to this reaction.^15,22–24

R = k θ_iso (1)

Assuming Langmuirian adsorption isotherms we obtain

θ_iso = (b_isoP_iso)/(1 + Σk_iP_i) (2)

where b and P have their usual meaning, i corresponds to all the reactants and products of the reaction, which are isopropanol, propene, diisopropyl ether, helium and water. Considering weak adsorption of all the reactants and products (1 ≫ Σk_iP_i), eqn. (1) obtains the form

R = k b_isoP_iso (3)

Then, expressing the partial pressure of isopropanol as a function of its initial pressure P⁰_iso, of the degrees of conversion, the selectivities of every product and the total pressure in the reactor P_t, as well as using the design-equation of the plug flow reactor (F dx = R dS, where F is the feed (moles s⁻¹) and S the surface area of the catalyst) as the one used in our case, we obtain after lengthy but rather trivial transformations eqn. (4) (all the above transformations are reported in detail in ref. 24).

where α and γ are the selectivities to propene and acetone, respectively, and x is the total conversion of isopropanol. For P_t = 727.5 mmHg, P⁰_iso = 33.16 mmHg, in our experiment we can easily rearrange eqn. (4) in the form where k = A exp(−E_app/RT), E_true is the true activation energy of the reaction, b_iso = exp[(−ΔH_iso)/RT], −ΔH_iso is the enthalpy of adsorption of isopropanol, and E_app is the apparent activation energy of the process related to E_true and ΔH by the relationship E_app = E_true − ΔH_iso.

Then, plots of the left hand part of eqn. (5)versus 1000/T can be used to obtain the apparent activation energy of the reaction E_app. Such plots are shown in Fig. 5. The calculated numerical values of E_app are listed in Table 2.

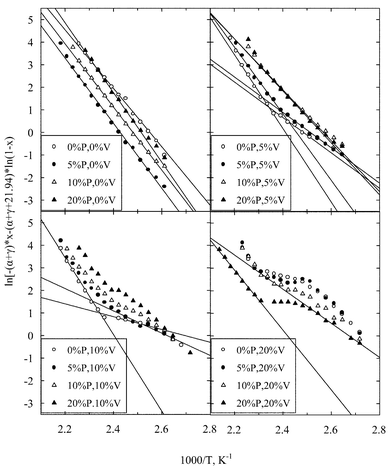Fig. 5 Arrhenius plots for the isopropanol decomposition drawn according to eqn. (5).

From the Arrhenius lines drawn in Fig. 5 it is immediately apparent that the vanadium containing catalysts behave in a totally different way, as compared to the samples without vanadium. Those plots indicate two regions of activation energy: The first one appears at high temperatures and high conversions and the other at low reaction temperatures and low conversions of isorpopanol. We believe that the two regions of activation energy which appear at higher temperatures are due to the alternation of kinetics. The first order kinetic eqn. (3) does not hold for the whole range of conversion. There are two possibilities. The first one is that isopropanol itself is strongly adsorbed at low T and low conversions on Al₁₀₀P_xV_y. If so, the kinetics should be zero order R = k and the apparent activation energy of the reaction E_app should equal E_true. The other possibility is that water, when produced in large quantities at higher conversion, acts inhibitively. Then, the apparent activation energy of the reaction should appear increased by an amount equal to that of the heat of water adsorption i.e.

E_app = E_true − ΔH_C3H8O + ΔH_H2O

while at high temperature

E_app = E_true − ΔH_C3H8O.

In other words, the difference between the two sets of activation energies on Al₁₀₀P_xV_y corresponds to the enthalpy of adsorption of water on the catalyst surface.

This peculiar behavior might also be connected with the heterogeneous spread of vanadium over the surface as small clusters of V₂O₅-like species, which affects the adsorption of reactant or/and products on the surface, and alters the reaction rate, the selectivity and the apparent activation energy of the reaction.

In Fig. 4b the values of E_app for low reaction temperatures and the selectivity to propene are depicted for the four groups of solids. The estimated apparent activation energies run parallel to the selectivity to the main product, i.e. propene. As mentioned above, the calculated values of E_app are related to the true activation energy E_true and the enthalpy of adsorption of isopropanol ΔH_iso. Catalysts with high surface acidity are expected to show higher catalytic activity, as well as higher negative values of ΔH_iso and as a result higher E_app values. For this reason, E_app runs parallel to the selectivity of propene which is the main product of the reaction.

Plotting the values of the pre-exponential factor versus the corresponding activation energies, a perfectly straight line is obtained (Fig. 6) which corresponds to a single compensation effect. According to Patterson et al.,²⁵ this happens because the variation of the strength of adsorption of the reactants and products affects the entropy of adsorption on the catalyst's surface. Arrhenius plots that obey the compensation effect must intersect at exactly the same point defining an “isokinetic temperature” and “isokinetic rate”. The isokinetic and compensation parameters are related to each other as follows:

Compensation effect : ln A = mE_app + C (6)

Isokinetic parameters : T_iso = (mR)⁻¹; ln(k_iso) = C (7)

Fig. 6 Compensation effect for the isopropanol decomposition over the Al–P–V catalysts.

From eqn. (7) and the estimated slope of the compensation effect line (Fig. 6) an “isokinetic temperature” of 424 K is calculated. It is remarkable that this value corresponds exactly to the reaction temperature where a changing of slope is observed at the Arrhenius plots in Fig. 5. Beyond this temperature, another reaction mechanism probably takes over, as discussed previously, with differentiated E_app and lnA. Therefore some compensation perhaps holds there which cannot be determined from the present set of data.

Conclusions

The following conclusions can be drawn from this work.

(i) The addition of phosphorus on γ-Al₂O₃ increases the acid sites per square metre of the Al₁₀₀P_xV_y solids and the same effect is also observed with the addition of vanadium.

(ii) The main products of the isopropanol decomposition were propene and di-isopropyl ether, with selectivity to propene between 50 and 100%.

(iii) We did not observe any direct correlation between the reaction rate and the number of acid sites for all tested catalysts. The samples with medium and high vanadium content showed a rather peculiar behavior, which might be due to poor dispersion of vanadium on the surface, forming V₂O₅-clusters.

(iv) The catalytic activity of the solids expressed as molecules decomposed per surface acid site per second shows maxima for the catalysts with the higher cumulative addition of phosphorus and vanadium, exactly at those P plus V concentrations that result in amorphous solids. The opposite behaviour was observed for the catalysts with 20% vanadium content.

(v) From the Arrhenius plots it was apparent that vanadium containing catalysts showed two regions of activation energy. The reaction temperature, which separated those regions, corresponds exactly to the isokinetic temperature of the reaction, as it was calculated from the compensation effect.

Acknowledgements

The authors thank Professor P. J. Pomonis for the helpful comments and discussions.

References

1. (a) M. J. Campelo, M. F. Bautista, A. Garcia, D. Luna, M. J. Marinas and A. A. Romero, Appl. Catal., A, 1998, 166, 39–45; (b) Robert A. W. Johnstone, Jun-Yao Liu and David Whittaker, J. Mol. Catal. A: Chem., 2001, 174, 159–168; (c) M. C. Fougret and F. W. Hölderich, Appl. Catal., A, 2001, 207, 295–301.
2. (a) K. G. Varshney, A. H. Pandith and U. Gupta, Langmuir, 1998, 14(26), 7353–7358; (b) Y. Makita, H. Kanoh, T. Hirotsu and K. Ooi, Chem. Lett., 1998, 1, 77–78.
3. (a) K. O. Miyai, Y. Makita and H. Kanoh, Sep. Sci. Technol., 1999, 34(6–7), 1133–1144; (b) D. M. Kaschak, S. A. Johnson, C. C. Waraksa, J. Pogue and T. E. Mallouk, Coord. Chem. Rev., 1999, 186, 403–416; (c) S. Oliver, A. Kuperman and A. G. Ozin, Angew Chem., Int. Ed. Engl., 1998, 37, 46–62.
4. (a) S. Oliver, A. Kuperman, N. Coombs, A. Lough and A. G. Ozin, Nature, 1995, 378, 47–50; (b) A. Stoch, W. Jastzebski, J. Stoch, J. Szaraniec, B. Trybalska and G. Kmita, J. Mol. Struct., 2000, 555, 375–382; (c) M. Nagano, T. Nakamura, T. Kokubo, M. Tanahashi and M. Ogawa, Biomaterials, 1996, 17, 1771–1777.
5. (a) A. G. Ozin, Acc. Chem. Res., 1997, 30, 17–27; (b) A. Choudhury, S. Natarajan and C. N. Rao, Inorg. Chem., 2000, 39, 4295–4304.
6. K. Tanabe, M. Misono, Y. Ono and Hattori, Studies in Surface Science and Catalysis, ed. B. Delmon and T. J. Yates, vol. 51, Amsterdam–Oxford–New York–Tokyo, 1990.
7. (a) L. M. Cornaglia, E. A. Lombardo, J. A. Andersen and J. J. Garcia Fierro, Appl. Catal., 1993, 100, 37–50; (b) N. S. Pavlova, A. V. Sadykov, V. G. Zabolotnaya, I. D. Kochubey, I. R. Maximovskaya, I. V. Zaikovskii, V. V. Kriventsov, V. S. Tsybulya, B. E. Burgina, M. A. Volodin, V. M. Chaikina, N. N. Kuznetsova, V. V. Lunin, D. Agrawal and R. Roy, J. Mol. Catal. A: Chem., 2001, 174, 159–168; (c) A. H. G. Mekhemer, K. H. A. Nohman, E. N. Fouad and A. H. Khalaf, Colloids Surf., A, 2000, 161, 439–446.
8. U. Ciesla, S. Schacht, D. G. Stucky, K. K. Unger and F. Schuth, Angew. Chem., Int. Ed. Engl., 1996, 35(5), 541–543.
9. (a) S. M. Wong, M. D. Antonelli and Y. J. Ying, Nanostruct. Mater., 1997, 9, 165–168; (b) E. Rodríguez-Castellón, J. Jiménez-Jiménez, A. Jiménez-López, P. Maireles-Torres, R. J. Ramos-Barrado, J. D. Jones and J. Rozière, Solid State Ionics, 1999, 125, 407–410.
10. L. M. Rodriguez, J. Alcaraz, M. Hernandez, M. Dufaux, Y. Ben Taarit and M. Vrinat, Appl. Catal., A, 1999, 189, 53.
11. K. J. Bartley, J. I. Ellison, A. Delimitis, J. C. Kiely, A.-Z. Isfahani, C. Rhodes and J. G. Hutchings, Phys. Chem. Chem. Phys., 2001, 3, 4606–4613.
12. (a) D. E. Petrakis, P. J. Pomonis and A. T. Sdoukos, J. Chem. Soc., Faraday Trans. 1, 1989, 85(10), 3173–3186; (b) E. D. Petrakis, M. J. Hudson, J. P. Pomonis, A. T. Sdoukos and T. V. Bakas, Colloids Surf., A, 1994, 90, 191; (c) D. E. Petrakis, M. J. Hudson, P. J. Pomonis, A. T. Sdoukos and T. V. Bakas, J. Mater. Chem., 1995, 5(11), 1975–1983.
13. (a) D. E. Petrakis, P. J. Pomonis and A. T. Sdoukos, J. Chem. Soc., Faraday Trans., 1991, 87(6), 901–905; (b) K. M. Kolonia, D. E. Petrakis, T. N. Angelidis, P. N. Trikalitis and P. J. Pomonis, J. Mater. Chem., 1997, 7(9), 1925–1931.
14. Petrakis E. Dimitris, Pashalidis Ioannis, Theocharis R. Charis, Hudson J. Michael and Pomonis J. Philip, J. Colloid Interface Sci., 1997, 185, 104–110.
15. D. E. Petrakis, P. J. Pomonis and A. T. Sdoukos, J. Chem. Soc., Faraday Trans., 1991, 87(9), 1439–1445.
16. R. D. Gougeon, P. R. Bodart, R. K. Harris, D. M. Kolonia, D. E. Petrakis and P. J. Pomonis, Phys. Chem. Chem. Phys., 2000, 2, 5286–5292.
17. K. M. Kolonia, D. E. Petrakis, T. C. Vaimakis, E. D. Economou and P. J. Pomonis, Thermochim. Acta, 1997, 293, 93–100.
18. E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373.
19. D. Chadwick, D. W. Aitchison, R. Badilla-Ohtbaum and L. Josefsson, in Preparation of Catalysis III, Studies in Surface Science and Catalysis, vol. 16, Elsevier, Amsterdam, 1983, p. 323.
20. A. Morales, M. M. Ramirez de Angelo and F. Hernandez, Appl. Catal., 1988, 41, 261.
21. G. C. Bond and S. Flamerz, Appl. Catal., 1987, 33, 219.
22. A. La Cinestra, P. Patrono, M. L. Berardelli, P. Galli, C. Ferragina and M. A. Massucci, J. Catal., 1987, 103, 346.
23. M. Richter and G. Ohlman, Appl. Catal., 1988, 36, 81.
24. A. K. Ladavos, P. N. Trikalitis and P. J. Pomonis, J. Mol. Catal. A: Chem., 1996, 106, 241.
25. W. R. Patterson and J. J. Rooney, J. Catal., 1994, 146, 310.

---