View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B207515F (Paper) Phys. Chem. Chem. Phys., 2003, 5, 203-207

Capillary condensation of hexafluoroethane in an ordered mesoporous silica

William D. Machin
Department of Chemistry, Memorial University of Newfoundland, St. John's, Newfoundland, Canada A1B 3X7

Received 31st July 2002 , Accepted 5th November 2002

First published on 20th November 2002

Abstract

A total of 43 adsorption isotherms are reported for hexafluoroethane (HFE) on an ordered mesoporous silica (MCM-41) at 2 K intervals for temperatures from 196 K to 280 K. All isotherms are reversible and, at lower temperatures, exhibit the abrupt step characteristic of capillary condensation in such adsorbents, but at higher temperatures both the extent and slope of the step decrease. The step is absent at temperatures greater than 255 K, here interpreted as the capillary critical temperature for first-order capillary condensation. Equations describing the capillary coexistence boundary and the rectilinear diameter are presented. Pore radii and pore volumes calculated from the isotherms are consistent with the assumption that capillary condensed HFE has essentially the same surface tension and density as bulk liquid over the entire temperature range. We conclude that capillary condensation at T[thin space (1/6-em)]>[thin space (1/6-em)]255 K occurs by a second-order process.

1 Introduction

Physical adsorption in mesoporous adsorbents such as silica gel or controlled-pore glass usually exhibits hysteresis.1 The extent of hysteresis decreases with increasing temperature and vanishes at a capillary critical temperature, Tcc, which is less than the critical temperature, Tc, of the bulk fluid.2–5 Theoretical arguments suggest that this phenomenon originates with shifted phase transitions arising from the influence of attractive fluid–wall interactions and that pore fluid at the capillary critical point should exhibit true critical behavior.6,7 However, other work suggests that the temperature at which hysteresis vanishes is not necessarily a true critical point.8,9

In contrast to conventional mesoporous silicas, highly ordered silicas such as MCM-41 may be prepared with parallel, uniform, cylindrical pores,10,11 and it has been suggested that such adsorbents may be suitable for fundamental studies on physical adsorption and capillary condensation.12 It has been observed that capillary condensation in ordered silicas is often reversible with hysteresis occurring at temperatures much less than predicted from theoretical arguments,13–15 whereas the capillary critical temperature of many adsorptives in other types of mesoporous adsorbents is reasonably well described by these theories.16–18

In this work, adsorption isotherms for hexafluoroethane on a mesoporous MCM-41 silica are reversible from 195 K to 280 K, but the characteristic step in the isotherm, indicative of first-order capillary condensation, is only observed at temperatures less than 255 K. We consider the nature of this phase transition and the processes that lead to pore filling at higher temperatures.

2 Experimental

The adsorbent was prepared using a sodium silicate solution (Aldrich, ca. 14% NaOH, ca. 27% SiO2) as a silica source and cetyltrimethylammonium bromide (CH3(CH2)15N(CH3)3Br, Aldrich) as template following the procedure given by Branton et al.13 The volumetric adsorption apparatus is constructed of stainless steel components and fittings. The pressure sensor (Paroscientific, Model 42K-101), dosing volume and associated bellows-seal metal valves are kept at a constant temperature (ca. 323 K), and the variable temperature bath surrounding the sample fits immediately below this constant temperature box. A more detailed description of the apparatus is presented elsewhere.19 To minimize potential dosing errors, adsorptives should have critical temperatures less than 323 K. Hexafluoroethane (HFE) meets this requirement (Tc[thin space (1/6-em)]=[thin space (1/6-em)]293.01 K) and is readily available in high purity (Matheson Halocarbon 116, 99.95%). It is also a large, non-polar, quasi-spherical molecule which simplifies analysis of the experimental results. Temperatures are measured with a platinum resistance thermometer to an accuracy of ca. ±0.002 K. At low temperatures where the density of the adsorbed fluid is much greater than that of the bulk vapour, the excess amount adsorbed is determined with an accuracy of 0.1% or better, but at higher temperatures and pressures this error may be larger. Estimated error in relative fugacity is ca. ±0.001.

The operating procedure is similar to that described previously.19 With a known amount of adsorptive in the system the temperature is decreased in ca. 2 K steps from the highest temperature to the lowest. At each step, temperature T, pressure P, and the adsorption excess ne are measured, then the process is reversed with temperature increasing in ca. 2 K steps. This overall process provides a sensitive test for the reversibility of the isotherms; if hysteresis is absent points obtained while increasing temperature coincide with those obtained while decreasing temperature. If hysteresis is present they do not. Runs carried out with different total amounts of adsorptive yield a pressure–temperature–amount adsorbed (P,T,ne) surface from which adsorption isotherms and isosteres may be obtained. Examples of each are shown in Figs. 1 and 2. In these figures and throughout the following discussion the total amount adsorbed, nt, is used, i.e.

 
nt[thin space (1/6-em)]=[thin space (1/6-em)]ne[thin space (1/6-em)]+[thin space (1/6-em)]Vpρvap(1)
where Vp is the pore volume (ca. 0.8 ml g−1). Bulk vapour density, ρvap, and fugacity f, are calculated using the virial coefficients reported by Hurly.20 At lower temperatures and pressures nt[thin space (1/6-em)]≅[thin space (1/6-em)]ne, but may be up to 10% larger at, for example, 280 K and 2000 kPa.


Adsorption isotherms, as total amount adsorbed vs. relative fugacity; ○, 196 K; ◇, 216 K; +, 236 K; ▷, 256 K; ●, 276 K. For each isotherm the solid line at low and intermediate coverages is calculated using the standard two parameter BET equation (eqns. (2)–(4)). At T < 255 K the dotted line indicates the characteristic abrupt step, and dashed lines show the plateau region for each isotherm.
Fig. 1 Adsorption isotherms, as total amount adsorbed vs. relative fugacity; ○, 196 K; ◇, 216 K; +, 236 K; ▷, 256 K; ●, 276 K. For each isotherm the solid line at low and intermediate coverages is calculated using the standard two parameter BET equation (eqns. (2)–(4)). At T[thin space (1/6-em)]<[thin space (1/6-em)]255 K the dotted line indicates the characteristic abrupt step, and dashed lines show the plateau region for each isotherm.

Adsorption isosteres for the following amounts adsorbed; ○, 2.2 mmol g−1; +, 3.2 mmol g−1; ●, 4.0 mmol g−1; ▷, 7.0 mmol g−1; ◇, 8.2 mmol g−1. These coverages illustrate isostere behaviour within (i) the initial monolayer–multilayer region, (ii) the capillary condensation region, and (iii) the plateau region. The vertical dotted line marks the position of the capillary critical temperature, 255 K.
Fig. 2 Adsorption isosteres for the following amounts adsorbed; ○, 2.2 mmol g−1; +, 3.2 mmol g−1; ●, 4.0 mmol g−1; ▷, 7.0 mmol g−1; ◇, 8.2 mmol g−1. These coverages illustrate isostere behaviour within (i) the initial monolayer–multilayer region, (ii) the capillary condensation region, and (iii) the plateau region. The vertical dotted line marks the position of the capillary critical temperature, 255 K.

3 Results

Forty-three isotherms at integer temperatures (2 K intervals) from 196 K to 280 K, have been derived from the combined adsorption runs (see Fig. 1). At lower temperatures the isotherms exhibit features characteristic of many adsorptives on MCM-41 type silicas with initial monolayer–multilayer growth at low relative fugacities leading to an abrupt, nearly vertical, step which is followed by a nearly horizontal plateau at higher relative fugacities. The height of the step and its slope both decrease at higher temperatures with the step becoming indistinct or absent for T[thin space (1/6-em)]>[thin space (1/6-em)]250 K. The standard BET equation1 provides an excellent description of each isotherm up to the onset of the step or well into the multilayer region when the step is absent, i.e.
 
nt/nm[thin space (1/6-em)]=[thin space (1/6-em)]C(f/f°)/{(1[thin space (1/6-em)]−[thin space (1/6-em)]f/f°)[1[thin space (1/6-em)]+[thin space (1/6-em)](C[thin space (1/6-em)]−[thin space (1/6-em)]1)(f/f°]}(2)
where nt is the total amount adsorbed at relative fugacity f/f°, nm is the monolayer capacity and C is a constant. The solid lines in Fig. 1 illustrate the goodness of fit of eqn. (2) to the experimental data. The BET parameters, C and nm, are given by
 
C[thin space (1/6-em)]=[thin space (1/6-em)]exp(−0.01234T[thin space (1/6-em)]+[thin space (1/6-em)]5.3414); ±1.7%(3)
 
nm(mmol g−1)[thin space (1/6-em)]=[thin space (1/6-em)]7.321[thin space (1/6-em)]−[thin space (1/6-em)]2.761[thin space (1/6-em)]×[thin space (1/6-em)]10−2T[thin space (1/6-em)]+[thin space (1/6-em)]4.379[thin space (1/6-em)]×[thin space (1/6-em)]10−5T2; ±0.027(4)

Molecular areas calculated from bulk liquid densities1,21 yield surface areas, S, ranging from 620–700 m2 g−1 with average S[thin space (1/6-em)]=[thin space (1/6-em)]646[thin space (1/6-em)]±[thin space (1/6-em)]21 m2 g−1.

For T[thin space (1/6-em)]<[thin space (1/6-em)]255 K the relative fugacity marking the lower position of the step is given by

 
fL/f°[thin space (1/6-em)]=[thin space (1/6-em)]3.516[thin space (1/6-em)]×[thin space (1/6-em)]10−3T[thin space (1/6-em)]−[thin space (1/6-em)]0.3877; ±0.0069(5)
and at the top of the step
 
fU/f°[thin space (1/6-em)]=[thin space (1/6-em)]4.090[thin space (1/6-em)]×[thin space (1/6-em)]10−3T[thin space (1/6-em)]−[thin space (1/6-em)]0.4799; ±0.0047(6)

Amounts adsorbed at saturation were obtained by extrapolation of the linear plateau region to f/f°[thin space (1/6-em)]=[thin space (1/6-em)]1, and these values are given by

 
ns (mmol g−1)[thin space (1/6-em)]=[thin space (1/6-em)]11.132(1[thin space (1/6-em)]−[thin space (1/6-em)]T/Tc)0.14; ±0.16(7)
where Tc is the bulk critical temperature, 293.01 K.21 The apparent pore volume, Vp, calculated from ns and bulk liquid density, increases slowly with temperature as
 
Vp (ml g−1)[thin space (1/6-em)]=[thin space (1/6-em)]1.590[thin space (1/6-em)]×[thin space (1/6-em)]10−3T[thin space (1/6-em)]+[thin space (1/6-em)]0.492; ±0.013(8)

Quoted uncertainties in the above parameters represent one standard deviation.

4 Discussion

The abrupt step observed with many adsorptives on MCM-41 type silicas is usually considered to arise from reversible capillary condensation of the adsorptive in uniform cylindrical mesopores.22 The step represents a tie-line between a less dense capillary gas phase and a dense capillary liquid phase in much the same way that a constant vapour pressure line ties low density vapour to high density liquid in corresponding pressure–density isotherms for bulk fluids. As temperature increases, the length of the tie-line (step height) decreases until it vanishes at Tcc, the capillary critical temperature. This behaviour is shown in Fig. 3. Also analgous to bulk behaviour, the average density along each tie-line (the rectilinear diameter), (nU[thin space (1/6-em)]+[thin space (1/6-em)]nL)/2, decreases slowly as
 
(nU[thin space (1/6-em)]+[thin space (1/6-em)]nL)/2[thin space (1/6-em)]=[thin space (1/6-em)]−2.441[thin space (1/6-em)]×[thin space (1/6-em)]10−3T[thin space (1/6-em)]+[thin space (1/6-em)]6.994; ±0.005(9)
and intersects the phase boundary line at the capillary critical temperature.23 The density difference, nU[thin space (1/6-em)]−[thin space (1/6-em)]nL, obeys the scaling law typical of bulk liquids, namely
 
nU[thin space (1/6-em)]−[thin space (1/6-em)]nL[thin space (1/6-em)]=[thin space (1/6-em)]k(1[thin space (1/6-em)]−[thin space (1/6-em)]T/Tcc)β, ±0.11(10)
where k is a constant (k[thin space (1/6-em)]=[thin space (1/6-em)]5.967) and the critical scaling parameter, β[thin space (1/6-em)]=[thin space (1/6-em)]0.37, which is reasonably close to 0.33, the theoretical value for bulk three-dimensional fluids.24 The phase boundary line in Fig. 3 (solid line) has been calculated using this equation and eqn. (9). The apparent capillary critical parameters are; Tcc[thin space (1/6-em)]=[thin space (1/6-em)]255 K and ρcc[thin space (1/6-em)]=[thin space (1/6-em)]6.372 mmol g−1 or ca. 7.2 mol L−1. The value of the capillary critical pressure will be considered later.
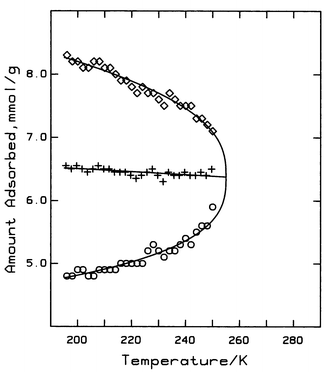The capillary coexistence curve for the first-order phase transition. ◇; amount adsorbed at the top, and ○; the amount adsorbed at the bottom of each step for isotherms at T < 255 K. The solid line passing through these points represents the phase boundary as calculated from eqns. (9) and (10). The rectilinear diameter (+), intersects the phase boundary line at the capillary critical point.
Fig. 3 The capillary coexistence curve for the first-order phase transition. ◇; amount adsorbed at the top, and ○; the amount adsorbed at the bottom of each step for isotherms at T[thin space (1/6-em)]<[thin space (1/6-em)]255 K. The solid line passing through these points represents the phase boundary as calculated from eqns. (9) and (10). The rectilinear diameter (+), intersects the phase boundary line at the capillary critical point.

One significant difference between the bulk and capillary phase transition is that the former occurs at constant fugacity whereas the latter does not (see Fig. 1). The slope, (nU[thin space (1/6-em)]−[thin space (1/6-em)]nL)/(fU/f°[thin space (1/6-em)]−[thin space (1/6-em)]fL/f°), of the capillary phase transition decreases with increasing temperature and becomes equal to the slope of the critical isotherm at ρcc, as shown in Fig. 4. Therefore, at the capillary critical point, the first derivative of fugacity with respect to density is finite, i.e. [∂f/∂ρ]cc[thin space (1/6-em)]>[thin space (1/6-em)]0, whereas the corresponding quantity for bulk fluid is equal to zero. Consequently, the compressibility of capillary fluid at the critical point is not infinite, and the capillary critical point cannot be a true critical point in the usual sense. As well, there may be other important differences between bulk and capillary fluid.


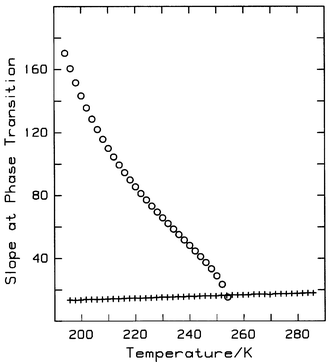Isotherm slope at the capillary phase transition. ○, step slope for T < 255 K; +, inferred (T < 255 K) or actual (T > 255 K) slope of the BET isotherm at the capillary critical density as calculated from eqn. (2).
Fig. 4 Isotherm slope at the capillary phase transition. ○, step slope for T[thin space (1/6-em)]<[thin space (1/6-em)]255 K; +, inferred (T[thin space (1/6-em)]<[thin space (1/6-em)]255 K) or actual (T[thin space (1/6-em)]>[thin space (1/6-em)]255 K) slope of the BET isotherm at the capillary critical density as calculated from eqn. (2).

Both surface tension and density of bulk liquids decrease with increasing temperature with the former becoming zero at the critical point. Capillary condensation and associated phenomena are therefore absent at supercritical temperatures. If similar behaviour occurs with capillary liquid then we might expect capillary condensation to be absent for all T[thin space (1/6-em)]>[thin space (1/6-em)]Tcc, and that the surface tension of capillary liquid to be significantly less than that of bulk liquid for T[thin space (1/6-em)]<[thin space (1/6-em)]Tcc. However, it is generally assumed1 that the surface tension of capillary liquid is essentially the same as that of bulk liquid, becoming zero only at the bulk critical temperature.19 Consequently, there are two possible situations; (i) capillary liquid exists only at temperatures less than the capillary critical temperature where its properties may differ significantly from bulk liquid, and (ii) capillary liquid exists at all temperatures less than the bulk critical temperature and its properties are essentially the same as bulk liquid. Two experimentally available quantities that may provide some insight into this question are pore radius and pore volume.

With all isotherms, adsorption starts with monolayer growth leading smoothly to multilayer formation (see Fig. 1), and at T[thin space (1/6-em)]<[thin space (1/6-em)]Tcc, first order capillary condensation occurs after the monolayer has been filled but before the second adsorbed layer has been completed. The top of the resulting step marks the point at which the pores are filled with capillary condensate. The pore liquid at this point, is under tension and further adsorption, along the plateau, proceeds by compression of the capillary liquid as saturation pressure is approached.1,25 With a rigid adsorbent having a fixed pore structure, the pore radii, rp, calculated using the relative fugacities at the top and bottom of the step should be constant, independent of temperature, when the appropriate surface tension, γ, and densities, ρ, are used in the Kelvin equation applicable to condensation in cylindrical mesopores,26i.e.

 
rp[thin space (1/6-em)]−[thin space (1/6-em)]1.5t[thin space (1/6-em)]=[thin space (1/6-em)]−2γ/[ΔρRT[thin space (1/6-em)]ln(f/f°)](11)

Here Δρ[thin space (1/6-em)]=[thin space (1/6-em)]ρ(liquid)[thin space (1/6-em)]−[thin space (1/6-em)]ρ(vapour), t is the thickness of the adsorbed film in contact with capillary condensate and may be estimated as

 
t[thin space (1/6-em)]=[thin space (1/6-em)]denx/nm(12)
where nx is the amount adsorbed at the base of the step, nm is the BET monolayer capacity and de is the equilibrium diameter (0.557 nm) of HFE.27 The results of this calculation, using bulk liquid values for surface tension and density22,28 are shown in Fig. 5. Over the temperature range 195 K to 250 K bulk liquid values yield nearly constant pore radii, rp[thin space (1/6-em)]=[thin space (1/6-em)]2.61[thin space (1/6-em)]±[thin space (1/6-em)]0.04 nm at the top of the step, and rp[thin space (1/6-em)]=[thin space (1/6-em)]2.49[thin space (1/6-em)]±[thin space (1/6-em)]0.06 nm at the base of the step. These values are in excellent agreement with the geometric pore radius, rg[thin space (1/6-em)]=[thin space (1/6-em)]2.62 nm, where rg[thin space (1/6-em)]=[thin space (1/6-em)]2Vp/S. It is unlikely that such good agreement would be found if surface tension of the capillary liquid differed significantly from bulk liquid. This result strongly suggests that the surface tension of capillary liquid HFE is the same as that of bulk liquid and, in particular, does not vanish at Tcc. Liquid density ρ, which also appears in eqn. (11), is expected to change rapidly in the vicinity of a true critical point23 and if capillary liquid density differs significantly from that of bulk liquid then anomalous values for both pore volume and pore radius should be evident, especially near Tcc. Neither anomaly is observed which suggests that capillary condensate at T[thin space (1/6-em)]>[thin space (1/6-em)]Tcc is liquid-like with surface tension and density essentially the same as bulk liquid over the entire temperature range, 195 K to 280 K. Since fugacity at the capillary critical point is less than fugacity at saturation pressure, the capillary condensate at this point should have a curved (hemispherical) liquid–vapour interface with the pressure difference, P(vapour)[thin space (1/6-em)]−[thin space (1/6-em)]P(liquid), given by the Laplace equation
 
ΔP[thin space (1/6-em)]=[thin space (1/6-em)]P(vapour)[thin space (1/6-em)]−[thin space (1/6-em)]P(liquid)[thin space (1/6-em)]=[thin space (1/6-em)]2γ/(rp[thin space (1/6-em)]−[thin space (1/6-em)]1.5t)(13)
where rp[thin space (1/6-em)]−[thin space (1/6-em)]1.5t is the radius of curvature of the hemispherical interface (see eqn. (11)). Therefore pressure within the liquid at the capillary critical point is ca. −9.30 MPa and the corresponding bulk phase pressure is 659 kPa.


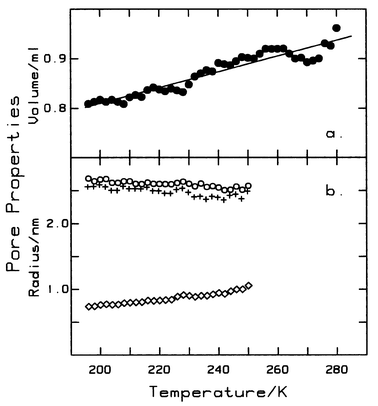(a) Pore volume, estimated by extrapolation of the plateau region to saturation pressure. The solid line represents values calculated from eqn. (8). Shortened plateau regions lead to increased scatter at higher temperatures. (b) Pore radii and film thickness; ○, pore radii calculated for the top and, +, for the bottom of each isotherm step. The difference between these two values is nearly constant, ca. 0.12 nm, showing that the range of pore sizes is very narrow. Also shown is the film thickness at the onset of each step (◇), as calculated from eqn. (12).
Fig. 5 (a) Pore volume, estimated by extrapolation of the plateau region to saturation pressure. The solid line represents values calculated from eqn. (8). Shortened plateau regions lead to increased scatter at higher temperatures. (b) Pore radii and film thickness; ○, pore radii calculated for the top and, +, for the bottom of each isotherm step. The difference between these two values is nearly constant, ca. 0.12 nm, showing that the range of pore sizes is very narrow. Also shown is the film thickness at the onset of each step (◇), as calculated from eqn. (12).

If pore-filling by first-order capillary condensation occurs only at temperatures less than Tcc, and if capillary fluid is liquid-like at higher temperatures, then for T[thin space (1/6-em)]>[thin space (1/6-em)]Tcc capillary condensation must proceed by a second-order process. Support for this model is provided by the adsorption isosteres (Fig. 2) and the isosteric heat of adsorption, qst, as a function of the amount adsorbed (Fig. 6). The former show no discontinuity at Tcc and the latter show that qstvs.nt, above and below the capillary critical temperature are essentially the same. There are three well-defined stages in the overall adsorption process; (i) mono-, multilayer formation at low coverage, with qst decreasing as the amount adsorbed increases, (ii) an exothermic peak as capillary condensation occurs, and (iii) decrease of qst to the enthalpy of evaporation of bulk liquid HFE as adsorption approaches saturation pressure. Similar heat–coverage curves have been reported by others.29


Isosteric heats of adsorption. This figure is derived from isosteres, such as those shown in Fig. 1. The dashed horizontal line indicates the enthalpy of vaporization of HFE.
Fig. 6 Isosteric heats of adsorption. This figure is derived from isosteres, such as those shown in Fig. 1. The dashed horizontal line indicates the enthalpy of vaporization of HFE.

With other silicas capillary condensation/evaporation almost invariably is accompanied by hysteresis, which vanishes only at the capillary critical temperature, Tcc. This point is well described by the equation6,9

 
Tcc[thin space (1/6-em)]=[thin space (1/6-em)]Tc[1[thin space (1/6-em)]−[thin space (1/6-em)]de/Rp](14)
When applied to the present results, this equation predicts a Tcc near 230 K, however hysteresis is absent even at temperatures as low as 195 K. It is not clear why this is so, but we note that pore size, more usefully expressed as reduced pore radius, Rp/de, appears to govern the occurrence of hysteresis in MCM-41 with hysteresis becoming common for adsorbents having larger reduced pore radii.22 It is our intention to continue work with this adsorbent using other adsorptives.

5 Conclusions

Capillary condensation of hexafluoroethane in this MCM-41 silica proceeds by a first-order process for T[thin space (1/6-em)]<[thin space (1/6-em)]255 K and by a second-order process at higher temperatures. Throughout the entire temperature range, 195 K to 280 K, capillary liquid has essentially the same properties as bulk liquid HFE and does not exhibit exceptional properties at the capillary critical point. The width of the pore size distribution determines the slope of the abrupt step in the isotherm at T[thin space (1/6-em)]<[thin space (1/6-em)]Tcc, and the step slope becomes equal to the slope of the critical isotherm at the capillary critical point. This implies that the range of pore sizes, as well as their absolute values, influence the extent of the first-order capillary condensation process and the location of the capillary critical point.

Acknowledgements

This work was supported in part by a grant from the Natural Sciences and Engineering Research Council of Canada.

References

  1. S. J. Gregg and K. S. W. Sing, in Adsorption, Surface Area and Porosity, Academic Press, New York, 2nd edn., 1982 Search PubMed.
  2. C. H. Amberg, D. H. Everett, L. H. Ruiter and F. W. Smith, in Solid/Gas Interface, Proceedings of the Second International Congress of Surface Activity, Academic Press, New York, 1957, vol. 2, pp. 3–16 Search PubMed.
  3. C. G. V. Burgess, D. H. Everett and S. Nuttal, Pure Appl. Chem., 1989, 61, 1845–1852 CAS.
  4. P. C. Ball and R. Evans, Langmuir, 1989, 5, 714–723 CrossRef CAS.
  5. W. D. Machin and P. D. Golding, J. Chem. Soc., Faraday Trans., 1990, 86, 175–179 RSC.
  6. R. Evans, U. M. B. Marconi and P. Tarazona, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 1763–1787 RSC.
  7. R. Evans, J. Phys.: Condens. Matter, 1990, 2, 8989–9007 Search PubMed.
  8. M. Thommes and G. H. Findenegg, Langmuir, 1994, 10, 4270–4277 CrossRef.
  9. W. D. Machin, Langmuir, 1999, 15, 169–173 CrossRef CAS.
  10. K. J. Edler, P. A. Reynolds, J. W. White and D. Cookson, J. Chem. Soc., Faraday Trans., 1997, 93, 199–202 RSC.
  11. C.-F. Cheng, D. H. Park and J. Klinowski, J. Chem. Soc., Faraday Trans., 1997, 93, 193–197 RSC.
  12. P. J. Branton, P. G. Hall and K. S. W. Sing, J. Chem. Soc., Chem. Commun., 1993, 1257–1258 RSC.
  13. P. J. Branton, K. S. W. Sing and J. W. White, J. Chem. Soc., Faraday Trans., 1997, 93, 2337–2340 RSC.
  14. K. Morishige, H. Fujii, M. Uga and D. Kinukawa, Langmuir, 1997, 13, 3494–3495 CrossRef CAS.
  15. P. J. Branton, D. G. Hall and K. S. W. Sing, in Characterisation of Porous Solids (IV), ed. B. McEnaney, T. J. Mays, J. Rouquerol, F. Rodriguez-Reinoso, K. S. W. Sing and K. K. Unger, Royal Society of Chemistry, Cambridge, 1997, pp. 98–102 Search PubMed.
  16. W. D. Machin and P. D. Golding, J. Chem. Soc., Faraday Trans., 1990, 86, 175–179 RSC.
  17. W. D. Machin, Langmuir, 1994, 10, 1235–1240 CrossRef CAS.
  18. R. J. Murdey and W. D. Machin, Langmuir, 1994, 10, 3842–3844 CrossRef CAS.
  19. W. D. Machin, Langmuir, 1999, 15, 169–173 CrossRef CAS.
  20. J. J. Hurly, Int. J. Thermophys., 1999, 20, 455–484 CAS.
  21. B. D. Smith and R. Srivastava, Thermodynamic Data for Pure Compounds, Part B, Elsevier, New York, 1986, p. 232 Search PubMed.
  22. F. Rouquerol, J. Rouquerol and K. Sing, in Adsorption by Powders and Porous Solids, Academic Press, London, 1999, pp. 415–425 Search PubMed.
  23. J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, in Molecular Theory of Gases and Liquids, John Wiley, New York, 1954, p. 362 Search PubMed.
  24. M. E. Fisher, J. Math. Phys., 1964, 5, 944–962 CrossRef.
  25. W. D. Machin and J. T. Stuckless, J. Chem. Soc., Faraday Trans. I, 1985, 81, 597–600 RSC G.H.
  26. G. H. Findenegg and M. Thommes, NATO ASI Ser., Ser. C, 197, 151–179 Search PubMed.
  27. D. Ben-Amotz and D. R. Herschbach, J. Phys. Chem., 1990, 94, 1038–1047 CrossRef CAS.
  28. C. L. Yaws, H.-C. Yang and X. Pan, Chem. Eng. (N. Y.), 1991, 98, 140–142, 144, 146, 148, 150 Search PubMed.
  29. P. L. Llewellyn, C. Sauerland, C. Martin, Y. Grillet, J. P. Coulomb, F. Rouquerol and J. Rouquerol, in Characterisation of Porous Solids IV, ed. B. McEnaney, T. J. Mays, J. Rouquerol, F. Rodriguez-Reinoso, K. S. W. Sing and K. K. Unger, Royal Society of Chemistry, Cambridge, 1997, pp. 111–117 Search PubMed.
This journal is © the Owner Societies 2003
Click here to see how this site uses Cookies. View our privacy policy here.