Ultrafast [2 + 2]-cycloaddition in norbornadiene

Abstract

Excitation of norbornadiene (bicyclo[2.2.1]hepta-2,5-diene) at 200 nm populates two states in parallel, the second ππ* state and a Rydberg state. We monitored both populations by transient nonresonant ionization. From the ππ* state the molecule relaxes in consecutive steps with time constants 5, 31 and 55 fs down to the ground-state surface, whereas the Rydberg population merges to the other path on the ππ* surface within 420 fs. The relaxation steps are discussed in terms of conical intersections (CoIns) between different surfaces. Information on them is inferred from known spectroscopy and, for the last CoIn, from published calculations on Dewar benzene→prismane conversion and on ethylene photodimerization for which norbornadiene with its two nonconjugated double bonds is a model. The calculation predicts symmetry breaking for this CoIn, the two ethylenes forming a rhombus. Although this distortion is hindered in norbornadiene by ring strain, this CoIn seems easily accessible as indicated by the short time (<55 fs) found for passing through it.

---

1 Introduction

Norbornadiene (bicyclo[2.2.1]hepta-2,5-diene, NBD in Scheme 1) is the prototype of a nonconjugated diene showing through-space interaction of the two double bonds. Its two ethylenic units are fixed in a spatial arrangement which seems to favor photochemical [2 + 2]-cycloaddition. The expected quadricyclane (tetracyclo[3.2.0.0^2,7.0^4,6]heptane, “Q”) is in fact the dominant photoproduct.¹ (For a review including derivatives see ref. 2.) In this work we investigate norbornadiene as a unimolecular model for photodimerization of ethylene and its derivatives. This is one of the textbook examples of pericyclic reactions photochemically allowed by the Woodward–Hoffmann rules (see e.g. ref. 3). It has been established by the work of Olivucci and co-workers that such nonadiabatic reactions pass through a conical intersection (CoIn) between the S₁ and S₀ potential energy surfaces, and that such CoIns generally control the photochemical pathways.⁴ Experimental work showed that many pericyclic CoIns are easily accessible, i.e. without energy of activation, giving rise to ultrafast processes.^5,6 In contrast to the assumption used in the derivation of the Woodward–Hoffmann rules, the molecular geometry at the CoIn in ethylene dimerization is not rectangular but distorted to a rhombus.^7,8 In view of the stiffness of norbornadiene, such a deformation may be expected to give rise to some activation energy. In the present experiment we found, however, a depopulation time of the S₁ state that is too short to be compatible with any substantial barrier. This result will also be discussed in view of the CoIn calculated for photochemical Dewar benzene→prismane conversion.⁹ This pair of molecules differs from norbornadiene and quadricyclane just by the lack of the CH₂ bridge.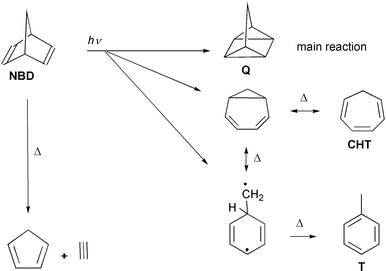

Scheme 1 Photochemical (arrows labelled with hν) and thermal reactions (Δ) of norbornadiene with supposed intermediates. The abbreviation NBD indicates norbornadiene, Q quadricyclane, CHT cycloheptatriene and T toluene.

The intramolecular [2 + 2]-photocycloaddition of norbornadiene is observed as the main photoreaction in solution,¹ but only to a minor extent (3% quantum yield¹⁰) in the gas phase where the dominating reaction is of the retro-Diels–Alder type, forming acetylene + cyclopentadiene.^11,12 We ascribe this fragmentation to a reaction in the hot ground state of the reactant (after internal conversion) or of a photoproduct, invoking collisional cooling to explain why it is largely suppressed in solution. Two more photoproducts, cycloheptatriene and toluene, are observed in small yield which is the same in the gas phase and in solution;^11,12 they must be attributed to photochemical (side) reactions competing with the [2 + 2]-addition.

The UV spectroscopy of norbornadiene has been carefully studied, with assignments being supported by CASPT2 calculations.^13,14 The two ethylenic double bonds give rise to two occupied π orbitals, the higher one (HOMO) belonging to the b₁ species in C_2v symmetry (antisymmetric combination of the two ethylenic contributions), whereas the lower unoccupied π-MO (LUMO) has b₂ symmetry¹⁴ (Scheme 2). The longest-wavelength transition is a weak diffuse band with a maximum at 236 nm; it corresponds to the symmetry-forbidden HOMO→LUMO (“first valence”, V₁) excitation of an A₂ state. This band was excited in most photochemical experiments. The next valence state (V₂, B₂ symmetry) is a superposition of the ππ*-excitations a₁→b₂ and b₁→a₂; the V₂ band is also weak and diffuse with a maximum near 213 nm and the 00 transition at 46290 cm⁻¹. It is superimposed by a Rydberg band [R(3s), B₁ symmetry, 00 transition at 45260 cm⁻¹] with extended vibrational structure, involving excitation of the HOMO to the Rydberg 3s orbital.

Scheme 2 Occupied and unoccupied π orbitals of norbornadiene composed of the localized ethylenic orbitals π_a and π_b of norbornadiene.

We investigated the dynamics of norbornadiene after excitation at 200 nm which populates both the R(3s) and V₂ states. Probing was carried out by ionizing with intense 800 nm pulses, detecting the yields of the ions mass-selectively. This nonresonant transient ionization has previously elucidated the dynamics also far from the Franck–Condon region (see e.g. the reviews in refs. 6 and 15). Also in the present case we were able to monitor the flow of population (in fact, of the populations of both initial states) all along the potential energy surfaces down to the ground state. Easily accessible conical intersections must be postulated to rationalize the ultrashort times found.

The molecule has already been investigated by transient ionization.^16,17 Excitation was by two 4 eV photons. The signals were interpreted in terms of two parallel retro-Diels–Alder reactions, one stepwise and one concerted. We suggest that an interpretation similar to ours is also appropriate for this experiment.

2 Experimental

The molecules were pumped in the gas phase at room temperature by a frequency-quadrupled pulse of a Ti–sapphire laser system (200 nm, 150 fs, 10⁹ W cm⁻²) and then probed by nonresonant multiphoton dissociative ionization at the fundamental wavelength (800 nm, 110 fs, 10¹³ W cm⁻²). The two beams were linearly polarized at an angle of 55° (“magic angle”) between each other in order to avoid time dependences induced by molecular rotation. The yields of the parent and fragment ions were measured mass-selectively as functions of the pump–probe delay time. In each pulse two ion signals were measured simultaneously by two boxcar integrators: not only an ion from norbornadiene (see Results), but also Xe⁺ which is due to nonresonant (1 + 4)-multiphoton ionization of Xe; it gives the time zero—the maximum of the Gaussian fit function—with a precision of ±1 fs and serves for synchronization of different scans with an accuracy of ± 2 fs. This error was found for the reproducibility from run to run in typically 10 runs. Although this high precision was necessary for distinguishing the different observation windows, it is worth noting that the exact positions and energetic limits of these windows on the potential surfaces are not known.

The shape of the Xe⁺ signal is expected to reflect the convolution of the 200 nm pulse with the fourth power of the 800 nm pulse. The shape (Gaussian) and width of the latter are known, so that the width of the former could be calculated. Ionization from the Franck–Condon region of norbornadiene requires two probe photons (energy 1.55 eV; the pump photon has 6.2 eV and the ionization energy is 8.69 eV^18,19), so that for the instrumental function we expect a Gaussian with a full width at half maximum of 163 fs resulting from convolution of the pump with the square of the probe. It is slightly broader than the Xe⁺ signal. For lower-energy locations (e.g., when the system reaches the ground state of the product) and a corresponding higher order of ionization, the instrumental function is again slightly narrower. These calculated functions, convoluted with exponentials (see Results), were used for fitting; varying the widths did not improve the fits.

All time constants were independent of the probe intensity which was varied by a factor of 3. The effective order for generating the parent ion by the probe was 2, as expected. The shape of the signals including the ratio of peak to pedestal (nonvanishing long-time signal) also did not depend on the pump intensity (varied by a factor of about 3). This is especially important for the pedestal and proves that it is produced by a single pump photon. At higher pump intensity it would be conceivable that two pump photons give rise to parent ions which are then photofragmented by the probe. This kind of pedestal in a fragment ion signal would not have a neutral precursor generated by 6.2 eV excitation, whereas in our experiment it has.

The experimental setup, special features of transient dissociative ionization including the effective time resolution and the method of assignment are discussed in ref. 20 in less detail, and also in refs. 5, 21 and 22, and are briefly reviewed in refs. 23 and 24.

Norbornadiene was used as commercially available (Fluka, stated purity 97%). A sample taken from the gas phase showed no impurity above 0.5% in gas-chromatographic mass-spectroscopic analysis.

3 Results

A typical time-of-flight mass spectrum observed 48 fs after the pump pulse is given in Fig. 1. Around this delay time, fragmentation is maximal. We investigated the signals C₇H₈⁺ (mass 92), C₇H₇⁺ (91), C₅H₆⁺ (66) and C₃H₄⁺ (40). The strongest peak (normalized to 1) is the parent ion (mass 92). The next strongest has mass 91 and an abundance of 0.12. The other investigated signals have intensities of 2 × 10⁻² (mass 66) and 10⁻⁴ (mass 40).

Fig. 1 Transient mass spectrum of norbornadiene recorded by photoionization by 800 nm at 48 fs after pumping at 200 nm. At this delay time, fragmentation reaches its maximum. The ion yields are normalized to the parent ion (mass 92).

The transient signals for three of these ions and for Xe⁺ (yielding the time zero and an indication of the instrumental function) are given in Fig. 2; mass 66 is not shown as it practically coincides with mass 91. All signals from a single neutral precursor (location on the potential energy surfaces) would be proportional to each other; obviously several such locations must be assumed, since the signals do not at all coincide. This is demonstrated, for instance, by the shift of the signal maxima, which are at 15, 55, 55 and 88 fs for masses 92, 91, 66 and 40, respectively.

Fig. 2 Time-resolved signals for norbornadiene. The signal for mass 66 (not shown) practically coincides with that for mass 91. The Xe⁺ signal gives the time zero and approximately the instrumental function. The upper three panels show how the signal is decomposed into contributions from paths 1 and 2; the residue (second panel) results from the full signal (first panel) by subtracting the curve (single exponential with convolution, broken line) fitted to its tail. See text for the functions (broken lines “path 2”) fitted to the residues. The mass 40 signal does not decay to 0 but to a “pedestal” of about 1% of the maximum (not visible on this scale).

For evaluation, we assume that the molecule reaches several locations (observation windows) i on the potential energy surfaces with lifetime τ_i. Since these times turn out to be very short, the transit time through the window gives a significant contribution to τ_i. Therefore, we do not distinguish the terms “lifetime” (time constant) and “traveling (transit) time”. The signals are then expressed as a sum of exponentials (with time constants τ_i) convoluted with the (Gaussian) pump and probe pulses. The exponential part of each signal is proportional to a linear combination of the time-dependent populations of each window, the coefficients containing the cross-sections ^mσ_i to produce an ion of mass m from window i. Each population is itself a sum of exponentials. Such sums result from rate equations for populations in locations connected by processes that are either consecutive or parallel or a combination of them. The fit procedure has been described in detail in ref. 20. In the following we only describe a modification specific to the given case.

Whereas the time constants, evaluated assuming consecutive or parallel processes, are the same, only the interpretation of the coefficients is different. We did not try evaluation with a purely consecutive model since it is known that excitation at 200 nm (pump laser) populates two states in parallel with roughly equal probability:¹³ a valence-excited state (V₂) and the Rydberg R(3s) state, the latter having the longer lifetime. This spectroscopic work also showed evidence that the R(3s) population is depleted to V₂,¹³ that is, the two initially separate paths merge on the V₂ surface. From bandwidths and comparison with two-photon ionization the R(3s)→V₂ relaxation can be estimated to take a time of the order of 1 ps [extrapolated from Fig. 9 of ref. 13 considering also the bandwidth assumed for their eqn. (1)] and the further decay to be faster.¹³ Therefore, we can expect that the R(3s) population gives rise to a signal (or signals, one of them being the parent ion) decaying with a long lifetime τ₁ (∼1 ps) and that each (fragment) signal from the subsequent locations shows the same time constant since the first step is rate determining. Indeed, all of the signals have a tail decaying with the same rate of (420 fs)⁻¹. Therefore, we can decompose all the signals into two contributions: paths 1 and 2. Path 1 describes the population flow from the R(3s) level, and the corresponding fraction is evaluated from the slow singly exponential decay (τ₁ = 420 fs) of each signal. The early part of this path 1 contribution to the signals is then calculated by convoluting this decay with the instrumental function (pump–probe correlation, see Experimental). The result (lines “path 1” in Fig. 2) is subtracted from the full signals. The residue (shown for mass 92 in the second panel of Fig. 2) is the contribution from path 2 that represents the flow of population from optical excitation of the V₂ state.

Whereas from path 1 we can extract only one time constant (τ₁), three additional ones (τ₂–τ₄) are found for path 2. They are deduced from the four residues, are much shorter than τ₁, as expected, and are consistent with consecutive population of four locations, the first one being obviously the Franck–Condon region of V₂ and the last one having “infinite” (τ₅ > 500 ps) lifetime; the latter time is obtained from the constant pedestal (very weak, not visible on the scale of Fig. 2) of the mass 40 signals (the heavier masses decay to 0), which contain contributions from both paths.

The value of τ₂ (5 fs) is obtained from simulating (with a singly exponential decay convoluted with the Gaussian instrumental function) the residue of the parent-ion signal (dotted line in Fig. 2). The fragment signals with masses 91 and 66 have identical time dependence; the two residues can be fitted with a triple exponential (with convolution), containing a main component with τ₃ = 31 fs, in addition to two weak components with τ₂ and τ₄. In a similar way, the main contribution to the residue signal of mass 40 is from the fourth window (τ₄ = 55 fs).

Table 1 summarizes the time constants τ_i and “contributions to the signal strengths” ^mc_i(j) resulting from these simulations. These “contributions” are products of ionization cross sections ^mσ_i with the relative populations p_j flowing in paths j = 1 and 2. The second line gives the lifetimes τ_i of the locations L_i. The columns below locations L₃–L₅ giving ^mc₃ − ^mc₅ are subdivided into contributions from paths 1 and 2. In fact, the curves 1 (Fig. 2) simulating the tails with time constant 420 fs only depend on the sum ^mc₃(1) + ^mc₄(1) + ^mc₅(1). The cross sections ^mσ_i (i = 3–5) must be identical for both paths since the same locations are involved. Therefore, we distributed the 420 fs signal contributions (path 1) over L₃–L₅ in the same ratio as in the residue signals (path 2); i.e., ^mc₃(1) ∶ ^mc₄(1) ∶ ^mc₅(1) = ^mc₃(2) ∶ ^mc₄(2) ∶ ^mc₅(2). Then the ratio p₁/p₂ of populations flowing in the two paths can be taken from ^mc_i(1)/^mc_i(2), i = 3–5. We find a value of 1.8 ± 0.3 for all fragments m. Using this ratio, we can also calculate from the signal contributions of the earlier locations L₁ and L₂ the ratio of ionization cross sections to be ⁹²σ₁/⁹²σ₂ ≈ 8.8×10⁻³.

Table 1 Lifetimes τ_i of the locations i on the potential energy surface and contributions ^mc_i(j) to selected ion signals (mass m, given with the formula) from paths j = 1 and 2. The error limits of τ_i are the standard deviations of the values determined in >10 runs from the fits described in the text

i	1	2	3		4		5
τ i /fs	420 ± 50	5 ± 5	31 ± 7		55 ± 7		>50 × 10^3
	Path 1	Path 2	Path 1	Path 2	Path 1	Path 2	Path 1	Path 2
C7H8^+ (92 u)	0.016	1.0	0	0	0	0	0	0
C7H7^+ (91 u)		0	1.0	0.55	0.108	0.061	0	0
C5H6^+ (66 u)		0	1.0	0.55	0.041	0.023	0	0
C3H4^+ (40 u)		0	0.102	0.075	1.0	0.55	0.0014	0.0008
400 nm:
C7H8^+ (20 °C)	0.413	1.0	0	0	0	0	0	0
(130 °C)	0.108	1.0	0	0	0	0	0	0

---

During the pump–probe overlapping time, and hence for the short time constants, one could worry that the high probe intensity may perturb the pump process. Therefore, we also compared the results with one-photon ionization at 400 nm at much lower intensity (≤10¹² W cm⁻²). It turned out that the time-resolved parent signal (that is, the only signal found under these conditions) was well fitted by the same two time constants (420 and 5 fs) as at the same mass with 800 nm probing. Only the ratio of ionization cross sections is much higher: ⁹²σ₁/⁹²σ₂ ≈ 0.23 at 400 nm. (As an explanation, we suppose that an intermediate resonance increases ⁹²σ₂ for two-photon ionization at 800 nm from location 2.) At higher temperature (∼130 °C) the ratio of contributions from path 1 to path 2 is reduced by a factor of 3.8, although the signals had the same time dependence at both temperatures. Since a spectrum is shifted to longer wavelength (and broadened) by heating, the reduction of this ratio indicates that excitation was indeed in the short-wavelength wing of the Rydberg band; thus any noticeable contribution from the long-wavelength wing of the next Rydberg band, R(3p), can be excluded.

4 Discussion

Although it is not necessary to know the mechanism of ionization and fragmentation in order to extract time constants from the measured data, such knowledge is helpful for assignment. In many molecules, fragmentation only occurs after ionization, and we assume this for the present case (see the discussion at the end of Section 4.3). Ionic fragmentation is caused by vibrational excess energy. There are three sources of such energy.²⁰

1. Electronic relaxation down the potential surfaces releases vibrational energy in the neutral molecule, and ionization transfers most of this energy to the ion; i.e., a hot neutral gives rise to a hot ion. Hence, the fragmentation pattern allows a rough estimation of the vibrational energy (and thus also the electronic energy, since the sum is constant) of the observation window in the neutral molecule. As long as this mechanism predominates, the observation windows are energy windows.

2. Vertical ionization from a strongly displaced location leads to a high-lying part of the ionic potential surface, and this excess energy can also contribute to fragmentation.

3. The ions themselves often have long-wavelength transitions and can absorb additional probe photons, thus giving rise to a distribution of excess energies and to a fragmentation pattern instead of a single fragment.

4.1 Assignment

As already inferred in Sections 1 and 3 from the absorption spectrum and as will be confirmed in this section, the pump pulse populates two states, namely R(3s) and V₂. The pathways of both populations must be assigned separately.

According to the principles above, the observation windows giving rise to the parent ions have the highest electronic energy (i.e., least amount converted to vibration) and cannot be much displaced compared with the ionic surface. We find two time constants from the parent ion, τ₁ = 420 and τ₂ = 5 fs (Table 1). The shorter one suggests a spectral (lifetime or dephasing) broadening of 1000 cm⁻¹ (see also below). Hence, it cannot belong to the Rydberg state, which shows pronounced vibrational structure in the spectrum with a width of about 100 cm⁻¹ (or 44 cm⁻¹ according to the analysis in ref. 13). Therefore, we assign τ₂ to a departure from the Franck–Condon region of the V₂ state (window or location L₂, start of path 2) and τ₁ to a departure from the R(3s) state (L₁, start of path 1). All the other times are much shorter than τ₁. They would not be observed if they belonged to pathway 1, i.e., to processes following departure from the R(3s) since otherwise the time dependence would be controlled by the rate-determining slowest step. Hence, the short times belong to path 2, and we will discuss this path first.

The next window (on path 2) with lifetime τ₃ = 31 fs must be lower in energy and/or shifted since no parent ion is observed from there. However, only a minor lowering and shift are needed since the parent ion only requires an excess energy of <0.9 eV for eliminating an H atom or acetylene molecule.²⁵ Therefore, we suggest that window 3 is still on the V₂ surface whose minimum is at 46290 cm⁻¹,¹³ 0.46 eV below the excitation energy, and is displaced in the C=C stretch direction compared with the ionic (and Rydberg) surface.¹³ (Note that the minimum of the Rydberg state has a similar energy, 45260 cm⁻¹,¹³ but the Rydberg surface is not shifted compared to the ionic surface, and the corresponding excess energy of 0.59 eV alone seems insufficient to fragment the ion.) The same considerations of energy and shift can be applied in order to rationalize why window 3 is not observed in probing by one-photon ionization at 400 nm (3.1 eV; ionization energy of norbornadiene: 8.7 eV^18,19). Also the width of spectral structure in the V₂ band agrees with this assignment: If L₃ were already on another surface, τ₂ = 5 fs would represent the V₂ lifetime which would cause a broadening of 1000 cm⁻¹, as mentioned. But a lifetime of τ₂ + τ₃ = 36 fs corresponds to a broadening of 140 cm⁻¹, compatible with the observed width of ∼300 cm⁻¹.¹³

In window 4 (τ₄ = 55 fs) fragmentation is substantially stronger than in the previous location: the ratio of signals of mass 40 and 66 increases by two orders of magnitude. Hence, this signal comes from a lower (possibly also shifted) state. On the other hand, this state is still excited since the signal decays to values near zero: After this decay (i.e., in L₅), the only detectable ion (mass 40) has decreased by three orders of magnitude; at this time obviously the ground state is reached, as can be concluded from the “infinite” (τ₅ > 500 ps) lifetime. The only excited state known from spectroscopy below those discussed is V₁. Its minimum seems to be around 4 eV or lower since the corresponding absorption band extends to about 300 nm. Therefore, we assign τ₄ to traveling along, and departure from, the V₁ surface. (For a modification, see Section 4.2.)

Path 1 describes the flow of population from the Rydberg state. The fact that we can detect only one time constant (τ₁) on this route does not imply that it is a one-step process. Generally, a path via shorter-lived intermediate states just shows the time behavior of the slowest step, as mentioned. Indeed, our signals provide evidence that the R(3s) state is depleted (within τ₁) to window 3, i.e., to the lower part of the V₂ surface from where the population then follows path 2. Within a given window (≥3) the fragmentation patterns (i.e., the ratios of the ion yields of the three fragments in the columns of the table) coincide for the two paths. This means that the signals belonging to the two paths originate from the same locations L₃–L₅ (or locations very similar in energy and shift) since fragmentation depends on the internal state. The previous evidence that R(3s) is depleted via V₂ came from UV spectroscopy in which the R(3s) lifetime was found to suddenly drop at an excess energy just sufficient to allow relaxation to the higher V₂ state.¹³

The assignment of the two pathways is summarized in Scheme 3. Whereas the horizontal represents the reaction coordinate (varying in direction), the vertical qualitatively indicates the electronic energy. For the unobserved parts (broken lines), see Section 4.2.

Scheme 3 Kinetic scheme showing that path 1 (beginning with τ₁) merges into path 2 (beginning with τ₂) just after the Franck–Condon region (FC) of the V₂ state. The electronic states are identified in Section 4.1, and S₁ is discussed in Sections 4.2 and 4.3. Broken lines indicate regions not directly detected. CoIn: conical intersection. See Scheme 1 for the abbreviations Q, NBD, T, CHT.

4.2 Pathways and potential energy surfaces

All transitions from surface to surface were found to take place in subpicosecond times. This is only possible if they pass through real crossings, i.e., through conical intersections (CoIns). τ₃ and τ₄ are even shorter than typical vibrational periods of backbone distortions. (100 fs would correspond to 333 cm⁻¹. For comparison: the wing-flapping vibration appearing in the R(3s) band has 375 cm⁻¹.) This means that in these cases the wave packet finds the outlet of the surface at the first attempt; in other words, the conical intersection is easily accessible, without any barrier.

However, the slightly longer τ₁ (420 fs) suggests that the R(3s)→V₂ relaxation (path 1) passes over a small barrier. This is in agreement with spectroscopic evidence for R(3s) lifetimes decreasing with excess energy.¹³ Although the lifetime of the lowest vibrational levels is long enough so that they could even give rise to observable fluorescence, it rapidly decreases above v = 4 of the wing-flapping vibration (deduced from band widths and comparison of one-photon absorption with resonance-enhanced multiphoton ionization). The spectroscopic barrier is thus just slightly larger than the energy difference (1030 cm⁻¹) of the two states. The observed band width of 44 cm⁻¹ at 200 nm is consistent with our τ₁ which would imply a lifetime broadening of 12 cm⁻¹. In spite of this agreement, we did not see any acceleration of this relaxation within the accuracy of 5% on heating to 130 °C. This probably means that the excess energy (∼0.5 eV) available in the wing-flapping mode is much more effective for R(3s)→V₂ relaxation than thermal (equipartitioned) energy would be. We also suggest that the relatively long time constant results in part not from activation energy but from entropy or a statistical factor which is temperature independent; such an effect can be expected since only one of the 39 internal coordinates can lead the wave packet around the lower cone of the CoIn. An entropy of activation for going around a conical intersection has previously been invoked for a charge-transfer reaction.²⁶ It may also be that the weakness of electronic interaction between Rydberg and valence states decreases the rate of radiationless transition between them.

The short time τ₁ + τ₂ = 36 fs assigned in Section 4.1 to the time of departure from V₂ indicates that there is no barrier before the outlet of the funnel (conical intersection). That is, there should be no dependence of lifetime and band width on excess energy, and the CoIn with V₁ should be near the V₂ minimum.

Generally, to rationalize the relaxation times, one should figure out the location of conical intersections, as already recommended in refs. 6 and 27 for instance. Unfortunately high-level quantum-chemical calculations for norbornadiene so far only concern the Franck–Condon region, and calculated surfaces are not available. But information is provided by the shifts derived from the spectra.¹³ Compared with the ground state, the Rydberg surface is mainly shifted in the direction of the wing-flapping mode, V₂ towards the C=C stretch (mixed with CH bending) and V₁ towards both. All these coordinates are totally symmetric (a₁). These shifts can be readily understood on the basis of the orbitals involved^13,14 (Scheme 2). On this basis one can figure out the potential energy curves shown in Fig. 3. All of the curves represent bottoms of valleys that are deep in the direction of the coordinate not indicated. The R(3s)/V₂ intersection implies a small activation energy, whereas the V₂/V₁ and V₁/S₀ intersections are near the V₂ and V₁ minima. In the subspace shown, the intersections would appear as lines. In fact, they are conical; for the second coordinate of the branching space one usually chooses the nonadiabatic coupling vector,²⁸ which is identical with the direction of strongest vibronic interaction of each state pair. It must have the symmetry species a₂, b₁ and a₂ in the three cases, respectively. Spectroscopic evidence indicates that the strongest R(3s)/V₂ interaction occurs along the a₂ mode of lowest-frequency¹³ that involves twisting of the six-membered ring.²⁹ As mentioned in the Introduction, according to calculations on ethylene dimerization, the S₁/S₀ CoIn is displaced from a symmetric geometry into another a₂ direction that involves a parallel shift of the two ethylenes against each other;^7,8 without such symmetry breaking, the excited- and ground-state surfaces do not come close enough together. In the S₁/S₀ CoIn calculated for Dewar benzene, the displacement involves both a₂ coordinates (Fig. 2i and 3 of ref. 9).

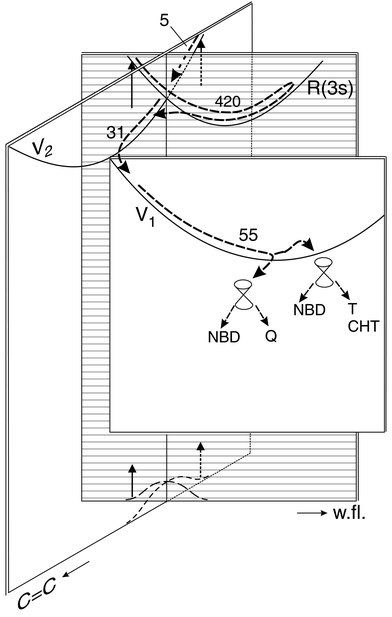Fig. 3 Suggested paths (numbers are times in fs) and potential energy surfaces (lines indicate bottoms of valleys). The two coordinates shown, both totally symmetric, are a C=C stretch mixed with CH bending and the wing-flapping (w.fl.) mode that causes the two ethylenic units to approach each other. In addition, each radiationless transition from surface to surface also requires an antisymmetric distortion (not shown). The initial excitation at 200 nm populates the R(3s) and V₂ states both beyond the Franck–Condon maximum; i.e., excitation starts from the wings of the S₀ vibrational wave function. The two paths merge on the V₂ surface. On V₁ there may be a branching towards two conical intersections (their displacements involve other coordinates) from where the products and the reactant are formed; however, between V₁ and these intersections, there may be a dark excited state (called S₁ in Scheme 3) that is not indicated here.

However, according to these calculations in the region of this CoIn the lowest excited state (S₁) is not V₁, but a two-electron excited state of A₁ symmetry.^7,8 Therefore, the path from V₁ to S₀ is not direct but passes (via a CoIn) through the S₁ (2A₁) state and from there (via a final CoIn) to S₀. This intermediate state is possibly not detected or distinguished from V₁ since it may have a similar energy or—more probably—because it may have a shorter lifetime. In order to avoid overloading, we have not shown the S₁ state in Fig. 3, although it is indicated in Scheme 3. The V₁/S₁ CoIn requires for symmetry reasons an a₂ distortion for the second coordinate, and according to the calculations^7,8 the subsequent S₁/S₀ CoIn is indeed displaced in an a₂ direction (rhombic distortion).

The two initial states are excited in the wings of their absorption bands; therefore the vertical arrows are drawn from the wing of the ground-state vibrational wave function. From the Rydberg state, path 1 leaves within τ₁ to the V₂ surface via a small barrier; passing below the intersection (as drawn) is enabled by an a₂ distortion. Then the wave packet joins path 1, traveling along and leaving from the V₂ surface within τ₃. Path 2 shows two observation windows on one surface. In previous cases where we observed such a phenomenon (e.g. in cyclohexadiene³⁰ or cycloheptatriene²²), a change of direction of motion was identified as the reason.

4.3 Relation to photochemistry

The last conical intersection can be associated with the main photochemical reaction, [2 + 2]-addition to form quadricyclane. In ethylene photodimerization, the upper state (S₁) is strongly lowered by symmetry breaking, resulting in a rhombic geometry with some 1–3 interaction.^7,8 In norbornadiene such an a₂ type distortion will cause ring strain that could cause a barrier or at least partially compensate the energy lowering of the S₁ (and V₁) state. (We note that another a₂ distortion also leads to 1–3 interaction and thus possibly contributes to decreasing the barrier: it corresponds to the mentioned a₂ mode that has the lowest frequency in S₀ and is a torsion of the six-membered ring.²⁹) Indeed, both a₂ displacements are involved in the S₁/S₀ CoIn calculated for Dewar benzene (see Fig. 2i and 3 of ref. 9). Furthermore, in ethylene dimerization the S₁ surface descends rather steeply on rhombic distortion, so that any added ring strain in the bicyclic compounds might not fully compensate this slope. Although on arriving at the V₁ or S₁ minimum the excess energy is rather large (∼2 eV), the short time (τ₄ = 55 fs and τ_S1 < 55 fs) for leaving the minimum implies that any barrier, if existent at all, must be minor. We suggest that the potential energy surface is rather flat in this region, a situation which can favor a branching of the path (see below).

It is interesting that the ring strain caused by such deformations can be mitigated by loosening or breaking the C(1)–C(7) bond. In fact, a barrier before the CoIn of Dewar benzene disappears when the bridge bond is included in the active space of the calculation. This bond is opened during the [1,3]-sigmatropic shift of the CH₂ bridge, a photochemical side reaction of norbornadiene (Scheme 1). The S₁/S₀ CoIn connected with this type of reaction has been calculated for a similar molecule, norbornene (bicyclo[2.2.1]hept-2-ene);³¹ the corresponding geometry involves a CH₂ group weakly bound to an allylic system containing the three carbons over which this group migrates. This calculation also suggests that one path on the lower cone of this CoIn can lead to complete breaking of this bond. In the case of norbornadiene, the CH₂ radical thus generated (Scheme 1) can be easily stabilized by a [1,2]-H shift on the ground-state surface to form toluene. So, we suggest that the path branches on the flat part of the S₁ (or V₁) surface, the main part going to a CoIn leading to [2 + 2]-addition (and to the reactant by branching at the CoIn) and the minor part to a CoIn that gives rise to (besides the reactant) a [1,3]-sigmatropic shift (primary product: bicyclo[4.1.0]hepta-2,4-diene = norcaradiene, which very rapidly rearranges to cycloheptatriene with an activation energy near zero,³² see Scheme 1) and to a diradical rearranging to toluene. The alternative that toluene is formed in the hot ground state of cycloheptatriene (see Scheme 1 and e.g. refs. 22 and 33 and the literature quoted therein) can be excluded since toluene formation is not suppressed or reduced in solution.^11,12

In contrast, formation of cyclopentadiene + acetylene in a retro-Diels–Alder reaction is reduced by a factor of 4 on going from the gas phase to solution.^11,12 The obvious interpretation is that this reaction takes place in the hot ground state of norbornadiene, formed along with the products from the S₁/S₀ conical intersections, and from hot quadricyclane. For both molecules this is the reaction of lowest activation energy.³⁴ (Roquitte assumed a reaction in a hot excited state instead.¹¹ But according to our data, these states are too short-lived so that cooling by a solvent cannot compete and there should be no solvent effect on this mechanism.) The reaction probably takes place in the range from tens to hundreds of picoseconds since it can in part compete with cooling in solution (which takes the order of 10 ps, see e.g. ref. 35). Our mass 40 signal is completely flat in the investigated region to 500 ps; however, we did not try hard to detect the process in this very weak signal. (In this region, it has only 10⁻⁶ of the maximum intensity of the parent, for instance.) Hence, from our data alone, we cannot exclude that there might also be a photochemical path for the retro-Diels–Alder reaction in addition to the thermal channel. However, in two similar cases, cyclohexene³⁶ and norbornene,³⁷ we showed that retro-Diels–Alder products were absent until at least 500 ps, a time long after the end of photochemical processes.

Previously, norbornadiene was excited to 8.1 eV by two photons at 307 nm and probed by ionization at 615 nm.^16,17 The signals decaying with time constants of 110 and 210 fs were interpreted in terms of retro-Diels–Alder splitting to cyclopentadiene + acetylene. However, the signal of mass 66 (cyclopentadiene⁺) practically coincides with that of mass 91; hence, obviously both signals have a larger neutral precursor than cyclopentadiene. As already described previously,^5,36,37 we suggest instead that the signals of refs. 16 and 17 reflect the decay of higher excited states of the intact molecule to lower ones (which are shorter-lived), from which normal photochemical reactions then take place.

5 Conclusion

It was already known from spectroscopy that the R(3s) state is depleted to the V₂ surface.¹³ Our data support the conclusion that the two paths merge on the V₂ surface and then pass through the same observation windows, as evidenced by the identical fragmentation patterns found in the corresponding windows of the two paths. It is remarkable that in path 1 we could monitor shorter-lived windows following the longer-lived Rydberg state; this was possible by comparison with path 2 (Section 3). However, the last window of both paths, the S₁ surface predicted by quantum chemistry, could not be detected probably just because its depletion is much faster than its population from the preceding V₁ surface. Nevertheless, it is reasonable to assume its existence and participation since models based on it have successfully explained slower photodimerizations and cycloadditions³⁸ (see also below). We expect that the participation of S₁ can be checked if less excess energy is deposited by pumping at longer wavelength, e.g., around 240 nm within the V₁ band.

The lifetimes found could be rationalized by conical intersections whose positions were mainly inferred from spectroscopic information. The longest, but still subpicosecond, time is that for R(3s)→V₂ relaxation. It was explained by a small activation energy and entropy along the path surrounding the lower cone of the R(3s)/V₂ CoIn. All the other processes occur with maximum rate, i.e., within a time shorter than a period of an appropriate vibration. This means that the corresponding CoIns are accessible without any barrier. For the last step, transition to the ground state, this was a surprise since the predicted geometry at the CoIn will cause some ring strain in norbornadiene. We concluded that the S₁ surface is relatively flat before this CoIn and that branching on this plateau can also explain two photochemical side reactions. In fact, the calculation gives such a flat region for the Dewar benzene→prismane system before the last CoIn,⁹ whereas for ethylene dimerization a rather steep descent is found in this region.^7,8

The model^3,38 that successfully explained (≥ nanosecond) photodimerization rates assumed that the two molecules (one of them excited) approaching each other first reach an excimer minimum. From there they climb over a barrier to a two-electron excited state (S₁) from where they relax to the ground state of product or reactant. This S₁ state correlates with two triplet-excited molecules at infinite distance. Considering the distance-dependent interaction between these two molecules allows an estimation of the location of the intersection between the S₁ and excimer surfaces. Low barriers are expected with low triplet and high singlet energies and if the electronic wave function is not very delocalized.³⁸ These prerequisites are found in norbornadiene. Realizing that the V₁ state can be considered as an excimer state—the transition dipole vectors of the two ethylenic units being coupled out of phase, resulting in an A₂ state—the model indeed seems applicable. It should only be supplemented by considering ring strain of the backbone.

Although there exist some photocycloadditions that take nanoseconds and longer³⁸ (owing to the mentioned barrier), subpicosecond times for dimerizations are not at all limited to norbornadiene, although a direct measurement has not been possible so far. For instance, in the case of cyclohexadiene²⁰ we argued that dimerization (which was observed) can only compete with the ultrafast unimolecular reactions of these molecules if it has a comparable rate.

References

1. W. G. Dauben and R. L. Cargill, Tetrahedron, 1961, 15, 197.
2. K. Maruyama and Y. Kubo, in Organic Photochemistry, edited by W. M. Horspool and P.-S. Song, CRC Press, Boca Raton, 1995, p. 222.
3. M. Klessinger and J. Michl, Excited states and photochemistry of organic molecules, VCH, New York, 1995.
4. F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321.
5. W. Fuß, P. Hering, K. L. Kompa, S. Lochbrunner, T. Schikarski and W. E. Schmid, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 500.
6. W. Fuß, S. Lochbrunner, A. M. Müller, T. Schikarski, W. E. Schmid and S. A. Trushin, Chem. Phys., 1998, 232, 161.
7. F. Bernardi, S. De, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1990, 112, 1737.
8. F. Bernardi, M. Olivucci and M. Robb, Acc. Chem. Res., 1990, 23, 405.
9. I. J. Palmer, M. Olivucci, F. Bernardi and M. A. Robb, J. Org. Chem., 1992, 57, 5081.
10. N. Ivanoff, F. Lahmani, J. F. Delouis and J. L. Le Gouill, J. Photochem., 1973/74, 2, 199.
11. B. C. Roquitte, J. Phys. Chem., 1965, 69, 2475.
12. B. C. Roquitte, J. Am. Chem. Soc., 1963, 85, 3700.
13. X. Xing, A. Gedanken, A.-H. Sheybani and R. McDiarmid, J. Phys. Chem., 1994, 98, 8302 and references cited therein.
14. B. O. Roos, M. Merchán, R. McDiarmid and X. Xing, J. Am. Chem. Soc., 1994, 116, 5927 and references cited therein.
15. W. Fuß, S. A. Trushin and W. E. Schmid, Res. Chem. Intermed., 2001, 27, 447.
16. B. A. Horn, J. L. Herek and A. H. Zewail, J. Am. Chem. Soc., 1996, 118, 8755.
17. E. W.-G. Diau, S. De Feyter and A. H. Zewail, Chem. Phys. Lett., 1999, 304, 134.
18. R. P. Frueholz, W. F. Flicker, O. A. Mosher and A. Kuppermann, J. Chem. Phys., 1979, 70, 1986.
19. G. Bieri, F. Burger, E. Heilbronner and J. P. Maier, Helv. Chim. Acta, 1977, 60, 2213.
20. W. Fuß, W. E. Schmid and S. A. Trushin, J. Chem. Phys., 2000, 112, 8347.
21. S. A. Trushin, W. Fuß and W. E. Schmid, Phys. Chem. Chem. Phys., 2000, 2, 1435.
22. S. A. Trushin, S. Diemer, W. Fuß, K. L. Kompa and W. E. Schmid, Phys. Chem. Chem. Phys., 1999, 1, 1431.
23. W. Fuß, W. E. Schmid and S. A. Trushin, Indian Soc. Radiat. Photochem. Sci. Bull., 2000, 11, 7.
24. S. A. Trushin, W. E. Fuß, K. K. Pushpa and W. E. Schmid, Study of ultrafast chemical dynamics by intense-laser field dissociative ionization, Minsk, Proc. SPIE, 2001, in the press.
25. S. Meyerson, J. D. McCollum and P. N. Rylander, J. Am. Chem. Soc., 1961, 83, 1401.
26. W. Rettig and G. Wermuth, J. Photochem., 1985, 28, 351.
27. W. Fuß, Y. Haas and S. Zilberg, Chem. Phys., 2000, 259, 273.
28. G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 1862.
29. R. A. Shaw, C. Castro, R. Dutler and H. Wieser, J. Chem. Phys., 1988, 89, 716.
30. M. Garavelli, C. S. Page, P. Celani, M. Olivucci, W. E. Schmid, S. A. Trushin and W. Fuß, J. Phys. Chem. A, 2001, 105, 4458.
31. S. Wilsey, K. N. Houk and A. H. Zewail, J. Am. Chem. Soc., 1999, 121, 5772.
32. M. Rubin, J. Am. Chem. Soc., 1981, 103, 7791.
33. U. Hold, T. Lenzer, K. Luther, K. Reihs and A. Symonds, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 552.
34. Z. Li and S. L. Anderson, J. Phys. Chem. A, 1998, 102, 9202.
35. J. Benzler, S. Linkersdörfer and K. Luther, J. Chem. Phys., 1997, 106, 4992.
36. W. Fuß, W. E. Schmid and S. A. Trushin, J. Am. Chem. Soc., 2001, 123, 7101.
37. W. Fuß, K. Pushpa, W. E. Schmid and S. A. Trushin, J. Phys. Chem. A, 2001, 105, 10640.
38. R. A. Caldwell, J. Am. Chem. Soc., 1980, 102, 4004.

---