Nondegenerate equilibrium in (2-propyl)cycloalkyl cations. Comparison of (2-propyl)cyclopentyl and (2-propyl)cyclohexyl cation using ¹³C NMR spectroscopy, equilibrium isotope effects and quantum chemical calculations

Abstract

Tertiary (2-propyl)cyclopentyl and (2-propyl)cyclohexyl carbocations were investigated by ¹³C NMR spectroscopy in superacid solution. Both ions undergo fast nondegenerate 1,2-hydride shifts to the corresponding 2-cycloalkyl-2-propyl cations. The direction of these equilibria depends on the size of the ring. The more stable isomer of the (2-propyl)cyclopentyl cation has the formal positive charge at the endocyclic carbon atom, while the more stable isomer of the (2-propyl)cyclohexyl cation has the formal charge at the exocyclic carbon atom. The dynamic NMR results were confirmed by NMR spectroscopic measurement of the equilibrium isotope effects and rationalized by quantum chemical calculations.

---

Introduction

Carbocations often show facile rearrangement reactions due to their shallow energy hypersurface. Typical examples for rapid nondegenerate rearrangements are 1,2-hydride shifts in tertiary carbocations A ⇋ B, such as in 2,3-dimethyl-3-pentyl cation, 2,3-dimethyl-2-hexyl cation¹ and in 2-aryl-3-methyl-2-butyl cations.²

Carbocations undergoing reversible rearrangements, which are fast relative to the NMR time scale, show NMR spectra with concentration weighted averaged chemical shifts for the interchanging sites. For a nondegenerate 1,2-hydride shift, such as A ⇋ B, the equilibrium constant K_eq = [B]/[A] ≠ 1 and two peaks are observed for all sites which are averaged by the fast hydride shift. These peaks show temperature dependent averaged chemical shifts. The peak for the carbocation center is shifted upfield and the peak for the β-carbon is shifted downfield compared to that of static carbocations.¹ In some carbocations nondegenerate equilibria have been detected by ¹H- and ¹³C-NMR spectroscopic methods, but often no details of those rearrangements are known.

We have investigated the 1,2-hydride shift equilibrium 1A ⇋ 1B of the 2-cyclopentyl-2-propyl cation 1A and the 1-(2-propyl)-cylopentyl cation 1B and the analogous rearrangement reaction 2A ⇋ 2B which equilibrates the 2-cyclohexyl-2-propyl cation 2A and the 1-(2-propyl)cyclohexyl cation 2B (Scheme 1) using high field ¹³C NMR spectroscopy, equilibrium isotope effects and quantum chemical calculations. Earlier NMR studies have indicated that the equilibrium 1A ⇋ 1B is moved toward the structure 1B in which the positive charge is located in the ring. On the contrary, for the equilibrium 2A ⇋ 2B the structure 2A with the positive charge on the exocyclic carbon was found to be more stable.^3,4

Scheme 1

The results we report in this study explain the different stabilities of alkyl-substituted five- and six-membered cycloalkyl cations 1B and 2B compared to the isomeric cycloalkyl-substituted 2-propyl cations 1A and 2A and give additional information on the stabilization modes and the structural and conformational consequences in these type of carbocations.

Results and discussion

The carbocations 1A/1B and 2A/2B and their isotopomers⁵ (1A-d₆/1B-d₆, 1A-d₄/1B-d₄, 2A-d₆/2B-d₆ and 2A-d₄/2B-d₄), as well as mixtures of deuterated and non-deuterated compounds were prepared from the corresponding alcohols with excess Lewis-acid SbF₅ and a 2 ∶ 1 mixture of SO₂F₂–SO₂ClF as solvent, using contemporary high vacuum matrix co-condensation techniques.⁶

The tertiary alcohols 1A–OH or 1B–OH, 1B-d₆–OH, 1A-d₄–OH, 2A–OH or 2B–OH, 2B-d₆–OH and 2A-d₄–OH, which were used as a precursors for the carbocations, were prepared by standard Grignard reaction from cyclopentyl- or cyclohexyl-chloride and acetone (1A–OH and 2A–OH) or acetone-d₆ (1A-d₆–OH, 2A-d₆–OH), and from β,β′-d₄-cyclopentanone or β,β′-d₄-cyclohexanone and 2-chloropropane (1B-d₄–OH, 2B-d₄–OH). ¹³C NMR spectra of the solutions of the carbocations were taken at different temperatures and assigned using standard techniques. Some representative spectra are shown in Fig. 1.

Fig. 1 ¹³C NMR spectra (100 MHz) of 1A/1B and 2A/2B in SO₂ClF–SO₂F₂ solution at selected temperatures.

Temperature dependent ¹³C NMR chemical shifts for 1A/1B and 2A/2B are given in Table 1.

Table 1 Temperature dependent ¹³C (100 MHz) NMR chemical shifts of cations 1A/1B and 2A/2B, and the corresponding equilibrium constants

		δ (ppm)
Cation	T/°C		C3,C4	C2,C5	C1	C1′	C2′,C3′	Δ = δ1 − δ1′ (ppm)	K obs ^a
a K obs = (δ1(A) − δ1′(A) + Δ)/(δ1(B) − δ1′(B) − Δ) where δ1′(A), δ1(A), δ1(B) and δ1′(B) are the calculated ^13C NMR chemical shifts (see Table 3) of the minimum energy structures 1A, 1B, 2A and 2B, respectively.
1A/1B	−127		26.73	58.61	332.73	64.24	20.76	268.50	28.97
	−120		2.71	58.33	329.73	66.86	21.04	259.99	21.38
	−112		26.70	58.08	326.55	69.78	21.34	256.77	16.56
	−105		26.70	57.76	322.48	73.42	21.74	249.06	12.81
	−97		26.67	57.38	318.27	77.21	22.06	241.06	10.24
	−86		26.67	56.97	315.56	79.88	22.54	235.68	7.16

---

		C4	C3,C5	C2,C6	C1	C1′	C2′,C3′
2A/2B	−122	24.78	25.87	35.34	81.67	316.20	42.46	−234.53	0.0131
	−115	24.76	25.91	35.55	83.89	314.01	42.22	−230.11	0.0222
	−106	24.72	25.86	35.81	86.59	311.18	41.94	−224.70	0.0336
	−99	24.69	26.02	36.04	89.04	308.65	41.67	−219.61	0.0442
	−86	24.63	26.15	36.51	94.28	303.27	41.12	−208.99	0.0676

---

The chemical shifts of the averaged signal of the interchanging sites depend on the equilibrium constant. The relative population of the two species A and B is given by the equilibrium constant K_eq = [B]/[A]. The averaged chemical shifts δ₁ and δ_1′ of the two peaks of a pair of carbons such as C1 and C1′ which are interchanged by the fast 1,2-hydride shifts are given in eqn. (1) and (2),

where δ₁(A) and δ_1′(A) represent the chemical shifts of carbons C1 and C1′ in the structure A, and δ₁(B) and δ_1′(B) represent the chemical shifts of the same carbons in the structure B. The equilibrium constant K_eq is obtained from the chemical shift difference Δ = δ₁ − δ_1′ for the two carbons according to eqn. (3).

Eqn. (3) can be applied to any two interchanging sites. If the chemical shift difference Δ between the two interchanging sites is small, however, the error of the equilibrium constant will be large. If an equilibrium is degenerate, structure A and B are identical, δ₁(A) − δ_1′(A) = δ₁(B) − δ_1′(B) = Δ and eqn. (3) converts to K_eq = (Δ + δ)/(Δ − δ).^7,8

For the determination of the experimental constant (K_obs) using eqn. (3), the ¹³C chemical shifts of the slow exchange limiting structures A and B are required. For low barrier rearrangement processes slow exchange spectra are often not accessible by experimental NMR spectroscopy in solution. The chemical shifts for these structures were therefore determined using quantum chemical calculations with the GIAO-B3LYP/6-311G(d,p) method for B3LYP/6-31G(d) optimized geometries. We have shown for a model set of alkyl carbocations by comparison of calculated chemical shifts with experimental shifts, that at this level of calculation, after applying a linear scaling method, an accuracy of Δδ < ±2 ppm is obtained.⁹

Geometry optimizations and frequency calculations for the structures involved in the equilibria 1A ⇋ 1B and 2A ⇋ 2B, respectively, were carried out at the B3LYP/6-31G(d) and MP2/6-31G(d) levels of theory using the Gaussian 98 program packages.¹⁰ The energies of the minimum structures of the carbocations 1A, 1B and 2A, 2B1, 2B2 are presented in Table 2. Selected bond lengths and angles are shown in Fig. 2 and 3.

Table 2 Total and relative energies for carbocations 1A, 1B, 2A, 2B1 and 2B2 and for transition state structures 1TS and 2TS in vacuum (ε = 1) and solvent (ε = 30.0)

	E gas/hartree		E solv/hartree^a		ΔEgas/kcal mol^−1		ΔEsolv/kcal mol^−1		E gas/hartree	ΔEgas/kcal mol^−1
Cation	B3LYP/631G(d) (ZPE)^b [NImag]^c	MP2/6-31G(d) (ZPE)^b [NImag]^c	B3LYP/631G(d) (ZPE)^b [NImag]^c	MP2/6-31G(d) (ZPE)^b [NImag]^c	B3LYP/6-31G(d) + ZPE	MP2/6-31G(d) + ZPE	B3LYP/6-31G(d) + ZPE	MP2/6-31G(d) + ZPE	MP4/6-31G(d)//MP2/6-31G(d) (ZPE)
a SCRF(IPCM) model and solvent relative permittivity of ε = 30.0 were used. B3LYP/6-31G(d) and MP2/6-31G(d) single point energy SCRF calculations were performed for B3LYP/6-31G(d) and MP2/6-31G(d) optimized geometries, respectively. b Zero point vibrational energy (not scaled) obtained from frequency calculation. c Number of imaginary frequencies obtained from frequency calculation.
1A	−313.610958	−312.451585	−313.682384	−312.522486	1.60	0	1.50	0	−312.573233	0.54
	(0.213313)	(0.218267)	(0.213313)	(0.218267)					(0.218267)
	[0]	[0]	[0]	[0]
1B	−313.612480	−312.448807	−313.684033	−312.520181	0	0.58	0	0.88	−312.572712	0
	(0.212465)	(0.216891)	(0.212465)	(0.216891)					(0.216891)
	[0]	[0]	[0]	[0]
1TS	−313.599733	−312.438571	−313.670599	−312.509886	7.25	5.82	6.82	6.08	−312.561922	5.60
	(0.210580)	(0.214935)	(0.210580)	(0.214935)					(0.214935)
	[1]	[1]	[1]	[1]
2A	−352.932279	−351.622437	−353.001729	−351.691344	0.29	1.34	0	4.56	−351.761354	1.19
	(0.242476)	(0.247539)	(0.242476)	(0.247539)					(0.247539)
	[0]	[0]	[0]	[0]
2B1	−352.934061	−351.625611	−353.001387	−351.699659	0	0	1.04	0	−351.764288	0
	(0.243784)	(0.248576)	(0.243784)	(0.248576)					(0.248576)
	[0]	[0]	[0]	[0]
2B2	−352.932552	−351.621897	−353.000229	−351.698550	0.12	1.69	0.94	0.06	−351.761334	1.21
	(0.242469)	(0.247558)	(0.242469)	(0.247558)					(0.247558)
	[0]	[0]	[0]	[0]
2TS	−352.918036	−351.610006	−352.987002	−351.679755	7.74	7.64	7.75	10.34	−351.748891	7.58
	(0.240094)	(0.245143)	(0.240094)	(0.245143)					(0.245143)
	[1]	[1]	[1]	[1]

---

Fig. 2 MP2/6-31G(d) optimized geometries of cations 1A, 1B and the transition state structure 1TS (B3LYP/6-31G(d) values in parentheses). Bonds involved in hyperconjugation are shown in black.

Fig. 3 MP2/6-31G(d) optimized geometries of cations 2A, 2B1 and 2B2 and the transition state structure 2TS (B3LYP/6-31G(d) values in parentheses). Bonds involved in hyperconjugation are shown in black.

The transition state structures 1TS for the rearrangement 1A ⇋ 1B and 2TS for the rearrangement 2A ⇋ (2B1 + 2B2)/2 were located and characterized as first order saddle points (NImag = 1) at the B3LYP/6-31G(d) and the MP2/6-31G(d) level. Selected bond lengths and angles are also shown in Fig. 2 and 3, respectively.

The optimized MP2/6-31G(d) geometries were subjected to single point energy calculations at MP4 level, thus our final level is MP4(SDTQ)/6-31G(d)//MP2/6-31G(d). The calculated ¹³C chemical shifts (δ_calc) at the GIAO-B3LYP/6-311G(d,p)//B3LYP/6-31G(d) level of theory and the scaled chemical shifts (δ_scaled) for the minimum energy structures are presented in Table 3.

Table 3 ¹³C NMR chemical shifts of 2-cyclopentyl-2-propyl cation (1A), 1-(2-propyl)cyclopentyl cation (1B), 2-cyclohexyl-2-propyl cation (2A) and 1-(2-propyl)cyclohexyl cation (2B1 and 2B2) calculated at the GIAO-B3LYP/6-311G(d,p)//B3LYP/6-31G(d) level (δ_calc) and the corresponding scaled values (δ_scaled),^a referenced to TMS^b

		Carbon atom
Cation			C3,C4^c	C2,C5^c	C1	C1′	C2′,C3′^c
a For the scaling equation and scaling parameter see ref. 9. b The absolute shielding values (^13C: 183.86; ^1H 31.92; ^29Si 339.94) for tetramethylsilane (TMS; Td symmetry) were obtained using the GIAO-B3LYP/6-311G(d,p)//B3LYP/6-31G(d) method. c Averaged chemical shift of the two corresponding carbon atoms.
1A	δ calc		36.22	47.00	86.85	299.25	39.98
	δ scaled		25.64	28.97	75.89	290.68	37.22
1B	δ calc		32.12	63.54	357.62	62.82	28.77
	δ scaled		26.77	56.65	348.06	56.07	17.25

---

		C1′	C3,C2^c	C2,C6^c	C1	C1′	C2′,C3′^c
2A	δ calc	28.17	31.02	44.05	85.99	325.30	46.52
	δ scaled	27.48	29.73	26.29	75.18	316.29	42.62
2B1	δ calc	32.19	60.65	59.67	333.66	65.39	24.54
	δ scaled	30.80	51.55	53.47	324.51	58.18	15.03
2B2	δ calc	27.17	33.02	58.91	345.56	68.68	23.63
	δ scaled	26.66	27.60	52.84	336.21	60.21	14.85

---

The 2-cyclopentyl-2-propyl cation (1A) ⇋ 1-(2-propyl)cyclopentyl cation (1B) rearrangement

The five signals which are observed in the ¹³C NMR spectrum of cation 1A/1B (Table 1, Fig. 1) show temperature dependent chemical shifts, indicating that the cation undergoes a reversible rearrangement which is fast on the NMR time scale. The two structures which are interchanged by a nondegenerate hydride shift are the 2-cyclopentyl-2-propyl cation (1A) and the 1-(2-propyl)cyclopentyl cation (1B). The relative shielding of the methylene groups C2/C5 (58.3 ppm, −120 °C, triplet) vicinal to the formal carbocation center C1 in 1B and the shielding of the methyl groups C2′/C3′(21.0 ppm, −120 °C, quartet) which are vicinal to the formal carbocation center C1′ in 1A indicate that in the equilibrium 1A ⇋ 1B the isomer 1B which has the formal charge located on the endocyclic C1 carbon atom is favoured. This is consistent with the observed temperature dependence of the chemical shifts (Table 1) and also in accord with earlier conclusions by Okazava and Sorensen,³ and Saunders et al.⁴ At higher temperatures the population of the less stable isomer 1A increases, affecting the averaged chemical shifts. The ring carbons C1, C2/C5 and C3/C4 move upfield and the exocyclic carbons C1′ and C2′/C3′ move downfield.

Both cation structures 1A and 1B have conformations favourable for β-CC-hyperconjugative stabilization of the positive charge (Fig. 2).¹¹ The cyclopentyl ring substituent of the 2-propyl cation 1A has an envelope conformation, carbons C1, C2, C3 and C5 are coplanar. The C1′–C2′–C3′ plane of the isopropyl group is perpendicular (87°) to C1–C2–C3–C5 thus the main axis of the formal vacant 2pπ orbital at carbon C1′ is eclipsed with the C1–C5 bond. Characteristic structural distortions in 1A accompany the hyperconjugative stabilization of the positive charge formally located at the C1′ carbon. The C1–C5 cyclopentyl bond (d(C1–C5) = 1.664 or 1.704 Å, at B3LYP/6-31G(d) and MP2/6-31G(d) level, respectively) is considerably elongated due to hyperconjugation (shown in black in Fig. 2) with the 2pπ orbital at the carbon C1′ as compared to the other vicinal cyclopentyl bond (d(C1–C2) = 1.539 or 1.520 Å; at B3LYP/6-31G(d) or MP2/6-31G(d) level of theory). Even more pronounced is the variance of the two bond angles C1′–C1–C5 (95.8 and 82.2°) and C1′–C1–C2 (123.7 and 125.7°) indicating the hyperconjugatively induced compression of the C1′–C1–C5 bond angle. The onset of bridging between C1′ and C5 is indicated by a shorter distance (d(C1′–C5) = 2.058 Å) as compared to d(C1′–C2) = 2.600 Å (MP2/6-31G(d) level).

The cyclopentyl cation structure 1B has a slightly twisted ring conformation. Carbon C4 is above and carbon C3 is below the plane C1–C2–C5–C1′. The β-C–C bond of one of the methyl groups (C2′–C1′) forms an angle of 90° to this plane, and is thus optimally aligned with the formally vacant 2p orbital at C1 for hyperconjugative interaction. This bond (d(C2′–C1′) = 1.583 or 1.578 Å) is elongated as compared to the C–C-bond to the other methyl group (d(C1′–C3′) = 1.536 Å or 1.527 Å) and has a reduced bond angle (C2′–C1′–C1, 103.9 or 102.3°) as compared to that of the other CH₃-group (C3′–C1′–C1, 116.0 or 116.2°, B3LYP/6-31G(d) or MP2/6-31G(d), respectively). The twisted ring conformation calculated for the 1-(2-propyl)cyclopentyl cation (1B) is in agreement with previous conclusions based on experimental NMR spectroscopic investigations of equilibrium isotope effects in β-CD₂- and CHD-deuterated isotopomers of the 1-methylcyclopentyl cation¹² and is also in accord with ab initio calculations for the twisted conformation of the parent cyclopentyl cation.¹³ The cyclopentyl cation 1B is calculated to be 1.6 kcal mol⁻¹ (B3LYP/6-31G(d)) or 0.5 kcal mol⁻¹ (MP4/6-31G(d)//MP2/6-31G(d)) more stable than the 2-propyl cation structure 1A, which is in accord with the experimental findings. At the MP2/6-31G(d)//MP2/6-31G(d) level, however, 1B is calculated to be 0.6 kcal mol⁻¹ less stable than 1A. As expected for such a flat energy surface, the energy differences show some dependence on the calculation method used. The μ-hydrido-bridged transition state structure 1TS (Fig. 2) is 7.3 kcal mol⁻¹ (B3LYP/6-31G(d)) or 5.6 kcal mol⁻¹ (MP4/6-31G(d)//MP2/6-31G(d)) higher in energy than 1B. This energy difference is a measure for the barrier of the 1,2-hydride shift intercoverting the structure 1B and 1A. No minimum energy structures with a conformation suitable for β-methine-C–H/C⁺-2pπ-hyperconjugation was found. Initial starting structures similar to 1A and 1B but with the β-C1–H and β-C1′–H-bond, respectively, aligned with the formally vacant 2pπ-orbital at the carbocation center, on geometry optimization, at the DFT-hybrid and MP2 level, converged to the β-CC hyperconjugation type minimum structures 1A and 1B respectively. Equilibrium constants K_obs for the equilibrium 1A ⇋ 1B were determined from ¹³C chemical shifts of the signals for C1 and C1′ measured between −127 and −86 °C (Table 1) using eqn. (3) and the scaled calculated chemical shifts for C1 and C1′ in 1A and 1B (Table 3). A linear van't Hoff plot (r = 0.999) was obtained plotting ln Kvs. 1/T. From the slope and the intercept the enthalpy ΔH° = −1.8 ± 0.4 kcal mol⁻¹ and the entropy ΔS° = 5.7 ± 0.3 cal K⁻¹mol⁻¹ were determined for the rearrangement reaction 1A ⇋ 1B.

The hydride shift 1A ⇋ 1B is fast on the NMR time scale even at the lowest temperatures (−127 °C) accessible in solution. Kinetic line broadening is observed for all but the peaks for C3,C4 at temperatures below −100 °C. The narrow temperature range (−127 to −86 °C) does not allow accurate line shape analysis, thus only the lower¹⁴ and the upper¹⁵ limits of the reaction rate at −127 °C were estimated to be 4.3 × 10⁴ < k < 9.0 × 10⁵.¹⁶ The corresponding limits for the free energy of activation at −127 °C are 5.0 < ΔG^‡ < 5.2 kcal mol⁻¹. This is in fair agreement with the calculated energy difference between 1B and 1TS (7.3 and 5.6 kcal mol⁻¹ at the B3LYP/6-31G(d) and MP4/6-31G(d)//MP2/6-31G(d) level, respectively). Above −100 °C a slow but irreversible rearrangement of 1A/1B to 1,2-dimethylcyclohexyl cation 5 was observed.¹¹ The rate constant for this rearrangement process 1A/1B → 5 at −99 °C is k = 2.7 × 10⁻³ s⁻¹, and ΔG^‡ (−99 °C) is 12.0 kcal mol⁻¹. The formation of carbocation 5 can be rationalized by a mechanism suggested in Scheme 2.

Scheme 2

At least two different pathways are possible. Both the expansion of the five membered ring of the 2-(2-cyclopentyl)propyl cation (1A) and 1,2-methyl shift in the 1-(2-propyl)cyclopentyl cation (1B) yield the tertiary carbocation 5, which is known to undergo a degenerate low barrier 1,2-hydride shift.¹⁵

The 2-cyclohexyl-2-propyl cation (2A) ⇋ 1-(2-propyl)cyclohexyl cation (2B) rearrangement

The ¹³C NMR spectrum of the mixture of 2-cyclohexyl-2-propyl cation (2A) and 1-(2-propyl)cyclohexyl cation (2B) shows six resonances with temperature dependent chemical shifts (Table 1, Fig. 1), proving the reversible rearrangement 2A ⇋ 2B, which is fast on the NMR time scale. The relative shielding of the methylene groups C2,C6 (35.3 ppm, −122 °C, triplet) vicinal to the formal carbocation center C1 in 2B and that of the methyl carbons C2′,C3′ (42.5 ppm, −122 °C, quartet) which are vicinal to the formal carbocation center C1′ in 2A indicate that the equilibrium 2A ⇋ 2B is shifted towards the isomer 2A which has a charge located on the exocyclic carbon C1′. This is consistent with the direction of the temperature dependent change of the averaged chemical shifts (Table 1). The averaged peaks for the ring carbons C1, C2/C6 and C3/C5 move downfield and the averaged peaks for the exocyclic carbons C1′ and C2′/C3′ move upfield at higher temperature as the population of the less stable isomer 2B is increasing. The averaged chemical shift for the methylene carbon C4, however, moves in the opposite direction to the shifts of the other ring carbons. We attribute this to an additional fast equilibrium of two conformational isomers (hyperconjomers) of the 1-(2-propyl)cyclohexyl cation 2B1 and 2B2 similar as reported for the 1-methylcyclohexyl cation.^17,18

Quantum chemical calculations at the DFT, MP2 and MP4 levels of theory reveal that, indeed, three different minimum structures of similar energy (Scheme 3, Table 2) are involved in equilibrium 2A ⇋ 2B (ΔEca. ±1 kcal mol⁻¹, at the MP4/6-31G(d)//MP2/6-31G(d) level).

Scheme 3

Two different conformations for the 1-(2-propyl)cyclohexyl cation, 2B1 and 2B2, and the 2-cyclohexyl-2-propyl cation 2A are presented in Fig. 3. The μ-hydrido-bridged structure 2TS was found as a stationary point and characterized as a transition state structure by frequency calculations (NImag = 1) at the B3LYP/6-31G(d) and MP2/6-31G(d) levels of theory (Fig. 3).

The 2-cyclohexyl-2-propyl cation 2A shows characteristic structural parameters which indicate a CC-hyperconjugative interaction of the formally empty 2pπ-orbital of the C⁺ carbon C1′ with one of the β-C–C bonds of the cyclohexyl ring. The interacting cyclohexyl C1–C6 bond is perpendicular (89°, at the MP2 level) to the C1–C2′–C3′ plane centered on the sp²-hybridized C⁺ carbon C1′, thus the C1–C6 bond is eclipsed to the formal vacant 2pπ orbital at C1′. The bond angle C6–C1–C1′ (94.9°) is reduced, the bond angle C5–C1–C1′ (121.1°) is increased compared to the C–C–C-bond angles (ca. 110°) of the cyclohexyl ring. The C1–C6 bond is elongated (1.626 Å) and the C1′–C1 bond is shortened (1.420 Å) as compared to the other cyclohexyl ring bonds (1.51–1.53 Å).

Both conformational isomers of the 1-(2-propyl)cyclohexyl cation, structures 2B1 and 2B2, have a chair conformation of the cyclohexyl ring. In 2B1 the axis of the formally empty 2pπ-orbital of the C⁺ carbon is in an equatorial-like position, close to parallel to the C2–C3–C4–C6 plane, while in the conformer 2B2, the empty 2pπ-orbital occupies the axial-like position. The structures 2B1 and 2B2 resemble the two conformations calculated for the 1-methylcyclohexyl cation.¹⁸ In both structures 2B1 and 2B2 one methyl group (C2′H₃) is oriented suitably for CC-hyperconjugation of the vacant C⁺-2pπ-orbital and the β-C1′–CH₃ bond. The C1′–C2′ bond to this methyl group is longer than the bond to the other methyl group (C3′H₃) (d(C1′–C2′) = 1.575 Å vs.d(C1′–C3′) = 1.525 Å in 2B1, and d(C1′–C2′) = 1.585 Å vs.d(C1′–C3′) = 1.525 Å in 2B2, at the MP2/6–31G(d) level). In the conformational isomer 2B1, the alignment of the C⁺-2pπ-orbital and the ring C2–C3 and C5–C6 carbon bonds allows additional stabilization of the positive charge by β-CC hyperconjugation. As a consequence the C2–C3 and C5–C6 bonds are elongated (1.587 Å) and the C1–C2 and C1–C6 bonds are shortened (1.450 Å) compared to the C3–C4 and C4–C5 bonds (1.52 Å). In the isomer 2B2 the two axial β-hydrogens at the methylene carbons C2 and C6 are aligned with the vacant C⁺-2pπ-orbital, thus involved in β-CH hyperconjugative stabilization of the positive charge. The C2–H and C6–H bonds are slightly longer (1.110 Å, at the MP2/6-31G(d) level) than the average of the other C–H bonds (1.094 Å) of the cyclohexyl ring. Similarly to 1A/1B, no minimum energy structures with a conformation suitable for β-methine-C–H/C⁺-2π-hyperconjugation was found.

The quantum chemical calculations show that the cation structure 2A and the structures 2B1 and 2B2 (Table 2) are very similar in energy. The small energy differences indicate a very flat energy surface. The order of relative energies calculated for the gas phase structures of 2A and 2B1/2B2 are not in accord with the experimental results which show that in solution 2A is preferred in the equilibrium (see Table 2). To estimate whether the effect of solvation^19,20 could change the relative order of energies for 2A, 2B1 and 2B2, self-consistent reaction field (SCRF) calculations with a static isodensity surface polarized continuum model (IPCM)²¹ were performed at B3LYP/6-31G(d) and MP2/6-31G(d) levels. A value of ε = 30.0 was used as an input parameter for a solvent relative permittivity. The relative permittivity of the solvent SO₂Cl₂ has been reported (ε = 9.1),²² but an excess of SbF₅ would create a more polar medium.¹⁸ The relative order of the energies in solution calculated at the B3LYP/6-31G(d) level of theory is in accord with the experimental findings (Table 1). Structure 2A in a solution is 1.0 kcal mol⁻¹ lower in energy than 2B1 and 0.9 kcal mol⁻¹ lower in energy than 2B2. Applying the solvent model calculation (SCRF = IPCM, ε = 30.0) to the cyclopentyl type carbocations 1A and 1B, however, does not change the relative order of their stability. The relative stability of 1B over 1A is 1.5 kcal mol⁻¹ in the gas phase and 1.6 kcal mol⁻¹ in the solution model calculation at the B3LYP/6-31G(d) level of theory (Table 2). Thus, for both carbocation systems 1A/1B and 2A/2B solvent model calculations at the B3LYP/6-31G(d) level are in qualitative agreement with the experiment.

The different temperature dependence for the cyclohexyl ring carbon of the equilibrating carbocations 2A/2B, i.e. the shielding of the averaged peak for C4 and the deshielding for the averaged peaks for C3/C5, C2/C6 and C1 can be explained taking into account the relative energies and the calculated and scaled chemical shifts of the structures 2A, 2B1 and 2B2 involved in the equilibrium process (Tables 2 and 3). Raising the temperature, the average shifts of the ring carbons C3/C5, C2/C6 and C1 increase, as the fraction of the lowest energy structure 2A decreases. The calculated shift for carbon C4 in the more stable 2B conformer, 2B1 (δ_scaled = 30.8 ppm), is only slightly downfield from the C4 shift in 2A (δ_scaled = 27.5 ppm), while the shift for carbon C4 in 2B2 (δ_scaled = 26.7 ppm) is slightly upfield from the signal for C4 in 2A. When the temperature is raised, the fraction of component 2B2 increases more than the fraction of its more stable conformational isomer 2B1 and the net effect is a slight shielding effect for the averaged peak of carbon C4. At higher temperatures the population of 2B1 (C3/C5, δ_scaled = 60.7 ppm) increases relative to 2A (C3/C5, δ_scaled = 29.7 ppm) causing deshielding of the peak for C3/C5, while an increase of the population of 2B2 (C3/C5, δ_scaled = 27.6 ppm) has the opposite effect, and causes an upfield shift of the C3/C5 peak. Even though the resulting averaged peak for the C3/C5 carbons is shifted downfield at higher temperatures, as expected due to increased charge at these positions, the change in chemical shift is very small (Δδ = 0.26 ppm for ΔT = 40 K). This is due to the large chemical shift difference between the C3/C5 signals of 2A and 2B1, (Δδ = 31 ppm), and the small chemical shift difference for the C3/C5 signals in 2A and 2B2 (Δδ = 2.1 ppm).

The three carbocation structures 2A, 2B1 and 2B2 involved in the equilibrium (Scheme 3) have the relative population: [2A] ∶ [2B1] ∶ [2B2] = 1 ∶ K₁ ∶ K₂. The averaged chemical shift of any carbon atom is given by eqn. (4),

where δ(2A), δ(2B1), and δ(2B2) represent the chemical shift of the carbon in the structures 2A, 2B1 and 2B2, respectively. Attempts to fit the corresponding equilibrium constants K₁ and K₂ (Scheme 3) led to considerable error, mainly due to the fact that both the relative energies (ΔE = 0.4 kcal mol⁻¹ at the B3LYP/6-31G(d) level) and the chemical shifts (Table 3) are very similar in both conformers 2B1 and 2B2. The equilibrium constants given in Table 1 represent the sum of the two equilibrium constants K_obs = K₁ + K₂ and were calculated using eqn. (3) with the approximation that K₁ = K₂. If K₁ is equal to K₂, the equilibrium constant for both processes 2A ⇋ 2B1 and 2A ⇋ 2B2 is K_obs/2. The corresponding thermodynamic parameters obtained from a van't Hoff plot (1/T plotted vs. ln (K_obs/2) are: ΔH = 2.5 ± 0.2 kcal mol⁻¹, and ΔS = −7.0 ± 0.8 cal mol⁻¹ K⁻¹ indicating that the structure 2A is energetically favoured over 2B1 and 2B2 by about 2 kcal mol⁻¹ which is in fair agreement with the calculated values (Table 2).

The ¹³C NMR spectra of cation 2 show line broadening at lower temperatures. The limits of the rate constants for the equilibration process 2A ⇋ (2B1 + 2B2)/2 were estimated to be similar to those of cation 1A/1B, 4.0 × 10⁴ < k_obs < 1.8 × 10⁶ (−122 °C). The rate constant k_obs refers to the sum of the overall rate constants for both processes 2A → 2B1 (k₁) and 2A → 2B2, (k₂). The single rate constants k₁ and k₂ are approximately k_obs/2. This limits the free energy of activation (ΔG^‡) at −122 °C for both processes to the range 4.3 < ΔG^‡ < 5.5 kcal mol⁻¹. This is somewhat lower than the calculated energy difference between 2A and 2TS (7.8 and 7.6 kcal mol⁻¹ at the B3LYP/6-31G(d) and MP4/6-31G(d)//MP2/6-31G(d) levels of theory, respectively).

Equilibrium isotope effects in the 1-(2-propyl)cyclopentyl-2-cyclopentyl-2-propyl cation and the 1-(2-propyl)cyclohexyl-2-cyclohexyl-2-propyl cation

The measurement of equilibrium isotope effects (EIE) on NMR spectra — the isotopic perturbation method — is a well established tool for the investigation of rapidly rearranging molecules which show averaged NMR signals.⁷ The deuterium EIE (K_H/K_D) is mainly vibrational in origin, caused by zero-point energy differences between exchanging sites. The heavier isotope deuterium prefers the site with the stiffer bond, where stretching and bending force constants are larger.²³

Therefore in deuterated carbocations where H and D are exchanged between a β-site loose-bonding situation and a stiffer bonding at a more remote site, the equilibrium is shifted towards the isotopomer with deuterium at the remote site.

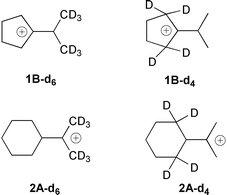
In the methyl hexadeuterated carbocation 1A-d₆/1B-d₆ and 2A-d₆/2B-d₆ the equilibria will be shifted towards the cation isomers 1B-d₆ and 2B-d₆, respectively. If the β-methylene positions, i.e. the ring-CH₂ groups are deuterated, as in 1-d₄ and 2-d₄, the corresponding equilibria will be shifted towards the 2-propyl cation isomers 1A and 2A, respectively.

In the ¹³C spectrum of a mixture of 1A/1B and 1A-d₄/1B-d₄ (Fig. 4a) the splitting between the C1 and C1′ peaks are smaller for 1A-d₄/1B-d₄ (Δ_D = 202.8 ppm at −130 °C) than for 1A/1B (Δ_H = 271.9 ppm at −130 °C), while in the ¹³C NMR spectrum of a mixture of 1A/1B and 1A-d₆/1B-d₆ (Fig. 4b) the splitting between the C1 and C1′ peaks are larger (Δ_D = 279.8 ppm at −127 °C) for 1A-d₆/1B-d₆ than for 1A/1B (Δ_H = 268.5 ppm at −127 °C).

Fig. 4 ¹³C NMR spectra (100 MHz) in SO₂ClF–SO₂F₂ solution: (a) the mixture of 1A/1B and tetradeuterated isotopomers 1A-d₄/1B-d₄ at −130 °C; (b) the mixture of 1A/1B and hexadeuterated isotopomers 1A-d₆/1B-d₆ at −127 °C.

These results are consistent only if C1 corresponds to the signal at lower field and C1′ to the signal at higher filed, i.e. the positive charge in the major isomer is located on C1. The EIE in the C2′,C3′-hexadeuterated cation 1A-d₆/1B-d₆ shifts the nondegenerate equilibrium between the isomeric structures A and B further towards the cyclopentyl cation structure B. This results in a further downfield shift of C1 and corresponding upfield shift of C1′, thus a larger splitting, as compared to the non-deuterated cation 1A/1B, is observed for the C1–C1′ peak pair. The equilibrium isotope effect for the equilibrium 1B ⇋ 1A is K_eq(H)/K_eq(D) = 0.478 at −112 °C, i.e. the average isotope effect per deuterium is 0.88 (K_H/K_D = 1.14 per deuterium). The EIE in the C2,C3-tetradeuterated cation 1A-d₄/1B-d₄ favours the 2-propyl cation isomer 1A-d₄. The concentration of isomer 1B-d₄ is decreased as compared to non-deuterated equilibrium 1A/1B. This results in an upfield shift of the C1 peak and a downfield shift of the C1′ peak, and in the ¹³C spectrum a reduced splitting for the C1 and C1′ peak pair is observed for 1A-d₄/1B-d₄ compared to the splitting for 1A/1B. The K_eq(H)/K_eq(D) = 4.54 at −116 °C (average EIE per deuterium K_H/K_D = 1.45). The larger average EIE per deuterium in the methylene deuterated cation 1A-d₄/1B-d₄ as compared to the methyl deuterated cation 1A-d₆/1B-d₆ is in accord with earlier conclusions comparing kinetic isotope effects in solvolysis reactions of β-methylene and β-methyl deuterated compounds.²⁴

The changes in the ¹³C NMR spectra of the deuterated isomers 2A-d₄/2B-d₄ and 2A-d₆/2B-d₆ are opposite compared to those of cations 1A-d₄/1B-d₄ and 1A-d₆/1B-d₆. For the C2,C6 methylene deuterated carbocation 2A-d₄/2B-d₄ (Fig. 5a) the shift difference between C1 and C1′ is larger (Δ_D = 246.4 ppm at −122 °C) than for 2A/2B (Δ_H = 234.5 ppm at −122 °C).

Fig. 5 ¹³C NMR (100 MHz) spectra in SO₂ClF–SO₂F₂ solution: (a) the mixture of 2A/2B and tetradeuterated isotopomers 2A-d₄/2B-d₄ at −122 °C; (b) the mixture of 2A/2B and hexadeuterated isotopomer 2A-d₆/2B-d₆ at −122°C.

For cation 2A-d₆/2B-d₆ the chemical shift difference (Fig. 5b) between C1 and C1′ is smaller (Δ_D = 196.5 ppm at −122 °C) than for the non-deuterated cation 2A/2B (Δ_H = 234.5 ppm at −122 °C). K_eq(D) < K_eq(H), the isotope effect favours structures of type B, thus the concentration of isomer A is lower compared to the non-deuterated cation. This shows that the peak at higher field arises from carbon C1′, while the peak at lower field is due to carbon C1. The EIE favours structures B, therefore C1′ is shifted upfield and C1 is shifted downfield in 2A-d₆/2B-d₆ and the splitting of the peak pair C1/C1′ is reduced as compared to the nondeuterated cation 2A/2B. The EIE for the 2A ⇋ (2B1/2B2)2 equilibria both favour the 2-propyl cation isomer 2A. The EIE for the 2A-d₆/2B-d₆ is K_eq(H)/K_eq(D) = 0.478 at −113 °C; the average isotope effect per deuterium of K_H/K_D = 1.13, while for the tetradeuterated carbocation 2A-d₄/2B-d₄, the EIE is K_eq(H)/K_eq(D) = 9.2 at −99 °C, which corresponds to K_H/K_D = 1.74 per deuterium.

Isodesmic reactions

The relative stabilities of the carbocation structures 1A/1B and 2A/2B1/B2 were evaluated from the isodesmic eqns. (5) and (6).

The relative energies calculated for the 2-cyclohexyl and 2-cyclopentyl substituted 2-propyl cations 2A and 1A and the corresponding hydrocarbons isopropylcyclopentane 6 and isopropylcyclohexane 7 (eqn. 5) indicate only a slight preference of the 2-cyclopentyl-2-propyl cation 1A (ΔE₁ (ε = 1.0) = −0.46 kcal mol⁻¹, ΔE₁ (ε = 30.0) = −1.56 kcal mol⁻¹) compared to the cyclohexyl substituted cation 2A. Thus the relative stability of the 2-(2-cycloalkyl)propyl cations 1A and 2A is not very sensitive to the ring size of the cycloalkyl substituent. A larger effect of the ring size, however, is found for 1-(2-propyl)-cycloalkyl cations 1B and 2B1, 2B2 (eqn. 5). The 2-propyl substituted cyclopentyl cation 1B is thermodynamically more stable than the 2-propyl substituted cyclohexyl-cation structures 2B1 and 2B2 (ΔE₂ (ε = 1.0) = −1.59 kcal mol⁻¹, ΔE₂ (ε = 30.0) = −4.16 kcal mol⁻¹ and ΔE₂ (ε = 1.0) = −1.76 kcal mol⁻¹, ΔE₂ (ε = 30.0) = −4.06 kcal mol⁻¹, respectively).

Conclusions

The nondegenerate 1,2-hydride shifts in (2-propyl)cyclopentyl and (2-propyl)cyclohexyl carbocations 1A/1B and 2A/2B were measured by dynamic ¹³C NMR spectroscopy in superacid solution. The direction of these equilibria depends on the size of the ring. The cyclopentyl cation 1B is more stable than the 2-propyl cation isomer 1A, but the 2-propyl cation 2A is more stable than the two hyperconjugative isomers (hyperconjomers) 2B1 and 2B2 of the cyclohexyl cation 2B. The results were confirmed by NMR spectroscopic measurements of deuterium equilibrium isotope effects (EIE) and rationalized by quantum chemical calculations of relative energies, geometries and NMR chemical shifts.

Acknowledgements

We gratefully acknowledge financial support by the DFG, the Fonds der Chemischen Industrie and the Ministry of Science and Technology of the Republic of Croatia (Grant No. 006151). V. V. thanks the Alexander von Humboldt Stiftung for a postdoctoral fellowship at Ulm university. We thank Thomas Nau, computer Center University of Ulm for local modifications of the Gaussian program suite.

References

1. G. A. Olah and D. J. Donovan, J. Am. Chem. Soc., 1977, 99, 5026.
2. D. A. Forsyth and Y. Pan, Tetrahedron Lett., 1985, 26, 4997.
3. N. E. Okazava and T. S. Sorensen, Can. J. Chem., 1982, 60, 2180.
4. M. Saunders, et al. unpublished results, Yale University; J. R. Lloyd, PhD Thesis, Yale University, 1978.
5. Only the labeled structures of the more stable structures in the equilibrium are presented.
6. M. Saunders and P. Vogel, J. Am. Chem. Soc., 1971, 93, 2559; D. Lenoir and H.-U. Siehl, Houben-Weyl: Methoden der Organischen Chemie, vol. E19C, Georg Thieme, Stuttgart, 1990; p. 26.
7. M. Saunders and H. A. Jiménez-Vazquez, Chem. Rev., 1991, 91, 375; H.-U. Siehl, Adv. Phys. Org. Chem., 1987, 23, 63.
8. Δ represents the chemical shift difference of the interchanging sites in the slow exchange limiting structures, and δ represents the experimental splitting of the interchanging sites..
9. V. Vrc̆ek, O. Kronja and H.-U. Siehl, J. Chem. Soc., Perkin Trans. 2, 1999, 1317.
10. Gaussian 98, Revision A.9, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian, Inc., Pittsburgh PA, 1998.
11. V. Vrc̆ek, H.-U. Siehl and O. Kronja, J. Phys. Org. Chem., 2000, 13, 616.
12. J. H. Botkin, D. A. Forsyth and D. J. Sardella, J. Am. Chem. Soc., 1986, 108, 2797.
13. P. v. R. Schleyer, C. Maerker, P. Buzek and S. Sieber, in Stable Carbocation Chemistry, Eds. G. K. S. Prakash and P. v. R. Schleyer, John Wiley & Sons, New York, 1997, ch. 2.
14. J. Sandström, Dynamic NMR spectroscopy, Academic Press, London, 1982, p. 77.
15. M. Saunders and M. R. Kates, J. Am. Chem. Soc., 1978, 100, 7082.
16. The lower limit: k > π/[(ν_1A(C1) − ν_1B(C1)], where ν_1A(C1) and ν_1B(C1) represent the calculated absorption frequencies of C1 in 1A and 1B respectively; The upper limit: k < π[ν_1A (C2′) − ν_1B (C2′)]²/2ω where ν_1A(C2′) and ν_1B(C2′) represent the frequencies of the C2′,C3′-methyl carbons sites in 1A and 1B and ω is the line broadening (7 Hz at −127 °C) observed for the methyl carbons C2′,C3′.
17. R. P. Kirchen, K. Ranganayakulu and T. S. Sorensen, J. Am. Chem. Soc., 1987, 109, 7811.
18. A. Rauk, T. S. Sorensen and P. v. R. Schleyer, J. Chem. Soc., Perkin Trans. 2, 2001, 869; A. Rauk, T. S. Sorensen, C. Maerker, J. W. de M Carnerio, S. Sieber and P. v. R. Schleyer, J. Am. Chem. Soc., 1996, 118, 3761.
19. W. L. Jorgensen, J. Am. Chem. Soc., 1977, 99, 280; C. Jenson and W. L. Jorgensen, J. Am. Chem. Soc., 1997, 119, 10846.
20. P. v. R. Schleyer, J. W. de M. Carnerio, W. Koch and D. A. Forsyth, J. Am. Chem. Soc., 1991, 113, 3990; P. R. Schreiner, D. L. Severance, W. L. Jorgensen, P. v. R. Schleyer and H. F. Schaefer III, J. Am. Chem. Soc., 1995, 117, 2663.
21. J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16098.
22. Handbook of Chemistry and Physics, 80th edn., Ed. D. R. Lide, CRC Press, New York, 1999–2000.
23. For general treatment of isotope effects see: J. Biegeleisen and M. Wolfsberg, Adv. Chem. Phys., 1958, 1, 15; L. Melander, Isotope Effects on Reaction Rates, Ronald Press, New York, 1960; Isotope Effects in Chemical Reactions, Eds. C. I. Collins and N. S. Bowman, ACS Monograph 167, Van Norstand Reinhold, New York, 1970; M. Wolfsberg, Acc. Chem. Res., 1972, 7, 225; L. Melander and W. H. Saunders, Jr., Reaction Rates of Isotopic Molecules, Wiley, New York, 1980.
24. V. J. Shiner, Jr., J. Am. Chem. Soc., 1961, 83, 240; V. J. Shiner, Jr. and J. S. Humphrey, Jr., J. Am. Chem. Soc., 1963, 85, 2146.

---

Footnote

† Electronic supplementary information (ESI) available: redundant coordinates for structures 1A, 1B, 1TS, 2A, 2B1, 2B2 and 2TS; van't Hoff plot for equilibrium 1A ⇋ 1B. See http://www.rsc.org/suppdata/p2/b1/b107756b/

---