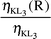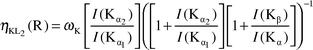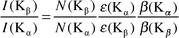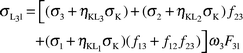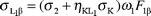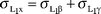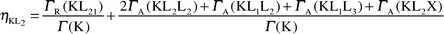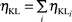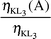Measurement of total, radiative and radiationless (Auger) vacancy transfer probabilities from K to Li sub-shells of Cs, Ba and La
Received
18th October 2001
, Accepted 17th April 2001
First published on 4th December 2001
Abstract
The vacancy transfer probabilities of K to L1, L2 and L3 shells were measured with a new approach. The measured L X-ray yields from targets excited by 59.5 keV incident photons, i.e., above the K edge of elements, were detected with a high-resolution Si(Li) detector. For comparison with experimental results, theoretical calculations were made using radiative and radiationless transitions. The radiative transitions of these elements were taken from the relativistic Hartree–Slater model. The radiationless transitions were taken from the Dirac–Hartree–Slater model. The measured results were found to be in good agreement with theoretical values.
Introduction
When an atom's K or L shell/sub-shell has been ionised, it is de-excited through radiative or radiationless (Auger) transitions. Knowledge of average vacancy distributions is important for the study of processes such as nuclear electron capture, internal conversion of γ-rays, the photoelectric effect and, in general, whenever primary vacancies produced in the shell must be distinguished from multiple ionization due to the decay of the inner vacancy.
The L X-ray and M X-ray production cross-sections and average L and M shell fluorescence yields were measured experimentally in recent years.1–7 Ertugrul et al.8 measured K to L shell radiative vacancy transfer probabilities for elements in the atomic number range 72 ≤ Z ≤ 92 using a cobalt-57 radioisotope source.
The enhancement effect of K to L shell vacancy transfer on the Kα to Lα intensity ratio was measured for lanthanides.9 The enhancement of Coster–Kronig transitions on L sub-shell X-rays was investigated for heavy elements in the atomic number range 79 ≤ Z ≤ 92.10 K to L shell11,12 and L to M shell13 vacancy transfer probabilities have been measured experimentally using two radioisotope sources. In addition, Puri et al.14 calculated vacancy transfer probabilities of K to L1, K to L2, K to L3, K to L, L1 to M1, L2 to M, L3 to M shells. The values of ηKLi
(i = 1, 2, 3) for elements in the atomic number
range 20 ≤ Z ≤ 94 have also been calculated.1 In these calculations, the contributions due to Auger and radiative transitions were derived using the best fitted experimental data on the fluorescence yields, and the intensity ratios of different components of K–LX (X = L, M, N…) Auger electrons to K X-rays are currently available.
In the earlier measurements11–13 two radioisotope sources for excitation of targets were used.11,12 The method was based on the number of L X-rays produced at the photon excitation energy below the K edge and at the excitation energy above the K edge, where the major contribution to L shell vacancies comes from the decay of K shell vacancies. In the present work, the vacancy probabilities of K to L1, K to L2 and K to L3 were measured using: Li sub-shell X-ray production cross-sections (σL1x, σL2x and σL3x); theoretical values of sub-shell photoionization cross-sections; sub-shell fluorescence yields; and Coster–Kronig transition probabilities. The measured values were compared with the calculated values deduced using Auger transitions15
and radiative X-ray emissions,16 and found to be in agreement.
Method and experimental measurements
Measurements of cross-sections for the production of Li sub-shell X-rays of Cs, Ba and La were made using the 241Am radioisotope and the experimental set-up shown in Fig. 1. In this set-up, 59.5 keV gamma rays emitted from a 100 mCi americium-241 point source were used for excitation of the target. The radioisotope of 241Am was completely (∼99.99%) filtered out with the help of graded filters of Pb, Cu and Al of thickness 0.1, 0.1 and 1 mm, respectively. The emitted L X-rays from the target were detected by a calibrated Si(Li) detector (active area = 12 mm2, sensitive depth = 3 mm, Be window thickness = 12.5 µm) with an energy resolution of approximately 160 eV at 5.96 keV. The measurement of L X-rays at the emission angle 90° accounts
for the anisotropic emission of Ll, Lα and L3β lines because the effects of anisotropy at angles smaller and greater than 90° compensate one another.17,18
 |
| | Fig. 1
Experimental set-up.
| |
High purity (99.9%) samples of thickness from 5 to 20 µg were used for the preparation of the targets. Each target was excited and the data were recorded for time intervals ranging from 3 to 12 h. Also, to minimize any systematic errors, the data for each target were taken on different occasions. A typical X-ray spectrum for La is shown in Fig. 2.
Data analysis
The experimental Li XRF cross-sections σLix were evaluated using the relation| |  | (1) |
where NLix is the number of counts per unit time under the photopeak corresponding to L X-rays of the elements, the product I0G is the intensity of the exciting radiation falling on the area of the target sample visible to the detector, εLix is the efficiency of the detector at the Lix X-ray energy of the element, t is the mass per area of the element in g cm−2, M is the atomic weight, NA is Avogadro's number and βLix is the self absorption factor for the incident and emitted Lix X-ray
photons. The values of βLix have been calculated by using the following expression obtained by assuming that the fluorescent X-rays are incident normally at the detector:| |  | (2) |
where μinc and μemt are the absorption coefficients at the incident and emitted X-ray photon energy, respectively (values are taken from the tables of Hubbell and Seltzer19), and θ1 are θ2 are the angles of incident photons and emitted X-rays with respect to the normal at the surface of the sample. In the present work, the values of I0GεLix were determined by collecting the K X-ray spectra of thin samples, Ti (99.9%), V (99%), Fe (99.9%),
Ni (99%), Zn (99.9%), As2O3
(99.9%), SeO2
(99.9%), KBr (99%) and SrCl2·6H2O (99.9%), in the same geometry in which the L XRP cross sections were measured using the equation:| |  | (3) |
where NKα, βKα and εKα have the same meaning as in eqn. (1) except that they correspond to K X-rays instead of the ith group of L X-rays. In the calculations, the theoretical values of Kα XRP cross sections were calculated using the equation| | 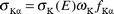 | (4) |
where σK(E) is the K
shell photoionization cross section20 for the elements at the excitation energy E, ωK is the K shell fluorescence yield from the tables of Krause21 and fKα is the fractional X-ray emission rate for Kα X-rays and is defined as:| |  | (5) |
where IKβ/IKα is the Kβ to Kα X-ray intensity ratio.16
In eqn. (1), the counts per unit time under the photopeak corresponding to Lix X-rays were evaluated according to the following.
(i) Because the L3l, L3α, Lβ and Lγ X-rays are well resolved the net counts were taken under the photopeak.
(ii) Because the L3β X-rays cannot be resolved they are found using NL3α, the net intensity with the following equation:
| | 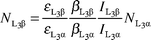 | (6) |
(iii) From this point, we can write
| |  | (7) |
| |  | (8) |
and
| | 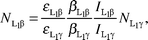 | (9) |
| | 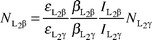 | (10) |
From eqns. (7)–(9)
| | 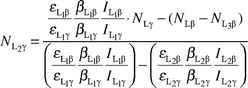 | (11) |
| |  | (12) |
where
εLix
(
i = 1, 2, 3 and x = α, β, γ) and
βLix are described in
eqn. (1), the
IL3β/
IL3α,
IL1β/
IL1γ and
IL2β/I
L2γ relative emission rates are given by the relationships:
| |  | (13) |
| |  | (14) |
| |  | (15) |
where
Γ(L
i–X
i) are the radiative emission rates, which are taken from the table of Scofield
16 and tabulated as relative radiative emission rates. The values of
NL3β,
NL2β,
NL2γ,
NL1β and
NL2γ involve the total L
3β, L
2β, L
2γ, L
1β and L
1γ X-rays originating from L
3, L
2 and L
1 sub-shells, for example,
NL1β =
NLβ3 +
NLβ4 +
NLβ9 +
NLβ10.
Table 1
L sub-shell X-ray production cross-sections with theoretical values
| |
σ
L3l/b atom−1a |
σ
L3α/b atom−1 |
σ
L3β/b atom−1 |
σ
L2β/b atom−1 |
σ
L2γ/b atom−1 |
σ
L1β/b atom−1 |
σ
L1γ/b atom−1 |
| Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
|
1 b (barn) = 10−28 m−2.
|
|
55Cs |
2.8 ± 0.3 |
2.8 |
73.6 ± 3 |
74 |
12.4 ± 0.8 |
12 |
40.7 ± 2 |
39 |
6.7 ± 0.8 |
6.3 |
8.3 ± 1 |
9.1 |
2.0 ± 0.2 |
2.3 |
|
56Ba |
3.2 ± 0.3 |
3.1 |
81.0 ± 5 |
79 |
13.5 ± 0.8 |
13 |
45.4 ± 3 |
44 |
7.7 ± 1 |
7.4 |
8.5 ± 1 |
8.7 |
2.3 ± 0.2 |
2.2 |
|
57La |
3.8 ± 0.4 |
3.7 |
94.5 ± 6 |
97 |
17.1 ± 1 |
17 |
52.2 ± 3 |
49 |
9.0 ± 1 |
8.7 |
9.6 ± 1 |
9.6 |
2.6 ± 0.2 |
2.5 |
Table 2
σ
L1x, σL2x and σL3x X-ray production cross-sections with theoretical values
| |
σ
L1x/b atom−1 |
σ
L2x/b atom−1 |
σ
L3x/b atom−1 |
| Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
|
55Cs |
11.3 ± 1 |
11.4 |
47.4 ± 3 |
45.3 |
88.8 ± 4 |
88.8 |
|
56Ba |
10.8 ± 1 |
10.9 |
53.1 ± 4 |
51.4 |
98.7 ± 6 |
95.1 |
|
57La |
12.5 ± 1 |
12.1 |
61.2 ± 4 |
57.7 |
115.4 ± 7 |
117.7 |
Table 3
Total vacancy transfer probabilities ηKLi
| |
η
KL1
|
η
KL2
|
η
KL3
|
| Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
|
55Cs |
0.051 ± 0.002 |
0.047 |
0.271 ± 0.01 |
0.302 |
0.545 ± 0.02 |
0.545 |
|
56Ba |
0.041 ± 0.002 |
0.045 |
0.304 ± 0.01 |
0.301 |
0.527 ± 0.02 |
0.542 |
|
57La |
0.045 ± 0.002 |
0.043 |
0.306 ± 0.01 |
0.300 |
0.540 ± 0.02 |
0.539 |
Table 4
Intensity ratios of K X-rays
| |
I(Kβ)/I(Kα) |
I(Kα2)/I(Kα1) |
I(K′β1)/I(Kα1) |
| Exp. |
Ref. 16
|
Ref. 16
|
Ref. 16
|
|
55Cs |
0.239 ± 0.014 |
0.2240 |
0.542 |
0.2807 |
|
56Ba |
0.243 ± 0.007 |
0.2273 |
0.543 |
0.2832 |
|
57La |
0.247 ± 0.010 |
0.2304 |
0.545 |
0.2857 |
Table 5
Radiative vacancy transfer probabilities ηKLi(R)
| |
η
KL2(R) |
η
KL3(R) |
| Exp. |
Theo. |
Exp. |
Theo. |
|
55Cs |
0.254 ± 0.01 |
0.255 |
0.469 ± 0.02 |
0.473 |
|
56Ba |
0.255 ± 0.01 |
0.257 |
0.470 ± 0.02 |
0.473 |
|
57La |
0.256 ± 0.01 |
0.258 |
0.470 ± 0.02 |
0.474 |
Table 6
Radiationless (Auger) vacancy transfer probabilities ηKLi(A)
| |
η
KL1(A) |
η
KL2(A) |
η
KL3(A) |
| Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
|
55Cs |
0.051 ± 0.002 |
0.047 |
0.047 ± 0.001 |
0.047 |
0.076 ± 0.003 |
0.072 |
|
56Ba |
0.041 ± 0.002 |
0.045 |
0.049 ± 0.002 |
0.044 |
0.058 ± 0.003 |
0.069 |
|
57La |
0.045 ± 0.002 |
0.043 |
0.048 ± 0.002 |
0.042 |
0.070 ± 0.003 |
0.065 |
| |

|

|

|
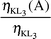
|

|
| Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
Exp. |
Theo. |
|
55Cs |
1 |
1 |
0.17 |
0.15 |
0.83 |
0.84 |
0.14 |
0.13 |
0.86 |
0.86 |
|
56Ba |
1 |
1 |
0.16 |
0.14 |
0.83 |
0.85 |
0.11 |
0.12 |
0.89 |
0.87 |
|
57La |
1 |
1 |
0.15 |
0.14 |
0.83 |
0.86 |
0.13 |
0.12 |
0.87 |
0.88 |
The ηKLi values were evaluated by the relations:
| |  | (16) |
| |  | (17) |
| |  | (18) |
The present values of
ηKL1
(for calculation of
ηKL2) and of
ηKL1 and
ηKL2
(for calculation of
ηKL3) were used in
eqns. (17) and (18), respectively. The experimental radiative transition probabilities were measured using the Kβ/Kα intensity ratio of these elements. For this the following equations were used
1,8| | 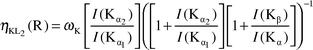 | (19) |
| |  | (20) |
where
ωK is the fluorescence yield of the K shell,
21I(Kα
2)/
I(Kα
1), and
I(Kβ
1)/
I(Kα
1) and
I(Kβ)/
I(Kα) are the intensity ratios of K X-rays.
I(Kα
2)/
I(Kα
1) and
I(Kβ
1)/
I(Kα
1) intensity ratios were taken from Scofield.
16 The
I(Kβ)/
I(Kα) intensity ratio is observed
by using the following relation:
| | 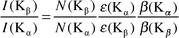 | (21) |
where
N(Kβ) and
N(Kα) are the net counts observed under the photopeaks corresponding to
I(Kβ) and
I(Kα) X-rays , respectively.
The radiationless (Auger) transition probabilities were found by using the equations:
| |  | (22) |
| |  | (23) |
| |  | (24) |
Theoretical calculations
In this work we calculated the theoretical L X-ray production cross-sections for the elements at the 59.5 keV incident photon energy using the following equations:| | 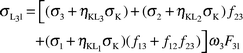 | (25) |
| |  | (26) |
| |  | (27) |
| |  | (28) |
| |  | (29) |
| | 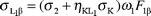 | (30) |
| |  | (31) |
where σi
(i = 1,
2, 3) is the L sub-shell photoionization cross section,20ωi
(i = 1, 2, 3) is the L sub-shell fluorescence yield,21fij
(i = 1, 2 and j = 2, 3) is the Coster–Kronig transition probability21 and Fij
(F3l, F3α, F3β,…) is the fraction of the radiative transition of the sub-shell Li
(i = 1, 2, 3) contained in the jth spectral line.
The Fij values are given by the following:
| |  | (32) |
| |  | (33) |
| |  | (34) |
| |  | (35) |
| |  | (36) |
| |  | (37) |
where
Γi
(
i = 1, 2, 3) is the total radiative width of the L
i sub-shell
16 and
Γ
(X
i–Y
j) is the partial
width.
From eqns. (25)–(32), we can obtain the following equations:
| |  | (38) |
| |  | (39) |
| | 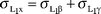 | (40) |
where the quantities are described earlier.
The K to Li sub-shell vacancy transfer probability is defined as the number of Li sub-shell vacancies produced in the decay of one K shell vacancy through radiative K–Li transitions or through Auger K–LiLj and K–LiX (X = M, N, O...) transitions. The average value of ηKLi is given by:
| |  | (41) |
where
ηKLi(R) and
ηKLi(A) are the radiative and Auger transition probabilities of the K to L
i sub-shells.
The ηKLi values have been calculated using the following equations:
| |  | (42) |
| | 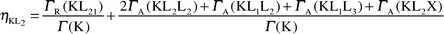 | (43) |
| |  | (44) |
where X = M, N, O and
| | 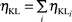 |
(45)
|
where
ΓR(KL
i) is the radiative K shell partial width,
ΓA(K–L
iL
j) and
ΓA(K–L
iX) are the radiationless partial widths and
Γ(K) is the total K level width. The radiative transition rates and Auger transition
rates have been tabulated by Scofield
16 and Chen
et al.,
15 respectively. In
eqns. (42)–(44), the first parts are the radiative transition probabilities and the second parts are the radiationless (Auger) transition probabilities.
Results and discussion
L sub-shell X-ray production cross-sections, total vacancy transfer probabilities, intensity ratios of K X-rays, radiative and radiationless (Auger) vacancy transfer probabilities are shown in Tables 1–6, respectively. The measured values of the K to Li sub-shell vacancy transfer probability for the elements Cs, Ba and La are listed in Table 3. The overall error in the measured values is estimated to be 3–7%. This error is attributed to the uncertainties in the different parameters used to deduce ηKLi values, namely, the error in the evaluation of the area under the K shell and L sub-shell X-ray peak (4%), the error in the absorption correction factor ratio (<1%) and other systematic errors (2–3%).
In earlier measurements, Puri et al.11 and Ertugrul et al.12 measured K to L shell vacancy transfer probabilities for elements in the atomic number range 37 ≤ Z ≤ 42 and 73 ≤ Z ≤ 92, respectively. Furthermore, from L to M shell vacancy transfer probabilities were measured for elements in the atomic number region 70 ≤ Z ≤ 92.13 In these measurements, the targets were excited by two energies that were below and above the K edge of the elements. In addition, the radiative vacancy transfer probabilities for K to L2, K to L3 and K to M shells were measured for elements in the atomic number range 69 ≤ Z ≤ 92 by using a Co-57 radioisotope.8 In the present study,
an Am-241 radioisotope source was used for excitation of targets. The experimental values, ηKL, were compared with the calculated values and found to be in good agreement with the calculated values for the elements. In the calculations, the K shell radiative rates, based on the relativistic Hartree–Slater theory, were taken from the tabulations of Scofield.16 The radiationless (Auger) transition rates, based on the relativistic Dirac–Hartree–Slater model were taken from Chen et al.15
When the excitation energy is above the K edge of an atom, a significant contribution to the L shell vacancy comes from the decay of K shell vacancies. To estimate this contribution, knowledge of K shell to Li sub-shell vacancy transfer probabilities, ηKLi, is required. While the Kα X-rays (Kα1 and Kα2) occur as a result of the transition of vacancy transfer from the L2 to K (Kα2) and L3 to K (Kα1) shells, the Kβ X-rays are formed as a result of the transition of vacancy transfer from the K shell to M, N and other higher shells. The fractional emission rate for Kα X-rays (fKα) gives information on the K to L2 and L3 radiative vacancy transfer. The fKα values for Cs, Ba and La were calculated as 0.816, 0.814
and 0.812, respectively. So, it can be said that the K shell vacancies decay to L2, L3 sub-shells and enhance L2, L3 sub-shell vacancies. A similar process occurs with radiationless transition. The K to L1 vacancy transfer is radiationless only. The K to L2 and L3 vacancy transfer is the sum of the radiative and radiationless transfer. As shown in Table 7, while the percentages of radiative transition from the L2 sub-shell into the K shell are 84%, 85% and 86% for Cs, Ba and La, respectively, the same quantities for the L3 sub-shell are 86%, 87% and 88%, respectively.
Because the total vacancy transfer from the K shell to L3 sub-shell is higher than the K shell to L1 sub-shell and K shell to L2 sub-shell, respectively, the L3 X-rays (Ll, Lα, some of Lβ) are the most enhanced. The counts of vacancy in the L3 sub-shell after photoionization are formed by primary ionization, K shell to L3 sub-shell vacancy transfer and L1 to L3 and L2 to L3 Coster–Kronig vacancy transfer. The percentages of the vacancies in the L3 sub-shell for Cs at 59.5 keV are calculated as 66%, 23%, 6% and 3.6% for K shell to L3 sub-shell vacancy transfer, L1 to L3 sub-shell Coster–Kronig vacancy transfer, L2 to L3 sub-shell Coster–Kronig transfer and primary ionization, respectively. Considering that the vacancies from K to
L1 and K to L2 vacancy transfer are carried out by the L1 to L3 , L2 to L3 and the L1 to L2 and L2 to L3 Coster–Kronig transitions (together), the enhancement of L3 X-rays by the K to Li sub-shell vacancy transfer are very important for L3 X-ray production cross sections. Similar calculations were made for L1 and L2 sub-shells of Cs. It is seen that the percentage of K to L1 vacancies in the L1 sub-shell vacancy is 34% and the percentage of K shell to L2 sub-shell vacancy and L1 to L2 Coster–Kronig vacancy in the L2 sub-shell are 86% and 7.5%, respectively. According to these results, when the K and L shell are excited together, the vacancy transfer of K to Li sub-shells should have a very
important role. For this reason, knowledge of the vacancy transfer is necessary. In this study, K to L1, K to L2 and K to L3 vacancy transfers (total, radiative and radiationless) were evaluated. Since a lot of physical parameters are calculated theoretically, this method can be called semi-empirical. However, K to L1, K to L2 and K to L3 vacancy transfer probabilities for total, radiative and radiationless transitions have been evaluated in this study for the first time.
References
- P. V. Rao, M. H. Chen and B. Crasemann, Phys. Rev. A, 1972, 5, 997 CrossRef.
- M. Ertugrul, Z. Phys. D, 1996, 38, 91 CrossRef CAS.
- H. S. Sohotko, R. Singh and N. P. S. Sidhu, X-Ray Spectrom., 1998, 17, 99.
- R. R. Garg, S. Puri, S. Singh, D. Mehta, J. S. Shahi, M. L. Garg, N. Singh, P. C. Mangal and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1992, 72, 147 Search PubMed.
- M. Ertugrul, E. Tırasoglu, Y. Kurucu, S. Erzeneoglu, R. Durak and Y. Sahin, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1996, 108, 18 Search PubMed.
- S. Puri, D. Mehta, N. Singh, P. C. Mangal and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1993, 73, 319 Search PubMed.
- R. R. Garg, S. Puri, S. Singh, D. Mehta, J. S. Shahi, M. L. Garg, N. Singh, P. C. Mangal and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1992, 72, 147 Search PubMed.
- M. Ertugrul, O. Dogan and O. Simsek, Radiat. Phys. Chem., 1997, 49, 221 CrossRef CAS.
- M. Ertugrul, J. Phys. B: At. Mol. Opt. Phys., 1995, 28, 4037 Search PubMed.
- M. Ertugrul, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1996, 119, 345 Search PubMed.
- S. Puri, D. Mehta, B. Chand, N. Singh and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1993, 73, 443 Search PubMed.
- M. Ertugrul, O. Dogan, O. Simsek, U. Turgut and H. Erdogan, Phy. Rev. A, 1997, 55, 303 Search PubMed.
- S. Puri, D. Mehta, B. Chand, N. Singh and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1993, 74, 347 Search PubMed.
- S. Puri, D. Mehta, B. Chand, N. Singh, J. H. Hubbell and P. N. Trehan, Nucl. Instrum. Meth. Phys. Res. Sect. B, 1993, 83, 21 Search PubMed.
- M. H. Chen, B. Crasemann and H. Mark, At. Nucl. Data Tables, 1979, 24, 13 Search PubMed.
- J. H. Scofield, At. Nucl. Data Tables, 1974, 14, 121 Search PubMed.
- M. Ertugrul and E. Buyukkasap, Appl. Spectrosc. Rev., 1997, 32, 175 Search PubMed.
- M. Ertugrul, E. Buyukkasap, Y. Sahin and H. Erdogan, Turk. J. Phys., 1997, 21, 175 Search PubMed.
-
J. H. Hubbell and S. M. Seltzer, National Institute of Standards and Technology, NIST IR 5632, 1995.
-
J. H. Scofield, UCRL No: 51326, 1973.
- M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 3307.
|
| This journal is © The Royal Society of Chemistry 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. 




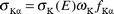

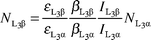


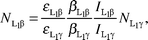
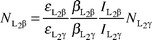
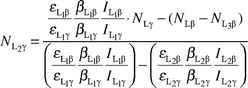




 ,
, 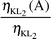 ,
,  ,
, 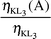 ,
,