Monochloramine loss in the presence of humic acid
Stephen E.
Duirk
,
Bertrand
Gombert
,
Junghoon
Choi
and
Richard L.
Valentine
*
Department of Civil and Environmental Engineering, University of Iowa, Iowa City, IA 52242-1527, USA. E-mail: richard-valentine@uiowa.edu; Fax: (319) 335-5660; Tel: (319) 335-5653
First published on 14th January 2002
Abstract
Free chlorine has been used extensively as a primary and secondary disinfectant for potable water. Where it is difficult to maintain a free chlorine residual or when disinfection by-products (DBPs) are of concern, monochloramine has been used to provide a stable disinfectant residual in distributions systems. Reactions of disinfectants, free chlorine or monochloramine, with natural organic matter (NOM) consequently result in the formation of DBPs such as trihalomethanes and haloacetic acids. However, few studies have focused on the fate and kinetics of monochloramine loss in the presence of reactive constituents such as NOM. Monochloramine is inherently unstable and decays even without reactive constituents present via a mechanism known as autodecomposition. Therefore, to predict monochloramine concentrations in the presence of NOM is clearly associated with the ability to adequately model autodecomposition. This study presents the results of a semi-mechanistic model capable of predicting the loss of monochloramine in the presence of humic material in the pH range of 6.55–8.33. The model accounts for both fast and a slow monochloramine demand to explain the loss of monochloramine over the pH range of this study. The formation of dichloroacetic acid was also predicted due to the ability of the model to differentiate monochloramine reaction pathways in the presence NOM. The results shown here demonstrate the ability of a semi-mechanistic model to predict monochloramine residuals and DBP formation in the presence of humic material.
Introduction
Free chlorine has been used as a primary disinfectant to inactivate microorganisms and to maintain a disinfectant residual in distribution systems. However, chlorination of potable water results in disinfection by-products such as trihalomethanes and haloacetic acids due to the free chlorine reacting with natural organic matter (NOM).1 Numerous empirical and semi-mechanistic chlorine decay models have been proposed to predict free chlorine demand or DBP formation in water treatment plants and more recently, in distribution systems.2 Most have focused solely on the loss of free chlorine in the presence of natural organic matter (NOM) or the formation of specific disinfection by-products primarily trihalomethanes (THMs). However, less work has focused on monochloramine loss in the presence of NOM.Monochloramine is rapidly replacing free chlorine as a disinfectant in distribution systems because it is believed to form less DBPs.3 Monochloramine is often used when chlorine residuals are difficult to maintain or when excessive DBPs are formed. However, the fate and kinetics of monochloramine loss in the presence of NOM has yet to be thoroughly investigated. Monochloramine loss in drinking water can be attributed to both autodecomposition and reaction with organic and inorganic constituents.4–7 Autodecomposition results in the preferential oxidation of the nitrogen in monochloramine (present in the N(III) state) to nitrogen gas (N2) and smaller quantities of nitrate (NO3−).8 However, monochloramine decay in the presence of NOM results in less nitrogen gas and increased quantities of ammonia and nitrate.4 It is believed that monochloramine reacts directly with the NOM; therefore, it is important to understand the effect NOM on the loss pathways of monochloramine. Since monochloramine autodecomposition does not result in DBPs, the ability to model both loss pathways is crucial to our understanding of monochloramine decay and disinfection by-product formation.
This study presents a semi-mechanistic model to explain monochloramine loss in the presence of NOM. The present work evaluated the effect of pH on the loss of monochloramine in the presence of a commercially available humic material, Aldrich humic acid (AHA). A semi-mechanistic model accounting for monochloramine autodecomposition (mechanistic) and loss pathways due to reactions of monochloramine with NOM (empirical) was developed. The semi-mechanistic model was then extended to predict dichloroacetic acid (DCAA) formation as a result of monochloramine reacting with the NOM over the pH range of this study. This confirms the ability of the model to predict monochloramine loss in the presence of NOM and formation of select haloacetic acids.
Experimental methods
The model waters were prepared using deionized water obtained from a Barnstead NANOpure II water system (Barnstead/Thermolyne Corp., Dubuque, IA). The glassware used in this studied was soaked in a concentrated free chlorine solution for 24 hours and rinsed with copious amounts of deionized water prior to use. The chemicals used in this study were all purchased through Fisher Scientific (Pittsburgh, PA) and certified ACS reagent grade.Monochloramine experiments were conducted using preformed monochloramine stock solution. The monochloramine stock solution was prepared using 5.64 mM ammonia and 3.7 mM hypochlorous acid to achieve the desired 0.7 Cl/N molar ratio. The stock solution was allowed to age for 60 min in 4 mM bicarbonate buffered water prior to use in any of the experiments at pH 8.5. An aliquot of the stock solution was added to the aqueous system which was then adjusted to the target pH. After the final pH was recorded, the initial monochloramine concentration was determined using N, N-diethyl-p-phenylenediamine (DPD)–ferrous ammonium sulfate (FAS) titrimetry .9 The solution was then transferred to 128 mL amber bottles and stored in a dark water bath at 25 ± 1 °C. The ionic strength in each experiment was adjusted to 0.1 M with the appropriate amount of sodium perchlorate.
Total organic carbon (TOC) was measured using a Shimadzu TOC 5000 (Shimadzu Scientific, Columbia, MD) which was standardized according to Standard Methods 505A.9 Total haloacetic acids (HAAs) were measured via gas chromatography with a HP 5890 GC in accordance with EPA method 552.2. UV absorbance and spectral characteristics of the natural organic mater were obtained through the use of a Shimadzu UV160U dual beam spectrophotometer.
Aldrich humic acid (AHA) was used as a model humic substance in this study (Aldrich Chemical Co., Milwaukee, WI). The AHA stock solution was purified to remove fulvic acid and heavy metals present in the powder salt from Aldrich.10 The purification procedure was performed by dissolving 1 g of the humic acid salt into 1 L of 0.01 M NaOH. The solution was mixed for approximately 2 h and centrifuged to remove any excess solids. The supernatant was then acidified to pH 1 with sulfuric acid to precipitate the humic acid. The acidified solution was then centrifuged and the supernatant was then discarded. The precipitated humic acid was then redissolved in 0.01 M NaOH. This procedure was then performed 4 more times to remove any additional fulvic acid. The final concentration of the AHA stock solution was 180 mg-C L−1 with a SUVA254 of 7.92 L mg m−1.
Model development
Monochloramine decay in the presence of humic materials occurs via two distinct pathways, autodecomposition and direct reaction with the NOM.4 Therefore, the ability to accurately predict autodecomposition in the presence of NOM is essential. Once autodecomposition is accounted for via a comprehensive mechanistic model, the loss of monochloramine due to direct reaction with NOM can be predicted and will provide a basis for DBP formation.Monochloramine autodecomposition is a very complicated reaction mechanism and has been well characterized3,11 (Table 1). The model includes four principle reaction schemes: (1) substitution/hydrolysis reactions involving free chlorine and ammonia or the chlorinated ammonia derivatives (reactions 1.1–1.4); (2) disproportionation reactions of chloramine species (reactions 1.5 and 1.6); (3) redox reactions that occur in the absence of measurable amounts of free chlorine (reactions 1.7–1.10); and (4) equilibrium reactions for pH dependent species (reactions 1.13–1.16).
| Reaction stoichiometry | Rate/equilibrium constant (25 °C) | Reference | |
|---|---|---|---|
| a k 5 = kH[H+] + kH2CO3[H2CO3] + kHCO3−[HCO3−]. b I represents the unidentified monochloramine autodecomposition intermediate. c Products include ammonia, chloride, and non-reactive NOM sites. | |||
| 1.1 | HOCl + NH3 → NH2Cl + H2O | k 1.1 = 1.5 × 1010 M−1 h−1 | 12 |
| 1.2 | NH2Cl + H2O → HOCl + NH3 | k 1.2 =7.6 × 10−2 h−1 | 12 |
| 1.3 | HOCl + NH2Cl → NHCl2 + H2O | k 1.3 = 1.0 × 106 M−1 h−1 | 13 |
| 1.4 | NHCl2 + H2O → HOCl + NH2Cl | k 1.4 = 2.3 × 10−3 h−1 | 13 |
| 1.5 | NH2Cl + NH2Cl → NHCl2 NH3 | a k 1.5 = pH dependent | 11 |
| 1.6 | NHCl2 NH3 → NH2Cl + NH2Cl | k 1.6 = 2.16 × 108 M−2 h−1 | 14 |
| 1.7 | NH2Cl + NHCl2 → N2 + 3H+ + 3Cl− | k 1.7 = 55.0 M−1 h−1 | 15 |
| 1.8 | NHCl2 + H2O → bI + 2HCl | k 1.8 = 4.0 × 105 M−1 h−1 | 16 |
| 1.9 | bI + NHCl2 → HOCl + N2 + HCl | k 1.9 = 1.0 × 108 M−1 h−1 | 15 |
| 1.10 | bI + NH2Cl → N2 + H2O + HCl | k 1.10 = 3.0 × 107 M−1 h−1 | 15 |
| 1.11 | NH2Cl + DOCr1 → cProducts | k doc1 = fit parameter | This work |
| 1.12 | NH2Cl + DOCr2 → cProducts | k doc2 = fit parameter | This work |
| 1.13 | HOCl ↔ H+ + OCl− | pKa = 7.5 | 17 |
| 1.14 | NH4+ ↔ H+ + NH3 | pKa = 9.3 | 17 |
| 1.15 | H2CO3 ↔ H+ + HCO3− | pKa = 6.3 | 17 |
| 1.16 | HCO3− ↔ H+ + CO32− | pKa = 10.3 | 17 |
The overall rate determining reaction at neutral to high pH for monochloramine loss is dichloramine formation.11 Dichloramine formation occurs via monochloramine hydrolysis (reactions 1.2 and 1.3) and by general acid catalyzed monochloramine disproportionation (reaction 1.5). Dichloramine formation is dependent on water quality conditions such as pH, ionic strength, temperature, and alkalinity. General acid catalyzed monochloramine loss is of importance because it suggests that a variety of proton donating species can accelerate monochloramine decay. A recent study investigated the effect of carbonate buffered waters on monochloramine decay.6 This study verified that carbonate species (carbonic acid and bicarbonate) act as a general acid catalyst determined previously from linear free energy relationships16 but was not experimentally validated.
A semi-mechanistic model portraying both the mechanistic autodecomposition pathway and empirical NOM pathway has been developed in accordance to the following assumptions. (1) A mechanistic model responsible for loss of monochloramine was adopted which accurately depicts monochloramine decay under a variety of water quality conditions such as pH, temperature, ionic strength, and buffer intensity. (2) Experimental observation has prompted the use of a two reactive fraction model, fast (S1) and slow (S2). Since a significant loss of monochloramine occurs within the first few minutes of contact time, two fractions have been employed in order to adequately describe monochloramine loss over the pH range of this study. S represents a percentage of the dissolved organic carbon (DOC) that exhibits reactivity towards monochloramine; therefore, S1 and S2 are dimensionless fitting parameters. Others working with free chlorine have also employed this assumption.2 (3) Monochloramine reacts directly with the humic material and assumed to be characterized as an elementary stoichiometric reaction. This assumption was based upon the experimental results found in this and in earlier studies.3,4
Monochloramine decay in the presence of AHA can be considered to be an observed second order reaction with respect to monochloramine. Reactions 1.11 and 1.12 show the assumed 1 to 1 elementary stoichiometry between monochloramine and both reactive fractions. (4) The reactive site concentrations are a function of the DOC. Therefore, each reactive fraction is calculated according to eqn. 1.
 | (1) |
 | (2) |
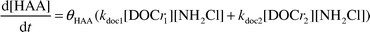 | (3) |
Results and discussion
Parameter estimation for the NOM rate constants and reactive fractions and model results
The stoichiometric equations (Table 1) were written as ordinary differential equations (ODEs) into a program called Scientist™,18 and ODE stiff equation solver. The rate constants and reactive fractions were fit using a modified Powel algorithm, which minimizes the sum squares residual error between the model results and experimental data. In the model, four fitting parameters exist: kdoc1, kdoc2, S1, and S2. The reactive site fractions are normalized to the DOC concentration, while the rate constants associated with each fraction mathematically co-vary. Therefore, numerous mathematical solutions exist for each parameter set, fast (kdoc1, S1) and slow (kdoc2, S2,), that are statistically feasible but not necessarily correct. The following methodology outlines the procedure used to determine the rate constants and reactive site fractions.The kdoc1 and S1 were assumed to be constant for each humic material regardless of pH. Therefore, the initial monochloramine demand was assumed to be the difference between the control and first actual monochloramine measurement in the presence of the humic material. Since this demand was extremely fast in the presence of the humic material, the initial monochloramine concentration in the control was assumed to be the initial monochloramine concentration in the NOM experiments. Therefore, the first actual sample to determine the monochloramine concentration taken from the reactors with humic material present showed that there was an extremely fast reactive fraction present consuming approximately 10% of the initial monochloramine dosed. This observation has also been noted by other researches working with both monochloramine and free chlorine in the presence of NOM.3,4,19,20 After the initial fast demand, the observed monochloramine demand in the presence of the humic material was constant over the rest of the experimental time frame. The initial demand data at pH 6.55, 7.6, and 8.33 was compiled into a singular data. The data was then evaluated by Scientist™ which minimized the sum squares residual error for both parameters simultaneously. The results of the parameterization for kdoc1 and S1 are shown in Table 2. The 0.02 site fraction corresponds to approximately 10% of the initial monochloramine concentration at this NOM concentration.
| pH | k doc1/M−1h−1 | S 1 | k obs/M−1h−1 | k MM/M−1h−1 | k doc2/M−1h−1 | S 2 | Apparent stoichiometry θDCAA | Fit parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k doc1 and S1: fitting parameters for fast reactive fraction, kdoc2 and S2: fitting parameters for slow reactive fraction, kobs: observed second order decay rate constant for monochloramine in the presence of AHA, kMM: forced second order decay rate constant obtained from mechanistic model results | |||||||||||||||||
| 6.55 | 9.0 × 104 | 0.02 | 949 | 372.6 | 314 | 0.15 | 83 | 103 | |||||||||
| 7.6 | 9.0 × 104 | 0.02 | 168 | 66.4 | 103 | 0.15 | 131 | 163 | |||||||||
| 8.33 | 9.0 × 104 | 0.02 | 80 | 20.3 | 60 | 0.15 | 225 | 154 | |||||||||
The parameterization for kdoc2 and S2 was relatively simple compared to the fast reactive fraction and rate constant. The main assumption was that only two pathways exist under the experimental conditions, which is autodecomposition and direct reaction with the NOM. Therefore, the observed second order rate constant (kobs), Table 2, for monochloramine decay in the presence of the humic material would then be the sum of the autodecomposition rate constant and kdoc2. The autodecomposition rate constant was determined from a forced second order plot of the mechanistic model predictions (kMM), Table 2. The slow reactive fraction rate constant (kdoc2) was initially determined at pH 7.6 and 8.33 by subtracting kMM found at each pH from kobs for each experiment prior to optimization. The slow reactive fraction (S2) was then fit using the least squares fitting algorithm in Scientist™. However, this was not case at pH 6.55. Once the slow reactive site fraction was determined at pH 7.6 and 8.33 for AHA, then the kdoc2 was fit using the least squares algorithm at pH 6.55. This assumes that S2 is not pH dependent and that any pH dependency on the reaction rate would be reflected in the rate constant. This simplifies the analysis by accounting for speciation of reactive sites with in the rate constant itself. The results of the above mention fitting procedure are shown in Table 2.
Model results at pH 6.55–8.33 can be seen in Fig. 1 for monochloramine loss with and without AHA present at 3.3 mg-C L−1. The model adequately predicts monochloramine loss over the entire pH range of this study. This demonstrates the ability of the model to predict residual monochloramine concentrations over the pH range and AHA concentration in this study.
![Monochloramine decay with and without AHA present at pH 6.55–8.33. [NH2Cl]o
≈ 0.0486 mM, CTCO3
= 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 oC, and [DOC]o
= 3.3 mg as C L−1. Lines represent model results.](/image/article/2002/EM/b106047n/b106047n-f1.gif) | ||
| Fig. 1 Monochloramine decay with and without AHA present at pH 6.55–8.33. [NH2Cl]o ≈ 0.0486 mM, CTCO3 = 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 oC, and [DOC]o = 3.3 mg as C L−1. Lines represent model results. | ||
Modeling select DBPs
The prominent HAA found in this study was dichloroacetic acid (DCAA). Since the semi-mechanistic model has been able to adequately predict both the autodecomposition and NOM monochloramine loss pathways, the possibility exists to predict the formation of select DBPs. Plotting the concentration of DCAA versus the amount of monochloramine reacted with the humic material and performing linear regression analysis could yield an apparent stoichiometry. The slope of each regression line in Fig. 2 represents the apparent stoichiometry with respect to DCAA formation for pH 6.55–8.33. In the model, this apparent stoichiometry was used to predict the formation of DCAA. θDCAA represents the apparent stoichiometric coefficient shown in eqn. 4.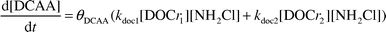 | (4) |
![DCAA formation versus monochloramine reacted with AHA at pH 6.55–8.33. [NH2Cl]o
≈ 0.0486 mM, CTCO3
= 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 °C, and [DOC]o
= 3.3 mg as C L−1.](/image/article/2002/EM/b106047n/b106047n-f2.gif) | ||
| Fig. 2 DCAA formation versus monochloramine reacted with AHA at pH 6.55–8.33. [NH2Cl]o ≈ 0.0486 mM, CTCO3 = 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 °C, and [DOC]o = 3.3 mg as C L−1. | ||
Table 2 shows the apparent stoichiometric coefficient (θDCAA) and the optimized formation coefficient found by Scientist™. The best fit parameter and θDCAA vary by less than 50%. Fig. 3 shows the model results obtained from optimized formation coefficient for monochloramine reacting with AHA over the pH range in this study. The model results follow the trend of DCAA formation for each pH with some initial over-prediction at pH 6.55. The model is capable of approximating DCAA formation using the apparent stoichiometry; however, some optimization of the formation coefficient was necessary to provide more accurate prediction for DBP formation.
![DCAA formation as a result of monochloramine reacting with AHA at pH 6.55–8.33. [NH2Cl]o
≈ 0.0486 mM, CTCO3
= 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 °C, and [DOC]o
= 3.3 mg as C L−1. Lines represent model results.](/image/article/2002/EM/b106047n/b106047n-f3.gif) | ||
| Fig. 3 DCAA formation as a result of monochloramine reacting with AHA at pH 6.55–8.33. [NH2Cl]o ≈ 0.0486 mM, CTCO3 = 4.0 mM, Ionic strength = 0.1 M, Temperature = 25 °C, and [DOC]o = 3.3 mg as C L−1. Lines represent model results. | ||
The monochloramine decomposition model was found to be very useful in predicting monochloramine residuals with out NOM present for pH 6.55–8.33. In the presence of AHA, a two reactive site model was employed to portray monochloramine loss in the presence of AHA under the same water quality conditions. The two reactive site model adequately predicted the loss of monochloramine with AHA present over the entire pH range of this study. Also, the formation of DCAA was adequately predicted by accounting for the amount of monochloramine that reacted directly with the humic material. Therefore, the semi-mechanistic monochloramine loss model was able to predict monochloramine residuals with and without NOM present as well as the formation of select DBPs. Future work will entail isolating different humic materials from other water sources, determining the rate constants and reactive site fractions for both the fast and slow reactive sites, modeling the formation of select DBPs, and correlating the results to experimentally determined humic properties such as SUVA254 and 13C NMR. Incorporation of humic material properties has the potential of transforming this model from a descriptive to a predictive model for monochloramine use in portable waters.
Acknowledgements
This work has been supported by EPA STAR Grant R826832-01-0.References
- D. A. Reckhow, P. C. Singer and R. L. Malcolm, Environ. Sci. Technol., 1990, 24(11), 1655–1664 CAS.
- J. N. McClellan, D. A. Reckhow, J. E. Tobiason, J. K. Edzwald and D. B. Smith, in Natural Organic Matter and Disinfection By-products Characterization and Control in Drinking Water. ed. S. E. Barret; S. W. Krasner and G. L. Amy, American Chemical Society: Washington DC, 2000. p 223–246 Search PubMed.
- R. L. Valentine, K. Ozekin and P. J. Vikesland, Chloramine Decomposition in Distribution System and Model Waters, AWWA Research Foundation, Denver, CO, 1998 Search PubMed.
- P. J. Vikesland, K. Ozekin and R. L. Valentine, Environ. Sci. Technol., 1998, 32(10), 1409–1416 CrossRef CAS.
- T. W. Trofe, G. W. Inman and J. D. Johnson, Environ. Sci. Technol., 1980, 14(5), 544–549 CAS.
- P. J. Vikesland, K. Ozekin and R. L. Valentine, Water Res., 2001, 35(7), 1766–1776 CrossRef CAS.
- D. W. Margerum, L. M. Schurter, J. Hobson and E. E. Moore, Environ. Sci. Technol., 1994, 28(2), 331–337 CAS.
- R. L. Valentine and G. G. Wilber, in Water Chlorination: Chemistry, Environmental Impact, and Health Effects, ed. R. L. Jolley, L. W. Condie, J. D. Johnson, S. Katz, R. A. Minear, J. S. Mattice and V. A. Jacobs, Lewis Publishers, Chelsea, MI, 1987; Vol. 6, pp. 819–832 Search PubMed.
- APHA, AWWA and WEF, 1992 Standard Methods for the Examination of Water and Wastewater. American Public Health Association, Washington DC, 15th edn., 1994 Search PubMed.
- Y. P. Chin and P. M. Gschwend, Geochem. Cosmochim. Acta., 1991, 55, 1309–1317 Search PubMed.
- C. T Jafvert and R. L. Valentine, Environ. Sci. Technol., 1992, 26(3), 577–586 CAS.
- J. C. Morris and R. A. Isaac. A Critical Review of Kinetic and Thermodynamic Constants for the Aqueous Chlorine-Ammonia System. In Water Chlorination Chemistry: Environmental Impact and Health Effects, Ann Arbor Science, Ann Arbor, MI, ed. R. L. Jolly, W. A. Burngs, J. A. Cotruvo, R. B. Cumming, J. S. Mattice and V. A. Jacobs, 1981, Vol 4, pp. 49–62, Search PubMed.
- D. W. Margerum, E. T. Gray, Jr. and R. P. Huffman, ACS Books, Washington, DC, in Organometals and Organometalloids: Occurrence and Fate in the Environment, ed. F. E. Brinkman and J. M. Bellama, pp. 278–291. Search PubMed.
- V. C. Hand and D. W. Margerum, Anal. Chem., 1983, 22(10), 1449–1456 CAS.
- S. F. Leao, Ph.D. Thesis, University of California, Berkeley, CA, 1981.
- R. L. Valentine and C. T. Jafvert, Environ. Sci. Technol., 1988, 22(6), 691–696 CAS.
- V. L. Snoeyink and D. Jenkins, Water Chemistry. Wiley, New York 1980 Search PubMed.
- Scientist, Version 2.02, software package, Micromath, Salt Lake City, UT, 1995 Search PubMed.
- G. V. Korshin, C. W. Li and M. M. Benjamin, Water Res., 1997, 31(7), 1787–1795 CrossRef CAS.
- C. W. Li, G. V. Korshin and M. M. Benjamin, Use of UV Spectroscopy to Characterize the Reaction Between NOM and Free Chlorine, Environ. Sci. Technol., 2000, 34(12), 2570–2575 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2002 |
