Role of halogen(I) cation-transfer mechanisms in water chlorination in the presence of bromide ion
Received
25th June 2001
, Accepted 22nd October 2001
First published on 20th December 2001
Abstract
Bromide ion is rapidly converted to HOBr via BrCl by reaction with HOCl. The subsequent slow reactions of (HOCl, OCl−)/(HOBr, OBr−) mixtures are monitored directly by multiwavelength UV–vis absorbance methods and simultaneously by ion chromatographic measurement of ClO2−, ClO3−, and BrO3−
(p[H+] 5.6–7.6). A first-order loss of HOCl is observed which is catalyzed by trace concentrations of Br− and BrCl. Chlorite ion forms first and is subsequently oxidized to ClO3−. The loss of HOBr is slower and is second-order in HOBr, so that BrO3− formation takes longer than ClO3− formation. Under the conditions of this work, the relative yield of BrO3− increases with
increase in pH. The decomposition of HOCl by bromide proceeds primarily by a series of halogen(I) cation-transfer reactions with subsequent halide release. The presence of HOCl increases the BrO3− yield three-fold from HOBr decay alone.
Introduction
Chlorine (typically 0.2–40 mg L−1)1 is one of the most common disinfectants used by water utilities.2 Aqueous chlorine hydrolyzes rapidly to HOCl and Cl− at pH 7 with a half-life of 0.1 s.3 The decay rate of HOCl, the main disinfectant in the absence of ammonia, is very slow,4 and sufficient amounts remain for effective disinfection. However, the decay of HOCl is accelerated by the presence of bromide ion. In natural waters, the bromide concentration varies from 0.01–3.0 mg L−1 in freshwater to 67 mg L−1 in seawater.5 HOCl and Cl2 react quickly with Br− to form BrCl, which rapidly hydrolyzes to HOBr and Cl−.6,7 Even when HOCl
is present in excess of total bromine, (where [Br]T = [HOBr] + [OBr−] + [BrCl] + [Br−]), an additional acceleration of the decay rate of HOCl is observed. The acceleration has been attributed to HOBr catalysis in previous work.8–10 Although the rates of decomposition of HOCl and HOBr are accelerated when both hypohalous acids are present, the rate dependence and reaction mechanism are not known. The present work shows that the HOCl decomposition is catalyzed by bromine species other than HOBr and proceeds by a series of halogen(I) cation-transfer reactions with subsequent halide ion release. The products of the decomposition of hypohalous acids [eqn. (1)] are chlorate ion (ClO3−)
and bromate ion (BrO3−).| |  | (1) |
BrO3− is a known carcinogen.11 For this reason, EPA has promulgated a 10 µg L−1 maximum contaminant level (MCL) for BrO3− in drinking water.12 The reaction mechanism for the decomposition of HOCl in the presence of Br− is important in order to understand the fate of disinfection byproducts in the environment. The kinetic information should be useful in regard to disinfection efficacy and factors that influence BrO3− formation.
Experimental
Reagents and materials
All solutions were prepared using distilled, deionized (18 MΩ cm) water. NaOCl was synthesized by bubbling chlorine gas (Matheson, UHP) through continuously stirred 0.30 M sodium hydroxide solution held at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. NaOCl solution (pH > 12) was standardized spectrophotometrically using the molar absorptivity of OCl− as 362 M−1 cm−1 at 292 nm.13
°C. NaOCl solution (pH > 12) was standardized spectrophotometrically using the molar absorptivity of OCl− as 362 M−1 cm−1 at 292 nm.13
Chromatographic standards were made from sodium salts (analytical reagent grade, dried at 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for 2 h), preserved with ethylenediamine,14 and used within four weeks of preparation. NaClO2 was purified and ClO2− standards were standardized spectrophotometrically using the molar absorptivity of ClO2− as 154 M−1 cm−1 at 260 nm.13
°C for 2 h), preserved with ethylenediamine,14 and used within four weeks of preparation. NaClO2 was purified and ClO2− standards were standardized spectrophotometrically using the molar absorptivity of ClO2− as 154 M−1 cm−1 at 260 nm.13
Methods and instrumentation
A ROSS® combination electrode was calibrated by titration of standardized perchloric acid and sodium hydroxide in media with a total ionic strength (μT) = 1.0 M (Na2SO4), to permit p[H+] to be calculated from the measured pH.
UV–vis spectra and kinetic scans were obtained on a PerkinElmer Lambda-9 UV–vis–NIR spectrophotometer. Ion chromatographic (IC) data were collected with a Dionex DX-500 HPLC. The separation method is an adaptation of EPA Method 300.1.14 Samples were injected via an autosampler (AS40) through a 25 µL injection loop onto quaternary amine anion exchange guard (AG9HC) and separation (AS9HC) columns. The analytes were eluted with 9.0 mM Na2CO3 at a 1.0 mL min−1 flow rate. Suppressed conductivity detection (ED40), with an ASRS-Ultra suppressor in the gas-assisted self-regeneration mode and a current of 100 mA, was used to detect the analytes.
To initiate the reaction, sodium bromide, in phosphate buffer ([PO4]T = [H2PO4−] + [HPO42−]), was added to a sodium hypochlorite solution. The reaction mixture was protected from light, stirred, and thermostatted at 25.0(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C or allowed to react at room temperature (22
°C or allowed to react at room temperature (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) where indicated. For analysis, aliquots were removed from the reaction mixture and quenched at timed intervals. To determine [HOCl]T and [HOBr]T
(where [HOX]T = [HOX] + [OX−], X = Cl, Br), a NaOH quench was applied to give pH > 12 so that all HOBr and HOCl were converted to OBr− and OCl−, respectively.
These samples were analyzed by UV–vis absorbance spectrophotometry with multiwavelength analysis. To calculate [HOCl]T and [HOBr]T, eqn. (2) was applied, where Aj = absorbance at wavelength j, ε(Cl)j and ε(Br)j are the molar absorptivities of OCl− and OBr−, respectively, at wavelength j, and j ranges from 280 to 340 nm (1 nm intervals).
°C) where indicated. For analysis, aliquots were removed from the reaction mixture and quenched at timed intervals. To determine [HOCl]T and [HOBr]T
(where [HOX]T = [HOX] + [OX−], X = Cl, Br), a NaOH quench was applied to give pH > 12 so that all HOBr and HOCl were converted to OBr− and OCl−, respectively.
These samples were analyzed by UV–vis absorbance spectrophotometry with multiwavelength analysis. To calculate [HOCl]T and [HOBr]T, eqn. (2) was applied, where Aj = absorbance at wavelength j, ε(Cl)j and ε(Br)j are the molar absorptivities of OCl− and OBr−, respectively, at wavelength j, and j ranges from 280 to 340 nm (1 nm intervals).
| |  | (2) |
To determine the products by IC, aliquots of the [HOCl]T/[Br]T reaction mixture were quenched by addition to sulfite in basic solution (10.5 < pH < 12). Sulfite reacts rapidly with OCl− and OBr−15,16 and prevents column oxidation by these hypohalites. The concentrations of ClO3− and BrO3− were determined directly. ClO2− reacts slowly with sulfite,17 but the peak areas are accurate if the sample is injected immediately after the quench. The total chloride is the sum of Cl− formed in the [HOCl]T/[Br]T reaction, the Cl− present in the OCl− stock solution, and the Cl− released from the reaction of [HOCl]T with SO32−.
The total bromide is the sum of the Br− formed in the [HOCl]T/[Br]T reaction, the Br− released from the reaction of BrO2− with SO32−, and the Br− released from the reaction of [HOBr]T with SO32−.
Results and discussion
Kinetic species distribution
The kinetic species distribution for the decomposition of [HOCl]T in the presence of [Br]T is shown in Fig. 1. The [HOCl]T decay and ClO3− formation both fit a first-order rate expression [eqn. (3)], where n is a stoichiometric factor.| |  | (3) |
The following integrated rate expressions [eqns. (4) and (5)] may be derived from the differential equation, where t = time, i = initial, and f = final.| |  | (4) |
| |  | (5) |
The observed rate constants (kobsHOCl) are calculated from the integrated rate expressions, where kobsHOCl = (3.63 ± 0.04) × 10−5 s−1 for [HOCl]T loss and kobsHOCl = (4.06 ± 0.08) × 10−5 s−1 for ClO3− formation at 25.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and μT = 1.0 M (Na2SO4). The precision given in the rate constants reflect the error in the curve fit. The agreement of the rate constants is about 10%, which is good considering two different methods were used to measure the kinetics.
°C and μT = 1.0 M (Na2SO4). The precision given in the rate constants reflect the error in the curve fit. The agreement of the rate constants is about 10%, which is good considering two different methods were used to measure the kinetics.
![a,b Kinetic species distribution for [HOCl]T/[Br]T reaction. Reaction conditions: 5.03 mM [HOCl]T, 0.508 mM [Br]T, 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22 °C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time.](/image/article/2002/EM/b105541k/b105541k-f1.gif) |
| | Fig. 1
a,b Kinetic species distribution for [HOCl]T/[Br]T reaction. Reaction conditions: 5.03 mM [HOCl]T, 0.508 mM [Br]T, 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time. °C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time.
| |
In contrast, the [HOBr]T decay and bromate formation fit second-order kinetics [eqn. (6)].
| |  | (6) |
The observed rate constants (
kobsHOBr) are measured from the integrated rate expressions [
eqns. (7) and (8)] and for the conditions given in
Fig. 1,
kobsHOBr = (1.77 ± 0.04) × 10
−2 M
−1 s
−1 for [HOBr]
T loss and
kobsHOBr = (1.7 ± 0.1) × 10
−2 M
−1 s
−1
for BrO
3− formation.
| |  | (7) |
| |  | (8) |
The ratio of [HOBr]
T reacted to [BrO
3−] formed is one while [HOCl]
T is present.
The kinetic traces for total chloride, total bromide, and chlorite are measured but not shown in Fig. 1 for clarity. The initial total chloride measured by IC agrees with the expected value. Also, the total bromide measured as a function of time agrees with [HOBr]T within the error of the analysis, which indicates that very little Br− or BrO2− builds up when HOCl is present. Chlorite ion is detected at the micromolar level near the beginning of the reaction and then decays.
Observed [HOCl]T decay rate constant dependence on [Br]T
The rate expression for the decay of [HOCl]T is first order in [HOCl]T and is not directly dependent on [HOBr]T, which also decays as shown in Fig. 1. Nevertheless, the observed first-order rate constants, kobsHOCl, do depend on [Br]T. Although [HOBr]T approximately equals [Br]T, minor species, such as Br− and BrCl, are believed to be important in the catalysis. The observed first-order rate constants for [HOCl]T decay were measured as a function of [Br]T
(0.36 M [PO4]T, p[H+] 7.00, [HOCl]T/[Br]T ≥ 4.0). The kobsHOCl values increase as [Br]T increases
as seen in Fig. 2. The data are fit to a quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2. The results of the fit are a = (6.5 ± 0.3) × 10−2 M−1 s−1 and b = 24 ± 1 M−2 s−1. The y-intercept, yo, is the [HOCl]T decay rate constant in the absence of [Br]T and is negligible with respect to kobsHOCl. The [HOCl]T decay rate constant in the absence of [Br]T has a third-order dependence on [HOCl]T
and can be calculated [eqns. (9)–(11), KaHOCl = 10−7.5 M].4| | 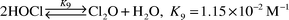 | (9) |
| |  | (10) |
| |  | (11) |
![Dependence of observed first-order rate constant for [HOCl]T decay on [Br]T, where [Br]T = [HOBr] + [OBr−] + [BrCl] + [Br−]. Reaction conditions: 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22 °C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl.](/image/article/2002/EM/b105541k/b105541k-f2.gif) |
| | Fig. 2
Dependence of observed first-order rate constant for [HOCl]T decay on [Br]T, where [Br]T = [HOBr] + [OBr−] + [BrCl] + [Br−]. Reaction conditions: 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl. °C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl.
| |
[Cl]T dependence of observed second-order rate constant for [HOBr]T decay and BrO3− yield
The observed rate of decay of HOBr in Fig. 1 is second order in [HOBr]T and is not affected by the large changes in HOCl concentration during its decay. Nevertheless, the observed values for these second-order rate constants (kobsHOBr, M−1 s−1) do depend on the initial concentrations of total chlorine ([Cl]T = [HOCl] + [OCl−] + [BrCl] + [Cl−], approximately 50%
[HOCl]T, 50%
[Cl−]) as shown in Fig. 3
(0.36 M [PO4]T, p[H+] 7.04, [HOBr]T,i = 0.504 mM).
The observed rate constant for [HOBr]T loss has a squared dependence in [Cl]T and the data are fit to the relationship (kobsHOBr = kHOBr + b[HOCl]T2) where kHOBr = (1.2 ± 0.3) × 10−2 M−1 s−1 and b = (1.06 ± 0.09) × 102 M−3 s−1. The curve-fitted y-intercept value (kHOBr) is in agreement with the expected second-order rate constant for HOBr disproportionation (kdisp = 0.015 M−1 s−1)
in the absence of HOCl [eqns. (12) and (13), where k1a = 2 × 10−3 M−1 s−1, kBP = 0.05 M−2 s−1, kBOH = 15 M−2 s−1, k1b = 6 × 10−7 M−1 s−1, KaHOBr = 10−8.59 M, and n
= 1].18| |  | (12) |
| |  | (13) |
The BrO3− yield in Fig. 3 is the percentage of initial [HOBr]T converted to BrO3− after 68 h total reaction time. The BrO3− yield increases with increasing initial [Cl]T.
![Dependence of observed second-order rate constant for [HOBr]T loss (○) and %BrO3− yield (×) on initial [Cl]T, where [Cl]T = [HOCl] + [OCl−] + [BrCl] + [Cl−]. kdisp at zero [Cl]T,i
(△) calculated by eqn. (13). %BrO3− yield at zero [Cl]T,i
(□) calculated by eqn. (1). Best fit line to [HOBr]T rate constant is curve fit to the following equation: kobsHOBr = kHOBr + b[Cl]T2,
where kHOBr = (1.2 ± 0.3) × 10−2 M−1 s−1 and b = (1.06 ± 0.09) × 102 M−3 s−1. %BrO3− = [BrO3−]/[HOBr]T,i after 68 h total reaction time. Reaction conditions: 0.504 mM [HOBr]T, 0.36 M [PO4]T, p[H+] 7.04(2), μT = 1.0 M (Na2SO4), 25.0(2) °C. Dashed line shows trend in data. Error bars represent error in kobsHOBr.](/image/article/2002/EM/b105541k/b105541k-f3.gif) |
| | Fig. 3
Dependence of observed second-order rate constant for [HOBr]T loss (○) and %BrO3− yield (×) on initial [Cl]T, where [Cl]T = [HOCl] + [OCl−] + [BrCl] + [Cl−]. kdisp at zero [Cl]T,i
(△) calculated by eqn. (13). %BrO3− yield at zero [Cl]T,i
(□) calculated by eqn. (1). Best fit line to [HOBr]T rate constant is curve fit to the following equation: kobsHOBr = kHOBr + b[Cl]T2,
where kHOBr = (1.2 ± 0.3) × 10−2 M−1 s−1 and b = (1.06 ± 0.09) × 102 M−3 s−1. %BrO3− = [BrO3−]/[HOBr]T,i after 68 h total reaction time. Reaction conditions: 0.504 mM [HOBr]T, 0.36 M [PO4]T, p[H+] 7.04(2), μT = 1.0 M (Na2SO4), 25.0(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Dashed line shows trend in data. Error bars represent error in kobsHOBr. °C. Dashed line shows trend in data. Error bars represent error in kobsHOBr.
| |
pH dependence of [HOCl]T/[Br]T reaction
The [HOCl]T and [HOBr]T decay rate constants were measured as a function of p[H+]. These results are shown in Fig. 4. The [HOCl]T decay rate constant is at a maximum near p[H+] 6.4. The [HOBr]T decay rate constant values maximize near p[H+] 7.5, which is consistent with eqn. (13).
![p[H+] dependence of observed rate constant (kobs) for [HOCl]T
(○) and [HOBr]T
(●). Error bars represent error in linear-least squares curve fit to kinetic traces. The lines show data trends. Reaction conditions: 7.3 mM [HOCl]T, 0.72 mM [Br]T, 0.36 M [PO4]T, μT = 1.0 M (Na2SO4), 25.0(2) °C.](/image/article/2002/EM/b105541k/b105541k-f4.gif) |
| | Fig. 4
p[H+] dependence of observed rate constant (kobs) for [HOCl]T
(○) and [HOBr]T
(●). Error bars represent error in linear-least squares curve fit to kinetic traces. The lines show data trends. Reaction conditions: 7.3 mM [HOCl]T, 0.72 mM [Br]T, 0.36 M [PO4]T, μT = 1.0 M (Na2SO4), 25.0(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C.
| |
The chlorate/bromate yields from the decomposition of HOCl in the presence of [Br]T were measured after a reaction period of 1 week. The results are shown in Table 1. The bromate yields increase with increasing pH, and chlorate yields decrease with increasing pH. The percent total halate ion yield is statistically constant (32.0 ± 0.3)%. This is consistent with the stoichiometry for hypohalous acid decomposition [eqn. (1)].
Table 1
Bromate and chlorate yield dependence on p[H+]a
| p[H+] |
%BrO3−b |
%ClO3−b |
%Total halate ionb |
Reaction conditions: 5.14 mM [HOCl]T and 0.518 mM [Br]T in 0.36 M [PO4]T, 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, μT = 1.0 M (Na2SO4). Yields were measured after 7 days total reaction time.
%XO3− = [XO3−] yield/([HOCl]T,i + [HOBr]T,i) × 100 (where X = Cl or Br). %Total halate ion = %BrO3− + %ClO3−. °C, μT = 1.0 M (Na2SO4). Yields were measured after 7 days total reaction time.
%XO3− = [XO3−] yield/([HOCl]T,i + [HOBr]T,i) × 100 (where X = Cl or Br). %Total halate ion = %BrO3− + %ClO3−.
|
| 5.57 |
3.92 |
27.9 |
31.8 |
| 5.88 |
4.36 |
27.8 |
32.2 |
| 6.23 |
4.81 |
27.5 |
32.3 |
| 6.59 |
5.37 |
26.9 |
32.3 |
| 6.94 |
5.93 |
26.2 |
32.1 |
| 7.29 |
6.44 |
25.2 |
31.6 |
| 7.60 |
7.23 |
24.7 |
31.9 |
Proposed mechanism and validation
The proposed mechanism is given in Table 2. The decay of [HOCl]T is first order while the decay in [HOBr]T is second order. The first-order fit to [HOCl]T is valid for at least three half-lives (87.5% loss). During this time, the [HOBr]T concentration decreases by 36%. If HOBr was catalyzing the reaction, its concentration would have to be constant to give a good first-order curve fit for the loss of HOCl. [HOBr]T is not constant, so this implies that no direct reaction between HOCl and HOBr occurs.
Table 2
Proposed mechanism for HOCl decomposition in the presence of [Br]T
| Reaction |
Rate constanta |
Ref. |
25.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, X = Cl or Br, μT = 0.5–1.0 M. °C, X = Cl or Br, μT = 0.5–1.0 M.
|

|
k
14 = 1.55 × 103 M−1 s−1 |
6,7 |
|
k
−14 = 5.2 × 107 M−1 s−1 |
|

|
k
15 = 3.0 × 106 s−1 |
7 |
|
k
−15 = 2.3 × 1010 M−2 s−1 |
|

|
k
16 > 106 M−1 s−1 |
This work |

|
k
18 = 2 × 10−3 M−1 s−1 |
18 |
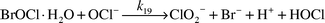
|
k
19 > 103 M−1 s−1 |
This work |

|
k
22 > 106 M−1 s−1 |
This work |

|
k
23 > 103 M−1 s−1 |
This work |
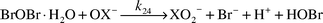
|
k
24 > 103 M−1 s−1 |
This work |

|
k
26 ≈ 97 M−1 s−1 |
13 |

|
k
30 = 17 M−1 s−1 |
9 |
Because HOBr does not directly react with HOCl and the HOCl decay rate constant depends on [Br]T, some other bromine species must be causing the HOCl decay. Upon reaction initiation, HOCl reacts with Br− to give BrCl [eqn. (14)].6
| |  | (14) |
Then, BrCl rapidly hydrolyzes to form HOBr [
eqn. (15)].
7 Trace amounts of Br
− and BrCl exist (approximately 10
−9 M under equilibrium conditions).
| |  | (15) |
BrCl is a very reactive species and we propose that BrCl rapidly reacts with OCl
− to form BrOCl [
eqn. (16)].
BrOCl is a known species in the gas phase.
19| |  | (16) |
Eqn. (17) describes the electronic rearrangement.
| | 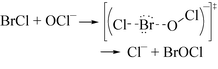 | (17) |
The bromine atom of BrCl, which is slightly positive, reacts with the nucleophilic oxygen on OCl
−. The mechanism is also favored because it is easier to expand the number of electrons around bromine than chlorine. The overall reaction in
eqn. (17) can be described as a
halogen cation-transfer (Br
+ transfer to OCl
−) with the loss of Cl
−.
If HOBr does not react with HOCl, then HOBr must decay by some other means. HOBr disproportionation is a second-order process and produces BrO2− and Br−
[eqn. (18)].18
| |  | (18) |
A second-order rate constant for HOBr disproportionation is calculated as shown in
eqns. (12) and (13). When HOCl is present,
n = 1, because HOCl rapidly converts the Br
− produced from disproportionation back to HOBr. The observed rate constant found in
Fig. 1, (1.77 ± 0.04) × 10
−2 M
−1 s
−1, is similar to the rate constant calculated
from
eqn. (13)
(
kdisp = 1.5 × 10
−2 M
−1 s
−1) and is in agreement when the low precision in the rate parameters and the differences in ionic strength are considered. This indicates that HOBr decay in the presence of HOCl is mainly due to disproportionation of HOBr.
Chlorite ion is detected in the [HOCl]T/[Br]T reaction mixtures at micromolar levels. Although BrOCl reactions have not been studied, BrOCl is expected to produce chlorite because the reaction of a similar species, Cl2O, with OCl− is known [eqn. (10)]. For these reasons, a BrOCl/OCl− reaction [eqn. (19)] is proposed.
| |  | (19) |
This reaction proceeds by a series of steps that are probably similar to the Cl
2O/OCl
− reaction.
4 The electronic rearrangement is shown by
eqns. (20) and (21). The bromine atom of BrOCl reacts with the oxygen atom of OCl
−.
| |  | (20) |
| |  | (21) |
HOCl is regenerated and the unstable intermediate, HOClOBr
−, dissociates to form ClO
2−, H
+, and Br
−.
The oxygen atom of OBr− should also be a good nucleophile, and for this reason a BrCl/OBr− reaction [eqn. (22)] and a BrOCl/OBr− reaction (23) could occur.
| |  | (22) |
| |  | (23) |
BrOBr could hydrolyze (with OX
− assistance, X = Cl or Br) to form Br
− and BrO
2−
[
eqn. (24)].
| |  | (24) |
In either case, Br
− rapidly forms so that HOBr is regenerated by the HOCl/Br
− reaction.
The kinetics for the HOCl/Br− reaction have been studied by Kumar and Margerum.6 The following rate expression for HOCl loss may be applied for the conditions in the present work [eqn. (25)], where k′ = 1.55 × 103 M−1 s−1, k′H = 1.32 × 106 M−2 s−1, k′P = 502 M−2 s−1.
| | 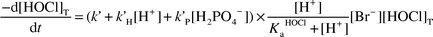 | (25) |
The bromide concentration at equilibrium conditions may be calculated from eqns. (14) and (15). This gives [Br−]eq = 4.7 × 10−9 M. If we apply this value to eqn. (25), the expected first-order rate constant for the HOCl/Br− reaction is 5.6 × 10−6 s−1. The rate constant measured (Fig. 1) is (3.63 ± 0.04) × 10−5 s−1, a factor of 6.5 larger. This suggests that Br− is not in equilibrium but that its concentration is at a higher, steady-state level.
ClO2− and BrO2− are rapidly oxidized by either HOBr or HOCl to form the final products, ClO3− and BrO3−. The ClO2− and BrO2− concentrations are small in comparison to [HOCl]T and [HOBr]T so that pseudo-first-order conditions prevail. Eqns. (26) and (27) represent the reaction and observed rate constant for the HOBr/ClO2− reaction,13 where k1 = 97 M−1 s−1, k2H/k−1 = 3.1 × 105 M−1, k2H2PO4/k−1 = 8.3 M−1, KaHOBr = 10−8.59 M.
At p[H+] = 7.0 (0.36 M [PO4]T), the observed rate constant for the HOBr/ClO2− reaction is kobs = 39.4[HOBr]T.
| |  | (26) |
| |  | (27) |
Eqns. (28)–(29) represent the reaction and observed rate constant for the HOCl/ClO
2− reaction,
20 where
k1 = 1.6 M
−1 s
−1,
k2H/
k−1 = 1.6 × 10
4 M
−1,
k2H2PO4/
k−1 = 8.5 M
−1,
KaHOCl = 10
−7.5 M.
| |  | (28) |
| |  | (29) |
At p[H
+] = 7.0 (0.36 M [PO
4]
T), the observed rate constant for the HOCl/ClO
2− reaction is
kobs = 0.146[HOCl]
T. As a result the HOBr/ClO
2− reaction dominates chlorate formation when [HOCl]
T/[HOBr]
T < 54. In
Fig. 1, this condition is satisfied for about 4 half-lives of [HOCl]
T decay.
Less kinetic information is known about reactions with bromite, but approximate rate constants are known. The rate constant for the HOCl/BrO2− reaction9 is 17 M−1 s−1
[eqn. (30)] and the rate constant for the HOBr/BrO2− reaction21 is 0.018 M−1 s−1
[eqn. (31)]. The result is that the HOCl/BrO2− reaction dominates bromate formation when [HOCl]T/[HOBr]T > 0.0053.
| |  | (30) |
| |  | (31) |
The final products are chlorate and bromate. By the mechanism given in
Table 2, the chlorate formation should follow the [HOCl]
T decay. The rate constants for chlorate formation and [HOCl]
T decay are relatively close. The rate constants for bromate formation and [HOBr]
T decay are in better agreement, which indicates that BrO
3− formation follows directly from [HOBr]
T decay. However, as [Cl]
T increases, more BrCl is available to react with OBr
− and/or form a higher steady-state amount of BrOCl. Then, the [HOBr]
T decay rate constant increases and more BrO
3− forms as [Cl]
T increases (as observed in
Fig. 3). For this reason, the BrCl/OBr
− reaction and
the BrOCl/OBr
− reaction become more important at higher [Cl]
T, and they cause the [Cl]
T2 dependence of
kobsHOBr.
The pH dependence of the observed rate constants for HOCl and HOBr decay show that the reaction rates are somewhat sensitive to pH. The pH dependence of HOBr decay rate constant follows the relationship given in eqn. (13). The HOCl decay rate constant should not decrease with decreasing pH according to eqn. (25). The observed pH dependence suggests that the OCl−/BrCl reaction [eqn. (16)] affects the observed HOCl decay rate at lower pH. At lower pH, less OCl− is available for reaction, which decreases the observed rate constant.
The pH dependence of the bromate/chlorate yields indicates bromate formation is favored at a high pH and chlorate formation at low pH. This can be explained in terms of the given mechanism. The disproportionation of HOBr [eqns. (12) and (13)] is general-base assisted and the HPO42− term (kBP) dominates the rate. As pH decreases (until p[H+] 6.4), the HOCl/Br− reaction rate constant increases while the HOBr self-disproportionation reaction rate constant decreases. Also, the [BrO3−]/[HOBr]T stoichiometry decreases from 1.0 (when HOCl is present) to 0.33 (when HOCl is absent). If the length of time for HOCl availability is shorter, then there is less time for bromate to be produced under high reaction stoichiometry
conditions. For this reason, the bromate yield is lower. However, the overall halate yield as a function of total hypohalous acid remains constant with pH, so that the relative chlorate yield increases as pH increases.
The [Br]T dependence of rate constant for [HOCl]T decay shows a squared term (Fig. 2). As [Br]T increases, the formation of Br2 is favored [eqns. (32) and (33)].7
| |  | (32) |
| |  | (33) |
As [Br]
T increases, the [BrCl]/[Br]
T ratio increases with a squared dependence on [Br]
T. This suggests that steady-state BrCl contributes to the rate-determining steps.
HOCl decay in the presence of environmentally relevant bromide ion and buffer levels
The bromide and chlorine concentrations in most of this work are higher than typical freshwater levels, because higher levels are needed for detailed kinetic analysis. However, the decay of [HOCl]T in low-level Br− concentrations was studied by following the decay of the [HOCl]T absorbance at 290 nm. At this wavelength, the [HOBr]T absorbance is negligible, so the [HOCl]T loss may be monitored directly. Fig. 5 shows the decay of HOCl in the presence 9.24 µM [Br]T and in zero [Br]T. The decay of HOCl with no Br− is expected to be third order, according to Gordon's mechanism [eqns. (9)–(11)].4
![Decomposition of 11.2 mM [HOCl]T in the presence of 9.24 µM [Br]T
(○) and 0 µM [Br]T
(△). Reaction conditions: 0.36 M [PO4]T, p[H+] 7.02, μT = 1.0 M (Na2SO4), 25.0(2) °C.](/image/article/2002/EM/b105541k/b105541k-f5.gif) |
| | Fig. 5
Decomposition of 11.2 mM [HOCl]T in the presence of 9.24 µM [Br]T
(○) and 0 µM [Br]T
(△). Reaction conditions: 0.36 M [PO4]T, p[H+] 7.02, μT = 1.0 M (Na2SO4), 25.0(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C.
| |
When the decomposition of [HOCl]T is measured in the presence of environmentally relevant [Br]T, the presence of [Br]T accelerates [HOCl]T decay (Fig. 5). We propose that very small amounts of BrCl catalyze the decomposition. However, a change in rate-controlling paths has occurred. Since the [HOCl]T/[HOBr]T ratio is greater than 54, HOCl, and not HOBr, reacts with ClO2− to form ClO3−.
Table 3 includes the ClO3− and BrO3− yields as a function of time for the decay of HOCl. The presence of 14.2 µM [Br]T results in a three-fold increase in the ClO3− yield in comparison to no added [Br]T. Also, the BrO3− yield is far above the MCL within 10 h. The AWWA Disinfection Committee Survey reported that 90% of water utilities employ a contact time (the time between the point of chlorine application and the first consumer) of 10 h.1
| Time/min |
0 µM [Br]T |
14.2 µM [Br]T |
| [ClO3−]/µM |
[ClO3−]/µM |
[BrO3−]/µM |
Reaction conditions: 5.07 mM [HOCl]T, 0.36 M [PO4]T, p[H+] 6.98, μT = 1.0 M (Na2SO4), 25.0(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C.
|
| 22 |
7.1 |
9.1 |
< 0.5 |
| 602 |
24.5 |
85.0 |
0.77 |
| 1005 |
31.1 |
132 |
1.2 |
| 1387 |
41.7 |
164 |
2.3 |
| 1787 |
57.8 |
200 |
2.8 |
| 2607 |
75.4 |
260 |
3.8 |
In this present work, pH control was achieved by the use of 0.36 M phosphate buffer. However, this level is much higher than expected for natural waters. Instead, carbonate buffers mediate pH in natural waters and the HCO3− concentration is typically about 1 mM.22 We can use this value to predict the pH effect on HOBr decomposition. By applying the Brønsted–Petersen relationship,23 the rate constant for HCO3− assistance of HOBr disproportionation can be calculated (kBHC = 0.030 M−2 s−1). Thus, the rate constant for HOBr disproportionation can be altered to account for carbonate buffers as in eqn. (34)
[kBC = 0.32 M−2 s−1,
other rate parameters are defined by eqns. (12) and (13)].18
| | 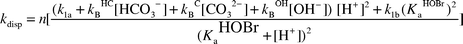 | (34) |
With the adjustment for
buffer type, the pH dependence of the observed rate constant for HOBr decay changes. HOBr decay is faster at low pH because the
k1a term dominates the rate. Therefore, BrO
3− production is slowest at high pH. Under typical drinking
water conditions (pH 6–8.5, [HCO
3−] = 1 mM), the presence of carbonate
buffer contributes very little to the rate of HOBr decay. For example, at pH 7.5, the HOBr decay rate constant in the presence of 0 mM and 1 mM HCO
3− is 1.7 × 10
−3 M
−1 s
−1.
However, as the pH and the carbonate
buffer concentration increase, the effect of CO
32− catalysis will be observed. CO
32− is a stronger Brønsted base than HCO
3−, and this increases the rate. As a result, at pH 9, the rate constant for HOBr decay doubles when the carbonate
buffer concentration is increased from 1 mM to 36 mM.
Conclusions
The reaction mechanism for the decomposition of [HOCl]T in the presence of moderate levels (0.1 mM–1.0 mM) of [Br]T is given. In contrast to previous work, no direct reaction is observed between the molecular species HOCl and HOBr. We propose that decomposition of HOCl in the presence of Br− proceeds by a series of halogen(I) cation-transfer reactions with halide ion release. Br− and BrCl occur in trace amounts and catalyze the HOCl decomposition. For example, in the presence of 9.2 µM Br−, the decay rate constant of HOCl (kobsHOCl = 1.9 × 10−6 s−1 at 11 mM [HOCl]T, p[H+] 7.0, 0.36 M [PO4]T, μT = 1.0 M,
25.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) is 25% greater than in the absence of Br−. HOBr decay is attributed to disproportionation except at high total chlorine concentrations. ClO3− and BrO3− are formed from the rapid reactions of HOBr with ClO2− and HOCl with BrO2−, respectively. For this reason, chlorate and bromate formation rates are directly related to the decay rates of HOCl and HOBr. The stoichiometry of the oxidation of HOBr to BrO3− is 1∶1 when HOCl is present because HOCl rapidly converts BrO2− to BrO3− and HOBr is regenerated by HOCl/Br− reaction [eqn. (35)].
°C) is 25% greater than in the absence of Br−. HOBr decay is attributed to disproportionation except at high total chlorine concentrations. ClO3− and BrO3− are formed from the rapid reactions of HOBr with ClO2− and HOCl with BrO2−, respectively. For this reason, chlorate and bromate formation rates are directly related to the decay rates of HOCl and HOBr. The stoichiometry of the oxidation of HOBr to BrO3− is 1∶1 when HOCl is present because HOCl rapidly converts BrO2− to BrO3− and HOBr is regenerated by HOCl/Br− reaction [eqn. (35)].| |  | (35) |
As a consequence, the BrO3−
yield from HOBr decay is higher in the presence of HOCl than in the absence of HOCl.
A pH dependence in the BrO3− and ClO3− yields was observed; for high [PO4]T, BrO3− is favored at higher pH and ClO3− is favored at lower pH. However, when carbonate buffer instead of phosphate buffer is present, the HOBr decay rate increases with decreasing pH. Carbonate buffer is more typically found in natural waters and increasing the pH of water treatment can help to minimize BrO3− formation.
Past work has focused on bromate formation in drinking water by ozonation of bromide-containing source water.24 This present work, however, shows that bromate formation in chlorination is possible and reaction pathways exist for bromate formation above the MCL. Fortunately, bromate formation is slower in hypochlorous acid than in ozone. Bromate formation in chlorinated systems can be limited by increasing pH, decreasing the concentration and contact time of [Cl]T, and decreasing buffer concentration. Therefore in the absence of other reactants, such as amines, organic matter, or light, the decomposition of HOCl in the presence of Br− may be an important pathway for BrO3− formation in drinking water.
Acknowledgements
This work was supported by NSF grant CHE-9818214 and by the Purdue Research Foundation. Preliminary studies were conducted by M. J. Tranovich (Senior Thesis, Purdue University, 1993).
References
-
G. C. White, Handbook of Chlorination and Alternative Disinfectants, Van Nostrand Reinhold, New York, 3rd edn., 1992, pp. 377–379 Search PubMed.
-
J. L. Oxenford, in Disinfection By-Products in Water Treatment, ed. R. A. Minear and G. L. Amy, Lewis Publishers, Boca Raton, FL, 1996, pp. 3–16 Search PubMed.
- T. X. Wang and D. W. Margerum, Inorg. Chem., 1994, 33, 1050 CrossRef CAS.
- L. C. Adam, I. Fábián, K. Suzuki and G. Gordon, Inorg. Chem., 1992, 31, 3534 CrossRef CAS.
-
(a)
P. Westerhoff, M. Siddiqui, J. Debroux, W. Zhai, K. Ozekin and G. Amy, in Critical Issues in Water and Wastewater Treatment, ed. J. N. Ryan and M. Edwards, ASCE, 1994, pp.
670–677 Search PubMed;
(b) S. W. Krasner, M. J. McGuire, J. G. Jacangelo, N. L. Patania, K. M. Reagan and E. M. Aieta, J. – Am. Water Works Assoc., 1989, 81, 41 Search PubMed;
(c)
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 1995 Search PubMed.
- K. Kumar and D. W. Margerum, Inorg. Chem., 1987, 26, 2706 CrossRef CAS.
- Q. Liu and D. W. Margerum, Environ. Sci. Technol., 2001, 35, 1127 CrossRef CAS.
- M. Lewin and M. J. Avrahami, J. Am. Chem. Soc., 1955, 77, 4491 CrossRef CAS.
-
T. F. Perrone, Ph.D. Thesis, Purdue University, 1999.
-
C. S. Furman, Ph.D.
Thesis, Purdue University, 1997.
- Y. Kurokawa, A. Maekawa, M. Takahashi and Y. Hayashi, Environ. Health Perspect., 1990, 87, 309 CAS.
-
Fed. Reg., 1998, 63(241), 69390 Search PubMed.
- C. S. Furman and D. W. Margerum, Inorg. Chem., 1998, 37, 4321 CrossRef CAS.
-
EPA method 300.1, US EPA,
Cincinnati, OH, 1997 Search PubMed.
- K. D. Fogelman, D. M. Walker and D. W. Margerum, Inorg. Chem., 1989, 28, 986 CrossRef CAS.
- R. C. Troy and D. W. Margerum, Inorg. Chem., 1991, 30, 3538 CrossRef CAS.
- L. C. Adam and G. Gordon, Anal. Chem., 1995, 67, 535 CrossRef CAS.
- R. C. Beckwith and D. W. Margerum, Inorg. Chem., 1997, 36, 3754 CrossRef CAS.
- J. B. Burkholder, G. Knight and J. J. Orlando, J. Photochem. Photobiol. A, 2000, 134, 133 CrossRef CAS.
- Z. Jia, D. W. Margerum and J. S. Francisco, Inorg. Chem., 2000, 39, 2614 CrossRef CAS.
- P. Engel, A. Oplatka and B. Perlmutter-Hayman, J. Am. Chem. Soc., 1954, 76, 2010 CrossRef CAS.
-
S. E. Manahan, Environmental Chemistry, Lewis Publishers, Boca Raton, FL, 7th edn., 2000, pp. 75–77 Search PubMed.
-
J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, McGraw-Hill, New York, 2nd edn., 1995, pp. 233–236 Search PubMed.
- M. S. Siddiqui, G. L. Amy and R. G. Rice, J. – Am. Water Works Assoc., 1995, 87, 58 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. NaOCl solution (pH > 12) was standardized spectrophotometrically using the molar absorptivity of OCl− as 362 M−1 cm−1 at 292 nm.13
°C. NaOCl solution (pH > 12) was standardized spectrophotometrically using the molar absorptivity of OCl− as 362 M−1 cm−1 at 292 nm.13
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for 2 h), preserved with ethylenediamine,14 and used within four weeks of preparation. NaClO2 was purified and ClO2− standards were standardized spectrophotometrically using the molar absorptivity of ClO2− as 154 M−1 cm−1 at 260 nm.13
°C for 2 h), preserved with ethylenediamine,14 and used within four weeks of preparation. NaClO2 was purified and ClO2− standards were standardized spectrophotometrically using the molar absorptivity of ClO2− as 154 M−1 cm−1 at 260 nm.13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C or allowed to react at room temperature (22
°C or allowed to react at room temperature (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) where indicated. For analysis, aliquots were removed from the reaction mixture and quenched at timed intervals. To determine [HOCl]T and [HOBr]T
(where [HOX]T = [HOX] + [OX−], X = Cl, Br), a NaOH quench was applied to give pH > 12 so that all HOBr and HOCl were converted to OBr− and OCl−, respectively.
These samples were analyzed by UV–vis absorbance spectrophotometry with multiwavelength analysis. To calculate [HOCl]T and [HOBr]T, eqn. (2) was applied, where Aj = absorbance at wavelength j, ε(Cl)j and ε(Br)j are the molar absorptivities of OCl− and OBr−, respectively, at wavelength j, and j ranges from 280 to 340 nm (1 nm intervals).
°C) where indicated. For analysis, aliquots were removed from the reaction mixture and quenched at timed intervals. To determine [HOCl]T and [HOBr]T
(where [HOX]T = [HOX] + [OX−], X = Cl, Br), a NaOH quench was applied to give pH > 12 so that all HOBr and HOCl were converted to OBr− and OCl−, respectively.
These samples were analyzed by UV–vis absorbance spectrophotometry with multiwavelength analysis. To calculate [HOCl]T and [HOBr]T, eqn. (2) was applied, where Aj = absorbance at wavelength j, ε(Cl)j and ε(Br)j are the molar absorptivities of OCl− and OBr−, respectively, at wavelength j, and j ranges from 280 to 340 nm (1 nm intervals).



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and μT = 1.0 M (Na2SO4). The precision given in the rate constants reflect the error in the curve fit. The agreement of the rate constants is about 10%, which is good considering two different methods were used to measure the kinetics.
°C and μT = 1.0 M (Na2SO4). The precision given in the rate constants reflect the error in the curve fit. The agreement of the rate constants is about 10%, which is good considering two different methods were used to measure the kinetics.
![a,b Kinetic species distribution for [HOCl]T/[Br]T reaction. Reaction conditions: 5.03 mM [HOCl]T, 0.508 mM [Br]T, 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22 °C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time.](/image/article/2002/EM/b105541k/b105541k-f1.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time.
°C. [HOCl]T, (□); [ClO3−]
(▲); [BrO3−]
(○); [HOBr]T
(△). [HOCl]T and [ClO3−] fit a first-order decay and formation, respectively. [HOBr]T and [BrO3−] fit a second-order decay and formation, respectively. Fig. 1b
is a detailed view of changes in [HOBr]T and [BrO3−] with time.



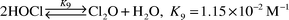


![Dependence of observed first-order rate constant for [HOCl]T decay on [Br]T, where [Br]T = [HOBr] + [OBr−] + [BrCl] + [Br−]. Reaction conditions: 0.36 M [PO4]T, p[H+] 7.00, μT = 1.0 M (Na2SO4), 22 °C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl.](/image/article/2002/EM/b105541k/b105541k-f2.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl.
°C, [HOCl]T/[Br]T > 4.0. Best fit line to quadratic equation: kobsHOCl = yo + a[Br]T + b[Br]T2, where a = (6.5 ± 0.3) × 10−2 M−1 s−1
and b = 24 ± 1 M−2 s−1. yo is calculated from eqn. (11) and equals 2.7 × 10−7 s−1 at [HOCl]T,i = 7.2 mM. Error bars represent error in kobsHOCl.


![Dependence of observed second-order rate constant for [HOBr]T loss (○) and %BrO3− yield (×) on initial [Cl]T, where [Cl]T = [HOCl] + [OCl−] + [BrCl] + [Cl−]. kdisp at zero [Cl]T,i
(△) calculated by eqn. (13). %BrO3− yield at zero [Cl]T,i
(□) calculated by eqn. (1). Best fit line to [HOBr]T rate constant is curve fit to the following equation: kobsHOBr = kHOBr + b[Cl]T2,
where kHOBr = (1.2 ± 0.3) × 10−2 M−1 s−1 and b = (1.06 ± 0.09) × 102 M−3 s−1. %BrO3− = [BrO3−]/[HOBr]T,i after 68 h total reaction time. Reaction conditions: 0.504 mM [HOBr]T, 0.36 M [PO4]T, p[H+] 7.04(2), μT = 1.0 M (Na2SO4), 25.0(2) °C. Dashed line shows trend in data. Error bars represent error in kobsHOBr.](/image/article/2002/EM/b105541k/b105541k-f3.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Dashed line shows trend in data. Error bars represent error in kobsHOBr.
°C. Dashed line shows trend in data. Error bars represent error in kobsHOBr.
![p[H+] dependence of observed rate constant (kobs) for [HOCl]T
(○) and [HOBr]T
(●). Error bars represent error in linear-least squares curve fit to kinetic traces. The lines show data trends. Reaction conditions: 7.3 mM [HOCl]T, 0.72 mM [Br]T, 0.36 M [PO4]T, μT = 1.0 M (Na2SO4), 25.0(2) °C.](/image/article/2002/EM/b105541k/b105541k-f4.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, μT = 1.0 M (Na2SO4). Yields were measured after 7 days total reaction time.
b %XO3− = [XO3−] yield/([HOCl]T,i + [HOBr]T,i) × 100 (where X = Cl or Br). %Total halate ion = %BrO3− + %ClO3−.
°C, μT = 1.0 M (Na2SO4). Yields were measured after 7 days total reaction time.
b %XO3− = [XO3−] yield/([HOCl]T,i + [HOBr]T,i) × 100 (where X = Cl or Br). %Total halate ion = %BrO3− + %ClO3−.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, X = Cl or Br, μT = 0.5–1.0 M.
°C, X = Cl or Br, μT = 0.5–1.0 M.




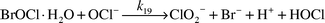


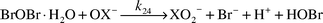





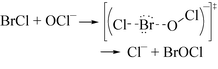







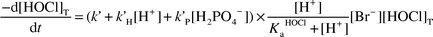








![Decomposition of 11.2 mM [HOCl]T in the presence of 9.24 µM [Br]T
(○) and 0 µM [Br]T
(△). Reaction conditions: 0.36 M [PO4]T, p[H+] 7.02, μT = 1.0 M (Na2SO4), 25.0(2) °C.](/image/article/2002/EM/b105541k/b105541k-f5.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
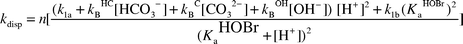
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) is 25% greater than in the absence of Br−. HOBr decay is attributed to disproportionation except at high total chlorine concentrations. ClO3− and BrO3− are formed from the rapid reactions of HOBr with ClO2− and HOCl with BrO2−, respectively. For this reason, chlorate and bromate formation rates are directly related to the decay rates of HOCl and HOBr. The stoichiometry of the oxidation of HOBr to BrO3− is 1∶1 when HOCl is present because HOCl rapidly converts BrO2− to BrO3− and HOBr is regenerated by HOCl/Br− reaction [eqn. (35)].
°C) is 25% greater than in the absence of Br−. HOBr decay is attributed to disproportionation except at high total chlorine concentrations. ClO3− and BrO3− are formed from the rapid reactions of HOBr with ClO2− and HOCl with BrO2−, respectively. For this reason, chlorate and bromate formation rates are directly related to the decay rates of HOCl and HOBr. The stoichiometry of the oxidation of HOBr to BrO3− is 1∶1 when HOCl is present because HOCl rapidly converts BrO2− to BrO3− and HOBr is regenerated by HOCl/Br− reaction [eqn. (35)].
