Theoretical study of the hydrogen abstraction by chlorine atoms for CH2BrCl and CHBrCl2
Received
14th September 2001
, Accepted 22nd October 2001
First published on 14th December 2001
Introduction
The hydrogen abstraction reactions of CH2BrCl and CHBrCl2 by Cl atoms, i.e.,| | 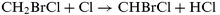 | (1) |
| |  | (2) |
are important in atmospheric chemistry due to their potential role in controlling the ozone concentration.1 Study of this kind of reaction can improve our understanding of the atmospheric lifetimes for these and related brominated compounds. In 1988, Tschuikow-Roux et al.2 measured the rate constants for reaction (1) as a function of temperature and obtained k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (6.46
(6.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2)
1.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 exp[(
10−11 exp[(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1502
1502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68)/T] cm3 molecule−1 s−1.
In 1998, Bilde et al.3 also measured the rate constants for both reactions and obtained k
68)/T] cm3 molecule−1 s−1.
In 1998, Bilde et al.3 also measured the rate constants for both reactions and obtained k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.2
(1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2)
0.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11
10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{(−1000
exp{(−1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82)/T} cm3 molecule−1 s−1 for the CH2BrCl
82)/T} cm3 molecule−1 s−1 for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction and k
Cl reaction and k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2.6
(2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4)
0.4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−12 exp{(−852
10−12 exp{(−852![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76)/T} cm3 molecule−1 s−1 for the CHBrCl2
76)/T} cm3 molecule−1 s−1 for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction by using relative rate methods. It can easily be seen that for reaction (1), the pre-exponential factor and activation energy of Tschuikow-Roux are somewhat
large. To our best knowledge, the theoretical C–H bond dissociation enthalpy of CH2BrCl has been estimated by Espinosa-Garcia et al.4 but the theoretical rate constants for the title reactions have not yet been studied theoretically. For the reactions of Cl with CH2BrCl and CHBrCl2
Cl reaction by using relative rate methods. It can easily be seen that for reaction (1), the pre-exponential factor and activation energy of Tschuikow-Roux are somewhat
large. To our best knowledge, the theoretical C–H bond dissociation enthalpy of CH2BrCl has been estimated by Espinosa-Garcia et al.4 but the theoretical rate constants for the title reactions have not yet been studied theoretically. For the reactions of Cl with CH2BrCl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , the Br-atom abstraction by Cl atoms is highly endothermic compared with the H-atom abstraction by Cl atoms, so these reactions can proceed via hydrogen abstraction.3 Thus it is necessary to investigate these reactions theoretically in order to reveal their mechanism.
, the Br-atom abstraction by Cl atoms is highly endothermic compared with the H-atom abstraction by Cl atoms, so these reactions can proceed via hydrogen abstraction.3 Thus it is necessary to investigate these reactions theoretically in order to reveal their mechanism.
Calculation methods
In this paper, standard ab initio and density functional theory (DFT) calculations are carried out with the Gaussian 98 program.5 Equilibrium geometries and frequencies of the stationary points (reactants, products, and transition states) are calculated by using Becke's half-and-half (BH&H)6 nonlocal exchange and the Lee–Yang–Parr (LYP)
7 nonlocal correlation functionals with the 6-311G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (d,p) basis set, which is denoted as BH&H-LYP/6-311
(d,p) basis set, which is denoted as BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p). At the same level, the minimum energy path (MEP) is obtained by the intrinsic reaction coordinate (IRC) method with a gradient step size of 0.05 u1/2a0
G(d,p). At the same level, the minimum energy path (MEP) is obtained by the intrinsic reaction coordinate (IRC) method with a gradient step size of 0.05 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . Furthermore, at 16 selected points (8 points in the reactant channel,
8 points in the product channel) along the MEP, the force constant matrices and the harmonic vibrational frequencies are calculated. For comparison, the equilibrium geometries of stationary points (reactants and products) are also optimized at the QCISD/6-311
. Furthermore, at 16 selected points (8 points in the reactant channel,
8 points in the product channel) along the MEP, the force constant matrices and the harmonic vibrational frequencies are calculated. For comparison, the equilibrium geometries of stationary points (reactants and products) are also optimized at the QCISD/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level. It should be noted that the difference in optimized geometries of reactants and products between the QCISD/6-311
G(d,p) level. It should be noted that the difference in optimized geometries of reactants and products between the QCISD/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) and BH&H-LYP/6-311
G(d,p) and BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) levels is small. Thus the geometries of the transition state and MEP obtained at the BH&H-LYP/6-311
G(d,p) levels is small. Thus the geometries of the transition state and MEP obtained at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level are used in further discussion. In order to obtain more accurate information on the energy, quadratic configuration interaction including single and double substitutions with a triple contribution [QCISD(T)]8 calculations
are performed using the 6-311
G(d,p) level are used in further discussion. In order to obtain more accurate information on the energy, quadratic configuration interaction including single and double substitutions with a triple contribution [QCISD(T)]8 calculations
are performed using the 6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) basis set at the BH&H-LYP MEP geometries. In order to obtain the rate constants theoretically, the POLYRATE-Version 8.4.1 program9 is employed with the aid of conventional transition state theory (TST) and the improved canonical variational transition state theory (ICVT) incorporating the small-curvature tunneling (SCT) correction methods proposed by Truhlar and co-workers.10,11 The rate constants are calculated in the temperature range 200–500 K by using mass-scaled Cartesian coordinates. The Euler single-step integrator with a step size of 0.0001 u1/2a0 is used to follow the MEP, and the generalized normal mode analysis is performed at every 0.01 u1/2a0
G(d,p) basis set at the BH&H-LYP MEP geometries. In order to obtain the rate constants theoretically, the POLYRATE-Version 8.4.1 program9 is employed with the aid of conventional transition state theory (TST) and the improved canonical variational transition state theory (ICVT) incorporating the small-curvature tunneling (SCT) correction methods proposed by Truhlar and co-workers.10,11 The rate constants are calculated in the temperature range 200–500 K by using mass-scaled Cartesian coordinates. The Euler single-step integrator with a step size of 0.0001 u1/2a0 is used to follow the MEP, and the generalized normal mode analysis is performed at every 0.01 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) .
.
Results and discussions
A. Stationary points
The optimized geometrical parameters of the reactants (CH2BrCl and CHBrCl2) and products (CHBrCl, CBrCl2 and HCl) at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level of theory are shown in Table 1, while those of the transition states are given in Table 2. The harmonic vibrational frequencies of all these species are presented in Table 3. For comparison, the available experimental values12–16 are also listed.
G(d,p) level of theory are shown in Table 1, while those of the transition states are given in Table 2. The harmonic vibrational frequencies of all these species are presented in Table 3. For comparison, the available experimental values12–16 are also listed.
Table 1 Calculated and experimental geometrical parameters (distances in Å and angles in degrees) of stable structures
| Species |
Geometrical parameters |
BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) G(d,p) |
QCISD/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) G(d,p) |
Exptl. |
| |
|
Ref. 12.
Ref. 13.
|
| CH2BrCl (Cs) |
r(CH) |
1.076 |
1.087 |
1.115a |
| |
r(CBr) |
1.934 |
1.941 |
1.928 |
| |
r(CCl) |
1.767 |
1.770 |
1.755 |
| |
∠HCH |
111.8 |
111.2 |
|
| |
∠HCBr |
107.3 |
107.3 |
109.3 |
| |
∠HCCl |
108.5 |
108.8 |
|
| CHBrCl (C1) |
r(CH) |
1.072 |
1.082 |
|
| |
r(CBr) |
1.860 |
1.871 |
|
| |
r(CCl) |
1.703 |
1.711 |
|
| |
∠HCBr |
116.9 |
116.6 |
|
| |
∠HCCl |
116.9 |
116.6 |
|
| |
∠BrCCl |
119.9 |
119.7 |
|
| CHBrCl2
(Cs) |
r(CH) |
1.074 |
1.084 |
|
| |
r(CBr) |
1.936 |
1.946 |
|
| |
r(CCl) |
1.764 |
1.768 |
|
| |
∠HCBr |
106.5 |
106.3 |
|
| |
∠HCCl |
107.8 |
107.9 |
|
| |
∠ClCCl |
111.5 |
111.5 |
|
| CBrCl2
(Cs) |
r(CBr) |
1.873 |
1.886 |
|
| |
r(CCl) |
1.712 |
1.720 |
|
| |
∠BrCCl |
117.5 |
117.2 |
|
| |
∠ClCCl |
116.9 |
116.6 |
|
| HCl |
r(HCl) |
1.276 |
1.276 |
1.275b |
Table 2 Optimized geometrical parameters (distances in Å and angles in degrees) of the transition states for both hydrogen abstraction reactions at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level
G(d,p) level
| Geometrical parameters |
ClBrHC⋯H′⋯Cl (C1) |
Cl2BrC⋯H′⋯Cl (Cs) |
| |
|
r(CH) |
1.078 |
|
|
r(CH′) |
1.324 |
1.288 |
|
r(CBr) |
1.886 |
1.904 |
|
r(CCl) |
1.723 |
1.734 |
|
r(H′Cl) |
1.506 |
1.539 |
| ∠HCH′ |
101.6 |
|
| ∠HCCl |
112.4 |
|
| ∠H′CCl |
106.7 |
104.8 |
| ∠H′CBr |
105.7 |
103.7 |
| ∠ClCCl |
|
113.8 |
| ∠HCBr |
111.9 |
|
| ∠CH′Cl′ |
174.2 |
177.6 |
L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δrCH′/δrH′Cl δrCH′/δrH′Cl |
1.22 |
0.81 |
Table 3 Calculated and experimental frequencies (cm−1) at stationary points
| Species |
BH&H-LYP/6-311G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (d,p) (d,p) |
Expt. |
| |
|
Ref. 14.
Ref. 15.
Ref. 16.
|
| CH2BrCl |
237, 633, 772, 889, 1209, 1322, 1507, 3225, 3308 |
229, 614, 744, 852, 1128,a 1231, 1482, 3003, 3066 |
| CHBrCl |
254, 450, 688, 887, 1273, 3315 |
866, 1196b |
| ClBrHC⋯H⋯Cl |
1359i, 78, 148, 251, 385, 700, 840, 893,1024, 1181, 1283, 3259 |
|
| CHBrCl2 |
225, 232, 346, 626, 761, 804, 1258, 1308, 3288 |
|
| CBrCl2 |
234, 246, 309, 447, 874, 926 |
|
| Cl2BrC⋯H⋯Cl |
1428i, 79, 93, 22, 234, 248, 397, 711, 812, 856, 1062, 1099 |
|
| HCl |
3045 |
2991c |
We first consider the static properties of the reactants and products. From Table 1, we can see that the theoretical bond lengths of reactants and products at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level are in excellent agreement with the QCISD results. The largest deviation of the bond angles is 0.6° for ∠HCH of CH2BrCl, and the largest bond length deviation is 0.013 Å for the C–Br bond in CBrCl2
G(d,p) level are in excellent agreement with the QCISD results. The largest deviation of the bond angles is 0.6° for ∠HCH of CH2BrCl, and the largest bond length deviation is 0.013 Å for the C–Br bond in CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . From Table 3, it is seen that the calculated frequencies of the reactants and products are 2–7% larger than the corresponding experimental values.14–16
. From Table 3, it is seen that the calculated frequencies of the reactants and products are 2–7% larger than the corresponding experimental values.14–16
Geometrical parameters of the transition states for both hydrogen abstraction reactions are listed in Table 2. In order to reflect the reactant- or product-like character of the forming transition state, we employ the parameter L,17 which is the ratio between the elongation of the C–H′ bond and the elongation of the Cl–H′ bond, L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr(C–H′)/δr(Cl–H′). We find L
δr(C–H′)/δr(Cl–H′). We find L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for reaction CH2BrCl
1 for reaction CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl and L
Cl and L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for reaction CHBrCl2
1 for reaction CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl, i.e., the H-abstraction transition state is reactant-like for the former reaction and product-like for the latter. It also can be seen that the transition state has C1
symmetry for reaction (1) and Cs symmetry for reaction (2). Both transition states are confirmed by normal-mode analyses, which present only one imaginary frequency. The angles between the breaking C–H′ bond and the nascent H′–Cl′ bond (∠CH′Cl′) are 174.2° for reaction (1), and 177.6° for reaction (2).
Cl, i.e., the H-abstraction transition state is reactant-like for the former reaction and product-like for the latter. It also can be seen that the transition state has C1
symmetry for reaction (1) and Cs symmetry for reaction (2). Both transition states are confirmed by normal-mode analyses, which present only one imaginary frequency. The angles between the breaking C–H′ bond and the nascent H′–Cl′ bond (∠CH′Cl′) are 174.2° for reaction (1), and 177.6° for reaction (2).
For both reactions, the reaction enthalpies and potential barriers calculated at the QCISD(T)//BH&H-LYP level with ZPE correction are listed in Table 4. For reactions (1) and (2), the enthalpies at 298 K are −4.18 and −6.88 kcal mol−1, respectively. This is in reasonable agreement with the corresponding experimental value −2.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.82 for reaction (1); we have not found an experimental result for reaction (2) in the recent literature. Table 4 also shows that the reaction potential barriers are 1.96 kcal mol−1 for reaction (1) and 0.67 kcal mol−1 for reaction (2).
2.82 for reaction (1); we have not found an experimental result for reaction (2) in the recent literature. Table 4 also shows that the reaction potential barriers are 1.96 kcal mol−1 for reaction (1) and 0.67 kcal mol−1 for reaction (2).
Table 4 Reaction enthalpies (ΔH2980), forward potential barriers (ΔEf)
(kcal mol−1) with ZPE correction for the two reactions
| |
|
BH&H-LYPa |
QCISD(T)//DFTb |
Expt.c |
| |
Calculated at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level.
Single point QCISD(T)/6-311 G(d,p) level.
Single point QCISD(T)/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) energy calculations at the BH&H-LYP/6-311 G(d,p) energy calculations at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) geometries.
Ref. 2. G(d,p) geometries.
Ref. 2.
|
CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHBrCl CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl HCl |
ΔH0298 |
−3.04 |
−4.18 |
−2.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8 2.8 |
| |
ΔEf |
4.08 |
1.96 |
|
CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBrCl2 CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl HCl |
ΔH0298 |
−6.39 |
−6.88 |
|
| |
ΔEf |
4.07 |
0.67 |
|
B. Minimum energy path
The changes in bond length along the IRC for the reactions of Cl with CH2BrCl and CHBrCl2 are plotted in Fig. 1. It is seen that as both reactions proceed, the active C–H′
(breaking) and Cl–H′
(forming) bond lengths change very smoothly up to s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.45 u1/2a0 for the CH2BrCl
−0.45 u1/2a0 for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction and −0.35 u1/2a0 for the CHBrCl2
Cl reaction and −0.35 u1/2a0 for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction. After that, both bonds change rapidly up to about s
Cl reaction. After that, both bonds change rapidly up to about s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 u1/2a0
0.5 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , then the changes become slow again. However, the remaining bond lengths are virtually unchanged over entire reaction processes.
, then the changes become slow again. However, the remaining bond lengths are virtually unchanged over entire reaction processes.
 |
| | Fig. 1 Changes in the bond length along the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) minimum energy path for (a) reaction (1) and (b) reaction (2) plotted vs. the reaction coordinate s in the mass weighted coordinates. G(d,p) minimum energy path for (a) reaction (1) and (b) reaction (2) plotted vs. the reaction coordinate s in the mass weighted coordinates. | |
Fig. 2 depicts the classical potential energy, VMEP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , the ground-state vibrational adiabatic potential energy, VaG
, the ground-state vibrational adiabatic potential energy, VaG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , and the zero-point energy for both reactions as functions of the intrinsic reaction coordinate s at the QCISD(T)/6-311
, and the zero-point energy for both reactions as functions of the intrinsic reaction coordinate s at the QCISD(T)/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level. For both reactions the ZPE shows a significant drop prior to the saddle point zone. Interestingly, we find that, for both reactions, the ground-state vibrational adiabatic potential surface has two barriers; one higher barrier at the entrance valley and the other in the transition state (s
G(d,p) level. For both reactions the ZPE shows a significant drop prior to the saddle point zone. Interestingly, we find that, for both reactions, the ground-state vibrational adiabatic potential surface has two barriers; one higher barrier at the entrance valley and the other in the transition state (s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 u1/2a0) of the MEP. But the two-barrier behavior is not remarkable for the CHBrCl2
0 u1/2a0) of the MEP. But the two-barrier behavior is not remarkable for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction. Such a two-barrier shape of VaG
has been revealed for the analogous reactions CH3X
Cl reaction. Such a two-barrier shape of VaG
has been revealed for the analogous reactions CH3X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl (X
Cl (X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F,18 Cl,19 Br19). According to the expression VaG
(s)
F,18 Cl,19 Br19). According to the expression VaG
(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VMEP
(s)
VMEP
(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZPE(s), the nonregular VaG shape may be attributed to the combination of two different factors: the low-energy barrier and the relatively large early drop of the zero-point energies prior to the saddle point zone.18 This kind of drop in the ZPE profile is usually a characteristic of H-abstraction reactions. Yet, when the drop in the ZPE profile is combined with a low, broad classical barrier profile (VMEP), it may cause a large variational effect. Thus the variational effect is
expected to be larger for the CHBrCl2
ZPE(s), the nonregular VaG shape may be attributed to the combination of two different factors: the low-energy barrier and the relatively large early drop of the zero-point energies prior to the saddle point zone.18 This kind of drop in the ZPE profile is usually a characteristic of H-abstraction reactions. Yet, when the drop in the ZPE profile is combined with a low, broad classical barrier profile (VMEP), it may cause a large variational effect. Thus the variational effect is
expected to be larger for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction than for the CH2BrCl
Cl reaction than for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction, since the former reaction has a broader VMEP with a smaller classical barrier than the latter one as shown in Fig. 2. The different variational effect will be presented in Section C.
Cl reaction, since the former reaction has a broader VMEP with a smaller classical barrier than the latter one as shown in Fig. 2. The different variational effect will be presented in Section C.
 |
| | Fig. 2
V
MEP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , ZPE, and VaG as a function of the reaction coordinate, s, at the QCISD(T)//BH&H-LYP level for (a) reaction (1) and (b) reaction (2). , ZPE, and VaG as a function of the reaction coordinate, s, at the QCISD(T)//BH&H-LYP level for (a) reaction (1) and (b) reaction (2). | |
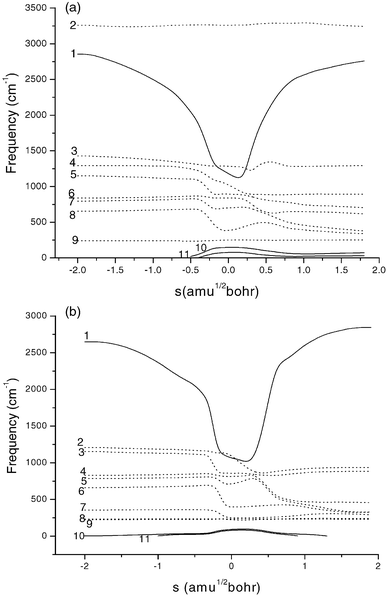
Fig. 3 shows the variations in generalized normal mode vibrational frequencies along the MEP for the two reactions. In the negative limit of s, the frequencies are associated with the reactants CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl and CHBrCl2
Cl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl, respectively. In the positive limit of s, the frequencies correspond to the products CHBrCl
Cl, respectively. In the positive limit of s, the frequencies correspond to the products CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl and CBrCl2
HCl and CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl. Now let us turn our attention to the frequencies in the vicinity of the transition states. For both reactions, when s approaches the saddle point zone, vibrational mode 1, which connects the frequency of the Cl–H′ stretching vibration of HCl with that of the C–H′ stretching vibration of CH2BrCl or CHBrCl2 drops sharply. From the above analysis it is reasonable to consider mode 1 as the “reactive mode”. For both reactions, the vibrational
modes 10 and 11 turn into translation or rotation in either reactant region or product region, and present a maximum near the saddle point. However, the increasing frequency of modes 10 and 11 does not fully compensate for the drop in the reactive mode 1, and thus the ZPE profile (Fig. 2) shows a noticeable drop with s.
HCl. Now let us turn our attention to the frequencies in the vicinity of the transition states. For both reactions, when s approaches the saddle point zone, vibrational mode 1, which connects the frequency of the Cl–H′ stretching vibration of HCl with that of the C–H′ stretching vibration of CH2BrCl or CHBrCl2 drops sharply. From the above analysis it is reasonable to consider mode 1 as the “reactive mode”. For both reactions, the vibrational
modes 10 and 11 turn into translation or rotation in either reactant region or product region, and present a maximum near the saddle point. However, the increasing frequency of modes 10 and 11 does not fully compensate for the drop in the reactive mode 1, and thus the ZPE profile (Fig. 2) shows a noticeable drop with s.
 |
| | Fig. 3 Generalized normal-mode vibrational frequencies for (a) reaction (1) and (b) reaction (2) as a function of the reaction coordinate, s. | |
To analyze further the reaction valley, the curvature term (k) of the reaction path as a function of s is plotted in Fig. 4. For both reactions, there are two peaks, one before the saddle point [s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.4 u1/2a0 for reaction (1) and −0.25 u1/2a0 for reaction (2)] and one after the saddle point [s
−0.4 u1/2a0 for reaction (1) and −0.25 u1/2a0 for reaction (2)] and one after the saddle point [s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 u1/2a0 for reaction (1) and 0.40 u1/2a0 for reaction (2)], due to strong coupling with C–H′
(in the reactant channel) and H′–Cl (in the product channel) stretch modes, respectively. This analysis
shows that the reaction path curvature should be taken into account in order to calculate the tunneling effect for both reactions, especially within low temperature regions. The tunneling effect on the rate constant for both reactions will be presented in Section C.
0.50 u1/2a0 for reaction (1) and 0.40 u1/2a0 for reaction (2)], due to strong coupling with C–H′
(in the reactant channel) and H′–Cl (in the product channel) stretch modes, respectively. This analysis
shows that the reaction path curvature should be taken into account in order to calculate the tunneling effect for both reactions, especially within low temperature regions. The tunneling effect on the rate constant for both reactions will be presented in Section C.
 |
| | Fig. 4 Reaction path curvatures (k) as a function of s. (⋯) reaction (1) and (—) reaction (2). | |
C. Rate constants
The rate constants of the forward reactions are calculated by using TST and ICVT with SCT correction for both hydrogen abstraction reactions over a wide temperature range from 200 to 500 K at the QCISD(T)//BH&H-LYP level. The calculated rate constants and the available experimental results for the two reactions are presented in Table 5 and Fig. 5. For reaction (1), there are two available experimental values measured by Tschuikow-Roux et al.2 and Bilde et al.3 The pre-exponential factor and activation energy of the former are somewhat larger than the later ones. Our calculated rate constants are in good agreement with both experimental results. The ratios between k(ICVT/SCT) and k(Expt) are 1.2, 1.4, 1.6, 2.0, 2.2, 2.4
and 2.6 at 217, 229, 250, 274, 296, 298 and 350 K, respectively. However, the temperature dependence of our rate constants is somewhat steeper than the measured one.3 For reaction (2)
(see Table 5(b) and Fig. 5(b)), only Bilde et al.3 measured the rate constants at five temperatures (217, 229, 250, 274 and 296 K) and the ratios of k(ICVT/SCT)/k(Expt)3 are 0.5, 0.6, 0.8, 0.9 and 1.1, respectively. Our calculated rate constants are also in good agreement with their measured values. Similar to reaction (1), the theoretical temperature dependence of the rate constants is also slightly steeper than the experimental one.
 |
| | Fig. 5 Computed ICVT/SCT rate constants as a function of 103/T and available experimental data for (a) reaction (1) and (b) reaction (2). | |
Table 5 Forward reaction rate constants (cm3 molecule −1 s −1) of (a) reaction (1) and (b) reaction (2) in the temperature range 200–500 K
|
T/K |
TST |
ICVT |
ICVT/SCT |
Ref. 2
|
Ref. 3
|
| |
| (a) |
|
|
|
|
|
| 200.0 |
8.83E-14 |
2.43E-14 |
7.51E-14 |
|
|
| 217.0 |
1.45E-13 |
5.11E-14 |
1.35E-13 |
|
1.11E-13 |
| 229.0 |
1.97E-13 |
8.12E-14 |
1.95E-13 |
|
1.37E-13 |
| 250.0 |
3.20E-13 |
1.67E-13 |
3.52E-13 |
|
2.25E-13 |
| 274.0 |
5.16E-13 |
3.33E-13 |
6.22E-13 |
2.69E-13 |
3.08E-13 |
| 296.0 |
7.57E-13 |
5.69E-13 |
9.76E-13 |
4.04E-13 |
4.47E-13 |
| 298.0 |
7.82E-13 |
5.95E-13 |
1.01E-12 |
4.18E-13 |
|
| 350.0 |
1.65E-12 |
1.56E-12 |
2.31E-12 |
8.84E-13 |
|
| 400.0 |
2.95 E-12 |
2.85E-12 |
3.86E-12 |
|
|
| 450.0 |
4.78E-12 |
4.69E-12 |
5.97E-12 |
|
|
| 500.0 |
7.25E-12 |
7.17E-12 |
8.72E-12 |
|
|
| (b) |
|
|
|
|
|
| 200.0 |
3.58E-13 |
8.01E-15 |
1.36E-14 |
|
|
| 217.0 |
4.69E-13 |
1.55E-14 |
2.43E-14 |
|
4.90E-14 |
| 229.0 |
5.57E-13 |
2.35E-14 |
3.51E-14 |
|
5.90E-14 |
| 250.0 |
7.34E-13 |
4.43E-14 |
6.21E-14 |
|
7.90E-14 |
| 274.0 |
9.72E-13 |
8.21E-14 |
1.09E-13 |
|
1.16E-13 |
| 296.0 |
1.22E-12 |
1.34E-13 |
1.70E-13 |
|
1.51E-13 |
| 298.0 |
1.25E-12 |
1.39E-13 |
1.77E-13 |
|
|
| 350.0 |
1.99E-12 |
3.50E-13 |
4.16E-13 |
|
|
| 400.0 |
2.91E-12 |
6.95E-13 |
7.95E-13 |
|
|
| 450.0 |
4.04E-12 |
1.21E-12 |
1.35E-12 |
|
|
| 500.0 |
5.40E-12 |
1.92E-12 |
2.09E-12 |
|
|
From Table 5(a), we can see that the ratio of k(TST)/k(ICVT) is in the range 3.6–1.0 for reaction (1) between 200 and 500 K; with increasing temperature the ratio decreases. This indicates that the variational effect is small for this reaction. However, the ratio of k(TST)/k(ICVT) is in the range 44.7–2.8 for reaction (2), which suggests a significant variational effect on the rate constants within the considered temperature range. The differences in the variational effect between the two reactions are consistent with their VMEP profile shapes, as discussed in Section B. For reaction (1), the ratio k(ICVT/SCT)/k(ICVT) is in the range 3.1–1.2 and for reaction (2), it is in the range 1.7–1.1 within the temperature range 200–500 K. This indicates that the small curvature tunneling effect on the rate constants is small for both reactions.
Conclusions
In this paper, the hydrogen abstraction reactions CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHBrCl
CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl and CHBrCl2
HCl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBrCl2
CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl are investigated theoretically. The respective forward potential barriers for both reactions calculated at the QCISD(T)//BH&H–LYP level are 1.96 and 0.67 kcal mol−1, and the respective reaction enthalpies are −4.18 and −6.88 kcal mol−1. The rate constants in the temperature range 200–500 K are calculated by conventional TST and the improved ICVT with SCT correction. For both reactions, the calculated rate constants are quantitatively in good agreement with the available experimental values over the measured temperature range although the temperature dependence of the theoretical rate constants is slightly steeper than the experimental results. The variational
effect on the calculation of rate constants for reaction (1) is large, whereas it is small for reaction (2). The tunneling corrections have only a small influence on the calculation of the rate constants for both reactions. Our results are helpful for further understanding of the mechanism of hydrogen abstraction reactions.
HCl are investigated theoretically. The respective forward potential barriers for both reactions calculated at the QCISD(T)//BH&H–LYP level are 1.96 and 0.67 kcal mol−1, and the respective reaction enthalpies are −4.18 and −6.88 kcal mol−1. The rate constants in the temperature range 200–500 K are calculated by conventional TST and the improved ICVT with SCT correction. For both reactions, the calculated rate constants are quantitatively in good agreement with the available experimental values over the measured temperature range although the temperature dependence of the theoretical rate constants is slightly steeper than the experimental results. The variational
effect on the calculation of rate constants for reaction (1) is large, whereas it is small for reaction (2). The tunneling corrections have only a small influence on the calculation of the rate constants for both reactions. Our results are helpful for further understanding of the mechanism of hydrogen abstraction reactions.
Acknowledgements
The authors thank Professor Donald G. Truhlar for providing the POLYRATE 8.4.1 program. This work is supported by the National Science Foundation of China (29892168, 20073014), Doctor Foundation by the Ministry of Education, Foundation for University Key Teacher by the Ministry of Education, and Key Subject of Science and Technology by the Ministry of Education of China.
References
- Global Ozone Research and Monitoring Project Report No. 37: Scientific Assessment of Ozone Depletion, World Meteorological Organization, 1994..
- E. Tschuikow-Roux, F. Faraji, S. Paddison, J. Niedzielski and K. Miyokawa, J. Phys. Chem., 1988, 92, 1488 CrossRef CAS.
- M. Bilde, T. J. Wallington, C. Ferronato, J. J. Orlando, G.
S. Tyndall, E. Estupiñan and S. Haberkorn, J. Phys. Chem. A, 1998, 102, 1976 CrossRef CAS.
- J. Espinosa-Garcia and S. Dobe, J. Phys. Chem. A, 1999, 103, 6387 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J.
R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Boboul, B. B. Stefnov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A.7, Gaussian, Inc., Pittsburgh, PA, 1998. Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968 CrossRef CAS.
-
Y.-Y. Chang, J. C. Corchado, P. L. Fast, J. Villa, W.-P. Hu, Y.-P. Liu, G. C. Lynch, C. F. Jackels, K. A. Nguyen, M. Z. Gu, I. Rossi, E. L. Coitino, S. Clayton, V. S. Melissas, B. J. Lynch, R. Steckler, B. C. Garrett, A. D. Isaacson and D. G. Truhlar, POLYRATE version 8.4.1, University of Minnesota, Minneapolis, 2000. Search PubMed.
-
D. G. Truhlar, A. D. Isaacson and B. C. Garrett, in The Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, FL, 1985, vol. 4, p. 65. Search PubMed.
- R. Steckler, W.-P. Hu, Y.-P. Liu, G. C. Lynch, B. C. Garrett, A. D. Isaacson, V. S. Melissas, D.-P. Lu, T. N. Troung, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1995, 88, 341 CrossRef CAS.
-
Numerical Data and Functional Relationship in Science and Technology, ed. K. H. Hellwege and A. M. Hellwege, Springer Verlag, Berlin, 1987, vol. 15 (supplement to Vol. II-17)..
-
K. P. Huber and G. Herzberg, Molecular Spectra and
Molecular Structure IV Constants of Diatomic Molecules, Van Nostrand Reinhold Co., New York, 1979. Search PubMed.
-
NIST Chemistry WebBook, NIST Standard Reference Database Number 69, February 2000 release, vibrational frequency data compiled by T. Shimanouchi..
- In NIST Chemistry WebBook, NIST Standard Reference Database Number 69, February 2000 Release, vibrational frequency data compiled by M. E. Jacox..
- M. W. Chase, Jr., C. A. Davies, J. R. Downey, Jr., D. J. Fryrip, R. A. McDonald and A. N. Syverud, JANAF Thermochemical Tables (3rd edn.), J. Phys. Chem. Ref. Data., 1985, 14, 1, Suppl. 1..
- M. Rayez, J. Rayez and J. Sawerysyn, J. Phys. Chem., 1994, 98, 11
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 CAS.
342 CAS.
- E. Rosenman and M. L. McKee, J. Am. Chem. Soc., 1997, 119, 9033 CrossRef CAS.
- J. F. Xiao, Z. S. Li, Y. H. Ding, J. Y. Liu, X. R. Huang and C. C. Sun, Phys. Chem. Chem. Phys., 2001, 3, 3955 RSC.
|
| This journal is © the Owner Societies 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level. The minimum energy path is obtained by the intrinsic reaction coordinate method at the same level, and the energies along the MEPs are further refined at the QCISD(T)/6-311
G(d,p) level. The minimum energy path is obtained by the intrinsic reaction coordinate method at the same level, and the energies along the MEPs are further refined at the QCISD(T)/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p)
(single-point) level. It is shown that the vibrational adiabatic potential energy curves for both reactions have two barriers. The rate constants are calculated using the improved canonical variational transition state theory with small-curvature tunneling correction within the temperature range 200–500 K. The
theoretical rate constants are quantitatively in good agreement with available experimental values, but the theoretical temperature dependence of the rate constants is somewhat steeper. Our results indicate that the variational effect is large for the Cl
G(d,p)
(single-point) level. It is shown that the vibrational adiabatic potential energy curves for both reactions have two barriers. The rate constants are calculated using the improved canonical variational transition state theory with small-curvature tunneling correction within the temperature range 200–500 K. The
theoretical rate constants are quantitatively in good agreement with available experimental values, but the theoretical temperature dependence of the rate constants is somewhat steeper. Our results indicate that the variational effect is large for the Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHBrCl2 reaction, whereas it is small for the Cl
CHBrCl2 reaction, whereas it is small for the Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH2BrCl reaction. For both reactions, the tunneling effect is small. Our results give further understanding of the mechanism of hydrogen abstraction reactions.
CH2BrCl reaction. For both reactions, the tunneling effect is small. Our results give further understanding of the mechanism of hydrogen abstraction reactions.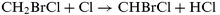

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (6.46
(6.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2)
1.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 exp[(
10−11 exp[(![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1502
1502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 68)/T] cm3 molecule−1 s−1.
In 1998, Bilde et al.3 also measured the rate constants for both reactions and obtained k
68)/T] cm3 molecule−1 s−1.
In 1998, Bilde et al.3 also measured the rate constants for both reactions and obtained k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.2
(1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2)
0.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11
10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{(−1000
exp{(−1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82)/T} cm3 molecule−1 s−1 for the CH2BrCl
82)/T} cm3 molecule−1 s−1 for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction and k
Cl reaction and k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2.6
(2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4)
0.4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−12 exp{(−852
10−12 exp{(−852![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76)/T} cm3 molecule−1 s−1 for the CHBrCl2
76)/T} cm3 molecule−1 s−1 for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction by using relative rate methods. It can easily be seen that for reaction (1), the pre-exponential factor and activation energy of Tschuikow-Roux are somewhat
large. To our best knowledge, the theoretical C–H bond dissociation enthalpy of CH2BrCl has been estimated by Espinosa-Garcia et al.4 but the theoretical rate constants for the title reactions have not yet been studied theoretically. For the reactions of Cl with CH2BrCl and CHBrCl2
Cl reaction by using relative rate methods. It can easily be seen that for reaction (1), the pre-exponential factor and activation energy of Tschuikow-Roux are somewhat
large. To our best knowledge, the theoretical C–H bond dissociation enthalpy of CH2BrCl has been estimated by Espinosa-Garcia et al.4 but the theoretical rate constants for the title reactions have not yet been studied theoretically. For the reactions of Cl with CH2BrCl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , the Br-atom abstraction by Cl atoms is highly endothermic compared with the H-atom abstraction by Cl atoms, so these reactions can proceed via hydrogen abstraction.3 Thus it is necessary to investigate these reactions theoretically in order to reveal their mechanism.
, the Br-atom abstraction by Cl atoms is highly endothermic compared with the H-atom abstraction by Cl atoms, so these reactions can proceed via hydrogen abstraction.3 Thus it is necessary to investigate these reactions theoretically in order to reveal their mechanism.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (d,p) basis set, which is denoted as BH&H-LYP/6-311
(d,p) basis set, which is denoted as BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p). At the same level, the minimum energy path (MEP) is obtained by the intrinsic reaction coordinate (IRC) method with a gradient step size of 0.05 u1/2a0
G(d,p). At the same level, the minimum energy path (MEP) is obtained by the intrinsic reaction coordinate (IRC) method with a gradient step size of 0.05 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . Furthermore, at 16 selected points (8 points in the reactant channel,
8 points in the product channel) along the MEP, the force constant matrices and the harmonic vibrational frequencies are calculated. For comparison, the equilibrium geometries of stationary points (reactants and products) are also optimized at the QCISD/6-311
. Furthermore, at 16 selected points (8 points in the reactant channel,
8 points in the product channel) along the MEP, the force constant matrices and the harmonic vibrational frequencies are calculated. For comparison, the equilibrium geometries of stationary points (reactants and products) are also optimized at the QCISD/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level. It should be noted that the difference in optimized geometries of reactants and products between the QCISD/6-311
G(d,p) level. It should be noted that the difference in optimized geometries of reactants and products between the QCISD/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) and BH&H-LYP/6-311
G(d,p) and BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) levels is small. Thus the geometries of the transition state and MEP obtained at the BH&H-LYP/6-311
G(d,p) levels is small. Thus the geometries of the transition state and MEP obtained at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level are used in further discussion. In order to obtain more accurate information on the energy, quadratic configuration interaction including single and double substitutions with a triple contribution [QCISD(T)]8 calculations
are performed using the 6-311
G(d,p) level are used in further discussion. In order to obtain more accurate information on the energy, quadratic configuration interaction including single and double substitutions with a triple contribution [QCISD(T)]8 calculations
are performed using the 6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) basis set at the BH&H-LYP MEP geometries. In order to obtain the rate constants theoretically, the POLYRATE-Version 8.4.1 program9 is employed with the aid of conventional transition state theory (TST) and the improved canonical variational transition state theory (ICVT) incorporating the small-curvature tunneling (SCT) correction methods proposed by Truhlar and co-workers.10,11 The rate constants are calculated in the temperature range 200–500 K by using mass-scaled Cartesian coordinates. The Euler single-step integrator with a step size of 0.0001 u1/2a0 is used to follow the MEP, and the generalized normal mode analysis is performed at every 0.01 u1/2a0
G(d,p) basis set at the BH&H-LYP MEP geometries. In order to obtain the rate constants theoretically, the POLYRATE-Version 8.4.1 program9 is employed with the aid of conventional transition state theory (TST) and the improved canonical variational transition state theory (ICVT) incorporating the small-curvature tunneling (SCT) correction methods proposed by Truhlar and co-workers.10,11 The rate constants are calculated in the temperature range 200–500 K by using mass-scaled Cartesian coordinates. The Euler single-step integrator with a step size of 0.0001 u1/2a0 is used to follow the MEP, and the generalized normal mode analysis is performed at every 0.01 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level of theory are shown in Table 1, while those of the transition states are given in Table 2. The harmonic vibrational frequencies of all these species are presented in Table 3. For comparison, the available experimental values12–16 are also listed.
G(d,p) level of theory are shown in Table 1, while those of the transition states are given in Table 2. The harmonic vibrational frequencies of all these species are presented in Table 3. For comparison, the available experimental values12–16 are also listed.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p)
G(d,p)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p)
G(d,p)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level
G(d,p) level
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δrCH′/δrH′Cl
δrCH′/δrH′Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (d,p)
(d,p)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level are in excellent agreement with the QCISD results. The largest deviation of the bond angles is 0.6° for ∠HCH of CH2BrCl, and the largest bond length deviation is 0.013 Å for the C–Br bond in CBrCl2
G(d,p) level are in excellent agreement with the QCISD results. The largest deviation of the bond angles is 0.6° for ∠HCH of CH2BrCl, and the largest bond length deviation is 0.013 Å for the C–Br bond in CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) . From Table 3, it is seen that the calculated frequencies of the reactants and products are 2–7% larger than the corresponding experimental values.14–16
. From Table 3, it is seen that the calculated frequencies of the reactants and products are 2–7% larger than the corresponding experimental values.14–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr(C–H′)/δr(Cl–H′). We find L
δr(C–H′)/δr(Cl–H′). We find L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for reaction CH2BrCl
1 for reaction CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl and L
Cl and L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for reaction CHBrCl2
1 for reaction CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl, i.e., the H-abstraction transition state is reactant-like for the former reaction and product-like for the latter. It also can be seen that the transition state has C1
symmetry for reaction (1) and Cs symmetry for reaction (2). Both transition states are confirmed by normal-mode analyses, which present only one imaginary frequency. The angles between the breaking C–H′ bond and the nascent H′–Cl′ bond (∠CH′Cl′) are 174.2° for reaction (1), and 177.6° for reaction (2).
Cl, i.e., the H-abstraction transition state is reactant-like for the former reaction and product-like for the latter. It also can be seen that the transition state has C1
symmetry for reaction (1) and Cs symmetry for reaction (2). Both transition states are confirmed by normal-mode analyses, which present only one imaginary frequency. The angles between the breaking C–H′ bond and the nascent H′–Cl′ bond (∠CH′Cl′) are 174.2° for reaction (1), and 177.6° for reaction (2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.82 for reaction (1); we have not found an experimental result for reaction (2) in the recent literature. Table 4 also shows that the reaction potential barriers are 1.96 kcal mol−1 for reaction (1) and 0.67 kcal mol−1 for reaction (2).
2.82 for reaction (1); we have not found an experimental result for reaction (2) in the recent literature. Table 4 also shows that the reaction potential barriers are 1.96 kcal mol−1 for reaction (1) and 0.67 kcal mol−1 for reaction (2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level.
b Single point QCISD(T)/6-311
G(d,p) level.
b Single point QCISD(T)/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) energy calculations at the BH&H-LYP/6-311
G(d,p) energy calculations at the BH&H-LYP/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) geometries.
c
Ref. 2.
G(d,p) geometries.
c
Ref. 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHBrCl
CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl
HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8
2.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBrCl2
CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl
HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.45 u1/2a0 for the CH2BrCl
−0.45 u1/2a0 for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction and −0.35 u1/2a0 for the CHBrCl2
Cl reaction and −0.35 u1/2a0 for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction. After that, both bonds change rapidly up to about s
Cl reaction. After that, both bonds change rapidly up to about s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 u1/2a0
0.5 u1/2a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , then the changes become slow again. However, the remaining bond lengths are virtually unchanged over entire reaction processes.
, then the changes become slow again. However, the remaining bond lengths are virtually unchanged over entire reaction processes.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) minimum energy path for (a) reaction (1) and (b) reaction (2) plotted vs. the reaction coordinate s in the mass weighted coordinates.
G(d,p) minimum energy path for (a) reaction (1) and (b) reaction (2) plotted vs. the reaction coordinate s in the mass weighted coordinates.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , the ground-state vibrational adiabatic potential energy, VaG
, the ground-state vibrational adiabatic potential energy, VaG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , and the zero-point energy for both reactions as functions of the intrinsic reaction coordinate s at the QCISD(T)/6-311
, and the zero-point energy for both reactions as functions of the intrinsic reaction coordinate s at the QCISD(T)/6-311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(d,p) level. For both reactions the ZPE shows a significant drop prior to the saddle point zone. Interestingly, we find that, for both reactions, the ground-state vibrational adiabatic potential surface has two barriers; one higher barrier at the entrance valley and the other in the transition state (s
G(d,p) level. For both reactions the ZPE shows a significant drop prior to the saddle point zone. Interestingly, we find that, for both reactions, the ground-state vibrational adiabatic potential surface has two barriers; one higher barrier at the entrance valley and the other in the transition state (s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 u1/2a0) of the MEP. But the two-barrier behavior is not remarkable for the CHBrCl2
0 u1/2a0) of the MEP. But the two-barrier behavior is not remarkable for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction. Such a two-barrier shape of VaG
has been revealed for the analogous reactions CH3X
Cl reaction. Such a two-barrier shape of VaG
has been revealed for the analogous reactions CH3X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl (X
Cl (X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F,18 Cl,19 Br19). According to the expression VaG
(s)
F,18 Cl,19 Br19). According to the expression VaG
(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VMEP
(s)
VMEP
(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZPE(s), the nonregular VaG shape may be attributed to the combination of two different factors: the low-energy barrier and the relatively large early drop of the zero-point energies prior to the saddle point zone.18 This kind of drop in the ZPE profile is usually a characteristic of H-abstraction reactions. Yet, when the drop in the ZPE profile is combined with a low, broad classical barrier profile (VMEP), it may cause a large variational effect. Thus the variational effect is
expected to be larger for the CHBrCl2
ZPE(s), the nonregular VaG shape may be attributed to the combination of two different factors: the low-energy barrier and the relatively large early drop of the zero-point energies prior to the saddle point zone.18 This kind of drop in the ZPE profile is usually a characteristic of H-abstraction reactions. Yet, when the drop in the ZPE profile is combined with a low, broad classical barrier profile (VMEP), it may cause a large variational effect. Thus the variational effect is
expected to be larger for the CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction than for the CH2BrCl
Cl reaction than for the CH2BrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl reaction, since the former reaction has a broader VMEP with a smaller classical barrier than the latter one as shown in Fig. 2. The different variational effect will be presented in Section C.
Cl reaction, since the former reaction has a broader VMEP with a smaller classical barrier than the latter one as shown in Fig. 2. The different variational effect will be presented in Section C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , ZPE, and VaG as a function of the reaction coordinate, s, at the QCISD(T)//BH&H-LYP level for (a) reaction (1) and (b) reaction (2).
, ZPE, and VaG as a function of the reaction coordinate, s, at the QCISD(T)//BH&H-LYP level for (a) reaction (1) and (b) reaction (2).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl and CHBrCl2
Cl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl, respectively. In the positive limit of s, the frequencies correspond to the products CHBrCl
Cl, respectively. In the positive limit of s, the frequencies correspond to the products CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl and CBrCl2
HCl and CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl. Now let us turn our attention to the frequencies in the vicinity of the transition states. For both reactions, when s approaches the saddle point zone, vibrational mode 1, which connects the frequency of the Cl–H′ stretching vibration of HCl with that of the C–H′ stretching vibration of CH2BrCl or CHBrCl2 drops sharply. From the above analysis it is reasonable to consider mode 1 as the “reactive mode”. For both reactions, the vibrational
modes 10 and 11 turn into translation or rotation in either reactant region or product region, and present a maximum near the saddle point. However, the increasing frequency of modes 10 and 11 does not fully compensate for the drop in the reactive mode 1, and thus the ZPE profile (Fig. 2) shows a noticeable drop with s.
HCl. Now let us turn our attention to the frequencies in the vicinity of the transition states. For both reactions, when s approaches the saddle point zone, vibrational mode 1, which connects the frequency of the Cl–H′ stretching vibration of HCl with that of the C–H′ stretching vibration of CH2BrCl or CHBrCl2 drops sharply. From the above analysis it is reasonable to consider mode 1 as the “reactive mode”. For both reactions, the vibrational
modes 10 and 11 turn into translation or rotation in either reactant region or product region, and present a maximum near the saddle point. However, the increasing frequency of modes 10 and 11 does not fully compensate for the drop in the reactive mode 1, and thus the ZPE profile (Fig. 2) shows a noticeable drop with s.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.4 u1/2a0 for reaction (1) and −0.25 u1/2a0 for reaction (2)] and one after the saddle point [s
−0.4 u1/2a0 for reaction (1) and −0.25 u1/2a0 for reaction (2)] and one after the saddle point [s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 u1/2a0 for reaction (1) and 0.40 u1/2a0 for reaction (2)], due to strong coupling with C–H′
(in the reactant channel) and H′–Cl (in the product channel) stretch modes, respectively. This analysis
shows that the reaction path curvature should be taken into account in order to calculate the tunneling effect for both reactions, especially within low temperature regions. The tunneling effect on the rate constant for both reactions will be presented in Section C.
0.50 u1/2a0 for reaction (1) and 0.40 u1/2a0 for reaction (2)], due to strong coupling with C–H′
(in the reactant channel) and H′–Cl (in the product channel) stretch modes, respectively. This analysis
shows that the reaction path curvature should be taken into account in order to calculate the tunneling effect for both reactions, especially within low temperature regions. The tunneling effect on the rate constant for both reactions will be presented in Section C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHBrCl
CHBrCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl and CHBrCl2
HCl and CHBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl
Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBrCl2
CBrCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl are investigated theoretically. The respective forward potential barriers for both reactions calculated at the QCISD(T)//BH&H–LYP level are 1.96 and 0.67 kcal mol−1, and the respective reaction enthalpies are −4.18 and −6.88 kcal mol−1. The rate constants in the temperature range 200–500 K are calculated by conventional TST and the improved ICVT with SCT correction. For both reactions, the calculated rate constants are quantitatively in good agreement with the available experimental values over the measured temperature range although the temperature dependence of the theoretical rate constants is slightly steeper than the experimental results. The variational
effect on the calculation of rate constants for reaction (1) is large, whereas it is small for reaction (2). The tunneling corrections have only a small influence on the calculation of the rate constants for both reactions. Our results are helpful for further understanding of the mechanism of hydrogen abstraction reactions.
HCl are investigated theoretically. The respective forward potential barriers for both reactions calculated at the QCISD(T)//BH&H–LYP level are 1.96 and 0.67 kcal mol−1, and the respective reaction enthalpies are −4.18 and −6.88 kcal mol−1. The rate constants in the temperature range 200–500 K are calculated by conventional TST and the improved ICVT with SCT correction. For both reactions, the calculated rate constants are quantitatively in good agreement with the available experimental values over the measured temperature range although the temperature dependence of the theoretical rate constants is slightly steeper than the experimental results. The variational
effect on the calculation of rate constants for reaction (1) is large, whereas it is small for reaction (2). The tunneling corrections have only a small influence on the calculation of the rate constants for both reactions. Our results are helpful for further understanding of the mechanism of hydrogen abstraction reactions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 CAS.
342 CAS.
