Method optimisation with the use of uncertainty budgets

Abstract

Uncertainty budgets can be used for a variety of situations, e.g. reporting the total uncertainty, calculating tolerance limits or method optimisation. In this paper it is demonstrated how the use of uncertainty budgets can help in reducing the total uncertainty of an analytical method, i.e. method optimisation. In this example it has been possible to reduce the total uncertainty of a concentration determination of hydrogen peroxide (by titration) from 2.7 × 10⁻² M to 3.93 × 10⁻³ M (or to about a 1/7) by changing the traceability chain and working with more pure reagents.

---

Introduction

By now most analytical chemists know of uncertainty budgets. Some scientists probably still see them as an unnecessary evil that is being forced on them. To some it might seem difficult to see the advantages of this technique. This paper is an attempt to illustrate the use of uncertainty budgets for method optimisation.

In any chemical analysis there are a large number of factors that contribute to the overall uncertainty; an uncertainty budget combines these contributions and gives an estimate of the total uncertainty. Below is shown an example of how uncertainty budgeting was used to optimise an analytical method.

The analytical method has deliberately been chosen to be a simple one, as it is the use of uncertainty budgets that is the key point of this paper.

The scope of the paper is to demonstrate the usefulness of uncertainty budgets, especially for the purpose of method optimisation. The technique of preparing the uncertainty budget itself is described in detail elsewhere (ISO ‘Guide to the Expression of Uncertainty in Measurement’ (GUM),¹ interpreted for chemistry in the EURACHEM Guide ‘Quantifying Uncertainty in Analytical Measurement’.²).

Method and results

The analysis method to be optimised is a titration of hydrogen peroxide. Ph. Eur. 3rd edn. 1997³ states the following method for determination of the strength of a 3% hydrogen peroxide solution: 10 gram hydrogen peroxide solution (3%) is weighed out; dilution to 100.0 ml with water10.0 ml is drawn; 20.0 ml of dilute sulfuric acid is added to the 10.0 ml; and the 30.0 ml is titrated with 0.02 M potassium permanganate. The concentration of hydrogen peroxide is calculated.

In order to calculate the uncertainty of the concentration of hydrogen peroxide found by the method, a model of how the result is obtained has to be deduced. The stoichiometry of the titration is:

2 KMnO₄ + 5 H₂O₂ + 6 H⁺ → 8 H₂O + 5 O₂ + 2 Mn²⁺ + 2 K⁺

From that, and from knowledge about titration, the following model is obtained:where c(H₂O₂) is the concentration of hydrogen peroxide, the 2.5 stems from the stoichiometry of the reaction, c(KMnO₄) is the concentration of the titer used, v(KMnO₄) is the volume of the titer, v(H₂O₂) is the volume of hydrogen peroxide and f(H₂O_2-dilution) is a correction factor, for the 30-fold dilution that is performed.

The different contributions to the total uncertainty of the concentration found by the analytical method are most easily shown in an Ishikawa diagram. An Ishikawa diagram is a tool to help the analyst remember and organise all uncertainty components. The diagram helps to prevent an uncertainty contribution being incorporated into the budget more than once. An Ishikawa diagram is produced by drawing an arrow for the measurand, and arrows leading to it are drawn for all the factors that influence the measurand. Likewise side arrows are drawn for the factors that influence those. In Fig. 1 an Ishikawa diagram for the titration of hydrogen peroxide is shown.

Fig. 1 Ishikawa diagram for the titration of hydrogen peroxide noting that, for example, the glassware in one branch of the Ishikawa diagram is not the same as glassware in another branch and that, on the branch for the concentration of KMnO₄, only one titration is included. A more thorough diagram for that branch is shown in connection with the description of the traceability chain.

After noting all the uncertainty contributions, the model is then used to calculate the uncertainty budget.

In this analysis method it is very important to know the correct concentration of potassium permanganate, otherwise the determination of the concentration of hydrogen peroxide will be incorrect. To make sure that the determination of the concentration of potassium permanganate is traceable in accordance with Ph. Eur., the concentration determination has to be performed by the steps demonstrated in Fig. 2.

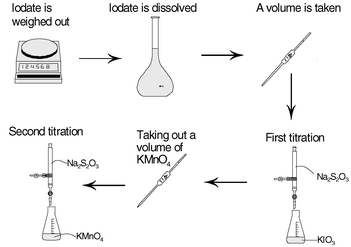Fig. 2 Steps in the process to achieve traceability for the titration of hydrogen peroxide according to Ph. Eur.

This will give rise to an expansion of the branch for the concentration of KMnO₄ in the Ishikawa diagram shown in Fig. 3.

Fig. 3 The extended Ishikawa diagram for the traceability of hydrogen peroxide.

In this traceability chain there are 3 titrations in order to determine the strength of hydrogen peroxide, each contributing to the total uncertainty.

A calculation of the uncertainty arising from this analysis is performed and shows a total uncertainty of 2.74 × 10⁻² M (the budget is shown in Table 1 given and examples of the calculations are in the Appendix); in Fig. 4 the uncertainty contributions from the different branches of the Ishikawa diagram are shown.

Fig. 4 Uncertainty contributions for the titration of hydrogen peroxide, with the traditional traceability chain.

The calculation of the uncertainty budget elucidated that the determination of the concentration of KMnO₄ accounted for by far the major part of the total uncertainty. The reason for this was the large number of steps in the traceability chain, and the purity of iodate, which was only 99.5% pure.

A closer inspection of the budget showed that an obvious way to reduce the total uncertainty was to alter the traceability chain.

A traceabilty chain where the concentration of KMnO₄ is determined by a single titration with a high purity sodium oxalate was suggested: the steps are shown in Fig. 5.

Fig. 5 Suggested steps in the new way of achieving traceability for the titration of hydrogen peroxide. With this traceability chain the Ishikawa diagram is reduced to the one first shown, with the addition of a purity term in the branch for concentration of calibrant.

The new traceability chain has one less titration and a higher purity of reagents (99.9% pure sodium oxalate). A calculation of the uncertainty budget for the same analysis method, with the new traceability chain, yielded a total uncertainty of 3.93 × 10⁻³ M. The calculation is shown in Table 2 in the Appendix. Fig. 6 shows the new uncertainty contributions.

Fig. 6 Uncertainty contributions with the suggested traceability chain.

The contribution to the overall uncertainty from the determination of the concentration of KMnO₄ is now comparable in size to the other contributions and the overall benefit is obvious.

Discussion and conclusions

Thus, the total uncertainty of the titration is reduced from 2.74 × 10⁻² M to 3.93 × 10⁻³ M or to about 1/7 of the original uncertainty. This large reduction was achieved merely by reducing the traceability chain by a titration step and working with purer chemicals, that is, changing from 99.5 to 99.9%. This may not seem a large change, but the effect on the uncertainty is dramatic.

The first uncertainty budget shows that the uncertainty contributions are distributed very unevenly, with a very large contribution from the determination of the concentration of KMnO₄ (calibration). As the traceability chain is altered, it can be seen that the uncertainty distributions become much more evenly distributed. After the alterations, it would be much more difficult to suggest ways to reduce the overall uncertainty, indicating that the process is closer to optimum.

In using uncertainty budgets it becomes very clear where the large contributions to the total uncertainty lie, which means that suggestions to reduce the total uncertainty will often follow naturally from the process of producing the uncertainty budget. This is why uncertainty budgets are such a useful tool in method optimisation. Uncertainty budgets make it possible to identify the key uncertainty contributions, to find the origin and reduce the contributions.

The uncertainty budget also have the benefit of including the total process, which means that the chemist becomes aware of the whole process and not just the analysis process, on which one would traditionally focus.

Another large advantage of producing uncertainty budgets is that contributions that logic would reject as being negligible, can actually have a large influence and should therefore be considered in method optimisation; this can be demonstrated by the uncertainty budget.

The example illustrates the value of taking time to analyse the unit operations in the method, including the traceability chain.

Appendix

Examples of how the uncertainty contributions have been found

To illustrate how the different uncertainty contributions have come about, two examples of that process are shown below. The examples are one for glassware and one for a balance: the rest of the contributions have been found in much the same way.

Uncertainty for the volume of the titer. In all volumetric glassware there has been included an uncertainty contribution to account for the fact that the glassware might be used at a temperature different from the one at which it has been calibrated. The thermal expansion coefficients for aqueous solutions are far greater than the one for glass, hence it is only necessary to account for the first.

The aqueous solutions are assumed to behave roughly like pure water. Pure water has a thermal expansion coefficient of 2.1 × 10⁻⁴ °C⁻¹. It is assumed that the temperature in the laboratory is within ±5 °C of 20 °C, which is the calibration temperature.

The remaining contributions to the uncertainty of the titer are: calibration of the burette (data sheet), uncertainty on the reading of the burette (deduced from the graduation of the burette) and an uncertainty on the visual determination of the end-point (has been estimated to one drop). The total uncertainty of the volume of the titer is:

Uncertainty of the mass of hydrogen peroxide. According to the EURACHEM guide,² the uncertainty of an analytical balance will consist of contributions from the readability, repeatability and the linearity. The size of these contributions can be found in the datasheet of the balance. Buoyancy is considered insignificant, as suggested in the EURACHEM guide.² The uncertainty contribution from the balance is calculated as:

Table 1 Uncertainty budget for the titration of hydrogen peroxide with traceability after Ph. Eur.

Uncertainty component	Estimates	Estimated or given uncertainty^a	Evaluation type (A/B) and/or expansion factor	Standard uncertainty u(xi)	Degree of freedom	Sensitivity coefficient	Contribution to the overall uncertainty
a Uncertainty contributions are found from literature (e.g., specifications), previous validation or separate uncertainty budgets, like the ones shown in the Appendix.
ctiter	0.02 M	6.17 × 10^−4 M	Mixed	6.17 × 10^−4 M	∞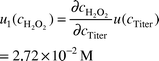
vtiter	17.65 ml	0.058 ml	Mixed	0.058 ml	∞
vH2O2	30 ml	0.037 ml	Mixed	0.037 ml	∞
fH2O2	30	5.85×10^−5	Mixed	5.85×10^−5	∞
u	0.88 M = 3%	—	—	—	—	—	2.74 × 10^−2 M
U	—	—	—	—	—	—	5.48 × 10^−2
Rel. U	—	—	—	—	—	—	6.22%

---

Table 2 Uncertainty budget for the titration of hydrogen peroxide with suggested traceability

Uncertainty component	Estimates	Estimated or given uncertainty^a	Evaluation type (A/B) and/or expansion factor	Standard uncertainty u(xi)	Degree of freedom	Sensitivity coefficient	Contribution to the overall uncertainty
a Uncertainty contributions are found from literature (e.g., specifications), previous validation or separate uncertainty budgets, like the ones shown in Appendix.
ctiter	0.02 M	5.5 × 10^−3 M	Mixed	5.47 × 10^−5 M	∞
vtiter	17.65 ml	0.058 ml	Mixed	0.058 ml	∞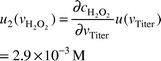
vH2O2	30 ml	0.037 ml	Mixed	0.037 ml	∞
FH2O2−opl	30	5.85×10^−5	Mixed	5.85×10^−5	∞
u	0.88 M = 3%	—	—	—	—	—	3.93 × 10^−3 M
U	—	—	—	—	—	—	7.86 × 10^−3 M
Rel. U	—	—	—	—	—	—	0.89%

---

References

1. Guide to the Expression of Uncertainty of Measurement, 1995, the guide is published by ISO in the name of the 7 organisations BIPM, IEC, IFCC, ISO, IUPAC, IUPAP and OIML, ISBN 92-67-10188-9.
2. Quantifying Uncertainty in Analytical Measurement, 2nd edn., 2000, the second edition of this guide has been prepared by the Eurachem Measurement Uncertainty Working Group in collaboration with members of CITAC and AOAC International and can be downloaded from: http://www.measurementuncertainty.org/mu/.
3. European Pharmacopoeia, 3rd edn., 1997, EDQM, Publications and Services, European Pharmacopoeia - BP 907, 226, avenue de Colmar, F-67029 Strasbourg Cedex 1, France.

---