Interaction of M³⁺ lanthanide cations with amide, urea, thioamide and thiourea ligands: a quantum mechanical study

Abstract

We report an ab initio quantum mechanical study on the interaction of M³⁺ cations (La³⁺, Eu³⁺, Yb³⁺) with model ligands L (L = amide, urea, thioamide and thiourea derivatives). The role of counterions and stoichiometry on ligand binding energies is investigated by a comparison of charged ML³⁺ complexes with the neutral MCl₃L and MCl₃L₂ ones. The calculations show that all ligands display strong interactions with the cation. Trends in binding energies in ML³⁺ (urea > thiourea > amide > thioamide) are found to differ from those of calculated protonation energies (thiourea > urea > thioamide > amide). Adding counterions or increasing the coordination number may also modify the relative affinities. Changes in structural parameters, electron transfer and polarization effects are analysed. The calculations reveal a striking difference in the binding mode of sulfur compared to oxygen ligands, and the role of steric repulsions in the first coordination sphere, due to counterions and increased coordination number. The results are discussed in the context of modelling complexes of lanthanide and actinides.

---

Introduction

The search for molecules that selectively complex lanthanides and actinides represents a challenging task from a basic point of view,¹ as well as for applications such as nuclear waste separation and minimization ^2,3 or design of photoactive systems.^4–7 Generally speaking, selective complexation in solution results from the interplay of features such as desolvation of the partners (solvent stripping from the cation and the ligand), conformational change of the ligand, and solvation of the formed complex, with possible counterion effects.⁸ One key requirement to form stable complexes is cation–ligand interactions that are strong enough to compete with the solvation forces. It is thus important to precisely assess the intrinsic energetic and stereochemical features of the elementary interactions between putative cations and the binding sites of the ligand. In the case of trivalent lanthanide or actinide ions, gas-phase data are not available from experiment. This led our group to undertake Quantum Mechanical (QM) computations to get information on structural, electronic and energetic features of non-covalent interactions between the metals and typical ligands. We recently reported QM ab initio studies on the interaction between the uranyl ⁹ and trivalent lanthanide cations ^10,11 M³⁺ with phosphoryl-containing R₃P[double bond, length half m-dash]O ligands (R = H, Me, Et, Ph, OMe). Ligands such as amide, pyridine, triazine or anisole derivatives were also considered.^12,13 In the series of phosphoryl ligands, we also investigated the effect of oxygen/sulfur substitution in R₃P[double bond, length half m-dash]O/R₃P[double bond, length half m-dash]S ¹⁴ and modelled the complexes with negatively charged “CYANEX-301” R₂PS₂⁻ ligands.¹⁵ Interest in sulfur compounds comes from the discovery of their extraction properties ^16,17 and, on a theoretical basis, from the HSAB concept according to which ligands are bases and cation are acids.^18–20 The softer character of sulfur, compared to oxygen, might be a source of selectivity among the M³⁺ lanthanides where the hardness decreases with the cation size (from La³⁺ to Lu³⁺) and for trivalent actinides which are presumably softer than lanthanides. We recently showed that, in addition to ligand basicity, electrostatic strain in the first coordination sphere is another source of ion–ligand discrimination in condensed phases.^11,15

The present paper extends the investigations on carbonyl derivatives: amide, thioamide, urea and thiourea complexes of lanthanide M³⁺ cations. Amide binding sites grafted on organized platforms such as calixarenes or resorcinarenes are good cation binders.^21,22 Calixarenes with urea or thiourea functionalized arms have been reported with the main focus on their hydrogen bonding capabilities, leading to supramolecular capsules or calixarene dimers ²³ as well as anion complexes in non-aqueous solution.^24,25 Thioamide calixarenes, like acyclic thioamides,^26–29 poorly extract M³⁺ lanthanide cations, compared to their amide analogues and prefer softer transition metals such as Cu²⁺, Pd²⁺, Cd²⁺ or Ag⁺.^30–32

In this study we compare the ligands (L) N,N′-dimethylacetamide (A) and its thioacetamide analogue (TA) with tetramethylurea (U) and its thiourea analogue (TU), shown in Fig. 1. They interact with typical lanthanide cations M³⁺ of decreasing size: La³⁺, Eu³⁺ and Yb³⁺. We first calculated the proton affinities E_prot of the four ligands, as it is generally believed that the proton basicities correlate with cation basicities. We next studied the intrinsic interaction energies ΔE between L and M³⁺, in the absence of other competing species, i.e. in the charged ML³⁺ complexes. Such complexes may poorly model, however, the species formed in condensed phases, where the coordination sphere of the cation is more or less saturated, and hard counterions also often bind to M³⁺. The effect of counterions is thus investigated in the neutral MCl₃L complexes of 1∶1 stoichiometry. Moving to higher stoichiometry in the MCl₃L₂ complexes gave further insights into the effect of cumulative ligands in the coordination sphere of M³⁺. For the three type of complexes, we focused on the interaction energies ΔE between L and the other part of the system, as defined in Fig. 2. Structural features of the complexes are also described, as they reveal the stereochemical requirements for ion binding. It will be shown that they are markedly dependent on the type of ligand L, as well as on the presence of the other coordinated species (counterions, other ligands). Electronic features of the systems and changes that occur upon complexation will be analysed by the changes in atomic charges.

Fig. 1 Simulated ligands: A, TA, U, TU.

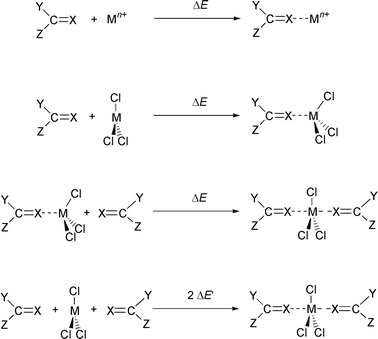Fig. 2 Definition of interaction energies ΔE and ΔE′ (X = O/S; Y, Z = Me/NMe₂).

Methods

The QM ab initio calculations were performed at the HF level using the Gaussian-94 and Gaussian-98 packages.^33,34 We showed that the HF results are comparable with those from MP2 or DFT calculations.^11,14 The 46 + 4f ⁿ core electrons of the lanthanide cations were described by the quasi relativistic pseudopotential of Dolg et al.^35,36 and the valence electrons by a (7s,6p,5d)/[5s,4p,3d] Gaussian basis set supplemented by one f polarization function of exponent 0.591, as optimized for La by Frenking et al.³⁷ The H, C, N, O, S and Cl atoms were described by the standard Dunning–Hay double-ζ basis set ³⁸ to which polarization functions (exponents being ζ_3dC = 0.75, ζ_3dN = 0.80_, ζ_3dO = 0.85, ζ_3dS = 0.532 and ζ_3dCl = 0.60) were added.

The geometries of the systems were fully optimized at the HF level using Berny’s algorithm without imposing symmetry constraints. Additional tests were performed with the MP2 and B3LYP-DFT methods. The interaction energies of the ligands L with M³⁺, MCl₃ and MCl₃L were calculated with respect to the corresponding optimized species. No basis set superposition error (“BSSE”) was systematically calculated because the BSSE is nearly constant within a given series.^11,13,14 The atomic charges were obtained by a Mulliken population analysis.

Results

The total energies of the optimized species are given in Table S1. In this section, we consider, unless otherwise specified, the HF results: interaction energies ΔE (see Table S2), optimized structural parameters and Mulliken charges (see Table S3). Figs. 3, 4, 6, 9 summarize the main energetic, structural and electronic features for L, LH⁺, ML³⁺, MCl₃ and MCl₃L₂ with M = La, Eu and Yb. Some DFT results are presented in the Discussion.

Fig. 3 Optimized L and LH⁺ species: distances (Å), angles (deg) and Mulliken charges (italics). Dipole moment of L (μ, Debye) and protonation energy (E_prot, kcal mol⁻¹; from HF/DZ*/HF/DZ* calculations without BSSE correction; see also Table 1 for MP2 and BSSE corrected energies).

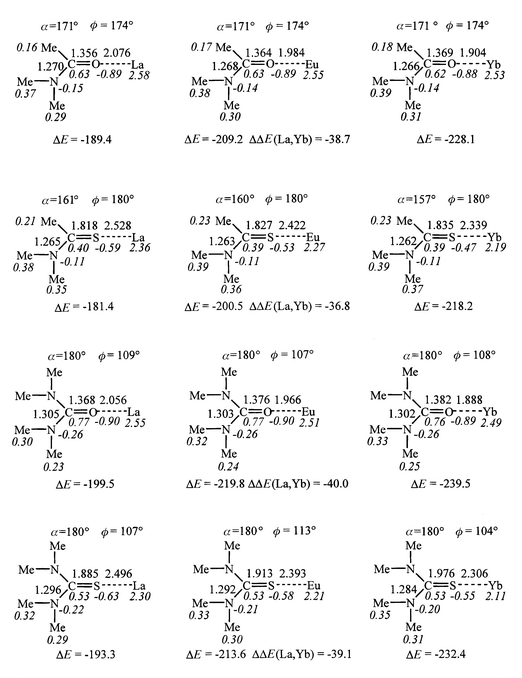Fig. 4 Optimized ML³⁺ complexes: distances (Å), angles (deg), Mulliken charges (italics). Interaction energies (ΔE, kcal mol⁻¹) between M³⁺ and L and ΔΔE(La, Yb).

1 . The free ligands and their protonation energies

The structures of the optimized ligands L and their protonated forms LH⁺ are displayed in Fig. 3. As shown by previous theoretical ³⁹ and experimental results,⁴⁰ protonation occurs at oxygen or sulfur, instead of at a nitrogen atom. The calculated protonation energies E_prot follow the sequence TU > U > TA > A, but the differences are small (6.3 kcal mol⁻¹ only along the series). The same sequence has been obtained at higher computational levels and by gas-phase experiments ⁴¹ and is confirmed by computations with BSSE correction at the HF level, as well as at the MP2 level (Table 1). Thus, sulfur ligands are somewhat more basic than the oxygen analogues (by 2.3 to 3.1 kcal mol⁻¹), and basicities are larger for NMe₂ than for Me carbon derivatives (by 3.2 to 4.0 kcal mol⁻¹). The higher basicity of sulfur, also observed for other series of compounds (e.g. ether/thioether, alcohol/thioalcohols,⁴² phosphoryl/thiophosphoryl ¹⁴) relates to its higher polarizability and to the more covalent character of the S–H bond, compared to O–H. Upon protonation, the C[double bond, length half m-dash]S bond lengthens less (by 0.07 to 0.09 Å) than does the C[double bond, length half m-dash]O bond (by about 0.10 Å). The greater basicity of sulfur also correlates with the higher dipole moment of TA and TU (5.4 and 5.0 D, respectively), compared to A and U (4.1 and 3.4 D, respectively), but not with the Mulliken charges on S/O atoms which yield opposite trends. Another distinct feature concerns the charge transfer Δq to the proton, larger (by about 0.3 e) in the sulfur compounds. In the latter, Δq stems mostly from the protonated centre (sulfur loses about 0.3 e), while in the oxygen compounds, the oxygen atom becomes more negative (by about 0.1 e) and the charge is transferred from the carbon substituents.

Table 1 Total and relative protonation energies (kcal mol⁻¹) from HF/DZ*/HF/DZ* and MP2/DZ*/HF/DZ* calculations without/with BSSE correction

	HF/DZ*/HF/DZ*		MP2/DZ*/HF/DZ*
Complex	ΔE/ΔEcor	ΔΔEM/ΔΔEcorM	ΔE/ΔEcor	ΔΔEM/ΔΔEcorM
(Me2N)MeCOH^+	−226.5/−226.2	0.0/0.0	−220.5/−218.8	0.0/0.0
(Me2N)MeCSH^+	−228.8/−228.6	−2.3/−2.4	−222.5/−221.0	−2.5/−2.2
(Me2N)2COH^+	−229.7/−229.4	−3.2/−3.2	−225.1/−223.4	−4.6/−4.6
(Me2N)2CSH^+	−232.8/−232.6	−6.3/−6.4	−228.1/−226.2	−7.6/−7.4

---

Interesting structural features are noticed in the series. The C[double bond, length half m-dash]O–H⁺ angles are comparable in the amide and urea acids (114°), as are the C[double bond, length half m-dash]S–H⁺ angles (97°) in the corresponding thio acids. A marked difference is observed between the acetamide AH⁺ and TAH⁺ acids and the urea UH⁺ and TUH⁺ analogues: in the former the proton sits in the plane of the carbonyl or thiocarbonyl groups, while in the latter it is slightly out of plane (the NC–XH dihedral angle is 161° in UH⁺ and 156° in TUH⁺), indicating some repulsion between the proton and the NMe₂ groups. Steric hindrance in the urea compounds is also revealed by their non-planarity, leading to almost C₂, instead of C_2v symmetry (excluding the proton). This non-planarity is consistent with previous studies on unsubstituted urea and thiourea (with NH₂, instead of NMe₂ groups),⁴³ as well as for cyclic analogues ⁴⁴ where the C–N rotational barriers are lower than in the amide analogues.

2 . The charged 1∶1 ML³⁺ complexes

According to the calculations, the attraction energies (−ΔE) between the ligands and the lanthanide cations are high (189 to 239 kcal mol⁻¹) and decrease in the order U > TU > A > TA. Thus, the four ligands bind lanthanide cations as efficiently as Me₃P[double bond, length half m-dash]S and Ph₃P[double bond, length half m-dash]S thiophosphoryl ligands (200 and 230 kcal mol⁻¹, respectively), and better than p-Me-pyridine (170 kcal mol⁻¹).¹³ The energy scale in this ligand series is similar (about 20 kcal mol⁻¹) for the three cations. This is comparable to the energy difference between H₂NMeC[double bond, length half m-dash]O and Me₂NMeC[double bond, length half m-dash]O acetamide ligands interacting with M³⁺ cations (about 22 kcal mol⁻¹) ¹³ and relatively small, compared to the energy scale in the cation series for a given ligand (from 37 to 40 kcal mol⁻¹). For a given ligand, ΔE increases with the cation hardness (La³⁺ < Eu³⁺ < Yb³⁺), as observed with all ML³⁺ systems simulated in similar conditions.^12,13 The ΔE(La, Yb) energy difference, which measures the cation selectivity for a given ligand, follows the same order as the ΔE values: it is largest for U and smallest for TA complexes. Thus, sulfur ligands display weaker M³⁺ affinities than oxygen ligands, in contrast to trends in proton affinities. A similarly contrasting trend has been recently reported for R₃P[double bond, length half m-dash]O vs. R₃P[double bond, length half m-dash]S ligands. ¹⁴ The difference is somewhat larger for amide (8 to 10 kcal mol⁻¹ for Avs.TA) than for urea derivatives (6 to 7 kcal mol⁻¹ for Uvs.TU). Thus, the M³⁺ basicities are more modulated by the Me/NMe₂ substitution at carbon than by the S/O substitution. The S/O cation basicity contrasts with observed trends on proton basicities (vide supra).

The oxygen/sulfur cation basicity can be qualitatively understood from the HSAB principle, according to which the hard M³⁺ ions prefer the hardest bases, i.e. oxygen rather than sulfur ligands, and from the higher electron donation and polarizability of NMe₂, compared to Me carbon substituents. There is thus no correlation between the dipole moments of L and the ΔE values (Figs. 3 and 4). The interaction energies ΔE are markedly dependent on polarization and charge transfer effects, as illustrated by changes in Mulliken charges. The cationic charge ranges from 2.58 (in LaA³⁺) to 2.11 e (in YbTU³⁺), as the result of electron transfer Δq from L. For a given ligand, Δq increases as ΔE, i.e. from La³⁺ to Yb³⁺, but the changes in the cation series are relatively small (0.05 to 0.19 e for a given ligand), compared to the Δq in the ligand series (0.24 to 0.42 e for a given cation). The transfer is larger with sulfur than with oxygen compounds (by 0.22 to 0.38 e) and larger for the NMe₂ than for the Me carbon substituted ones (by 0.03 to 0.08 e). Thus, the order of M³⁺ basicities does not simply follow the order of the Δq values.

The second important effect concerns the polarization of L by the cation. We notice that in all ML³⁺ complexes the cation sits in the plane of the molecule, which leads to the most effective polarization. In the U and TU complexes, the cation lies on the C[double bond, length half m-dash]O or C[double bond, length half m-dash]S axis, while in the amide A and TA complexes, it is somewhat trans to the C–N bond: the C[double bond, length half m-dash]O–M angle is 171° with the three cations, while the C[double bond, length half m-dash]S–M angle ranges from 157° (with Yb) to 161° (with La). The trans position is favoured by polarization effects (NR₂ is more polarizable than Me) and by steric effects (the Me side is less hindered). Thus, cation coordination is much more linear than proton coordination, due to the different nature of the bonds. As a result of polarization, the q_O or q_S charges are more negative in ML³⁺ than in uncomplexed L, while the adjacent carbon is more positive. As the S atom transfers more charge to the cation than does the O atom, the charge increase Δq_S is smaller than the Δq_O increase. As a result of polarization and charge transfer effects, the Me_N and Me_C groups are also more positive in ML³⁺ than in L.

Concerning the structure of the complexes, we notice that the M–S bonds are about 0.5 Å longer than the M–O ones, while in a cation series, these bonds are shortest with the smallest ion (Yb) and longest with La (by about 0.2 Å). For a given type of binding site (X = O/S), the stronger the interaction energy ΔE, the shorter is the X–M bond: with M = La, the bond variation ranges from 0.02 (X = O) to 0.03 Å (X = S).

The strong electronic perturbations of L that occur upon coordination to the cation also translate into large geometry changes: the C[double bond, length half m-dash]O and C[double bond, length half m-dash]S bonds lengthen, while the N–C bonds shorten, following trends suggested by the stabilization of the ionic form of the complex (Fig. 5). In the ML³⁺ complexes, the C[double bond, length half m-dash]O and C[double bond, length half m-dash]S bonds are even longer than in the corresponding protonated C[double bond, length half m-dash]OH⁺ and C[double bond, length half m-dash]SH⁺ species (see Figs. 3 and 4). They increase in the order La³⁺ < Eu³⁺ < Yb³⁺ in the cation series (by about 0.01 Å) and upon Me→NMe₂ carbon substitution (by about 0.01 Å). Thus, compared to the free ligands, the largest deformation Δd is observed in the thiourea complex YbTU³⁺ (0.30 Å), while in the corresponding oxygen complex, Δd is only 0.18 Å. These deformations again contrast with those observed upon protonation, where C[double bond, length half m-dash]S was less elongated than C[double bond, length half m-dash]O. Lanthanide cation coordination results mostly from electrostatic interactions, while protonation involves more covalent binding.

Fig. 5 Schematic representation of electronic effects in the ML³⁺ complexes.

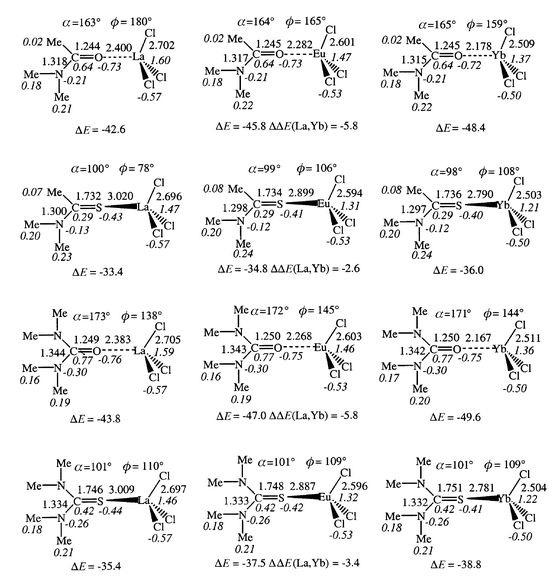Fig. 6 Optimized MCl₃L complexes: distances (Å), angles (deg), Mulliken charges (italics). Interaction energies (ΔE, kcal mol⁻¹) between MCl₃ and L and ΔΔE(La, Yb).

3 . The neutral MCl₃L complexes. Effects of counterions

Addition of a ligand L to a neutral MCl₃ salt leads to MCl₃L complexes, where the electrostatic interactions between the MCl₃ moiety and L are of the dipole–dipole type, and therefore are weaker than the charge–dipole M³⁺ ⋯ L interactions in the ML³⁺ complexes. As a result, the interaction energies ΔE with L drop markedly from ML³⁺ to MCl₃L (by a factor of 4.4 to 4.8 for oxygen ligands and 5.4 to 6.1 for sulfur ligands) where ΔE values range from −33 to −50 kcal mol⁻¹ (Fig. 6). Thus, the preference of oxygen to sulfur ligands (by 8 to 12 kcal mol⁻¹) is retained and, in most cases, enhanced in the presence of counterions. On the other hand, the NMe₂/Me substituent effect at carbon drops on going from ML³⁺ (14 to 10 kcal mol⁻¹) to MCl₃L complexes (3 to 1 kcal mol⁻¹). Thus, in the presence of counterions, the effect of O/S substitution becomes larger than the effect of NMe₂/Me carbon substitution, in relation to the different nature of ligand binding in ML³⁺vs. MCl₃L complexes. As a result, the ligand affinity for a given cation increases in the order TA < TU < A < U in MCl₃L complexes, i.e. in a different sequence to the ML³⁺ complexes (TA < A < TU < U). We suggest that the A/TU inversion and the weaker preference for urea, compared to amide derivatives (1–3 kcal mol⁻¹ only) are due to destabilizing interactions between the anions and the NMe₂ groups in the urea compounds (vide infra). These repulsions are antagonistic to the stabilization energy that would result from the larger electron donating capability and polarizability of NMe₂ compared to Me.

Adding counterions to the ML³⁺ complexes retains the same order of cation affinities for a given ligand (La³⁺ < Eu³⁺ < Yb³⁺), but the La/Yb binding selectivity ΔΔE(La,Yb) drops markedly (from 37–40 kcal mol⁻¹ in ML³⁺ to 3–6 kcal mol⁻¹ in MCl₃L). Again, the larger (or smaller) the interaction energy ΔE, the larger (or weaker) is the ion selectivity.

The reduced interactions in MCl₃L, compared to ML³⁺, translate into larger metal–ligand distances: the S–M bonds lengthen more (by 0.45 to 0.51 Å) than the O–M bonds (by 0.27 to 0.33 Å), and the lengthening increases from Yb to La. The geometry of the ligand is also less perturbed in MCl₃L than in ML³⁺.

The cation binding mode of L is very different in MCl₃L from that in the ML³⁺ complexes. First, the α angle between M with the C[double bond, length half m-dash]X bond deviates more from linearity. For instance, the C[double bond, length half m-dash]O–M angle is about 164° in the amide EuCl₃A complex and 172° in the urea complex UEuCl₃. In sulfur complexes, the C[double bond, length half m-dash]S–M angle is 98 to 101°, i.e. closer to the value in the protonated LH⁺ forms than in ML³⁺. Moving from linear to bent coordination is indicative of enhanced covalent binding and of reduced polarization interactions in the MCl₃L complexes.

The second striking feature concerns the co-planarity of M and the ligands. In one case only (LaCl₃A complex) the cation sits in the plane of the ligand. In all other cases, it is slightly out of plane, as measured by the ϕ dihedral angles (ϕ = NC–XM; see definition in Fig. 7 and values in Fig. 6). In EuCl₃A and YbCl₃A, M is close to the plane of the ligand (ϕ = 160°). This contrasts with the thioamide analogues MCl₃TA where the cation sits nearly perpendicular to the plane of the TA ligand (ϕ ranges from 78 to 108°). Among the urea complexes, non-planarity is again much more pronounced for sulfur complex MCl₃TU (ϕ = 110°; see Fig. 8) than for the oxygen MCl₃U complexes (ϕ = 138 to 145°). These results suggest that the chloride anions interact repulsively with the ligand, and that the repulsions are larger for the NMe₂ than for the Me carbon substituent, and larger for sulfur than for oxygen ligands where the coordination is more linear.

Fig. 7 Definition of non-linear (α) and out of plane (ϕ) cation coordination.

Fig. 8 Structure of the EuCl₃TU complex.

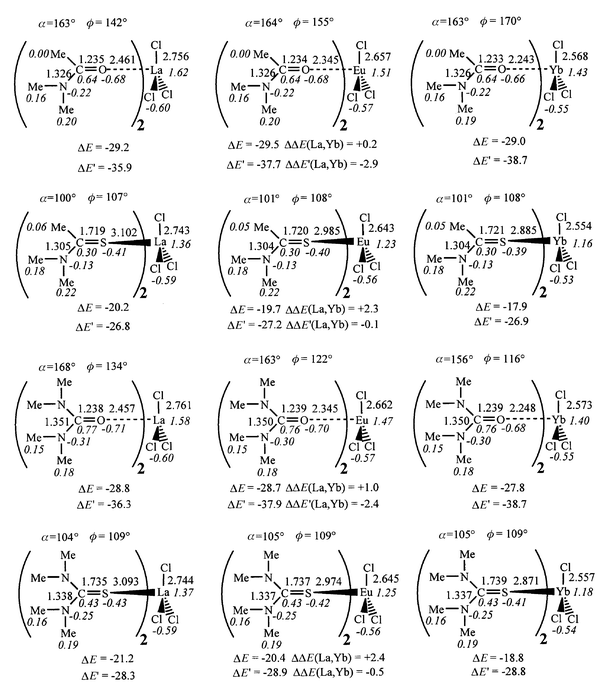Fig. 9 Optimized MCl₃L₂ complexes: distances (Å), angles (deg), Mulliken charges (italics). Interaction energies (ΔE, kcal mol⁻¹) between MCl₃L and L, ΔE′ and ΔΔE(La, Yb).

The importance of repulsive interactions between the anions and the amide substituents is supported by the two following “computer experiments”. We first optimized the thioformamide (TFA = Me₂NHC[double bond, length half m-dash]S) EuCl₃TFA complex, where repulsions between the H atom on the carbon and the anions should be minimal, and found that the Eu atom sits indeed exactly in the plane of TFA (the NC–SEu angle is 180°). Furthermore, the binding energy of TFA is slightly better (by 0.1 kcal mol⁻¹) than the binding of the TA, despite the lower polarizability and donating capability of the H atom, compared to the Me group. This is indicative of an intrinsic preference for in-plane binding and of repulsive interactions between the carbon substituent (Me of TA, or NMe₂ of U or TU) and the counterions. The second test was run on the thiourea complex EuCl₃TU, which was optimized with the Eu atom respectively “in-plane” (NC–SEu angle constrained at 0°) and “perpendicular to the plane” of the ligand (NC–SEu angle constrained at 90°). The “in plane” binding turns out to be 6.7 kcal mol⁻¹ less stable than the “perpendicular” binding. The corresponding C[double bond, length half m-dash]S–Eu angle is more open for the planar binding (129°) than for the “perpendicular” binding (102°), also indicating larger repulsions in the former. The out-of-plane metal binding to sulfur ligands is also observed in solid state structures of analogous complexes (vide infra).

The Mulliken charges also reveal the difference in ligand binding to MCl₃, compared to M³⁺. We first notice that, in relation to the electron donation from the anions to the metal (0.50 to 0.43 e per chloride), the metal charge is much less positive (1.6 to 1.2 e) in the MCl₃L than in ML³⁺ complexes. The MCl₃ moiety is pyramidal (the X–M–Cl angle ranges from 99 to 103°), leading to a dipole which interacts with the L ligand much less than does the “naked” M³⁺ cation. As a result, the charge transfer from L drops from ML³⁺ (0.42–0.89 e) to MCl₃L (0.11–0.29 e). It is larger for sulfur than for oxygen ligands (0.15 e) and similar for NMe₂ and Me substituted carbon. Also, the charge of the coordinated atoms (X = O/S) lies between the charge in MCl₃L and uncomplexed L, due to the reduced contribution of polarization effects.

4 . Neutral MCl₃L₂ complexes

Adding a second ligand to the MCl₃L complex leads to a coordination number of five, closer to the coordination in condensed media. The corresponding binding energy ΔE has been compared to the average binding energy per ligand ΔE′ (Table S2 and Fig. 9), ΔE′ being somewhat larger than ΔE (by 7 to 11 kcal mol⁻¹). We first discuss the ΔE binding energy, which ranges from 18 to 29 kcal mol⁻¹ for all MCl₃L₂ complexes. The drop in ΔE from the first to the second ligand is more pronounced for oxygen (65%) than for sulfur compounds (55%) and for the Yb cation, which is complexed best by all the ligands in the ML³⁺ and MCl₃L series. This leads to a levelling of all ΔE values and to inversions compared to the MCl₃L complexes. With the four ligands, the ΔΔE(La,Yb) difference becomes positive (from 0.5 to 2.4 kcal mol⁻¹), which means that L binds better to the lanthanum than to the ytterbium for the MCl₃L complexes. We suggest that this inversion stems from “strain repulsion” in the first coordination sphere of the cation, which is antagonistic to the metal–ligand and metal–anion attractions. These repulsions are most effective with the smallest cation Yb. Thus, the order of metal affinities is Yb < Eu < La for the TA, U and TU ligands. With the A ligand, the ΔΔE(La,Yb) is smallest (0.5 kcal mol⁻¹) and europium is slightly preferred (Yb < La < Eu). Thus, increasing the coordination number of the metal does not simply scale down the ligand binding energies, but modulates the order of ion discrimination for a given ligand. For a given metal, the preference for oxygen vs. sulfur ligands is retained (by about 10 kcal mol⁻¹) and the ligands bind in the order TA < TU < U < A. The A/U order is thus different from the order in the MCl₃L complexes, but in both cases, the differences ΔΔE(A, U) and ΔΔE(TA, TU) are small (about 1 kcal mol⁻¹).

Looking at the ΔE′ average interaction energy per ligand yields similar conclusions to the ΔE energies, as far as the comparison of ligands for a given metal is concerned (Fig. 9). The U/A order is inversed but the difference in ΔE as well as in ΔE′ values is small (from 0.0 to 1.2 kcal mol⁻¹). The order in the cation series for a given L also differs somewhat. In most cases, binding to ytterbium is preferred over lanthanum, but the difference is small (from 0.1 to 2.9 kcal mol⁻¹). This is because the ΔE′ energies lie between the ΔE values in MCl₃L₂ and in MCl₃L, and contain therefore relatively more attraction (which favour Yb) than repulsion (which favour La) contributions.

Some features may also be noticed concerning the structure of MCl₃L₂ complexes. Although no symmetry was imposed during the minimization, the two optimized ligands are related by a C₂ symmetry axis and the MCl₃ moiety is planar. The zero dipole moment of MCl₃ explains, in addition to the ligand–ligand repulsions, the weaker binding of L. As a result, the metal–ligand distances are longer in MCl₃L₂ than in MCl₃L (by 0.06 to 0.08 Å with oxygen ligands and by 0.08–0.09 Å with sulfur ligands). The ligand structures are also less perturbed than in MCl₃L: the C[double bond, length half m-dash]O and C[double bond, length half m-dash]S bonds are shorter, and the C–N bonds are longer (by about 0.01 Å), being much closer to the structures of uncomplexed L. The cation binding mode is very close to that found in MCl₃L complexes. In the oxygen complexes, the C[double bond, length half m-dash]O–M angles are almost linear (156 to 168°) and the cation sits closer to the plane of the amide A (ϕ = 142 to 170°) than in the case of the urea U ligand (ϕ = 116 to 134°). In the sulfur complexes, the C[double bond, length half m-dash]S–M angles are bent (100 to 105°) and the cation sits nearly perpendicular to the plane of the ligands (ϕ = 107 to 109°).

The trends in Mulliken charges in the cation series, as well as in the ligand series, remain the same in MCl₃L₂ as in the MCl₃L series. The electron transfer per ligand is larger with sulfur (0.20 to 0.23 e) than with oxygen (0.09 to 0.13 e) ligands, and larger with NMe₂ than with Me carbon substituents. This is slightly less than in MCl₃L complexes. Notice also that electron donation from the chloride ions is smaller in MCl₃L₂ than in MCl₃L and smaller with oxygen than with sulfur ligands. As a result, the metal charge is reduced upon addition of a second ligand to the sulfur complexes, but increased for oxygen complexes.

Discussion and conclusion

We report consistent calculations on the lanthanide complexes of two important classes of carbonyl ligands, amide and urea, respectively, and of their thio analogues. When compared to other ligands such as pyridine derivatives, anisole and phosphoryl compounds,^12,13 the results show that these molecules are good ligands for trivalent lanthanide cations.

Proton vs. cation affinity of the ligands

Comparison with protonation energies allows one to gain insights into possible correlations between the ligand proton basicities and cation basicities. We notice that correlations are generally indirectly inferred from measurements involving weak interactions in solution with Lewis acids (e.g. with SbCl₅ or I₂ ^20,45) or with hydrogen bonded molecules. Concerning the amide/thioamide comparison, the hydrogen bonding formation constants in CCl₄ solution are larger for the former ligands,^46,47 as supported by theoretical investigations on related systems.^48,49 This order of hydrogen bonding contrasts with the order of protonation energies calculated by us and by others,⁴⁷ according to which thio compounds are preferred. Generally speaking, proton basicities involve major electronic perturbations of the ligand and may not correlate with hydrogen bonding which leads to minor perturbations only.

The next stage is to consider the ligand affinities for hard cations. As shown by experiments on gas-phase lithium basicities,^50,51 fair correlations with proton affinities can be observed for homogeneous classes of ligands, but correlations involving different classes are less good. Our calculations show that the interactions with lanthanide cations are markedly modulated by the presence of counterions and by the stoichiometry. Intrinsically, for ML³⁺ complexes, the cation prefers the harder oxygen ligands to their sulfur analogues, following an opposite trend to the proton basicities. The difference stems from the less covalent character of the metal–ligand bond compared with the proton–ligand bond, and from marked polarization effects in ML³⁺. As counterions are added to the system, the ligand formally binds to a neutral MCl₃ salt, leading to reduced interactions. This leads to an amplification of the sulfur/oxygen discrimination, and a reduction of substituent effects at carbon. The order of cation affinities is the same in both ML³⁺ and MCl₃L complexes, following the ion hardness (Yb³⁺ > Eu³⁺ > La³⁺).

The relative interactions of sulfur vs. oxygen ligands with “acids” A (A = H⁺, M³⁺, MCl₃) can be assessed via the isodesmic reaction shown in Fig. 10 where X = Me vs. NMe₂. The results (Table 2) confirm that the proton prefers the softer sulfur ligands, while the M³⁺ and MCl₃ “acids” prefer the harder oxygen ligands, the effect being more pronounced with the amide A (X = Me) than with the urea U (X = NMe₂) ligands. This observation is also more pronounced with MCl₃ than with the M³⁺ acid, due to more repulsive interactions between the counterions and the sulfur ligands. Thus, counterions and cumulative interactions in the first coordination sphere of the cation play an important role in ion discrimination by a given ligand, as well as on ligand recognition by a given ion. As shown by recent NMR studies on calixarene–CMPO derivatives, the nature of the lanthanide complexes also depends on the presence of competing binders such as polar solvent molecules, or hard anions.⁵² Our calculations demonstrate how counterions modulate the nature of metal–ligand bonds and lead to a reversal of ion binding affinities: the intrinsically preferred Yb³⁺ cation is less well bound in the presence of counterions and other ligands than the sterically more accessible La³⁺ cation.

Table 2 Energies E_iso (kcal mol⁻¹) of the isodesmic reaction (XMe)C[double bond, length half m-dash]O + (XMe)C[double bond, length half m-dash]S–A→(XMe)C[double bond, length half m-dash]O–A + (XMe)C[double bond, length half m-dash]S

		Acid A
X	Y	H^+	La^3+	Eu^3+	Yb^3+	LaCl3	EuCl3	YbCl3
Me	NMe2	2.3	−8.0	−8.7	−9.9	−9.2	−11.0	−12.4
NMe2	NMe2	3.1	−6.2	−6.2	−7.1	−8.4	−9.5	−10.8

---

Fig. 10 Isodesmic reaction used to compare the interaction of “acids” (A = H⁺, M³⁺, MCl₃) with oxygen vs. sulfur “bases”.

Structural features of the complexes

Counterions and stoichiometry also change the structure of the coordinated ligand, which is less perturbed in MCl₃L and MCl₃L₂ than in the ML³⁺ complexes, where polarization effects are magnified. Thus, comparisons with solid state structures or with structures in condensed phases should be done with the most saturated (here, MCl₃L₂) species. We previously discussed the structure of acetamide complexes, showing good agreement between calculated and X-ray structures.¹³ A review of amide complexation can be found in ref. 53 and typical features of A and U complexes are reported in Table 3. We notice that in most solid state structures, the anions are directly coordinated to the metal, and the C[double bond, length half m-dash]O–M angles are bent. One exception concerns the M(ClO₄)₃U₆ complexes (M = Er; Yb) where this angle is linear as in the optimized MU³⁺ species. Experimental results on Yb(ClO₄)₃U₆ at different temperatures also reveal thermal effects on bond lengths (the Yb–O distance ranges from 2.18 Å at −158 °C to 2.13 Å at 70 °C). The calculated structures of LaCl₃A and of YbCl₃A agree within 0.03–0.05 Å with the X-ray structures of the corresponding La and Yb complexes. The experimental structures of the Sm and Er complexes of A are also close to those optimized for the corresponding (and similar in size) metals Eu and Yb.

Table 3 Structural features of complexes of A and U in the solid state (retrieved from the Cambridge Crystallographic Database) ⁶⁷

Refcode	Formula	CN	M ⋯ O/Å	O[double bond, length half m-dash]C/Å	α/deg	ϕ/deg	Ref.
a X-Ray structure at −60 °C.
CAXYIJ	La((^iPrO)2PS2)3A2	8	2.41–2.43	1.21–1.26	144–166	99–113	68
CIDJUU	Sm(NO3)3A3	9	2.31–2.32	1.21–1.27	140–155	116–175	69
CIDKAB	Er(NO3)3A3	9	2.24–2.29	1.23–1.31	140–163	111–156	69
JAQCIN ^a	Yb(Ni(CN)4)ClA4	7	2.20–2.27	1.27–1.33	133–160	121–145	70
LELBOT	Ce(C5H5)3U	4	2.46	1.26	155	97	71
WEHTOS	Ce(picrate)3U3	6	2.37–2.42	1.22–1.26	143–172	98–104	72
LELBUZ	Nd(C5H5)3U	4	2.44	1.26	154	100	71
WEHTUY	Nd(picrate)3U3	6	2.36–2.40	1.23–1.25	142–158	96–106	72
TMUNEU	Eu(NO3)3U3	9	2.30–2.35	1.23–1.27	143–170	98–118	73
HURERC	Er(ClO4)3U6	6	2.18–2.20	1.27–1.30	178–179	95–114	74
VITTIB	Yb(ClO4)3U6	6	2.17	1.27	177	142	75

---

Consideration of other amide complexes of the cations under study retrieved from the Cambridge Crystallographic Database reveals some disparity between the experimental M–O distances, and general agreement with the optimized distances in MCl₃L₂. This is observed for M = La (25 structures, La–O = 2.39–2.61 Å; average = 2.50 Å, to be compared with the optimized distance of 2.46 Å), M = Eu (17 structures, Eu–O = 2.31–2.51 Å, average = 2.40 Å; optimized value is 2.35 Å) and M = Yb (6 structures; Yb–O = 2.24–2.46 Å; average = 2.30 Å; calculated value is 2.24 Å). Similar features are found for urea complexes with Eu or Yb, or the related Ce (close to La), Nd (close to Eu) or Er (close to Yb) analogues.

For the sulfur compounds, no solid state structure could be found that can be directly compared with the calculated ones. For instance, in the Gd³⁺ and Sm³⁺ complexes of TU, the ligands are bidentate (via S and N atoms) and achieve bridging coordination to two cations.⁵⁴ The corresponding M–S distances (2.94 and 3.06 Å) are close to the optimized Eu–S distance of 2.97 Å. Structures of lanthanide complexes of negatively charged dithiocarbamate RR’NCS₂⁻ ligands have also been reported,^55,56 but the metal–ligand distances are shorter than with the neutral TA or TU ligands (by 0.12 Å with M = La and 0.17 Å with M = Yb), in accord with the stronger attractions to the metal.

Another interesting aspect of metal binding concerns the co-planarity of the cation with the ligand. The planar binding in ML³⁺ complexes contrasts with the out-of-plane binding, especially with sulfur ligands in the presence of counterions. According to a recent review,⁵³ out-of-plane binding is not uncommon for amide ligands and is shown by our calculations to be induced by other coordinated species. Out-of-plane coordination is most pronounced with thiourea TU, in accord with the more bent C[double bond, length half m-dash]S–M angle, which also leads to enhanced repulsions between the anions and the NMe₂ urea substituents. Although no structure was found for similar lanthanide complexes, a number of thiourea halide complexes with such a deformation have been reported, with M = Sb (ϕ = 94–114°),^57–59 Os (ϕ = 94–97°),⁶⁰ Re (ϕ = 101–143°),^61,62 Ru (ϕ = 94°),⁶³ Pt (ϕ = 114°),⁶⁴ Zn (ϕ = 119–150°) ⁶⁵ and Hg (ϕ = 99–159°).⁶⁶ Noteworthy are the soft character of these metals and the presence of coordinated (generally halide) counterions. There are structures, however (M = Cu, Au, W, Mo, Rh), where the metal is more co-planar with thioamide or thiourea ligands (ϕ > 160°). According to our study, out-of-plane binding is not an intrinsic feature of the metal–thiourea bond, but results from avoiding repulsions in the planar binding mode. We suggest that monitoring the stereochemistry of metal–ligand interactions via preorganized arrangements of the latter (e.g. on calixarene or resorcinarene platforms) might lead to ion discrimination by oxygen/sulfur binding sites. The binding mode of counterions clearly contributes to that process.

Computational aspects

Concerning the computations, we previously found that the conclusions obtained on similar amide, phosphoryl and pyridine lanthanide complexes from HF calculations are validated by MP2 and B3LYP-DFT calculations.^11,13–15 We decided however to reoptimize the four EuCl₃L complexes to compare the interaction energies ΔE and structures. It can be seen from Table 4 that the HF vs. DFT ΔE values differ by at most 1.4 kcal mol⁻¹ and the order of the ligand binding sequence is identical. Table 4 also confirms that BSSE corrections at the HF or DFT level are relatively small and nearly constant, yielding nearly identical differences in binding energies ΔE. HF vs. DFT optimized distances differ by 0.01 to 0.03 Å. The Eu ⋯ L and Eu–Cl distances are somewhat shorter and the C[double bond, length half m-dash]O and C[double bond, length half m-dash]S bonds are longer in the DFT optimized structures, but the structural trends are the same with both methods (Table 5). Trends concerning the non-linearity of the C[double bond, length half m-dash]X–M angles are also similar (α angles differ by 2 to 12°). In the DFT structures the cation is somewhat more out of the plane of the ligands (ϕ angles differ by 3 to 35°), and this non-planarity is more pronounced with the sulfur compounds, as found in the HF calculations and in the solid state structures. Another issue concerns the representation of the lanthanide cations, where it would be desirable to compare the large core ECPs used here to small core ones. In the case of the Eu³⁺ ⋯ O[double bond, length half m-dash]PH₃ complex, the two types of representations were found to lead to similar results,¹⁰ but this question remains to be more systematically investigated.

Table 4 Comparison of HF vs. DFT interaction energies ΔE (kcal mol⁻¹) in EuCl₃L complexes. ΔΔE_M are the differences in ΔE, relative to the AEuCl₃ complex. Uncorrected/BSSE corrected energies

Complex	ΔE/ΔEcor	ΔΔEM/ΔEcorM
HF/DZ*//HF/DZ*
(Me2N)MeCO ⋯ EuCl3	−45.8/−43.2	0.0/0.0
(Me2N)MeCS ⋯ EuCl3	−34.8/−31.3	+11.0/+11.9
(Me2N)2CO ⋯ EuCl3	−47.0/−44.5	−1.2/−1.3
(Me2N)2CS ⋯ EuCl3	−37.5/−34.0	+8.3/+9.2
DFT/DZ*//DFT/DZ*
(Me2N)MeCO ⋯ EuCl3	−44.4/−40.3	0.0/0.0
(Me2N)MeCS ⋯ EuCl3	−33.5/−29.8	+10.9/+10.5
(Me2N)2CO ⋯ EuCl3	−46.8/−42.6	−2.4/−2.3
(Me2N)2CS ⋯ EuCl3	−37.9/−33.9	+6.5/+6.4

---

Table 5 Comparison of HF vs. DFT optimized structures and Mulliken charges q of L and EuCl₃L complexes

	M–X/Å	C–X/Å	M–Cl/Å	α/deg	ϕ/deg	X–M–Cl/deg	q(M)	q(X)	q(C)	q(Cl)
HF/DZ*
(Me2N)MeCO	—	1.205	—	—	—	—	—	−0.48	0.54	—
(Me2N)MeCS	—	1.667	—	—	—	—	—	−0.35	0.22	—
(Me2N)2CO	—	1.205	—	—	—	—	—	−0.48	0.66	—
(Me2N)2CS	—	1.677	—	—	—	—	—	−0.36	0.36	—
(Me2N)MeCO ⋯ EuCl3	2.282	1.245	2.601	164	165	100	1.47	−0.73	0.64	−0.53
(Me2N)MeCS ⋯ EuCl3	2.899	1.734	2.594	99	106	102	1.31	−0.41	0.29	−0.53
(Me2N)2CO ⋯ EuCl3	2.268	1.250	2.603	172	145	101	1.46	−0.75	0.77	−0.53
(Me2N)2CS ⋯ EuCl3	2.887	1.748	2.596	101	109	102	1.32	−0.42	0.42	−0.53
DFT/DZ*
(Me2N)MeCO	—	1.233	—	—	—	—	—	−0.35	0.29	—
(Me2N)MeCS	—	1.675	—	—	—	—	—	−0.25	0.05	—
(Me2N)2CO	—	1.233	—	—	—	—	—	−0.35	0.31	—
(Me2N)2CS	—	1.684	—	—	—	—	—	−0.27	0.07	—
(Me2N)MeCO ⋯ EuCl3	2.264	1.266	2.570	162	130	101	1.04	−0.49	0.39	−0.42
(Me2N)MeCS ⋯ EuCl3	2.851	1.731	2.563	96	100	103	0.91	−0.28	0.11	−0.42
(Me2N)2CO ⋯ EuCl3	2.252	1.274	2.574	160	130	101	1.02	−0.51	0.39	−0.42
(Me2N)2CS ⋯ EuCl3	2.839	1.747	2.567	99	112	103	0.91	−0.29	0.10	−0.42

---

To conclude, we emphasize the importance of computational approaches to study cation complexes of increasing complexity and to compare the intrinsic binding features of various classes of ligands used in the complexation and liquid–liquid extraction of lanthanide and actinide cations. Such computations should contribute to a better understanding of the structural and energetic features of the complexes and the basis of efficient complexation and separation of lanthanides and actinides by known or putative ligands.

Acknowledgements

The authors are grateful to EEC (FIKW-CT-2000-0088) and PRACTIS for support, and to IDRIS and Université Louis Pasteur for allocation of computer resources. F. B. is grateful to the French ministry of Research for a grant.

References

1. V. Alexander, Chem. Rev., 1995, 95, 273.
2. L. Cecille , M. Casarci and L. Pietrelli , New Separation Chemistry Techniques for Radioactive Waste and Other Specific Applications, 1991, Commission of the European Communities, Elsevier Applied Science, London, New York..
3. G. R. Choppin and K. L. Nash, Radiochim. Acta, 1995, 70/71, 225.
4. G. R. Choppin and D. R. Peterman, Coord. Chem. Rev., 1998, 174, 283.
5. N. Sabbatini, A. Mecati, M. Guardigli, V. Balzani, J. M. Lehn, R. Ziessel and R. Ungaro, J. Lumin., 1991, 48-49, 463.
6. W. D. J. Horrocks and D. R. Sudnik, J. Am. Chem. Soc., 1979, 101, 334.
7. D. Parker and J. A. G. Williams, J. Chem. Soc., Dalton Trans., 1996, 3613.
8. J. M. Lehn, Struct. Bonding (Berlin), 1973, 161, 1.
9. F. Hutschka, L. Troxler, A. Dedieu and G. Wipff, J. Phys. Chem. A, 1998, 102, 3773.
10. L. Troxler, A. Dedieu, F. Hutschka and G. Wipff, THEOCHEM, 1998, 431, 151.
11. R. Schurhammer, V. Erhart, L. Troxler and G. Wipff, J. Chem. Soc., Perkin Trans. 2, 1999, 2515.
12. M. Baaden, F. Berny, C. Boehme, N. Muzet, R. Schurhammer and G. Wipff, J. Alloys Compd., 2000, 303–304, 104.
13. F. Berny, N. Muzet, L. Troxler, A. Dedieu and G. Wipff, Inorg. Chem., 1999, 38, 1244.
14. C. Boehme and G. Wipff, J. Phys. Chem. A, 1999, 103, 6023.
15. C. Boehme and G. Wipff, Inorg. Chem., 1999, 38, 5734.
16. J. Chen, Y. Zhu and R. Jiao, Sep. Sci. Technol., 1996, 31, 2724.
17. C. Hill, C. Madic, P. Baron, M. Ozawa and Y. Tanaka, J. Alloys Compd., 1998, 271–273, 159.
18. R. G. Pearson , Hard and Soft Acids and Bases, Dowdon, Hutchinson and Ross Publ., Stroudsburg, PA, 1973..
19. G. R. Choppin , in Principles of Solvent Extraction, ed. J. Rydberg, C. Musikas and G. R. Choppin, M. Dekker, New York, pp. 71–100, 1992..
20. R. D. Hancock and A. E. Martell, Chem. Rev., 1989, 89, 1875 and references cited therein..
21. F. Arnaud-Neu, S. Barboso, F. Berny, A. Casnati, N. Muzet, A. Pinalli, R. Ungaro, M.-J. Schwing-Weill and G. Wipff, J. Chem. Soc., Perkin Trans. 2, 1999, 1727.
22. A. M. Kervey , M.-J. Schwing-Weill and F. Arnaud-Neu , in Comprehensive Supramolecular Chemistry, ed. J. L. Atwood, J. E. D. Davies, D. D. McNicol, F. Vögtle and J.-M. Lehn, Pergamon, New York, 1996, pp. 537–603..
23. J. J. Gonzales, R. Ferdani, E. Albertini, J. M. Blasco, A. Arduini, A. Pochini, P. Prados and J. de Mendoza, Chem. Eur. J., 2000, 6, 73.
24. J. W. M. Nissink, H. Boerrigter, W. Verboom, D. N. Reinhoudt and J. H. van der Maas, J. Chem. Soc., Perkin Trans. 2, 1998, 2623.
25. H. Boerrigter, L. Grave, J. W. M. Nissink, L. A. J. Chrisstoffels, J. H. van der Maas, W. Verboom, F. de Jong and D. N. Reinhoudt, J. Org. Chem., 1998, 63, 4174.
26. F. Z. El Aamrani, A. Kumar and A. M. Sastre, New J. Chem., 1999, 23, 517.
27. A. Ceresa and E. Pretsch, Anal. Chim. Acta, 1999, 395, 41.
28. T. Kowalik-Jankowska, M. Jasionowski, L. Lankiewicz and H. Kozlowski, J. Inorg. Biochem., 1997, 45.
29. J. S. Kim, M. H. Cho, J. H. Cho, J. H. Lee, R. A. Bartsch, Y. I. Lee and I. H. Kim, Talanta, 2000, 51, 99.
30. R. J. W. Lugtenberg, R. J. M. Egberink, J. F. J. Engbersen and D. N. Reinhoudt, J. Chem. Soc., Perkin Trans. 2, 1997, 1353.
31. F. Arnaud-Neu, G. Barrett, D. Corry, S. Cremin, G. Ferguson, J. F. Gallagher, S. J. Harris, M. A. McKervey and M.-J. Schwing-Weill, J. Chem. Soc., Perkin Trans. 2, 1997, 575.
32. W. Wroblewski and Z. Brzozka, Anal. Chim. Acta, 1996, 326, 163.
33. M. J. Frisch , G. W. Trucks , H. B. Schlegel , P. M. W. Gill , B. G. Johnson , M. A. Robb , J. R. Cheeseman , T. Keith , G. A. Petersson , J. A. Montgomery , K. Raghavachari , M. A. Al-Laham , V. G. Zakrzewski , J. V. Ortiz , J. B. Foresman , C. Y. Peng , P. Y. Ayala , W. Chen , M. W. Wong , J. L. Andres , E. S. Replogle , R. Gomperts , R. L. Martin , D. J. Fox , J. S. Binkley , D. J. Defrees , J. Baker , J. P. Stewart , M. Head-Gordon , C. Gonzalez and J. A. Pople , Gaussian 94, Revision B.2, Gaussian, Inc., Pittsburgh, PA, 1995..
34. M. J. Frisch , G. W. Trucks , H. B. Schlegel , G. E. Scuseria , M. A. Robb , J. R. Cheeseman , V. G. Zakrzewski , J. A. Montgomery Jr. , R. E. Stratmann , J. C. Burant , S. Dapprich , J. M. Millam , A. D. Daniels , K. N. Kudin , M. C. Strain , O. Farkas , J. Tomasi , V. Barone , M. Cossi , R. Cammi , B. Mennucci , C. Pomelli , C. Adamo , S. Clifford , J. Ochterski , G. A. Petersson , P. Y. Ayala , Q. Cui , K. Morokuma , D. K. Malick , A. D. Rabuck , K. Raghavachari , J. B. Foresman , J. Cioslowski , J. V. Ortiz , B. B. Stefanov , G. Liu , A. Liashenko , P. Piskorz , I. Komaromi , R. Gomperts , R. L. Martin , D. J. Fox , T. Keith , M. A. Al-Laham , C. Y. Peng , A. Nanayakkara , C. Gonzalez , M. Challacombe , P. M. W. Gill , B. Johnson , W. Chen , M. W. Wong , J. L. Andres , M. Head-Gordon , E. S. Replogle and J. A. Pople , Gaussian 98, Revision A.5, Gaussian, Inc., Pittsburgh, PA, 1998..
35. M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730.
36. M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1993, 85, 441.
37. A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111.
38. T. H. Dunning and P. J. Hay , in Methods of Electronic Structure Theory. Modern Theoretical Chemistry 3, ed. H. F. Schaefer III, Plenum Press, New York, 1977, pp. 1–28..
39. F. Wang, S. Ma, D. Zhang and R. G. Cooks, J. Phys. Chem. A, 1998, 102, 2988.
40. G. A. Olah, A. Burrichter, G. Rasul, K. O. Christe and G. K. S. Prakash, J. Am. Chem. Soc., 1997, 119, 4345.
41. J.-L. M. Abboud, A. Mo, J. L. G. de Paz, M. Yanez, M. Esseffar, W. Bouab, M. El-Mouhtadi, R. Mikhlisse, E. Ballesteros, M. Herreros, H. Homan, C. Lopez-Mardomingo and R. Notario, J. Am. Chem. Soc., 1993, 115, 12468.
42. P. Kebarle, Annu. Rev. Phys. Chem., 1977, 28, 445.
43. W. Kim, H.-J. Lee, Y. S. Choi, J.-H. Choi and C.-J. Yoon, J. Chem. Soc., Faraday Trans., 1998, 94, 2663.
44. E. Kleinpeter, J. Mol. Struct., 1996, 380, 139.
45. V. Gutman , The Donor–Acceptor Approach to Molecular Interactions, Plenum Press, New York, 1980..
46. C. Laurence, M. Berthelot, Y. J. Le Questel and M. L. El Ghomari, J. Chem. Soc., Perkin Trans. 2, 1995, 2075 and references cited therein..
47. B. K. Min, H.-J. Lee, Y. S. Choi, J. Park, C.-J. Yoon and J.-A. Yu, THEOCHEM, 1998, 471, 283.
48. R. J. Boyd, THEOCHEM, 1985, 133, 45.
49. A. Masunov and J. J. Dannenberg, J. Phys. Chem. B, 2000, 104, 806.
50. P. Burk, I. A. Koppel, I. Koppel, R. Kurg, J.-F. Gal, P.-C. Maria, M. Herreros, R. Notario, J.-L. M. Abboud, F. Anvia and R. W. Taft, J. Phys. Chem. A, 2000, 2824.
51. R. W. Taft, F. Anvia, J.-F. Gal, S. Walsh, M. Capon, M. C. Holmes, K. Hosn, G. Oloumi, R. Vasanwala and S. Yazdani, Pure Appl. Chem., 1990, 62, 17.
52. B. Lambert, V. Jacques, A. Shivanyuk, S. E. Matthews, A. Tunayar, M. Baaden, G. Wipff, V. Böhmer and J.-F. Desreux, Inorg. Chem., 2000, 39, 2033.
53. O. Clement, B. M. Rapko and B. P. Hay, Coord. Chem. Rev., 1998, 170, 203.
54. M. Geissinger and J. Magull, Z. Anorg. Allg. Chem., 1996, 622, 734.
55. T. D. Tilley, R. A. Andersen, A. Zalkin and D. H. Templeton, Inorg. Chem., 1982, 21, 2644.
56. H. Jinshun, L. Shanhuo, W. Manfang, Z. Qianer and L. Jiaxi, Wuji Huaxue Xuebao (J. Inorg. Chem.), 1987, 3, 1.
57. B. Rubin, F. J. Heldrich, W. K. Dean, D. J. Williams and A. Viehbeck, Inorg. Chem., 1981, 20, 4434.
58. E. Hough and D. G. Nicholson, J. Chem. Soc., Dalton Trans., 1981, 2083.
59. P. Berges , W. Hinrichs , J. Kopf , D. Mandak and G. Klar , J. Chem. Res., 1985..
60. T. Lis and P. Starynowicz, Acta Crystallogr., Sect. C, 1985, 41, 1299.
61. T. Lis, Acta Crystallogr., Sect. B, 1976, 32, 2707.
62. T. Lis, Acta Crystallogr., Sect. B, 1977, 33, 944.
63. D. P. Fairlie, W. A. Wickramasinghe, K. A. Byriel and H. Taube, Inorg. Chem., 1997, 36, 2242.
64. U. Bierbach, T. W. Hambley, J. D. Roberts and N. Farrell, Inorg. Chem., 1996, 35, 4865.
65. I. Potocnak, M. Dunaj-Jurco, V. Petricek and J. Cernak, Acta Crystallogr., Sect. C, 1994, 50, 1902.
66. M. Cannas, F. A. Devillanova, G. Marongiu and G. Verani, J. Inorg. Nucl. Chem., 1981, 43, 2383.
67. F. Allen and O. Kennard, Chem. Des. Autom. News, 1993, 8, 31.
68. K. Nagai, Y. Sato, S. Kondo and A. Ouchi, Bull. Chem. Soc. Jpn., 1983, 56, 2605.
69. M. D. Matheus, J. L. Brianso, X. Solans, G. Germain and J. P. Declercq, Z. Kristallogr., 1983, 165, 233.
70. D. W. Knoeppel, J. Liu, E. A. Meyers and S. G. Shore, Inorg. Chem., 1998, 37, 4828.
71. A. Domingos, N. Marques, A. P. D. Matos, M. G. Silva-Valenzuela and L. B. Zinner, Polyhedron, 1993, 12, 2545.
72. C. Barberato and E. Castellano, Acta Crystallogr., Sect. C, 1994, 50, 351.
73. C. Chieh, G. E. Toogood, T. D. Boyle and C. M. Burgess, Acta Crystallogr., Sect. B, 1976, 32, 1008.
74. L. A. Aslanov, V. M. Ionov and S. S. Sotman, Kristallografiya, 1976, 21, 1200.
75. T. Y. Lyubeznova, V. I. Ponomarev and L. A. Aslanov, Kristallografiya, 1990, 35, 746.

---

Footnote

† Tables S1–S3 are available as supplementary data. For direct electronic access see http://www.rsc.org/suppdata/p2/b0/b006585o/

---