Micromachined impedance spectroscopy flow cytometer for cell analysis and particle sizing

Abstract

A new cytological tool, based on the micro Coulter particle counter (μCPC) principle, aimed at diagnostic applications for cell counting and separation in haematology, oncology or toxicology is described. The device measures the spectral impedance of individual cells or particles and allows screening rates over 100 samples s⁻¹ on a single-cell basis. This analyzer is intended to drive a sorting actuator producing a subsequent cell separation. Size reduction and integration of functions are essential in achieving precise measurements and high throughput. 3D finite element simulations are presented to compare various electrode geometries and their influence on cell parameters estimation. The device is based on a glass-polyimide microfluidic chip with integrated channels and electrodes microfabricated at the length scale of the particles to be investigated (1–20 μm). A laminar liquid flow carries the suspended particles through the measurement area. Each particle’s impedance signal is recorded by a differential pair of microelectrodes using the cell surrounding media as a reference. The micromachined chip and processing electronic circuit allow simultaneous impedance measurements at multiple frequencies, ranging from 100 kHz to 15 MHz. In this paper, we describe the microfabrication and characterisation of an on-chip flow-cytometer as the first building block of a complete cell-sorting device. We then discuss the signal conditioning technique and finally impedance measurements of cells and particles of different sizes and types to demonstrate the differentiation of subpopulations in a mixed sample.

---

Introduction

Two complementary approaches have been developed in parallel for the measurement of the cell electrical properties. The first consists of using extracellular electrodes along with complex excitation and signal analyses techniques. The second uses pipette microelectrodes to connect the cell interior and permits trans-membrane measurements with a more direct analysis (i.e. patch clamp). Both techniques provided some noteworthy contribution to explore physiological properties (ionic transfer mechanisms, muscle contraction, etc.). Accurate acquisition of cell and membrane data with patch-clamp techniques is a lengthy sequential process, which is not well adapted to diagnostic applications.

Alternatively to these electrical methods, the use of fluorescent markers in combination with fluorescent activated cell sorting (FACS) allows very fast and precise screening and sorting with throughputs in the 10⁴ s⁻¹ range. This technique faces two major drawbacks: first it requires cell modification by markers and antibodies, which may imply alteration of the system under study; second the equipment is rather expensive and complex to operate.

Recently, it has been demonstrated that micro-machining technologies may alleviate some of the problems encountered in ‘macroscale’ flow-cytometry. On-chip integration of microfluidics and microelectrodes has already been reported for stationary cell measurements, trapping and sorting. The article by Ayliffe et al.¹ presented the first stationary single cell impedance spectrum discrimination in micromachined channels. As for dielectrophoretic cell manipulation the group of Prof. Fuhr has demonstrated many impressive actuators such as the AC octode field cages, which allow precise particle positioning² as well as cell alignment and sorting capability.³ Three other designs of micromachined particle counters^4–7 have been presented so far, starting with the one presented by Larsen,⁵ but no measurements with a standard physiological saline solution of conductivity σ_sol = 1.6 S m⁻¹ and no evidence of cell differentiation have been published to date. Dielectrophoresis and electrorotation methods to characterise the cell’s electrical parameters have also been demonstrated lately but even automated microsystems take several minutes per cell.⁸ Other techniques are under development including electrokinetic effects, cell fusion and electroporation.^9–11

Because the integration of microelectrodes in capillary channels allows manipulation and detection at a single particle level without the inherent complexity of optical tools, it is possible to consider numerous diagnostic and research applications in oncology, haematology or toxicology, to name but a few, where a cytometry chip, such as the one presented here, would permit automated and highly controlled treatment and measurement of biological cell characteristics at a much lower cost. Still, the use of transparent substrate and cover materials allow the combination of electric impedance and optical detection techniques (fluorometry) to permit measurement crosschecking.

Principle

The common attribute of impedance flow cytometry devices is that they are all liable to measure the size of the cell under consideration. Thus, it has to be determined with a maximum precision as it can significantly influence estimation of the other parameters of interest. Essentially, the measurement consists in determining the impedance change ΔR due to the particle passing through an aperture placed between two electrodes. In a microchannel the aperture is inbuilt and the remaining question is: where do we put the electrodes? Channel walls appear to be the best solution to achieve a high ΔR/R ratio by placing the electrodes as close as possible to each other and concentrating the current lines on the cell.

The measurements are realised by sensing the differential variation of impedance Z_AC − Z_BC into two successive channel segments as the cell passes consecutively into each one (Fig. 1a). This method was preferred over the use of a separate reference channel because the cell’s properties can be measured directly against its surrounding media. Another advantage derives from the fact that the measurement and reference electrodes are inherently switched; any uneven drift of the electrode properties can be sensed and corrected, as both signal maxima should be of the same amplitude. Furthermore, the speed of the particle can be determined, as the distance between the two measurement areas and time t_tr separating both signal spikes are known (Fig. 1b). Consequently, information of the cell’s height in the channel can be derived from the flow speed profile. It is important to note that when flow speed is sufficient, hydrodynamic focusing compensates the sedimentation force and moves the particles away from the fringing electrical field at the edges of the electrodes. The probability of having two cells simultaneously in the sensing area is remote as it has a small volume (∼30 pl) compared to the cell density in the prepared solution (∼1/600 pl⁻¹). The charge transfer between the metal electrodes and the solution takes place at low voltage [∼100 mV_pp (millivolts peak–peak)] and relatively high frequencies (>100 kHz), it is therefore possible to consider a simple model of the electrode/electrolyte interface (Fig. 2a). Only a non-faradic AC current, which charges and discharges the double layer capacitance C_dl, is considered.¹² The cell is presented as a uniform, spherical cytoplasm of conductivity σ_c (typically 0.5 S m⁻¹) surrounded by a very thin non-conductive membrane, having a capacitance per unit area C_m (typically 1 μF cm⁻²). The resistance R_sol of the fluid surrounding the cell is related to the conductivity σ_sol of the phosphate buffered saline (∼1.6 S m⁻¹).

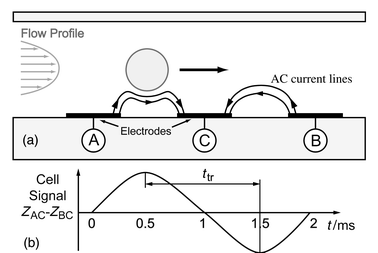Fig. 1 (a) Side schematic view of the microchannel showing a particle passing over three electrodes (A, B and C). The impedance signal is measured differentially (Z_AC − Z_BC). Hydrodynamic focusing is used to center the particle in the channel. (b) Impedance signal. As the distance between the two measurement areas and time t_tr separating the signal spikes are known, the speed of the particle can be calculated. In this type of sequential differential sensor the reference and measurement electrodes are inherently switched, revealing uneven drift of electrode properties.

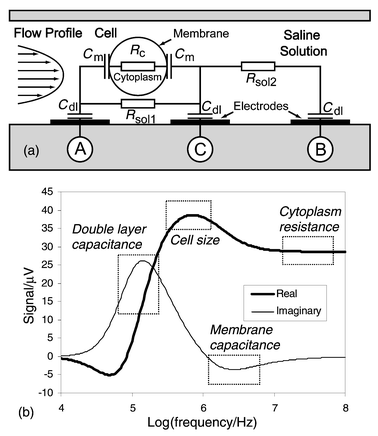Fig. 2 (a) Simplified electrical model of the impedance change in the detection area in the presence of a cell. (b) Simulated complex impedance spectrum of the cell as simulated using a SPICE model for a 10 μm diameter cell. The sensor is connected using a symmetric bridge configuration. Rectangles indicate frequencies of interest for cell discrimination.

Models and simulations

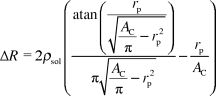
In the case of a classical Coulter counter the change in impedance ΔI due to the presence of a spherical particle of radius r_p can be calculated using the following equation:¹³
where ρ_sol is the resistivity of the phosphate buffered saline and A_C is the cross sectional area of the channel (20 × 20 μm²). This model supposes that no current passes through the cell, which is only valid for low excitation frequencies.

The use of electrodes on the bottom of the channel results in a non-uniform current distribution across the channel’s height. To take this effect into consideration and study the influence of an off-centered particle, the resistance variation can either be calculated analytically in 2D for infinite electrode length using Schwartz–Christoffel conformal mapping¹⁴ or simulated using 3D finite elements.

A first set of 3D simulations (using the FEMLAB^® toolkit) has been carried out using partial differential equations for a conductive media and assuming that no electrical current flows through the spherical particle. This assumption is true for frequencies below the cell characteristic frequency R_cC_m reported to be in the 2–3 MHz range.¹⁵ The electrode capacitance was measured on the microfabricated devices and can be neglected for frequencies above 100 kHz (Fig. 3). A fixed potential is applied to the two electrodes, all other boundaries are considered insulating; the particle resistivity ρ_p is either given the same value as the solution ρ_sol, or ρ_p = ∞, which correspond to the absence or presence of the cell in the detection area respectively. The current in the sensor is calculated using the solution’s Lagrange multiplicators on the electrode surface; this method yields a higher precision than the integration of current density. The channel resistance is derived from this value and the applied potential. Simulations are performed for a 20 × 20 μm² channel, 20 μm electrode dimensions and particles of 5, 8 and 10 µm in diameter. Three electrode geometries are compared to the analytical solution (Table 1). The difference between the simulations for the up- and downstream positioned electrodes and the analytical model can be attributed to the inhomogeneous current density around the cell and the high cell/channel size ratio. This case is merely theoretical but gives a good approximation for electrode geometries covering 3 or 4 sides of the channel. Microfabrication of the planar electrodes used for the two other geometries is considered to be easier and more precise but both result in a lower ΔR/R ratio.

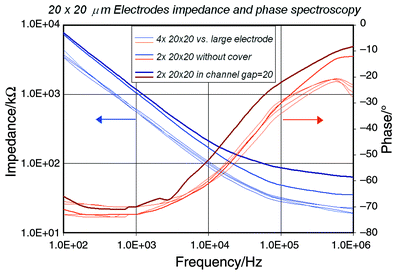Fig. 3 Impedance of 20 × 20 μm² electrodes measured with a large Pt electrode and within an open and closed channel. Measurements were performed with an HP 4284A precision LCR meter.

Table 1 Summary of the FEM results and analytical equation comparing 3 electrodes geometries for different cell sizes. Channel and electrodes have a 20 × 20 μm area; interelectrode distance is 20 μm. The results of the up- and downstream FEM geometry differs from the analytical model by about 20%, one explanation is the inhomogeneous current density in the channel cross section around the cell. The other two geometries produce a lower impedance change but are preferred for microfabrication.

Cell size/µm	Up- and downstream electrodes (analytic)		Up- and downstream electrodes (FEM)		Parallel overlap electrodes (FEM)		Coplanar electrodes (FEM)
	R/kΩ	ΔR (%)	R/kΩ	ΔR (%)	R/kΩ	ΔR (%)	R/kΩ	ΔR (%)
No cell	31.25	—	31.25	—	21.66	—	58.35	—
5	31.51	0.85	31.62	1.19	21.84	0.84	58.70	0.60
8	32.41	3.73	32.80	4.97	22.31	3.03	59.75	2.40
10	33.68	7.78	34.40	10.11	23.02	6.30	61.37	5.18

---

A second set of simulations is used to determine the influence of the particle height on the impedance variation ΔR in the coplanar electrodes case (i.e. most sensitive). A particle of 10 µm is placed at different heights near to the channel’s centre between the electrodes. A high frequency model of a cell is also simulated by assuming that the membrane capacity is shorted and a cell interior conductivity is σ_c = 0.5 S m⁻¹. The same meshing is used for the three simulations realized for each particle position (i.e. about 70000 elements using an adaptive solver). The results (Fig. 4) show, as expected, that the cell’s influence on the channel resistance is smaller for the high-frequency model and decreases for higher cell position. Interestingly, the HF/LF ratio, known as cell opacity, is barely influenced by the cell position.

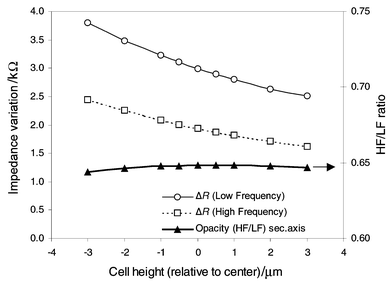Fig. 4 Simulated differential impedance for high and low frequencies as a function of passing cell height in a coplanar electrode geometry (20 × 20 μm²). These results were obtained using finite element modelling of the channel conductance (∼70000 elements) for each cell position using an insulated and conductive model for the cell (r = 5 μm, σ_c = 0.5 S m⁻¹). The centre of the channel is chosen as origin. Both impedance curves present an important dependence on cell position whereas their ratio (known as opacity) is barely influenced.

Another use of the FEM simulations is to study the fringing effect at the electrodes edges and around the particle, as it is assumed to be more important with microelectrodes and capillary channels than for the standard Coulter counter (i.e. large electrodes and aperture). Existing Coulter analysers use an edit system to reject the particles passing near the aperture border; this system was reported to induce some bias in population sizing.¹⁶

Frequency sweep SPICE simulations (Fig. 2b) of the sensor in a bridge circuit configuration using the above results and measured electrode characteristics reveal frequencies of interest for cell parameter estimation. At low frequencies the signal is screened by the electrodes’ double layer capacitance. The first resistive maximum between 100 kHz and −1 MHz is related to the cell size. The cell membrane shows a reactance peak for frequencies between 2 and 5 MHz. High-frequency impedance is related to the cell internal cytoplasm conductance.

Materials and methods

Channel and electrode design

Different electrode configurations and channel designs were initially investigated using two and four point measurement or standard bridge configurations. These methods did not give satisfactory results because of the high noise level and drift requiring too frequent bridge balancing. A better approach consists in realising an entirely symmetrical bridge using one half of the differential sensor in each branch. A single chip can be used alone (Fig. 5a), the channel being covered by a PDMS sheet with inlet holes and molded connectors. The fluidic path is designed with an axial symmetry, which permits the use a second chip, flipped and rotated by 180°, to realize the lid and top electrodes (Fig. 5b). A total of 8 electrodes are available on the current chip design (Fig. 6). The measurement uses three electrodes and shielding is performed by large grounding electrodes up- and downstream of the channel. Some designs also include an experimental negative dielectrophoresis sorting device downstream of measurement channel.

Fig. 5 (a) The microfabricated chip with a PDMS cover and molded fluidic connections. (b) Chip-on-chip configuration designed with two outlets, top and bottom electrodes and an experimental sorting chamber. The two chips are assembled by pressure contact during a final 300 °C cure under N₂. A grid design was used to allow the evacuation of the evaporated solvent.

Fig. 6 Microfabricated sensors showing the measurement channel with integrated coplanar 20 × 20 μm² electrodes as well as shielding electrodes. The fork in the middle provides a separated ground electrode for each of the two sensing areas.

Chip microfabrication

The process used to manufacture the structures requires only two masks. A 0.5 mm thick 4″ float-glass wafer serves as the substrate. The first deposited layer consists of a thin metal film, which is patterned by lift-off (Fig. 7a) using a reversible photo resist (AZ 5214, 1.4 μm,) to realize the portion of the electrode in contact with the solution inside the channel as well as chip contacts. The electrode material (Fig. 7b,c) is sputtered Ti–Pt (Balzers 450, 50–150 nm). To define the channel we used a photosensitive polyimide precursor (PI-2732, Dupont, 10–15 μm), which is patterned to define the channel geometry (Fig. 7d) and cured under nitrogen atmosphere at 300 °C. At this stage, an optional thin layer of platinum black can be electrodeposited on the electrode surface exposed to the channel in order to increase the electrode's effective area and thereby reduce the double layer impedance. This treatment has shown to reduce the electrode impedance by a factor of 100 and more but could yield an uneven electrode polarisability.¹² Similarity of electrode properties was studied on 4 different electrodes and chips. Measurements made with an HP 4284A precision LCR meter showed very low deviation (Fig. 3) and demonstrated that for frequencies above 100 kHz the influence of the electrode double layer capacitance is considerably reduced (i.e. the channel impedance is essentially resistive as 1/jωC_dl → 0). The chips can be used individually using a PDMS cover or in a chip-on-chip configuration requiring the final cure to be performed under mechanical pressure.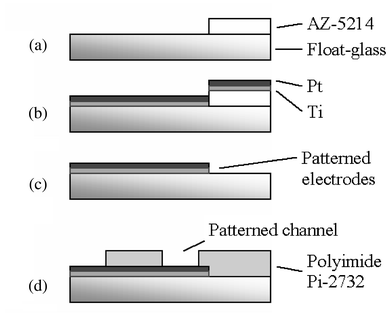

Fig. 7 The process flow for the chip uses two masks: one to define the Ti–Pt electrodes, the other to pattern the polyimide channel walls. See text for details.

Electronics and processing

Many different approaches can be used to efficiently measure the spectral impedance of the passing cell. One method consists of generating a short electrical pulse (i.e. ideally a Dirac pulse) as the cell passes in the detection area and performing a fast Fourier transform to directly recover the full impedance spectra.¹⁷ The main inconvenience of this technique is that the pulse’s energy is not equally distributed throughout the spectrum and should be limited to avoid electrode damage; thus resulting in poor signal-to-noise ratio for high frequency values. The chosen alternative is to produce a continuous excitation signal by summing two or more sine functions at frequencies of specific interest. This method allows for a good signal-to-noise ratio when combined with a synchronous demodulation technique already used by Hoffmann and Britt in 1978.¹⁸ This paper was also the first to present microelectrodes integrated inside the detection channel, which was realised by ceramic and platinum layers assembly prior to drilling. The generated signal is injected in the sensor through two precision resistors R_b, which form a Wheatstone bridge with the sensor chip (Fig. 8). The bridge sensitivity would be maximized if both resistors R_b were chosen equal to the channel (∼50 kΩ). However, the current chip connection causes some parasitic capacitances (∼20 pF) and demands the use of 1 kΩ resistors in order to preserve the desired signal bandwidth. To permit further processing the differential signal is amplified with a high frequency instrumentation amplifier and a second amplification stage resulting in a total gain of 330. A high pass filter followed by a synchronous demodulation yields two signals proportional to the real and imaginary part of the channel impedance variation for each excitation frequency. Finally, a low pass filter removes high frequency noise and the signal is decoupled, digitised and transferred to a computer for further analysis. Software has been developed to automate parameter extraction from the acquired data. The amplitudes, speeds and other user-defined parameters can be visualized and statistically analysed.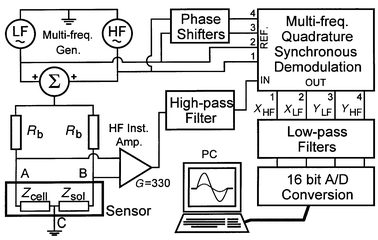

Fig. 8 Excitation, amplification and synchronous demodulation diagram of the multi-frequency detection circuit. The sample data is digitised and stored on a computer for visualisation and further processing.

Results and discussion

Measurements have been performed with calibrated latex beads of 5 and 8 μm (Serva) in diameter, human erythrocytes as well as erythrocyte ghost cells (i.e. having had their content removed). They were diluted in standard PBS (Sigma, NaCl 120 mmol l⁻¹, KCl 2.7 mmol l⁻¹, phosphate buffer 10 mmol l⁻¹, pH 7.4) the conductance of which was measured at about 1.6 S m⁻¹. The particles were flown through the microchannel detection area at speeds ranging from 4 to 160 mm s⁻¹. Thus, the Reynolds number is between 0.08 and 3.2, meaning that a laminar flow is expected, which is verified by the optical tracking of particle trajectories in the channel. The protruding electrode height of 200 nm as compared to the 20 μm channel will not observably affect the flow dynamics and particles position above the electrodes. However, the shear forces due to the quadratic flow speed profile has been shown to considerably affect the cell shape in channels of 10 μm or smaller.¹⁹ In the present case, the shape of the passing particle is highly position dependent and thus stresses the need of proper particle focusing.

The latex beads were used to determine whether our system was able to differentiate particles of different sizes. The high electrical impedance makes them ideal for calibration purpose over the whole excitation spectrum. The 5 and 8 μm beads were mixed in a 4∶1 ratio. Transit time of the passing beads is plotted versus the real part of the signal for an excitation frequency of 1.7 MHz (Fig. 9). Some sampling limitation effect is observed for time measurement due to the data acquisition rate of 20000 s⁻¹. The 5 μm beads speed range is relatively broader than the 8 μm beads, which indicates that the actual design of the channel is too short to establish hydrodynamic focusing for the smallest particles. However, the observation that, according to the flow profile, the slower cells are located lower in the channel and thus result in a higher signal is clearly verified for both cell sizes. The 8 μm beads can be clearly differentiated but are very irregular in amplitude. Since the speed of these particles is stable, it indicates that small height variations are more critical for large particles.

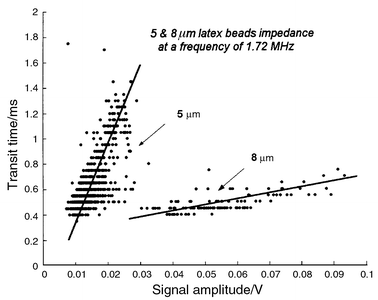Fig. 9 Transit time and measured amplitude signal of 5 and 8 μm latex beads (2000 recorded events). The particles were mixed in a PBS solution and passed in the measurement channel excited with 1.72 and 15 MHz excitation signals. The small beads present relatively broad distribution of transit times, this is attributed to an insufficient channel length to establish hydrodynamic focusing for this particle size. The fastest cells are located higher in the channel and thus produce a lower signal in particular for 8 μm beads. The time quantification effect is due to the data aquisition sampling rate of 20 kHz.

A second measurement procedure was established to discriminate normal erythrocytes from erythrocytes ghost cells. The ghost cells were prepared by dilution in demineralised water 1∶4 and suspended in a PBS solution after centrifugation. Confocal microscopy imaging was used to determine ghosts size (∼6 μm) prior to measurement with our system (Fig. 10). We first recorded 2000 events of a solution containing normal erythrocytes with two simultaneous excitation frequencies (1.72 and 15 MHz) (Fig. 11a). The ghost cells were then mixed in a 1∶4 ratio and 2000 new events were recorded under the same conditions. A scatter plot (Fig. 11b) makes it possible to discriminate the two populations: the ghost cells present lower high-frequency impedance as the conductivity of the cell interior is reported to be similar to that of the solution.¹⁵ The ghost cell size is estimated to about 6 μm, by comparison with the low-frequency amplitude signal of the measured latex calibrated beads.

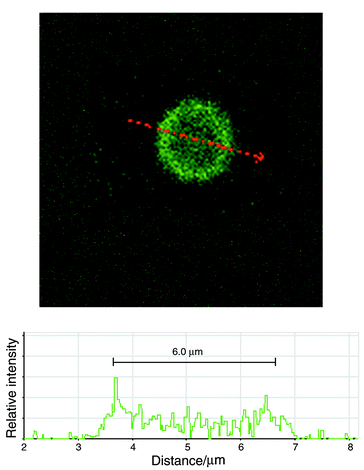Fig. 10 Confocal microscope image of a ghost erythrocyte cell using C-12 fluorescein (Molecular Probe). The C-12 was dissolved in DMSO up to a concentration of 12 mM. The ghost cells were incubated with the C-12 fluorescein at a 10 mM concentration. The image was taken on an Axiovert 100M.

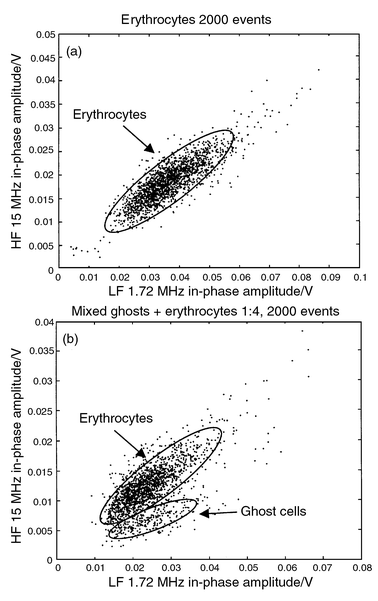Fig. 11 (a) Signal in-phase amplitude of 2000 erythrocytes recorded simultaneously for 2 frequencies. (b) Ghost cells were then mixed with erythrocytes in a 1∶4 ratio and another 2000 events were recorded. The ghost cell cytoplasm conductance is similar to that of the buffer solution resulting in a lower HF/LF ratio. The cell size can be estimated (using the low-frequency impedance amplitude) to about 6 μm, compared to the 5 and 8 μm calibration beads.

Conclusion

The chip and related electronic circuit have demonstrated that a micromachined cell impedance analyser can discriminate between different cells types and particle sizes with rates over 100 samples s⁻¹. Although the system requires some optimisation to allow classification on a single cell basis, it can already be used for counting, sizing and population study. The use of finite elements modelling of the channel impedance variation has shown that the analytical expression underestimates the effect due to the inhomogeneous current density around the particle and at the electrode edges. Different electrode geometries influence has also been compared by these means. Using top and bottom sets of electrodes, speed compensation and efficient hydrodynamic focusing of our system is expected to yield more accurate cell positioning and to alleviate many of the related problems. Placing electrodes inside the channel offers significant advantages as it allows single cell tracking, which is a major requirement in order to drive a future micromachined cell-sorting device. Another benefit is the measurement of the double differential cell signal; it is preferred as it increases the resolution, avoids eventual offset problems in using a ground reference and provides useful information on the particle speed.

Our system is still in the development stage and we have many important improvements in mind for new chip designs and processing as well as electronic connection and amplification. A newly built electronic and connection system is anticipated to significantly reduce parasitic capacitance and thus allow more precise measurements as well as excitation frequencies up to 200 MHz. Electrode impedance can be reduced using platinum black electroplating and should allow measurements down to 10 kHz only limited by the time the cells are present in the detection area. The use of top and bottom electrodes as well as trans-impedance amplification should also yield some significant signal improvement. A higher excitation signal can also increase resolution provided that it won’t alter the microelectrodes too quickly.

Acknowledgement

The authors are grateful to the CMI-EPFL cleanroom staff for support in micromachining processing and to M. Wütrich, M. Baumgartner, A.-P. Tairi ,Y. Leung-ki, O. Dubochet, U. Seger and the groups of Prof. F. Wurm and Prof. H. Vogel for their assistance in various aspects of this project. This work has been partially supported by LEISTER.

References

1. H. E. Ayliffe, A. B. Frazier and R. D. Rabbitt, IEEE J. Microelectromech. Syst., 1999, 8(1), 50 .[*][*] Significant reference.
2. T. Schnelle, T. Muller and G. Fuhr, J. Electrost., 2000, 50(1), 17 .[*] Significant reference.
3. S. Fiedler , S. G. Shirley, T. Schnelle and G. Fuhr, Anal. Chem., 1998, 70(9), 1909 .[*][*] Significant reference.
4. S. Gawad, M. Heuschkel, Y. Leung-Ki, R. Iuzzolino, L. Schild, P. Lerch and P. RenaudFabrication of a microfluidic cell analyzer in a microchannel using impedance spectroscopy, in IEEE-EMBS Conference on Microtechnologies in Medicine and Biology, 2000, Lyon, France.
5. U. D. Larsen, G. Blankenstein and S. Ostergaard, Microchip Coulter particle counter, in Proceedings Transducers, Chicago, USA, 1997.[*] Significant reference.
6. M. Koch, A. G. R. Evans and A. Brunnschweiler, Design and fabrication of a micromachined Coulter counter, in Proceedings Micromechanics Europe, Ulvik, Norway, 1998.
7. C. K. Fuller, J. Hamilton, H. Ackler and P. R. C. GascoyneMicrofabricated multi-frequency particle impedance characterization system, in Micro Total Analysis Systems, Kluwer, Enschede, Netherland, 2000.
8. J. Gimsa , T. Muller, T. Schnelle and G. Fuhr, Biophys. J., 1996, 71(1), 495.
9. D. P. Schrum , C. T. Culbertson, S. C. Jacobson and J. M. Ramsey, Anal. Chem., 1999, 71, 4173.
10. P. C. H. Li and D. J. Harrison, Anal. Chem., 1997, 69, 1564.
11. Y. Murakami , K. Motohashi, K. Yano, K. Ikebukuro, K. Yokoyama, E. Tamiya and I. Karube, J. Biotechnol., 1994, 34, 35.
12. C. D. Ferris, Introduction to Bioelectrodes, Plenum Press, New York, 1974.
13. M. Koch, A. G. R. Evans and A. Brunnschweiler, Microfluidic Technology and Applications, Baldock Research Studies Press Ltd., 2000.
14. A. R. Varlan, P. Jacobs and W. Sansen, Sens Actuators B, 1996, 34(1–3), 258.
15. H. P. Schwan, Adv. Biol. Med. Phys., 1957, 5, 147.
16. T. Allen, Particle Size Measurement, Chapman and Hall, London, 4th edn., 1990.
17. Y. Liu, E. Abel, J. Belch and R. J. Tweedie Method of and apparatus for determining a property of a sample, (US5691633), 1997.
18. R. A. Hoffman and W. B. Britt, J. Histochem. Cytochem., 1978, 27(1), 234 .[*][*] Significant reference.
19. K. Tsukada , E. Sekizuka, Ch. Oshio and H. Minamitani, Microvascular Res., 2001, 61, 231.

---