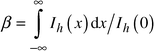Superhard materials based on the solid solution SiC–C†
Oleksandr O.
Mykhaylyk‡
a and
Mykola P.
Gadzira
b
aDepartment of Chemistry, University
of Cambridge, Lensfield Road, Cambridge, UK CB2 1EW
bInstitute for Problems of Materials
Science, Ukrainian National Academy of Sciences, Krzhyzhanivskogo 3, 252680, Kyiv, Ukraine
First published on 3rd October 2000
Abstract
Recently, a fine powder of the SiC–C solid solution, where superstoichiometric carbon atoms in the SiC crystal structure are arranged either as planar defects (diamond-like layers) or as non-correlated point defects, was synthesised. The dynamics of the SiC–C powder sintering and different sintering conditions under high pressures (2–8 GPa) and temperatures (1273–2073 K) are analysed by hardness measurements and by X-ray powder diffraction methods. The strains of the SiC–C crystal structure are characterised by classical and modified Williamson–Hall plots and by the dislocation model of the strain anisotropy. A correlation between microstructure parameters and the hardness of the material was established. The main cause of the work hardening of the SiC–C ceramics is the growth of the dislocation density in the SiC–C crystal structure during high pressure and temperature sintering. The presence of the planar carbon defects plays a key role in the work hardening of the SiC–C ceramics. The highest hardness found for ceramics based on the SiC–C solid solution was 41.4 GPa (Vickers indentation at 2 kg loading).
Introduction
Silicon carbide (SiC) exists in a number of polytypic forms,1 which are virtually stoichiometric when synthesised under equilibrium conditions. According to ref. 2, the deviations from the SiC composition are less than 10−5 at.%. Recently, due to the non-equilibrium conditions of a self-propagated synthesis (SHS) and using a thermal exfoliated graphite (TEG) in the reactant mixture as the carbon component, a cubic silicon carbide possessing a lower lattice parameter [a = 0.4353(1) nm] in comparison with standard β-SiC§ was obtained.3 On the basis of an X-ray crystal structure analysis, Raman scattering spectra4 and microhardness measurements,5 it was concluded that a SiC–C solid solution had been formed, in which the superstoichiometric carbon atoms occupy the silicon sub-lattice of the SiC structure and form diamond-like C–C bonds from sp3-hybridized orbitals. These conclusions were confirmed by theoretical work,6 where, using the self-consistent ab initio linearized ‘muffin-tin’ orbital method, the electronic structure of superstoichiometric silicon carbide was studied. Moreover, the authors concluded that superstoichiometric SiCx 〉 1.0 formation can be energetically favourable under non-equilibrium synthesis conditions.Further investigation of the microstructural characteristics of the SiC–C solid solution7 has shown a more complicated arrangement of the superstoichiometric C atoms in the silicon carbide structure. Carbon atoms can be arranged either as infinite defects (diamond-like carbon layers) after synthesis or as non-correlated point defects (in particular, carbon antisites) after sintering of the synthesized powder under high pressures (4–8 GPa) and temperature (2073 K). Also, considerable variation of the SiC–C structural strain and strain anisotropy was found with different sintering conditions. Such behavior of the microstructure characteristics could be connected with changes in the dislocation density. The latter has a huge influence on the mechanical properties of materials.8 In a preliminary study,9 the sintering conditions which produced SiC–C ceramics characterized by Vickers hardness values of more than 40 GPa (for a range of loads between 2–10 kg) were established, however, a systematic investigation was not carried out to elucidate the nature of the hardness. The present work is devoted to an analysis of the microstructure characteristics and mechanical properties of the SiC–C ceramics sintered under high pressures and temperatures.
Experimental
The initial powder of the SiC–C solid solution was synthesised from a mixture of elemental silicon powder and TEG. The size of the powder particles was 〈0.5 µm. The details of the preparation of the SiC–C solid solution powder are described elsewhere.4 The crystal structure of the cubic silicon carbide–carbon solid solution was characterised by the lattice parameter a = 0.43540(2) nm and the presence of stacking faults identified by a diffraction peak at d = 0.266 nm and the hkl-dependent behaviour of the peak broadening.7The SiC–C solid solution powder was sintered under high pressure and temperature in the ranges 2–8 GPa and 1273–2073 K, respectively, using a DO-044 one-axis press equipped with a high-pressure ‘toroid’-type camera, a pyrophillite container with graphite heater and NaCl pressure medium (a schematic of the high-pressure cell is presented in ref. 9). The precision of the pressure and temperature measurements were ±0.3 GPa and ±50 K, respectively. The duration of the sintering was varied from 5 to 60 s.
Hardness (HV) measurements were performed by the Vickers indentation method using a pyramidal diamond penetrator. A hardness tester (TP-7R-1) was used to apply a 2.0 kg load. Such loading allowed a good quality of indentation for virtually all of the samples investigated. It should be noted that some of the sintered samples displayed a sharp indentation at loadings of more than 20.0 kg.
The powder diffraction data were collected on a DRON-UM1 powder diffractometer [graphite diffracted-beam monochromator, Cu-Kα radiation, λ(Kα1) = 0.15405981 nm]. The divergence of the incident beam was 0.6° and the receiving-slit width was 0.015 or 0.15°. Throughout the experiment the ambient temperature was maintained at 293(1) K. The adjustment of the diffractometer is described in ref. 7
The position (2θ), full width at half maximum (FWHM), shape of individual Bragg reflections and the unit-cell parameters were obtained by means of the CSD program package.10 Line profiles were modeled by a pseudo-Voigt function and, since almost all lines were effectively symmetric, the asymmetric parameter was not used in fittings. Taking into account the presence of stacking faults in the crystal structure of SiC–C, the sinθ002/sinθ111 ratio¶ was estimated. In the case of deformation faults, according to ref. 11, the necessary corrections were input in the peak positions before lattice parameter calculations.
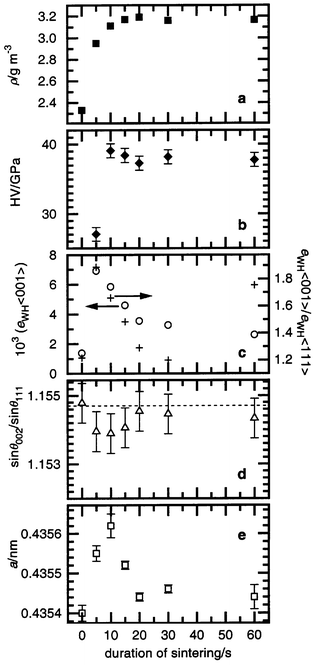
The microstructural properties (strain and crystallite size) of the SiC–C samples were characterised by the dependence of physical broadening βf (see Appendix) on d* (= 2sinθ/λ). In principle, two pairs of reflections of different orders, such as 111 and 222 or 002 and 004, allow the classical Warren–Averbach analysis to be carried out, however, in our case, the overlapping tails of the 111 and 002 line profiles and satellite peak at d = 0.266 nm induced by stacking faults made them unsuitable for the Fourier method. Thus, only Williamson–Hall analysis12 was carried out. A straight line is drawn through the data points in a plot of βf(d*) versusd*, with the intercept of the ordinate being interpreted as 1/DWH and the slope as (2π)1/2eWH, where DWH and eWH (= Δd/d) are the size and strain parameters, respectively. Most of the samples show strain anisotropy and the spread of βf was too large to apply the straight-line approximation in the Williamson–Hall analysis for all sets of peaks. In these cases, we determined the strain parameter for directions 〈001〉 (eWH〈001〉) and 〈111〉 (eWH〈111〉) and the coefficient of the strain anisotropy (ksa = eWH〈001〉/eWH〈111〉) was used.
Results and discussion
1 Influence of the duration of sintering on the hardness of SiC–C ceramics
Preliminary investigations of the SiC–C solid solution powder sintered at high pressures (ca. 4 GPa) and high temperatures (1300–2000 K) showed9 the consolidation and formation of these ceramics is completed during 60 s. Also, the optimal pressure (4 GPa), at which ceramics having high hardness are formed, was found. At such pressures and a temperature of 1673 K, we could obtain good quality samples without cracks after different durations of sintering up to the above-mentioned time period. Crystal structure investigations and hardness measurements for these samples allow us to analyze the hardening of SiC–C ceramics in the process of sintering.The density of the sintered samples shows an asymptotic dependence on duration of sintering through 20 s treatments (Fig. 1a) giving close to theoretical values (standard β-SiC has density ρ = 3.21 g cm−3, in our case a lattice parameter of a = 0.4354 nm and composition Si1 − xC1 + x where x = 0.0077 gives a density equal to this), demonstrating the formation of ceramics almost without pores. A similar dependence was observed for the hardness of the sintered material (Fig. 1b), although there is a slight increase in hardness in the range 10–15 s.
 | ||
| Fig. 1 Macrocharacteristics of the SiC–C ceramics sintered at 4 GPa, 1673 K in dependence on duration of sintering: density (a), hardness (b) and the SiC–C crystal structure characteristics: strain and strain anisotropy (c), stacking faults (d), lattice parameter (e). | ||
At the same time, microstructure analysis leads to the following conclusions: a considerable growth of strain takes place during the first seconds of the sintering followed by a monotonic decrease in the further stages (Fig. 1c and 2). Such a dependence of strain on duration of sintering is connected with the formation of new dislocations in the SiC–C crystal structure during the first stage of sintering at high pressure, and then a decrease in dislocation density due to annealing and stabilization processes under the influence of the high temperature. In addition, we consider that after achievement of the critical value of the dislocation density at 5 s, according to Teylor's or Mott's theory,3 the plastic flow (deformation) of SiC–C is developed, which is followed by the growth of the material density up to the theoretically acceptable level (Fig. 1a). The presence of deformations at the beginning of the sintering is confirmed by the growth of deformation stacking faults in the face centered cubic (f. c. c.) SiC–C crystal structure (Fig. 1d).
 | ||
| Fig. 2 The integral breadth βfversusd* plot for diffraction profiles (hkl given below) of the SiC–C samples sintered at 4 GPa, 1673 K after different times of treatment. Dotted lines have been used in the Williamson–Hall analysis for single cubic structure directions (〈111〉 and 〈001〉). | ||
The distinctive feature of the SiC–C crystal structure after high
pressure and temperature sintering is a considerable strain anisotropy (Fig. 1c and 2): the strain parameter for 〈001〉
directions (eWH〈001〉) is higher than
for 〈111〉 directions (eWH〈111〉)
and, therefore, their ratio (ksa) is greater
than one. This is a usual effect for f. c. c. structures13
and is caused by dislocation formation in favorable crystallographic directions.
This phenomenon is general in all systems containing strain caused by dislocations.
As in other diamond-like structures,14
dislocations in cubic SiC lie preferentially in the Peierls valleys, being
of the type {111}, 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉.15
It was noted that the strain anisotropy of the SiC–C crystal structure
depends on the duration of sintering. There is a growth of the anisotropy
within the first seconds of treatment then a decrease followed by growth again (Fig. 1d). Such behavior can be described
by the peculiarity of dislocation formation at hardening, named stage III.16 At high pressures, a cellular dislocation structure
consisting of densely packed cell walls oriented along {111} forms in the
SiC–C crystal structure. The latter is a cause of the considerable anisotropy
during the first seconds of the sintering (Fig. 1c).
After a longer period of sintering, the presence of plastic deformation initiated
by the high dislocation density destroys the cellular structure. This effect
is observed experimentally as a decrease in the strain anisotropy within 20 s
of the sintering beginning (Fig. 1c).
After all processes of sintering in the material have stabilized (consolidation,
grain and boundary formation), the cellular dislocation structure is
ordered in the SiC–C and the high anisotropy is achieved (Fig. 1c, point at 60 s).
10〉.15
It was noted that the strain anisotropy of the SiC–C crystal structure
depends on the duration of sintering. There is a growth of the anisotropy
within the first seconds of treatment then a decrease followed by growth again (Fig. 1d). Such behavior can be described
by the peculiarity of dislocation formation at hardening, named stage III.16 At high pressures, a cellular dislocation structure
consisting of densely packed cell walls oriented along {111} forms in the
SiC–C crystal structure. The latter is a cause of the considerable anisotropy
during the first seconds of the sintering (Fig. 1c).
After a longer period of sintering, the presence of plastic deformation initiated
by the high dislocation density destroys the cellular structure. This effect
is observed experimentally as a decrease in the strain anisotropy within 20 s
of the sintering beginning (Fig. 1c).
After all processes of sintering in the material have stabilized (consolidation,
grain and boundary formation), the cellular dislocation structure is
ordered in the SiC–C and the high anisotropy is achieved (Fig. 1c, point at 60 s).
The lattice parameters of the SiC–C in the starting powder and in the samples sintered for 20 s or longer are virtually identical (Fig. 1e). After a short sintering time, elevation of the SiC–C lattice parameter is observed. Such behavior of the lattice parameter cannot be interpreted unambiguously. However, a possible mechanism could be as a result of the plastic flow (deformation) of the SiC–C particles at the beginning of the sintering slip by planar carbon interlayers. This will result in a decrease in the crystallite size and the quantity of superstoichiometric carbon in the structure. The latter will increase the lattice parameter. Eventually, resublimation of the SiC–C particles leads to growth of the crystallites and a recovery of the lattice parameter. However, the destruction of the SiC–C solid solution accompanied by the formation of a ‘pressed’ graphite is sometimes irreversible during high pressure and temperature sintering.5
Thus, macrocharacteristics (hardness and density) and microcharacteristics (lattice parameter, strain and strain anisotropy of the crystal structure) show that the main processes of the SiC–C powder sintering take place within 60 s or less. During this time, the consolidation of material, growth of the hardness, increase of the dislocation density in the SiC–C crystal structure and an ordering of the dislocation structure occur.
2 Mechanical properties of SiC–C ceramics sintered under different conditions
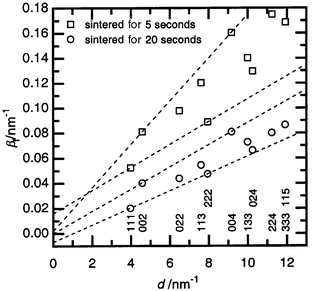
Sintering at different pressures and temperatures, but for the same duration (60 s) when ceramic formation is finished, allows the samples to be plotted on a P versus T diagram (Fig. 3) and an estimate of the influence of treatment conditions on mechanical properties to be made. It should be noted that this diagram is not a thermodynamic equilibrium diagram. The lattice parameter of the SiC–C solid solution is virtually unaffected by the conditions of treatment.7 Increasing the sintering temperature at the same pressure leads to lower hardness. In general, the samples having lower hardness (32–35 GPa) lie at the top left corner of the diagram on one side of the dashed line and those having higher hardness (ca. 41 GPa) lie on the other side in the bottom right corner. | ||
| Fig. 3 The P–T diagram for SiC–C powder sintering conditions. The hardness value (HV) and coefficient of the strain anisotropy of the SiC–C crystal structure (ksa) for sintered material are given for each point. The dashed line is discussed in the text. * denotes specimens for which the hardness could not be measured because of cracking of the sample. | ||
The microstrain analysis shows a substantial difference in eWH
between these two groups of samples (Table 1, Fig. 4). The samples characterized by a
lower hardness have a small eWH strain value, less than
for the starting powder. It was suggested7
that such behavior of the structural strain is caused by an increase in the
diffusion of superstoichiometric C atoms in the silicon carbide structure.
The latter destroys the planar carbon clusters in the initial SiC–C
structure, which at the same time decreases the dislocation density and, therefore,
the strains. In contrast to the former group, the samples characterized by
a high hardness have a large eWH parameter. This suggests
that such sintering conditions boost the formation of new dislocations creating
the additional strain fields in the structure of the SiC–C solid solutions.
The strain anisotropy observed in these samples indicates the presence of
dislocations, mainly in glide systems of type {111}, 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉.
Due to the planar carbon clusters located in the cubic SiC structure parallel
to {111}, the probability of such dislocations appearing in this situation
grows. The plot of hardness versus strain parameter eWH〈001〉
(or eWH〈111〉)
for all samples shows a direct dependence between the two parameters (Fig. 5). The increase in the hardness with
increasing strain confirms that the main cause of the work hardening of the
SiC–C ceramics is growth of the dislocation density. Thus, the presence
of the planar carbon defects plays a major role in the work hardening of the
SiC–C sintered material. This suggests that the main cause of the higher
hardness of the SiC–C ceramics sintered at 4 GPa, 1673 K
for 10–15 s in comparison with those sintered for 60 s (see
item 1 of this section and Fig. 1b)
is the higher dislocation density in the SiC–C crystal structure (Fig. 1c).
10〉.
Due to the planar carbon clusters located in the cubic SiC structure parallel
to {111}, the probability of such dislocations appearing in this situation
grows. The plot of hardness versus strain parameter eWH〈001〉
(or eWH〈111〉)
for all samples shows a direct dependence between the two parameters (Fig. 5). The increase in the hardness with
increasing strain confirms that the main cause of the work hardening of the
SiC–C ceramics is growth of the dislocation density. Thus, the presence
of the planar carbon defects plays a major role in the work hardening of the
SiC–C sintered material. This suggests that the main cause of the higher
hardness of the SiC–C ceramics sintered at 4 GPa, 1673 K
for 10–15 s in comparison with those sintered for 60 s (see
item 1 of this section and Fig. 1b)
is the higher dislocation density in the SiC–C crystal structure (Fig. 1c).
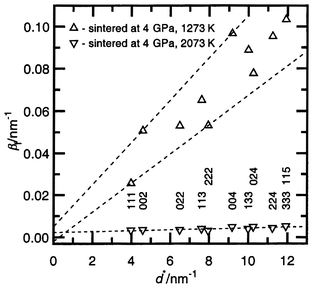 | ||
| Fig. 4 The integral breadth βfversusd* plot for diffraction profiles (hkl given below) of the SiC–C samples sintered at 4 GPa (1273 and 2073 K) for 60 s. Dotted lines have been used in the Williamson–Hall analysis for the single cubic structure direction (〈111〉 and 〈001〉). | ||
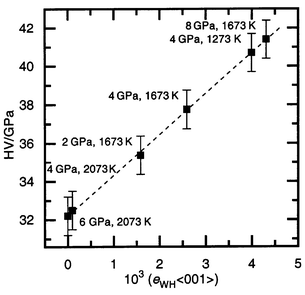 | ||
| Fig. 5 Plot of hardness (HV) versus strain parameter of the SiC–C crystal structure for the 〈001〉 direction (eWH〈001〉). The conditions of sintering are given beside each point. The dashed line is discussed in the text. | ||
| Conditions of sintering | 103 (eWH〈001〉) | 103 (eWH〈111〉) | k as |
|---|---|---|---|
| a The anisotropy was not observed and data correspond to all of the crystallographic directions. | |||
| 2 GPa, 1673 K | 1.59 | 1.20 | 1.32 |
| 4 GPa, 2073 Ka | 0.09(2) | 0.09(2) | ca. 1 |
| 6 GPa, 2073 Ka | 0.39(4) | 0.39(4) | ca. 1 |
| 4 GPa, 1273 K | 4.00 | 2.77 | 1.44 |
| 8 GPa, 1673 K | 4.31 | 3.43 | 1.26 |
| 4 GPa, 1673 K | 2.59 | 1.48 | 1.75 |
| 8 GPa, 2073 K | 0.67 | 0.22 | 2.99 |
The C–C single bonds may also play some part in the hardening of SiC. The samples sintered at 4 GPa and 2073 K, in which strains are not revealed by X-ray measurements (Table 1, Fig. 4), have the lowest hardness; 32.2 GPa (Fig. 5). It should be suggested that there is virtually no dislocation hardening and, as shown in ref. 7, we obtain the substitutional solid solution Si1 − xC1 + x, where superstoichiometric carbon atoms are distributed randomly (not as planar defects). At the same time, the controlled sintering of standard β-SiC [a = 0.4359(1) nm, grain size <0.5 µm and stacking faults present] at different pressures and temperatures allow us to get samples characterized by a hardness <31 GPa, that is slightly lower than the hardness of the above samples of sintered SiC–C. Such comparisons suggest that the presence of randomly distributed carbon atoms in the silicon sub-lattice of the SiC have a weak influence on the hardness, that is, an order of magnitude smaller than the work hardening by dislocations.
Concluding remarks
Recently, a dislocation model of the strain anisotropy, in particular for f. c. c. crystal structures, was developed13,17,18 and a simple procedure (modified Williamson–Hall plot) was presented for the rationalisation of anisotropic strain broadening in terms of the anisotropic contrast effect of dislocations. The dislocation contrast factors [C(g), where g is a diffraction vector] are compiled as functions of the elastic constants.13 On the basis of the above-mentioned works, the contrast factors for {111}, a/2〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉
glide system were calculated using anisotropic elastic constants for cubic
silicon carbide||
and taking into account the notation for the parabolic dependence of the breadth (βf)
in the d*C(g)1/2
scale13,18 the value of the anisotropic
parameter (ksa = eWH〈001〉/eWH〈111〉)
was estimated. The limits of the ksa value in the terms
of the mentioned works are expressed as:
10〉
glide system were calculated using anisotropic elastic constants for cubic
silicon carbide||
and taking into account the notation for the parabolic dependence of the breadth (βf)
in the d*C(g)1/2
scale13,18 the value of the anisotropic
parameter (ksa = eWH〈001〉/eWH〈111〉)
was estimated. The limits of the ksa value in the terms
of the mentioned works are expressed as: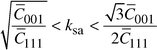 | (1) |
Attempts to use the dislocation model and modified Williamson–Hall
analysis for our measurements showed that only samples characterized by a
high anisotropic parameter and a long duration of sintering (Table 1, the sintering at 4 GPa, 1673 K
and at 8 GPa, 2073 K) show a smooth variation of integral
breadth (βf) with d*C(g)1/2.
The crystal structures of the SiC–C in the other samples probably have
extra dislocation-like lattice defects, beside the glide system {111}, 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉,
and additional correction of the dislocation model is necessary. As an example,
the results of the modified Williamson–Hall analysis for SiC–C
sintered at 4 GPa, 1673 K are presented in Fig. 6.
More detailed descriptions of the parameters are given in ref. 13 and 18, from which the symbols
used in these work are taken. Taking into account the notation in ref. 22, the peak from
the overlapping of 333 and 115 reflections is excluded in analysis. Because
of stacking faults in the SiC–C crystal structure, according to ref. 11, 13 and 18,
the necessary corrections to βf were incorporated
in the calculations. The classical Williamson–Hall plot of βf
reveals a strong spreading of the points (Fig. 6a).
The plot of βfversusH2
according to eqn. (13) inref. 13
(Fig. 6b) allows q to be estimated.**
The best linear regression is obtained with the value α 〈 1.1 × 10−5 nm−2
(α = D−2),
that is, a true particle size of D 〉 300 nm
and a stacking fault parameter β′ close to 0.007, providing q = 2.0(4).
The best fit of the modified Williamson–Hall plot with quadratic regression (Fig. 6c) is obtained at q = 1.73
and β′ = 0.01. The straightforward
interpretation of the obtained value of q is that the preliminary
dislocations in the SiC–C crystal structure after sintering at 4 GPa,
1673 K for 60 s are screw dislocations and the quantitative
ratio between screw and edge dislocations is about 3∶1. The intersection
of the regression curve at d* = 0 (Fig. 6c) gives an average true particle
size of 330 nm, in good agreement with transmission electron microscopy
observations in earlier work.5 However, in
spite of the excellent fit obtained in the former analysis, in order to apply
the dislocation model strain anisotropy to all samples to understand the whole
picture of dislocation formation in the SiC–C crystal structure after
high pressure and temperature sintering, additional assumptions about the
dislocation structure, besides the glide system {111}, 〈
10〉,
and additional correction of the dislocation model is necessary. As an example,
the results of the modified Williamson–Hall analysis for SiC–C
sintered at 4 GPa, 1673 K are presented in Fig. 6.
More detailed descriptions of the parameters are given in ref. 13 and 18, from which the symbols
used in these work are taken. Taking into account the notation in ref. 22, the peak from
the overlapping of 333 and 115 reflections is excluded in analysis. Because
of stacking faults in the SiC–C crystal structure, according to ref. 11, 13 and 18,
the necessary corrections to βf were incorporated
in the calculations. The classical Williamson–Hall plot of βf
reveals a strong spreading of the points (Fig. 6a).
The plot of βfversusH2
according to eqn. (13) inref. 13
(Fig. 6b) allows q to be estimated.**
The best linear regression is obtained with the value α 〈 1.1 × 10−5 nm−2
(α = D−2),
that is, a true particle size of D 〉 300 nm
and a stacking fault parameter β′ close to 0.007, providing q = 2.0(4).
The best fit of the modified Williamson–Hall plot with quadratic regression (Fig. 6c) is obtained at q = 1.73
and β′ = 0.01. The straightforward
interpretation of the obtained value of q is that the preliminary
dislocations in the SiC–C crystal structure after sintering at 4 GPa,
1673 K for 60 s are screw dislocations and the quantitative
ratio between screw and edge dislocations is about 3∶1. The intersection
of the regression curve at d* = 0 (Fig. 6c) gives an average true particle
size of 330 nm, in good agreement with transmission electron microscopy
observations in earlier work.5 However, in
spite of the excellent fit obtained in the former analysis, in order to apply
the dislocation model strain anisotropy to all samples to understand the whole
picture of dislocation formation in the SiC–C crystal structure after
high pressure and temperature sintering, additional assumptions about the
dislocation structure, besides the glide system {111}, 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉,
are needed.
10〉,
are needed.
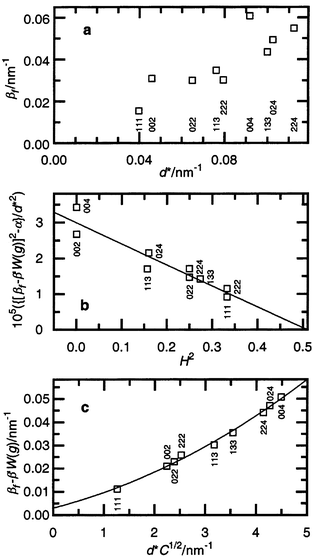 | ||
| Fig. 6 The βf of the SiC–C sintered at 4 GPa, 1673 K in the classical Williamson–Hall plot (a), in a scale of H2 = {(h2k2 + h2l2 + k2l2)/(h2 + k2 + l2)} (b) and according to the modified Williamson–Hall plot (c). Because of stacking faults the necessary correction to βf is applied to plots (b) and (c) (y-axis). | ||
The present results also show that the usual technique of X-ray diffraction measurements can be applied successfully in the analysis of the fine structure of diffraction peak broadening. However, a good quality standard specimen is necessary for this analysis.
In general, the following conclusions can be made:
(i) The sintering and formation of the SiC–C ceramics at high pressures (4–8 GPa) and temperatures (1273–2073 K) is complete after a few tens of seconds.
(ii) The hardness (HV) of the sintered SiC–C ceramics is higher than that of standard SiC ceramics and lies in the interval 32 GPa 〈 HV 〈 41.5 GPa (Vickers measurement at 2 kg loading), the highest hardness has been achieved by sintering at 8 GPa, 1673 K and 4 GPa, 1273 K.
(iii) The main cause of work hardening of SiC–C ceramics is the growth of the dislocation density in the SiC–C crystal structure during high pressure and temperature sintering. The presence of the planar carbon defects plays a key role in the work hardening of SiC–C ceramics through dislocations.
(iv) The dislocations in the SiC–C crystal structure are
similar to those of more conventional, plastically-deformable materials
and lie preferentially in the Peierls valley, parallel to the 〈![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10〉
direction in the {111} glide plane of the cubic structure.
10〉
direction in the {111} glide plane of the cubic structure.
(v) Randomly distributed carbon atoms in the silicon sub-lattice of SiC have a weak influence on the hardness of SiC–C ceramics, an order of magnitude smaller than the work hardening by dislocations.
Determination of the physical broadening of the diffraction peaks
The integral breadths of the observed diffraction peaks are determined as:The observed intensity profile Ih(x) is the convolution of the physical profile of the diffraction reflection If(x) and the instrumental function of the equipment Ig(x):
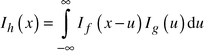 | (2) |
The physical broadening of the peak is expressed as:
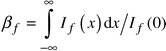 | (3) |
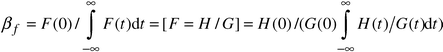 | (4) |
Acknowledgements
The authors thank Dr O. O. Bochechka for help in the preparation of the sintered samples. O. O. M. is grateful to the Royal Society and NATO for a Postdoctoral Fellowship award.References
- A. R. Verma and P. Krishna, Polymorphism and Polytypism in Crystals, John Wiley, New York, 1966. Search PubMed.
- J. A. Lely, Ber. Dtsch. Keram. Ges., 1955, 32, 229 Search PubMed.
- N. F. Gadzyra, G. G. Gnesin, A. V. Andreyev, V. G. Kravets and A. A. Kasjanenko, Inorg. Mater., 1996, 32, 721 Search PubMed.
- M. Gadzira, G. Gnesin, O. Mykhaylyk and O. Andreyev, Diamond Relat. Mater., 1998, 7, 1466 CrossRef CAS.
- M. Gadzira, G. Gnesin, O. Mykhaylyk, V. Britun and O. Andreyev, Mater. Lett., 1998, 35, 277 CrossRef CAS.
- A. L. Ivanovskii, N. I. Medvedeva and G. P. Shveikin, Russ. Chem. Bull., 1999, 48, 612 Search PubMed.
- O. O. Mykhaylyk and M. P. Gadzira, Acta Crystallogr., Sect. B, 1999, 55, 297 CrossRef.
- L. M. Clarebrough and M. E. Hargreaves, in Progress in Metal Physics, ed. B. Chalmers and R. King, Pergamon Press, London, 1959, vol. 8, p. 1. Search PubMed.
- N. F. Gadzyra, G. G. Gnesin and A. A. Mikhailik, Inorg. Mater., 1999, 35, 1054 Search PubMed.
- L. G. Akselrud, Yu. N. Grun, P. Y. Zavalii, V. K. Pecharskii and V. S. Fundamentskii, Twelfth European Crystallographic Meeting, Moscow, USSR, August 20–29, 1989: Collected abstracts, Oldenburg, München, 1990, vol. 3, p. 155. Search PubMed.
- B. E. Warren, X-Ray Diffraction, Addison-Wesley, Reading, MA, 1969. Search PubMed.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22 Search PubMed.
- T. Ungar, I. Dragomir, A. Revesz and A. Borbely, J. Appl. Crystallogr., 1999, 32, 992 CrossRef CAS.
- H. Alexander, in Dislocations in Solids, ed. F. R. N. Nabarro, Elsevier Science Publishers B.V., Amsterdam, 1986, vol. 7, p. 113. Search PubMed.
- X. J. Ning and P. Pirouz, J. Mater. Res., 1996, 11, 884 CAS.
- A. S. Argon and P. Haasen, Acta Metall. Mater., 1993, 41, 3289 Search PubMed.
- T. Ungar and G. Tichy, Phys. Status Solidi A, 1999, 171, 425 CrossRef CAS.
- T. Ungar, S. Ott, P. G. Sanders, A. Borbely and J. R. Weertman, Acta Mater., 1998, 46, 3693 CrossRef CAS.
- W. R. L. Lambrecht, B. Segall, M. Methfessel and M. van Schilfgaarde, Phys. Rev. B, 1991, 44, 3685 CrossRef CAS.
- K. Karch, P. Pavone, W. Windle, O. Schutt and S. Strauch, Phys. Rev. B, 1994, 50, 17054 CrossRef CAS.
- W. Li and T. Wang, Phys. Rev. B, 1999, 59, 3993 CrossRef CAS.
- T. Ungar, M. Leoni and P. Scardi, J. Appl. Crystallogr., 1999, 32, 290 CrossRef CAS.
Footnotes |
| † Basis of a presentation given at Materials Discussion No. 3, 26–29 September 2000, University of Cambridge, UK. |
| ‡ Permanent address: Institute for Problems of Materials Science, Ukrainian National Academy of Sciences, Krzhyzhanivskogo 3, 252680 Kyiv, Ukraine. E-mail: oom65@usa.net. |
| § Powder Diffraction File No. 29-1129; a = 0.43589(1) nm; the wavelength for Cu-Kα radiation was taken to be 0.154178 nm [λ(Kα1) = 0.154051 nm]. |
| ¶ The ratio sinθ002/sinθ111 = 1.1547 is constant for a cubic structure and does not depend on the lattice parameter, but it increases due to deformation stacking faults leading to the displacement of the 111 and 002 peaks.11 |
| || Due to the unavailability of single crystals of β-SiC (and also the SiC–C solid solution) of the required size, direct determination of the full set of elastic constants for this material is not possible. In our analysis we used the following elastic constants for cubic silicon carbide: c11 = 390, c12 = 142 and c44 = 256 GPa, obtained in ref. 19 from sound velocities in the hexagonal polytype and cited as experimental results for β-SiC in many works.20,21 |
| ** q is a constant depending on the elastic constants of the crystal and, for pure edge or pure screw dislocations in the cubic silicon carbide, qedge = 1.023 or qscrew = 2.063, respectively. |
| This journal is © The Royal Society of Chemistry 2001 |