Electrical properties of the oxygen-deficient perovskites, Ca₂Mn_2 − xNb_xO_γ: 0 ≤ x ≤ 1.2, with Mn valence varying from +2.0 to +4.0

---

Abstract

The electrical conductivity of a range of ceramics of general formula Ca₂Mn_2 − xNb_xO_γ, with x and γ as variables, was measured using impedance spectroscopy. All materials were semiconducting but conductivity decreased with both increasing x and decreasing γ, both of which involved a gradual decrease in oxidation state of Mn from +4 in CaMnO₃ to +2 in Ca₂Mn_0.8Nb_1.2O_5.8. Possible factors that control the conductivity are discussed; electrons in e_g orbitals of Mn appear not to be involved directly; instead, conduction appears to depend either on the degree of t_2g–Op_π–t_2g orbital overlap or on σ d–p overlap, with donation of electrons from oxygen into the bonds involving e_g orbitals. In both cases, the conductivity is influenced mainly by Mn–O–Mn distances and unit cell dimensions. For compositions of intermediate oxygen content γ, it was difficult to obtain materials that were electrically homogeneous due to oxygen content gradients; thus, samples prepared by partial reduction in H₂ were more heavily reduced at the grain surfaces than in the grain interiors. Since the conductivity was very sensitive to γ, impedance spectroscopy provided a valuable method to investigate oxygen inhomogeneity. Two types of sample inhomogeneity were characterized: those with reduced surfaces and oxidized cores and vice versa, those with oxidized surfaces and reduced cores.

---

Introduction

The perovskite structure is able to tolerate great variations in its stoichiometry, especially oxygen content. Oxygen deficiency has attracted much attention because of its association with a range of phenomena, such as mixed electronic–ionic conduction, superconductivity, giant magnetoresistance and catalytic activity. In perovskites which contain transition metals, especially Cr, Mn, Fe, Co and Ni, the existence of mixed or intermediate valence states is critical for those properties.^1–5

The Ca₂Mn_2 − xNb_xO_γ system: 0 ≤ x ≤ 1.2, can accommodate up to 20% vacancies at oxygen sites and Mn occurs in valence states ranging from +2 to +4.⁶ Mn and Nb are disordered over the B-sites, at least for composition x = 1.0.⁷ Depending on the average B-cation composition and oxygen content, two solid solutions form: an extensive orthorhombic GdFeO₃-type solid solution over the range 0 ≤ x ≤ 1.2 with zero or small oxygen deficiency, and a closely-related, grossly oxygen-deficient solid solution over the range 0.3 ≤ x ≤ 0.8 with a simple cubic perovskite structure. The unit cell volume, V, and the orthorhombic distortion of the perovskite unit cell due to tilting of MnO₆ octahedra vary with x, γ and Mn valency, as follows: (i) with increasing x (and decreasing Mn valency) at γ = 6, V and the orthorhombic distortion increase; (ii) on removal of oxygen (and decrease in Mn valency), V increases but the orthorhombic distortion decreases.

Several factors influence the electronic conductivity of transition metal oxides. For the present mixed valence Mn oxides, these include: Mn valence state, Nb content, unit cell size and Mn–O–Mn bond angles. Taguchi⁸ studied CaMnO_3 − δ with Mn valence ranging from +3.7 to +3.94 and found the conductivity to depend on the oxygen content; on reduction, σ increased, suggesting an n-type conduction mechanism. By contrast, the conductivity of composition x = 1.0, with Mn valence in the range +2.8 to +3.0, decreased on reduction; however, oxygen loss occurred preferentially from surface and grain boundary regions leading to oxygen concentration gradients through the samples.

In order to understand which parameters control the conductivity of Ca₂Mn_2 − xNb_xO_γ, a number of fully and partially oxidised samples with x = 0.5 and 1.2 have been studied and the results compared with those for x = 0.0 and 1.0. For x = 0.5, γ varies over the range 5.0 ≤ γ ≤ 6.0 and the average Mn valence varies from +2.3 to +3.7; the structure changes from orthorhombic GdFeO₃-type to cubic perovskite type with decreasing γ. For x = 1.2, the orthorhombic GdFeO₃ structure is retained over the range 5.8 ≤ γ ≤ 6.0 and the Mn valence varies from +2.0 to +2.5. On reoxidation, Ca₂Mn_0.8Nb_1.2O_5.8 forms a poorly characterized, oxygen-rich phase of nominal composition Ca₂Mn_0.8Nb_1.2O_6.2 with Mn valence +3.0; this loses the oxygen excess at higher temperatures and reforms single phase Ca₂Mn_0.8Nb_1.2O_6.0.

Experimental

Compositions Ca₂Mn_2 − xNb_xO_γ were prepared, as previously,^6,7 from CaCO₃, MnO₂ and Nb₂O₅, which were mixed and fired, first at 900 °C and then at 1250 to 1350 °C in steps of 50 °C with intermediate regrinding. Products were heated finally at 1400 °C for 3 days and quenched in air. Pellets of 3–8 mm diameter and 1–2 mm thickness were cold-pressed at ∼200 MPa, sintered overnight at 1400 °C and quenched in air; typical pellet densities were 70–80% of theoretical.

In order to vary the oxygen content, pellets were post-reaction heat-treated in O₂, N₂ and 10% H₂/90% N₂. In high pressure O₂, pellets were heated at 5 °C min⁻¹ to 800 °C, held for 16 h and cooled at 2 °C min⁻¹ in a Morris Research Furnace, HPS-5015E7. The maximum pressure was ∼100 atm at 800 °C. In flowing N₂, pellets were heated at 10 °C min⁻¹ to 1100 °C, held for 10 h and cooled at 2 °C min⁻¹. Heat treatments in H₂/N₂ were carried out in a Stanton Redcroft TG-DTA 1500 which allowed the weight losses to be determined in situ. Samples were heated at 10 °C min⁻¹ to temperature, cooled at 20 °C min⁻¹ to ∼350 °C and more slowly thereafter to room temperature. The oxygen partial pressure in these experiments was not buffered since the TG furnace was not leak-proof. The results cannot be related to a particular oxygen partial pressure, therefore, and partially-reduced samples in particular may not have reached a homogeneous, equilibrium state; there was evidence in some cases that grain boundaries were more heavily reduced than grain cores, giving rise to oxygen concentration gradients. Nevertheless, this method was effective as a means of varying the oxygen content and average Mn oxidation state.

Oxygen contents of various pellets were determined from the weight loss during complete reduction of Mn³⁺ and Mn⁴⁺ to Mn²⁺ in 10% H₂/90% N₂. Pellets were heated at 10 °C min⁻¹ until the weight remained constant; it was assumed then that all Mn was reduced to Mn²⁺. From the total weight loss, the initial oxygen content was calculated. Phase identity and purity were determined by X-ray diffraction, using a Hägg–Guinier camera and CuKα₁ radiation.

For impedance measurements, organo-Ag paste electrodes were attached to opposite pellet faces and dried at 180 °C for 1 h in order to remove organic residue. Thin gold strips were held to the sample by pressure. For measurements over the range 298–793 K, the conductivity jig was inserted in a vertical tube furnace; for measurements at 200–300 K, the jig was fixed inside a Dewar flask containing a dry-ice/acetone liquid bath. An Oxford Optistat Cryostat with an IT C4 temperature controller was employed for data collection at T ≥ 83 K. Measurements in the furnace and dry-ice/acetone were carried out in air; those in the cryostat used N₂. Data were collected over the frequency range 10⁻² to 10⁷ Hz using Solartron 1250/1287 and Hewlett-Packard 4192A LF Impedance Analysers. All data were corrected for sample geometry.

At this point, it is necessary to comment on the correction of electrical data for sample geometry. Conductivities are calculated from resistance data using:

where l is the thickness and A the area of the pellet; R_corrected is, effectively, the resistivity ρ of the sample, i.e. the resistance for unit geometry. In this paper, we prefer the use of R_corrected rather than ρ. Since various components contribute to the overall pellet response, e.g. bulk, grain boundary and electrode/sample interface, for accurate analysis each region should be considered separately taking into account the geometry of that region. Usually these geometries are not known and quantitative corrections for geometry cannot be made. Parameters of regions which have been corrected for overall pellet geometry have to be treated with caution, particularly grain boundary conductivities, because grain boundary regions are usually much thinner than bulk regions. Capacitance data are also corrected for overall pellet geometry but, by assuming a typical permittivity value, ε′ ∼ 10, for different regions of the sample, the dimensions of the regions responsible for the different C values can be estimated approximately. A useful parameter which is independent of geometry is the relaxation time or time constant of each RC element, estimated from f_max data of peaks in Z″, M″ plots. f_max is geometry-independent because f_max = (2πRC)⁻¹. Since C has the units F cm⁻¹ and R has units Ω cm, the product RC is independent of geometry. We have not carried out computer fitting to the impedance data since the main purpose is to establish general trends in composition and temperature dependence rather than accurate quantification of parameters for individual samples.

Results

Composition x = 0.5

Electrical characterisation of composition x = 0.5 was carried out on four pellets: as-prepared (quenched in air from 1400 °C) and after post-reaction heat-treatment in O₂, N₂ and 10% H₂/90% N₂. In H₂/N₂, it was more difficult to reduce a pellet than a finely powdered sample; the pellet had to be heated to higher temperature in order to obtain the same oxygen content and took longer to equilibrate at a given temperature. It is shown later that the oxygen content may vary significantly throughout a pellet, making it difficult to obtain homogeneous samples during reduction. From TG, the as-prepared pellet and pellets annealed in O₂ and N₂ all had oxygen contents, γ, close to 6.0 and Mn in valence state ∼+3.7. The pellet heated in H₂/N₂ had γ ∼ 5.34(2) and Mn valence state +2.8.

The three pellets with γ = 6.0 were highly conducting at room temperature and, therefore, were measured at low temperatures in the cryostat. Fig. 1 shows the impedance complex plane plot for the as-prepared pellet at 83 K. The total resistance was obtained from the intercept with the Z′ axis and was R_total ∼ 10.5 kΩ cm. Note that for these and all subsequent plots, the R and C data were corrected for pellet geometry. Three responses were partially resolved in the plot. The initial assumption was made that these data can be represented by an equivalent circuit composed, ideally, of three parallel RC elements in series, Fig. 1 inset. The low frequency response was assigned to element R₁C₁, the intermediate frequency response to R₂C₂ and the high frequency response to R₃C₃. Arcs, attributed to R₂C₂ and R₃C₃, were poorly resolved and, therefore, R₂ and R₃ values (Table 1) were obtained only approximately; however, R₃ is larger than R₂ and R₁, indicating that R₃C₃ is the most resistive element in this sample at this temperature. From the Z″, M″ spectroscopic plots of the same data, Fig. 2, the high frequency peak had capacitance C₃ ∼ 9 pF, calculated from the relation

and was assigned to the bulk response. The two other impedance responses had higher capacitances, C₁ ∼ 20 nF and C₂ ∼ 200 pF, and were tentatively assigned to electrode–sample contact and grain boundary regions, respectively. The data were not corrected for the blank parallel capacitance of the jig, since it was found to be only a few pF.

Fig. 1 Composition x = 0.5, heated in air at 1400 °C: impedance complex plane plot at 83 K. Inset: equivalent circuit representing three parallel RC elements in series.

Fig. 2 Composition x = 0.5, heated in air at 1400 °C: combined spectroscopic Z′′, ○, M′′, ●, plot at 83 K; same data as used in Fig. 1.

Table 1 Composition x = 0.5; R and C values for as-prepared and heat-treated samples

	O2 (83 K)	air (83 K)	N2 (83 K)	H2/N2 (250 K)	H2/N2 (170 K)
a From M″ data.
R total/kΩ	11.5	10.5	21.7	185
R 1/kΩ	2.0(3)	2.6(1)	7.9(7)	10(3)
R 2/kΩ	2.9(3)	2.2(1)	8.0(7)	35(6)
R 3/kΩ	6.6(3)	5.7(3)	5.8(7)	140(6)	8100(400)
R 4/kΩ					20(10)^a
C 1/nF cm^−1	8(4)	15(6)	5(2)	200(50)
C 2/nF cm^−1	0.7(2)	1.1(5)	0.05(2)	1.4(4)
C 3/pF cm^−1	10(3)	9(3)	14(4)	9(2)	16(4)
C 4/pF cm^−1				4	5(1)^a

---

If R₁C₁ were associated with a non-ohmic electrode contact, the associated resistance should increase as the applied voltage is decreased. In Fig. 3, a decrease in amplitude of the ac voltage from 1 V to 100 mV led to a significant increase of R₁; R₂ and R₃ did not vary. When Au paste or In–Ga eutectic were applied as electrodes, similar effects were seen but with an even higher value for R₁. Therefore, R₁C₁ represents a non-ohmic contact at the electrode/sample interface. All subsequent measurements were carried out using Ag electrodes and an ac voltage of 1 V. This reduced the magnitude of R₁ but did not cause any changes to R₂ and R₃.

Fig. 3 Composition x = 0.5, heated in air at 1400 °C: data at 83 K for applied ac voltages of 100 mV, ●, and 1 V, ○.

Impedance plots at 83 K for pellets annealed in O₂ and N₂ were broadly similar to those of the as-prepared sample. For the pellet treated in O₂, R values were similar, Table 1. For the pellet treated in N₂, R₃ changed little but R₁ and R₂ increased significantly and had values similar to R₃. C₁ and C₃ showed little variation after heat treatment in O₂ and N₂, whereas C₂, assigned to the grain boundary region, varied from 0.03–0.07 nF in N₂ to 0.5–0.9 nF in O₂ and 0.6–1.6 nF in air, indicating that the grain boundary layers were relatively thin after treatment in air and O₂, but became thicker in N₂.‡ This appears to be because the grain boundary regions are oxygen-deficient and increase in thickness, due to a small amount of O₂ loss, on heating in N₂.

The fourth pellet, with γ = 5.34, was much more resistive, Table 1. C₃ was similar to the bulk capacitance of oxidised compositions; C₁ and C₂ were larger but from their magnitudes can still be attributed to an electrode/sample interface and a grain boundary, respectively. M″ data, Fig. 4, show a main peak at 3 MHz and a poorly resolved shoulder peak at 200 kHz. The shoulder occurs at a similar position to the main peak of the Z″ spectrum and was attributed to element R₃C₃. The M″ maximum at 3 MHz was assigned to a second bulk element, R₄C₄. Bulk M″ peaks were better separated at lower temperatures which indicates that R₃ has a greater temperature dependence and therefore higher activation energy than R₄ as shown by Arrhenius plots of f_max for the Z″ (R₃C₃) and M″ (R₄C₄) peaks, Fig. 5. If it is assumed that C₃ and C₄ are independent of temperature, then the activation energies, E_a, for f_max correspond to those for the respective R values. E_a for R₄C₄ (0.13 eV) is smaller than for R₃C₃ (0.21 eV) and higher than for R₃C₃ in fully oxidised samples (0.09 eV, see later). Values of R₄ and C₄ calculated from M″ data are shown in Table 1. R₄ is much smaller than R₃ and R₃C₃ is therefore the more resistive bulk region. From the observed dependence of resistance on oxygen content, it appears that R₃C₃ corresponds to the outer grain region which is more reduced than the inner R₄C₄ grain core. The value of C₄ is smaller than that of C₃; consequently, the reduced, outer region is thinner than the less-reduced core.

Fig. 4 Composition x = 0.5, heat-treated in H₂/N₂ at 580 °C: combined spectroscopic M′′, Z′′ plot at 250 K.

Fig. 5 Arrhenius plots of log f_max for bulk responses, R₃C₃ and R₄C₄, of composition x = 0.5, heat-treated in air, ●, O₂, □, N₂, ▽, and H₂/N₂; R₃C₃ (white circles) and R₄C₄ (grey circles). Average Mn valence states, +3.7 and +2.8, for different data sets are indicated.

Bulk and grain boundary conductivities, σ₃ and σ₂, of all four samples are plotted in Arrhenius format in Figs. 6a and b: note that the σ₂ data refer to the overall geometry of the pellet and not to that of the grain boundary region. Samples annealed in air, O₂ and N₂ with Mn average valence state +3.7 had similar bulk conductivities and E_a, ∼0.09 eV. After reduction in H₂/N₂ to give Mn average valence state +2.8, σ₃ decreased drastically and E_a increased to ∼0.23 eV although the Arrhenius plot may be slightly curved. The variation in activation energies between oxidised and reduced samples may either indicate the existence of distinct conduction mechanisms in samples with different Mn average valencies, or that the difficulty of electron hopping between adjacent Mn atoms is composition-dependent. This is discussed later (Fig. 11) where it is concluded that a single conduction mechanism occurs.

Fig. 6 Arrhenius plots of (a) bulk and (b) grain boundary conductivities, σ₃ and σ₂, of composition x = 0.5, heat treated in air, ●, O₂, □, N₂, ▽ and H₂/N₂, ○.

Grain boundary conductivities, σ₂, Fig. 6b, are similar for samples heated in air and O₂, but decrease significantly in N₂ and greatly in H₂/N₂. E_a values are similar for samples heated in air, O₂ and N₂ (∼0.09 eV), but much larger in H₂/N₂. Since activation energies for bulk and grain boundary regions in air, O₂ and N₂ are similar, 0.09 eV, the conduction mechanism is the same in both regions.

A schematic model for conduction through partially reduced grains is shown in Fig. 7a. Grain shells (R₃C₃) are more resistive than cores (R₄C₄) and where possible, charge carriers travel through the inner bulk regions. It is shown later that this is not always the case and the conduction path may vary greatly depending on the thermal history. XRD of the reduced pellet showed a cubic pattern, similar to those for oxygen-deficient samples with x = 0.5.⁷ However, the lines were diffuse, probably due to variation of γ within the sample bulk.

Fig. 7 Conduction pathways through inhomogeneous grains: (a) partially reduced grain after heat-treatment of a fully oxidised sample in H₂/N₂; (b) partially re-oxidised grain after heating of a reduced composition in air.

Composition x = 1.2

In Nb-rich compositions, the oxygen content varies over a smaller range than in Mn-rich compositions.⁷ Two pellets were prepared: the as-prepared pellet had γ = 6.0 and Mn valence state +2.5; the other pellet was reduced in H₂/N₂, had γ = 5.8 and all Mn reduced to Mn²⁺. Note that +2.5 is not the highest average valence state of Mn which can be achieved for this cation composition; on heating the reduced sample in air, the average Mn oxidation state increases to +3.0 to yield a metastable phase of composition Ca₂Mn_0.8Nb_1.2O_6.2. This excess oxidation is important for the interpretation of impedance data, as seen later.

The −Z″, Z′ plane for the as-prepared pellet at 278 K showed a large arc with R ∼ 3.9 MΩ cm and C ∼ 2(3) pF, which was assigned to the bulk region, R₃C₃. A second, small arc at low f had ∼10 nF, and was attributed to either the grain boundary, R₂C₂, or the electrode/sample interface, R₁C₁; it was not investigated further.

The reduced pellet with γ = 5.8 was the most resistive sample investigated. The −Z″, Z′ plane (not shown) had a single arc with R₃ ∼ 9.4 MΩ cm and C ∼ 5–9 pF at 508 K, Table 2. M″ data (not shown) showed a single, symmetric peak attributed to R₃C₃; in this case, the sample bulk appeared not to separate into regions of different oxygen content on reduction.

Table 2 Composition x = 1.2; R and C values for as-prepared, γ = 6.0, and reduced, γ = 5.8, pellet

	Air (278 K)	Air (472 K)	H2/N2 (508 K)
R 1,2/kΩ		2.6(1)
R 3/kΩ	3900(300)	4.8(3)	9400(400)
C 1,2/nF cm^−1		10(2)
C 3/pF cm^−1	2(3)		7(2)

---

C ₃ showed little variation with temperature and was 2–7 pF for as-prepared and reduced pellets. Bulk conductivities, σ₃, are given in Arrhenius format in Fig. 8. For γ = 6.0, data, *, fell on a straight line with E_a ∼ 0.39 eV and were reversible on cooling. Data for γ = 5.8, however, showed more complex behaviour, attributed to partial reoxidation of the sample ≥400 °C. On first heating, ●, data fell on a fairly straight line, possibly slightly curved, with activation energy ∼0.84 eV. On annealing at 400 °C overnight, its conductivity increased (→) and variable temperature data ■, ○ fell on a second straight line with decreased E_a ∼ 0.55 eV. At T > 400 °C, a further jump in conductivity occurred, – – –, with a new activation energy of ∼0.23 eV. In order to exclude any possible influence of the Ag electrode on these conductivity data, especially for samples heated >400 °C, a second set of experiments was performed in which electrodes (of InGa alloy) were added only after the heat treatments >400 °C. Similar trends to those shown in Fig. 8 were obtained, thus showing that the conductivity increases were unaffected by the electrode. From the general trend of increased conductivity with increased oxygen contents, some oxidation of the sample had clearly occurred at >400 °C. However, X-ray patterns of the initial, reduced sample and after the second cooling were identical, and so oxygen uptake was probably limited to the grain boundaries, forming relatively thin conductive regions. C₃ remained small and was similar to that in the as-prepared sample, Table 2. From this, we suggest that charge carriers travel along conductive surface regions, bypassing the more resistive inner bulk region, Fig. 7b; thus, C₃ still refers to the bulk of the sample, which includes both the conductive surface layers and the less conductive grain cores.

Fig. 8 Arrhenius plots and activation energies of bulk conductivities, σ₃, for compositions x = 1.2: γ = 6.0, *, and γ = 5.8 during first (filled symbols) and second (open symbols) heating, ● ○, and cooling, ■ □, cycles.

The activation energy decreased greatly during reoxidation of the grain surfaces, Fig. 8, so much so that, after heating >400 °C, it was smaller than that of the as-prepared sample. Since E_a decreases with increasing oxygen content, it seems likely that the oxygen content in the outer surface region was larger, i.e.γ > 6.0, than in the as-prepared sample. It was shown previously⁶ that an anomalously high oxygen content is achieved on oxidation at intermediate temperatures, ∼750 to 1000 °C; these are much higher temperatures than achieved during the present impedance measurements, 400 to 470 °C, which may therefore be high enough to oxidise the grain boundary/grain surfaces but not the entire sample.

CaMnO_3.0

A pellet of CaMnO_3.0 with Mn valence state +4.0 was prepared.⁶ The −Z′′, Z′ plane at 83 K is given in Fig. 9 for two applied voltages, 100 mV and 1 V. The total resistance was ∼70 Ω cm and varied greatly with applied voltage; thus the arcs seen in Fig. 9 represent the electrode/sample interface. The resistance of the sample, given by the high frequency intercept of the arcs, is ∼42 Ω. The electrical properties could not be further investigated with the frequencies available and it is not known whether any grain boundary resistance contributed to the sample resistance, but certainly the bulk resistance is ≤42 Ω at 83 K. This is much lower than reported for CaMnO_3 − δ by Taguchi (R ∼ 10 kΩ cm at T ∼ 160 K).⁸ The reason for this discrepancy is not known; it may involve differences in oxygen content in the different samples.

Fig. 9 CaMnO_3.0, prepared in O₂: impedance complex plane plot at 83 K, with applied ac voltages of 100 mV, ○, and 1 V, ●.

Discussion

In the present family of materials, complex electrical characteristics were apparent but some general trends may be seen: (i) with increasing x, and decreasing Mn valency at γ = 6.0, both R and E_a increase, Fig. 10; (ii) with decreasing γ and Mn valency at constant x, both R and E_a increase (Figs. 6 and 10 and ref. 7). From the composition and temperature dependence of conductivity, deductions about the conduction mechanism may be made and the role of parameters that influence the conductivity may be considered.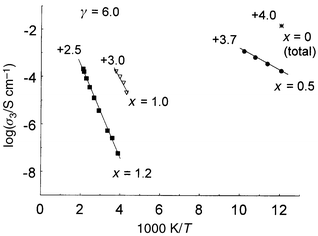

Fig. 10 Arrhenius plots of bulk conductivities, σ₃, for fully oxidised compositions, Ca₂Mn_2 − xNb_xO_6.0: x = 0.5, ●; x = 1.0, ▽; x = 1.2, ■. Total σ for CaMnO_3.00, *.

Conduction mechanisms

For all the materials studied, apart from CaMnO₃ for which we have few data, the conductivity is thermally activated and the Arrhenius plots are generally linear. Although σ and E_a vary with composition, the conductivity pre-exponential factor A, from σ = A exp(−E_a/kT), is almost constant, Fig. 11. Hence, the number of mobile carriers is constant and the conductivity is governed entirely by the ease of hopping, E_a. The conductivity is therefore intrinsic since there is no evidence for any extrinsic region in which carrier concentration varies. Since the conductivity is thermally activated and intrinsic, the mechanism involves the hopping of localised electrons or small polarons, rather than conduction through delocalised bands. Since the carrier concentration is independent of composition, it is inappropriate to refer to the conduction mechanism as p-type, even though the conductivity increases with increasing average oxidation state of Mn.

Fig. 11 Pre-exponential factor, A, as a function of Mn valency.

Mn 3d orbital interactions

The details of the conduction mechanism can be discussed in terms of electron configurations of Mn ions and possible interactions involving the 3d orbitals. If we assume a high spin configuration for octahedrally coordinated Mn, consistent with magnetic susceptibility data for Ca₂MnNbO_γ,⁷ and neglecting any Jahn–Teller splitting, then the energy level diagrams for the various Mn ions are: Mn²⁺: t_2g³ e_g²; Mn³⁺: t_2g³ e_g¹; Mn⁴⁺: t_2g³ e_g⁰. It is usually assumed that the electrons responsible for conductivity are those in the highest occupied levels, since electrons in lower levels are increasingly localised or in levels that are fully occupied. For example, the electronic conduction in GMR manganates with Mn in a mixed +3/+4 valence state is explained by assuming that t_2g³ electrons are localised with a spin of S = 3/2, while e_g electrons are strongly hybridised with the oxygen 2p state, Fig. 12a, forming a σ d–p bond between Mn and O;^1,10,11 e_g electrons hop from Mn³⁺ to Mn⁴⁺via the bridging oxygen, so that effectively Mn³⁺ and Mn⁴⁺ ions change places. The difficulty in applying this model to the present materials is that conductivity is greatest when Mn is in the +4 state, for which the e_g orbitals are empty. If, however, some partial occupancy of e_g orbitals occurs, through contribution of oxygen 2p electrons to the σ d–p bonds, then would be forced to conclude that, effectively, oxygen 2p electrons are responsible for the high conductivity in CaMnO₃.

Fig. 12 Possibilities of Mn d-orbital interactions in a simple cubic AMnO₃ perovskite structure: (a) e_g–p_σ–e_g overlap of Mn ions with oxygen (σ-bond), (b) t_2g–p_π–t_2g overlap of Mn ions with oxygen (π-bond) and (c) direct t_2g–t_2g overlap between Mn ions across the unit cell face diagonal.

Alternatively, the t_2g rather than the e_g electrons may be responsible for the conductivity. The relative disposition of t_2g orbitals on adjacent Mn atoms in a simple perovskite structure suggests two possible modes of orbital interaction.

First, t_2g orbitals may overlap with the O p_π orbitals in directions parallel to the unit cell edges, Fig. 12b. This situation is comparable to that in tungsten bronzes, A_xWO₃ with A = alkali metals or protons,^12,13 in which t_2g–p_π–t_2g overlap is responsible for metallic conductivity. WO₃ (x = 0) has an empty W 5d (t_2g) band and is insulating. Reduction of W⁶⁺ to W⁵⁺ (increasing x) introduces electrons into the 5d (t_2g) band and at high x, a Mott transition to a metallic state occurs. This model may be considered for the present system in which the t_2g band is half-filled for d³, d⁴ and d⁵ high spin Mn; conduction through the t_2g orbitals is possible in all three cases but the materials are semiconducting rather than metallic, which might indicate that the t_2g–p_π–t_2g orbital overlap is poor. The increase of conductivity on oxidation could correlate with an increase in t_2g–p_π–t_2g orbital overlap due to reduction in unit cell dimensions. Factors that influence orbital separation are discussed later.

It might also be considered whether t_2g orbitals interact directly across the unit cell face diagonal, as occurs in some rocksalt structures, e.g. TiO, Fig. 12c. In TiO, the t_2g conduction band, resulting from direct t_2g–t_2g overlap, is 1/3 full (d² Ti) and gives rise to metallic conduction.¹² In the present system, the Mn–Mn distance across the cell face diagonal is larger than in rocksalt structures (approximately twice as long) and direct t_2g–t_2g overlap appears unlikely.

To a first approximation, then, it is concluded that conduction in the present materials may involve either the t_2g electrons through t_2g–p–t_2g orbital overlap or the e_g orbitals through σ d–p orbital overlap, with electrons provided primarily by oxygen. Enormous variations in conductivity are seen with changing valence of Mn; since the number of t_2g and oxygen p electrons is constant, the activation energy and, hence, the conductivity must be controlled by the separation of orbitals on adjacent atoms.

Mn 3d-orbital separation

In considering the separation of orbitals on adjacent atoms, two factors are potentially important: the size/charge of Mn and the unit cell dimensions. First, the idealised cation radius of Mn in octahedral coordination decreases on oxidation, from 0.83 Å (Mn²⁺) to 0.53 Å (Mn⁴⁺).¹⁴ Consequently, with increasing charge of Mn, the d electrons should be held more tightly to the nucleus, the orbital extent and overlap should decrease and conductivity through the d orbitals should decrease. The exact opposite occurs, however, as the conductivity increases with Mn oxidation state. Alternatively, with increasing occupation of e_g orbitals in the sequence Mn⁴⁺–Mn³⁺–Mn²⁺, the ionic size of Mn increases but the spatial extent of the t_2g orbitals might decrease because of electron–electron repulsion, and hence t_2g orbitals on adjacent Mn ions become more separated. The latter situation would be consistent with the present data; conductivity is lowest when all Mn is in valence state +2 and possesses the highest number of e_g electrons.

Second, an increase in unit cell dimensions must increase interatomic distances and, therefore, increase the orbital separation. In the present materials, the unit cell expands on increasing x and decreasing γ, both of which are associated with a decrease in Mn valence. Fig. 13 shows that activation energies increase non-linearly with the average perovskite unit cell dimension, a_p = ³√V. For small interatomic distances with a higher degree of orbital overlap, E_a is relatively small and varies little with unit cell size; for large interatomic distances and poor orbital overlap, E_a depends increasingly strongly on a_p. This simple correlation, Fig. 13, indicates that interatomic distance may be the main factor that determines electronic conductivity in the present system.

Fig. 13 Variation of E_a with perovskite unit cell dimension, ³√V.

Tilting of octahedra in the GdFeO₃-type structure

We may also consider the possible influence of non-linearity of Mn–O–Mn bonds due to tilting of MnO₆ octahedra in the orthorhombic solid solutions with the GdFeO₃ structure and the absence of tilting in the reduced, cubic solid solutions. Cubic structures with a Mn–O–Mn bond angle of 180 °C would maximise the Mn–O–Mn σ and π orbital interactions. In structures with tilted octahedra, the Mn–O–Mn bond angles deviate from 180 °C, give poorer σ and π orbital overlap and increased localisation of d-electrons.^15,16

Conductivity data do not indicate a major influence of octahedral tilting on conductivity. For x = 0.5, as oxygen is removed from the structure, the orthorhombicity decreases and a transition to a simple cubic structure occurs. At the same time, a decrease in conductivity with increased activation energy is observed which is perhaps the opposite of what would be predicted. Also, there is no obvious correlation between the degree of orthorhombicity (greatest for x = 1.2, γ = 6) and conductivity (greatest for x = 0, γ = 6).^7,17,18

Oxygen vacancies

Some compositions were oxygen-deficient and contained 3–11% oxygen vacancies. The role of oxygen vacancies may be discussed in terms of e_g–p_σ–e_g or t_2g–p_π–t_2g orbital overlap which, on removal of oxygen from the structure, may prevent d–p–d interactions and interrupt electron hopping between the metal ions, leading to low conductivity. This is consistent with the observed decrease of conductivity with increasing oxygen deficiency.

Nb content

We can discount any major effect of inert Nb⁵⁺ ions on the conductivity, provided that there are sufficient Mn–Mn or Mn–O–Mn close contacts to give a 3D hopping pathway through the structure for electrons. Assuming a random distribution of Mn and Nb over the B-sites, the question of whether Mn–Mn or Mn–O–Mn interactions can occur depends on composition and is essentially a percolation problem; provided there is sufficient Mn present to provide a percolation pathway, then dc conduction is possible and should be fairly insensitive to the Nb content. For the present materials, the entire range, 0 ≤ x ≤ 1.2, is within the percolation limit.

High spin Mn³⁺

We may also consider whether, in situations where all Mn is in the +3 state, any anomalies in the electrical properties are expected. There is some evidence for this in f_max data for the bulk conductivities shown in Fig. 14. The activation energy for the data set with valence state +3 is anomalously high and out of sequence with the remaining data; it could be that, for this composition, the unit cell is locally distorted, perhaps with a structural elongation associated with a local Jahn–Teller effect, and this gives rise to a small increase in Mn–Mn separations, and hence an increase in activation energy.

Fig. 14 Arrhenius plots of log f_max (obtained from M′′ or Z′′ data) for bulk responses in the Ca₂Mn_2 − xNb_xO_γ system: x = 0.5, γ = 6.0, ●, and γ = 5.34 with the two bulk responses, ○ and ●; x = 1.0, γ = 6.0, ▽; x = 1.2, γ = 6.0, ■, and γ = 5.8, □.

Conclusions

The variation of conductivity with composition in the Ca₂Mn_2 − xNb_xO_γ system may be discussed in several ways. The increase of conductivity on oxidation of Mn is often explained by the concept of p-type hopping conduction,¹⁹ but this model cannot explain the high values of conductivity when Mn has valency +4.0. We found no evidence that Mn electrons in the e_g orbitals are responsible for conduction. Instead, either oxygen p electrons forming σ d–p bonds with e_g orbitals or t_2g electrons linking through oxygen p_π orbitals are the conducting species. Direct t_2g–t_2g orbital interactions between Mn ions across the unit cell face diagonal are unlikely because of the large Mn–Mn interatomic distance. Conductivities depend on the degree of d–p orbital overlap, which is influenced directly by Mn–O–Mn distances and, hence, unit cell dimensions. There was no systematic dependence of conductivity on Mn–O–Mn bond angle but the octahedral tilt angles may be too small to have a significant effect.

The electrical characteristics of ceramic samples depended very much on sample history. Samples that were partially reduced [in situ reduction in H₂/N₂ in TG experiments] were particularly complex, probably because reduction commenced at the grain surfaces, giving rise to oxygen gradients and non-equilibrium structures. Similarly, reduced samples that were allowed to partially reoxidise gave rise to samples that were electrically inhomogeneous. In both cases, impedance measurements provided a sensitive indicator of sample inhomogeneity. Most of the data reported here are for samples that were fully oxidized or fully reduced; their results provided a framework on which to explain the behaviour of more complex inhomogeneous samples of intermediate oxygen content.

References

1. C. N. R. Rao, A. K. Cheetham and R. Mahesh, Chem. Mater., 1996, 8, 2421.
2. R.-F. Huang and W. Y. Howng, J. Mater. Res., 1996, 11, 3077.
3. W. T. A. Harrison, T. H. Lee, Y. L. Yang, D. P. Scarfe, L. M. Liu and A. J. Jacobson, Mater. Res. Bull., 1995, 30, 621.
4. B. Ma and U. Balachandran, J. Electroceram., 1998, 2, 135.
5. P. Hagenmuller, M. Pouchard and J. C. Grenier, Solid State Ionics, 1990, 43, 7.
6. A. Kruth, U. Guth and A. R. West, J. Mater. Chem., 1999, 9, 1579.
7. A. Kruth, M. Tabuchi, U. Guth and A. R. West, J. Mater. Chem., 1998, 8, 2515.
8. H. Taguchi, Phys. Status Solidi A, 1985, 88, K79.
9. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132.
10. J. B. Goodenough, Prog. Solid State Chem., 1971, 5, 149.
11. P. D. Battle, D. E. Cox, M. A. Green, J. E. Millburn, L. E. Spring, P. G. Radaelli, M. J. Rosseinsky and J. F. Vente, Chem. Mater., 1997, 9, 1042.
12. J. A. Duffy, Bonding, Energy Levels & Bands in Inorganic Solids, Longman Scientific & Technical, Essex, 1990..
13. N. S. P. Bhuvanesh and J. Gopalakrishnan, J. Mater. Chem., 1997, 7, 2297.
14. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751.
15. H. Taguchi, J. Solid State Chem., 1996, 124, 360.
16. P. M. Woodward, Acta. Crystallogr., Sect. B, 1997, 53, 44.
17. A. Kruth and A. R. West, unpublished work..
18. S. K. Mishra and S. Satpathy, Phys. Rev. B, 1998, 58, 7585.
19. J. Töpfer, J. P. Doumerc and J. C. Grenier, J. Mater. Chem., 1996, 6, 1511.

---

Footnotes

† Basis of a presentation given at Materials Discussion No. 3, 26–29 September 2000, University of Cambridge, UK.

‡ Since C data are corrected for overall pellet geometry and the permittivity values, ε′, of different regions of the pellet are likely to be similar, then the capacitance values give an approximate idea of the thickness of each region.⁹

---