The structure and dynamics of cationic zirconocene complexes with phenyl coordination![[hair space]](https://www.rsc.org/images/entities/h2_char_200a.gif) †
†
Michael
Bühl
* and
Jörg
Saßmannshausen
Max-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, D-45470, Mülheim an der Ruhr, Germany
First published on 13th December 2000
Abstract
Density functional computations (BP86/ECP1 and B3LYP/II level) have revealed that the phenyl group in [Zr(η-C5H5)(η-C5H4CR2C6H5)Me]+ (R = H) is coordinated to the Zr atom via one of the phenyl carbon atoms, rather than via an agostic Zr–H contact, as suggested previously. A stationary point with such an agostic interaction is the transition structure for phenyl rotation with a barrier higher than 50 kJ mol−1 (B3LYP/II level), consistent with results from dynamic NMR spectroscopy for a closely related compound (R = Me). The structural assignments are supported by the good accord between the computed (GIAO-B3LYP/II level) and experimental NMR chemical shifts. A second dynamic process with a very similar activation barrier is indicated to involve dissociation of the coordinated phenyl moiety from the Zr atom and inversion at the latter. The same structural motif (i.e. η1-bonded aryl group) is also found for the [Zr(η-C5H4CH2C6H5)2]2+ dication.
Introduction
Structure determination in solution is difficult, in particular for reactive intermediates of fleeting existence. The only hope in most cases is to revert to closely related model systems that are stable enough to be characterised. One such example is the solvated alkylzirconocene cation, [ZrCp2Me(solv)]+ (Cp = cyclopentadienyl-type ligand), believed to be a key intermediate in homogeneous olefin polymerisation with Kaminski-type zirconocene catalysts.1,2 Since most of these polymerisations are conducted in toluene or other aromatic solvents, it is of interest to elucidate the nature of the interaction between the zirconocene center and an arene. To this end, special zirconocene derivatives with CMe2Ph groups tethered to the Cp ring have recently been investigated.3 Based on the 1H and 13C NMR spectra of [Zr(η-C5H5)(η-C5H4CMe2C6H5)Me]+1 and derivatives thereof, structures with an intramolecular agostic interaction between the Zr atom and one of the phenyl hydrogen atoms in ortho position have been proposed (Scheme 1).3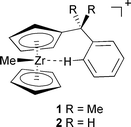 | ||
| Scheme 1 | ||
Computational chemistry has contributed significantly to the understanding of many aspects of homogeneous olefin polymerisation.4 Suggested mechanisms and intermediates could be corroborated by use of the modern tools of density-functional theory (DFT). We now apply these well established methods5 to study the intramolecular Zr–phenyl coordination in [Zr(η-C5H5)(η-C5H4CH2C6H5)Me]+2, a slightly simplified model for 1 which lacks the two methyl groups in the benzyl bridge. Optimised structures are assessed by comparison of computed chemical shifts with experimental δ values, a combined approach that has evolved into a useful structural tool.6 The calculations reported here show that a stationary point with an agostic Zr–H interaction can be excluded, and indicate that a η1 coordination to a phenyl carbon atom is favored instead.
Computational details
Geometries have fully been optimised without symmetry constraints (except 4a and 4b for which C2 symmetry was imposed) at the BP86/ECP1 level, i.e. employing the exchange and correlation functionals of Becke![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 7 and Perdew,8 respectively, together with a fine integration grid (75 radial shells with 302 angular points per shell), relativistic MEFIT effective core potentials with the corresponding valence basis sets for Zr
7 and Perdew,8 respectively, together with a fine integration grid (75 radial shells with 302 angular points per shell), relativistic MEFIT effective core potentials with the corresponding valence basis sets for Zr![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 (contraction scheme [6s5p3d]), and standard 6-31G* basis set
9 (contraction scheme [6s5p3d]), and standard 6-31G* basis set![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 10 for C and H. Geometries are given as ESI
10 for C and H. Geometries are given as ESI![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) † in the form of cartesian coordinates. The stationary points were characterised as minima or transition states by analytical harmonic frequencies (zero or one imaginary frequency, respectively), which were also used without scaling for zero-point and thermal corrections.
† in the form of cartesian coordinates. The stationary points were characterised as minima or transition states by analytical harmonic frequencies (zero or one imaginary frequency, respectively), which were also used without scaling for zero-point and thermal corrections.
Magnetic shieldings σ have been evaluated for the BP86/ECP1 geometries using a recent implementation of the GIAO (gauge-including atomic orbitals)-DFT method,11 involving the functional combinations according to Becke (hybrid)12 and Lee, Yang, and Parr![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 13 (denoted B3LYP), together with basis II, i.e. a [12s9p5d] all-electron basis for Zr, contracted from the (17s13p9d) set14 and including two diffuse p and one diffuse d function
13 (denoted B3LYP), together with basis II, i.e. a [12s9p5d] all-electron basis for Zr, contracted from the (17s13p9d) set14 and including two diffuse p and one diffuse d function![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 15 (exponents 0.11323, 0.04108, and 0.0382), and the recommended IGLO-basis II16 on C and H. This particular combination of functionals and basis sets has proven quite effective for chemical shift computations for transition-metal complexes.171H and 13C chemical shifts have been calculated relative to benzene as primary reference (absolute shieldings σ 24.3 and 45.5, respectively, at the same level) converted into the TMS scale using the experimental δ values of benzene (7.3 and 128.5, respectively). 91Zr chemical shifts are reported relative to [Zr(C5H5)2Br2], with σ = 1720.3 at the same level. All computations employed the GAUSSIAN 98 program package,18 except for the topological analyses (Bader analyses)
15 (exponents 0.11323, 0.04108, and 0.0382), and the recommended IGLO-basis II16 on C and H. This particular combination of functionals and basis sets has proven quite effective for chemical shift computations for transition-metal complexes.171H and 13C chemical shifts have been calculated relative to benzene as primary reference (absolute shieldings σ 24.3 and 45.5, respectively, at the same level) converted into the TMS scale using the experimental δ values of benzene (7.3 and 128.5, respectively). 91Zr chemical shifts are reported relative to [Zr(C5H5)2Br2], with σ = 1720.3 at the same level. All computations employed the GAUSSIAN 98 program package,18 except for the topological analyses (Bader analyses)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 19 which were performed using MORPHY.20
19 which were performed using MORPHY.20
Energies are reported at the BP86/ECP1 and B3LYP/II levels, corrected for the BP96/ECP1 zero-point energies. For the [Zr(η-C5H5)2Me(C6H6)]+ complex the association energies have been corrected for the basis-set superposition error by the counterpoise method.21
Results and discussion
An initial optimisation of complex 2 starting from a configuration as depicted in Scheme 1, i.e. with an agostic Zr–H interaction, collapsed to a minimum devoid of such an interaction, but with a close contact between Zr and one ortho-carbon atom of the phenyl ring (2b, Fig. 1, Zr–C1 2.612 Å). The coordination mode of the phenyl moiety in 2b can be characterised as η1 since all other Zr–C(Ph) distances are much larger than 3 Å (also, the H atom attached to C1 is bent away from Zr, by ca. 15° out of the Ph plane).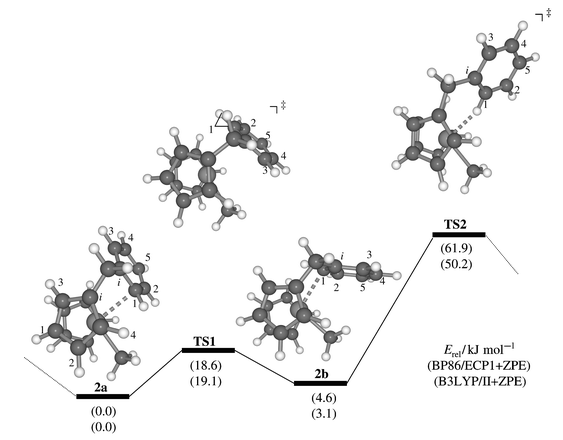 | ||
| Fig. 1 Stationary points and schematic potential energy surface for phenyl rotation in cation 2; in parentheses, relative energies at the BP86/ECP1 (top) and B3LYP/II levels (bottom), including zero-point corrections. | ||
Further exploration of the potential energy surface revealed the presence of at least one other minimum wherein the Zr atom is attached to the other ortho-carbon (2a, Zr–C1 2.629 Å) and which is slightly lower in energy (by ca. 3–5 kJ mol−1, Fig. 1). A transition state connecting these two minima, TS1, was located which is characterised by a loosely η3-coordinated phenyl ring (the distances between Zr and C1, Ci, and C3 are 2.995, 2.840, and 3.246 Å, respectively). As the resulting barrier is only 19 kJ mol−1, rapid equilibration between the two isomers is to be expected on the NMR timescale.
A second transition state between complexes 2a and 2b, TS2, is considerably higher in energy, ca. 50–62 kJ mol−1, depending on the DFT procedure (Fig. 1). This stationary point resembles the Zr–H agostic intermediate proposed earlier (Scheme 1), and has a Zr–H distance of 2.201 Å. While the interconversion viaTS1 is a slippage of the Zr along one side of the phenyl ring, the process viaTS2 scrambles both sides of the latter. This scrambling is in line with dynamic NMR spectra of 1 and its derivatives where coalescence of the o,o′ and m,m′ resonances can be observed at higher temperatures (around −10 °C). A preliminary line-shape analysis afforded an estimate for the free energy of activation of this process of around ca. 50(1) kJ mol−1, in good accord with the B3LYP value.22 This analysis also afforded evidence for a second dynamic process (see below).
Chemical shifts of these minima and transition structures are summarised in Table 1, together with the experimental data for complex 1. The δ value of the phenyl hydrogen in 1 position is of particularly diagnostic value: this proton is computed to be highly shielded in the H-agostic TS2, and much less so in the other, η-bonded structures, which are thus in better accord with experiment. Among the 13C shifts, that of the Zr–bonded methyl carbon is the most sensitive; again the largest deviation from experiment is found for TS2. The latter also performs significantly worse than 2a,2b or TS1 in terms of the mean absolute deviations from experiment (see |Δδ| values in Table 1). The presence of a purely agostic Zr–H interaction between the metal and the phenyl ring as in TS2 can thus be refuted on the basis of these NMR data.
| Nucleus | TS2 | TS1 | 2b | 2a |
expt.(1)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a |
|---|---|---|---|---|---|
| a From reference 3. b Assignment according to the derivative bearing a Me group at Ph C5. c Largest absolute deviation from experiment (in parentheses: mean absolute deviation). | |||||
| 1H | |||||
| Ph H1 | −1.2 | 6.3 | 3.1 | 5.6 | 6.3 |
| Ph H2 | 6.8 | 7.6 | 8.0 | 7.6 | 7.8 |
| Ph H3 | 7.4 | 6.3 | 7.3 | 7.2 | 7.3 |
| Ph H4 | 7.6 | 7.7 | 8.1 | 8.0 | 8.1 |
| Ph H5 | 7.4 | 7.4 | 7.4 | 7.7 | 7.7 |
| Cp′ H1 | 5.8 | 5.9 | 6.0 | 6.0 |
6.2![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ H2 | 7.4 | 5.8 | 5.8 | 6.5 |
6.4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ H3 | 6.9 | 5.8 | 5.9 | 5.7 |
5.9![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ H4 | 7.2 | 6.7 | 6.5 | 6.7 |
7.0![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp H(av.) | 6.6 | 6.0 | 6.4 | 5.7 | 5.8 |
| CH3 (av.) | 2.2 | 1.0 | 0.3 | 1.3 | 0.7 |
|Δδ|max (av.)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c |
7.5 (1.30) | 1.0 (0.34) | 3.2 (0.54) | 0.9 (0.25) | |
| 13C | |||||
| Ph Ci | 144.3 | 125.1 | 143.8 | 128.2 | — |
| Ph C1 | 123.5 | 118.7 | 114.8 | 113.0 | 114.1 |
| Ph C2 | 129.6 | 138.5 | 136.9 | 141.4 | 139.4 |
| Ph C3 | 131.6 | 130.4 | 128.6 | 133.1 | 128.2 |
| Ph C4 | 135.2 | 141.5 | 146.9 | 144.1 | 140.9 |
| Ph C5 | 131.2 | 131.5 | 129.2 | 129.8 | 128.8 |
| Cp′ Ci | 147.1 | 121.1 | 123.2 | 119.6 | — |
| Cp′ C1 | 107.1 | 115.1 | 111.7 | 112.2 |
111.9![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ C2 | 129.1 | 114.7 | 115.7 | 119.3 |
117.8![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ C3 | 114.7 | 102.7 | 106.5 | 103.5 |
102.1![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ C4 | 122.9 | 122.0 | 123.4 | 118.3 |
114.5![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp C(av.) | 118.7 | 116.3 | 115.2 | 115.9 | 115.1 |
| CH3 | 66.0 | 47.0 | 53.2 | 49.3 | 46.2 |
|Δδ|max (av.)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c |
19.8 (8.3) | 7.5 (2.5) | 8.9 (3.0) | 4.9 (2.1) | |
| 91Zr | 646 | 290 | 317 | 328 | — |
Another experimental observable is in line with such an assignment, namely the 1JCH coupling constant between Ph C1 and H1, recorded for a derivative of complex 1 bearing an additional Me group at the phenyl ring in 5 position. The value of 148 Hz is somewhat reduced with respect to the other phenylic CH-coupling constants of the same molecule (163–174 Hz),3 but much smaller 1JCH values of the order of 100 Hz are observed when the corresponding hydrogen atom is involved in a strong agostic bond to the metal.23
No unambiguous decision can be made between the three η-bonded structures on the basis of the mean absolute deviations. Owing to the low barrier viaTS1, the system is fluxional on the NMR timescale in the region between 2a and 2b. We note, however, that the best accord with experiment is obtained for the lowest minimum, 2a. The slightly higher-lying isomer 2b is disfavored by the large discrepancy encountered for the chemical shift of Ph H1, |Δδ| > 3 ppm (first entry in Table 1). Despite the much longer Zr–C(phenyl) distances in TS1 as compared to 2a, the chemical shifts computed for these two structures do not differ much. We are quite confident that the potential energy surface is correctly described, at least in a qualitative sense, at the DFT level employed, i.e. that 2a should be the equilibrium structure. Very likely, 2a is a good representation of the geometry of 1 and derivatives in solution. It cannot be excluded, however, that solvent and temperature effects could produce an averaged structure closer to that of TS1. The fluxionality described by TS1, if retained in the real system 1, would add to the dynamics and lability![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 3 of zirconocene cations with phenyl coordination.
3 of zirconocene cations with phenyl coordination.
No evidence for Zr–H interactions in complexes 2a and 2b can be detected via topological analyses of the B3LYP/II total electron densities: in either structure, a bond path extends from Zr to the nearest ortho-carbon atom of the phenyl ring, not to the proton attached to this carbon. The notable shielding of the Ph H1 resonance in 2b is not due to a specific interaction with the Zr, but is most likely a consequence of paratropic current loops around the metal. Such a mechanism has been shown to be responsible for the negative “hydridic” shift in the proton NMR spectra of transition-metal hydrides.24
For the Zr–H agostic transition structure TS2 very similar 13C chemical shifts between δ 130 and 135 are computed for the resonances of the unsubstituted phenylic carbon atoms Ph C2–C5 (Table 1). In contrast, a more pronounced alternation of these values between δca. 128 and 141 is observed experimentally. Such a pattern could be indicative of noticeable Wheland character for the cation (B, in Scheme 2), similar to suggestions forwarded for rhodium complexes with pincer ligands.25 For the latter, support for such an interpretation came from an enhanced acidity of the complexes (cf. C, in Scheme 2). However, our computations provide no evidence for a particularly high acidity in 2a, as the corresponding deprotonated, ortho-metallated species [Zr(η-C5H5)(η-C5H4CH2C6H4)Me] is found higher in energy by 1051 kJ mol−1 (BP86/ECP1 level without zero-point correction; cf. 807 kJ mol−1 for protonated benzene at the same level). There is precedence for at least one related ortho-metallated benzyl–Cp complex in the literature, namely in the case of [Fe(CO)2(η-C5Me4CH2C6H4)].26
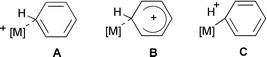 | ||
| Scheme 2 | ||
The same structural motif as in complexes 1, 2, and their derivatives should also be present in the dication [Zr(η-C5H4CMe2C6H5)2]2+3, the synthesis of which has recently been reported.27 For the corresponding model compound [Zr(η-C5H4CH2C6H5)2]2+ two minima, 4a and 4b, with the same phenyl bonding modes as in 2a and 2b could be located (C2 symmetry imposed, Fig. 2). Compared to the latter, the energy separation between 4a and 4b is larger, ca. 14–18 kJ mol−1. The 1H chemical shifts computed for 4a fit much better than those of 4b to the experimental data of 3 (Table 2), in particular the Ph H1 resonance.
| Nucleus | 4b | 4a |
expt. (3)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a |
|---|---|---|---|
| a From reference 27. b Assignment of positions 2 and 4 reversed (see text). c Largest absolute deviation from experiment (in parentheses: mean absolute deviation). | |||
| 1H | |||
| Ph H1 | 2.5 | 6.0 | 6.8 |
| Ph H2 | 7.5 | 8.1 | 8.2 |
| Ph H3 | 7.4 | 7.6 | 7.5 |
| Ph H4 | 8.4 | 8.6 | 8.3 |
| Ph H5 | 7.3 | 8.1 | 7.9 |
| Cp′ H1 | 7.3 | 6.8 | 6.9 |
| Cp′ H2 | 6.6 | 3.5 |
3.9![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ H3 | 6.7 | 6.3 | 6.3 |
| Cp′ H4 | 6.4 | 6.6 |
6.6![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
|Δδ|max (av.)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c |
4.3 (1.06) | 0.8 (0.22) | |
| 13C | |||
| Ph Ci | 151.1 | 132.5 | 144.4 |
| Ph C1 | 118.4 | 112.8 | 113.4 |
| Ph C2 | 138.4 | 146.0 | 143.0 |
| Ph C3 | 129.6 | 136.8 | 129.8 |
| Ph C4 | 153.6 | 152.2 | 144.6 |
| Ph C5 | 130.5 | 133.0 | 130.3 |
| Cp′ Ci | 135.6 | 124.2 | 134.1 |
| Cp′ C1 | 116.9 | 119.5 | 119.1 |
| Cp′ C2 | 123.6 | 133.3 |
127.6![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
| Cp′ C3 | 115.2 | 111.8 | 109.0 |
| Cp′ C4 | 120.4 | 117.2 |
114.0![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b |
|Δδ|max. (av.)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c |
9.0 (4.2) | 11.6 (4.9) | |
| 91Zr | 149 | 226 | — |
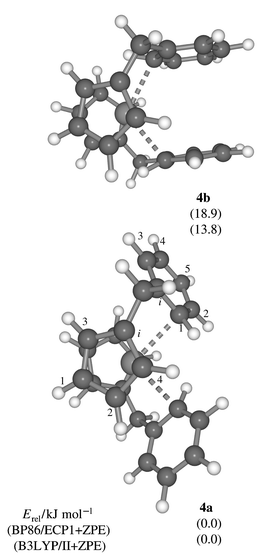 | ||
| Fig. 2 Minima for dication 4 (C2 symmetry, BP86/ECP1 level). | ||
Two proton assignments of the Cp ring probably need to be reassigned: the exceptionally shielded resonance at δ 3.9 has been attributed to Cp′ H4, whereas for 4a such a low-frequency shift is computed for Cp′ H2 (Table 2). The original assignments have been based on the assumption that anisotropy effects of the Ph group would be most prominent for the Cp ring attached to it. Inspection of the molecular geometry, however, reveals that Cp′ H2 is in close proximity to the phenyl ring of the other ligand and well inside its shielding cone (this feature is not immediately apparent from the orientation in Fig. 2). Thus, the published assignments![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 27 of Cp′ H4 and H2 need to be reversed. In 2a one of the Cp H atoms experiences a similar shielding, δ 3.4, which is responsible for the 0.7 ppm low-frequency shift of the averaged Cp H signal with respect to that of 2b (Table 1), a situation reminiscent of the well known ASIS (aromatic solvent induced shift) effect in 1H NMR spectroscopy.28
27 of Cp′ H4 and H2 need to be reversed. In 2a one of the Cp H atoms experiences a similar shielding, δ 3.4, which is responsible for the 0.7 ppm low-frequency shift of the averaged Cp H signal with respect to that of 2b (Table 1), a situation reminiscent of the well known ASIS (aromatic solvent induced shift) effect in 1H NMR spectroscopy.28
The computed δ(13C) values of structures 4a,,4b compiled in Table 2 are less conclusive. Both isomers show fairly large maximum and average deviations, as compared to those of 2a, 2b in Table 1. For the more stable form 4a the largest errors are found for both types of ipso-carbon atoms. Most remaining resonances agree better with experiment than those of 4b, provided the experimental assignments of Cp′ C2 and Cp′ C4 are switched (which would be consistent with the 1H data as the 13C resonances were assigned via CH correlation). Unfortunately, no distinction between 4a and 4b can be made on the basis of the 13C NMR data. Also, it cannot be excluded that other isomers may noticeably be populated under the experimental conditions. Indeed, another minimum was located (4c, not shown in Fig. 2) with one Ph ring oriented as in 2a and the other as in 2b, which was found to be between 5.1 (BP86) and 3.1 kJ mol−1 (B3LYP) above 4a. Neither the appropriately averaged chemical shifts of 4c nor those of a 4∶1 mixture between 4a and 4c (estimated from the B3LYP value and a Boltzmann distribution at −10 °C) performed significantly better than those of 4a in Table 2.
For completeness, the 91Zr chemical shifts are included in Tables 1 and 2. Trends in δ(91Zr) of zirconocenes have been reproduced computationally at Hartree–Fock and DFT levels.29 A substantial deshielding of the Zr in TS2 is computed, δ 649, similar to the value predicted for the unsolvated [Zr(η-C5H5)2Me]+5 cation, δca. 700.29a The electron deficiency of the metal is considerably reduced in the η-bonded species TS1 and 2a, 2b, as judged by their lower δ(91Zr) values around 300 ppm (Table 1), but appears to be larger than that in the [Zr(η-C5H5)2Me(THF![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) )]+ adduct (THF = tetrahydrofuran), for which a value of δ 115 has been reported.30 Intermediate δ(91Zr) values of 149 and 226 are obtained for 4a, 4b (Table 2). Unfortunately, based on the computed electric field gradients and the expected enhanced molecular correlation times,29a2b and 4b should have much broader metal resonances than [Zr(η-C5H5)2Me2], for which Δν1/2 is 2.5 kHz at room temperature.29a Thus, it appears unlikely that the 91Zr NMR resonances of 2 and 4, much less those of the larger 1 and 3, could be detected.
)]+ adduct (THF = tetrahydrofuran), for which a value of δ 115 has been reported.30 Intermediate δ(91Zr) values of 149 and 226 are obtained for 4a, 4b (Table 2). Unfortunately, based on the computed electric field gradients and the expected enhanced molecular correlation times,29a2b and 4b should have much broader metal resonances than [Zr(η-C5H5)2Me2], for which Δν1/2 is 2.5 kHz at room temperature.29a Thus, it appears unlikely that the 91Zr NMR resonances of 2 and 4, much less those of the larger 1 and 3, could be detected.
Finally it should be noted that the situation in the experiments may actually be more complex than assumed in the computations for the free cations. Attempts to produce cation 2 were thwarted by stability problems of the corresponding precursor, and no unambiguous evidence for phenyl coordination was found in cations produced from potential precursors of 4.31 Apparently, the benzylic hydrogens in 2 and 4 can be involved in undesired side reactions and need to be blocked, for instance by methyl substitution. Nevertheless, the electronic and geometric structures of the as yet unknown cations 2 and 4, and in particular the nature of the Zr–phenyl interaction, should be very similar to those of the observed and closely related species 1 and 3.
Besides the phenyl rotation viaTS2 in Fig. 1, which only scrambles the o,o′ and m,m′ phenyl resonances, a second dynamic process can be detected in the temperature-dependent NMR spectra of complex 1, namely scrambling of the two methyl groups at the bridge between Cp and Ph. The linewidths of these methyl signals can be analysed and fitted reasonably well, affording a scrambling barrier of 53.0 kJ mol−1.22 This value is very similar to, albeit slightly higher than, that of phenyl rotation, ca. 50 kJ mol−1. A plausible mechanism for methyl scrambling involves dissociation of the phenyl group from the metal, inversion at Zr, and coordination of the phenyl group “from the other side” (see Scheme 3).
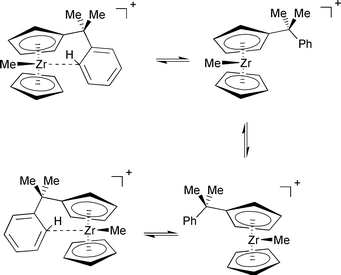 | ||
| Scheme 3 | ||
The process was not studied for complex 2 due to the manifold of possible pathways (involving rotamers about the Zr–Cp axis or the Cp-CMe2Ph bond), which would make an explicit treatment of dynamics desirable. However, an upper limit for this barrier can be estimated from model calculations for [Zr(η-C5H5)2Me]+5 and its benzene adduct, [Zr(η-C5H5)2Me(C6H6)]+6. Optimisation of the latter afforded a η1-coordinated adduct![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 32 similar to 2a, also when starting from a Zr–H agostic structure. The computed binding energy of benzene in 6 is substantial, between 68.8 and 55.2 kJ mol−1 (BP86/ECP1 and B3LYP/II levels, respectively, including counterpoise and zero-point corrections). Cationic Group IV metal complexes with three ligands in pyramidal orientation can easily invert via a planar metal center when π-donating ligands are present.33 Indeed, a very small barrier not exceeding 2 kJ mol−1 is obtained for zirconocene 5 (Fig. 3). Thus, the first step in the sequence in Scheme 3 should be rate-determining, namely dissociation of the coordinated aryl ring. The overall barrier for the whole process should be of the same order of magnitude as the binding energy of benzene in 6.34 Incidentally, the B3LYP value for the latter, 55.2 kJ mol−1, fits very well to the experimental barrier of 53 kJ mol−1.
32 similar to 2a, also when starting from a Zr–H agostic structure. The computed binding energy of benzene in 6 is substantial, between 68.8 and 55.2 kJ mol−1 (BP86/ECP1 and B3LYP/II levels, respectively, including counterpoise and zero-point corrections). Cationic Group IV metal complexes with three ligands in pyramidal orientation can easily invert via a planar metal center when π-donating ligands are present.33 Indeed, a very small barrier not exceeding 2 kJ mol−1 is obtained for zirconocene 5 (Fig. 3). Thus, the first step in the sequence in Scheme 3 should be rate-determining, namely dissociation of the coordinated aryl ring. The overall barrier for the whole process should be of the same order of magnitude as the binding energy of benzene in 6.34 Incidentally, the B3LYP value for the latter, 55.2 kJ mol−1, fits very well to the experimental barrier of 53 kJ mol−1.
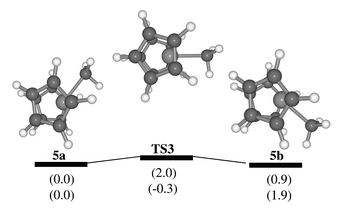 | ||
| Fig. 3 Stationary points and schematic potential energy surface for inversion at the metal in the parent zirconocene cation 5; in parentheses, relative energies at the BP86/ECP1 (top) and B3LYP/II levels (bottom), including zero-point corrections. | ||
Are complexes 1 and 2 good structural models for the interaction of cationic zirconocenes with aromatic solvents? A superposition of 2a and 6 is displayed in the upper part of Fig. 4. Clearly, the coordination about Zr is very similar in both cases, even though the Zr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⋯
⋯![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C(benzene) separation in 6, 2.698 Å, is somewhat longer than the corresponding distance in 2a, 2.629 Å. Apparently, the methylene bridge in 2a enforces a somewhat shorter contact between Zr and the aryl moiety. When an ethyl bridge is used instead, i.e. in [Zr(η-C5H5)(η-C5H4CH2CH2C6H5)Me]+7, the coordination geometry about Zr approaches that in 6 (see the superposition in the lower half of Fig. 4). Suitably substituted analogs of 7 would thus appear to be promising synthetic targets.
C(benzene) separation in 6, 2.698 Å, is somewhat longer than the corresponding distance in 2a, 2.629 Å. Apparently, the methylene bridge in 2a enforces a somewhat shorter contact between Zr and the aryl moiety. When an ethyl bridge is used instead, i.e. in [Zr(η-C5H5)(η-C5H4CH2CH2C6H5)Me]+7, the coordination geometry about Zr approaches that in 6 (see the superposition in the lower half of Fig. 4). Suitably substituted analogs of 7 would thus appear to be promising synthetic targets.
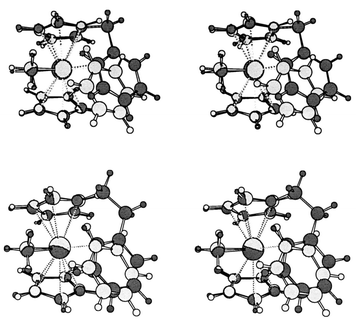 | ||
| Fig. 4 Stereoview of the superimposed BP86/ECP1 structures of complex 2a (dark gray) and the benzene complex 6 (light gray). | ||
Conclusion
We have applied a combination of DFT computations and NMR chemical shifts to elucidate the structure of [Zr(η-C5H5)(η-C5H4CH2C6H5)Me]+2, an important model for the interaction between a cationic zirconocene center and an arene. The phenyl moiety is not attached to the metal via an agostic Zr–H interaction, as suggested previously, but is bound in a η1 fashion to one of the phenyl carbon atoms. However, a loosely η3-bonded transition structure TS1 is not much higher in energy (ca. 19 kJ mol−1) and cannot fully be excluded on the basis of the computed NMR chemical shifts. TS1 describes the slippage of the zirconocene moiety along the phenyl ring, a hitherto undetected detail of the dynamics of zirconocene complexes with arene coordination. Two distinct dynamic processes are found experimentally and can be modeled computationally. The first is essentially a rotation of the coordinated phenyl group via Zr–H agostic transition structure TS2; the second probably involves dissociation of the phenyl ring from the Zr and inversion at the latter. In both processes the bond between Zr and the phenyl carbon atom is cleaved, consistent with the similar activation barriers derived from dynamic NMR spectroscopy.The same salient structural features as in the minima 2a,, 2b, in particular the η1 coordination of the aryl group, are apparent in the bis-coordinated analogue [Zr(η-C5H4CH2C6H5)2]2+4. The results can be transferred to the experimentally accessible derivatives 1 and 3, and should be of significance for the nature of the bonding and the dynamic behavior in zirconocene–arene adducts believed to be involved in homogeneous olefin polymerisation with Kaminski-type catalysts.
Acknowledgements
M. B. wishes to thank Professor W. Thiel for his continuing support and the Deutsche Forschungsgemeinschaft for a Heisenberg fellowship. Computations were performed on Compaq XP1000 and ES40 workstations at the MPI Mülheim. We thank Dr Mynott for analysis of the variable-temperature NMR spectra and for stimulating discussions.References
- H.-H. Brintzinger, D. Fischer, R. Mülhaupt, B. Rieger and R. M. Waymouth, Angew. Chem., Int. Ed. Engl., 1995, 34, 1143 CrossRef CAS.
- M. Bochmann, J. Chem. Soc., Dalton Trans., 1996, 225 Search PubMed.
- L. H. Doerrer, M. L. H. Green, D. Häußinger and J. Saßmannshausen, J. Chem. Soc., Dalton Trans., 1999, 2111 RSC.
- See for instance A. K. Rappé, W. M. Skiff and C. J. Casewit, Chem. Rev., 2000, 100, 1435 CrossRef CAS; K. Angermund, G. Fink, V. R. Jensen and R. Kleinschmidt, Chem. Rev., 2000, 100, 1457 CrossRef CAS; M. S. W. Chan, K. Vanka, C. C. Pye and T. Ziegler, Organometallics, 1999, 18, 4624 CrossRef CAS and references cited therein..
- See for instance: W. Koch and M. Holthausen , A Chemist’s Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2000. Search PubMed.
- M. Bühl , in Encyclopedia of Computational Chemistry, eds. P. v. R Schleyer, N. L. Allinger, P. A. Kollman, T. Clark, H. F. Schaefer, J. Gasteiger and P. R. Schreiner, Wiley, Chichester, 1998, pp. 1835–1845. Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822 CrossRef; J. P. Perdew, Phys. Rev. B, 1986, 34, 7406 CrossRef.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123 CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257 CrossRef CAS; P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS.
- J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- H. Horn , unpublished work; ; A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 Search PubMed.
- S. P. Walch, C. W. Bauschlicher and C. J. Nelin, J. Chem. Phys., 1983, 79, 3600 CrossRef CAS.
- W. Kutzelnigg , U. Fleischer and M. Schindler , in NMR Basic Principles and Progress, Springer-Verlag, Berlin, 1990, vol. 23, pp. 165. Search PubMed.
- This is true in particular for the δ(metal) values; for the ligand shifts, other DFT variants would also be appropriate, see for instance M. Bühl, M. Kaupp, V. G. Malkin and O. L. Malkina, J. Comput. Chem., 1999, 20, 91 CrossRef CAS.
- GAUSSIAN98, M. J. Frisch , G. W. Trucks , H. B. Schlegel , G. E. Scuseria , M. A. Robb , J. R. Cheeseman , V. G. Zakrzewski , J. A. Montgomery , R. E. Stratman , J. C. Burant , S. Dapprich , J. M. Millam , A. D. Daniels , K. N. Kudin , M. C. Strain , O. Farkas , J. Tomasi , V. Barone , M. Cossi , R. Cammi , B. Mennucci , C. Pomelli , C. Adamo , S. Clifford , J. Ochterski , G. A. Petersson , P. Y. Ayala , Q. Cui , K. Morokuma , D. K. Malick , A. D. Rabuck , K. Raghavachari , J. B. Foresman , J. Cioslowski , J. V. Ortiz , A. G. Baboul , B. B. Stefanov , C. Liu , A. Liashenko , P. Piskorz , I. Komaromi , R. Gomperts , R. L. Martin , D. J. Fox , T. Keith , M. A. Al-Laham , C. Y. Peng , A. Nanayakkara , C. Gonzalez , M. Challacombe , P. M. W. Gill , B. G. Johnson , W. Chen , M. W. Wong , J. L. Andres , C. Gonzales , M. Head-Gordon , E. S. Replogle and J. A. Pople , Gaussian, Inc., Pittsburgh, PA, 1998. Search PubMed.
- R. W. F. Bader , Atoms In Molecules. A Quantum Theory, Clarendon Press, Oxford, 1990; Search PubMed; R. W. F. Bader, Chem. Rev., 1991, 91, 893 Search PubMed.
- P. L. A. Popelier, Comput. Phys. Commun, 1996, 93, 212 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
- R. J. Mynott , personal communication. The spectra, obtained by J. S. during the work reported in ref. 3, were analysed in the temperature region between −50 and +10 °C; a more accurate determination of the activation parameters and a more detailed study of the dynamic processes were hampered by the presence of impurities and the lack of suitable spectra at higher temperatures, due to the limited stability of the compounds..
- See for instance: J. Schottek, G. Erker and R. Fröhlich, Eur. J. Inorg. Chem., 1998, 551 CrossRef CAS.
- Y. Ruiz-Morales, G. Schreckenbach and T. Ziegler, Organometallics, 1996, 15, 3920 CrossRef CAS.
- A. Vigalok, O. Uzan, L. J. W. Shimon, Y. Ben-David, J. M. L. Martin and D. Milstein, J. Am. Chem. Soc., 1998, 120, 12539 CrossRef CAS.
- J. P. Blaha, J. C. Dewan and M. S. Wrighton, Organometallics, 1986, 5, 899 CrossRef CAS.
- M. L. H. Green and J. Saßmannshausen, Chem. Commun., 1999, 115 RSC.
- P. Laszlo, Prog. Nucl. Magn. Reson. Spectrosc., 1967, 3, 231 CrossRef CAS.
- (a) M. Bühl, G. Hopp, W. von Philipsborn, S. Beck, M.-H. Prosenc, U. Rief and H.-H. Brintzinger, Organometallics, 1996, 15, 778 CrossRef; (b) M. Bühl, J. Phys. Chem. A, 1997, 101, 2514 CrossRef.
- A. R. Siedle, W. M. Lamanna, R. A. Newmark and J. N. Schroepfer, J. Mol. Catal. A: Chem., 1998, 128, 257 CrossRef CAS.
- M. Bochmann, M. H. L. Green, A. K. Powell, J. Saßmannshausen, M. U. Triller and S. Wocadlo, J. Chem. Soc., Dalton Trans., 1999, 43 RSC.
- Similar structures have been found for analoguous complexes of Ti and Zr with toluene: M. S. W. Chan, K. Vanka, C. C. Pye and T. Ziegler, Organometallics, 1999, 18, 4624 CrossRef CAS.
- P. Margl, L. Q. Deng and T. Ziegler, Organometallics, 1998, 17, 93.
- Entropy favors benzene dissociation in complex 6,, however, and the corresponding computed ΔG values are reduced to ca. 22 (BP86) and 9 kJ mol−1 (B3LYP), at −50 °C. Since the particle number is conserved in Scheme 3, entropic effects should be much smaller for 1..
Footnote |
| † Electronic supplementary information (ESI) available: cartesian coordinates for complexes 2a, 2b, 4a–c, 5a,b and 6 and transition states TS1, TS2 and TS3 in x, y, z format. See http://www.rsc.org/suppdata/dt/b0/b007748h/ |
| This journal is © The Royal Society of Chemistry 2001 |
