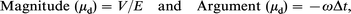Electroacoustic estimates of non-ionic surfactant layer thickness on emulsion drops
Linggen
Kong
,
James K.
Beattie
* and
Robert J.
Hunter
School of Chemistry F11, Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersity of Sydney, Sydney, NSW 2006, Australia. E-mail: beattiej@chem.usyd.edu.au
ersity of Sydney, Sydney, NSW 2006, Australia. E-mail: beattiej@chem.usyd.edu.au
First published on 7th December 2000
Abstract
The effects of an adsorbed non-ionic surfactant [nonyl phenol ethoxylate (C9ϕEN) (N = 100)] on the electroacoustic signals of hexadecane-in-water emulsion droplets were studied. The emulsions were prepared in the presence of two levels of sodium dodecyl sulfate (SDS), both well below the c.m.c. The dynamic mobility of the oil droplets was measured using a flow-through version of the AcoustoSizer. Adsorption of the non-ionic surfactant produced significant changes in the dynamic mobility of the particles and these were interpreted in terms of O'Brien's gel layer model. The model allows an estimate to be made of the elasticity and the approximate thickness of the adsorbed polymer layer and the influence which it has in moving the plane of shear out from the droplet surface. The SDS concentration had little effect on the polymer layer thickness which was also stable with time.
1 Introduction
In order to stabilise oil-in-water emulsions, ionic surfactant or macromolecular non-ionic surfactants are normally used to create a barrier between the oil droplets. The former provides a repulsive force between the electrical double layers on the drops (electrostatic stabilisation), whilst the latter imparts stability by a steric mechanism. Mixtures of surfactants have attracted more attention in recent years, not only because the materials used in commercial applications are impure but, more importantly, because different mixed surfactants can provide enhanced performance. A range of techniques has been applied to determine the mechanisms of adsorption and to measure the properties of adsorbed layers on various surfaces.1–4 But due to the lack of suitable experimental techniques, the adsorption of mixed surfactants at the oil/water interface has received much less attention.In this work, the adsorption of nonyl phenol ethoxylate (C9ϕEN; N = 100) on emulsion droplets previously formed in the presence of SDS has been investigated by electroacoustics. In this technique, a quantity known as the dynamic mobility, μd, is measured by subjecting the sample to a high frequency electric field. The applied field causes the particles to oscillate between the electrodes, generating pressure changes in the dispersion which propagate as sound waves. This is referred to as the electrokinetic sonic amplitude (ESA) effect.5,6 The velocity of the particles in response to the field, as a function of the applied frequency, comprises the dynamic mobility spectrum, μd, of the material. The value of μd is related to both the zeta potential and the size of the colloidal particles so these quantities can be obtained from the frequency dependence of the ESA signals.7
The oil droplets were generated in a homogeniser in the presence of SDS so this anionic surfactant was adsorbed at the interface first, but not in sufficient quantities to completely saturate the surface. With increasing concentration of the non-ionic surfactant, the drops became coated with an adsorbed layer that altered the electroacoustic behaviour drastically. Our objective was to determine the effects of the adsorbed layer on the dynamic mobility and hence to measure the layer thickness and its elasticity under different conditions.
2 Theory
2.1 Electroacoustics
Electroacoustic measurements were made with a prototype of a flow-through version of the AcoustoSizer (Colloidal Dynamics Inc., Rhode Is, USA). The principles of the method have been described elsewhere.5–7 There are two steps needed to determine the particle size and zeta potential from the ESA signals. First, the dynamic mobility is obtained from the ESA signal. The dynamic mobility is the ac analogue of the mobility determined by standard electrophoretic methods (i.e. the ratio of the particle velocity to the magnitude of the applied field). When an ac field of strength E is applied to a colloid, it causes the particles to move with a sinusoidal velocity (amplitude V). If the frequency ω of the applied field is sufficiently high, inertia forces will cause the particle to lag the applied field by a time Δt. The dynamic mobility is thus a complex quantity defined by:
where the argument is in radians.
The AcoustoSizer measures the ESA signals at eleven frequencies from 1 to 20 MHz from which the corresponding dynamic mobility values are obtained. Measurements on the SDS covered drops allow determination of both the zeta potential and the size of the droplets in emulsions of concentrations from 2% up to about 50% volume fraction.8 We assume that subsequent addition of the non-ionic surfactant to the preformed emulsions does not result in any change in the size of the particles since they are not subjected to any substantial energy input.
The presence of a layer of polymeric material on the surface of the droplets has a profound effect on the motion of the fluid in the neighbourhood of the droplet surface and this in turn affects both the magnitude and the phase of the dynamic mobility. The influence of the adsorbed layer can be examined by calculating the ratio: μd(coated)/μd(uncoated). This ratio, in effect, represents the electroacoustic behaviour of the adsorbed layer itself. The ratio provides two quantities as a function of frequency: (i) the ratio of the magnitudes and (ii) the difference in the phase angles. To understand these quantities we employ O'Brien's ‘gel layer ’ model1 of the effect of the adsorbed polymer layer.
2.2 The gel layer model
The effect of an adsorbed layer of neutral polymer or non-ionic surfactant can be described1 by an extension of the Smoluchowski theory for the motion of fluid adjacent to a charged surface under the influence of a tangential electric field. O'Brien first shows that, in the absence of the polymer, the inertia forces induced by the alternating field can be neglected, so that the net force on a block of fluid is the same as for the static electro-osmotic case. The standard Smoluchowski relation (Δus = εζ/η) therefore applies to the flow field in the absence of the polymer. He then sets up a model for the distribution of polymer segments in the neighbourhood of the droplet surface and examines the forces on the polymer induced by the fluid flow, and the reaction forces of the polymer segments on the fluid. Provided that the zeta potential is not too high, so that the Debye–Hückel theory applies, the velocity jump across the polymer layer (Δu) is then found to be:

| (1) |
where γ is the effective elastic shear modulus of the polymeric surfactant, which is the ratio of shear stress to shear strain,9κ is the Debye–Hückel parameter and d is the dynamic outer layer thickness. The parameter k is given by

| (2) |
where η is the viscosity and α is the drag coefficient, which is the force per unit volume per unit velocity applied by the fluid to the polymer chain. In order to evaluate the ratio in eqn. (1) we require estimates of κ, k, α, γ and d. The Debye–Hückel parameter, κ, is known from the electrolyte concentration:
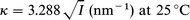
| (3) |
where I is the ionic strength. As k is given by eqn. (2), the only unknowns are α, γ and d. O'Brien1 uses an order of magnitude estimate to show that α is related to the polymer chain dimensions by

| (4) |
where s is the radius of the chain and L is its length. These can be calculated from the bond lengths and angles. The coil diameter, dc, is estimated from literature values for the random coil configuration. A program written by O'Brien calculates the velocity jump given in eqn. (1) from three parameters: the non-dimensional drag coefficient α*, the relaxation frequency ω0 and the ratio κd of the ‘gel layer ’ thickness, d, to the electrical double layer thickness. The non-dimensional quantity is defined as

| (5) |
The relaxation frequency ω0 (in unit of s−1) is given by the expression

| (6) |
In the absence of experimental data for the shear modulus (and hence ω0) the value of ω0 was determined as the point where the peak in the argument of the dynamic mobility ratio μd(coated)/μd(uncoated) occurs. Once ω0 has been set there are still two parameters, α* and κd, to adjust in order to fit the phase angles. However, since α* = αd2/η and α/η can be estimated using eqn. (4), only the thickness, d, of the outer polymeric surfactant layer is adjustable. Hence d is adjusted to match the change in peak heights at different polymeric surfactant concentrations.
Finally, with these two parameters set, an estimate is made of the ratio of the magnitudes from eqn. (1) and this turns out to be too large. The theory underestimates the reduction in mobility magnitude caused by the gel layer, although the theoretical magnitude curves resulting from the above procedure were of the same shape as the experimental curves.
This kind of underestimate could be due to the fact that the segments of the non-ionic surfactant are not homogeneously distributed as is assumed in the theory, but are much denser near the surface. Such a dense layer has the effect of displacing the shear plane by a distance Δ, and this causes a uniform reduction in the theoretical mobility magnitudes. To incorporate this shear plane displacement into the gel layer theory, the theoretical magnitudes were multiplied by the appropriate exp(−κΔ) factor for each curve. This amounts to assuming, as noted above, the validity of the Debye–Hückel approximation for the diffuse layer potential.
A consistent evaluation of the factor Δ over the frequency range for a particular magnitude ratio was obtained from the experimentally determined magnitude of the mobility ratio and the uncorrected theoretical magnitude of the velocity jump across the gel layer, using the expression
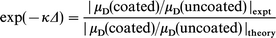
| (7) |
where the subscript “theory” refers to the case Δ = 0. This calculation was applied at several frequencies within each curve to obtain an average value for the correction factor. In the system studied, five frequencies (2.30, 3.49, 5.79, 9.50 and 15.64 MHz) were selected. This correction resulted in very good agreement with the experimental magnitudes at all concentrations. An estimate of the dynamic inner layer thickness Δ follows directly from the evaluation of exp(−κΔ). The total adsorbed layer thickness is then equal to the sum of d and Δ.
There have been earlier studies of the thickness of adsorbed polymer layers and their influence on the position of the shear plane from dc (static) electrophoresis results.10 In order to obtain the static electrophoretic thickness, an effective static mobility thickness Δs can be calculated by setting ω = 0 in eqn. (1), with the exp(−κΔ) correction (eqn. (7)). The formula then reduces to

| (8) |
where k is now equal to
2.3 Evaluation of structure parameters for non-ionic surfactants
Although the C9ϕEN molecules are surfactants, the EN group itself is a small polymer and hence the molecules may assume a range of conformations in solution, from fully extended to random coil.11 The treatment of the non-ionic surfactant in the system as random coils for the estimation of the α/η parameter therefore seems reasonable.Fig. 1 is a schematic view of the C9ϕEN molecular structure.12,13 The length of an ethylene oxide segment was calculated to be 0.35 nm, and the length of the C9ϕO chain was 0.88 nm, giving a total chain length of (0.35N + 0.88) nm in general agreement with literature values.14 The maximum s value is equal to half the height of the para-branched-alkyl radical side chain, i.e. s = 0.267 nm. For the estimation of dc, the effect of the C9ϕ group was neglected and the molecules were treated as random coils of poly(ethylene oxide) (PEO). The coil diameter was equated with the unperturbed rms end-to-end distance, r0 (nm), of the PEO chain,15 which was calculated from the molecular weight Mr using the formula:16

| (9) |
 | ||
| Fig. 1 Calculation of s and L for C9ϕEN by molecular structure. | ||
For C9ϕEN, N = 100 (N100), the molecular weight is 4620, giving dc as 5.1 nm, and the radius of the surfactant chain s and its length L are 0.27 and 35.9 nm, respectively. Consequently, α/η equals 0.038 nm−2. It is the coil diameter that determines the adsorption density of the N100 on the drop surface. Fig. 2 shows schematically the relative sizes of the different constituents, more or less to scale. The emulsion drop radius is so large compared to the molecular dimensions that the surface is considered flat. Note, however, that only a very occasional N100 molecule goes into the surface and the effect on the packing of the SDS heads is minimal. The SDS is well below saturation level at 1 mM but is close to saturation at 3 mM.
 | ||
| Fig. 2 Schematic view of adsorption of SDS and C9ϕEN on oil droplet. | ||
3 Experimental
3.1 Instruments and chemicals
The experimental set-up has been shown schematically elsewhere.8 The instrument was calibrated at 25°C as recommended by the manufacturer. The pH, conductivity and temperature of the emulsions were measured electronically (TPS Model 901-N pH-Conductivity-Temp Meter) using probes immersed in the circulation cell. The ESA signals were observed by oscilloscope (468 Digital Storage Oscilloscope, Tektronix, Inc., Oregon, USA). The measurement operation was controlled by the main control block (Colloidal Dynamics Inc., RI, USA) and function generation block (RITEC Advanced Measurement System, RAM-10000). The emulsion was circulated by a peristaltic circulating pump (Amicon CH-2A Concentrator). The temperature of samples was controlled by a refrigerated circulator (Julabo F20-HC).All reagents used were AR grade. n-Hexadecane was from Sigma with a minimum purity of 99%. SDS (Sigma, approx. 99% GC) was used without further purification. Sodium chloride was from Ajax chemicals (min. 99.9%). C9ϕEN was obtained from ICI Australia Operations Pty. Ltd., with an N value of 100. High purity Milli-Q water (Millipore) was used for all solutions; its resistivity was above 18.2 MΩ cm.
3.2 Methods
The calculation of zeta potential and size from the measured dynamic mobility is comparatively straightforward for a dilute uncoated system (6%). The relevant relationship is given by O'Brien et al.7 and is built into the instrument software.
4 Results
4.1 Concentration effects
Fig. 3 shows the dynamic mobility spectra including magnitude and argument for the N100 system with 1 mM SDS. The sample without N100 is used to measure the size of the emulsion drops.7 It can be seen that with increasing N100 concentration, the magnitude decreases substantially. The argument is unaffected at 0.1 mM and shows the typical increase in phase lag with frequency due to the inertia effect. At higher non-ionic surfactant concentrations the argument becomes more positive and increases with increasing polymer addition, showing a pronounced maximum in the region of 4 MHz. These effects are made clearer in Fig. 4 in which the ratio of the coated to the uncoated system is plotted, and a comparison is made between the experimental data (symbols) and the gel layer theory (lines) for the dynamic mobility ratio at six different N100 concentrations. | ||
| Fig. 3 Variation of dynamic mobility with frequency and N100 concentration, SDS 1 mM, N100 was added after the emulsification and measured 1 h later. | ||
 | ||
| Fig. 4 Comparison of gel layer theory (lines) with experimental data (symbols) for the dynamic mobility ratio μD(coated)/μD(uncoated) for N100, which was added after the emulsification and measured 1 h later; SDS 1 mM. κ = 0.255 nm−1; (a) ω0 = 0.5 s−1, d = 2.1 nm, Δ = 0.83 nm, Δs = 0.92 nm; (b) ω0 = 3.0 s−1, d = 7.3 nm, Δ = 2.23 nm, Δs = 4.09 nm; (c) ω0 = 5.0 s−1, d = 8.0 nm, Δ = 2.93 nm, Δs = 5.15 nm; (d) ω0 = 7.5 s−1, d = 8.6 nm, Δ = 3.91 nm, Δs = 6.46 nm; (e) ω0 = 8.0 s−1, d = 8.7 nm, Δ = 4.32 nm, Δs = 6.93 nm; (f) ω0 = 8.5 s−1, d = 8.8 nm, Δ = 4.46 m, Δs = 7.13 nm. | ||
At the lowest concentration (0.10 mM) the magnitude of the mobility ratio was independent of frequency with a value of about 0.80, showing a 20% reduction in mobility compared to the uncoated particles but no significant phase angle difference. As the concentration was increased, the magnitude decreased and showed an increasingly strong dependence on the applied frequency. The arguments of the mobility ratio were also affected by the increasing concentration of N100. A well-defined trend with frequency developed, consisting of a phase lead which increased progressively with concentration and with a peak increasing from 6 to 12 MHz. At 0.50 mM N100, the phase lead was almost 19° at the peak with respect to the particles covered with only SDS. Both the magnitude and the phase signals show a plateau effect at the higher levels of the non-ionic surfactant.
When the SDS concentration was increased to 3 mM, the dynamic mobility spectra were very similar to those of SDS 1 mM. The comparison with the gel layer model is shown in Fig. 5. It should be mentioned here that with the increase of SDS concentration from 1 to 3 mM, the particle size decreased from 0.56 to 0.36 μm (zeta potentials remained at − 105 ± 5 mV) as measured by the AcoustoSizer. So, for the higher SDS system, smaller particles were obtained and consequently a larger droplet surface was provided.
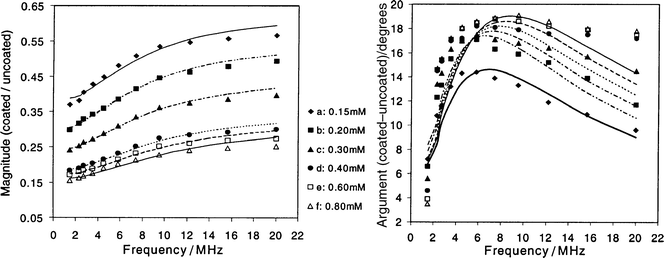 | ||
| Fig. 5 Comparison of gel layer theory (lines) with experimental data (symbols) for the dynamic mobility ratio μD(coated)/μD(uncoated) for N100, which was added after the emulsification and measured 1 h later; SDS 3 mM. κ = 0.294 nm−1; (a) ω0 = 4.0 s−1, d = 7.3 nm, Δ = 1.58 nm, Δs = 3.33 nm; (b) ω0 = 4.5 s−1, d = 8.0 nm, Δ = 2.07 nm, Δs = 4.16 nm; (c) ω0 = 5.0 s−1, d = 8.1 nm, Δ = 2.73 nm, Δs = 4.87 nm; (d) ω0 = 5.5 s−1, d = 8.2 nm, Δ = 3.61 nm, Δs = 5.80 nm; (e) ω0 = 6.0 s−1, d = 8.3 nm, Δ = 3.79 nm, Δs = 6.03 nm; (f) ω0 = 6.5 s−1, d = 8.4 nm, Δ = 3.99 m, Δs = 6.28 nm. | ||
4.2 Time effects
After the samples were stored in the laboratory environment for 8 days, they were measured again. The dynamic mobility ratios![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. frequency and N100 concentration are shown in Fig.
6 and 7 for the 1 and 3 mM SDS levels respectively. Compared with the results measured immediately after the N100
addition, for both series, the magnitude ratios went down
slightly and the argument difference increased only by a few
degrees.
s. frequency and N100 concentration are shown in Fig.
6 and 7 for the 1 and 3 mM SDS levels respectively. Compared with the results measured immediately after the N100
addition, for both series, the magnitude ratios went down
slightly and the argument difference increased only by a few
degrees.
 | ||
| Fig. 6 Comparison of gel layer theory (lines) with experimental data (symbols) for the dynamic mobility ratio μD(coated)/μD(uncoated) for N100, which was added after the emulsification and measured 8 days later; SDS 1 mM. κ = 0.255 nm−1; (a) ω0 = 0.5 s−1, d = 4.5 nm, Δ = 1.51 nm, Δs = 2.16 nm; (b) ω0 = 3.5 s−1, d = 7.9 nm, Δ = 2.65 nm, Δs = 4.82 nm; (c) ω0 = 5.0 s−1, d = 8.5 nm, Δ = 3.73 nm, Δs = 6.23 nm; (d) ω0 = 5.5 s−1, d = 8.9 nm, Δ = 4.58 nm, Δs = 7.30 nm; (e) ω0 = 6.0 s−1, d = 9.0 nm, Δ = 5.03 nm, Δs = 7.81 nm; (f) ω0 = 6.5 s−1, d = 9.1 nm, Δ = 5.08 m, Δs = 7.92 nm. | ||
 | ||
| Fig. 7 Comparison of gel layer theory (lines) with experimental data (symbols) for the dynamic mobility ratio μD(coated)/μD(uncoated) for N100, which was added after the emulsification and measured 8 days later; SDS 3 mM. κ = 0.294 nm−1; (a) ω0 = 4.0 s−1, d = 7.8 nm, Δ = 2.22 nm, Δs = 4.21 nm; (b) ω0 = 4.5 s−1, d = 8.3 nm, Δ = 2.80 nm, Δs = 5.04 nm; (c) ω0 = 5.0 s−1, d = 8.4 nm, Δ = 3.30 nm, Δs = 5.59 nm; (d) ω0 = 5.5 s−1, d = 8.5 nm, Δ = 4.04 nm, Δs = 6.38 nm; (e) ω0 = 6.0 s−1, d = 8.6 nm, Δ = 4.32 nm, Δs = 6.72 nm; (f) ω0 = 6.5 s−1, d = 8.7 nm, Δ = 4.37 m, Δs = 6.82 nm. | ||
4.3 Layer thickness
The calculated adsorbed layer thicknesses are shown in Fig. 8 and 9 for the two systems. When the SDS was 1 mM, the permeable outer layer d increased abruptly from 2 to 7 nm as the N100 increased from 0.10 to 0.15 mM and reached a maximum of around 8.5 nm at the higher N100 concentrations. For the 3 mM SDS, the d value was much the same, so the SDS concentration had little effect on the outer layer thickness. | ||
| Fig. 8 Outer layer thickness d as a function of N100 concentration for the systems with SDS concentration (●) 1 mM and (□) 3 mM, measured at A, 1 h and B, 8 days later. | ||
 | ||
| Fig. 9 Inner layer thickness Δ and static mobility thickness Δs as a function of N100 concentration measured at A, 1 h and B, 8 days later. (●) Δ at SDS 1 mM; (□) Δ at SDS 3 mM; (♦) Δs at SDS 1 mM; (△) Δs at SDS 3 mM. | ||
The dense inner layer became thicker with increasing N100 for both systems, and Δ for the 1 mM SDS was slightly larger (∽0.5 nm) than for the 3 mM SDS at the same concentration of N100. The overall layer thickness (d + Δ) increased with the N100 concentration reaching a plateau value of 13 ± 1 nm at the higher concentrations. Again for the 1 mM SDS the layer thickness was perhaps 1 nm larger than for the 3 mM SDS.
It can be seen from Fig. 9 that the effective static mobility thickness Δs increased gradually with increase in N100 for both systems, and again showed a plateau at higher N100 concentrations. In addition, both d and Δ became slightly larger with time, as did Δs. In most cases the changes were small (<10%) but for the lowest N100 level and 1 mM SDS, the total layer thickness doubled over 8 days, suggesting that the 1 h equilibration time might not have been long enough for that system to reach adsorption equilibrium.
5 Discussion
In assessing the results of applying the gel layer model there are two major considerations. First, the model is set up and the parameters are set in terms of ‘order of magnitude’ estimates of the effects involved. The distances and thicknesses of the layers are therefore indicative rather than definitive. This applies particularly to the parameter d and the drag coefficient, α; the magnitude of Δ is less problematic. The second point is that the estimates are averaged over the surface area of the droplets. As the polymer concentration is increased, the degree of coverage of the surface increases until, at the plateau, we may assume that coverage by the non-ionic surfactant is complete. This is expected to occur when the hydrophilic coils are in more or less close contact. As was noted above, the number of adsorbed non-ionic surfactant molecules is quite small, relative to the number of SDS molecules adsorbed. Finding room for the nonyl-phenol head groups is not a problem, even when the SDS concentration is at 3 mM and the droplet surface is almost saturated with SDS molecules.For the system with 1 mM SDS the drop radius was 0.56 μm and, taking an adsorbed area per SDS molecular of 0.55 nm2,3,19,20 implies that, at 6% volume fraction, the surface is only about half covered. Table 1 shows some basic parameters for SDS and C9ϕEN adsorption on the oil drops. It can be calculated that 1.94 mM SDS is needed for full coverage at a radius of 0.28 μm.
| Adsorption area of SDS molecular | A SDS/nm2 | 0.55 |
| (assumed) | ||
| Total length of SDS molecular | L SDS/nm | 1.50 |
| Radius of SDS sulfate head group | r SDS/nm | 0.15 |
| Total length of N100 molecular | L N100/nm | 35.88 |
| Coil radius of N100 molecular | R coil/nm | 2.55 |
| Radii of N100 hydrophobic head | (r1/r2)/nm | 0.27/0.37 |
| (ellipse) | ||
| SDS bulk concentration | 1 mM | 3 mM |
| Oil drop radius/μm | 0.28 | 0.18 |
| Area (%) covered by SDS molecular | 52 | 99 |
| Area (%) occupied by SDS sulfate | 7 | 13 |
| head group | ||
| SDS needed for full coverage/mm | 1.94 | 3.02 |
At 3 mM SDS the drop diameter is 0.36 μm and the coverage would appear to be near to saturation (∽99%), but there still remains room between the SDS head groups for nonyl phenol head groups needed to saturate the surface of the drop with the non-ionic surfactant in the manner described above. Although the sulfate groups each occupy an area of 0.55 nm2, there is still a significant distance between them because it is the lateral repulsion between the charges rather than the physical size of the SO4 group which determines the minimum area. The distance between the SDS heads is approximately 0.55 nm, which is twice the radius of the nonyl phenol ethyoxylate chain s, so the area defined by four SDS heads is more than enough for a nonyl phenol ethyoxylate head to penetrate. Indeed, it has been argued12 that the insertion of the hydrophobic group of the non-ionic surfactant between two sulfates may possibly pull them together through the formation of an electron donor–acceptor (EDA) complex between the phenolic group and the nearby sulfate head groups.
At concentrations below the plateau level the polymer coverage is expected to be patchy and the estimated thicknesses are averages for the covered and ‘bare ’ surface. It is, therefore the values at the final coverage levels which give the most useful insight into the disposition of the polymer at the interface because here the arrangement is fairly uniform. The values of about 4 nm for Δ and about 9 nm for d should be seen as the most significant and they agree reasonably well with the values of 3 and 11.5 nm, respectively, observed by Carasso et al.1 in their corresponding electroacoustic study of the adsorption of this non-ionic surfactant on the silica surface. The plateau adsorption is reached at rather higher N100 levels on silica (0.9 mM) and the slight differences in d and Δ values suggest that the hydrophilic part of the molecule can sit closer to the hydrophobic emulsion surface than to the silica surface.
The interpretation of the other parameters is also best done under plateau adsorption conditions. The values of ω0 in the plateau region are from 5–10 s−1, corresponding to a shear modulus of order 5–10 mN m−2 which is orders of magnitude smaller than the values observed by Buscall et al.21 for ordered latex systems interacting through repulsive double layer forces. The portion of the PEO chain in the outer region of the gel layer is apparently offering minimal resistance to the water flow but that minimal restraint can still be detected by the electroacoustic signal. The increase in shear modulus with increasing non-ionic surfactant concentration is to be expected since it corresponds to the gradual establishment of the non-ionic surfactant monolayer. Studies of the effects of adsorbed non-ionic surfactants on vesicles22 show a similar effect but both the surfactant concentration (70–200 mM) and the resulting moduli (5–50 N m−2) are much greater. At the surfactant concentrations used in the present study the normal methods of measuring the rigidity modulus are too insensitive to provide data. The drag parameter, α, was estimated from the known dimensions of the PEO residue so it should have the right order of magnitude but there is little information in the literature with which to compare it.
The effective static thickness of the inner region Δs is somewhat larger than Δ but less than the total layer thickness, Δ + d, which is to be expected. It measures the total effect of the adsorbed polymer on the electrokinetic potential, ζ, and includes both the physical shift in the shear plane Δ, plus a contribution (of about 2 nm) for the enhanced viscosity due to polymer chains in the neighbouring solution.
6 Conclusions
This work discusses the effect of non-ionic surfactant adsorption on the electroacoustic behaviour of a hexadecane-in-water emulsion in the presence of SDS, and provides information about the properties of the adsorbed surfactant layer. The gel layer theory developed by O'Brien1 is capable of describing the effect of the adsorbed surfactant layer on the dynamic mobility of a particle and provides information about the elasticity and thickness of the adsorbed layer. The apparent inner and the outer layer thickness increase with increase in the nonyl phenol ethoxylate concentration as the polymer layer becomes progressively more complete. There was no obvious increment of layer thickness with time over a period of 8 days. The effective static mobility thickness, Δs, was calculated for each adsorption measurement, and it was roughly 2 nm more than the dense inner layer Δ. It is the Δs value which should be compared with estimates of this quantity from other situations such as small-angle neutron scattering, photon correlation spectroscopy, NMR spectroscopy, IR spectroscopy, ellipsometry and sedimentation/diffusion studies.1–4,23–32 The electroacoustic technique, in particular the dynamic mobility spectrum, appears to be an effective method for studying the adsorption of non-ionic surfactants at the oil/water interface.Acknowledgements
This work has been supported by a Gritton Research Scholarship for L. Kong. The authors would like to thank Dr. R. W. O'Brien and Dr. G. G. Warr for helpful advice and discussions.References
- M. L. Carasso, W. N. Rowlands and R. W. O'Brien, J. Colloid Interface Sci., 1997, 193, 200 CrossRef CAS.
- E. Dickinson, Colloids Surf. B, 1999, 15, 161 CrossRef CAS.
- E. Staples, J. Pensold and I. Tucker, J. Phys. Chem. B, 2000, 104, 606 CrossRef CAS.
- T. J. Barnes and C. A. Prestidge, Langmuir, 2000, 16, 4116 CrossRef CAS.
- R. J. Hunter, in Modern Characterisation Methods of Surfactant Systems, ed. B. P. Binks, Marcel Dekker, New York, 1999, p. 521. Search PubMed.
- R. J. Hunter, Colloids Surf. A, 1998, 141, 37 CrossRef CAS.
- R. W. O'Brien, D. W. Cannon and W. N. Rowlands, J. Colloid Interface Sci., 1995, 173, 406 CrossRef CAS.
- L. Kong, J. K. Beattie and R. J. Hunter, Chem. Eng. Process., 2001, 40, in the press CrossRef.
-
F. W. Sears, M. W. Zemansky
and H. D. Young, Uni
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersity Physics, Addison Wesley, London, 1987, p. 297. Search PubMed.
ersity Physics, Addison Wesley, London, 1987, p. 297. Search PubMed. - D. E. Brooks, J. Colloid Interface Sci., 1973, 43, 687, 700, 714.
- J. S. Clunie and B. T. Ingram, in Adsorption from Solution at the Solid/Liquid Interface, ed. G. D. Parfitt and C. H. Rochester, Academic Press, London, 1983. Search PubMed.
- B. Jönsson, B. Lindman, K. Holmberg and B. Kronberg, Surfactants and Polymers in Aqueous Solution, Wiley, Chichester, 1998, p. 358. Search PubMed.
- The Merck Index, Merck & Co., Inc., USA, 11th edn., 1989, p. 1056, No. 6599. Search PubMed.
- G. Urbina-Villalba, I. Reif, M. L. Márquez and E. Rogel, Colloids Surf. A, 1995, 99, 207 CrossRef CAS.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, New York, 1987, vol. 1. Search PubMed.
- M. Kurata, Y. Tsunashima, M. Iwama and K. Kamada, in Polymer Handbook, ed. J. Brandrup and E. H. Immergut, Wiley-Interscience, New York, 1975, p. IV-45. Search PubMed.
- Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 75th edn. 1995, pp. 3–183. Search PubMed.
- AcoustoSizer User's Manual, Matec Applied Sciences, USA, 1995, App. C. Search PubMed.
- H. Gerrens and G. Hirsch, in Polymer Handbook, ed. J. Brandrup and E. H. Immergut, Wiley-Interscience, New York, 1975, p. II-485. Search PubMed.
- F. van Voorst Vader, Trans. Faraday Soc., 1960, 56, 1067 RSC.
- R. Buscall, J. W. Goodwin, M. W. Hawkins and R. H. Ottewill, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 2873 RSC.
- H. Hoffmann, S. Hofmann and U. Kästner, in Hydrophilic Polymers, ed. J. E. Glass, American Chemical Society, Washington, DC, 1996, p. 235. Search PubMed.
- Y. Fang and D. G. Dalgleish, J. Colloid Interface Sci., 1993, 156, 329 CrossRef CAS.
- P. L. Dubin and P. Tong, in Colloid–Polymer Interactions, ACS Symposium Series 532, American Chemical Society, Washington, DC, 1993. Search PubMed.
- G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Chapman & Hall, London, 1993, ch. 6. Search PubMed.
- E. Killmann, H. Maier and J. A. Baker, Colloids Surf., 1987, 31, 51 CrossRef.
- J. A. Baker and J. C. Berg, Langmuir, 1988, 4, 1055 CrossRef CAS.
- J. Lee, P. A. Martic and J. S. Tan, J. Colloid Interface Sci., 1989, 131, 252 CrossRef CAS.
- J. A. Shar, T. M. Obey and T. Cosgrove, Colloids Surf. A, 1998, 136, 21 CrossRef CAS.
- J. A. Baker, R. A. Pearson and J. C. Berg, Langmuir, 1989, 5, 339 CrossRef CAS.
- M. Malmsten, P. Linse and T. Cosgrove, Macromolecules, 1992, 25, 2474 CrossRef CAS.
- T. Cosgrove, J. Chem. Soc., Faraday Trans., 1990, 86, 1323 RSC.
| This journal is © the Owner Societies 2001 |