Molecular simulation of adsorption equilibria of xylene isomer mixtures in faujasite zeolites. A study of the cation exchange effect on adsorption selectivity
Véronique Lachet†, Séverine Buttefey, Anne Boutin* and Alain H. Fuchs
Laboratoire de Chimie Physique (UMR 8000 CNRS), Bâtiment 350, Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersité de Paris-Sud, 91405, Orsay, France. E-mail: boutin@lcp.u-psud.fr
ersité de Paris-Sud, 91405, Orsay, France. E-mail: boutin@lcp.u-psud.fr
First published on 4th December 2000
Abstract
Grand canonical ensemble Monte Carlo simulations of the adsorption properties of several model faujasite zeolites were performed using the statistical bias method. The results enable a better understanding of the effect of cation exchange in the selective adsorption of binary mixtures of para- and meta-xylene isomers. The NaY/KY reversal of adsorption selectivity (from m- to p-xylene) can be accounted for by a simultaneous change in the size of the cation and a displacement of the potassium cation towards the centre of the supercage; this gives rise to a complete rearrangement of the adsorption potential energy surface. BaX is shown to be selective in p-xylene because of the sufficient size of the barium cation. Increasing the number of cations in the NaY faujasite model had a similar effect on selectivity to increasing the cation size. On the basis of our simulations, we predict that NaX should be only weakly selective in favour of one or the other xylene isomer. We also predict that adding a small amount of water molecules could enhance the adsorption selectivity in favour of p-xylene.
I. Introduction
Zeolitic materials and related open-framework inorganic materials are gaining increasing importance in ion exchange, molecular sieving and catalysis. In these processes adsorption and transport of the guest molecules play a crucial role. While the macroscopic science of this field is well developed, there is a need for a more fundamental microscopic understanding of the phenomena as well as a means for predicting thermodynamics and transport properties in a variety of guest–host systems.The
properties of confined fluids are well described by analytical
theory in the case of model mesoporous materials such
as slit pores or cylinders only. Atomic details need to be taken
explicitly into account in order to reproduce the adsorption
properties of fluids in micropores. Molecular simulation, in
conjunction with experiments, has played an important role in
the past few years in developing our understanding of the relation between microscopic and macroscopic properties of confined
molecular fluids in zeolitic materials. Recently developed
techniques have allowed the simulation of complex systems
that a few years ago were considered impossible to study ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia computer simulation.
ia computer simulation.
The separation of p-xylene from m-xylene (and other C8 aromatics) is performed on the industrial scale using selective adsorption in synthetic faujasite zeolite.1 It has been shown experimentally that the nature and the number of cations lead to selective properties for one isomer or another (m- or p-xylene).2–7 However the adsorption selectivity mechanism is not yet understood and analytical theories fail to predict equilibrium adsorption selectivity from single component adsorption data.
Different aspects of the xylene/faujasite system have been studied at low molecular loading by molecular dynamics8 and at high loading by grand canonical9–12 and canonical13 Monte Carlo simulations. In most of these studies only single component (either m- or p-xylene) adsorption properties were investigated.
In a recent paper,12 we have reported a grand canonical Monte Carlo (GCMC) simulation of a binary mixture of m- and p-xylene in NaY and KY faujasites. Using statistical biasing together with a full-scale guest–host semi-empirical potential and realistic framework geometries, we were able to reproduce the experimentally observed adsorption selectivity of NaY in favour of m-xylene and the reversal of selectivity in the case of KY. A tentative explanation of this phenomena has been provided in terms of the occupation of the potential energy surface wells (adsorption sites). However our understanding of the reasons why an extra-framework cation exchange in the zeolite can lead to a reversal of adsorption selectivity in the binary mixture is still poor. Cation exchanges in zeolites are usually accompanied by some change in the structural parameters of the system. It is thus not clear whether the changes in adsorption properties are mostly related to the change in nature of the cation (size and valence) or to the change in zeolite structure, or both. In order to clear up this point we have performed GCMC simulations on several simplified models of faujasite zeolite in which one parameter was changed at a time, with the aim of understanding the effect of cation exchange in the selective adsorption of binary mixtures of p- and m-xylene isomers.
II. Simulation details
II.1. Zeolite models
Zeolites are porous crystalline aluminosilicates. The framework consists of tetrahedral aluminium and silicon atoms bridged by oxygen atoms. The presence of aluminium atoms introduces charge defects, which are compensated with some non-framework cations (sodium, potassium, barium . . .). The X and Y faujasite zeolites display cubic crystalline lattices. The microporous network is made of cuboctahedral sodalite cages with a diameter of about 6.5 Å. These cages are linked together in a tetrahedral arrangement by six oxygen atom rings and form large cavities, named supercages. The supercages have a diameter of about 12.5 Å. They are interconnected in a tetrahedral arrangement by “windows” of diameter ∽7.5 Å. One cubic unit cell contains 8 sodalite cages and 8 supercages. The ratio of silicon to aluminium atoms and the number of cations vary from one faujasite to another. A faujasite is named Y (X) when it has a Si/Al ratio greater (lower) than 1.5. A substantial number of diffraction studies have examined the location of extra-framework cations in faujasite-type zeolites, including hydrated and dehydrated forms of zeolites X and Y.14–21Five different simplified zeolite models were used in this work, corresponding to different types of extra-framework cations as well as different cation distribution and location. In these “thought experiments”, each model framework displays exactly the same crystalline structure. The models differ from one another in the nature and location of the extra-framework cations only. The characteristic features of these models are summarised in Table 1 and described in more detail below.
Extra-framework cations were considered to be fixed in the simulations, whatever the amount of xylene loading. Changes in the cation location upon adsorption has not been observed experimentally in the dehydrated xylene/faujasite systems. This only happens when a small amount of water is present in the system.
In the KYm model the site II cation coordinates have been taken from Mortier et al.17 Using such coordinates, a site II in KYm is located ∽0.8 Å closer to the centre of the supercage compared to the site II in NaYm. No other structural changes were made between NaYm and KYm model structures.
The model called NaXm1 displays a full occupancy of the cationic sites I, II and III (site III is in the supercage symmetrically centred on the sodalite four-ring) i.e. 16, 32 and 48 Na+ in sites I, II and III respectively.
The second model, called NaXm2, displays a partial occupancy of sites III (32 cations) and full occupancies of sites I′(32) and II(32). A random distribution of sites III was achieved, with 4 sites occupied out of 6 available within each supercage. This new distribution is much closer to that observed experimentally19–21 but it introduces some periodic defects due to the partial occupancy of crystallographic sites.
In this work, the zeolite structure, including the cations, was considered to be rigid. Framework expansion or contraction upon adsorption has been reported experimentally. This effect is weak in the case of xylene in faujasite (0.1%15 to 1%22 contraction of the unit cell parameter) and for this reason has not been taken into account in the simulations. One unit cell of zeolite (8 supercages) was used to construct the simulation box and periodic boundary conditions were applied.
II.2. Interatomic potential function
The adsorbate–zeolite potential function used in this work has been described in detail elsewhere.10–12 It takes into account the interaction between each atom of the adsorbate molecule and each zeolite species and includes Coulombic, induction, dispersion and repulsion terms: | (1) |
The subscripts i and j stand for the atoms of the adsorbate molecule and the zeolite species, respectively. The dispersion coefficients (C6, C8 and C10) were estimated from knowledge of the dipole polarizabilities and the partial charges of all the interacting species as described by Pellenq and Nicholson.23 The repulsive parameters Aij and bij for a pair of heteroatoms ij were estimated from those of the ii and jj pairs using the second of the four combination rules proposed by Böhm and Ahlrichs:24
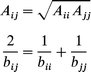 | (2) |
The full potential function could thus be determined from knowledge of 4 parameters per atom only. The partial charge, the dipole polarizability and the two repulsive parameters of each atom are given in Table 2.
| q/e | α/Å3 | Aii/108 K | bii/Å−1 | ||
|---|---|---|---|---|---|
| T | 1.396 | 0.44 | 11.5 | 7.26 | |
| NaYm | O | −0.823 | 1.11 | 4.87 | 4.16 |
| KYm | Na | 1.0 | 0.15 | 1.46 | 3.78 |
| MYm | K | 1.0 | 0.78 | 1.46 | 3.4 |
| M | 1.0 | 0.15 | 1.46 | 3.02–3.97 | |
| BaXm | T | 1.2 | 0.44 | 11.5 | 7.26 |
| NaXm1 | O | −0.85 | 1.11 | 4.87 | 4.16 |
| NaXm2 | Ba | 2.0 | 1.50 | 1.46 | 2.46 |
| Na | 1.0 | 0.15 | 1.46 | 3.78 | |
Xylene isomers were assumed to be rigid planar molecules. The intermolecular potential was taken from the Optimised Potentials for Liquid Simulations (OPLS) proposed by Jorgensen.25
Ewald sums were used to calculate the Coulomb and induction terms. The Ewald parameter α was equal to 0.19 Å−1 and the k vectors were such that k ∈ [ − 3,3].
II.3. Bias grand canonical Monte Carlo (BGCMC) calculation
GCMC simulations have proven to be successful in predicting adsorption thermodynamics of a variety of simple sorbates (argon, methane26,27) in zeolites. Attempts to apply the normal GCMC technique to larger sorbates (benzene,28 xylene, chain molecules29) are bound to be frustrated by low acceptance rates of the insertion and deletion steps. In our study of xylene isomers in faujasites, these rates fell below 10−3% at high loading. Thus, in order to sample the grand canonical ensemble correctly, the use of biased insertions and deletions was found to be necessary.The
first bias consisted in reducing the volume V
in which
insertions were attempted. In normal GCMC, these insertions
are attempted uniformly throughout the volume of a unit cell
of zeolite. However, much of this volume (sodalite cages,
volume filled by atoms of the framework, etc.) is inaccessible
to xylene molecules. In the case of xylenes in NaY, the volume
of the simulation box (one unit cell) is V
= 15352 Å3 and the accessible
volume is reduced to
Vacc
= 6919 Å3. The second bias
was the cavity-bias proposed by Mezei.30 In this method, insertions
are only attempted in regions of the accessible volume
where cavities of radius R![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) Rc exist. Such cavities can accommodate
a particle insertion. In the case of xylene molecules,
Rc
= 3.5 Å, which corresponds to the nearest neighbour
distance in the xylene centre of mass pair distribution function.
The third bias used here was an orientational bias.31
In the case of a particle insertion, the method consisted in generating
k trial orientations (k
= 10 in our work), and choosing
the new configuration out of these k trials with an energetic
criterion. More details about our biased algorithms can be found
in ref. 10 and 11.
Rc exist. Such cavities can accommodate
a particle insertion. In the case of xylene molecules,
Rc
= 3.5 Å, which corresponds to the nearest neighbour
distance in the xylene centre of mass pair distribution function.
The third bias used here was an orientational bias.31
In the case of a particle insertion, the method consisted in generating
k trial orientations (k
= 10 in our work), and choosing
the new configuration out of these k trials with an energetic
criterion. More details about our biased algorithms can be found
in ref. 10 and 11.
III. Results and discussion
The adsorption of xylene isomers in NaY and KY zeolites has been studied in some detail in our previous work.10–12 A good agreement between simulation and experiment has been obtained using the NaYm and KYm model described above. In the present work we have studied in detail the effect of extra-framework cation size, nature (monovalent![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. divalent), location
and number.
s. divalent), location
and number.III.1. Effect of the extra-framework cation size
In this section, we are interested in studying the influence of extra-framework cation size on adsorption capacity and selectivity. We have thus used the MYm models, which differ only in cation size. The starting point of our simulation was the NaYm model. By gradually decreasing the bcation–cation repulsive parameter from 3.97 to 3.02 Å−1 we have increased the cation size. All other potential and structural parameters were kept constant. In order to illustrate the effect of increasing the cation size, the xylene carbon–cation dispersion–repulsion interactions are plotted on Fig. 1 for different values of the bcation–cation parameter. It is worth noting that both the well depth and the equilibrium distance were affected by such a change. A ∽0.4 Å−1 decrease in the b parameter can be viewed as a ∽0.5 Å increase in the cation radius. One might have envisaged modifying the potential in such a way that the depth of the potential stays the same while only the size varies. This has not been done here since we were mainly interested in understanding how adsorption was modified by changing the nature of the cation with no other changes in the framework model. | ||
| Fig. 1 Xylene carbon–cation dispersion–repulsion interactions plotted for different values of the bcation–cation parameter. All other potential and structural parameters were kept constant. | ||
GCMC simulations of pure component adsorption have been performed using these MYm models at 423 K. Maximum loading of m- and p-xylene are shown in Fig. 2 for different b values. A decrease is seen in the adsorption capacities as the cation radius increases (i.e. as b decreases). This effect is stronger for m- than for p-xylene. Therefore zeolite models with smaller cations adsorb more m- than p-xylene whereas with larger cations the reverse trend is observed.
 | ||
| Fig. 2 Maximum loading of m and p-xylene and selectivity for different b values. | ||
Adsorption of equimolar binary mixtures has also been performed using such MYm models. The corresponding p/m-xylene selectivities at maximum loading (see Fig. 2) have been calculated using the equation:
 | (3) |
where Xi and Yi are the molar fractions of component i in the adsorbed phase and in the gas phase respectively.
The MYm model with b = 3.78 Å−1 (corresponding exactly to the NaYm model) exhibits a selectivity for the m-xylene isomer (αpx/mx = 0.49) as observed experimentally for the NaY zeolite.2,4 No selectivity was found (αpx/mx≈1) for all smaller b values used.
Two MYm models with b = 3.78 and 3.40 Å−1, corresponding to sodium and potassium cations respectively, have been studied in more detail. Adsorption isotherms of pure components in both models have been calculated at 423 K and compared to the corresponding experimental results (in NaY and KY)32 (see Fig. 3). Adsorbed quantities obtained using these two zeolite models agree reasonably well with experiment. Co-adsorption isotherms have also been calculated for different vapour compositions. The selectivity diagram is plotted in Fig. 4. The MYm model with b = 3.78 Å−1 (i.e. Na cation) leads to a good agreement with experiment whereas the MYm model with b = 3.4 Å−1 (i.e. K cation) is unable to reproduce at all the selectivity for p-xylene isomer observed experimentally. This latter model reproduces reasonably well the pure component behaviour but fails to do so for mixture properties.
 | ||
| Fig. 3 Adsorption isotherms of pure components in the two MYm models calculated at 423 K and compared to the corresponding experimental results (in NaY and KY).32 An expanded scale is shown for the low-pressure region in the left-hand part of the figure. | ||
 | ||
| Fig. 4 Selectivity diagrams for the MYm, KYm and BaXm models and comparison with the experimental results. | ||
In the MYm models, a unique adsorption site, called site II, was observed for both isomers. Xylene molecules were located near a cation in site II, the plane of the aromatic ring being nearly parallel to the six T-ring framework windows. More details on this can be found in ref. 12. The distance between the xylene centre of mass and cations in sites II depends on the value of the b repulsive parameter (see Fig. 5(a)). This distance increases with the cation size. The distance between the xylene centre of mass and the 3-fold axis (the [111] direction) is represented in Fig. 5(b). We notice that this distance increases as the cation size increases. Also, as the cation size increases, xylene molecules become more and more delocalized and tend to sit near the centre of the supercage. For small cations, (i.e. Na, b = 3.78 Å−1), the adsorption site II can accommodate up to 4 molecules per supercage with only weak steric hindrance. The observed selectivity is, in this case, mainly due to energetic effects since the adsorption site is found to be more favourable for meta isomer (energy of about − 12450 K) than for para isomer (energy ∽ − 11337 K) (see Fig. 6). As the cation size increases, i.e. for b = 3.4 Å−1, the energy of the adsorption sites does not change much (−12000 K and − 11300 K for m- and p-isomers respectively). However, the displacement of adsorbed molecules near the centre of the supercage creates some steric hindrance between molecules and leads to a decrease in the adsorbed quantities and a cancelling of the adsorption selectivity.
 | ||
| Fig. 5 (a) Distribution of the distance between the xylene centre of mass and the nearest cation in site II for the two MYm models. (b) Distribution of the distance between the xylene centre of mass and the crystallographic axis (111). | ||
 | ||
| Fig. 6 Potential energy of the adsorption sites of m-xylene and p-xylene in KYm and BaXm. | ||
In summary, an increase of the cation size only reduces the adsorbed quantities but does not lead to a selectivity in favour of the p-isomer as observed experimentally in the case of KY zeolite. We have thus checked the influence of the cation location on the selectivity results, since it is known experimentally that the crystallographic cation sites for potassium and sodium differ slightly from each other.
III.2. Effect of the extra-framework cation location
Two zeolite models, MYm (b = 3.4 Å−1) and KYm, have been compared. They differ only in the location of site II. In the KYm sites II are ∽0.8 Å closer to the centre of the supercage compared to the MYm model. In these cases the cation size is identical for the two models and corresponds to the potassium cation. The pure component adsorption isotherms obtained using the MYm (b = 3.4 Å−1) model are shown in Fig. 3. The adsorption isotherms calculated using the KYm model have been published elsewhere.12 The two models lead to very similar results. The number of adsorbed xylene molecules does not seem to depend strongly on the position of the cations. Co-adsorption isotherms have also been calculated for different vapour compositions. The KYm model leads to a qualitative agreement with the experimental behaviour (Fig. 4). This zeolite model is selective for p-xylene. Whereas these two models gave similar pure component adsorption properties, the co-adsorption properties were quite different. This is due to the fact that the two models display rather different adsorption sites.In the case of the KYm model, three adsorption sites have been observed for both isomers (see Fig. 6). Site II is no longer a stable adsorption site. The lowest-energy adsorption site is named II/III. It corresponds to a molecule adsorbed near the crystallographic site III (which is not occupied by a cation in this model), between two sites II, the aromatic ring being perpendicular to the four-membered window of the zeolite. The second site called site II/W can be viewed as a distorted site II. In the third site (called site W), the molecules are located in the circular 12-membered windows joining two supercages. Snapshots of the p-xylene adsorbed in sites II/III, II/W, W were shown in ref. 12.
The change in the adsorption properties on going from NaY to KY (reversal of selectivity) can only be accounted for by a simultaneous increase in the cation size and a displacement of the cations to the centre of the supercage.
III.3. Effect of the extra-framework cation valence
In order to study the effect of the cation valence we have also studied the adsorption of xylene isomers in the BaX zeolite. The BaXm model has been constructed using the crystallographic coordinates of the NaY zeolite replacing the Na+ by Ba2+ cations (see description of the model above). We have used a barium polarizability of 1.5 Å3 and the repulsive b parameter for cations was equal to 2.46 Å−1. The adsorption isotherms of pure component are shown in Fig. 7. Very good agreement is observed for the m-xylene isomer whereas some discrepancy is observed for the p-xylene. It is worth mentioning that the structural model chosen here does not strictly correspond to the experimental refined structure of BaX.18 We have seen in the case of KY that a small displacement of site II cations may lead to significant differences in adsorption properties. Thus, even if the framework structure and crystallographic site II of NaY and BaX are close to each other, a more realistic BaX structure model should be tested in a future work.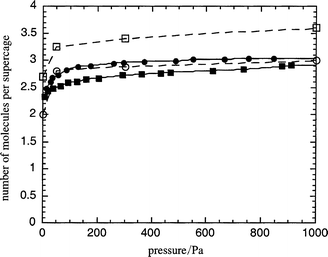 | ||
| Fig. 7 Simulated (open symbols) and experimental (filled symbols) adsorption isotherms at 423 K for pure p-xylene (squares) and pure m-xylene (circles) in the BaX zeolite. | ||
The selectivity diagram obtained using this BaXm model is shown in Fig. 4. This model leads to a selectivity in favour of p-xylene as observed experimentally for the BaX zeolite. The adsorption sites are very similar to those observed in KYm. The adsorption site energies are shown in Fig. 6. The selectivity mechanism is the same for KYm and BaXm models.12
In contrast with the KY zeolite case, here we did not have to modify the barium cations location in order to reproduce the experimentally observed selectivity in favour of p-xylene. A rather large divalent cation located at 6 Å from the centre of the supercage has more or less the same effect as a large monovalent cation located at 5.2 Å from the supercage centre. However, for quantitative agreement to be obtained it would be necessary to use a more realistic model.
III.4. Effect of the number of extra-framework cations
In order to study the influence of the number of cations on the adsorption properties, we have compared the adsorption in NaY and NaX zeolites. The NaXm1 and NaXm2 models (described above) have been studied (see Table 1). In the NaXm1 model, all the I, II and III sites were occupied whereas, in the NaXm2 model all the sites II and I′ were fully occupied but the sites III were only partially occupied. Co-adsorption isotherms have been computed and the results have been compared to those obtained for NaYm. The number of adsorbed molecules of each isomer depend on the occupancy of sites III (see Fig. 8). When sites III were occupied, the number of adsorbed molecules decreased. A decrease of 50% in the number of adsorbed molecules was observed when sites III were all occupied. | ||
| Fig. 8 Evolution of the maximum adsorption capacity for the pure components and of the selectivity for binary mixture with an increasing number of cations in site III. The NaYm model corresponds to zero occupancy, NaXm2 to 32 sodium cations in site III and NaXm1 to 48 cations in site III. | ||
The adsorption selectivity also depends on the occupancy of the sites III. When there were no cation in sites III (model NaYm), the zeolite was selective in m-xylene (αpx/mx = 0.49). When sites III were partially occupied (model NaXm2), the zeolite showed almost no selectivity (αpx/mx = 1.22). The occupancy of all the sites III (model NaXm1) leads to a selectivity in favour of the p-xylene (αpx/mx = 1.92).
Three adsorption sites were observed for both isomers in NaXm models. Two of them corresponded to sites W and II/III observed in the KYm and BaXm models. The third site is a site III located between two sites II and the xylene molecule is parallel to the four-membered window of the zeolite. This site was only occupied when the cation crystallographic site was also occupied.
We have compared the maximum loading obtained with the two NaXm models with the NaX zeolite experimental results.32 Experimentally, the NaX zeolite can adsorb 2.69 p-xylene and 2.56 m-xylene per supercage. In NaXm2, the zeolite can adsorb up to 2.87 p-xylene and m-xylene per supercage whereas in the model NaXm1, 1.67 p-xylene and 1.71 m-xylene per supercage were adsorbed. NaXm2 displays a much better agreement with experiment, from both the cation distribution and the equilibrium adsorption properties. We thus predict, from the above simulations, that NaX should only be weakly selective in favour of one or the other xylene isomer. This seems to be in agreement with experiment.1
IV. Discussion and conclusion
The simulation results obtained here enable a better understanding of the observed trends in adsorption selectivity of m-and p-xylene isomers mixtures in faujasites.Y faujasites with small monovalent cations (LiY4 and NaY2,4) are selective for m-xylene. This is due to the fact that there is enough room in these systems to accomodate up to 4 xylene molecules per supercage, all molecules being adsorbed in site II. The m-xylene isomer adsorbs more strongly than p-xylene in site II, whatever the loading. This is mainly because m-xylene can find different orientations in which both methyl groups interact favourably with oxygen atoms of the framework. In the case of p-xylene, only one methyl group at a time can find a favourable position with respect to the oxygen atoms. The preferential adsorption of m-xylene in these small cations-Y zeolites is presumably due to this simple energetic effect.
It seems now clear that the NaY/KY reversal of adsorption selectivity cannot be accounted for by a change in the size of the cation alone. For this phenomenon to be observed in the simulations one must also bring the potassium cation towards the centre of the supercage (as observed experimentally). The effect of this is to destabilize adsorption site II because molecules in site II can no longer interact favourably with the oxygen atoms of the framework. This gives rise to a complete rearrangement of the adsorption potential energy surface. Three new adsorption sites are created (two of them could be viewed as “distorted” sites II). In addition the adsorption capacity of the supercages decreases and steric hindrance between adsorbed molecules becomes stronger. A combination of energetic and steric effects makes the adsorption of p-xylene more favourable than m-xylene at high loading in this system. Y faujasites with larger cations (RbY4 and CsY4) are also selective for p-xylene, presumably for the same reasons.
BaX provides an interesting case since the number of cations in this system is the same as in NaY. The exchange of Na+ by Ba2+ should have two opposite effects. The first is electrostatic and tends to stabilize the adsorption site II. The other is steric in nature and tends to destabilize site II, since Ba2+ is much larger than Na+. Our results show that the second effect greatly outweighs the first. It seems that sufficiently large cations, whatever their valence, destabilize adsorption site II finally leading to selective adsorption in favour of p-xylene.
Another way of producing a rearrangement of the adsorption potential energy surface is to create favourable adsorption sites III in the zeolite by increasing the number of cations. Everything occurs as if adsorption sites II and III in NaX models compete with each other and this leads to strong steric hindrance at high loading. Introducing cations in sites III has a similar effect on selectivity to increasing the cation size. On the basis of our simulations, we predict that NaX should only be weakly selective in favour of one or the other xylene isomer.
Finally, a way of increasing steric hindrance in the supercages and displacing the adsorbed molecules towards the supercage centre would be to add a small amount of water molecules, which are known experimentally to adsorb close to the site II cations. In this way the effective diameter of the cations would be increased and the xylene molecules would be pushed further away from the framework atoms. This could result in an enhancement of the adsorption selectivity in favour of p-xylene. Our next step will be to simulate xylene adsorption in prehydrated faujasites. In these systems cation mobility will be taken into account, as one expects cation location to change because of the adsorbed water molecules.
Some progress has been made here in the understanding of how adsorption selectivity of xylene isomers is generated in faujasite zeolites, depending on the nature and number of extraframework cations. Molecular simulation should now become a useful tool, not only for rationalising the known experimental facts, but also to make some predictions.
Acknowledgements
We wish to thank the Institut Français du Pétrole for financial support through a BDI/CNRS grant for S.B. and for a generous allocation of computer time. Bernard Tavitian is gratefully acknowledged for fruitful discussions.References
- R. W. Neuzil, U.S. Pat.
3 558
730; 3 558 732 and 3 626 020, 1971 Search PubMed; G. Ash, K. Barth, G. Hotier, L. Mank and P. Renard, Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . Inst. Fr. Pét., 1994, 49, 541 Search PubMed.
. Inst. Fr. Pét., 1994, 49, 541 Search PubMed. - V. Cottier, J.-P. Bellat, M.-H. Simonot-Grange and A. Méthivier, J. Phys. Chem. B, 1997, 101, 4798 CrossRef CAS.
- D. M. Ruthven and M. Goddard, Zeolites, 1986, 6, 275 CrossRef CAS.
- K. Iwayama and M. Suzuki, Stud. Surf. Sci. Catal., 1994, 83, 243 Search PubMed.
- E. Santacesaria, M. Morbidelli, P. Danise, M. Mercenari and S. Carra, Ind. Eng. Chem. Process Des. De
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1982, 21, 440 Search PubMed.
., 1982, 21, 440 Search PubMed. - R. Hulme, R. E. Rosensweig and D. M. Ruthven, Ind. Eng. Chem. Res., 1991, 30, 752 CrossRef CAS.
- C. Pichon, A. Méthivier and M.-H. Simonot-Grange, Langmuir, 2000, 16, 1931 CrossRef CAS.
- G. Schrimpf, B. Tavitian and D. Espinat, J. Phys. Chem., 1995, 99, 10932 CrossRef CAS.
- R. J.-M. Pellenq, B. Tavitian, D. Espinat and A. H. Fuchs, Langmuir, 1996, 12, 4768 CrossRef CAS.
- V. Lachet, A. Boutin, B. Tavitian and A. H. Fuchs, J. Phys. Chem. B, 1998, 102, 9224 CrossRef CAS.
- V. Lachet, A. Boutin, B. Tavitian and A. H. Fuchs, Faraday Discuss., 1997, 106, 307 RSC.
- V. Lachet, A. Boutin, B. Tavitian and A. H. Fuchs, Langmuir, 1999, 15, 8678 CrossRef CAS.
- T. Kitagawa, T. Tsunekawa and K. Iwayama, Microporous Mater., 1996, 7, 227 CrossRef CAS.
- W. J. Mortier, Compilation of Extra-Framework Sites in Zeolites, Butterworth, Guildford, 1982. Search PubMed.
- A. N. Fitch, H. Jobic and A. Renouprez, J. Phys. Chem., 1986, 90, 1311 CrossRef CAS.
- G. R. Eulenberger, D. P. Shoemaker and J. G. Keil, J. Phys. Chem., 1967, 71, 1812 CrossRef CAS.
- W. J. Mortier, H. J. Bosman and J. B. Uytterhoeven, J. Phys. Chem., 1972, 76, 650 CrossRef CAS.
- L. Uytterhoeven, D. Dompas and W. J. Mortier, J. Chem. Soc., Faraday Trans., 1992, 88, 2753 RSC.
- D. H. Olson, Zeolites, 1995, 15, 439 CrossRef CAS.
- G. Vitale, C. F. Mellot, L. M. Bull and A. K. Cheetham, J. Phys. Chem. B, 1997, 101, 4559 CrossRef CAS.
- L. Zhu and K. Seff, J. Phys. Chem. B, 1999, 103, 9512 CrossRef CAS.
- M. Czjzek, H. Fuess and T. Vogt, J. Phys. Chem., 1991, 95, 5255 CrossRef CAS.
- R. J.-M. Pellenq and D. Nicholson, J. Phys. Chem., 1994, 98, 13339 CrossRef CAS.
- H. Böhm and R. Ahlrichs, J. Chem. Phys., 1982, 77, 5068.
- W. L. Jorgensen and T. B. Nguyen, J. Comput. Chem., 1993, 14, 195 CrossRef CAS.
- V. Lachet, A. Boutin, R. J.-M. Pellenq, D. Nicholson and A. H. Fuchs, J. Phys. Chem., 1996, 100, 9006 CrossRef CAS.
- D. Douget, R. J.-M. Pellenq, A. Boutin, A. H. Fuchs and D. Nicholson, Mol. Simul., 1996, 17, 255 Search PubMed.
- R. Q. Snurr, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1993, 97, 13742 CrossRef CAS.
- B. Smit, Mol. Phys., 1995, 85, 153 CAS.
- M. Mezei, Mol. Phys., 1980, 40, 901 CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, 1996. Search PubMed.
- J.-P. Bellat, M.-H. Simonot-Grange and S. Jullian, Zeolites, 1995, 15, 124 CrossRef CAS; J.-P. Bellat and M.-H. Simonot-Grange, Zeolites, 1995, 15, 219 CrossRef CAS.
Footnote |
| † Present address: Institut Français du Pétrole, 1-4 avenue du Bois Préau, 92852 Rueil Malmaison Cedex, France. |
| This journal is © the Owner Societies 2001 |
