Electronically nonadiabatic transitions in a collinear H2 + H+ system: Quantum mechanical understanding and comparison with a trajectory surface hopping method
V. G.
Ushakov†
,
Katsuyuki
Nobusada‡
* and
V. I.
Osherov†
Department of Theoretical Studies, Institute for Molecular Science, Myodaiji, Okazaki, 444-8585, Japan. E-mail: nobusada@sci.hokudai.ac.jp
First published on 4th December 2000
Abstract
Electronically nonadiabatic transitions in a collinear H2 + H+ system have been studied both quantum mechanically and with classical mechanics using a diatomics-in-molecules type potential energy surface fitted to recent ab initio data. The quantum dynamical calculations are carried out by employing a standard close-coupling method in hyperspherical coordinates and the quasiclassical trajectory calculations were carried out with a basic surface hopping method. Special emphasis is placed on qualitative analysis of the physical mechanisms of the electronically nonadiabatic transitions. To make such an analysis, the basic idea proposed by Nobusada et al. (K. Nobusada, O. I. Tolstikhin and H. Nakamura, J. Chem. Phys., 1998, 108, 8922) in the study of vibrationally nonadiabatic transitions is applied, and also the reaction dynamics is visualized in detail by using classical trajectories. It is found that the electronically nonadiabatic transition occurs in a rather narrow configuration space and its reactivity depends strongly on the initial vibrational state of H2.
I Introduction
Accurate theoretical calculations of quantum reaction dynamics have become feasible. A number of calculations for triatomic1 and also polyatomic1–3 systems have been carried out. Most of these reactions are usually assumed to occur on the ground adiabatic potential energy surface (PES) only. Although several groups have carried out accurate quantum mechanical calculations of electronically nonadiabatic reactions,4–13 the detailed quantum dynamics of those reactions have not yet been well analyzed. On the other hand, a quasiclassical trajectory surface hopping (TSH) method has been much more extensively applied to reactions accompanying electronically nonadiabatic transitions.14–19 The TSH method has the advantage of visualizing reaction dynamics more clearly and is very helpful if the method is used together with a quantum approach to elucidate the reactions accompanying electronically nonadiabatic transitions.In the present study, we apply quantum and classical mechanical approaches to a reactive collinear system of H2 + H+ accompanying electronically nonadiabatic transitions. It is still demanding to make exact (especially quantum mechanical) calculations of the electronically nonadiabatic transition in a full 3D system. Even though we can accomplish such tough calculations, qualitative understanding of the mechanisms is not sufficient. Therefore, we analyze the present collinear H3+ system in detail and get a deeper insight into electronically nonadiabatic transitions. The quantum dynamical calculations are carried out by using a standard time-independent close-coupling method in hyperspherical coordinates and the classical calculations by the TSH method. In both calculations the new diatomics-in-molecules (DIM)20,21 type PES is employed. The DIM PES is con structed by fitting a 3 × 3 DIM type matrix to recent ab initio data calculated by Ichihara and Yokoyama.22 In this paper, we place special emphasis on qualitative analysis of the mechanisms of electronically nonadiabatic reactions. From a quantum mechanical viewpoint, we aim to conceptualize electronically nonadiabatic transitions by taking advantage of a basic idea, which was previously established by Nobusada et al. to treat vibrationally nonadiabatic transitions.23–25 On the other hand, from a classical mechanical viewpoint, we visualize the dynamics more clearly by analyzing the classical trajectories.
This paper is organized as follows. In the next section, we define the present collision system and describe the DIM PES of the system. The methods of the quantum mechanical and classical TSH calculations are given in Section III. In Section IV, the results obtained by the quantum and classical dynamical calculations are discussed in detail. A comparison between the two results is also made in this section. The concluding remarks are given in Section V.
II Physical system and potential energy surfaces
In the present study, we chose a collinear H2 + H+ reactive collision system accompanying electronically nonadiabatic transitions, i.e., charge transfer. This system has two different electronic channels in the energy range considered:

| (1) |
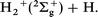
| (2) |
If we assume that all three hydrogen atoms are distinguishable, there are four different processes in this collision system, exchange and nonexchange without charge transfer and exchange and nonexchange with charge transfer. In the following discussions, we distinguish between these four processes. The present collision system is described by using the DIM PES. The DIM PESs of H3+ have already been reported.26,27 To reconstruct the DIM PES, however, we fit the 3 × 3 minimal DIM potential to recent ab initio data for the ground and first excited states of H3+ calculated in 734 physically important nuclear configurations.22 The fitting procedure is fulfilled in a framework of the simple many body expansion method28 by adding correcting polynomials described below. The 3 × 3 DIM Hamiltonian matrix is given by

| (3) |
Here,

| (4) |

| (5) |

| (6) |
where i, j, k(i≠j≠k) = 1, 2, 3 and ri,j,k are internuclear distances of the diatoms. 1Σg+ represents the ground electronic state of H2, and 2Σg+ and 2Σu+ represent the ground and first excited electronic states of H2+, respectively. Functional forms of these states are given by
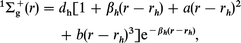
| (7) |

| (8) |

| (9) |
where a = 1.13804 and b = 0.52961, and the other diatomic parameters are listed in Table 1. Three-body terms Ch,g,u in eqn. (4)–(6) decrease exponentially to zero when one of the atoms moves away from the other two. The three-body terms are explicitly given by
| h | g | u | |
|---|---|---|---|
| d | −0.17445 | 0.10272 | 0.62871 |
| β | 2.09607 | 0.71935 | 0.87080 |
| r | 1.40104 | 2.00313 | 0.34405 |

| (10) |
Here Pl is the cubic polynomial which is represented in the following form taking account of the symmetry of H3+:
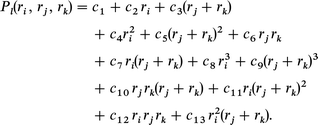
| (11) |
The fitting parameters cn(n = 1–14) defined for each l( = h, g, u) are given in Table 2.
| h | g | u | |
|---|---|---|---|
| c 1 | 8.13033 | −6.22155 | −3.94414 |
| c 2 | −3.02555 | 3.70543 | 0.57600 |
| c 3 | 1.65898 | −1.98676 | 0.32953 |
| c 4 | 0.93108 | −1.96016 | 0.01044 |
| c 5 | 0.92263 | −2.08734 | 0.03277 |
| c 6 | −0.36808 | 5.76902 | −0.06461 |
| c 7 | −1.77260 | 1.77340 | −0.10262 |
| c 8 | −0.12637 | 0.17791 | −0.00117 |
| c 9 | 0.11083 | 0.21520 | −0.00541 |
| c 10 | −0.34325 | −1.03671 | 0.01565 |
| c 11 | −0.30780 | −0.01557 | 0.00594 |
| c 12 | 0.44247 | −0.20215 | −0.00982 |
| c 13 | 0.30672 | −0.04772 | 0.00182 |
| c 14 | 0.78463 | 0.93662 | 0.58787 |
We plot contour maps of the H3+ DIM PES for the ground state in Fig. 1 and for the first excited state in Fig. 2 as a function of u1 and u2, where u1 is the mass-scaled distance between H and the center-of-mass of H2+ and u2 is the mass-scaled H–H internuclear distance. The ground PES has a deep well at u1≈2.5 a0 and u2≈1.4 a0 corresponding to the stable H3+ triatomic complex. On the other hand, the first excited PES is generally repulsive, at least in the energy region considered.
 | ||
| Fig. 1 Contour map of the ground electronic state of H3+ as a function of u1 and u2, where u1 is the mass-scaled distance between H and the center-of-mass of H2+, and u2 is the mass-scaled H–H internuclear distance. The thick broken curves indicate the seam lines. The contour lines are drawn in eV relative to the lowest vibrational state of H2. | ||
 | ||
| Fig. 2 As Fig. 1 but for the first excited state. | ||
III Calculations of reaction dynamics on multi-potential energy surfaces
A Quantum mechanical treatment
The Schrödinger equation taking account of nuclear and electron motions is given by

| (12) |
where T(r) and K(Rel) are the kinetic energy parts with respect to nuclear and electron motions, respectively. Here, r( = r1, r2, r3) and Rel respectively indicate sets of nuclear and electron coordinates. V(r, Rel) is the interaction potential as a function of r and Rel, and E is the total energy measured from the lowest vibrational state of H2. If we consider a collinear H3+ system, eqn. (12) is easily rewritten by using the hyperspherical coordinates in a usual way:

| (13) |
where
μ is the characteristic mass,
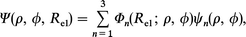
| (14) |
where Φn(Rel; ρ, ϕ) is the electronic basis set forming the DIM Hamiltonian of eqn. (3) and ψn(ρ, ϕ) is the nuclear basis function. After substituting eqn. (14) into eqn. (13), we obtain the following set of coupled differential equations given by

| (15) |
where Umn( = 〈Φm∣Hel(ρ, ϕ, Rel)∣Φn〉) is represented by eqn. (3). Without difficulty eqn. (15) is further rewritten into a set of coupled equations with respect to ρ if ψn(ρ, ϕ) is expanded in terms of proper basis sets as a function of ϕ. Then, we solve these coupled equations using the R-matrix propagation method29 up to the asymptotic region along ρ and obtain the S-matrix by imposing a proper scattering boundary condition there.
B Trajectory surface hopping approach
We carry out the classical calculations by employing a primitive TSH method described elsewhere.14 To obtain quantitative results, we should use the improved TSH methods.15,17,19 However, in this paper we do not intend to make a quantitative comparison between the quantum and classical results. The electronically nonadiabatic transition probability between the two PESs is evaluated by using the Landau–Zener (LZ) formula at every position where the classical trajectory crosses the seam line. The LZ parameters are determined by interpolating the adiabatic PESs in the section normal to the seam line. Whether the surface hop actually occurs or not is determined by comparing the magnitude of the LZ nonadiabatic transition probability with random numbers (i.e., an anteater method).IV Results
A Quantum mechanical description of electronically nonadiabatic transitions
Fig. 3 shows the vibronic adiabatic potential energy curves as a function of ρ. The vibrational quantum numbers of H2 and H2+ are indicated on the right-hand edge. The curves are roughly categorized into two types of diabatic curves; (i) those having deep potential wells and (ii) simply repulsive curves. All the potential curves asymptotically correlate to definite H2 or H2+ vibrational energy levels and are double degenerate. However, the diabatic curves correlating to H2 split into two at small ρ. This is simply energy splitting, well known in the case of a double well potential. These splittings are mainly responsible for the atom exchange process. In the region of E≳1.8 eV and 7≲ρ/a0≲10, many avoided crossings are located between the adiabatic potential curves. As will be described below, these avoided crossings play a very important role in electronically nonadiabatic transitions. | ||
| Fig. 3 Vibronic adiabatic potential energy curves as a function of ρ. Vibrational quantum numbers of H2 and H2+ are indicated on the right-hand edge. | ||
In Fig. 4(a)–(d), we show the quantum mechanical probabilities of three inelastic collision processes for H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2–5) as a function
of the total energy. The three processes are exchange and
nonexchange with charge transfer, and exchange without charge
transfer. Here, it should be noted that all the probabilities
are smoothed out because the original raw data give a huge
number of (Feshbach) resonances owing to the deep potential
well shown in Fig. 3. All the quantum probabilities reported
below are similarly smoothed out. These figures indicate
two interesting features: (i) Some representative maximum
peaks appear. (ii) The three processes compete with each
other strongly, depending on the initial vibrational state of H2.
These characteristic features are qualitatively interpreted
in terms of the idea proposed by Nobusada et al. in the study
of electronically adiabatic rearrangement reactions.23–25 In their
papers, they demonstrated that the rearrangement reactions
were regarded as vibrationally nonadiabatic transitions
occurred at some important avoided crossings. Let us first
consider the dynamical feature of (i) mentioned above. To relate
the electronically nonadiabatic transitions to specific avoided
crossings, we pick up several avoided crossings from Fig.
3. Fig. 5 is a magnification of Fig. 3 to show such avoided crossings more clearly, labeled a–d. We can roughly ascribe the main maximum peaks labeled in Fig. 4 to these specific avoided
crossings. In fact, each main peak position approximately
corresponds to the energy positions of the avoided crossings
a–d. To confirm the above explanations more quantitatively,
we evaluate the electronically nonadiabatic transition
p at these crossings by introducing the a2
parameter,
which judges the significance of avoided crossings.30
According to the semiclassical analysis by Zhu et al.,30
effective
nonadiabatic transitions (0.005≲p≲0.96) occur in the range 0.05≲a2<100.
The present a2 parameters are 0.402 (crossing a), 0.246 (crossing b), 0.265 (crossing c), and 0.287 (crossing d).
These results clearly indicate that electronically nonadiabatic
transitions occur effectively at these avoided crossings.
The representative maximum peaks in Fig. 4 appear as a result
of these effective electronically nonadiabatic transitions.
= 2–5) as a function
of the total energy. The three processes are exchange and
nonexchange with charge transfer, and exchange without charge
transfer. Here, it should be noted that all the probabilities
are smoothed out because the original raw data give a huge
number of (Feshbach) resonances owing to the deep potential
well shown in Fig. 3. All the quantum probabilities reported
below are similarly smoothed out. These figures indicate
two interesting features: (i) Some representative maximum
peaks appear. (ii) The three processes compete with each
other strongly, depending on the initial vibrational state of H2.
These characteristic features are qualitatively interpreted
in terms of the idea proposed by Nobusada et al. in the study
of electronically adiabatic rearrangement reactions.23–25 In their
papers, they demonstrated that the rearrangement reactions
were regarded as vibrationally nonadiabatic transitions
occurred at some important avoided crossings. Let us first
consider the dynamical feature of (i) mentioned above. To relate
the electronically nonadiabatic transitions to specific avoided
crossings, we pick up several avoided crossings from Fig.
3. Fig. 5 is a magnification of Fig. 3 to show such avoided crossings more clearly, labeled a–d. We can roughly ascribe the main maximum peaks labeled in Fig. 4 to these specific avoided
crossings. In fact, each main peak position approximately
corresponds to the energy positions of the avoided crossings
a–d. To confirm the above explanations more quantitatively,
we evaluate the electronically nonadiabatic transition
p at these crossings by introducing the a2
parameter,
which judges the significance of avoided crossings.30
According to the semiclassical analysis by Zhu et al.,30
effective
nonadiabatic transitions (0.005≲p≲0.96) occur in the range 0.05≲a2<100.
The present a2 parameters are 0.402 (crossing a), 0.246 (crossing b), 0.265 (crossing c), and 0.287 (crossing d).
These results clearly indicate that electronically nonadiabatic
transitions occur effectively at these avoided crossings.
The representative maximum peaks in Fig. 4 appear as a result
of these effective electronically nonadiabatic transitions.
 | ||
| Fig. 4 Quantum probabilities of exchange with charge transfer (solid line), nonexchange with charge transfer (dotted line), and exchange without charge transfer (broken line) as a function of the total energy. Initial vibrational states of H2 are (a) 2, (b) 3, (c) 4 and (d) 5. Some representative maximum peaks are labeled as a–d. | ||
 | ||
| Fig. 5 Magnification of Fig. 3 showing some avoided crossings much more clearly. These avoided crossings are labeled with notation corresponding to those of Fig. 4. | ||
We now explain the reason for the characteristic feature (ii)
listed above by drawing sections of the ground and first
excited PESs of H3+ in Fig. 6 as a function of ϕ/π at ρ
= 6, 8 and 14 a0.
The reagent and product channels are well separated by the potential
barrier. The potential barrier of the first excited PES
is so high that the exchange reaction cannot occur, at least
in the energy range considered. On the other hand, the barrier
of the ground PES becomes lower with decreasing
ρ and then the exchange reaction seems to occur easily on the ground PES. Combining these sections of the PESs with the
vibronic adiabatic potential curves in Fig. 3, we analyze the
quantum dynamics of H3+. Let us follow the vibronic adiabatic
potential energy curves correlating to H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽3) in Fig. 3. These
potential curves do not have important avoided crossings
at which the electronically nonadiabatic
transitions occur
effectively. Therefore, the reaction for H2(
⩽3) in Fig. 3. These
potential curves do not have important avoided crossings
at which the electronically nonadiabatic
transitions occur
effectively. Therefore, the reaction for H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽3) + H+ occurs mainly
on the ground PES corresponding to the solid
line in Fig. 6. As mentioned above, the exchange reaction on
the ground PES can occur at small ρ. In fact, exchange without
charge transfer occurs easily when
⩽3) + H+ occurs mainly
on the ground PES corresponding to the solid
line in Fig. 6. As mentioned above, the exchange reaction on
the ground PES can occur at small ρ. In fact, exchange without
charge transfer occurs easily when ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽3 as shown in Fig. 4(a)
and (b) (see broken lines). However, charge transfer
also occurs even when
⩽3 as shown in Fig. 4(a)
and (b) (see broken lines). However, charge transfer
also occurs even when ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2 or 3. This is because the vibrational
excitation occurs during the collision and then the system
has a chance to encounter the important avoided crossings
shown in Fig. 5. Nevertheless, this process is minor and
thus the probability of charge transfer is much smaller than
that of exchange without charge transfer in the case of H2(
= 2 or 3. This is because the vibrational
excitation occurs during the collision and then the system
has a chance to encounter the important avoided crossings
shown in Fig. 5. Nevertheless, this process is minor and
thus the probability of charge transfer is much smaller than
that of exchange without charge transfer in the case of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽3) + H+. Next, we follow the vibronic adiabatic potential
energy curves correlating to H2(
⩽3) + H+. Next, we follow the vibronic adiabatic potential
energy curves correlating to H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽4). Differently from the case
of H2(
⩽4). Differently from the case
of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif)
![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) 3) + H+, these curves encounter the important avoided
crossings shown in Fig. 5. As mentioned above, electronically
nonadiabatic transitions occur efficiently at these
crossings. Thus, the sum of the probabilities for the two charge transfer
processes (solid line + dotted line) is larger than that for H2(
3) + H+, these curves encounter the important avoided
crossings shown in Fig. 5. As mentioned above, electronically
nonadiabatic transitions occur efficiently at these
crossings. Thus, the sum of the probabilities for the two charge transfer
processes (solid line + dotted line) is larger than that for H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ⩽3) + H+. In particular, Fig. 4(c) and (d) show that
nonexchange with charge transfer occurs more efficiently
than exchange with charge transfer. This is because the charge
transfer occurs effectively in the entrance channel and
then the collsion system is repelled backwards on the first
excited PES owing to the high potential barrier, as mentioned
above.
⩽3) + H+. In particular, Fig. 4(c) and (d) show that
nonexchange with charge transfer occurs more efficiently
than exchange with charge transfer. This is because the charge
transfer occurs effectively in the entrance channel and
then the collsion system is repelled backwards on the first
excited PES owing to the high potential barrier, as mentioned
above.
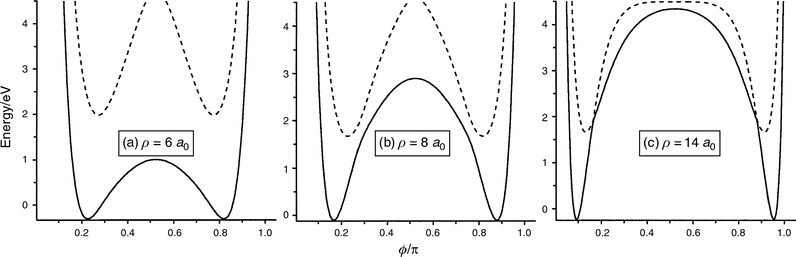 | ||
| Fig. 6 Sections of the present PESs of the ground (solid line) and first excited (dotted line) states at ρ = (a) 6, (b) 8 and (c) 14 a0 as a function of ϕ/π. | ||
B Classical mechanical description of electronically nonadiabatic transitions
Fig. 7 show the classical mechanical probabilities of four collision processes for the initial vibrational states of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2, 4 and
6) as a function of the collision energy Ecol
. The dynamics of
these processes is illustrated in Fig. 8 by showing the corresponding
typical classical trajectories. The seam lines are the same
as those shown in Fig. 1 and 2. As clearly seen from these
figures, the dynamics depends strongly on the initial vibrational
state of H2. The dynamical features are explained qualitatively
as follows.
= 2, 4 and
6) as a function of the collision energy Ecol
. The dynamics of
these processes is illustrated in Fig. 8 by showing the corresponding
typical classical trajectories. The seam lines are the same
as those shown in Fig. 1 and 2. As clearly seen from these
figures, the dynamics depends strongly on the initial vibrational
state of H2. The dynamical features are explained qualitatively
as follows.
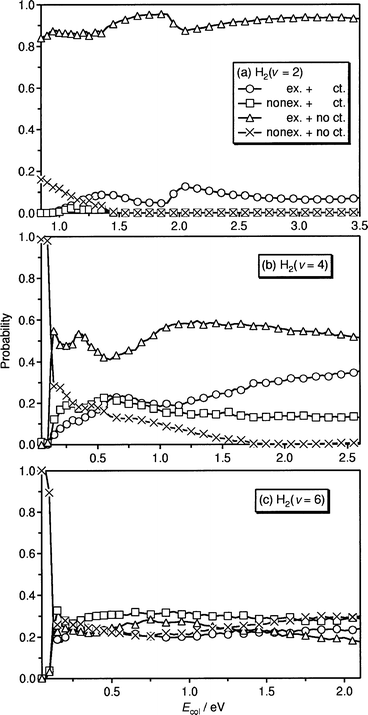 | ||
| Fig. 7 Classical probabilities of four processes of exchange with charge transfer (○), nonexchange with charge transfer (□), exchange without charge transfer (△), nonexchange without charge transfer ( × ) as a function of the collision energy. Initial vibrational states of H2 are (a) 2, (b) 4 and (c) 6. | ||
 | ||
Fig. 8
Typical classical trajectories for some representative initial conditions of (a) H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2); Ecol
= 1.1 eV, (b) H2(
= 2); Ecol
= 1.1 eV, (b) H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 4); Ecol
= 1.5 eV and (c) H2(
= 4); Ecol
= 1.5 eV and (c) H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 6); Ecol
= 1 eV as a function of u1 and u2. The thick broken curves represent the seam lines.
= 6); Ecol
= 1 eV as a function of u1 and u2. The thick broken curves represent the seam lines.
| ||
The dynamics is fully diabatic in the asymptotically far
region of the entrance channel. Thus, if the vibration amplitude
is so large, i.e., H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) >4), that the trajectories can cross the
seam line, the electronically nonadiabatic transition probability
is equal to unity. As the atom and the diatom are close to
each other, the dynamics transforms from diabatic to adiabatic
and then the electronically nonadiabatic transition probability
tends to be zero. Since the split between the ground and
first excited PESs along the seam line becomes narrower exponentially,
the transformation from diabatic to adiabatic occurs
in a rather limited region of the valley at u1∽8 a0. This
small region plays a very important role because it determines
whether or not the effective electronically nonadiabatic transitions
occur. In the following discussions, we further analyze
the details of the electronically nonadiabatic transitions
by showing the three typical cases for H2(
>4), that the trajectories can cross the
seam line, the electronically nonadiabatic transition probability
is equal to unity. As the atom and the diatom are close to
each other, the dynamics transforms from diabatic to adiabatic
and then the electronically nonadiabatic transition probability
tends to be zero. Since the split between the ground and
first excited PESs along the seam line becomes narrower exponentially,
the transformation from diabatic to adiabatic occurs
in a rather limited region of the valley at u1∽8 a0. This
small region plays a very important role because it determines
whether or not the effective electronically nonadiabatic transitions
occur. In the following discussions, we further analyze
the details of the electronically nonadiabatic transitions
by showing the three typical cases for H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2), then H2(
= 2), then H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 6),
and finally H2(
= 6),
and finally H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 4).
= 4).
![[italic v]](https://www.rsc.org/images/entities/b_char_e0f5.gif) = 2) + H+.
Since the vibration amplitude is
small in the entrance channel, as shown in Fig. 8(a), the trajectories cannot cross the seam line. This means that the
dynamics proceeds only on the ground PES and thus the electronically
nonadiabatic transitions do not occur in the
entrance channel. The trajectories on the ground PES reach
the deep potential well at u1≲6 a0 and then most of the trajectories enter the product channel out of the potential well. Since
the present reactive system is symmetric, there exists also
the same small region in the product channel where the effective electronically nonadiabatic transitions occur. The collision
system in the deep potential well has a chance to be vibrationally
excited and as a result the vibration amplitude
becomes
large. If the outgoing trajectory passes the above small
region in the product channel and crosses the seam line, the
electronically nonadiabatic transition can occur. This process
ends in the exchange with charge transfer. The trajectory corresponding to this process is clearly illustrated in Fig. 8(a).
Fig. 8(a) shows the two typical outgoing trajectories starting
from the initial condition of H2(
= 2) + H+.
Since the vibration amplitude is
small in the entrance channel, as shown in Fig. 8(a), the trajectories cannot cross the seam line. This means that the
dynamics proceeds only on the ground PES and thus the electronically
nonadiabatic transitions do not occur in the
entrance channel. The trajectories on the ground PES reach
the deep potential well at u1≲6 a0 and then most of the trajectories enter the product channel out of the potential well. Since
the present reactive system is symmetric, there exists also
the same small region in the product channel where the effective electronically nonadiabatic transitions occur. The collision
system in the deep potential well has a chance to be vibrationally
excited and as a result the vibration amplitude
becomes
large. If the outgoing trajectory passes the above small
region in the product channel and crosses the seam line, the
electronically nonadiabatic transition can occur. This process
ends in the exchange with charge transfer. The trajectory corresponding to this process is clearly illustrated in Fig. 8(a).
Fig. 8(a) shows the two typical outgoing trajectories starting
from the initial condition of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2) and Ecol
= 1.1 eV. Exchange
with charge transfer is a rather minor process and exchange
without charge transfer occurs much more frequently.
= 2) and Ecol
= 1.1 eV. Exchange
with charge transfer is a rather minor process and exchange
without charge transfer occurs much more frequently.
![[italic v]](https://www.rsc.org/images/entities/b_char_e0f5.gif) = 6) + H+.
In these collisions the initial vibration
amplitude is so large that the trajectories can cross the
seam line in the entrance channel, as shown in Fig. 8(c). Thus,
the dynamics proceeds fully diabatically up to u1∽8 a0 where the
electronically nonadiabatic transition probability changes sharply
from unity to zero. As frequently mentioned in this paper,
this rather narrow region determines whether the processes
occur on the ground or the excited PES. If the system remains
on the ground PES, the subsequent process is similar to
the previous case of H2(
= 6) + H+.
In these collisions the initial vibration
amplitude is so large that the trajectories can cross the
seam line in the entrance channel, as shown in Fig. 8(c). Thus,
the dynamics proceeds fully diabatically up to u1∽8 a0 where the
electronically nonadiabatic transition probability changes sharply
from unity to zero. As frequently mentioned in this paper,
this rather narrow region determines whether the processes
occur on the ground or the excited PES. If the system remains
on the ground PES, the subsequent process is similar to
the previous case of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2) + H+. However, if the electronically
nonadiabatic transition occurs in this narrow region, the collision system is repelled backwards by the high
repulsive potential barrier on the excited PES. This dynamics is one
of the typical processes in the H2(
= 2) + H+. However, if the electronically
nonadiabatic transition occurs in this narrow region, the collision system is repelled backwards by the high
repulsive potential barrier on the excited PES. This dynamics is one
of the typical processes in the H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 6) + H+ collision system. In
fact, the probability for nonexchange with charge transfer
increases much more than that of H2(
= 6) + H+ collision system. In
fact, the probability for nonexchange with charge transfer
increases much more than that of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2) + H+. The trajectories
repelled backwards have another chance of electronically nonadiabatic transition. If the system is electronically de-excited
to the ground state from the upper state, the dynamical
process ends in the nonexchange without charge transfer.
= 2) + H+. The trajectories
repelled backwards have another chance of electronically nonadiabatic transition. If the system is electronically de-excited
to the ground state from the upper state, the dynamical
process ends in the nonexchange without charge transfer.
As
shown in Fig. 7(c), the three inelastic processes of
exchange and nonexchange with charge transfer, and
exchange without charge transfer have the same energetic
threshold (∽0.1 eV). This threshold is caused by the low potential
barrier (∽0.1 eV) at u1∽9 a0 in the entrance channel (see Fig. 1). A similar energetic threshold will be also seen
in the case of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 4) + H+.
= 4) + H+.
![[italic v]](https://www.rsc.org/images/entities/b_char_e0f5.gif) = 4) + H+.
This
collision process is intermediate
between the two described above. In the far asymptotic region
in the entrance channel, the trajectories cannot cross the seam
line, as shown in Fig. 8(b), but have a chance to cross the line
as the line gradually curves. If the electronically nonadiabatic
transition occurs before the exchange, the trajectories are
repelled backwards owing to the high potential barrier of the
excited PES. On the other hand, if the system enters the deep
potential well on the ground PES, the subsequent processes
are similar to the previous cases. Reflecting the present intermediate
collision process, exchange without charge transfer is
still a major process as for the case of H2(
= 4) + H+.
This
collision process is intermediate
between the two described above. In the far asymptotic region
in the entrance channel, the trajectories cannot cross the seam
line, as shown in Fig. 8(b), but have a chance to cross the line
as the line gradually curves. If the electronically nonadiabatic
transition occurs before the exchange, the trajectories are
repelled backwards owing to the high potential barrier of the
excited PES. On the other hand, if the system enters the deep
potential well on the ground PES, the subsequent processes
are similar to the previous cases. Reflecting the present intermediate
collision process, exchange without charge transfer is
still a major process as for the case of H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2) + H+ but the other three processes gradually occur.
= 2) + H+ but the other three processes gradually occur.
B.4 Comparison with the quantum mechanical results
We end this section by comparing the classical results with the quantum ones. Fig. 9 shows the quantum and classical probabilities for H2(![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) = 2, 4 and 6) + H+ as a function of the collision
energy. The processes of exchange and nonexchange with charge
transfer, and exchange without charge transfer are plotted.
As was expected, the classical method reproduces the quantum
results on average. In particular, however, the classical
mechanical approach breaks down at small
= 2, 4 and 6) + H+ as a function of the collision
energy. The processes of exchange and nonexchange with charge
transfer, and exchange without charge transfer are plotted.
As was expected, the classical method reproduces the quantum
results on average. In particular, however, the classical
mechanical approach breaks down at small ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) and near the threshold energy, and of course does not reproduce the resonance
structures.
and near the threshold energy, and of course does not reproduce the resonance
structures.
 | ||
| Fig. 9 Comparison of the quantum and classical probabilities for exchange and nonexchange with charge transfer, and exchange without charge transfer. Initial vibrational states of H2 are (a) 2, (b) 4 and (c) 6. | ||
V Concluding remarks
We have analyzed quantum and classical reaction dynamics accompanying electronically nonadiabatic transitions in a col linear H2 + H+ collision system. The quantum mechanical calculations are based on the standard close-coupling method in hyperspherical coordinates and the classical mechanical ones have been carried out by using a TSH method. We have also reconstructed the DIM potential energy surface of H3+ by using recent ab initio data. Special emphasis is placed on a qualitative understanding of the mechanisms of the electronically nonadiabatic transitions.In the quantum mechanical studies, we made use of a basic idea previously proposed by Nobusada et al. in analyzing electronically adiabatic rearrangement reactions. This basic idea has been found to work well, even in the reactive system accompanying electronically nonadiabatic transitions. The electronically nonadiabatic transitions occur at some specific avoided crossings located in a rather narrow configuration space. As a result, the charge transfer probabilities have representative maximum peaks, and the reactivity of the processes depends strongly on the initial vibrational state of H2. We have also found that the electronically nonadiabatic transition and the exchange process occur at different configuration space. The present analysis will be very helpful in the 3D H3+ system when we obtain the adiabatic potential energy curves of the 3D system.
The TSH method successfully visualizes the reaction dynamics clearly by illustrating the trajectories and thus gives helpful insights into the electronically nonadiabatic transition. Similarly to the quantum results, the classical analysis also reveals that the nonadiabatic transitions occur in a rather narrow region and the reactivity depends on the initial condition. The present TSH method is not suitable to obtain quantitative results for the following reasons: (i) The electronically nonadiabatic transitions are allowed only at predefined crossing seam lines. This restriction would be less accurate in the 3D system. (ii) The electronically nonadiabatic transition probability is estimated by the L/Z formula which is invalid in the energetically threshold and classically forbidden region. These problems have been quite well resolved by improving the TSH method.15,17,19 We are currently improving the primitive TSH method in the classically forbidden region by using the Zhu–Nakamura formula.30
Acknowledgements
The authors thank Professor H. Nakamura for his useful comments. This work was partially supported by a Research Grant 10440179 and by a Grant-in-Aid for Scientific Research on Priority Area “Molecular Physical Chemistry” from The Ministry of Education, Science, Culture and Sports of Japan.References
- J. Z. H. Zhang, Theory and Application of Quantum Molecular Dynamics, World Scientific, Singapore, 1999, and references therein. Search PubMed.
- D. C. Clary, J. Phys. Chem., 1994, 98, 10678 CrossRef CAS.
- J. M. Bowman and G. C. Schatz, Annu. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . Phys. Chem., 1995, 46, 169 Search PubMed.
. Phys. Chem., 1995, 46, 169 Search PubMed. - M. Gilibert and M. Baer, J. Phys. Chem., 1994, 98, 12822 CrossRef CAS.
- M. Gilibert and M. Baer, J. Phys. Chem., 1995, 99, 15748 CrossRef CAS.
- I. Last, M. Gilibert and M. Baer, J. Chem. Phys., 1997, 107, 1451 CrossRef CAS.
- S. L. Mielke, G. J. Tawa, D. G. Truhlar and D. W. Schwenke, Chem. Phys. Lett., 1995, 234, 57 CrossRef CAS.
- G. C. Schatz, J. Phys. Chem., 1995, 99, 7522 CrossRef CAS.
- C. S. Maierle, G. C. Schatz, M. S. Gordon, P. McCabe and J. N. L. Connor, J. Chem. Soc., Faraday Trans., 1997, 93, 709 RSC.
- G. C. Schatz, P. McCabe and J. N. L. Connor, Faraday Discuss., 1998, 110, 139 RSC.
- T. W. J. Whiteley, A. J. Dobbyn, J. N. L. Connor and G. C. Schatz, Phys. Chem. Chem. Phys., 2000, 2, 549 RSC.
- M. H. Alexander, H.-J. Werner and D. E. Manolopoulos, J. Chem. Phys., 1998, 109, 5710 CrossRef CAS.
- T. Takayanagi, Y. Kurosaki and A. Ichihara, J. Chem. Phys., 2000, 112, 2615 CrossRef CAS.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562 CrossRef CAS.
- N. C. Blais and D. G. Truhlar, J. Chem. Phys., 1983, 79, 1334 CrossRef CAS.
- J. R. Stine and J. T. Muckerman, J. Phys. Chem., 1987, 91, 459 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- S. Chapman, Ad
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . Chem. Phys., 1992, 82, 423 Search PubMed.
. Chem. Phys., 1992, 82, 423 Search PubMed. - J.-Y. Fang and S. Hammes-Schiffer, J. Chem. Phys., 1999, 110, 11166 CrossRef CAS.
- J. C. Tully, Ad
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . Chem. Phys., 1980, 42, 63 Search PubMed.
. Chem. Phys., 1980, 42, 63 Search PubMed. - P. J. Kuntz, in Theory of Chemical Reaction Dynamics, ed. M. Bare, CRC, Boca Raton, FL, 1985, vol. I, p. 71. Search PubMed.
- A. Ichihara and K. Yokoyama, J. Chem. Phys., 1995, 103, 2109 CrossRef CAS.
- K. Nobusada, O. I. Tolstikhin and H. Nakamura, J. Chem. Phys., 1998, 108, 8922 CrossRef CAS.
- K. Nobusada, O. I. Tolstikhin and H. Nakamura, J. Phys. Chem. A, 1998, 102, 9445 CrossRef CAS.
- K. Nobusada, H. Nakamura, Y. Lin and B. Ramachandran, J. Chem. Phys., 2000, 113, 1018 CrossRef CAS.
- R. K. Preston and J. C. Tully, J. Chem. Phys., 1971, 54, 4297 CrossRef CAS.
- Ch. Schlier, U. Nowotny and E. Teloy, Chem. Phys., 1987, 111, 401 CrossRef CAS.
- J. N. Murrell and S. Carter, J. Phys. Chem., 1984, 88, 4887 CrossRef CAS.
- K. L. Baluja, P. G. Burke and L. A. Morgan, Comput. Phys. Commun., 1982, 27, 299 CrossRef.
- C. Zhu, H. Nakamura and K. Nobusada, Phys. Chem. Chem. Phys., 2000, 2, 557 RSC.
Footnotes |
| † Present address: Institute of Chemical Physics, Russian Academy of Sciences, Moscow, Russia. |
| ‡ Present address: Division of Chemistry, Graduate School of Science, Hokkaido University, Sapporo 060-0810, Japan. |
| This journal is © the Owner Societies 2001 |

