Dynamical structure of AgxCu1−xI (x = 0.99–0.80) in ionic and superionic phases studied by solid 63Cu and 127I NMR spin–lattice relaxation time measurements
Motohiro
Mizuno
*,
Atsuki
Hirai
,
Hidekazu
Matsuzawa
,
Kazunaka
Endo
and
Masahiko
Suhara
Department of Chemistry, Faculty of Science, Kanazawa Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersity, Kanazawa, 920-1192, Japan. E-mail: mizuno@wriron1.s. kanazawa-u.ac.jp
ersity, Kanazawa, 920-1192, Japan. E-mail: mizuno@wriron1.s. kanazawa-u.ac.jp
First published on 6th December 2000
Abstract
The temperature dependences of the 63Cu and 127I NMR spin–lattice relaxation time T1 and the 63Cu NMR spin–lattice relaxation time in a rotating frame T1ρ were measured for AgxCu1−xI (x = 0.99–0.80). In the γ phase, T1 and T1ρ were dominated by the lattice vibration at low temperatures. The minimum of T1ρ caused by the diffusion of the Cu ion was observed at ca. 360 K. The temperature dependence of T1ρ in the range 420–300 K can be explained in terms of a distribution of correlation times which arises from a distribution of activation energies for the ionic diffusion. The mean and the width of the distribution for the activation energies increased with increasing Cu concentration. The rapid T1 decrease observed above ca. 400 K can be attributed to the motion of the thermally generated defects. The enthalpy for the formation of the defect was estimated as 120 ± 10 kJ mol−1 from 63Cu NMR T1 and T1ρ values. In the α phase, the relaxation of the 63Cu nucleus was in the fast motion region and the activation energy of the ionic diffusion was determined as 7 ± 1 kJ mol−1 from the temperature dependence of 63Cu NMR T1.
Introduction
It is well known that AgI and CuI are superionic conductors that achieve a highly conducting state![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia phase transitions
and that an anomalous increase in the defect concentration
occurs near the transition temperature to the superionic
phase.1–6 However, the crystal structures and the paths of
ionic diffusion in the superionic phases of these compounds
are different.7–9 The superionic phase of AgI is the α-phase where
the iodine ions form a body-centered cubic structure, whereas
that of CuI is the α′-phase where the iodine ions form a face-centered
cubic structure.7–9 These differences are considered
to be attributable to the size and electronic structure of the diffusing
ions. In order to understand how the nature of these ions
relates to ionic diffusion and the formation of defects,
study of the transport properties of the cations in the mixed crystal,
AgxCu1−xI, is important. Kusakabe et al. investigated
the crystal structure and ionic diffusion for AgxCu1−xI using electrical
conductivity, heat capacity and X-ray diffraction methods.10–14
We analyzed the crystal structure of AgxCu1−xI
by using 63Cu NMR and X-ray diffraction methods.15–17
We clarified the sites of the Cu and Ag ions in AgxCu1−xI by analyzing the observed 63Cu NMR chemical shift using
ab initio MO calculations. In the present work, we study the
influence of doped Cu ions on ionic diffusion and the formation
of defects in AgxCu1−xI by using 63Cu and 127I NMR. The
63Cu and 127I NMR spin–lattice relaxation time T1 and the
63Cu NMR spin–lattice relaxation time in the rotation frame
T1ρ were measured for AgxCu1−xI (x
= 0.99–0.80). In this range
of x, AgxCu1−xI transforms with increasing temperature from
the γ phase, which has a zinc-blende structure, into the α phase
ia phase transitions
and that an anomalous increase in the defect concentration
occurs near the transition temperature to the superionic
phase.1–6 However, the crystal structures and the paths of
ionic diffusion in the superionic phases of these compounds
are different.7–9 The superionic phase of AgI is the α-phase where
the iodine ions form a body-centered cubic structure, whereas
that of CuI is the α′-phase where the iodine ions form a face-centered
cubic structure.7–9 These differences are considered
to be attributable to the size and electronic structure of the diffusing
ions. In order to understand how the nature of these ions
relates to ionic diffusion and the formation of defects,
study of the transport properties of the cations in the mixed crystal,
AgxCu1−xI, is important. Kusakabe et al. investigated
the crystal structure and ionic diffusion for AgxCu1−xI using electrical
conductivity, heat capacity and X-ray diffraction methods.10–14
We analyzed the crystal structure of AgxCu1−xI
by using 63Cu NMR and X-ray diffraction methods.15–17
We clarified the sites of the Cu and Ag ions in AgxCu1−xI by analyzing the observed 63Cu NMR chemical shift using
ab initio MO calculations. In the present work, we study the
influence of doped Cu ions on ionic diffusion and the formation
of defects in AgxCu1−xI by using 63Cu and 127I NMR. The
63Cu and 127I NMR spin–lattice relaxation time T1 and the
63Cu NMR spin–lattice relaxation time in the rotation frame
T1ρ were measured for AgxCu1−xI (x
= 0.99–0.80). In this range
of x, AgxCu1−xI transforms with increasing temperature from
the γ phase, which has a zinc-blende structure, into the α phase
![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia a coexistent α
+
γ phase.18 For the relaxation of 63Cu NMR in the γ phase,
two processes are considered.1 One is due to the hopping
of a Cu atom between the cubic lattice sites and the other
is caused by the defect motion.19
Usually, the former process
occurs at a lower frequency than the latter. Therefore,
the former and latter processes are considered to affect
T1ρ
and T1, respectively. When the relaxation of nuclei is caused by
ionic diffusion, T1
and T1ρ sometimes deviate from the Bloembergen,
Purcell and Pound (BPP) theory.20 Such deviations can be explained
by a distribution of correlation times. In this
case, T1 in a log(T1)
ia a coexistent α
+
γ phase.18 For the relaxation of 63Cu NMR in the γ phase,
two processes are considered.1 One is due to the hopping
of a Cu atom between the cubic lattice sites and the other
is caused by the defect motion.19
Usually, the former process
occurs at a lower frequency than the latter. Therefore,
the former and latter processes are considered to affect
T1ρ
and T1, respectively. When the relaxation of nuclei is caused by
ionic diffusion, T1
and T1ρ sometimes deviate from the Bloembergen,
Purcell and Pound (BPP) theory.20 Such deviations can be explained
by a distribution of correlation times. In this
case, T1 in a log(T1) ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. (1/T) plot and T1ρ in a log(
T1ρ)
s. (1/T) plot and T1ρ in a log(
T1ρ) ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. (1/T) plot show an asymmetric temperature dependence with a steeper slope on the high-temperature side of the minimum.21–23 We discuss
the distribution of the barrier height for ionic diffusion
in the γ phase calculated from 63Cu NMR T1ρ values. The ionic
diffusion in the α phase is also discussed on the basis of the
63Cu NMR T1 values.
s. (1/T) plot show an asymmetric temperature dependence with a steeper slope on the high-temperature side of the minimum.21–23 We discuss
the distribution of the barrier height for ionic diffusion
in the γ phase calculated from 63Cu NMR T1ρ values. The ionic
diffusion in the α phase is also discussed on the basis of the
63Cu NMR T1 values.
Experimental
The AgxCu1−xI crystals were prepared by the melt annealing method as described earlier.15–1763Cu and 127I NMR were measured with a CMX-300 spectrometer at 79.12 and 59.73 MHz, respectively. A single π/2 pulse and a (π/2)x–τ–(π/2)y–τ–acquisition pulse sequence were used for the measurements of the 63Cu and 127I NMR spectra, respectively. The T1 measurements were made by using the inversion recovery method in the temperature range 523–173 K. The π/2 pulse widths were 3 and 4 μs for 63Cu and 127I, respectively. τ was 30 μs. T1ρ was measured at a spin-locking rf field of 31 G in the γ phase.Results
63Cu NMR
The temperature dependences of the 63Cu NMR T1 and T1ρ are shown in Fig. 1. Below ca. 280 K, T1 and T1ρ are considered to be dominated by the lattice vibration, since T1 and T1ρ agreed well and were proportional to T−2. Above ca. 280 K, T1ρ decreased rapidly with increasing temperature and showed a minimum at ca. 360 K. In this temperature range, T1ρ is considered to be dominated by the fluctuation of the quadrupole interaction and the dipole interaction due to the hopping of a Cu ion.1 For all compounds, except x = 0.99, T1ρ deviated from BPP behavior and the slope of the temperature dependence of T1ρ became steeper on the high-temperature side of the minimum. In the case of x = 0.85, the activation energies estimated from the slope of the temperature dependence of T1ρ were 51 kJ mol−1 on the low-temperature side and 82 kJ mol−1 on the high-temperature side. These temperature dependences of T1ρ can be explained by the distribution of the correlation times which arises from the distribution of the activation energies for the diffusion of the Cu ions.21–23 Above ca. 400 K, T1 decreased rapidly with increasing temperature. For AgI and CuI, the defects increase the anomaly at temperatures approaching the transition to a superionic phase.1–6 Therefore, T1 is considered to be dominated by the fluctuation of the electric field gradient at the Cu nuclei due to the defect motion.1,19 The open circles in Fig. 1 show the temperature dependence of T1 in the α phase. T1 in the α phase was shorter than that in the γ phase and increased with increasing temperature. These results suggest that T1 is dominated by fast ionic diffusion in the α phase. | ||
| Fig. 1 Temperature dependences of 63Cu NMR T1 and T1ρ for AgxCu1−xI (x = 0.99–0.80). The open and the closed circles show T1 above and below Tc, respectively. The triangles show T1ρ. The solid and the broken lines show the theoretical fitting to the observed T1 and T1ρ, respectively. | ||
127I NMR
The 127I NMR spectrum could not be observed in the α phase. Fig. 2 shows the temperature dependence of 127I NMR T1 for the x = 0.99 compound. T1 was proportional to T−2 below ca. 280 K and decreased rapidly above ca. 300 K. 127I NMR T1 can be explained by fluctuation of the electric field gradient at the 127I nuclei due to lattice vibration and defect motion, in analogy with 63Cu NMR T1. Fig. 3 shows the ratio of T1 for 63Cu and 127I (T1(63Cu)/T1(127I)). Below ca. 280 K, where the lattice vibration is considered to dominate the relaxation of both nuclei, T1(63Cu)/T1(127I) was constant. Above ca. 300 K, T1(63Cu)/T1(127I) increased rapidly with increasing temperature. These results, which indicate that the defect motion affects more strongly the relaxation of 127I than that of 63Cu, are connected with the fact that the distance between the Ag or Cu defect and the I atom is shorter than that between the defect and the Cu atom in the regular site. | ||
| Fig. 2 Temperature dependence of 127I NMR T1 in the γ phase of Ag0.99Cu0.01I. The solid line shows the theoretical fitting to T1 below 280 K by using T1 = aT−2. | ||
 | ||
| Fig. 3 Temperature dependence of the ratio of 63Cu and 127I NMR T1 for Ag0.99Cu0.01I. | ||
Discussion
Motion of Cu ions and defects in the γ phase
In order to relate the results of 63Cu T1ρ and T1 to the dynamical properties of the diffusing ions and defects, we consider two relaxation processes. One is due to the hopping Cu ion. The hopping Cu ion undergoes fluctuations of the electric field gradient and the magnetic dipole field and these fluctuations cause the relaxation of the Cu nuclei. The other is caused by fluctuation of the electric field gradient at the 63Cu nuclei on the regular sites due to motion of the defect. In general, the fluctuation of the local field for the second process is faster than for the first process.1 Therefore, T1ρ and T1 are predicted to be sensitive to the two different processes. For the relaxation due to the hopping motion of the Cu ion, the correlation time τa corresponds to the time between hops of a Cu ion and assuming an Arrhenius relation can be expressed as

| (1) |
where τa0 and Ea are the correlation time at infinite temperature and the activation energy for the hopping motion of the Cu ion, respectively. When a distribution of τa is caused by a distribution of Ea, T1ρ is represented by21–23
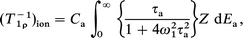
| (2) |
where Ca is the average change in the dipole and the quadrupole interactions for the Cu nuclei due to the hopping motion and ω1 is the locking rf frequency. For the present case, we assume a Gaussian distribution of Ea and the distribution function Z is written as21–23

| (3) |
where Em and Eb are the mean of the activation energies and the half width at half height of the distribution, respectively.
For the relaxation due to the motion of the defect, the correlation time τd is the time between hops of the defect and is connected with τa by1

| (4) |
where nd is the atomic fraction of defects. The relaxation rate due to the motion of the thermally generated defect, which dominates T1 on the high-temperature side in the γ phase, is written as21–23
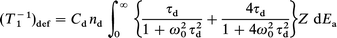
| (5) |
where Cd and ω0 are the average change in the quadrupole interaction for the 63Cu nuclei due to defect diffusion and the angular NMR frequency. The atomic fraction of thermally generated defects is represented by

| (6) |
where
ΔH is the enthalpy for the formation of the Frenkel defect.
Since nd![[double less-than, compressed]](https://www.rsc.org/images/entities/char_2aa1.gif) 1 holds in the γ phase,3–5ω0τd
1 holds in the γ phase,3–5ω0τd![[double less-than, compressed]](https://www.rsc.org/images/entities/char_2aa1.gif) 1 is predicted and eqn.
(5) is rewritten as19,21–23
1 is predicted and eqn.
(5) is rewritten as19,21–23

| (7) |
The contribution of the lattice vibration to T1 is written as

| (8) |
The temperature dependence of T1ρ and T1 can be explained by
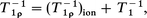
| (9) |

| (10) |
The fitting calculations of T1ρ and T1 were performed using eqn. (1)–(10) with Ca, τa0, Em, Eb, Cdnd*2, ΔH and a as parameters. The parameters which give the minimum of ∑[(log(T1)obs − log(T1)cal)2 + (log(T1ρ)obs − log(T1ρ)cal)2] were obtained by using the software package MultiSimplex for the optimization. The broken and the solid lines in Fig. 1 show the theoretical fitting curves for T1ρ and T1, respectively. The parameters obtained are shown in Table 1. The ΔH value obtained, which was almost constant at 120 ± 10 kJ mol−1, is comparable to those of the silver halides [AgCl (140 kJ mol−1), AgBr (110 kJ mol−1), β-AgI (79 kJ mol−1)].6,24 From a molecular dynamics (MD) study of β-AgI, ΔH for the octahedral site and the tetragonal site were obtained as 53 and 115 kJ mol−1, respectively.3–5 ΔH obtained by this work agrees with the latter value. In a similar manner to AgxCu1−xI (x = 0.99–0.80), the 63Cu NMR T1 for CuI decreased rapidly above ca. 400 K.1 Therefore, it is predicted that the 63Cu NMR T1 is mainly dominated by the dynamics of the defect in the tetrahedral site and the enthalpy for the formation of this defect is little affected by the different cations.
| Ag0.99Cu0.01I | Ag0.95Cu0.05I | Ag0.90Cu0.10I | Ag0.85Cu0.15I | Ag0.80Cu0.20I | |
|---|---|---|---|---|---|
| C a/s−2 | (3.0 ± 0.3) × 109 | (7.0 ± 0.5) × 109 | (8.0 ± 0.5) × 109 | (1.0 ± 0.2) × 1010 | (7.0 ± 0.5) × 109 |
| C d n d *2/s−2 | (4.0 ± 0.4) × 1023 | (1.0 ± 0.2) × 1024 | (4.0 ± 0.4) × 1022 | (1.2 ± 0.2) × 1023 | (7.5 ± 0.5) × 1022 |
| E m/kJ mol−1 | 70 ± 2 | 75 ± 2 | 75 ± 2 | 80 ± 2 | 80 ± 2 |
| E b/kJ mol−1 | ≃0 | 1.5 ± 0.2 | 2.5 ± 0.2 | 5.0 ± 0.5 | 5.5 ± 0.5 |
| τ a0/s | (1.5 ± 0.3) × 10−16 | (4.0 ± 0.5) × 10−17 | (5.0 ± 0.4) × 10−17 | (2.5 ± 0.5) × 10−17 | (3.0 ± 0.5) × 10−17 |
| ΔH/kJ mol−1 | 120 ± 5 | 125 ± 5 | 115 ± 5 | 125 ± 5 | 125 ± 5 |
| a/s−1 K−2 | (5.5 ± 0.3) × 10−4 | (5.5 ± 0.3) × 10−4 | (5.5 ± 0.3) × 10−4 | (5.0 ± 0.3) × 10−4 | (5.0 ± 0.3) × 10−4 |
Fig. 4 shows the distribution of Ea. Although the distribution of Ea was not seen in the x = 0.99 compound, the mean and width of the distribution of Ea for the other compounds increased gradually with increasing Cu concentration. These phenomena are considered to be closely related to the size of the cations. Since the ionic radius of the Cu ion is less than that of the Ag ion, the lattice constant of AgxCu1−xI decreases with increasing Cu concentration.15 Therefore, the decrease in the available space for ionic diffusion due to the increase in Cu concentration is predicted to cause the increase in the mean and the width of the activation energy. The diffusion constant DNMR was derived from τa0, Em and Eb using the equation
 | ||
| Fig. 4 Distribution of the activation energies (Ea) for the hopping of the copper ion in the γ phase. | ||

| (11) |

| (12) |
where 〈r2〉 is the mean square jump distance, which was estimated as 2.1 × 10−19 m2 from the distance between the nearest regular Ag ion sites in γ-AgI. Fig. 5 shows the temperature dependence of DNMR . The diffusion constant Dσ can be obtained from the electrical conductivity, using the Nernst–Einstein relation:
 | ||
| Fig. 5 Temperature dependence of the diffusion constant (DNMR) in the γ phase of AgxCu1−xI obtained from 63Cu NMR T1ρ. | ||
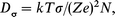
| (13) |
where σ, Ze and k are the conductivity, the charge of the diffusing ion and Boltzmann's constant, respectively. The number of diffusing ions per unit volume N was estimated as 1.5 × 1028 m−3 using the crystal structure of γ-AgI. From the value of the electrical conductivity for AgxCu1−xI (x = 1.0– 0.6) measured by Kusakabe et al.,14Dσ is found to be of the order of 10−14 m2 s−1 at 370 K. These results are in agreement with the value of DNMR. Dσ represents the total diffusion of the Ag and Cu ions, whereas DNMR is a constant for the diffusion of the Cu ion. The agreement of both constants suggests that the mobility of the Cu ion is nearly the same as that of the Ag ion in the γ phase.
Ionic diffusion in the α phase
The activation energy of the ionic diffusion in the α phase Eaα was obtained from the temperature dependence of T1 by assuming an Arrhenius relation. Eaα shows an almost constant value of 7 ± 1 kJ mol−1. The Eaα value obtained from the 63Cu NMR T1 was smaller than that (∽10 kJ mol−1) determined from the electrical conductivity.14 The result from the electrical conductivity measurements suggests that the activation energy of the Cu ion is the same as that of the Ag ion in the α phase.14 Therefore, the deviation is considered to reflect the difference between the ionic motions which are observed by NMR and by electrical conductivity. The correlation time of NMR is considered to be mainly dominated by short-range hopping in the α phase. On the contrary, the electrical conductivity is predicted to be determined by long-range diffusion of the Ag and Cu ions.Conclusions
(1) The distribution of the activation energy for diffusion of the Cu ion in the γ phase was studied by 63Cu NMR T1ρ. The mean and the width of the distribution for the activation energy increased with increasing Cu concentration.(2) The diffusion constant of the Cu ion in the γ phase was estimated from 63Cu NMR T1ρ. The agreement of the diffusion constants from 63Cu NMR and electrical conductivity measurement shows that the mobilities of the Cu and Ag ions are nearly the same in the γ phase.
(3) The rapid increase in the number of defects near the transition temperature to a superionic phase was confirmed by 63Cu NMR T1. The enthalpy of formation of the Frenkel defect in the γ phase of AgxCu1−xI (x = 0.99–0.80) was almost independent of the Cu concentration.
(4) The activation energy estimated from 63Cu NMR T1 in the α phase shows the barrier height for the short-range hopping of the cations.
References
- J. B. Boyce and B. A. Huberman, Solid State Commun., 1977, 21, 31 CrossRef CAS.
- S. Miyake, S. Hoshino and T. Takenaka, J. Phys. Soc. Jpn., 1952, 7, 19 Search PubMed.
- J.-S. Lee, S. Adams and J. Maier, J. Phys. Chem. Solids, 2000, 61, 1607 CrossRef CAS.
- F. Zimmer, P. Ballone, J. Maier and M. Parrinello, J. Chem. Phys., 2000, 112, 6416 CrossRef CAS.
- N. Hainovsky and J. Maier, Phys.
Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . B, 1995, 51, 15789 Search PubMed.
. B, 1995, 51, 15789 Search PubMed. - R. J. Cava and E. A. Rietman, Phys. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . B, 1984, 30, 6896 Search PubMed.
. B, 1984, 30, 6896 Search PubMed. - S. Hoshino, J. Phys. Soc. Jpn., 1957, 12, 315 Search PubMed.
- S. Hoshino, T. Sakuma and Y. Fujii, Solid State Commun., 1977, 22, 763 CrossRef CAS.
- W. Bührer and W. Hälg, Electrochim. Acta, 1977, 22, 701 CrossRef.
- M. Kusakabe, Y. Ito and S. Tamaki, J. Phys. Condens. Matter, 1996, 8, 6851 CrossRef CAS.
- M. Kusakabe, Y. Ito, M. Arai, Y. Shirakawa and S. Tamaki, Solid State Ionics, 1996, 86, 231 Search PubMed.
- M. Kusakabe, Y. Ito, M. Arai, Y. Shirakawa and S. Tamaki, Solid State Ionics, 1996, 92, 135 Search PubMed.
- M. Kusakabe, Y. Ito and S. Tamaki, J. Phys. Soc. Jpn., 1996, 65, 3220 Search PubMed.
- M. Kusakabe, Y. Shirakawa, S. Tamaki and Y. Ito, J. Phys. Soc. Jpn., 1995, 64, 170 Search PubMed.
- T. Ida, K. Endo, M. Suhara, M. Kenmotsu, K. Honda, S. Kitagawa and H. Kawabe, Bull. Chem. Soc. Jpn., 1999, 72, 2061 CrossRef CAS.
- K. Endo, T. Ida, J. Kimura, M. Mizuno, M. Suhara and K. Kihara, Chem. Phys. Lett., 1999, 308, 390 CrossRef CAS.
- J. Kimura, T. Ida, M. Mizuno, K. Endo, M. Suhara and K. Kihara, J. Mol. Struct., 2000, 522, 61 CrossRef CAS.
- J. Nölting, Ber. Bunsen-Ges. Phys. Chem., 1964, 68, 932 Search PubMed.
- M. H. Cohen and F. Reif, in Solid State Physics, ed. F. Seitz and D. Turnbull, Academic Press, New York, 1957, vol. 5, p. 321. Search PubMed.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys.
Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1948, 73, 679 Search PubMed.
., 1948, 73, 679 Search PubMed. - I. Svare, F. Borsa, D. R. Torgeson and S. W. Martin, Phys. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) .
B, 1993, 48, 9336 Search PubMed.
.
B, 1993, 48, 9336 Search PubMed. - S. Sen, A. M. George and J. F. Stebbins, J. Non-Cryst. Solids, 1996, 197, 53 Search PubMed.
- S. Sen and J. F. Stebbins, Phys. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . B, 1997, 55, 3512 Search PubMed.
. B, 1997, 55, 3512 Search PubMed. - J. K. Aboagye and R. J. Friauf, Phys.
Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1975, 11, 1654 Search PubMed.
., 1975, 11, 1654 Search PubMed.
| This journal is © the Owner Societies 2001 |
