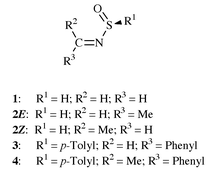
Theoretical investigation on the conformational preferences of sulfinimines
Prasad V. Bharatam*, Punam Uppal, Amita Kaur and Damanjit Kaur
Department of Chemistry, Guru Nanak Dev University, Amritsar, 143 005, India
First published on UnassignedUnassigned23rd December 1999
Abstract
The potential energy surfaces of sulfinimine, H2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) NS(O)H, 1, and methylsulfinimine, MeHC
NS(O)H, 1, and methylsulfinimine, MeHC![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) NS(O)H, 2, have been searched, using the ab initio MO and Density Functional Methods, to study the conformational preferences. Complete optimizations at HF/6-31G*, HF/6-31+G*, MP2/6-31+G* and B3LYP/6-31+G* levels on 1 showed that there are three minima on the path of rotation around N–S bond in 1. A conformer with synperiplanar arrangement, with the C–N–S–O torsional angle close to 13°, has been found to be the most preferred. Repulsions between the lone pairs of electrons present on N, S and O atoms are responsible for the observed conformational preferences of 1. The N–S bond rotational barrier in 1 is 9.16 kcal mol−1 at the B3LYP/6-31+G*(+ZPE) level. This high energy barrier can be attributed to the nN → σ*SO negative hyperconjugation and to the repulsive interactions between the lone pairs of electrons. The planar N-inversion barrier in 2Z is 18.72 kcal mol−1 at the B3LYP/6-31+G* (+ZPE) level, comparable to experimental values.
NS(O)H, 2, have been searched, using the ab initio MO and Density Functional Methods, to study the conformational preferences. Complete optimizations at HF/6-31G*, HF/6-31+G*, MP2/6-31+G* and B3LYP/6-31+G* levels on 1 showed that there are three minima on the path of rotation around N–S bond in 1. A conformer with synperiplanar arrangement, with the C–N–S–O torsional angle close to 13°, has been found to be the most preferred. Repulsions between the lone pairs of electrons present on N, S and O atoms are responsible for the observed conformational preferences of 1. The N–S bond rotational barrier in 1 is 9.16 kcal mol−1 at the B3LYP/6-31+G*(+ZPE) level. This high energy barrier can be attributed to the nN → σ*SO negative hyperconjugation and to the repulsive interactions between the lone pairs of electrons. The planar N-inversion barrier in 2Z is 18.72 kcal mol−1 at the B3LYP/6-31+G* (+ZPE) level, comparable to experimental values.
Introduction
Sulfinimines (thiooxime S-oxides, N-alkylidenesulfinamides)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 are important species belonging to the general class of N-sulfur binding imines, R2C
1 are important species belonging to the general class of N-sulfur binding imines, R2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) NS(O)nR (n = 0,1,2). There is current interest in these compounds
NS(O)nR (n = 0,1,2). There is current interest in these compounds![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2 with the recognition of their ability stereoselectively to produce amines
2 with the recognition of their ability stereoselectively to produce amines![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 3 and their application in the preparation of amino acids.4 Sulfinimines show exceptional facial selectivity apart from reactions with several nucleophiles.2–12 Sulfinimines are also found to be excellent intermediates for the preparation of asymmetric aziridines,6 which in turn are important starting materials for the preparation of alkaloids, amino acids, and β-lactam antibiotics, etc. One of the important reactions of aldehyde derived sulfinimines is to produce, on heating, sulfenic acids which are key intermediates in many biological transformations.7 Recycling of sulfinimines and removal of sulfinyl auxiliaries can readily be carried out under mild reaction conditions.8 In the recent past sulfinimines have been successfully employed in the synthesis of several types of amino acids,4,9
α-aminophosphonic acids,10 the taxol side chains,11 arylpyrrolines,12 azomethine ylides,5aetc.
3 and their application in the preparation of amino acids.4 Sulfinimines show exceptional facial selectivity apart from reactions with several nucleophiles.2–12 Sulfinimines are also found to be excellent intermediates for the preparation of asymmetric aziridines,6 which in turn are important starting materials for the preparation of alkaloids, amino acids, and β-lactam antibiotics, etc. One of the important reactions of aldehyde derived sulfinimines is to produce, on heating, sulfenic acids which are key intermediates in many biological transformations.7 Recycling of sulfinimines and removal of sulfinyl auxiliaries can readily be carried out under mild reaction conditions.8 In the recent past sulfinimines have been successfully employed in the synthesis of several types of amino acids,4,9
α-aminophosphonic acids,10 the taxol side chains,11 arylpyrrolines,12 azomethine ylides,5aetc.The N-sulfinyl auxiliary, S(:)(O)R group, in sulfinimines increases the electrophilicity of the N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C unit and also prevents competitive enolization of this unit.2 The dπ–pπ bonding between sulfur and N
C unit and also prevents competitive enolization of this unit.2 The dπ–pπ bonding between sulfur and N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) CR2 had been expected to be the origin of this increased electrophilicity.13a Davis et al. have suggested that conjugation between the C
CR2 had been expected to be the origin of this increased electrophilicity.13a Davis et al. have suggested that conjugation between the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N and the S
N and the S![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O bonds through the N–S bond is absent in sulfinimines, but localized p–d π interactions between nitrogen and sulfur are responsible for the transfer of electronic effects through the N–S bond.13 They also found that the localized p–d π interactions between nitrogen and sulfur are maximum when the nitrogen atom has sp2 character.13a If this p–d π interaction is important, the N–S single bond rotation in sulfinimines should be high and the charge distribution should show strong variations during rotation. Reed and Schleyer have shown that in N–S interactions of sulfenamides, and in hypervalent sulfur compounds, the d-orbital participation should not be invoked and the observed high barriers are due to negative hyperconjugation.14 The C–N–S–O unit in sulfinimine is often represented as if it has a synperiplanar (s-cis) arrangement. The stereo and facial selectivities observed in the reactions of sulfinimines have been explained assuming synperiplanar arrangement.3–6 Crystal structures of only two sulfinimines, 3 and 4, are known. 3 but not 4 has a synperiplanar arrangement. Is there any preference for the C–N–S–O unit of sulfinimine towards synperiplanar arrangement? If so, what is the origin of such a preference? What is the importance of negative hyperconjugation in these molecules? To address these questions and to understand the electron distribution in these molecules, we have performed quantum chemical calculations on 1 and studied the N–S bond rotational path in 1.
O bonds through the N–S bond is absent in sulfinimines, but localized p–d π interactions between nitrogen and sulfur are responsible for the transfer of electronic effects through the N–S bond.13 They also found that the localized p–d π interactions between nitrogen and sulfur are maximum when the nitrogen atom has sp2 character.13a If this p–d π interaction is important, the N–S single bond rotation in sulfinimines should be high and the charge distribution should show strong variations during rotation. Reed and Schleyer have shown that in N–S interactions of sulfenamides, and in hypervalent sulfur compounds, the d-orbital participation should not be invoked and the observed high barriers are due to negative hyperconjugation.14 The C–N–S–O unit in sulfinimine is often represented as if it has a synperiplanar (s-cis) arrangement. The stereo and facial selectivities observed in the reactions of sulfinimines have been explained assuming synperiplanar arrangement.3–6 Crystal structures of only two sulfinimines, 3 and 4, are known. 3 but not 4 has a synperiplanar arrangement. Is there any preference for the C–N–S–O unit of sulfinimine towards synperiplanar arrangement? If so, what is the origin of such a preference? What is the importance of negative hyperconjugation in these molecules? To address these questions and to understand the electron distribution in these molecules, we have performed quantum chemical calculations on 1 and studied the N–S bond rotational path in 1.
Sulfinimines with unsymmetrical substituents on carbon have been shown to be capable of existing as rapidly equilibrating E/Z mixtures, because the planar inversion barrier is only 13–17 kcal mol−1.1,2,14 This is much lower than the N-inversion barrier in methanimine (≈30 kcal mol−1).15a The observed small inversion barriers have been attributed to the p–d π interactions in the transition state.14 The sulfinimines derived from aldehydes are expected to exist only in their E conformation.1,2 Though initially this stability has been attributed to the intramolecular hydrogen bonding,1 later based on crystal structure data such a possibility was ruled out.2 Since the d–p π interactions are shown to be unimportant by Reed and Schleyer,14 what are the reasons for the low N-inversion barriers in sulfinimines? We have been working on the N-inversion barriers, and C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N rotational barriers of several imines and related compounds, to understand the electron distribution in these molecules.15 In continuation of our efforts, to understand the inversion barriers in sulfinimines and the origin of the preference of the E isomer in the aldehyde based sulfinimines, we have performed quantum chemical calculations on 2 and studied the N-inversion process.
N rotational barriers of several imines and related compounds, to understand the electron distribution in these molecules.15 In continuation of our efforts, to understand the inversion barriers in sulfinimines and the origin of the preference of the E isomer in the aldehyde based sulfinimines, we have performed quantum chemical calculations on 2 and studied the N-inversion process.
Computational details
Ab initio![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 16 and Density Functional (DFT)
16 and Density Functional (DFT)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 17 calculations have been carried out using the GAUSSIAN 94W
17 calculations have been carried out using the GAUSSIAN 94W![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 18 package, the windows version of GAUSSIAN 94 suite of programs, on an IBM compatible PC Pentium-100MHz with 64 MB memory and 1 GB disk space. Complete optimizations have been performed on sulfinimine, 1 methylsulfinimine, 2, their rotational and E/Z isomerization conformers and corresponding transition states using the HF/6-31G*
18 package, the windows version of GAUSSIAN 94 suite of programs, on an IBM compatible PC Pentium-100MHz with 64 MB memory and 1 GB disk space. Complete optimizations have been performed on sulfinimine, 1 methylsulfinimine, 2, their rotational and E/Z isomerization conformers and corresponding transition states using the HF/6-31G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 19 basis set. Since these molecules possess four lone pairs and that too on adjacent atoms, inclusion of diffuse functions in the basis set is important
19 basis set. Since these molecules possess four lone pairs and that too on adjacent atoms, inclusion of diffuse functions in the basis set is important![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 16 and hence all the structures have completely been optimized at HF/6-31+G* level also. To study the effect of electron correlation on the geometries and energies, full optimizations have been performed using MP2/6-31+G* and the density functional method,17 defining the exchange functionals according to Becke’s three parameter formulation (B3)
16 and hence all the structures have completely been optimized at HF/6-31+G* level also. To study the effect of electron correlation on the geometries and energies, full optimizations have been performed using MP2/6-31+G* and the density functional method,17 defining the exchange functionals according to Becke’s three parameter formulation (B3)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 20a,b and the correlation functionals according to the Lee, Yang, Parr (LYP) formulation
20a,b and the correlation functionals according to the Lee, Yang, Parr (LYP) formulation![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 20c,d and using the 6-31+G* basis set. Frequencies were computed analytically for all optimized species at HF/6-31G* and HF/6-31+G* levels in order to characterize each stationary point as a minimum or a transition state and to determine the zero point vibrational energies (ZPEs).21 The ZPE values obtained at HF/6-31G* and HF/6-31+G* levels have been scaled by factors of 0.9135 and 0.9153 respectively.22 Atomic charges in all the molecules were obtained using the Natural Population Analysis (NPA) method
20c,d and using the 6-31+G* basis set. Frequencies were computed analytically for all optimized species at HF/6-31G* and HF/6-31+G* levels in order to characterize each stationary point as a minimum or a transition state and to determine the zero point vibrational energies (ZPEs).21 The ZPE values obtained at HF/6-31G* and HF/6-31+G* levels have been scaled by factors of 0.9135 and 0.9153 respectively.22 Atomic charges in all the molecules were obtained using the Natural Population Analysis (NPA) method![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 23 within the Natural Bond Orbital (NBO) model using HF/6-31+G* geometries and MP2/6-31+G** densities to understand the electron distribution in these molecules. Semi-empirical AM1 calculations
23 within the Natural Bond Orbital (NBO) model using HF/6-31+G* geometries and MP2/6-31+G** densities to understand the electron distribution in these molecules. Semi-empirical AM1 calculations![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 24 have been performed on 1–4 using the MOPAC package.25 The geometrical parameters obtained at HF/6-31+G* level and the energies obtained at B3LYP/6-31+G* (+ZPE) level will be used in the discussion unless otherwise specifically mentioned.
24 have been performed on 1–4 using the MOPAC package.25 The geometrical parameters obtained at HF/6-31+G* level and the energies obtained at B3LYP/6-31+G* (+ZPE) level will be used in the discussion unless otherwise specifically mentioned.Results and discussion
Structures and charges
Theoretical calculations on 1 at various levels have been performed to select a suitable method for sulfinimines and the results are reported in Table 1. Here, the study is mainly focused on the synperiplanar arrangement of 1 because it is the most stable arrangement on the S–N rotational path (see below). The N–S and S![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O bond distances are found to be highly sensitive to the method used. The N–S and S–O bond distances are very large when d orbitals are not included in the basis set. After including the d orbitals in the form of polarization functions (HF/6-31+G*), the N–S and S–O distances became comparable to those reported for 3 and 4 using crystallographic methods (Table 2).2,26 After including the electron correlation, using the MP2, B3LYP and B3PW91 methods, the N–S and S–O distances became longer, due to the overestimation of the repulsive interactions between the lone pairs on N, S and O.27 The important geometrical data of 1, 2E and 2Z are given in Fig. 1. A comparison of the important geometric parameters of 1, 2E, 2Z (obtained using the HF/6-31+G* method) with the crystal structure data of 3 and 4 is given in Table 2, which shows excellent agreement.
O bond distances are found to be highly sensitive to the method used. The N–S and S–O bond distances are very large when d orbitals are not included in the basis set. After including the d orbitals in the form of polarization functions (HF/6-31+G*), the N–S and S–O distances became comparable to those reported for 3 and 4 using crystallographic methods (Table 2).2,26 After including the electron correlation, using the MP2, B3LYP and B3PW91 methods, the N–S and S–O distances became longer, due to the overestimation of the repulsive interactions between the lone pairs on N, S and O.27 The important geometrical data of 1, 2E and 2Z are given in Fig. 1. A comparison of the important geometric parameters of 1, 2E, 2Z (obtained using the HF/6-31+G* method) with the crystal structure data of 3 and 4 is given in Table 2, which shows excellent agreement.
| Method | NS–S3 | S3–O4 | N2–S3–O4 | C1–N2–S3–H5 | C1–N2–S3–O4 | Total energy |
|---|---|---|---|---|---|---|
| HF/3-21G | 1.826 | 1.653 | 104.9 | 118.3 | 9.4 | −563.368522 |
| HF/6-31G | 1.834 | 1.704 | 105.7 | 119.6 | 12.9 | −566.152387 |
| HF/6-31+G | 1.831 | 1.714 | 105.6 | 120.0 | 14.6 | −566.163415 |
| B3LYP/6-31+G | 2.038 | 1.686 | 102.9 | 112.4 | 7.8 | −567.865456 |
| HF/3-21G* | 1.695 | 1.475 | 110.3 | 122.0 | 11.4 | −563.546194 |
| HF/6-31G* | 1.700 | 1.469 | 111.3 | 122.4 | 12.9 | −566.329301 |
| HF/6-31+G* | 1.699 | 1.473 | 111.1 | 122.3 | 13.7 | −566.338033 |
| MP2/6-31+G* | 1.761 | 1.507 | 112.1 | 122.6 | 14.2 | −566.947879 |
| B3LYP/6-31+G* | 1.769 | 1.505 | 112.3 | 121.7 | 13.3 | −567.995342 |
| B3PW91/6-31+G* | 1.751 | 1.500 | 112.4 | 121.9 | 13.5 | −567.876556 |
| Parameter | 1![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 2E![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 2Z![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 3![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | 4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c |
|---|---|---|---|---|---|
| a Theoretical values obtained at the HF/6-31+G* level.b From the supplementary material of ref. 2.c From ref. 26.d Implied from the text of ref. 2. | |||||
C1![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N2 N2 | 1.254 | 1.257 | 1.258 | 1.271 | 1.282 |
| N2–S3 | 1.699 | 1.695 | 1.684 | 1.704 | 1.714 |
S3![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O4 O4 | 1.473 | 1.475 | 1.475 | 1.474 | 1.484 |
| S3–H5 | 1.339 | 1.339 | 1.336 | — | — |
O4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) H6 H6 | 2.398 | 2.371 | — | 2.376 | — |
| C1–N2–S3 | 117.1 | 117.5 | 126.0 | 116.6 | 119.6 |
| N2–S3–O4 | 111.1 | 111.3 | 114.8 | 111.8 | 103.4 |
| N2–S3–H5(or C5) | 91.3 | 91.6 | 90.6 | — | 97.1 |
| C1–N2–S3–O4 | 13.7 | 13.7 | 26.3 | ≈0![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) d d | 158.0 |
| C1–N2–S3–H5 | 122.3 | 122.3 | 134.4 | — | 91.9 |
 | ||
| Fig. 1 Important geometric parameters and numbering scheme of sulfinimine 1, and methylsulfinimine 2E, 2Z, and the transition state for the N-inversion (2tsi) between 2E and 2Z at various levels of ab initio calculations. Distances are in Å and angles in °. The C–N–S–O and C–N–S–H torsional angles are represented as ω1 and ω2 respectively. | ||
The dihedral angle between the C–N–S and the N–S–O planes in 1 is in the range of 7.8–14.6° at various levels of theory (Table 1). Similarly, the C–N–S–O torsional angles in 2E and 2Z at HF/6-31+G* level are 13.7 and 26.3° respectively (Table 2). The small torsional angles of 1 and 2 are comparable to those of the reported crystal structure of 3, shown to have s-cis arrangement.2 Stable structures of 1–4 have been studied using the semi-empirical AM1 method. These calculations show C–N–S–O torsional angles of 8.9, 7.0, 3.2, 23.0° for 1–4 respectively. The N–S bond lengths in 1, 2E and 2Z respectively are 1.699, 1.695 and 1.684 Å (Fig. 1). These values are only slightly shorter than the N–S single bond distance (1.709 Å) in H2N–SH, and are much longer than the N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) S double bond distance (1.537 Å) in HN
S double bond distance (1.537 Å) in HN![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) S, both obtained at HF/6-31+G* level. The N–S bond distances in 1, 2E and 2Z are slightly longer than the N–S single bond length in (1.677 Å) in sulfinamide, H2N–S(O)H at HF/6-31+G* level.15e This indicates that the N–S bond in sulfinimines is of the order of a single bond only.
S, both obtained at HF/6-31+G* level. The N–S bond distances in 1, 2E and 2Z are slightly longer than the N–S single bond length in (1.677 Å) in sulfinamide, H2N–S(O)H at HF/6-31+G* level.15e This indicates that the N–S bond in sulfinimines is of the order of a single bond only.
To understand the electron distribution in these molecules, we have performed atomic charge calculations on 1, 2E and 2Z using the NPA method; the atomic charges are given in Table 3. From the data it is clear that the sulfur atom has a strong positive charge (more than 1 unit) in all the molecules. This is because two electronegative elements are attached to the highly polarizable sulfur. The oxygen atom is highly electron dense, the charge on it being close to unity in all the structures. This clearly indicates that the S–O bond in sulfinimines is strongly polarized. The S–O interaction may be described as a single bond with an additional electrostatic interaction between the two atoms. This is consistent with similar observations in sulfoxides, sulfonium ylides and sulfilimines.28 The charges on the hydrogen atoms attached to sulfur in 1 and 2 are only slightly positive whereas those on hydrogen atoms attached to carbon are strongly positive. This indicates that the sulfur atom does not pull electron density from the hydrogen in spite of the strong positive charge on itself. This might originate from the large size of the sulfur atom.
| Atom/group | 1 | 2E | 2Z | 2tsi |
|---|---|---|---|---|
| C1 | −0.114 | 0.103 | 0.124 | 0.196 |
| N2 | −0.615 | −0.666 | −0.678 | −0.781 |
| S3 | 1.774 | 1.241 | 1.241 | 1.319 |
| O4 | −0.940 | −0.974 | −0.981 | −0.978 |
| H5 | 0.065 | 0.054 | 0.061 | 0.049 |
| H6 | 0.210 | 0.211 | 0.212 | 0.182 |
| H7/Me | 0.217 | 0.032 | 0.021 | 0.013 |
N–S Rotational barriers
To understand the origin for the preference of synperiplanar arrangement in sulfinimines,3–6 we have studied the N–S bond rotational process in 1.15e Complete optimizations at HF/6-31G*, HF/6-31+G* and B3LYP/6-31+G* levels showed that there are three minima corresponding to three rotamers of sulfinimine, 1, along the N–S bond rotational path. Using the AM1, HF/6-31+G and B3LYP/6-31+G levels, however, we could not locate any N–S bond rotamer for 1. The geometric parameters of the rotamers, 1r1 (same as 1), 1r2, 1r3, and the three transition states on the N–S bond rotational path 1tsr1, 1tsr2, 1tsr3 obtained at HF/6-31+G* are given in Table 4. The absolute energies and ZPE values obtained at various levels are given in Table 5 and the relative energies in Table 6. Fig. 2 shows the potential energy surface for the N–S bond rotational path at various levels. There is a potential well around the rotational structure 1r1, on the potential energy surface as can be seen from Fig. 2 and Table 6. The N–S bond rotamers 1r2 and 1r3 are 8.90 and 7.20 kcal mol−1 higher in energy compared to 1. The rotamer 1r3 has only a transient existence as indicated by the very small barrier of 0.01 kcal mol−1 at HF/6-31+G* level to go to the rotamer 1r1.29 The application of ZPE correction results in negative barrier for the conversion of 1r2 to 1r1. This only reconfirms the transient existence of 1r1. Though rotamer 1r2 is relatively more stable, the barrier heights for the conversion into 1r1 (0.30 kcal mol−1) and 1r3 (0.88 kcal mol−1) are very small. These small values indicate that 1r2 and 1r3 are thermodynamically unstable.| Parameter | 1r1 | 1tsr1 | 1r2 | 1tsr2 | 1r3 | 1tsr3 |
|---|---|---|---|---|---|---|
| a The C–N–S–O torsional angle shows that this is actually in the range of anticlinal. | ||||||
C1![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N2 N2 | 1.251 | 1.253 | 1.251 | 1.251 | 1.254 | 1.255 |
| N2–S3 | 1.698 | 1.712 | 1.699 | 1.713 | 1.719 | 1.720 |
S3![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O4 O4 | 1.473 | 1.471 | 1.467 | 1.463 | 1.467 | 1.469 |
| S3–H5 | 1.339 | 1.350 | 1.351 | 1.344 | 1.338 | 1.337 |
| C1–H6 | 1.089 | 1.084 | 1.085 | 1.087 | 1.084 | 1.084 |
| C1–H7 | 1.077 | 1.078 | 1.078 | 1.077 | 1.078 | 1.078 |
| C1–N2–S3 | 117.1 | 118.2 | 120.3 | 118.5 | 114.4 | 114.3 |
| N2–S3–O4 | 111.1 | 108.4 | 108.3 | 108.2 | 108.6 | 108.8 |
| N2–S3–H5 | 91.3 | 95.4 | 96.0 | 94.3 | 91.5 | 91.5 |
| H6–C1–N2 | 123.3 | 124.2 | 124.3 | 124.7 | 124.1 | 124.2 |
| H7–C1–N2 | 118.1 | 118.7 | 118.8 | 118.7 | 118.7 | 118.7 |
| C1–N2–S3–O4 | −13.7 | 75.9 | 111.6 | 164.4 | 245.2 | 256.1 |
| C1–N2–S3–H5 | −122.3 | 327.6 | 2.5 | 55.7 | 137.1 | 148.0 |
| H6–C1–N2–S3 | −2.5 | 1.7 | −2.7 | ![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) −3.4 −3.4 | ![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) −0.9 −0.9 | ![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) −1.2 −1.2 |
| H7–C1–N2–S3 | 178.0 | 181.9 | 177.7 | 176.8 | 179.0 | 178.6 |
 | ||||||
| Compound | HF/6-31+G | B3LYP/6-31+G | HF/6-31G* | HF/6-31+G* | MP2/6-31+G* | B3LYP/6-31+G* | ZPE![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a |
|---|---|---|---|---|---|---|---|
| a Obtained at the HF/6-31+G* level and scaled by 0.9153.22 | |||||||
| 1r1 | −566.163415 | −567.865456 | −566.329301 | −566.338033 | −566.947879 | −567.995342 | 28.28 |
| 1r2 | −566.314057 | −566.323203 | −566.932785 | −567.981107 | 27.87 | ||
| 1r3 | −566.316765 | −566.326103 | −567.983794 | 27.99 | |||
| 1tsr1 | −566.143586 | −567.845731 | −566.313138 | −566.322610 | −566.932096 | −567.979994 | 27.81 |
| 1tsr2 | −566.312138 | −566.321303 | −566.931122 | −567.980017 | 27.57 | ||
| 1tsr3 | −566.316607 | −566.326082 | −567.983516 | 27.91 | |||
| Compound | HF/6-31+G![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | B3LYP/6-31+G![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | HF/6-31G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | HF/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | MP2/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | B3LYP/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a |
|---|---|---|---|---|---|---|
| a Corrected using ZPE obtained at HF/6-31+G*.b Corrected using ZPE obtained at the same level as that of optimization. | ||||||
| 1r1 | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) | 0.00 (0.00) |
| 1r2 | 9.57 (9.11) | 9.31 (8.90) | 9.47 (9.06) | 8.93 (8.52) | ||
| 1r3 | 7.87 (7.58) | 7.49 (7.20) | 7.25 (6.96) | |||
| 1tsr1 | 10.14 (9.46) | 9.68 (9.20) | 9.90 (9.43) | 9.63 (9.16) | ||
| 1tsr2 | 12.44 (11.73) | 12.37 (11.66) | 10.77 (9.99) | 10.50 (9.78) | 10.51 (9.80) | 9.62 (8.91) |
| 1tsr3 | 7.97 (6.91) | 7.50 (7.12) | 7.42 (7.05) | |||
 | ||
Fig. 2 Potential energy surface for the N–S bond rotational process in sulfinimine, 1, obtained at HF/6-31G* (—), HF/6-31+G* (.........), B3LYP/6-31+G* (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ), MP2/6-31+G*//HF/6-31+G* (- - - -) levels. ), MP2/6-31+G*//HF/6-31+G* (- - - -) levels.
| ||
1tsr2 with antiperiplanar arrangement has highest energy on the PE surface. 1tsr1 with lone pairs on nitrogen and sulfur cis to each other also is equally high in energy. The N–S rotational barriers at HF/6-31G*, HF/6-31+G*, MP2/6-31+G*//HF/6-31+G* and MP2/6-31+G* levels respectively are 10.77, 10.50, 10.55 and 10.51 kcal mol−1. At the B3LYP/6-31+G* level the barrier has been reduced to 9.62 kcal mol−1. After including the ZPE corrections, the values are slightly reduced. At the B3LYP/6-31+G*(+ZPE) level, 1tsr1 becomes the highest energy transition state. When the d-orbital participation is not included (i.e. at HF/6-31+G, B3LYP/6-31+G levels) the N–S bond rotational barriers are about 12.4 kcal mol−1. If p–d π interactions are present along the N–S bond, the N–S bond rotational barriers should increase after inclusion of the d orbitals in the basis set. Inclusion of the d orbitals in the form of polarization functions decreases the rotational barrier. This indicates that N–S p–d π interactions are absent in sulfinimines.
The calculated N–S rotational barriers are high compared to single bond rotations of many other bonds. An analysis of the geometrical features of the most stable rotamers of 5–7 (Fig. 3) indicates that the lone pairs on nitrogen and sulfur try to be farthest apart, as in 5.15e But when oxygen atoms are involved, structures with the lone pair on N and the oxygen atom trans are found to be most stable. Houk et al. have reported the conformational PE surface of N-methylmethanesulfonamide.30a They also have observed that when the nitrogen lone pair is further away from the oxygen lone pairs unfavorable electrostatic interactions are reduced and such a structure is preferred even though it has an eclipsed arrangement.30a Considering this, it may be concluded that in sulfinimines a structure with lowest repulsive interactions between the lone pair on nitrogen and the negatively charged oxygen should be preferred and that is the reason why 1 and 2 have synperiplanar arrangements. In addition, in 1r1, nN → σ*SO negative hyperconjugation![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 14 is present, which gives partial double bond character to the structure. The presence of negative hyperconjugation is evident from the smaller N–S distances, larger N–S–O bond angles and larger N–S bond polarization in 1r1 as compared to the rotamers 1r2 and 1r3. The energy of stabilization due to the anomeric effect in 1 has been estimated using isodesmic eqn. (1). The stabilization energies at HF/6-31+G*, MP2/6-31+G* and B3LYP/6-31+G* levels respectively are 2.60, 6.20 and 4.94 kcal mol−1.
14 is present, which gives partial double bond character to the structure. The presence of negative hyperconjugation is evident from the smaller N–S distances, larger N–S–O bond angles and larger N–S bond polarization in 1r1 as compared to the rotamers 1r2 and 1r3. The energy of stabilization due to the anomeric effect in 1 has been estimated using isodesmic eqn. (1). The stabilization energies at HF/6-31+G*, MP2/6-31+G* and B3LYP/6-31+G* levels respectively are 2.60, 6.20 and 4.94 kcal mol−1.
 | ||
| Fig. 3 Important geometrical parameters of the most stable arrangements of sulfenamide, 5, sulfinamide, 6, and sulfonamide, 7, obtained at HF/6-31+G* level. Distances are in Å and angles are in °. | ||
H2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N–S(O)R + NH3 → H2N–S(O)R + H2C N–S(O)R + NH3 → H2N–S(O)R + H2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) NH NH | (1) |
In 1r1 the C–N–S–O torsional angle is −13.7°. When this torsional angle was forced to be 0.0° an increase in energy up to 0.7 kcal mol−1 was observed. The deviation from complete planarity might be due to the repulsions between the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N unit and the S–O unit of the sulfinimines. If repulsions between the C
N unit and the S–O unit of the sulfinimines. If repulsions between the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N and S–O unit are the only reason for this deviation, a structure with a C–N–S–O torsional angle of about +13.7° also should have been observed on the PE surface. However, such an arrangement would increase the proximity of the lone pairs on nitrogen and sulfur and becomes unstable. Hence, a trade off among various repulsive interactions between the lone pairs of electrons on N, S and O and the anomeric effect provides a semi-rigid C–N–S–O backbone for sulfinimines, giving a synperiplanar arrangement, which is responsible for the facial selectivity and stereoselectivity observed in the reactions. The S–N rotational barrier in sulfinimine 1 is higher than that in sulfinamide 6 by about 1.3 kcal mol−1 at the HF/6-31+G* level.15e This higher barrier might originate from the in plane π character induced by the nN → σ*SO negative hyperconjugation in 1 which is absent in 6. In conclusion, there is an out-of-plane C
N and S–O unit are the only reason for this deviation, a structure with a C–N–S–O torsional angle of about +13.7° also should have been observed on the PE surface. However, such an arrangement would increase the proximity of the lone pairs on nitrogen and sulfur and becomes unstable. Hence, a trade off among various repulsive interactions between the lone pairs of electrons on N, S and O and the anomeric effect provides a semi-rigid C–N–S–O backbone for sulfinimines, giving a synperiplanar arrangement, which is responsible for the facial selectivity and stereoselectivity observed in the reactions. The S–N rotational barrier in sulfinimine 1 is higher than that in sulfinamide 6 by about 1.3 kcal mol−1 at the HF/6-31+G* level.15e This higher barrier might originate from the in plane π character induced by the nN → σ*SO negative hyperconjugation in 1 which is absent in 6. In conclusion, there is an out-of-plane C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N π bond, in-plane N–S π character due to negative hyperconjugation in 1 and because these two interactions are in orthogonal planes no C–N–S π delocalization should be expected.
N π bond, in-plane N–S π character due to negative hyperconjugation in 1 and because these two interactions are in orthogonal planes no C–N–S π delocalization should be expected.
Inversion barriers
In simple sulfinimines the N-inversion and C–N rotation processes go through same transition state and hence the two processes are indistinguishable. The transition state for inversion in 1, i.e.1tsi, could be located only at the HF/6-31G* level.31 To obtain a clear understanding of the inversion process in sulfinimines we have performed calculations on methylsulfinimine, 2, where the geometrical isomers 2E and 2Z can be clearly distinguished.31 The absolute energies of 2E, 2Z, and 2tsi are given in Table 7 and the relative energies are given in Table 8. The Z isomer is 4.68 kcal mol−1 higher in energy than the E isomer. The energy difference between 2E and 2Z can mainly be attributed to the repulsions between the Me and S(O)H groups in 2Z. The N2–C1–C7 angles in 2E and 2Z at HF/6-31+G* level are 121.5 and 131.7° respectively. Similarly, the C1–N2–S3 angles in 2E and 2Z respectively are 117.5 and 126.0° (Fig. 1). There is a large increase (Table 9) in these two angles as the molecule flips from 2E to 2Z. This is due to the increased repulsions between the Me and S(O)H groups in the 2Z arrangement.| Method | 2E | 2Z | 2tsi |
|---|---|---|---|
a A scaling factor of 0.9153 has been used![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 22 on the values calculated using the HF/6-31+G* level. NIF = Number of imaginary frequencies. 22 on the values calculated using the HF/6-31+G* level. NIF = Number of imaginary frequencies. | |||
| HF/6-31+G | −605.195836 | −605.188599 | −605.144107 |
| HF/6-31G* | −605.375659 | −605.367155 | −605.331358 |
| HF/6-31+G* | −605.384832 | −605.375927 | −605.341654 |
| MP2/6-31G*//HF/ | −606.121885 | −606.113324 | −606.078140 |
| 6-31+G* | |||
| MP2/6-31+G**// | −606.163799 | −606.155281 | −606.120032 |
| HF/6-31+G* | |||
| MP2/6-31+G* | −606.126576 | −606.117851 | −606.082429 |
| B3LYP/6-31+G* | −607.322206 | −607.314783 | −607.283602 |
ZPE![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a (NIF) a (NIF) | 45.41 (0) | 45.43 (0) | 44.50 (1) |
| Method | 2E → 2Z | 2E → 2tsi | 2Z → 2tsi |
|---|---|---|---|
| a ZPE values obtained at the HF/6-31+G* level.b ZPE values obtained at the same level as that of optimization. | |||
HF/6-31+G![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 4.54 (4.50) | 32.46 (31.66) | 27.92 (27.16) |
HF/6-31G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | 5.34 (5.37) | 27.80 (26.98) | 22.46 (21.61) |
HF/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | 5.59 (5.61) | 27.09 (26.27) | 21.50 (20.66) |
MP2/6-31+G*//HF/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 5.37 (5.39) | 27.45 (26.63) | 22.08 (21.24) |
MP2/6-31+G**//HF/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 5.34 (5.36) | 27.46 (26.64) | 22.11 (21.27) |
MP2/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 5.47 (5.49) | 27.70 (26.79) | 22.23 (21.30) |
B3LYP/6-31+G*![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 4.66 (4.68) | 24.22 (23.40) | 19.56 (18.72) |
| Geometrical Parameters | Atomic charges | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | 2Z → 2tsi | 2E → 2tsi | 2E → 2Z | Atom | 2E → 2Z | 2E → 2tsi | 2Z → 2tsi |
C1![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N2 N2 | −0.021 | −0.021 | 0.001 | C1 | 0.021 | 0.093 | 0.072 |
| N2–S3 | −0.082 | −0.093 | −0.011 | N2 | −0.013 | −0.116 | −0.103 |
S3![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O4 O4 | −0.010 | −0.010 | 0.000 | S3 | 0.000 | 0.078 | 0.078 |
| C1–N2–S3 | 54.0 | 62.5 | 8.5 | O4 | −0.007 | −0.003 | 0.004 |
| N2–S3–O4 | −0.9 | 2.6 | 3.5 | H5 | 0.008 | −0.004 | −0.012 |
| H6–C1–N2 | 5.8 | −1.3 | −7.1 | H6 | 0.002 | −0.028 | −0.030 |
| C7–C1–N2 | −6.7 | 3.5 | 10.2 | C7 | −0.034 | −0.015 | 0.019 |
| C1–N2–S3–O4 | −70.4 | −57.8 | 12.6 | H8 | −0.001 | 0.003 | 0.004 |
| C1–N2–S3–H5 | −70.5 | −58.4 | 12.1 | H9 | 0.020 | −0.004 | −0.024 |
| H6–C1–N2–S3 | 68.6 | −112.3 | 179.1 | H10 | 0.004 | −0.004 | −0.007 |
| C7–C1–N2–S3 | 68.8 | −112.2 | −180.9 | ||||
The structural features of 2tsi, the transition state connecting the minima 2E and 2Z are given in Fig. 1.32 The C1–N2–S3 angle in 2tsi is close to 180°. In 2tsi the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N, N–S, S–O bond lengths have been reduced in comparison to those of 2E (Table 9). This is a consequence of the change of hybridization around N from sp2 to sp, which increases the s character on the nitrogen and thus the electronegativity of N in 2tsi. Analysis of the atomic charge data indicates that there is an alternative charge localization in 2tsi in comparison to that of 2E (Table 9), i.e. the positive charges on C and S and the negative charges on N and O have increased appreciably. Hence, the reduction in the C
N, N–S, S–O bond lengths have been reduced in comparison to those of 2E (Table 9). This is a consequence of the change of hybridization around N from sp2 to sp, which increases the s character on the nitrogen and thus the electronegativity of N in 2tsi. Analysis of the atomic charge data indicates that there is an alternative charge localization in 2tsi in comparison to that of 2E (Table 9), i.e. the positive charges on C and S and the negative charges on N and O have increased appreciably. Hence, the reduction in the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N, N–S, S–O bond distances can be attributed to the increased coulombic attractions between neighboring atoms.
N, N–S, S–O bond distances can be attributed to the increased coulombic attractions between neighboring atoms.
The inversion barrier in 2E to give 2Z is calculated to be about 27.80 kcal mol−1 at the HF/6-31G* level. After including diffuse functions on non-hydrogen atoms, the inversion barrier is slightly reduced to 27.09 kcal mol−1. Inclusion of electron correlation increases the inversion barrier to 27.45 kcal mol−1 at the MP2/6-31+G*//HF6-31+G* level. Complete optimizations at the MP2/6-31+G* level do not improve the situation. However, the density functional methods at the B3LYP/6-31+G* level reduce the inversion barrier to 24.22 kcal mol−1. After including the ZPE corrections, the inversion barriers are reduced at all levels. The inversion barriers for the reverse process, i.e.2Z → 2tsi → 2E, are 21.30 and 18.72 kcal mol−1 at MP2/6-31+G* (+ZPE) and B3LYP/6-31+G* (+ZPE) levels respectively. 2E may be considered as a model for the aldehyde derived sulfinimines, where a hydrogen atom is cis to the sulfinyl group along the C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N axis and 2Z may be taken as a model for the unsymmetrical sulfinimines
N axis and 2Z may be taken as a model for the unsymmetrical sulfinimines![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2 where a non-hydrogen group is cis to the sulfinyl group. Hence, the energy difference between 2Z and 2tsi can be compared to the planar inversion barriers reported for the unsymmetrical sulfinimines using the NMR coalescence methods.2 The theoretically obtained inversion barriers become comparable to the experimentally observed inversion barriers (13–17 kcal mol−1) at the B3LYP/6-31+G* optimization level.
2 where a non-hydrogen group is cis to the sulfinyl group. Hence, the energy difference between 2Z and 2tsi can be compared to the planar inversion barriers reported for the unsymmetrical sulfinimines using the NMR coalescence methods.2 The theoretically obtained inversion barriers become comparable to the experimentally observed inversion barriers (13–17 kcal mol−1) at the B3LYP/6-31+G* optimization level.
In the absence of d-orbital participation as in the HF/6-31+G level, the inversion barrier is high (32.46 kcal mol−1). This indicates that the d orbitals on sulfur play an important role in reducing the N-inversion barriers in sulfinimines as suggested from the experimental observations.14 The reduction in the N–S distance during inversion is quite large in 2tsi in comparison to 2E and 2Z. This might be due to the formation of additional π bonds in 2tsi. To estimate the extent of additional π interactions we have calculated N–S rotational barriers in 2tsi by performing partial optimization calculations at MP2/6-31+G and MP2/6-31+G* levels. The N–S rotation barrier at the MP2/6-31+G level is 11.08 kcal mol−1 and is associated with an increase in the N–S distance by 0.51 Å. After including the d-orbital participation, the N–S rotation barrier increased to about 16.11 kcal mol−1 (ΔN–S = 0.056 Å). This indicates that, in 2tsi, p–d π interactions are present and these stabilize the inversion transition state causing a reduction in the N-inversion barriers in sulfinimines in comparison to simple imines.
The O4![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) H6 non-bonded distance in 1 is 2.398 Å and in 2E it is 2.371 Å. In 3, crystal data show that the non-bonded H
H6 non-bonded distance in 1 is 2.398 Å and in 2E it is 2.371 Å. In 3, crystal data show that the non-bonded H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O distance is 2.376 Å,2 indicating a good agreement between the experimental and theoretical data. Davis et al. have argued that “this non-bonded distance is too large for there to be any hydrogen bonding interaction”.2 O4 is highly negatively charged and H6 is reasonably positively charged. Hence, it is possible that there is some non-bonded electrostatic interaction between the two atoms. Table 10 lists the atomic charges on H6 and O4 in 1 and 1tsr2 and variation in them as a function of the N–S bond rotation. During rotation the negative charge on O4 and the positive charge on H6 decreases, indicating that the electrostatic interaction which is present in 1 gets disrupted on rotation. It should be noted that the H6 in aldehyde derived sulfinimines is not attached to an electronegative element like oxygen but attached to a carbon atom, which is a very weak hydrogen bond donor. The C–H
O distance is 2.376 Å,2 indicating a good agreement between the experimental and theoretical data. Davis et al. have argued that “this non-bonded distance is too large for there to be any hydrogen bonding interaction”.2 O4 is highly negatively charged and H6 is reasonably positively charged. Hence, it is possible that there is some non-bonded electrostatic interaction between the two atoms. Table 10 lists the atomic charges on H6 and O4 in 1 and 1tsr2 and variation in them as a function of the N–S bond rotation. During rotation the negative charge on O4 and the positive charge on H6 decreases, indicating that the electrostatic interaction which is present in 1 gets disrupted on rotation. It should be noted that the H6 in aldehyde derived sulfinimines is not attached to an electronegative element like oxygen but attached to a carbon atom, which is a very weak hydrogen bond donor. The C–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O hydrogen bonding interactions are known in the literature and the hydrogen bond distances in such cases have been reported to be in the range of 2.2–2.9 Å.33 The observed H6
O hydrogen bonding interactions are known in the literature and the hydrogen bond distances in such cases have been reported to be in the range of 2.2–2.9 Å.33 The observed H6![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O4 distances in 1, 2E and 3 are within the expected range of C–H
O4 distances in 1, 2E and 3 are within the expected range of C–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O hydrogen bond distances and are close to the H
O hydrogen bond distances and are close to the H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O van der Waals distances (2.2 to 2.4 Å) indicating the possibility of electrostatic interactions. The expected stabilization due to such interaction is in the order of 1–2 kcal mol−1 only.29 Formation of sulfenic acids from aldehyde derived sulfinimines on heating (Scheme 1) can be explained only when there is some electrostatic interaction between the H and O atoms.1b Hence, the observed preference for the aldehyde derived sulfinimines to show E conformation might be attributed to this electrostatic interaction in addition to the minimization of steric repulsions in this configuration.
O van der Waals distances (2.2 to 2.4 Å) indicating the possibility of electrostatic interactions. The expected stabilization due to such interaction is in the order of 1–2 kcal mol−1 only.29 Formation of sulfenic acids from aldehyde derived sulfinimines on heating (Scheme 1) can be explained only when there is some electrostatic interaction between the H and O atoms.1b Hence, the observed preference for the aldehyde derived sulfinimines to show E conformation might be attributed to this electrostatic interaction in addition to the minimization of steric repulsions in this configuration.
| Atomic charges | |||
|---|---|---|---|
| Atom | 1r1 | 1tsr2 | Variation 1r1 → 1tsr2 |
| O4 | −0.973 | −0.948 | 0.025 |
| H6 | 0.206 | 0.171 | −0.035 |
 | ||
| Scheme 1 | ||
The crystal structure of 3 has a synperiplanar arrangement whereas 4 does not. The difference between the two is only a Me group attached to the iminic carbon atom. From the studies on 2Z it is clear that the bulky Me group causes an increase in the C–N–S–O torsional angle due to the steric interactions between Me and S(O)H. Considering the structure of 4, we have tried to locate the N–S bond rotamers of 2Z at HF/6-31+G* and AM1 levels: all our efforts proved futile. Dihedral angle constrained optimizations on 2E and 2Z do not show any other minima. Similarly we could not locate any N–S bond rotamers on the PE surface of 4 using the AM1 method. This indicates that, under the gas phase conditions, only the synperiplanar arrangement is preferred for sulfinimines. However, in the solid phase, crystal lattice forces are present in addition to the possibility of intermolecular interactions.34 These additional forces might result in stability of an isomer of 4 with non-synperiplanar arrangement.
Conclusion
The structural aspects of sulfinimine, 1, and methylsulfinimine, 2, the N–S bond rotational isomers of 1, the E/Z isomerization pathway of 2 and the charge distribution in them have been studied using ab initio and DFT methods. The geometrical parameters for 1 and 2 obtained at the HF/6-31+G* level match well with the crystallographic results for 3 and 4. There are three minima on the N–S bond rotational path, but two of them can only have a transient existence. The N–S bond rotational barrier in 1 is 9.16 kcal mol−1 at the B3LYP/6-31+G* (+ZPE) level. Sulfinimines have a natural tendency to prefer a semi rigid synperiplanar arrangement. The origin of this preference can be attributed to (1) the repulsions among the lone pairs of electrons present on the N, S and O atoms, (2) the nN → σ*SO negative hyperconjugation and (3) the intramolecular C–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) O electrostatic interactions (only in the case of sulfinimines derived from aldehyde). The semi rigidity of the C–N–S–O unit is responsible for the stereoselectivity and facial selectivity of sulfinimines.
O electrostatic interactions (only in the case of sulfinimines derived from aldehyde). The semi rigidity of the C–N–S–O unit is responsible for the stereoselectivity and facial selectivity of sulfinimines.The N-inversion barrier in 2Z is calculated to be 18.72 kcal mol−1 at the B3LYP/6-31+G* (+ZPE) level which is comparable to the experimental values. The inversion barriers in sulfinimines are smaller as compared to simple imines. This is due to (1) the lowering of the transition state because of increased d orbital participation in addition to the increased coulombic interactions and (2) the destabilization of the ground state because of increased steric repulsions as a function of the size of the R group cis to the sulfinyl group. Atomic charge calculations show that the S–O bond is strongly polar. The sulfinyl group in sulfinimines polarizes the C–N bond while withdrawing electrons through the inductive effect; this leads to the Michael acceptor character of sulfinimines.
Acknowledgements
The authors acknowledge the critical comments given by one of the reviewers, which helped in improving the quality of the paper. P. V. B. and D. J. K. thank Department of Science and Technology, New Delhi for research grant. P. U. thanks Council for Scientific and Industrial Research, New Delhi for a Senior Research Fellowship.References
- (a) F. A. Davis, A. J. Friedman and E. W. Kluger, J. Am. Chem. Soc., 1974, 96, 5000 CrossRef CAS; (b) F. A. Davis, A. J. Friedman and U. K. Nadir, J. Am. Chem. Soc., 1978, 100, 2844 CrossRef CAS.
- F. A. Davis, R. E. Reddy, J. M. Szewczyk, G. V. Reddy, P. S. Portonova, H. Zhang, D. Fanelli, R. T. Reddy, P. Zhou and P. J. Carrol, J. Org. Chem., 1997, 62, 2555 CrossRef CAS supplementary material and refs. therein.
- (a) R. Annunziata, M. Cinquini and F. Cozzi, J. Chem. Soc., Perkin Trans. 1, 1982, 339 RSC; (b) D. H. Hua, S. W. Miao, J. S. Chen and S. Iguchi, J. Org. Chem., 1991, 56, 4 CrossRef CAS; (c) D. R. J. Hose, M. F. Hahon, K. C. Molloy, T. Raynham and M. Wills, J. Chem. Soc., Perkin Trans. 1, 1996, 691 RSC; (d) T.-K. Yang, R.-Y. Chen, D.-S. Lee, W.-S. Peng, Y.-Z. Jiang, A.-Q. Mi and T.-T. Jong, J. Org. Chem., 1994, 59, 914 CrossRef CAS.
- F. A. Davis, P. Zhou and B.-C. Chen, Chem. Soc. Rev., 1998, 27, 13 RSC and refs. therein..
- (a) A. Viso, R. F. de la Pradilla, C. Guerrero-Strachan, M. Alonosa, M. Martinez-Ripoll and I. Andre, J. Org. Chem., 1997, 62, 2316 CrossRef CASand refs. therein; (b) K. Burger, J. Albanbauer, F. Kafig and S. S. Penninger, Liebigs Ann. Chem., 1977, 624 Search PubMed; (c) T. Yoshida, S. Naruto, H. Uno and H. Nishimura, Chem. Pharm. Bull., 1982, 30, 2820 Search PubMed; (d) M. Cinquini and F. Cozzi, J. Chem. Soc., Chem. Commun., 1977, 723 RSC.
- J. L. G. Ruano, I. Fernandez, M. d. P. Catalina and A. A. Cruz, Tetrahedron: Asymmetry, 1996, 7, 3407 CrossRef CAS; J. L. G. Ruano, I. Fernandez and C. Hamdouchi, Tetrahedron Lett., 1995, 36, 295 CrossRef CAS; F. A. Davis, G. V. Reddy and H. Liu, J. Am. Chem. Soc., 1995, 117, 3651 CrossRef CAS; F. A. Davis, P. Zhou and G. V. Reddy, J. Org. Chem., 1994, 59, 3243 CrossRef CAS; F. A. Davis and P. Zhou, Tetrahedron Lett., 1994, 35, 7525 CrossRef CAS; F. A. Davis, P. Zhou, C. H. Liang and R. E. Reddy, Tetrahedron: Asymmetry, 1995, 6, 1511 CrossRef CAS; F. A. Davis and G. V. Reddy, Tetrahedron Lett., 1996, 37, 4349 CrossRef CAS; F. A. Davis, H. Liu and G. V. Reddy, Tetrahedron Lett., 1996, 37, 5473 CrossRef CAS.
- For leading references on the chemistry of sulfenic acids see F. A. Davis, L. A. Jenkins and R. L. Billimers, J. Org. Chem., 1986, 51, 1033 Search PubMed.
- F. A. Davis, R. E. Reddy and J. M. Szewczyk, J. Org. Chem., 1995, 60, 7037 CrossRef CAS.
- For leading references on the synthesis of amino acids using sulfinimines see refs. 3(b), 4, 8 also ref. 11 below and F. A. Davis, P. S. Portonova, R. E. Reddy and Y.-H. Chiu, J. Org. Chem., 1996, 61, 440 Search PubMed; J. Jiang, K. Schumacher, M. M. Joullie, F. A. Davis and R. E. Reddy, Tetrahedron Lett., 1994, 35, 2121 CrossRef CAS; F. A. Davis, J. Szewczyk and R. E. Reddy, J. Org. Chem., 1996, 61, 2222 CrossRef CAS; T. Fujisawa, Y. Kooriyama and M. Shimizu, Tetrahedron Lett., 1996, 37, 3881 CrossRef CAS; F. A. Davis and R. E. Reddy, Tetrahedron: Asymmetry, 1994, 5, 955 CrossRef CAS.
- M. Mikalajczyk, P. Lyzwa, J. Drabowicz, M. W. Wieczorek and J. Blaszczyk, Chem. Commun., 1996, 1503 RSC; I. M. Lefebvre and S. A. Evans, J. Org. Chem., 1997, 62, 7532 CrossRef CAS.
- F. A. Davis, T. R. Reddy and R. E. Reddy, J. Org. Chem., 1992, 57, 6387 CrossRef CAS.
- T. Balasubramanian and A. Hassner, J. Org. Chem., 1996, 37, 5755 CrossRef CAS.
- (a) F. A. Davis, J. M. Kaminski, E. W. Kluger and H. S. Freilich, J. Am. Chem. Soc., 1975, 97, 7085 CrossRef CAS; (b) F. A. Davis and E. W. Kluger, J. Am. Chem. Soc., 1976, 98, 302 CrossRef CAS.
- A. E. Reed and P. v. R. Schleyer, J. Am. Chem. Soc., 1987, 109, 7362 CrossRef CAS; Inorg. Chem., 1988, 27, 3696. Search PubMed; J. Am. Chem. Soc., 1990, 112, 1434. Search PubMed.
- (a) The N-inversion barriers in methanimine are 31.14 and 30.28 kcal mol−1 at HF/6-31+G* and MP2/6-31+G*//HF/6-31+G* levels respectively; ; (b) K. Lammertsma and B. V. Prasad, J. Am. Chem. Soc., 1994, 116, 642 CrossRef; (c) B. V. Prasad, P. Uppal and P. S. Bassi, Chem. Phys. Lett., 1997, 276, 31 CrossRef CAS; (d) B. V. Prasad, G. Grover, P. Uppal and D. Kaur, J. Mol. Struct. (THEOCHEM), 1999, 458, 227 CrossRef CAS; (e) B. V. Prasad , P. Uppal and D. Kaur , unpublished results; ; (f) B. V. Prasad , S. Kumar and M. P. Mahajan , Tetrahedron, 1998 Search PubMedsubmitted for publication..
- W. J. Hehre , L. Radom , P. v. R. Schleyer and J. A. Pople , Ab Initio Molecular Orbital Theory, Wiley-Interscience, New York, 1986; Search PubMed; J. B. Foresman and E. Frisch , Exploring Chemistry with Electronic Structure Methods, Gaussian Inc., Pittsburgh, 2nd edn., 1996. Search PubMed.
- R. G. Parr and W. Yang , Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989; Search PubMed; L. J. Bartolotti and K. Fluchick , in Reviews in Computational Chemistry, vol. 7, eds. K. B. Lipkowitz and D. B. Boyd, VCH, New York, 1996, pp. 187–216. Search PubMed.
- Gaussian 94, Revision B.2, M. J. Frisch , G. W. Trucks , H. B. Schlegel , P. M. W. Gill , B. G. Johnson , M. A. Robb , J. R. Cheeseman , T. Keith , G. A. Petersson , J. A. Montgomery , K. Raghavachari , M. A. Al-Laham , V. G. Zakrzewski , J. V. Ortiz , J. B. Foresman , C. Y. Peng , P. Y. Ayala , W. Chen , M. W. Wong , J. L. Andres , E. S. Replogle , R. Gomperts , R. L. Martin , D. J. Fox , J. S. Binkley , D. J. Defrees , J. Baker , J. P. Stewart , M. Head-Gordon , C. Gonzalez and J. A. Pople , Gaussian, Inc., Pittsburgh, PA, 1995. Search PubMed.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213 CrossRef CAS.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1980, 37, 785 CrossRef; (d) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- J. S. Binkley and J. A. Pople, Int. J. Quantum Chem., 1975, 9, 229 CrossRef CAS; J. A. Pople and J. S. Binkley, Int. J. Quantum Chem. Symp., 1976, 10, 1 Search PubMed.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS; A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- M. J. S. Dewar, E. G. Zoebisch and E. F. Healy, J. Am. Chem. Soc., 1985, 107, 3902 CrossRef.
- MOPAC semi-empirical package obtained from Quantum Chemistry Program Exchange (QCPE No. 455), Indiana University, Bloomington, IN..
- P. D. Robinson, D. H. Hua, J. S. Chen and S. Saha, Acta Crystallogr., Sect. C, 1991, 47, 594 CrossRef.
- G. Böttger, A. Geisler, R. Fröhlich and E.-U. Würthwein, J. Org. Chem., 1997, 62, 6407 CrossRef.
- G. H. Whitham , Organosulfur Chemistry, Oxford Science Publications, Oxford, 1995. Search PubMed.
- Using complete optimizations at MP2/6-31+G* level, 1r3 and 1tsr3 could not be located on the PE surface. All attempts to locate these structures using the Eigenvalue Following (EF) procedures also failed to find them. Finally as shown in Fig. 2, partial optimization with constrained CNSO dihedral angles also failed to show any minimum corresponding to 1r3..
- (a) J. L. Radkiewicz, M. A. Michael, E. Goldstein and K. N. Houk, J. Org. Chem., 1998, 63, 1419 CrossRef CAS; (b) S. Lacombe, M. Loudet, A. Dargelos and E. Robert-Banchereau, J. Org. Chem., 1998, 63, 2281 CrossRef CAS.
- The calculations at HF/6-31+G*, B3LYP/6-31+G* and MP2/6-31+G* levels did not lead to any such stationary point. This may be a limitation of the optimization procedure. The important geometric parameters of 1tsi obtained at the HF/6-31G* level are C–N 1.232, N–S 1.607, S–O 1.458 Å, N–S–O 114.7°, C–N–S 180.05°, C–N–S–O 138.0° and C–N–S–H 246.9°. Normal mode analysis of the negative frequency of 1tsi (at HF/6-31G* level) and 2tsi (at HF/6-31G*level) showed vibration corresponding to N-inversion and C
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N rotation..
N rotation.. - The structural features of 2tsi do appear to connect 2E and 2Z. We have tried to locate other possible structures of 2tsi. All other apparently possible structures converged to 2tsi on complete optimization.
- G. R. Desiraju, Acc. Chem. Res., 1991, 24, 290 CrossRef CAS.
- R. D. Bindal, J. T. Golab and J. A. Katzenellenbogen, J. Am. Chem. Soc., 1990, 112, 7861 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2000 |