Kinetic investigation of the reduction of pinacolone by borane catalyzed by oxazaborolidines in THF. Hydride shift as rate determining step

Abstract

The kinetics of the reduction of the ketone pinacolone (P) by borane (B) catalyzed by the oxazaborolidines (OAB) (S)-1-methyl-3,3-diphenylperhydropyrrolo[1,2-c][1,3,2]oxazaborolidine and (S)-2,4-dimethyl-3,3-diphenyl-1,3,2-oxazaborolidine have been studied in THF. The findings are discussed in comparison with the kinetic results obtained previously for the same reaction using two different OABs as catalysts (C). The reaction order in the ketone P changes in the series of OABs from first-order to zero-order. This surprising behaviour excludes the addition of P to the binary complex C–B forming the ternary complex P–C–B as the rate determining step. However, the kinetic data are consistently explained if the intramolecular hydride shift in P–C–B with subsequent rearrangement leading to the complex of monoalkoxyborane and catalyst is assumed to be rate determining. The rate equations of the catalytic reactions of the four OABs, the corresponding ee values, and apparent activation energies are given.

---

Introduction

The development in organic chemistry during the last decades has led to various methods for asymmetric synthesis.^1–5 One of them is the reduction of prochiral ketones catalyzed by oxazaborolidines (OAB).^1,6 This reaction is widely used due to its very high enantioselectivity and excellent ee. Itsuno et al. started working with OABs in 1981 and used them to introduce defined chirality to alcohols.^7–13 A little later Corey et al. developed a conclusive mechanism for the OAB catalyzed reaction.^1,14,15 Since this time there have even been attempts to immobilize OABs on polymeric supports.^16–20 Borane sources other than BH₃–THF have also been examined.^20–27 The principal intermediates of the reaction sequence are known from experimental ^{6,14,15,28–33} as well as theoretical investigations.^6,28,34–41 However, the rate determining step of the catalytic reaction is still unknown. The addition of the ketone to the borane–catalyst complex forming a ternary complex or the subsequent hydride shift are assumed to determine the rate of the catalytic process.^1,25,38

Few kinetic studies investigating the dependence of the reaction rate on the concentrations of catalyst and reagents, which could give further insight into the mechanism of the catalyzed reaction, have been published, although such information is also of particular interest for finding the optimum reaction conditions. Recently, we published the first detailed kinetic study on the reduction of a ketone by borane catalyzed by oxazaborolidines in THF.⁴² The direct, uncatalyzed reduction, which competes with the catalytic cycle leading to a decrease in enantioselectivity, was also investigated.⁴³ Pinacolone was used as prochiral ketone, (S)-1-phenyl-3,3-diethylperhydropyrrolo[1,2-c][1,3,2]oxazaborolidine 1a and (S)-1,3,3-triphenylperhydropyrrolo[1,2-c][1,3,2]oxazaborolidine 1b as catalysts, see Scheme 1. It was shown by the analysis of the kinetic data that the reaction of ketone P and binary complex catalyst–borane leading to the complex catalyst–monoalkoxyborane is rate determining with both OABs. Actually this reaction consists of the reaction steps ketone addition, hydride shift, and rearrangement. Based on the kinetic data, however, it was not possible to distinguish which of the single steps is rate determining. In order to increase our knowledge about the OAB catalyzed reduction of ketones, we extended the kinetic investigations and report in the present paper our results with (S)-1-methyl-3,3-diphenylperhydropyrrolo[1,2-c][1,3,2]oxazaborolidine 1c and (S )-4-methyl-2,5,5-triphenyl-1,3,2-oxazaborolidine 1d, see Scheme 1.

Scheme 1

Results and discussion

Rates of reaction

Borane (B) exists in THF (T) as a 1∶1 BH₃–THF complex (= B–T).^44–49 In our previous investigations we observed that the direct borane reduction of pinacolone (P) as well as the catalyzed reduction occurred much slower if we used freshly prepared, pure B–T instead of commercial B–T as reducing agent.⁴³ It was shown that a contaminant, the stabilizer NaBH₄ of the commercial reagent, leads to a change in the reaction kinetics and to much faster reactions. Therefore, we performed all our further experiments with pure B–T.^50,51Fig. 1 shows representative kinetic traces of the overall reaction of P with B–T in the presence of catalyst (C) OAB 1c at 20 °C.

Fig. 1 Kinetic traces of the reduction of P by borane in THF catalyzed by OAB 1c at 20 °C. [C]_o = 0.0025 mol dm⁻³; [B–T]_o = 0.405 (upper trace), 0.115 mol dm⁻³ (lower trace).

The time required for 50% conversion of the ketone in the presence of the overall concentration [C]_o = 0.0025 mol dm⁻³ of OAB catalyst 1c amounts to τ_1/2 = 11 s at [B/T]_o = 0.405 mol dm⁻³ and to 29 s at [B/T]_o = 0.115 mol dm⁻³. Without catalyst the corresponding conversions of P require about 460 and 1600 s. Thus, a strong acceleration of the reaction is caused already at this low concentration of OAB 1c. A closer look at Fig. 1 demonstrates that both kinetic curves distinctly deviate from first-order behavior. The reaction rates are almost constant in the beginning and decrease distinctly only after about 50% conversion of P. In this respect we notice a significant difference from OABs 1a and 1b, for which the reaction was in a good approximation first-order in the ketone P. With OAB 1c, however, the reaction is between zero-order and first-order in P. An even stronger shift in the direction of zero-order kinetics is observed with OAB 1d. As is demonstrated by the kinetic traces of Fig. 2, the reaction rates decrease only slightly during almost the complete course of reaction until about 95% of P is consumed.

Fig. 2 Kinetic traces of the reduction of P by borane in THF catalyzed by OAB 1d at 20 °C. [C]_o = 0.0050 mol dm⁻³; [B–T]_o = 0.455 mol dm⁻³.

Because of the approximate zero-order character of the reaction, the time required for 50% conversion of P changes strongly with the initial concentration [P]_i. At [C]_o = 0.0050 mol dm⁻³ of OAB 1d and [B/T]_o = 0.455 mol dm⁻³τ_1/2 amounts to 60 s for [P]_i = 0.134 mol dm⁻³ and to only 7.5 s for [P]_i = 0.016 mol dm⁻³ at 20 °C. Without catalyst the corresponding conversion of P is achieved after about 410 s. Again, we observe a strong acceleration of the reaction, which is, however, weaker than in the case of OAB 1c.

The lack of first-order kinetics prevents the determination of rate constants. Instead, reaction rates r = −d[P]/dt have been determined as slopes of linear least squares fits to the kinetic traces, describing the consumption of P over about 25% conversion of P with OAB 1c and 50% conversion of P with OAB 1d. The direct reduction of P by B–T, competing with the actual catalytic process, is considered by calculation of the corresponding rate r_d = k_d f[P]_i[B–T]_o with k_d = 0.0037 dm³ mol⁻¹ s⁻¹ (20 °C).⁴³ The factors f = 0.9 (OAB 1c) and f = 0.75 (OAB 1d) indicate that the mean concentration of P in the linear range of the reaction rate is lower than [P]_i. Thus, we obtain the rate of the catalytic reaction as r_c = r − r_d. The importance of the correction by r_d generally increases with increasing [P]_i, [B–T]_o and decreasing [C]_o. The ratio r_d/r ranges only from 0.01 to 0.08 for OAB 1c, but becomes important with 0.01 ≤ r_d/r ≤ 0.4 for OAB 1d.

Kinetic scheme

It was previously shown by us that the following three reactions R1 to R3 with corresponding rate constants k₁ to k₃ (20 °C) are sufficient for a simulation of the experimental kinetic curves of the direct borane reduction by numerical integration.⁴²

B–T + P → M–T k₁ = 0.0037 dm³ mol⁻¹ s⁻¹ (R1)

M–T + P → D–T k₂ = 0.003 dm³ mol⁻¹ s⁻¹ (R2)

2 M–T → D–T + B–T k₃ = 0.2 dm³ mol⁻¹ s⁻¹ (R3)

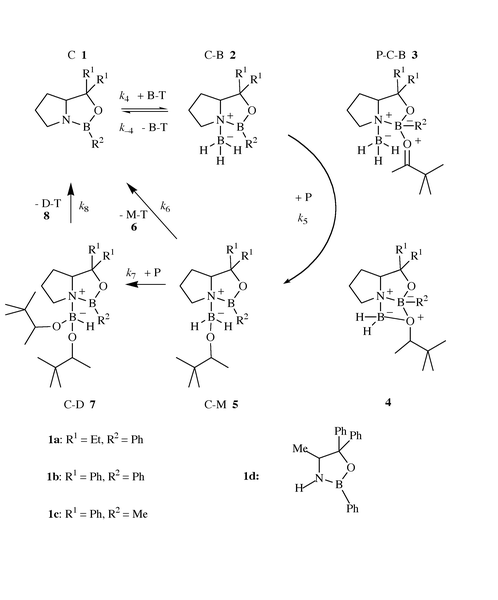
M–T represents the monoalkoxyborane–THF complex derived from P (M = mono(3,3-dimethyl-2-butoxy)borane). D–T is the corresponding dialkoxyborane complex. Dialkoxyboranes are the only reaction products formed in the direct borane reduction of ketones.^28,52 The distribution reaction to trialkoxyborane is too slow and must therefore not be considered.^43,53 Reaction R1 describes the main part of the overall direct reduction of P. Scheme 1 presents a simplified catalytic cycle for the reduction, which considers the results of experimental and theoretical studies and which proved to be sufficient to interpret the results with OABs 1a and 1b.

The reversible addition of borane to the catalyst C 1 forms the complex C–B 2 in reaction R4. It has been shown by NMR spectroscopy of solutions of C–B in THF ¹⁵ and by single-crystal X-ray spectroscopy of solid C–B ^28,33 that BH₃ is coordinated to the nitrogen atom of the OAB ring in C–B. Since the lone pair electrons of the nitrogen can no longer be shared with the boron atom of the heterocycle, the acidity of the boron atom of the OAB ring is distinctly increased in C–B relative to C.¹ The ketone P couples with the sterically better accessible free electron pair of the oxygen to the electrophilic ring-boron of C–B to form the ternary complex P–C–B 3.^1,32,34 It is generally accepted that hydride transfer occurs from the NBH₃ unit of P–C–B to the carbonyl carbon via a six-membered cyclic transition state.^{1,14,15,31,40} The hereby formed intermediate 4 rearranges to yield the monoalkoxyborane adduct C–M of the oxazaborolidine catalyst. Since we observed only very small spectral changes in the reaction spectra of the catalytic cycle, we assume for the complex C–M in THF at room temperature structure 5, which is very similar to the structure 2 of complex C–B.⁴² C–M reacts with THF and dissociates into C and M–T 6 in reaction R6 or adds and reduces a second ketone molecule and yields the dialkoxyborane adduct C–D 7 in the reaction sequence R7, which is very similar to the first reaction sequence R5 of the catalytic cycle. Finally, C–D reacts with T and dissociates into C and D–T 8. Thus, in addition to the direct borane reduction reactions R4 to R8 had to be considered for a quantitative description of the kinetics.⁴²

C + B–T ⇌ C–B + T K₄ = k₄/k₋₄ (R4)

C–B + P → C–Mk₅ (R5)

C–M + T → C + M–Tk₆ (R6)

C–M + P → C–Dk₇ (R7)

C–D + T → C + D–Tk₈ (R8)

Besides k₁, k₂, and k₃ the rate constants k₄ and k₋₄ and thus the equilibrium constant K₄ of the borane addition of the catalyst had been determined for OAB 1b.⁴² Based on these known constants it was actually possible to resolve the experimental kinetics by numerical integration, since experimental kinetic traces had been recorded in dependence of [B/T]_o, [C]_o and [P]_i.⁴² It was shown by the analysis of the numerical integration data that reaction R5 is rate determining in the catalytic process. Actually, R5 is a reaction sequence which is composed of several steps, the addition of P to C–B 2 yielding P–C–B 3, and the hydride shift to 4 with subsequent rearrangement of 4 forming C–M 5. Eqn. (1) was derived for the rate r_c of the catalyzed reaction, which was found to be first-order in P with OABs 1a and 1b.

r_c = k₅(K₄/[T])[B–T]_o[P][C]_o/{1 + (K₄/[T])[B–T]_o} (1)

Already Figs. 1 and 2 reveal that the catalytic reaction is not first-order in P with OABs 1c and 1d. Thus, we notice distinct changes in the reaction kinetics of the OAB catalyzed reduction of P by B–T. We have no reason to assume important changes in the kinetic scheme of the catalytic cycle, if we compare OABs 1a and 1b with 1c and 1d. However, the graduated shift from first-order kinetics to zero-order kinetics in P demonstrates that the addition of P to C–B forming the ternary complex P–C–B cannot be the rate determining step. Thus, the intramolecular hydride shift in the ternary complex P–C–B with subsequent rearrangement forming C–M must be rate determining. Therefore, it is necessary to split reaction R5 into reaction R5a, the reversible addition of P to C–B, and reaction R5b, the rate determining hydride shift with subsequent rearrangement producing C–M.

C–B + P ⇌ P–C–BK_5a (R5a)

P–C–B → C–Mk_5b (R5b)

If C–M reacts much faster than it is formed, then a stationary state is established, in which reaction R5b is rate determining. Then, the rate k_5b[P–C–B] becomes equal to the rate r_c of the OAB catalyzed consumption of P. Since we put together hydride shift and rearrangement in one reaction R5b, the result of the formal kinetic treatment would be the same if the last step, the rearrangement, but not the hydride shift were rate determining which, however, appears to be less realistic. P–C–B is formed in the two coupled equilibrium reactions R4 and R5a. As long as the conditions [P] ≫ [C]_o, [B–T]_o ≫ [C]_o and [B–T]_o ≪ [T] = 12.3 mol dm⁻³ hold true, the equilibrium concentration [P–C–B] and the rate r_c of the catalytic reaction are described by eqns. (2) and (3), respectively.

[P–C–B] = (K₄/[T])[B–T]_oK_5a[P][C]_o/{1 + (K₄/[T])[B–T]_o(1 + K_5a[P])} (2)

r_c = k_5b(K₄/[T])[B–T]_oK_5a[P][C]_o/{1 + (K₄/[T])[B–T]_o(1 + K_5a[P])} (3)

Eqn. (3) simplifies with k₅ = k_5bK_5a to Eqn. (1), if K_5a[P] ≪ 1. Then, the catalyzed reaction becomes first-order in P, as was actually found with OABs 1a and 1b. Eqn. (1) is also derived if the addition of P to C–B is the rate determining step. Thus, we realize that we cannot distinguish on the basis of the kinetics which is first-order in P and follows Eqn. (1), whether the addition of P to C–B or the subsequent hydride shift is the rate determining step. However, since we observe a shift in direction to zero-order kinetics in P with OABs 1c and 1d, the addition of P to C–B cannot be rate determining. Instead, the hydride shift with subsequent rearrangement has to be assumed to be rate determining. Eqn. (3) but not Eqn. (1) can describe a kinetics which is zero-order in P.

The spectrophotometric determination of K₄, k₄ and k₋₄ failed for the OABs 1c and 1d, since the spectral changes following the addition of borane are too fast and/or too small to be measured with sufficient accuracy with our stopped-flow apparatus. Furthermore, the kinetic scheme becomes more complex with the replacement of reaction R5 by the reactions R5a and R5b. Thus, it is not surprising that the kinetics of the reduction of P catalyzed by OABs 1c and 1d cannot be resolved by numerical integration. Therefore, we will discuss the kinetic data in the following paragraphs on the basis of eqn. (3).

Kinetics of the reduction of P catalyzed by OAB 1c

Eqn. (3) describes the variation of r_c with the overall concentrations of C and B–T as well as the concentration of P. Fig. 3 illustrates the dependence of r_c on [C]_o for constant [B–T]_o and [P]_i = 0.11 mol dm⁻³.

Fig. 3 Rates of the catalyzed reaction as a function of the overall catalyst concentration, OAB 1c. [P]_i = 0.11 mol dm⁻³; [B–T]_o = 0.62, 0.405, 0.23, 0.115 mol dm⁻³ (from top to bottom).

The experiments performed with [B–T]_o = 0.405 and 0.23 mol dm⁻³ and varying catalyst concentrations demonstrate that actually a linear correlation exists, i.e., the reaction is first-order in catalyst. Thus, it is reasonable to analyze in the further discussion rates of the catalyzed reaction, which are normalized to the catalyst concentration: k′ = r_c/[C]_o. In Fig. 3 the r_c values determined for only one single catalyst concentration at [B–T]_o = 0.62 and 0.115 mol dm⁻³ are also given. The slopes of the interconnecting lines and both linear least squares fits correspond to normalized rates at constant pinacolone concentration k′_P, which we indicate by the subscript P. The values of k′_P increase with increasing [B–T]_o. Fig. 4 illustrates the dependence of k′_P on [B–T]_o for [P]_i = 0.114 and [P]_i = 0.046 mol dm⁻³.

Fig. 4 Normalized rates of the catalyzed reaction as a function of the overall borane concentration, OAB 1c. [P]_i = 0.114 (upper curve), 0.046 mol dm⁻³ (lower curve).

Despite the scatter of the data it is obvious that the dependence of k′_P on [B–T]_o weakens distinctly with increasing [B–T]_o. Considering that [P] is constant, we rearrange eqn. (3) and derive eqn. (4), which gives an analytical expression for the dependence of k′_P on [B–T]_o at constant [P]_i.

k′_P = f₁[B–T]_o/(1 + f₂[B–T]_o) (4)

f₁ = k_5bK_5a(K₄/[T])[P] (4a)

f₂ = K₄/[T] + K_5a(K₄/[T])[P] (4b)

The curves of Fig. 4 describing the experimental data have been calculated with the constants f₁ = 10 M⁻¹ s⁻¹ and f₂ = 5.0 M⁻¹ at [P]_i = 0.114 mol dm⁻³ and f₁ = 6.0 M⁻¹ s⁻¹ and f₂ = 3.5 M⁻¹ at [P]_i = 0.046 mol dm⁻³. Eqn. (4a) demands direct proportionality of f₁ with [P], which seems to be fulfilled. The corresponding slope is k_5bK_5a(K₄/[T]) = 90 M⁻² s⁻¹. If we calculate the straight line connecting the two data points f₂;[P]_i according to eqn. (4b) we obtain as slope K_5a(K₄/[T]) = 36 M⁻² and as intercept (K₄/[T]) = 1.8 M⁻¹. From these results we finally get k_5b = 2.5 s⁻¹, K_5a = 20 M⁻¹ and K₄ = 23.

The analysis of the normalized rates k′_B, determined at constant B–T concentration, with respect to their dependence on the concentration of pinacolone allows a test of the consistency of evaluation. Taking [B–T]_o as constant, we derive eqn. (5) as an analytical expression for the dependence of k′_B on [P]_i at constant [B–T]_o.

k′_B = g₁g₂[P]_i/(1 + g₂[P]_i) (5)

g₁ = k_5b (5a)

g₂ = (K₄/[T])[B–T]_oK_5a/{1 + (K₄/[T])[B–T]_o} (5b)

Thus, only parameter g₂ should vary with [B–T]_o. Fig. 5 shows the dependence of k′_B on [P]_i for three different constant borane concentrations.

Fig. 5 Normalized rates of the catalyzed reaction as a function of the initial pinacolone concentration, OAB 1c. [B–T]_o = 0.62, 0.23, 0.115 mol dm⁻³ (from top to bottom).

The lines drawn in Fig. 5 roughly describe the experimental data. They have been calculated by eqn. (5) with g₁ = 2.5 s⁻¹ and g₂ = 11.0 M⁻¹ ([B–T]_o = 0.62 mol dm⁻³), g₂ = 6.0 M⁻¹ (0.23) and g₂ = 3.4 M⁻¹ (0.115). Using eqns. (5a) and (5b) and the above derived values of k_5b, K_5a and K₄/[T] we calculate g₁ = 2.5 s⁻¹, g₂ = 10.5 M⁻¹ ([B–T]_o = 0.62 mol dm⁻³), g₂ = 5.8 M⁻¹ (0.23) and g₂ = 3.4 M⁻¹ (0.115). Hence, it is actually possible to describe both the dependence of k′_P on [B–T]_o and the dependence of k′_B on [P]_i with the common set of constants of k_5b = 2.5 s⁻¹, K_5a = 20 M⁻¹ and K₄ = 23 for OAB 1c. Thus, the evaluation appears to be consistent.

It has to be noted that the value of K₄ obtained from the kinetic analysis of the catalyzed reduction of P is by one order of magnitude smaller than the value K₄ = 260, which was determined by Mathre et al. studying the concentration dependent changes of the NMR spectrum of the 1∶1 complex of OAB 1c and BH₃ in THF-d₈ at 25 °C.²⁸ The reason for that discrepancy is not fully understood. We tried to determine the equilibrium constant K₄ spectrophotometrically. However, the spectral changes following the addition of borane to OAB 1c are too fast to be measured time-resolved with our stopped-flow apparatus. We observed slow spectral changes developing during the time scale of several minutes. The corresponding slow reaction, however, cannot be of relevance for the catalyzed reaction, which occurs on a faster time scale with conversions Δ[P] ≥ 20[C]_o, indicating borane–catalyst turnover numbers of at least 10 during one or two minutes, see Fig. 1. Since the time span between sample preparation and NMR measurement was probably distinctly longer than some seconds, the relevance of the corresponding value of K₄ for the kinetics of the catalyzed reaction has to be questioned.

Kinetics of the reduction of P catalyzed by OAB 1d

Both kinetic traces of Fig. 2 indicate that the reaction catalyzed by OAB 1d is almost zero-order in pinacolone. This conclusion is supported by the quantitative evaluation. Fig. 6 plots rates r_c determined at constant [B–T]_o = 0.23 mol dm⁻³ but different catalyst concentrations of [C]_o = 0.0010, 0.0025 and 0.0050 mol dm⁻³versus [P]_i.

Fig. 6 Rates of the catalyzed reaction as a function of the initial pinacolone concentration, OAB 1d. [B–T]_o = 0.23 mol dm⁻³; [C]_o = 0.0050, 0.0025, 0.0010 mol dm⁻³ (from top to bottom).

No significant dependence of r_c on [P]_i can be seen in the pinacolone concentration range investigated. According to eqn. (3), r_c becomes independent of [P] only if K_5a[P] ≫ 1 andK_5a[P](K₄/[T])[B–T]_o ≫ 1 hold true. Then, eqn. (3) simplifies to r_c ≈ k_5b[C]_o and r_c should also be independent of [B–T]_o. Because of the constancy of the r_c data of Fig. 5 it is reasonable to calculate average values, covering the whole investigated pinacolone concentration range. Fig. 7 shows the plot of the average values of r_cversus [C]_o at constant [B–T]_o = 0.23 mol dm⁻³.

Fig. 7 Rate of the catalyzed reaction as a function of the overall catalyst concentration, OAB 1d. Values of r_c are averages of the r_c data in the 0.015 ≤ [P]_i ≤ 0.13 mol dm⁻³ concentration range of Fig. 6; [B–T]_o = 0.23 mol dm⁻³.

A strong linear correlation is obtained in agreement with the expectations based on eqn. (3). k_5b = 0.17₄ s⁻¹ results as slope. Further experiments have been carried out at [B–T]_o = 0.445 mol dm⁻³ and [C]_o = 0.0050 mol dm⁻³. The rate r_c was again found to be independent of [P]_i between 0.015 and 0.13 mol dm⁻³. The mean value of k′ = r_c/[C]_o = 0.20₅ s⁻¹ yields a further estimate of k_5b. Both results differ only in the mutual limits of experimental error. Thus, we obtain as average k_5b = 0.2 s⁻¹ for OAB 1d.

Comparison of the catalysts

The catalyzed reaction is first-order in P for OABs 1a and 1b. The corresponding rate follows Eqn. (1), which allows no distinction as to whether the addition of P to C–B forming P–C–B (R5a) or the hydride shift with subsequent rearrangement (R5b) is the rate determining step. However, the change from first- to zero-order kinetics in P observed with OABs 1c and 1d definitely indicates for these catalysts reaction R5b to be rate determining. Thus, for the first time it is shown that the hydride shift with subsequent rearrangement determines the rate of the catalytic process. Since we see no reason why the chemistry developing at the OAB catalyst should change from OAB 1a to 1d, we conclude that the reaction R5b is rate determining for all OABs investigated by us and use eqn. (3) as a common base for the comparison of the catalysts.

For OABs 1a and 1bK_5a[P]_i ≪ 1 and hence K_5a ≤ 2 M⁻¹ must hold true, since only in this case the catalyzed reaction becomes first-order in P in the investigated concentration range. For OAB 1cK_5a = 20 M⁻¹ was obtained and for OAB 1dK_5a[P]_i ≫ 1 corresponding to K_5a ≥ 100 M⁻¹ results. It is the question, how this strong variation of the equilibrium constant of the addition of P to C–B can be understood. The excellent effectiveness of the enantioselectively catalyzed reduction of prochiral ketones by OABs is based on the almost perfect application of the lock and key principle, which implies that for each OAB–borane complex (lock) the highest effectiveness is only obtained with an optimum fitting substrate (key). Besides electronic and structural properties of the OAB–borane complex C–B the structure of the substrate P has to be taken into account. The magnitude of the value of K_5a seems to be determined by steric restrictions hindering the access of the oxygen atom of the bulky pinacolone molecule to the ring boron atom in the case of the rather rigid bicyclic OABs 1a, 1b and 1c. According to AM1 calculations,⁵⁴ the bond between the ring boron atom and its substituent stands almost perpendicular to the plane of the oxazaborolidine ring. Therefore, the access of P to C–B is rather restricted for the OABs 1a and 1b, which have a phenyl substituent bound to the ring boron atom. The restriction is smaller for OAB 1c, since the phenyl substituent is replaced by a methyl substituent at the ring boron, leading to a larger value of K_5a. Because of the missing structure stabilizing effect of the fused second ring, the flexibility of the monocyclic OAB 1d is increased, possibly allowing for the larger value of K_5a due to the better accessibility of the ketone P to the ring boron atom, despite its phenyl substituent.

The equilibrium constant of the borane addition to the catalyst was recently spectrophotometrically determined by us as K₄ = 220 for OAB 1b.⁴² This value is one order of magnitude larger than the value of K₄ = 23 presently obtained for OAB 1c. Because of the smaller steric hindrance to the addition of borane to the nitrogen atom in OAB 1c reasons other than steric ones must be responsible for the smaller value of K₄. Possibly, the basicity of the nitrogen atom is decreased in 1c compared with 1b due to the replacement of the phenyl substituent at the ring boron atom by the methyl substituent, which is the weaker electron donor.

The rate constant of the hydride shift amounts to k_5b = 2.5 s⁻¹ for OAB 1c and 0.2 s⁻¹ for OAB 1d. This difference is the main reason why 1c is the better catalyst. Electronic as well as steric factors may influence the graduation in k_5b. A detailed interpretation of this interesting effect could eventually be given on the basis of high level theoretical calculations.

The comparison of the catalytic effect of the OABs depends on the experimental conditions of the reactions, as the reaction kinetics change in the series of catalysts. For OABs 1a and 1b second-order rate constants of catalysis k_c have recently been calculated for constant [B–T]_o from the pseudo-first-order rate constants k_p1 and k_d of the overall and of the direct borane reduction, respectively, by k_c = (k_p1 − k_d)/[C]_o, whereby k_c depends on [B–T]_o.⁴² Values of k_c = 0.23 dm³ mol⁻¹ s⁻¹ (OAB 1a, [B–T]_o = 0.26 mol dm⁻³, 0.08 ≤ [P]_i ≤ 0.12 mol dm⁻³) and k_c = 9 dm³ mol⁻¹ s⁻¹ (OAB 1b, [B–T]_o = 0.23 mol dm⁻³, 0.08 ≤ [P]_i ≤ 0.14 mol dm⁻³) resulted at 20 °C. These data can be used to calculate the normalized rate k′ of the catalytic reaction as k′ = k_c[P]_i. We obtain at [B–T]_o = 0.26 mol dm⁻³k′ = 0.23[P]_i s⁻¹ for OAB 1a and k′ = 9[P]_i s⁻¹ for OAB 1b. For OAB 1ck′ = 16[P]_i/(1 + 6.4[P]_i) s⁻¹ and for OAB 1d finally k′ = 0.20 s⁻¹ results in the 0.015 ≤ [P]_i ≤ 0.13 mol dm⁻³ range at [B–T]_o = 0.26 mol dm⁻³. Thus, the catalytic activity of the OABs decreases in the series 1c ≈ 1b > 1d ≫ 1a.

We performed as complementary to the kinetic experiments ee determinations at 20 °C under the experimental conditions [C]_o = 0.0050, [P]_i = 0.10, and [B–T]_o = 0.23 mol dm⁻³. The following ee values (%) have been obtained: 61 (OAB 1a), 96 (OAB 1b), 97 (OAB 1c), and 85 (OAB 1d). The fact that the graduation of ee values follows the same sequence as the graduation of catalytic activity strongly indicates a close relationship between the two quantities. However, it should be noted that these graduations hold true for pinacolone. The investigation of other ketones will probably result in different graduations.

Temperature dependence

The kinetic investigation revealed that the rate of the catalytic reactions depends in a complex manner on equilibrium and rate constants. Therefore, temperature dependent measurements only lead to apparent activation energies, which may even depend on [P] and [B–T]_o. Since they cannot be directly related with one defined reaction step, these values are of more practical interest but less suited for a discussion of a particular transition state.

Measurements of the overall reaction rates r have been performed with OABs 1c and 1d at intervals of 5 °C from 10 to 30 °C. The temperature dependent rate of the direct borane reduction of P was calculated using the previously determined rate constant k_d = 0.0037 dm³ mol⁻¹ s⁻¹ (20 °C) and the corresponding activation energy of E_a = 54.3 kJ mol⁻¹. The rate of the catalytic reaction was obtained for each temperature as r_c = r − r_d. From Arrhenius type plots of ln (r_c) versus 1/T apparent activation energies “E_a” have been obtained, which are collected together with calculated values of k′ in Table 1. As expected, with all catalysts the apparent activation energies are smaller than the activation energy of the direct reduction.

Table 1 Normalized rates k′ = r_c/[C]_o (20 °C) and apparent activation energies “E_a” of the reduction of pinacolone by borane catalyzed by OABs in THF. k′ calculated for [P] = 0.1 mol dm⁻³, [B–T]_o = 0.23 mol dm⁻³. The “E_a” data have been determined at [P]_i = 0.1 mol dm⁻³ and at the specified values of [B–T]_o

Catalyst	k′/s^−1	“Ea”/kJ mol^−1	[B–T]o/mol dm^−3
a Calculated from the kc data of ref. 42.
OAB 1a ^a	0.0060	35 ± 6	0.50
OAB 1b ^a	0.23	26 ± 5	0.42
OAB 1c	0.97	44 ± 4	0.23
OAB 1d	0.20	41 ± 9	0.23

---

Conclusions

The reaction order in the ketone P changes in the series of OABs from first-order to zero-order. This kinetic result demonstrates for the first time that it is not the addition of P to the binary complex C–B but the hydride shift in the ternary complex P–C–B with subsequent rearrangement which is the rate determining step in the OAB catalyzed reduction of pinacolone.

Experimental

Techniques

Melting points were measured with a Büchi 510 apparatus and are uncorrected. FT-infrared spectra were recorded with a Nicolet Magna FT-IR spectrometer. ¹H NMR and ¹³C NMR spectra were recorded on a Bruker AM 270 spectrometer. Chemical shifts are reported in ppm and were referenced to the residual CHCl₃ resonances (7.26 ppm/77.00 ppm). Elemental analyses were obtained with a Perkin-Elmer CHNO/S-Analysator 2400 II or a Heraeus CHN-Rapid. Optical rotations were measured at 20 °C in CHCl₃ on a Perkin-Elmer 241 polarimeter. The reactions were followed spectrophotometrically using a stopped flow apparatus and a computerized Hewlett-Packard HP8452A diode array spectrophotometer as described earlier.^42,43 The handling of the materials and the preparation of the solutions was done under Ar to avoid contamination by water. If not otherwise stated, all kinetic experiments were carried out at 20 °C.

Determination of enantiomeric excess

The procedure for the determination of ee values under the conditions of our stopped-flow experiments was the same for all catalysts. Solution 1 (50 ml) contained [C]_o = 0.010 and [B–T]_o = 0.455 mol dm⁻³ and solution 2 (50 ml) [P] = 0.20 mol dm⁻³. 1 ml of each solution was mixed in the stopped flow apparatus at 20 °C. The mixing was repeated every 60 s until the entire solutions had reacted. The reaction mixture (100 ml) was quenched by 10 ml of water and refluxed for 1 h to destroy the unreacted borane and to transform the dialkoxyboranes to the product alcohol 3,3-dimethylbutan-2-ol (pinacolyl alcohol). Finally the solution was distilled. The fraction at ≥72 °C contained pinacolyl alcohol and THF as checked by ¹H NMR spectroscopy. The THF was removed from 40 ml of this fraction in a rotary evaporator. The residue was separated by using a column of packed Kieselgel F60 and hexane–ethyl acetate (ratio 3∶1). The progress was controlled by gas chromatography (conditions: column Lipodex E of Machery + Nagel/Düren, injector block 100 °C, flame ionisation injector block 200 °C, oven 50 °C at isothermal cond., pressure of H₂ carrier gas 45 kPa, approx. split ratio 60∶1). 0.5 g of the isolated pinacolyl alcohol (4.9 mmol) were dissolved in 10 ml of dry CH₂Cl₂. Then 2.5 ml of dry pyridine and 2.55 g acetic anhydride (25 mmol, 5 eq.) were added. The solution was stirred at room temperature for 5 h, forming pinacolyl acetate. Then 5 ml of 2 M HCl were added and the solution was washed several times with ether. The combined ether phases were washed with 1 M NaOH and brine. After drying over K₂CO₃ the ether was removed in vacuo. The residue was separated from pyridine by chromatography (column of packed Kieselgel F60, solvent hexane–ethyl acetate, ratio 3∶1). The pinacolyl acetate passes the column first (R_f = 1), pyridine is slower (R_f = 0.5). After separation, the solvent hexane–ethyl acetate is removed at 40 °C at 200 mbar. The yellow volatile liquid residue is purified pinacolyl acetate (yield ca. 270 mg), characterized by ¹H NMR spectroscopy. The ester was separated into its enantiomers by using the above described GC method. Based on the integrals over the peaks of the R (retention time 6.5–6.69 min) and the S enantiomer (retention time 7.15–7.5 min), we found that in every case mainly the R configuration of pinacolyl alcohol was formed.

Preparations

(S)-(−)-2-(1-Hydroxy-1,1-diphenylmethyl)pyrrolidine, BH₃–THF and 3,3-dimethylbutan-2-one (pinacolone).. These were prepared and/or purified as described previously.^42,43

L-Alanine methyl ester hydrochloride.¹⁰. 17.82 g (0.2 mol) of L-alanine suspended in 150 ml methanol were cooled to −20 °C. 20 ml (0.276 mol, 1.4 eq.) of thionyl chloride were added during 90 min by using an addition funnel. The resulting clear solution was brought back to room temperature and then heated to 80 °C for 2.5 h. After reaching room temperature again the product was washed with methanol. The solvent was removed under reduced pressure and the remaining residue (clear oil) was dried in vacuo to give 27.54 g of a white solid product in 98% yield. Mp 103 °C; [α]₅₈₉ = +8.2°, c = 1.52 (MeOH, 20 °C); ¹H NMR (CDCl₃, 270 MHz): δ = 8.8–8.6 (s, br, 2H), 4.4–4.24 (m, 1H), 3.8 (s, 3H), 1.74 (d, J = 7.5 Hz, 3H); ¹³C NMR (CDCl₃, 270 MHz): δ = 170.5, 53.2, 49.3, 16; Anal. Calcd for C₄H₁₀NO₂Cl: C, 34.42; H, 7.22; N, 10.03. Found: C, 33.84; H, 7.09; N, 10.01%.

(S)-2-Amino-1,1-diphenylpropan-1-ol.¹⁰. 350 ml of a 25% solution (0.64 mol) of PhMgCl in THF was cooled using an ice bath. A continuous Ar flow through the three-necked flask was established to ensure exclusion of moisture. Then 14 g (100.3 mmol) of L-alanine methyl ester hydrochloride were added in small portions. The resulting (still cooled) mixture was stirred for 1 h. Then it was heated to 80–90 °C and refluxed for 4 h. At room temperature 150 ml of saturated NH₄Cl and 20 ml conc. HCl were added stepwise, turning the indicator litmus to red. Then 100 ml of aqueous 25% NH₄OH were added until alkaline reaction was reached. The THF phase was separated and the aqueous phase was extracted three times by using 100 ml ethyl acetate each time. The combined organic phases were washed with brine and dried with MgSO₄. The solution was filtered and rewashed with a small amount of ethyl acetate. Removal of the organic solvents under reduced pressure resulted in a yellow–orange solution. The crude product was purified by Kugelrohr distillation (80–115 °C, 0.7 mbar) to give a yellow–white product. White crystals could be obtained by recrystallization from n-hexane–MeOH (12∶1) in 52% yield. Mp 98–100 °C (100–102 °C);¹⁰ [α]₅₈₉ = −92°, c = 1.35 (CHCl₃, 20 °C); ¹H NMR (CDCl₃, 270 MHz): δ = 7.65 and 7.48 (each ψd, J = 8 Hz, total 4H), 7.4–7.12 (m, 5H), 4.16 (ψq, 1H), 1.4–1.05 (s, br, 1H), 0.96 (d, J = 7.5 Hz, 3H); ¹³C NMR (CDCl₃, 270 MHz): δ = 147, 144.7, 128.4, 128, 126.7, 126.4, 125.9, 125.4, 78.4, 51.9, 17.2; Anal. Calcd for C₁₅H₁₇NO: C, 79.26; H, 7.54; N, 6.16. Found: C, 79.21; H, 7.56; N, 6.15%.

Preparation of the oxazaborolidine catalysts 1c and 1d.^15,55. In a dry 100 ml Schlenk flask 2.0 mmol of the amino alcohol and 2.1 mmol of boronic acid (1c: methylboronic acid, 1d: phenylboronic acid) were suspended in 40 ml of dry toluene. The mixture was heated to reflux in an atmosphere of argon for 14 h under azeotropic removal of water, which was trapped by 10 g of 4 Å molecular sieves placed in a pressure equalizing dropping funnel between the flask and the condensor. The toluene was then removed in vacuo and the residue purified by Kugelrohr distillation (170–175 °C/0.5 mbar for 1c and 185–190 °C/0.5 mbar for 1d) to give the pure oxazaborolidines (1c: white crystals, 1d: yellow solid) in nearly quantitative yields.
(S)-1-Methyl-3,3-diphenylperhydropyrrolo[1,2-c][1,3,2]oxazaborolidine 1c.. Mp 73–75 °C (74–86 °C);¹⁵ [α]₅₈₉ = −211.5°, c = 1.58 (CHCl₃, 20 °C); ¹H NMR (CDCl₃, 270 MHz): δ = 7.65–7.1 (m, 10H), 4.35 (dd, J = 5.6 and 9.8 Hz, 1H), 3.44–3.32 (m, 1H), 3.1–2.95 (m, 1H), 1.9–1.55 (m, 3H), 0.9–0.75 (m, 1H), 0.4 (s, 3H); ¹³C NMR (CDCl₃, 270 MHz): δ = 147.8, 143.9, 128.2, 128.1, 127.7, 127.1, 126.5, 126.3, 126.2, 125.8, 87.8, 72.6, 42.9, 30.2, 26.4.
(S)-4-Methyl-2,5,5-triphenyl-1,3,2-oxazaborolidine 1d.. [α]₅₈₉ = −182°, c = 0.54 (CHCl₃, 25 °C); ¹H NMR (CDCl₃, 400 MHz): δ = 7.92 (m, 2H), 7.75 (m, 2H), 7.56–7.61 (m, 11H), 4.66 (q, 1H), 3.9 (s, br., 1H), 0.99 (d, 3H); ¹³C NMR (CDCl₃, 100 MHz): δ = 147, 143, 133.9, 130.4, 129, 128.4, 128.2, 128, 127.8, 127.6, 127.1, 126.7, 126.4, 126.1, 125.9, 125.5, 125.4, 89.9, 59.3, 22.5.

Acknowledgements

Generous financial support by the Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie, grant nos. 03D0029B3 and 03D0029A0, and by the Adolf Messer Stiftung is gratefully acknowledged. We also thank the Fonds der Chemischen Industrie for support.

References

1. E. J. Corey and C. J. Helal, Angew. Chem., 1998, 110, 2093; Angew. Chem., Int. Ed. Engl., 1998, 37, 1986..
2. D. Valentine and J. W. Scott, Synthesis, 1978, 329.
3. V. K. Singh, Synthesis, 1992, 605.
4. L. Deloux and M. Srebnik, Chem. Rev., 1993, 93, 763.
5. Y. H. Kim, D. H. Park, I. S. Byun, I. K. Yoon and C. S. Park, J. Org. Chem., 1993, 58, 4511.
6. S. Wallbaum and J. Martens, Tetrahedron: Asymmetry, 1992, 3, 1475.
7. S. Itsuno, Y. Sakurai, K. Ito, A. Hirao and S. Nakahama, Bull. Chem. Soc. Jpn., 1987, 60, 395.
8. A. Hirao, S. Itsuno, S. Nakahama and N. Yamazaki, J. Chem. Soc., Chem. Commun., 1981, 315.
9. S. Itsuno, K. Ito, A. Hirao and S. Nakahama, J. Chem. Soc., Chem. Commun., 1983, 469.
10. S. Itsuno, M. Nakano, K. Miyazaki, H. Masuda and K. Ito, J. Chem. Soc., Perkin Trans. 1, 1985, 2039.
11. S. Itsuno, Y. Sakurai, K. Shimizu and K. Ito, J. Chem. Soc., Perkin Trans. 1, 1990, 1859.
12. S. Itsuno, A. Hirao, S. Nakahama and N. Yamazaki, J. Chem. Soc., Perkin Trans. 1, 1983, 1673.
13. S. Itsuno, K. Ito, A. Hirao and S. Nakahama, J. Org. Chem., 1984, 49, 555.
14. E. J. Corey, R. K. Bakshi and S. Shibata, J. Am. Chem. Soc., 1987, 109, 5551.
15. E. J. Corey, R. K. Bakshi and S. Shibata, J. Am. Chem. Soc., 1987, 109, 7925.
16. S. Itsuno, T. Wakasugi, K. Ito, A. Hirao and S. Nakahama, Bull. Chem. Soc. Jpn., 1985, 58, 1669.
17. S. Itsuno, K. Ito, A. Hirao and S. Nakahama, J. Chem. Soc., Perkin Trans. 1, 1984, 2887.
18. S. Itsuno, M. Nakano, K. Ito, A. Hirao, M. Owa, N. Kanda and S. Nakahama, J. Chem. Soc., Perkin Trans. 1, 1985, 2615.
19. C. Cazé, N. El Moualij, P. Hodge, C. J. Lock and J. Ma, J. Chem. Soc., Perkin Trans. 1, 1995, 345.
20. C. Franot, G. B. Stone, P. Engeli, C. Spöndlin and E. Waldvogel, Tetrahedron: Asymmetry, 1995, 6, 2755.
21. G. B. Stone, Tetrahedron: Asymmetry, 1994, 5, 465.
22. A. M. Salunkhe and E. R. Burkhardt, Tetrahedron Lett., 1997, 38, 1523.
23. E. J. Corey and J. O. Link, J. Am. Chem. Soc., 1992, 114, 1906.
24. E. J. Corey and R. K. Bakshi, Tetrahedron Lett., 1990, 31, 611.
25. E. J. Corey, J. O. Link and R. K. Bakshi, Tetrahedron Lett., 1992, 33, 7107.
26. E. J. Corey and J. O. Link, Tetrahedron Lett., 1992, 33, 3431.
27. E. J. Corey and C. J. Helal, Tetrahedron Lett., 1995, 36, 9153.
28. D. J. Mathre, A. S. Thompson, A. W. Douglas, K. Hoogsteen, J. D. Carroll, E. G. Corley and E. J. J. Grabowski, J. Org. Chem., 1993, 58, 2880.
29. A. W. Douglas, D. M. Tschaen, R. A. Reamer and Y.-J. Shi, Tetrahedron: Asymmetry, 1996, 7, 1303.
30. J. G. Quallich, J. F. Blake and T. M. Woodall, J. Am. Chem. Soc., 1994, 116, 8516.
31. G. J. Quallich and T. M. Woodall, Tetrahedron Lett., 1993, 34, 4145.
32. E. J. Corey, X.-M. Cheng, K. A. Cimprich and S. Sarshar, Tetrahedron Lett., 1991, 32, 6835.
33. E. J. Corey, M. Azimioara and S. Sarshar, Tetrahedron Lett., 1992, 33, 3429.
34. V. Nevalainen, Tetrahedron: Asymmetry, 1991, 2, 429.
35. V. Nevalainen, Tetrahedron: Asymmetry, 1993, 4, 1597.
36. V. Nevalainen, Tetrahedron: Asymmetry, 1994, 5, 289.
37. V. Nevalainen, Tetrahedron: Asymmetry, 1996, 7, 2655.
38. L. P. Linney, C. R. Self and I. H. Williams, J. Chem. Soc., Chem. Commun., 1994, 1651.
39. L. P. Linney, C. R. Self and I. H. Williams, Tetrahedron: Asymmetry, 1994, 5, 813.
40. D. Liotta and D. K. Jones, Adv. Mol. Modelling, 1995, 3, 1.
41. D. K. Jones, D. C. Liotta, I. Shinkai and D. J. Mathre, J. Org. Chem., 1993, 58, 799.
42. R. Schmidt, H. Jockel, H.-G. Schmalz and H. Jope, J. Chem. Soc., Perkin Trans. 2, 1997, 2725.
43. H. Jockel and R. Schmidt, J. Chem. Soc., Perkin Trans. 2, 1997, 2719.
44. C. F. Lane, Chem. Rev., 1976, 76, 773.
45. J. R. Elliot, W. L. Roth, G. F. Roedel and E. M. Boldebuck, J. Am. Chem. Soc., 1952, 74, 5211.
46. C. Than and H. Morimoto, J. Org. Chem., 1995, 60, 7503.
47. C. Camacho, G. Uribe and R. Contreras, Synthesis, 1982, 1027.
48. A. T. Whatley and R. N. Pease, J. Am. Chem. Soc., 1954, 76, 835.
49. B. Rice, J. A. Livasy and G. W. Schaeffer, J. Am. Chem. Soc., 1955, 77, 2750.
50. H. C. Brown , Hydroboration, W. A. Benjamin Inc., New York, 1962, p. 18..
51. G. F. Freegard and L. H. Long, Chem. Ind., 1963, 471.
52. H. C. Brown, H. I. Schlesinger and A. B. Burg, J. Am. Chem. Soc., 1939, 61, 673.
53. J. D. Pasto and B. Lepeska, J. Am. Chem. Soc., 1976, 98, 1091.
54. HyperChem software package release 4.5, 1995, Hypercube, Inc., Waterloo, Ontario..
55. D. J. Mathre, T. K. Jones, L. C. Xavier, T. J. Blacklock, R. A. Reamer, J. J. Mohan, E. T. T. Jones, K. Hoogsteen, M. W. Baum and E. J. J. Grabowski, J. Org. Chem., 1991, 56, 751.

---