Probing the magnetizability distribution of ferrocene as determined via anisotropic contributions to the NMR shielding and its application to several substituted ferrocenes
Leonidas Phillips*a, Gary R. Dennisb and Manuel J. Aroneya
aSchool of Chemistry, University of Sydney, Sydney, 2006, Australia
bDepartment of Chemistry, University of Western Sydney-Nepean, Kingswood, 2747, Australia
First published on UnassignedUnassigned21st January 2000
Abstract
Molecular magnetic anisotropies of ferrocene derivatives are derived from solution-state measurements of the Cotton–Mouton and Kerr constants. A calculation is presented of chemical shifts induced at the hydrogen and carbon nuclei, arising from the experimental magnetic anisotropy. Ferrocene, ruthenocene and analogously substituted benzenes were also examined. Comparisons of the chemical shifts were used to probe the effects of metal–carbon bonding in the metallocenes. The experimental chemical shifts for pentamethylferrocene have been interpreted, allowing for magnetic anisotropy contributions, to give carbon atom charges that are in close agreement with predictions from the measured electric dipole moment.
Following recent work1 in this series,1–6 the mean magnetizability (or susceptibility), χ, for a number of substituted ferrocenes was investigated in terms of a perturbation, λ, to the metal–ring bonding introduced to bring the experimental and predicted results into agreement. It was considered that a more sensitive probe of the magnetic environment of the ferrocenyl nucleus would be the anisotropy in the magnetizability, Δχ, rather than the λ corrections to the isotropic value. Considerable electron reorganization is known to occur along the metal–ring axis in ferrocene and ruthenocene,6 M(η5-C5H5)2, M=Fe or Ru, respectively, following coordination. The purpose of this paper is to explore the magnetic anisotropy and other physical properties of both free and complexed rings in these systems. One such property is the NMR chemical shift, which for the ring nuclei of the cyclopentadienyl rings, displays a significant shielding contribution compared to equivalently substituted benzenes. This shielding can arise from a number of causes, including diamagnetic shielding from the metal or diminution of the classic aromatic ring current.
Experimental
The solute molar Cotton–Mouton constant at infinite dilution, ∞(mC2), from which the solute magnetizability anisotropy can be derived, is obtained from experimental observables by eqn. (1)6,7| ∞(mC2)=sC1(1−β−Fγ+δ⊥)M2 | (1) |
where subscripts 1 and 2 refer in turn to solvent and solute; sC1 is the specific Cotton–Mouton constant of the solvent; β and γ are derived from the incremental densities and refractive indices of the solutions of graded concentration,8 which have been presented earlier;6,9δ⊥ derives from the incremental Cotton–Mouton constants for the solutions;10F is a solvent constant;11 and M2 is the molecular weight of the solute. Some of these parameters for the metallocenes studied here are collected in Table 1.
| Metallocene | 1015(ΔC12/w2)w2=0b/m A−2 | δ⊥ | 1027∞(mC2)w2=0/m5 A−2 mol−1 | 1029 Δχ/J T−2 molecule−1 |
|---|---|---|---|---|
| a Reliable measurements could not be made for decachloroferrocene due to solubility limitations.b w2 refers to the solute weight fraction.c Data from ref. 6. | ||||
| Fe(η5-C5Me5)2 | 2.25±0.09 | −12.9±0.5 | 33.4±1.4 | 77.6±3.6 |
| Fe(η5-C5H5)(η5-C5Me5) | −2.52±0.21 | 14.5±1.2 | −32.1±2.8 | −101±11 |
| Fe(η5-C5H5)2c | −4.33±0.24 | 24.9±1.4 | −39.3±2.1 | −92.2±0.6 |
| Fe(η5-C5H5)(η5-C5Cl5) | −1.07±0.26 | 6.2±1.5 | −19.5±5.2 | −140±40 |
| Ru(η5-C5H5)2c | −2.06±0.22 | 11.8±1.3 | −23.5±2.4 | −53.3±6.0 |
The substituted ferrocenes were purified2 by vacuum sublimation and/or recrystallization. Solutions were prepared and manipulated under nitrogen. Cyclohexane, an inert solvent for such studies, was purified and dried by distillation under nitrogen from phosphorus pentoxide.
The NMR chemical shifts of the metallocenes were recorded on either a Joel FX-60Q, XLFT-100 or a Bruker WM-400 spectrometer; all chemical shifts are referenced to TMS. The measured shifts (δ) for the metallocenes and reference benzene compounds are given in Table 2.
| Molecule | Nucleus | 13C shift/ppmb | 1H shift/ppm |
|---|---|---|---|
| a In C6D12 solvent except as noted otherwise.b The 13C shifts, apart from those of Ru(η5-C5H5)2 and C6Me6, are from ref. 9.c In C6D6 solvent. | |||
| Fe(η5-C5Me5)2 | *C5Me5 | 78.73 | — |
| Me | 9.84 | 1.64 | |
| Fe(η5-C5H5)(η5-C5Me5) | *C5Me5 | 80.29 | — |
| C5H5 | 71.53 | 3.55 | |
| Me | 11.66 | 1.87 | |
| Fe(η5-C5H5)2 | C5H5 | 68.28 | 4.04 |
| Fe(η5-C5H5)(η5-C5Cl5) | C5Cl5 | 88.18 | — |
| C5H5 | 79.64 | 4.26 | |
| Fe(η5-C5Cl5)2c | C5Cl5 | 90.56 | — |
| Cr(η6-C6H6)2 | C6H6 | 74.90 | 4.26 |
| Cr(η6-C6H6)2c | C6H6 | 74.93 | 4.213 (T=323 K) |
| 4.223 (T=298 K) | |||
| 4.227 (T=278 K) | |||
| Ru(η5-C5H5)2 | C5H5 | 70.42 | 4.43 |
| C6H6 | C6H6 | 128.79 | 7.16 |
| C6Me6 | *C6Me6 | 131.78 | — |
| Me | 16.68 | 2.14 | |
| C6Cl6 | C6Cl6 | 133.15 | — |
Theoretical
For the axially symmetric molecules investigated, each of which has a threefold or higher-order rotation axis (subscripted z), the classical statistical mechanical expression for the Cotton–Mouton constant reduces to:10,12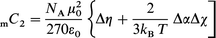 | (2) |
where NA, kB, ε0, μ0 and T have their usual meanings,2Δα(=αzz−αxx) and Δχ(=χzz−χxx) are the anisotropies in the optical polarizability and susceptibility, respectively. The tensor Δη, describing the temperature-independent contribution to the Cotton–Mouton constant, has been shown to be negligible for such highly anisometric systems.12–14
To obtain the magnetizability anisotropy from mC2, the sign of the polarizability anisotropy must be known with reference to molecular orthogonal axes. Earlier analysis of the polarizabilities of methylated ferrocenes9 enabled the sign of Δα to be specified for decamethylferrocene, Fe(η5-C5Me5)2. For ferrocene and ruthenocene, the sign of Δχ had earlier been established from crystal state studies.6
In order to develop a physical model that would provide insight into the relationship between experimentally determined Δχ values and NMR shifts, the following argument was adopted. The chemical shift is often deconvoluted into contributions arising from purely empirical components, e.g. local atomic properties or neighbouring environment factors. Of the latter, those originating from the presence of delocalized electrons or due to the presence of a magnetically anisotropic group are the most relevant. We define the term σΔχ to represent the contribution to the shielding arising from the magnetic anisotropy of a group or bond. This includes the magnetic field arising from electrons not centred on the atom in question or its bonding electrons. McConnell15 and Pople16 were the first to quantify this factor. For an axially symmetric group or bond, G, the magnetic point dipole induced at the origin by the randomly oriented magnetic field will produce a secondary field at some nucleus, N, remote from it. Choosing a coordinate system with the major axis along the bond direction, McConnell has advanced the following expression (in SI units)
 | (3) |
where Δχ is the magnetic anisotropy of the group or bond G; R is the distance between the resonant nucleus and the centre of the induced magnetic dipole of G; θ is the angle between R and the symmetry axis of G. Note that for a dipolar field to be an accurate approximation, the distance R must be large in relation to the orbital radius of G, typically R>0.3 nm.
A more rigorous approach has been advanced by Stiles and co-workers.17–19 However, for a description of σΔχ that is suitably tractable in relation to the available data, the treatment of ApSimon and co-workers.20–23 was preferred. According to this scheme, the dipole is no longer considered a point, but rather is assigned a length S, which is taken to be 75% of half the bond length. This empirical choice of S was adopted for C–C and C–H together with the directional bond magnetic susceptibilities of Davies.24 The non-point dipole equation in SI units is
 | (4) |
where χ‖ is the magnetic susceptibility of the bond along the bond axis, χ⊥ is the magnetic susceptibility in a direction perpendicular to the bond axis and Δχ is the magnetic anisotropy, in units of J T−2 molecule−1. The distances R and S are in metres, θ is the inclination of the vector R to the axially symmetric bond axis to which χ‖, χ⊥ and Δχ refer. The point of origin of the induced dipole, of length S, is chosen to be the centre of the bond. This same origin determines the distance R to the nucleus being investigated. For the metallocenes the delocalized bonding between the cyclopentadienyl rings and the metal commends the metal–ring distance as the appropriate measure of the bond length. The cyclopentadienyl–metal bond, which contains the magnetically anisotropic C–C linkages as well as bonding to the electron-rich metal, would dominate the molecular anisotropy.
Hence, by using the experimentally determined molecular magnetic anisotropy and mean magnetizability to represent the delocalized metal–ring bond, a reasonable estimate of the chemical shift arising from the magnetically anisotropic metal–ring bond can be ascertained. As was applied to the electric polarizability studies9 of these axially symmetric molecules (i.e., αxx=αyy or χxx=χyy), the parallel and perpendicular magnetizability components of the metal–ring bond are derived from the following molecular relations:
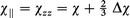 | (5) |
 | (6) |
where χ=(χzz+2χxx)/3 and Δχ=(χzz−χxx) for the axial symmetry present in these molecules.
Results and discussion
The NMR chemical shift has a dependence upon both the local electric field due to neigbouring dipolar bonds and to the magnetic anisotropy of the metal–ring bond.25 –28 Contributions arising from higher orders of the electric field are expected to be small for the metallocenes of this study.29 The geometry of ferrocene is such that the protons and iron atom are on a surface at which the interaction of their atomic charges with the molecular electronic quadrupole moment30 is nullified, i.e. the cone about the iron atom for which θ= cos−1(1/√3)=54.7°. Due to the structural similarities, this simplification is also expected to apply reasonably well to the persubstituted ferrocenes. The carbon Cp atoms lie very close31 to this surface (within 18°). This configuration also means that there will be negligible screening due to a magnetic point dipole centred on the iron atom. The overall result is to make the ring carbons, protons and/or substituents, sensitive probes of the magnetic environment associated with the delocalized metal–ring bond.The purely electronic contribution to the 13C NMR shielding would be determined by the charge and associated bond polarization, while effects due to the magnetic anisotropy of bonds can play a significant role for hydrogen atoms.32,33 For carbon nuclei the effect on the chemical shift due to the contri bution arising from σΔχ (being independent of the nature of the atom) will be a much smaller perturbation, amounting to between 2–10% of the observed chemical shift. The results are compiled in Table 3 for both the proton and carbon nuclei of these molecules.
| Molecule | 1029 Δχ /J T−2 molecule−1 | 1029χxx /J T−2 molecule−1a | 1029χzz /J T−2 molecule−1a | S/10−10 mb | RH/10−10 m (θ/deg.)c | σΔχ (1H)/ppmc | RH/10−10 m (θ/deg.)c | σΔχ (13C)/ppmc |
|---|---|---|---|---|---|---|---|---|
| a The components χxx and χzz are calculated using eqns. (5) and (6). Values of the mean magnetizability are given in ref. 1.b The induced dipole length S is calculated from 75% of half the metal–cyclopentadienyl ring bond length for the metallocenes with the origin located at the midpoint of this bond. For the benzene compounds, S is taken as the same ratio of the ring radius (equal to the C–C bond length). The electron diffraction-derived values are used for Fe(η5-C5Me5)2 ,37 Fe(η5-C5H5)231,37 and Ru(η5-C5H5)231 since they would better reflect the solution-state structure. For Fe(η5-C5H5)(η5-C5Me5) the crystallographic values derived earlier2 were employed.c The chemical shifts are calculated using eqn. (4) and published geometries2,31,37–39 where available, or assumed values as outlined in the following table notes d and e. The quoted uncertainties are based on the errors in Δχ and χ. The symbols Me and Cp refer to the methyl and cyclopentadienyl ring protons respectively, while the asterisked carbon refers to the resonant nucleus.d The ferrocene geometry is assumed in Fe(η5-C5H5)(η5-C5Cl5).e In this model the geometry of the C5H5–Fe system is taken to be the same as that of C5H5–Fe of pentamethylferrocene, while that of C5–Fe in C5Cl5–Fe is analogous to that of C5Me5–Fe in pentamethylferrocene.f Ref. 40.g Ref. 41.h Ref. 42.i Ref. 43. | ||||||||
| Fe(η5-C5Me5)2 | 77.6±3.6 | −392±8 | −314±9 | 0.6233 | 3.410 (74.2) | Me: 1.00±0.04 | 1.479 (55.8) | *C5Me5: −1.46±0.19 |
| 2.866 (71.3) | Me: 1.74±0.06 | |||||||
| Fe(η5-C5H5)(η5-C5Me5) | −101±11 | −253±12 | −354±14 | 0.6236 | 2.249 (68.9) | Cp: −0.10±0.28 | 1.452 (55.1) | C5H5: −6.91±0.43 |
| 0.6154 | 3.169 (74.2) | Me: −0.34±0.11 | 1.451 (55.6) | *C5Me5: −6.47±0.43 | ||||
| 0.6154 | 2.839 (72.5) | Me: −0.34±0.15 | ||||||
| Fe(η5-C5H5)2 | −92.2±0.6 | −179±5 | −271±5 | 0.6229 | 2.309 (69.7) | Cp: −0.44±0.16 | 1.452 (55.6) | C5H5: −5.39±0.26 |
| Fe(η5-C5H5)(η5-C5Cl5) | −140±40 | −350±18 | −490±29 | 0.6229d | Cp: −0.16±0.86 | C5H5, C5Cl5: −9.2±1.4 | ||
| 0.6236e | Cp: −0.15±0.90 | C5H5: −9.6±1.3 | ||||||
| 0.6154e | C5Cl5: −9.0±1.3 | |||||||
| Ru(η5-C5H5)2 | −53.3±6 | −280±6 | −334±7 | 0.6837 | 2.524 (68.8) | Cp: 0.60±0.11 | 1.526 (53.3) | C5H5: −5.82±0.21 |
| C6H6 | −106±4f | −55.5±1.7g | −161.5±2.8 | 0.5239 | 2.481 (90) | C6H6: −1.78±0.09 | 1.397 (90) | C6H6: −3.55±0.67 |
| C6Me6 | −136±7f | −157±10h | −294±11 | 0.5213 | 3.084 (90) | Me: −1.12±0.11 | 1.39 (90) | *C6Me6: 5.95±2.2 |
| 2.93 (90) | Me: −1.25±0.13 | |||||||
| C6Cl6 | −144±10f | −194±12i | −338±14 | 0.5224 | 1.393 (90) | C6Cl6: 9.5±2.8 | ||
The difference between the magnetic anisotropies of free and complexed rings can be probed by examining changes in σΔχ between similarly substituted ferrocene and benzene molecules. The latter represents a close, if imperfect, approximation to the free uncoordinated C5H5 ligand. For the benzene molecules the magnetic origin is taken to be the centre of the ring, while the induced dipole length is taken as 75% of half the ring radius. These results are presented in Table 4. In absolute magnitude, the largest calculated differences occur in the cyclopentadienyl framework carbon atoms, with a calculated shielding shift of from 1.8 ppm for ferrocene to 12.4 ppm for the methylated carbons of pentamethylferrocene, Fe(η5-C5H5)(η5-C5Me5), relative to the carbons of the free benzene ring. Since the ferrocenyl carbons are directly bonded to the iron, it is expected that they would be most affected by the magnetic anisotropy of the metal–ring bond. Examinin g the calculated chemical shift differences ΔσΔχ, given in Table 4, we observe a relatively large variation upon complexation.
| Metallocene | Benzene | Differencesa/ppm | H in Me | CnHn*b | C in Me | Cn*Men | Cn*Hn | Cn*Cln |
|---|---|---|---|---|---|---|---|---|
| a Δ refers to the difference given by the ferrocene shift minus the corresponding benzene shift; e.g. from Table 3, for Me(H) in Fe(η5-C5Me5)2 relative to C6Me6, ΔσΔχ=1.00−(−1.12) ppm=2.12 ppm. Δδ is obtained in an analogous manner from the δ values in Table 2. The error in Δδ for protons is ±0.01 ppm, while for carbon it is ±0.05 ppm; * refers to the resonant nucleus.b n=5 refers to the cyclopentadienyl ring while n=6 refers to the benzene ring.c The geometry based on the pentamethylferrocene molecule is used for these calculations.d For this molecule the Cotton–Mouton constant could not be determined due to solubility limitations. | ||||||||
| Fe(η5-C5Me5)2 | C6Me6 | ΔσΔχ | 2.12±0.12 | — | 2.99±0.14 | −7.41±2.2 | — | — |
| Δδ | −0.50 | — | −6.84 | −53.05 | — | — | ||
| Fe(η5-C5H5)(η5-C5Me5) | C6H6, C6Me6 | ΔσΔχ | 0.78±0.14 | 1.68±0.29 | 0.91±0.20 | −12.4±2.2 | −3.36±0.8 | — |
| Δδ | −0.27 | −3.61 | −5.02 | −51.49 | −57.26 | — | ||
| Fe(η5-C5H5)2 | C6H6 | ΔσΔχ | — | 1.34±0.18 | — | — | −1.84±0.72 | — |
| Δδ | — | −3.12 | — | — | −60.51 | — | ||
| Fe(η5-C5H5)(η5-C5Cl5) | C6H6, C6Cl6 c | ΔσΔχ | — | 1.63±0.90 | — | — | −6.05±1.46 | −18.5±3.1 |
| Δδ | — | −2.90 | — | — | −49.15 | −44.97 | ||
| Fe(η5-C5Cl5)2 | C6Cl6 | ΔσΔχ | — | — | — | — | d | — |
| Δδ | — | — | — | — | — | −42.59 | ||
When the ΔσΔχ differences are compared to the experimental differences (Δδ) for the 13C resonances in Cp, which range from ca. 49 to 60 ppm, it is apparent that some other factor, apart from any magnetic anisotropy dependent shift, causes the major part of the shielding in the complexed species.
It is known, however, that eqns. (3) and (4) are valid within a series of homologous compounds.34 To examine the validity of our approach, differences between the chemical shifts within the ferrocene derivatives themselves were also obtained and are presented in Table 5. In this Table the differences between calculated and experimental shifts are much smaller and they are of comparable magnitude. For the pentasubstituted molecules, the presence of internal metal–ligand dipole moments of opposite orientation with regard to the protonated cyclopentadienyl ring may generate chemical shifts arising from an electric field contribution that have not been quantified in this treatment.
| Ferrocene 1 | Ferrocene 2 | Differencesa/ppm | H in Me | C5H5* | C in Me | C5*Me5 | C5*H5 | C5*Cl5 |
|---|---|---|---|---|---|---|---|---|
| a Δ′ refers to the difference given by the Ferrocene 1 shift minus the corresponding Ferrocene 2 shift (both from Table 3). The error in Δ′δ for protons is ±0.01 ppm, while for carbon it is ±0.05 ppm. | ||||||||
| Fe(η5-C5H5)(η5-C5Me5) | Fe(η5-C5Me5)2, Fe(η5-C5H5)2 | Δ′σΔχ | −1.34±0.12 | 0.34±0.32 | −2.08±0.16 | −5.01±0.47 | −1.52±0.50 | — |
| Δ′δ | 0.23 | −0.49 | 1.82 | 1.56 | 3.24 | — | ||
| Fe(η5-C5H5)(η5-C5Cl5) | Fe(η5-C5Cl5)2, Fe(η5-C5H5)2 | Δ′σΔχ | — | 0.3±0.9 | — | — | −4.2±1.3 | — |
| Δ′δ | — | 0.22 | — | — | 11.35 | −2.38 | ||
An independent check is required to test the validity of the model presented. In assessing the contribution of an electric field arising from intramolecular charge separation to the chemical shift of a ring carbon atom, we must consider the factors affecting the observed resonance. As has been indicated by the significant differences between ΔσΔχ and Δδ in Table 4, large shielding contributions arise from bonding to the metal. These factors will be dependant on: (i) the metal orbitals with which the ring carbon interacts, (ii) the nature of the atom bonded to the ring carbon, i.e. proton, carbon or chlorine, (iii) the contribution from the magnetic field of the metal–ring bond and (iv) any interannular charge displacement.
A comparison is made of intramolecular charge distributions from experimental dipole moments with those obtained by deconvoluting the 13C chemical shifts (δ) into component contributions according to eqn. (7):
| δ=σΔχ+σElectronic+σFramework | (7) |
where δ is the experimentally determined NMR chemical shift, σΔχ, is given in Table 3 and equates to point (iii), σElectronic is the screening effect of molecular electronic charges as covered in point (iv), and σFramework covers the screening of the ring carbon arising from bonding to both the iron atom and the ring substituent. The σFramework term pertains to the electronic backbone of the molecule and encompasses both points (i) and (ii) above. For example, it can be accounted for in pentamethylferrocene by comparing the 13C resonances of this molecule with those of ferrocene and decamethylferrocene.
Due to the symmetry and planarity of the Cp ring and the ring substituents of ferrocene, pentamethylferrocene and decamethylferrocene, the experimental dipole moment3 can be taken to directly reflect the charge difference between the protonated and methylated rings of pentamethylferrocene. A similar approach could not be applied to the chlorinated series since the structures could not be determined†; the unavailability of the Cotton–Mouton constant for decachloroferrocene, Fe(η5-C5Cl5)2, also prevented the determination of σΔχ for this molecule. The following argument is restricted to ferrocene and the methylated ferrocenes.
We define a corrected chemical shift, δ′, as the difference between the experimental NMR shift, δ, and the magnetic anisotropy contribution, σΔχ. The difference Δδ′ is that between δ′ of corresponding C5H5 or C5Me5 rings of pentamethylferrocene, decamethylferrocene and ferrocene resonances. The quantity Δδ′ should then represent the electric field effect σElectronic upon the chemical shift for each type of ring. The final difference between the Δδ′ of the protonated and methylated rings will directly report on the charge difference arising from any interannular charge donation. Using the proportionality constant of −160 ppm electron−1,32,35 the Δδ′ in Table 6 will translate to an equivalent electric charge of 0.011±0.004 electrons per carbon atom.
| Metallocene | Ring | δa /ppm | σΔχb /ppm | δ′c /ppm | Δδ′d /ppm | Δδ′(C5H5)−Δδ′(C5Me5)e |
|---|---|---|---|---|---|---|
| a δ refers to the experimental chemical shift given in Table 2.b σΔχ is given in Table 3.c δ′ is defined to equal δ−σΔχ for either the C5H5 or C5Me5 ring systems.d Δδ′ is the difference between the pentamethylferrocene ring δ′ and the corresponding homoannular ferrocene δ′ value.e A proportionality constant of −160 ppm per electron was used to convert the magnetic resonance shift to a corresponding electric charge. | ||||||
| Fe(η5-C5H5)2 | C5H5 | 68.28 | −5.39 | 73.67 | ||
| 4.77±0.50 (C5H5) | ||||||
| Fe(η5-C5H5)(η5-C5Me5) | C5H5 | 71.53 | −6.91 | 78.44 | −1.80±0.69 ppm | |
| Fe(η5-C5H5)(η5-C5Me5) | C5Me5 | 80.29 | −6.47 | 86.76 | =0.011± 0.004 electrons | |
| 6.57±0.47 (C5Me5) | ||||||
| Fe(η5-C5Me5)2 | C5Me5 | 78.73 | −1.46 | 80.19 | ||
This means that the ring carbon atoms are experiencing a chemical shift arising from a charge of 0.0112±0.0043 electrons. Now turning to the dipole moment data3 and the crystal structure2 it is found that the assigned charges, required to reproduce the measured dipole moment of (3.00±0.07)×10−30 C m, are not sensitive to the charge locations within the rings of the molecule. Thus, by fixing a single point charge in the ring or partitioning the charge between the ring carbon atoms, we determine a total charge of 0.056±0.001 electrons per ring. Assigning this charge to the ring carbons results in an average ring carbon charge of 0.0112±0.0003 electrons per ring carbon atom, in excellent accord with the value determined from the corrected 13C resonance differences.
The outcome of this analysis is that the model presented for the σΔχ determinations is self-consistent and reproduces the magnetic shielding fairly accurately for distances of the order of several bond lengths. Furthermore, the sense of the dipole moment is determined from the chemical shift analysis, such that the negative end is located in the C5H5 ring of pentamethylferrocene and the positive end lies in the C5Me5 ring. This is in accord with the hyperconjugative character of alkyl groups,36 feeding electronic charge into the conjugated aromatic system across to the C5H5 ring.
Acknowledgements
Helpful discussions with Associate Professors F. Separovic and M. K. Cooper on the general trend of the NMR parameters and the syntheses, respectively, are gratefully acknowledged. Thanks must go to Professor N. J. Hush for discussing the electric field dependence, to Professor G. L. D. Ritchie for allowing the use of the Cotton–Mouton effect apparatus, and especially to Dr B. Cornell for support and the use of computing facilities.References
- L. Phillips, J. Chem. Soc., Dalton Trans., 1994, , 3257 RSC.
- L. Phillips, A. R. Lacey and M. K. Cooper, J. Chem. Soc., Dalton Trans., 1988, 1383 RSC.
- L. Phillips and S. W. Filipczuk, J. Mol. Liq., 1991, 47, 261 CrossRef CAS.
- S. W. Filipczuk and L. Phillips, J. Mol. Liq., 1994, 59, 13 CrossRef CAS.
- K. N. Brown, P. T. Gulyas, P. A. Lay, N. S. McAlpine, A. F. Masters and L. Phillips, J. Chem. Soc., Dalton Trans., 1993, 835 RSC.
- G. L. D. Ritchie, M. K. Cooper, R. L. Calvert, G. R. Dennis, L. Phillips and J. Vrbancich, J. Am. Chem. Soc., 1983, 105, 5215 CrossRef CAS.
- R. J. W. Le Fèvre, P. H. Williams and J. M. Eckert, Aust. J. Chem., 1965, 18, 1133.
- C. G. Le Fèvre and R. J. W. Le Fèvre, in Techniques of Chemistry, ed. A. Weissberger, Wiley–Interscience, New York, 1972, Pt. IIIc, vol. 1, ch. 6, p. 399. Search PubMed.
- L. Phillips and G. R. Dennis, J. Chem. Soc., Dalton Trans., 1995, 1469 RSC.
- M. P. Brereton, M. K. Cooper, G. R. Dennis and G. L. D. Ritchie, Aust. J. Chem., 1981, 34, 2253 CAS.
- M. R. Battaglia and G. L. D. Ritchie, J. Chem. Soc., Faraday Trans. 2, 1977, 73, 209 RSC.
- P. B. Lukins, A. D. Buckingham and G. L. D. Ritchie, J. Phys. Chem., 1984, 88, 2414 CrossRef CAS.
- A. D. Buckingham, W. H. Prichard and D. H. Whiffen, Trans. Faraday Soc., 1967, 63, 1057 RSC.
- H. Kling, E. Dreier and W. Hüttner, J. Chem. Phys., 1983, 78, 4309 CrossRef CAS.
- H. M. McConnell, J. Chem. Phys., 1957, 27, 226 CrossRef CAS.
- J. A. Pople, Proc. R. Soc. London, A, 1957, 239, 550 Search PubMed.
- A. D. Buckingham and P. J. Stiles, Mol. Phys., 1972, 24, 99 CAS.
- J. W . Perram and P. J. Stiles, Proc. R. Soc. London A, 1976, 349, 125 Search PubMed.
- P. J. Stiles, Chem. Phys. Lett., 1975, 30, 259 CrossRef CAS.
- J. W. ApSimon, W. G. Craig, P. V. Demarco, D. W. Mathieson, L. Saunders and W. B. Whalley, Chem. Commun., 1966, , 359 RSC.
- J. W. ApSimon, W. G. Craig, P. V. Demarco, D. W. Mathieson, A. K. G. Nasser, L. Saunders and W. B. Whalley, Chem. Commun., 1966, , 754 RSC.
- J. W. ApSimon, W. G. Craig, P. V. Demarco, D. W. Mathieson, L. Saunders and W. B. Whalley, Tetrahedron, 1967, 23, 2339 and 2357 CrossRef CAS.
- J. W. ApSimon, P. V. Demarco, D. W. Mathieson, W. G. Craig, A. Karim, L. Saunders and W. B. Whalley, Tetrahedron, 1970, 26, 119 CrossRef CAS.
- D. W. Davies, Mol. Phys., 1963, 6, 489 CAS.
- R. J. Pugmire and D. M. Grant, J. Am. Chem. Soc., 1968, 90, 697 CrossRef CAS.
- G. L. Nelson, G. C. Levy and J. D. Cargioli, J. Am. Chem. Soc., 1972, 94, 3089 CrossRef CAS.
- V. Graves and J. J. Lagowski, Inorg. Chem., 1976, 15, 577 CrossRef CAS.
- J. Evans and J. R. Norton, Inorg. Chem., 1974, 13, 3042 CrossRef CAS.
- J. G. Batchelor, J. H. Prestegard, R. J. Cushley and S. R. Lipsky, J. Am. Chem. Soc., 1973, 95, 6358 CrossRef CAS.
- A. D. Buckingham, in Physical Chemistry. An Advanced Treatise, ed. H. Eyring, D. Henderson and W. Yost, Academic Press, New York, 1970, vol. 4, ch. 8, p. 349. Search PubMed.
- A. Haaland and J. E. Nilsson, Acta Chem. Scand., 1968, 22, 2653 Search PubMed.
- H. Spiesecke and W. G. Schneider, Tetrahedron Lett., 1961, , 468 CrossRef CAS.
- P. C. Lauterbur, J. Am. Chem. Soc., 1961, 83, 1838 CrossRef CAS.
- H. Spiesecke and W. G. Schneider, J. Chem. Phys., 1961, 35, 722 CrossRef CAS.
- G. A. Olah and G. D. Mateescu, J. Am. Chem. Soc., 1970, 92, 1430 CrossRef CAS.
- C. A. Coulson, in Valence, ed. R. McWeeny, Oxford University Press, Oxford, 3rd edn., 1979, ch. 12, pp. 381–383. Search PubMed.
- A. Almenningen, A. Haaland, S. Samdal, J. Brunvoll, J. L. Robbins and J. C. Smart, J. Organomet. Chem., 1979, 173, 293 CrossRef CAS.
- P. Seiler and J. D. Dunitz, Acta Crystallogr., Sect., B, 1979, 35, 1068 CrossRef.
- D. P. Freyberg, J. L. Robbins, K. N. Raymond and J. C. Smart, J. Am. Chem. Soc., 1979, 101, 892 CrossRef CAS.
- G. L. D. Ritchie and J. Vrbancich, Aust. J. Chem., 1982, 35, 869 CAS.
- A. A. Bothner-By and J. A. Pople, Annu. Rev. Phys. Chem., 1965, 16, 43 CrossRef CAS.
- R. J. W. Le Fèvre and D. S. N. Murthy, Aust. J. Chem., 1966, 19, 179 CAS.
- G. Foex, Constantes Sélectionées, Diamagnétisme et Paramagnétisme: Tables de Constantes et Données Numériques, Masson, Paris , 1957, ch. 1. Search PubMed.
Footnote |
| † Several unseccessful attempts were made to determine X-ray crystal and electron diffraction structures in our own and other laboratories. |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2000 |
