Neutron reflectivity studies of the structure of polymer/polymer and polymer/substrate interfaces at the nanometer level

Abstract

We review the use of neutron reflectivity as a probe of organic thin films, concentrating on its application to study buried interfaces in thin polymer films. For an interface between immiscible polymers of relatively low molecular weight, we find a width greater than that observed for higher molecular weight species, and we find that the width grows with time either logarithmically or following a weak power law. The conformation of a layer of very high molecular weight polymer chains chemically grafted to a silicon interface and coated by a chemically different polymer matrix is studied as a function of temperature, which controls the thermodynamic interaction between the grafted chains and the chemically different matrix chains. At high temperatures the layer abruptly changes from an extended conformation to one with a sharp interface with the matrix layer.

---

Introduction

Neutron reflection as a probe of interfaces and thin films

Neutron reflection has emerged in the last fifteen years as a powerful tool for the study of surface and interface structure in organic thin films. The wavelength of cold neutrons is of the order of a few tenths of nanometers, and this sets the length-scales probed by reflection experiments; typically such an experiment is sensitive to structural features perpendicular to the plane of the film with length scales between 0.5 and 50 nm. Two other advantages of neutrons make them particularly suited to studying organic thin films: their penetrating power is substantially greater than, for example, X-rays, so it is straightforward to study buried interfaces, and the great difference in neutron scattering length density between deuterium and hydrogen makes possible experiments using isotopic substitution.

Fig. 1 shows a schematic diagram of a neutron reflectivity experiment as it would be carried out at a pulsed neutron source such as ISIS at the Rutherford Appleton Laboratory.¹ A white neutron beam, with a wavelength range of order 2–6 Å or so, is incident on the sample at a grazing angle of incidence, which is typically between 0.3 and 1.5°. Neutrons specularly reflected are detected and sorted by wavelength using their time-of-flight. If one is interested solely in the specular reflection a single detector can be used, but often a linear or two dimensional position sensitive detector is used instead, which has the advantage that the intensity of neutrons scattered out of the specular direction can also be monitored. After data processing the output of the instrument is a graph of the reflection coefficient of the neutrons as a function of their wavelength, or perhaps more conveniently as a function of the change in wave-vector on reflection—the scattering vector Q, which is related to the wavelength of the neutrons λ and the grazing angle of incidence θ by the expression Q = [4π sin(θ)]/λ.

Fig. 1 Schematic diagram of a neutron reflectometer—CRISP, at the Rutherford Appleton Laboratory.

Interpretation of neutron specular reflectivity data is relatively straightforward in principle. Neutrons interact with matter only via nuclear forces; the interaction with a nucleus of a given isotope is characterised by the scattering length. The range of the interaction is very small compared to the wavelength of the neutron; in these circumstances the interaction of the neutron with matter can be represented by the interaction with a smooth Fermi pseudo-potential. The value of this potential in a region of space is determined by the total density of scattering lengths summed over all the nuclei in that region. Thus the problem of propagation of neutrons through matter is reduced to one of solving Schrödinger's equation for a potential whose value can be determined for a given material knowing its density and isotopic composition. If one considers reflection from a film that only has composition variations perpendicular to the plane of the film, then one can separate the variables in Schrödinger's equation to arrive at a one dimensional equation, which can be solved to give the reflection coefficient as a function of the scattering vector Q and the potential as a function of perpendicular distance from the surface V(z). This potential is itself related by simple arithmetic to the concentration profiles of the isotopes making up the sample.

In practice data analysis has a number of difficulties. Firstly, since the reflectivity profile is determined only by the potential V(z) if the sample contains more than two unknown compositions then the composition profile cannot be uniquely determined. Secondly, there is no reliable way of inverting a neutron reflectivity profile to recover a unique potential profile V(z); instead a plausible trial function needs to be used as a starting point and its parameters refined until a best fit is achieved between the experimental and predicted reflectivity profiles. This means that neutron reflectivity is quite unsuitable for analyzing films of unknown composition; instead it should be considered as a tool for characterising the structure of thin films at high resolution when their morphology is already known at some coarse level and one has some knowledge of the materials from which they are composed. Neutron reflection is at its most powerful when samples are specially made for the technique, preferably using a scheme of labeling selected components with deuterium substituted for hydrogen. In addition, any additional information that can be obtained about the sample from other techniques, for example a total film thickness as obtained from ellipsometry, is invaluable in aiding data analysis.

Among the areas for which neutron reflection has proved valuable in the study of organic thin films are the characterisation of interfaces between immiscible polymers, including their modification by interfacially active materials such as block copolymers, the study of segregation to surfaces and interfaces in mixed polymer films, and the study of the self-assembly of block copolymers into lamellar phases. Early work was reviewed in a comprehensive article by Russell;² for a more recent review concentrating on work carried out at the Rutherford Laboratory see Penfold et al.¹

In this article we highlight the value of neutron reflection for the study of organic thin films by presenting recent data in two areas, the structure of the interface between two immiscible, amorphous polymer thin films, and the conformation of chains grafted at an interface between an inorganic substrate and a thin polymer film.

The interface between immiscible polymer thin films

The interface between two polymers which are immiscible in the bulk is not atomically sharp; a broadening of such an interface, by increasing the number of configurations available to chains near the interface, increases the entropy sufficiently to offset the larger number of energetically unfavourable interactions between segments of the immiscible polymers. An accurate statistical mechanical theory of this effect was developed by Helfand,³ but using the techniques available at the time it was not possible to test this quantitatively. It was realised soon after the development of neutron reflectivity as a technique for interfacial analysis that this was an ideal application; the predicted length scale of the interfacial broadening, in the range 20–50 Å, fell within the range for which neutron reflectivity is most sensitive. Two groups made measurements on the interface between polystyrene and poly(methyl methacrylate), and despite using different materials and different instruments found results identical within error.^4,5 The interfacial profile could be described by a so-called tanh profile, given by eqn. (1),

where the width of the interface 2w_I took the value 50 Å. The agreement between the two experiments was encouraging, as was the fact that the value was of the correct order of magnitude predicted by theory, but less encouraging was the fact that the exact value predicted by theory was 30 Å. The discrepancy is much larger either than the experimental error of the measurements (which is of order ±5 Å) or the uncertainties in the values of the parameters needed to go into the theory.

Recent work has clarified the origin of this discrepancy.^6–8 The self-consistent field theory approach of Helfand is a mean-field theory, and as such it neglects the effects of thermodynamic equilibrium fluctuations. Although these experiments are conducted a long way away from a critical point, so that bulk composition fluctuations should not be important, it turns out that interfacial fluctuations of the interface are always significant. These fluctuations take the form of capillary waves with a wide range of wavelengths and random directions and phases, whose amplitudes are given by the principle of equipartition of energy. The interface can thus be thought of as being composed of an intrinsically diffuse interface, characterised by a certain interface width w_I, which itself is roughened by the superposition of random capillary waves (see Fig. 2). It can be shown that the total width of the interface, taking account of both the intrinsic diffuseness and the capillary waves, can be written as eqn. (2).

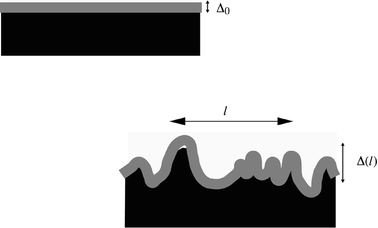Fig. 2 The capillary wave picture of an interface between immiscible polymers. In the mean field picture (top) a planar interface is characterised by a certain intrinsic diffuseness Δ₀. This picture needs to be modified to account for capillary waves (bottom)—superposed on the intrinsic diffuseness is a roughness due to thermally excited capillary waves. The total measured roughness Δ(l) depends on the lengthscale l of the largest wavelength capillary wave which contributes to the roughness.

In this equation Δ is the total root mean squared roughness of the interface as measured, for example, by neutron reflectivity. The contribution of the intrinsic diffuseness to this roughness is measured by Δ₀, which is related to the intrinsic interface width 2w_I by eqn. 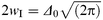(3).

σ₀ is the interfacial tension between the two immiscible phases. A curious feature of eqn. (2) is that when one sums over all possible capillary waves, the total contribution to the width of the interface diverges logarithmically. Thus an additional length-scale, l, must be introduced to cut off the divergence—this represents the longest wavelength of capillary wave contributing to the roughness. The origin of this cut-off varies with the system under investigation and the technique used to measure it. Ultimately, very large capillary waves would be suppressed by gravity; for typical polymer systems this cut-off length would correspond to about 10 mm. In a neutron reflectivity experiment, contributions to the roughness arising from capillary waves with a wavelength larger than the lateral coherence length of the neutrons will not contribute to the roughness as measured by the reflectivity; this provides an effective cut-off determined by the geometry of the collimation of the neutrons which is of the order of microns. Finally, if one of the two films is very thin, dispersion forces acting across the film can act in the same way as gravity to suppress the capillary waves; this leads to a cut-off which depends on film thickness and thus an apparent interface width that varies logarithmically with the film thickness. Such a dependence has been observed,⁸ and indeed this dependence provides the strongest evidence for the importance of capillary waves in broadening the interface. These experiments show that the self-consistent field theory modified by the capillary wave correction does account quantitatively for observed interface widths between immiscible polymer films.

In this paper we consider a problem with two new aspects—we look at interfaces between immiscible polymers at much lower molecular weight than our previous experiments, and we explicitly consider the time dependence of the development of the interface. The classical self-consistent field theory considers polymers in the limit of infinitely high molecular weight; for finite molecular weights we expect the interface to be somewhat broader. The corrections to the infinite molecular weight result should be of order (χN)⁻¹, where N is the degree of polymerisation and χ is the Flory–Huggins interaction parameter, but there is disagreement on the precise form of the correction.^9–11 Some experimental results have been obtained, but only in the case where the molecular weight of only one of the polymers was reduced.¹² These results showed semi-quantitative agreement with the prediction of Broseta, but this was without properly taking into account the correction for capillary waves. Ultimately, if the molecular weight is very low we reach the critical point for miscibility, at which the interfacial width diverges to infinity. According to mean field theory the interfacial width in the critical region takes the form of eqn. (4),

where χ_crit is the value of the Flory–Huggins interaction parameter at the critical point.¹³ This expression must in reality be modified to take into account both capillary waves and bulk composition fluctuations, with the effect that very close to the critical point the mean-field exponent of −½ will be replaced by a non-classical exponent.¹⁴

The dynamics of the formation of interfaces between immiscible polymers are not currently well understood. In the limit of large degrees of immiscibility, a narrow intrinsic interface may come to equilibrium quite rapidly as the formation of such an interface—whose width is much smaller than the overall chain dimensions—will be governed by polymer motion on the segment level rather than by the diffusion of whole chains. On the other hand, the broadening of the interface by capillary waves will take much longer as the growth of these waves requires hydrodynamic flows of the polymer melt. In fact, on dimensional grounds one can argue that the largest wavelength of capillary wave l(t) that has had time to come to equilibrium after time t must scale like eqn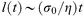. (5),

where η is the viscosity of the polymer and σ₀ is the interfacial tension. If this time dependent length is regarded as the cut-off length for capillary waves in eqn. (2) then we arrive at the prediction that the time dependence of the growth of the interfacial width for highly immiscible polymers should be essentially logarithmic. Such a dependence has indeed been observed for the time dependence of the development of interfacial width between high molecular weight polystyrene and PMMA.¹⁵

The situation must be different for polymer pairs closer to their critical point, where the initial diffusive broadening of the interface must be significant. Here theory predicts that the broadening of the interface follows a power law time dependence with exponent 0.25.¹⁶ Experiments have been done in this regime for polymers of high molecular weight but small unfavourable thermodynamic interactions; one set of data is in agreement with this prediction,¹⁷ while another suggested a slightly higher exponent of 0.34.¹⁸ These theories, however, do not take into account fluctuations, either of the bulk composition or of the position of the interface.

The conformation of chains grafted at an interface between a polymer film and an inorganic substrate

The interface between a polymer thin film and a substrate can be rather easily modified by arranging for some polymer chains to be physically adsorbed or chemically grafted to the substrate. If the grafting is done in such a way that polymer chains are attached to the interface by one end, with the rest of the chain able to interpenetrate the free polymer that makes up the film (the ‘matrix'), the resulting grafted layer is often known as a ‘polymer brush'; such a layer may be useful for stabilising the film against dewetting¹⁹ or modifying the adhesion between the film and the substrate.²⁰ Indeed, a polymer brush may be considered to be a simple, well-controlled model for the types of interphase that occur in composite materials.

The conformation of polymers arises from a balance between the configurational entropy of the chains in the brush, which resists their being stretched too far out into the matrix, the excluded value interaction between different segments in the same brush chain, which tends to make the brush stretch out to minimise these interactions, and the nature of the interaction between the brush chains and the matrix chains.^21,22 If this interaction is favourable, so that the free energy is reduced if the brush and matrix chains mix, then the brush chains will tend to stretch out into the matrix forming a diffuse, extended layer. On the other hand, if the interaction is unfavourable, the brush chains will shrink back towards the substrate, forming a much more compact layer with a sharper interface with the matrix. Indeed, in some circumstances one expects a brush in a very unfavourable matrix to develop a lateral, microphase separated structure of ‘bundles'.²³ Theories exist which predict the brush structure as a function of the molecular weight of the brush chains and the matrix chains, the density of grafting of the brush and the Flory interaction parameter between segments of the brush and matrix chains.²⁴ An important qualitative distinction is illustrated in Fig. 3. For relatively low grafting densities (top), the grafted chains are too far away to interact with each other and we have a series of grafted coils whose conformation is not strongly perturbed from bulk conformations (this situation has been referred to in the literature as ‘mushrooms'). As the grafting density increases (centre), the individual grafted chains start to overlap. However, if the molecular weight of the matrix chains is relatively high the excluded volume interactions between segments in different grafted chains are screened, and the conformation of individual grafted chains is still not strongly perturbed. This situation changes when a certain critical grafting density is reached, and excluded volume interactions force the grafted chains to stretch out into the matrix, forming a stretched brush.

Fig. 3 Schematic of the conformation of grafted chains as a function of grafting density and quality of thermodynamic interaction with the matrix. At low grafting densities, the chains do not interact and adopt conformations close to ideal random walks (top)—in this situation the chains are referred to as ‘mushrooms'. As the grafting density increases the chains physically overlap (centre), but the conformations remain unperturbed as long as the matrix chains screen out the excluded volume interaction between segments of the grafted chains. When the screening is no longer effective (bottom) the excluded volume interaction forces the chains to stretch out, resulting in a ‘brush'.

In previous work we have used neutron reflectivity to characterise both physically and chemically grafted polymer brushes in the case where the matrix polymer was chemically identical to the brush polymers, though not necessarily of the same molecular weight.^25,26 A brush in a matrix of comparable molecular weight formed a relatively compact layer, extending a distance of the order of a radius of gyration into the matrix. As the matrix molecular weight was decreased, the brush became more extended and its interface with the matrix more diffuse, reflecting the growing importance of the excluded volume interaction between brush segments as the matrix polymer became more like a good solvent. The segment density profiles of the polymer brushes were in quantitative agreement with the results of self-consistent field theory. In another set of experiments, we looked at the situation where the matrix polymer and grafted polymer were chemically different.²⁷ Here, we chose a situation in which the thermodynamic interaction between the brush chain and the matrix chain could be changed by changing the temperature; the brush chains were polystyrene, while the matrix was poly(vinyl methyl ether) (PVME). At low temperatures, the interaction between polystyrene and PVME is favourable, the two polymers being completely miscible. As the temperature is increased the interaction becomes less favourable, with a lower critical solution temperature appearing in the phase diagram. When we increased the temperature from room temperature, we measured a gradual and reversible change in conformation of the brush. At low temperatures, the interaction was favourable, and the brush was relatively compact, with a sharp interface with the matrix polymers. Raising the temperature resulted in the brush collapsing to a much more compact state. These results could be accounted for using a scaling theory to describe the stretched brush.

In this paper we present results for the temperature response of a very high molecular weight brush grafted at a substantially lower density than these earlier measurements. Anticipating the results, we find in this case rather different results to the situation for a lower molecular brush at a higher grafting density. Rather than having a gradual collapse of the brush over a wide temperature, we get a much more abrupt change. This is perhaps more closely analogous to the way the chain dimensions of an isolated chain in bulk would change, with a sharp coil/globule transition, reflecting the fact that for these less densely grafted chains interactions between different grafted chains are much less important.

Experimental

Preparation of polymer bilayers

For the experiments probing the interface between immiscible polymers, poly(methyl methacrylate) (PMMA) and deuterated polystyrene (dPS) were bought from Polymer Laboratories. The polymers had been prepared by anionic polymerisation, and had molecular weights of 10 000 (dPS) and 7600 (PMMA), and polydispersity indices of 1.1 or less. To make the bilayer samples, a PMMA film of thickness around 2200 Å was spun cast onto a 5 cm silicon wafer, which previously had been cleaned using a nitric acid–hydrogen peroxide solution. A dPS film of thickness around 1400 Å was spun cast onto a glass slide and then transferred onto the PMMA film by floating it off the glass onto a water bath and picking it up from the surface of the water with the PMMA covered silicon. The samples were then dried in a vacuum oven at 60 °C, before being annealed at various temperatures for various times.

Preparation of grafted polymer layers

The starting point for the chemically grafted layers was deuterated polystyrene with a carboxy end group, purchased from Polymer Laboratories. This had been synthesised by anionic polymerisation, and had a molecular weight of 760 000. A previously published procedure was used to link a triethoxysilane group to the chain via the carboxy group;²⁶ reaction of the triethoxysilane group with silanol groups at the surface of the native oxide of the silica grafts the polymer chain to the substrate. The grafting was achieved by spin-coating a solution of the triethoxysilane terminated polystyrene in toluene onto the surface of a cleaned silicon wafer to form a polymer layer about 500 Å in thickness. This sample was then annealed at a temperature above the glass transition temperature of the polystyrene, allowing the end-groups to find their way to the substrate and react. Unreacted polymer was removed by repeated washing with toluene. The grafted dPS layer was then coated with a spin-coated layer of poly(vinyl methyl ether) (PVME), obtained from Scientific Polymer Products, with a nominal weight average molecular weight of 99 000 and a polydispersity index of 2.1. The thickness of this layer was around 5000 Å.

Neutron reflectivity measurements and analysis

After annealing, the samples were analysed by neutron reflectivity at the spallation source ISIS at the Rutherford Appleton Laboratory, on one or other of the two reflectometers CRISP and SURF. Both instruments are time-of-flight instruments operating with a wavelength range of about 0.5 to 6.5 Å. In order to obtain data over a sufficiently wide range of scattering wavevectors Q it is necessary to obtain data at two or three angles of incidence between 0.25 and 1.5°, giving a Q range between 0.008 and 0.3 Å⁻¹. Data analysis is carried out using a computer program which calculates reflectivities according to a recursive algorithm and adjusts the parameters of a model profile to obtain a best fit with data.

Results and discussion

The interface between low molecular weight, immiscible polymers

Fig. 4 shows reflectivity profiles obtained for a bilayer sample of dPS and PMMA, in this case following annealing at 120 °C for times up to two hours (successive curves have been shifted down a factor of 10 for clarity). The profiles show a reflectivity of unity at low values of Q; this corresponds to total external reflection of the neutron beam. Above a critical value of Q the reflectivity falls away rapidly, with oscillations arising from interference from waves reflected from the top surface and the dPS/PMMA interface. As the interface between dPS and PMMA becomes less sharp on annealing, the visibility of the fringes at high values of Q decreases; fitting the curve to a simple two layer model with gaussian roughness between the two layers allows one to extract the value of the interfacial roughness with some precision. Fig. 5 shows the fitted values of interfacial roughness as a function of annealing time. The values for annealing times of 60 and 150 min are the same within error at Δ = 28 ± 3 Å. This would correspond to a value of the width of a tanh profile, as defined by eqn. (1), of 2w_I = 70 Å. This is significantly bigger than the value of 50 Å obtained for high molecular weight polymers,^4,5 showing already that molecular weight does have a significant effect on the interfacial width.

Fig. 4 Reflectivity curves as measured for a bilayer consisting of a thin film of deuterated polystyrene, of molecular weight 10 000, on a film of poly(methyl methacrylate), molecular weight 7600, supported on a silicon substrate. The curves are measured following different annealing times at 120 °C. Successive reflectivity curves are shifted downwards by a factor of ten for clarity; the top curve is for an annealing time of 5 min, and successive curves, reading downwards, are for annealing times of 10, 20, 45, 60 and 150 min.

Fig. 5 Interfacial roughness between films of deuterated polystyrene and poly(methyl methacrylate) as a function of annealing time at 120 °C, as determined from the neutron reflectivity curves shown in Fig. 4. The solid line is a fit to a logarithmic growth law, while the dotted line is a fit to a power law; see text for details.

Broseta's theory⁹ predicts an intrinsic interface width of 44 Å for this combination of molecular weights, corresponding to a contribution to the roughness of 17.6 Å. Thus the observed roughness must include a substantial contribution from capillary waves, which we can estimate as 22 Å (this is obtained by subtracting in quadrature the theoretical intrinsic roughness from the experimental value). To make a theoretical estimate of the contribution of capillary waves to the roughness we need to know the lateral coherence length of the neutrons and the interfacial tension. Our previous experiments indicated a value of 20 µm for the coherence length;⁸ (the calculation does not require a highly precise value as l appears inside a logarithm). The interfacial tension is more difficult, as this itself depends on molecular weight. Broseta et al.⁹ have given a formula for the molecular weight dependence, from which we estimate a value of 0.7 mJ m⁻². Using these values, we find that the contribution of capillary waves to the interfacial width—the second term in eqn. (2)—is 32 Å, substantially bigger than that we have deduced. There are three possible explanations. The first is that the Broseta theory overestimates the increase in interfacial width that results from finite molecular weight. The second is that our estimate of the interfacial tension is too low. The third is that the upper cut-off length l we have chosen is too large, either because we have overestimated the lateral coherence length of the neutrons, or because the sample has not yet reached equilibrium.

More insight is obtained when the kinetics are considered. Fig. 5 shows that an interfacial roughness value of around 10 Å is attained rather rapidly, with a subsequent increase towards the equilibrium value over a time of the order of an hour or so. We can interpret this in terms of the capillary wave picture by assuming that the intrinsic interface width is achieved relatively fast, and that the subsequent slow rise in interfacial thickness is due to capillary waves of progressively larger wavelength coming to equilibrium. As discussed in the introduction, we can interpret eqn. (2) as applying to the non-equilibrium case by assuming that the cut-off length l is interpreted as a time-dependent length representing the longest wavelength that has had a chance to come to equilibrium. This predicts a logarithmic dependence on time; the solid line on Fig. 5 shows the best fit of such a law to our data, showing satisfactory agreement. If the dependence of the cut-off length on time is linear this fit implies an interfacial tension of 0.43 mJ m⁻², of the right order of magnitude but somewhat smaller than we estimated above. We should, however, be cautious about this interpretation, as it is difficult on limited data to distinguish between logarithmic growth and a weak power law. The dotted line shows a best power law fit, with growth proportional to t^0.28. The exponent of 0.28 is close to the value of 0.25 predicted for the growth of interfacial width in near-critical interfaces. Thus it is difficult with the present set of data and our current level of theoretical understanding to distinguish definitely between these two approaches.

High molecular weight polymer grafted at a polymer/non-polymer interface

We now move on to consider the interface between a polymer film and an inorganic substrate as modified by a grafted polymer layer. In this case experiments were done in which a grafted polystyrene layer in a poly(vinyl methyl ether) matrix was heated in situ during the neutron reflectivity run. Fig. 6 shows the neutron reflectivity profiles obtained for one such sample, for which the thickness of the dPS grafted layer before coating was 66 Å. The profiles show little change as the sample is heated from room temperature to 100 °C. However, when it is heated from 100 to 110 °C a dramatic change occurs: the reflectivity drops away at the critical Q more quickly and a fringe develops. This is diagnostic of a much more abrupt layer forming; from the fits indicated by solid lines the volume fraction profiles in Fig. 7 were obtained. These show that at low temperatures the grafted layer formed a diffuse layer whose size is comparable to the unperturbed radius of gyration of the grafted chains, 234 Å. But at high temperatures the grafted chains collapse to form a layer with a sharper interface with the matrix. Interestingly, rather than collapsing to a compact layer against the substrate, the volume fraction of grafted chains at the surface is substantially less than unity. One possible way to account for this surprising result is that the grafted chains have microphase separated, forming bundles of dPS close to the wall, with much of the wall in direct contact with the PVME matrix.²³ In the future it might be possible to examine such scenarios using off-specular neutron scattering. This technique in principle can probe the lateral structure of thin films,²⁸ though experimental difficulties have so far inhibited its widespread use.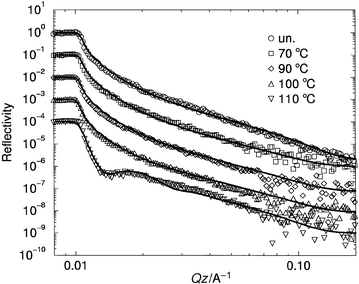

Fig. 6 Reflectivity curves for an end-grafted layer of deuterated polystyrene, molecular weight 760 000, in a matrix of poly(vinyl methyl ether), as a function of temperature. Successive reflectivity curves are shifted downwards by a factor of ten for clarity.

Fig. 7 Volume fraction profiles of an end-grafted layer of deuterated polystyrene in a matrix of poly(vinyl methyl ether) as a function of temperature, as extracted from the neutron reflectivity curves shown in Fig. 6. The solid line is the volume fraction profile which fits the data for room temperature and all temperatures up to 100 °C, and the dotted line is the profile at 110 °C.

Conclusion

Neutron reflectivity provides a powerful way of characterising buried interfaces in thin polymer films. For well characterised samples, it is possible to probe such interfaces with nanometer resolution. We have illustrated this for two systems; in one we study the structure of the interface between two immiscible polymer films. Here neutron reflectivity reveals that in addition to an intrinsic diffuseness the interface has thermally excited capillary waves, which play an important role both in determining the total width of the interface at equilibrium and in controlling its dynamics. In the other experiments we study the conformation of a layer of polymer chains chemically grafted to a substrate; the structure of such a layer responds to a changing thermodynamic interaction between free and grafted chains. In the future we can expect neutron reflectivity to be applied to similar problems in a wider variety of systems, and for the technique to be developed in a way which will provide a greater understanding of interfaces in these systems. This will include the use of off-specular neutron reflectivity to obtain information on in-plane correlations, and greater use of kinetic and real-time measurements to probe dynamics.

References

1. J. Penfold, R. M. Richardson, A. Zarbakhsh, J. R. P. Webster, D. G. Bucknall, A. R. Rennie, R. A. L. Jones, T. Cosgrove, R. K. Thomas, J. S. Higgins, P. D. I. Fletcher, E. Dickinson, S. J. Roser, I. A. McLure, A. R. Hillman, R. W. Richards, E. J. Staples, A. N. Burgess, E. A. Simister and J. W. White, J. Chem. Soc., Faraday Trans., 1997, 93, 3899.
2. T. P. Russell, Mater. Sci. Rep., 1990, 5, 171.
3. E. Helfand and Y. Tagami, J. Chem. Phys., 1971, 56, 3592.
4. M. L. Fernandez, J. S. Higgins, J. Penfold, R. C. Ward, C. Shackleton and D. Walsh, Polymer, 1988, 29, 1923.
5. S. P. Anastasiadis, T. P. Russell, S. K. Satija and C. F. Majkrzak, J. Chem. Phys., 1990, 92, 5677.
6. K. R. Shull, A. M. Mayes and T. P. Russell, Macromolecules, 1993, 26, 3929.
7. A. N. Semenov, Macromolecules, 1994, 27, 2732.
8. M. Sferrazza, C. Xiao, R. A. L. Jones, J. Penfold and J. Webster, Phys. Rev. Lett., 1997, 78, 3693.
9. D. Broseta, G. H. Fredrickson, E. Helfand and L. Leibler, Macromolecules, 1990, 23, 132.
10. A. V. Ermoshkin and A. N. Semenov, Macromolecules, 1996, 29, 6294.
11. H. Tang and K. F. Freed, J. Chem. Phys., 1991, 94, 6307.
12. D. W. Schubert and M. Stamm, Europhys. Lett., 1996, 35, 419.
13. K. Binder, J. Chem. Phys., 1983, 79, 6387.
14. J. S. RowlinsonB. Widom, Molecular theory of capillarity, Clarendon Press, Oxford, 1982..
15. M. SferrazzaR. A. L. JonesJ. PenfoldD. BucknallJ. R. P. Webster, to be published. .
16. S. Puri and K. Binder, Phys. Rev. B: Condens. Matter, 1991, 44, 9735.
17. B. Guckenbiehl, M. Stamm and T. Springer, Phys. B, 1994, 198, 127.
18. U. Steiner, G. Krausch, G. Schatz and J. Klein, Phys. Rev. Lett., 1990, 64, 1119.
19. R. Yerushalmi-Rozen, J. Klein and L. J. Fetters, Science, 1994, 263, 793.
20. J. W. Smith, E. J. Kramer and P. J. Mills, J. Polym. Sci., Part B: Polym. Phys., 1994, 32, 1731.
21. P. G. de Gennes, Macromolecules, 1980, 13, 1069.
22. H. R. Brown, K. Char and V. R. Deline, Macromolecules, 1990, 23, 3383.
23. C. Yeung, A. C. Balazs and D. Jasnow, Macromolecules, 1993, 26, 1914.
24. K. R. Shull, J. Chem. Phys., 1991, 94, 5723.
25. T. Nicolai, C. J. Clarke, R. A. L. Jones and J. Penfold, Colloids Surf. A: Physicochem. Eng. Aspects, 1994, 86, 155.
26. C. J. Clarke, R. A. L. Jones, J. Edwards and J. Penfold, Macromolecules, 1995, 28, 2048.
27. M. Sferrazza, R. A. L. Jones and D. B. Bucknall, Phys. Rev. E, 1999, 59, 4434.
28. M. Sferrazza, M. Heppenstall-Butler, R. Cubitt, D. Bucknall, J. Webster and R. A. L. Jones, Phys. Rev. Lett., 1998, 81, 5173.

---

Footnote

† Basis of a presentation given at Materials Chemistry Discussion No. 2, 13–15 September 1999, University of Nottingham, UK.

---