In situ characterization of phospholipid coated electrodes†
Philip N. Bartletta, Karen Bracea, Ernesto J. Calvob and Roberto Etcheniqueb
aDepartment of Chemistry, University of Southampton, Southampton, UK SO17 1BJ
bDepartamento de Quimica Inorganica, Analítica y Quimica Fisica, Universidad de Buenos Aires, AR-1428, Buenos Aires, Argentina
First published on UnassignedUnassigned22nd December 1999
Abstract
Four in situ techniques, quartz crystal microbalance, electrochemical impedance spectroscopy, ellipsometry and atomic force microscopy, have been used to study the deposition of dioleoylphosphatidylglycerol (DOPG) films from vesicle solution onto 1-decanethiol coated gold surfaces. The experiments show that, although no one technique can give an unequivocal picture of the deposition process and structure of the final film, by combining the results from the four different techniques a consistent picture emerges. Initially, over the first 200 s a monolayer of DOPG is formed on the 1-decanethiol coated surface. Then at longer times and in the presence of 0.1 M NaCl and 0.1 M TRIS buffer at pH 8 a further bilayer of DOPG is deposited on top of this initially formed monolayer. Evidence for this is provided by the quartz crystal microbalance measurements and from atomic force microscopy. The results from electrochemical impedance measurements and ellipsometry are consistent with these findings but these two methods are less able to distinguish between the formation of the monolayer and subsequent deposition of the bilayer on top of the monolayer. For DOPG films, where the head group is negatively charged at pH 8, the ionic strength of the solution has an important effect in controlling the deposition of the bilayer on top of the initially formed monolayer.
Introduction
Phospholipid membranes assembled on to a rigid support are more stable and easier to use than conventional phospholipid membrane assemblies such as black lipid membranes and Langmuir–Blodgett films. In addition to fundamental biological research, supported phospholipid membranes have potential applications as biosensors for the numerous biologically significant analytes that act at, or within, the cell membrane. Examples include the use of supported phospholipid membranes incorporating membrane bound enzymes as amperometric biosensors,1 their use with ion channel switches,2–6 and to detect the binding of species to membrane bound binding sites.7,8 Our interest is in developing electrochemical microsensors for the rapid determination of phospholipase enzyme activity9 where the high sensitivity of electrochemical methods could provide an inexpensive and simple alternative to more established analytical techniques.As a part of this research program it is necessary to characterize the assembly of supported phospholipid membranes onto alkanethiol coated electrode surfaces and to study their subsequent removal by reaction with phospholipase enzymes added to the contacting solution. In this paper we describe the results of our studies of the self-assembly of dioleoylphosphatidylglycerol (DOPG) films from vesicle solution on to 1-decanethiol coated gold electrodes using a range of in situ techniques. DOPG has a negatively charged head group at pH 8 and contains a cis double bond half way down both of the C18 alkyl chains. As a result the phase transition temperatures of bilayers of such lipids are below 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C10 and so we assume that all our experiments are conducted with lipid layers in the liquid state. In this paper we show that, whilst the interpretation of the results of any one technique are ambiguous, by combining together results from several different techniques we are able to produce a coherent and consistent picture of these thin films and their assembly.
°C10 and so we assume that all our experiments are conducted with lipid layers in the liquid state. In this paper we show that, whilst the interpretation of the results of any one technique are ambiguous, by combining together results from several different techniques we are able to produce a coherent and consistent picture of these thin films and their assembly.
Electrochemical impedance spectroscopy (EIS) measurements have been extensively used to characterize the integrity of supported phospholipid membranes and to try to model their behavior in terms of the thickness and permittivity of the lipid layer as well as the number and resistance of pores or pinhole defects in the films.3–9,11 Although the different authors use different equivalent circuit models the analyses are all based on an assumed model for the structure of the supported lipid layer. Quartz crystal microbalance (QCM) measurements are well suited to the measurement of the assembly of supported lipid membranes and their properties but the interpretation of the results can be complex. Early studies utilized the Sauerbrey equation to relate the frequency shift of the microbalance directly to mass changes but more recent studies have demonstrated that changes in the viscoelastic properties of these layers can be equally significant.12–16 Since a full description of the layer requires a knowledge of at least four parameters (the film thickness, density and the real and imaginary components of the shear modulus of the film at 10 MHz) and because only two parameters are readily available from the QCM measurement (the real and imaginary components of the electroacoustic impedance at the resonant frequency) the interpretation of the QCM measurements is also model dependent. Surface plasmon resonance (SPR) measurements have widely been used to characterize the kinetics of the self assembly of lipid layers, formed from vesicles, on to coated gold surfaces and to characterize the interactions of these supported lipid layers with solution species.17–22 Whilst the SPR method is well suited to real-time measurements in order to extract average layer thicknesses from the experimental results it is necessary to assume a value for the refractive index of the layer. Spectral ellipsometry22 or surface plasmon resonance spectroscopy21 have been used for the simultaneous independent determination of the refractive index and thickness of these films but both techniques are too slow to allow kinetic measurements. Neither SPR nor ellipsometry gives any information about the number or size of defects within the films. Atomic force microscopy studies23–26 and surface force measurements24 have been used to characterize phospholipid and mixed phospholipid layers assembled on mica surfaces. These studies have generally used films formed by Langmuir–Blodgett deposition. For lipids which form solid films under the conditions of the AFM experiment stable images were obtained but for liquid phase films the layers were easily disrupted by the AFM tip.26
In this paper we present the result of a study of the kinetics of self-assembly of dioleoylphosphatidylglycerol layers on to 1-decanethiol coated gold surfaces using a quartz crystal microbalance, electrochemical impedance spectroscopy, ellipsometry, and atomic force microscopy.
Experimental
Chemicals
Dioleoylphosphatidylglycerol (20 mg cm−3 methanol, Sigma) and 1-decanethiol (Aldrich) were used as received. All electrolyte solutions were a mixture of TRIS buffer (pH 8.0, 0.1 M), prepared from tris(hydroxymethyl)aminomethane (Aldrich, Ultrapure) and HCl (BDH AnalaR, 37%), containing NaCl (0.1 M). All aqueous solutions were prepared using deionized water from a Whatman RO 50 and Stillplus water purification system.Preparation of alkanethiol/phospholipid-coated electrode
The alkanethiol monolayer was deposited onto a freshly cleaned gold electrode via a standard self-assembly procedure. For electrochemical impedance spectroscopy and quartz crystal microbalance experiments, the cleaning procedure consisted of cycling the electrode potential in 0.1 M sulfuric acid (0.01 M in the case of the QCM electrodes) between 0.0 and +1.3 V vs. SCE at 0.1 V s−1 for a minimum of three potential cycles. The electrode potential was then held at +0.1 V vs. SCE for 1 min to ensure complete reduction of the surface before use. Care was taken to avoid electrode/air contact by keeping a drop of solution over the electrode. The electrode was then carefully rinsed in ethanol, immersed in a freshly prepared solution of the alkanethiol in ethanol (1 mM), and left for a minimum of 12 h. The modified electrode was soaked in ethanol for 30 min, dried under argon for 5 min, and stored in deionized water.A fresh vesicle solution was prepared via fast injection of the phospholipid methanol solution into electrolyte (final phospholipid concentration 30 μg cm−3). Phospholipid deposition onto the alkanethiol-coated gold electrode was followed by EIS and QCM at 25 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C respectively.
°C respectively.
Quartz crystal microbalance (QCM)
Fast quartz crystal impedance measurements which allowed the real time measurement of both R and XL were performed using a system described elsewhere.27,28 Briefly, a 10 MHz sinusoidal voltage (5 mV peak to peak) generated by a voltage controlled oscillator connected to the D/A output of a Keithley Data Acquisition System 575 was applied to the crystal. Both the input, Vi, and output, Vo, voltage moduli were amplified (MAX436 radio frequency operational amplifier) and rectified with an ideal diode circuit based on an LH0024 operational amplifier. The resulting signals were measured with an A/D converter of the Keithley Data Acquisition System 575. An AT-386 computer was used to generate the perturbation ac signal and to calculate the ratio of the circuit transfer function modulus, |Vo/Vi|, as a function of the VCO output signal frequency. The sample rate was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1, so that a complete transfer function spectrum (50 kHz and 100 points) was acquired in 10 ms.
000 s−1, so that a complete transfer function spectrum (50 kHz and 100 points) was acquired in 10 ms.In order to correct for any shift of the VCO the extreme frequencies were measured with a HP5334B frequency meter via an IEEE-488 interface. Calibration of the dc rectified signals was achieved with the read level functions of the HP5334B to the amplified radio frequency signals used for frequency measurement.
The transfer function spectrum, the modulus of Vo/Vi, as a function of frequency around 10 MHz was obtained in real time for the quartz crystal in contact with the solution.
AT-cut 10 MHz quartz crystals machine polished to 1 μm (International Crystal Manufacturing Company Inc., Oklahoma City, USA; 14 mm diameter, 0.165 mm thick) were used throughout. The gold working electrode area for these crystals is 0.196 cm2. The surface roughness was calculated to be 1.2 using AFM measurements. The crystals were mounted by means of ‘O'-ring seals with only one face in contact with the electrolyte, this electrode acted as a common ground.
Electrochemical impedance spectroscopy (EIS)
A standard three electrode arrangement, consisting of a gold working electrode, a platinum mesh counter electrode and a purpose built low resistance AgCl-coated Ag wire (area≈0.5 cm2) as a reference electrode, was used for all ac measurements. The gold working electrodes used for EIS experiments were constructed from gold wire (Aldrich, 99.999% purity, 1.0 mm diameter) set in epoxy resin (Streurs Epofix Kit) and polished down to 0.05 μm using alumina slurries (Buehler Micropolish on Buehler Microcloth).For all experiments, the alkanethiol-coated electrode was held at a dc bias of +0.1 V vs. Ag/AgCl to prevent any potential drift and possible voltage-dependent degradation of the alkanethiol and phospholipid-coated electrode. Before and after phospholipid deposition, impedance measurements were taken between 1 Hz and 60 kHz using a frequency response analyser (Solartron 1250) connected to a purpose built potentiostat under computer control. The generator signal was ±20 mV rms and the response signal was averaged over 1000 measurements. Phospholipid deposition was followed by recording repeated impedance measurements at 90 Hz averaged at each time interval over 50 measurements.
Ellipsometry
Measurements were performed using a rotating analyzer ellipsometer built in house29 using a He/Ne laser light source (632.8 nm) at an angle of incidence of 70°. The sample was a gold film evaporated onto chromium-coated glass that had been cleaned in ‘piranha' solution (2:1 mixture of concentrated sulfuric acid and 30% hydrogen peroxide. CAUTION: piranha solution reacts violently with most organic materials) prior to alkanethiol self-assembly. Phospholipid deposition onto the alkanethiol-coated gold was recorded in situ by adding vesicle solution to electrolyte (5 μg cm−3).Atomic force microscopy (AFM)
AFM measurements were performed using a magnetically driven MAC Mode PicoSPM (Molecular Imaging, Phoenix, AZ) fitted with a PicoScan controller and with MacLever (Molecular Imaging) of normal spring constant (0.1 N m−1). The system has been described elsewhere30 and allows the measurement of the topography of soft samples. Tip oscillation frequency was 89 kHz and tip force typically 1 nN. All measurements were performed in air at room temperature.The substrates used for AFM measurements were gold films (2.25 cm2) sputtered onto chromium-coated glass. The films were supplied by Metallhandel Schröer GmbH, Germany and were annealed for 2 min in a hydrogen flame immediately before use. This was considered to be sufficient cleaning for alkanethiol self-assembly.
QCM Theory
The QCM data were analysed in terms of a modified lumped-element Butterworth van Dyke (BVD) electrical equivalent circuit.28,31 It consists of a static capacitance in parallel with a motional branch. The static capacitance C0 is the result of two capacitances in parallel: the capacitance that arises between the electrodes located on opposite sides of the insulating quartz and the parasitic capacitance due to the cables and connections.31 According to Martin et al.,32 the total capacitance of the motional arm C is considered to be equal to the capacitance of the quartz. The motional arm impedance is the sum of the impedances due to the unperturbed, or bare, quartz with LQ, RQ and CQ, the liquid load with Ll and Rl and the viscoelastic film load with Lf and Rf (Z =Zq + Zl + Zf). The motional arm lumped-elements, R, L, and the static capacitance, C0, of the modified BVD equivalent circuit were obtained by non-linear fitting of the experimental transfer function spectrum data, |Vo /Vi|(ω), using the analytical expression for the BVD transfer function, eqn. (1) | (1) |
For a system of two non piezoelectric layers attached to the quartz resonator, a viscoelastic film (f) and a viscous liquid electrolyte overlayer (l), Granstaff and Martin33 derived an expression for the total electrical equivalent impedance Z in terms of the surface mechanical impedance ZM, eqn. (2)
 | (2) |
The mechanical impedance of each non piezoelectric layer on the quartz is given by33 eqn. (3)
 | (3) |
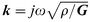 , the wave propagation constant, and d is the thickness of the non-piezoelectric layer of density ρ.
, the wave propagation constant, and d is the thickness of the non-piezoelectric layer of density ρ.If two non-piezoelectric layers are successively attached to the crystal, the expression (4) describes the surface impedance33
 | (4) |
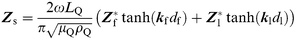 | (5) |
Use of eqn. (5) also assumes additivity of the surface film (Zf) and liquid electrolyte (Zl) mechanical impedances in eqn. (4) which is valid for |Zf≫Zl| or for very thin films (df → 0).33 For aqueous electrolytes |Zl| ≈ 280 Ω and G = jωη where η is the viscosity of water and the film impedance Zf at 10 MHz can be obtained by subtracting the impedance due to the newtonian liquid electrolyte, (ca.XLf≈Rf) from the surface impedance ZS due to film and liquid. Since the surface films formed by the 1-decanethiol and DOPG are thin (<10 nm) we assume that additivity applies in our experiments.
Results
We have used a number of complimentary in situ techniques to characterize the assembly of dioleoylphosphatidylglycerol layers from vesicle solution onto 1-decanethiol coated gold surfaces. We begin by considering the quartz crystal microbalance measurements.Quartz crystal microbalance measurements
Following self assembly of the 1-decanethiol monolayer onto the QCM, the lipid layer was deposited onto the crystal from a vesicle solution containing 30 μg cm−3 DOPG. Fig. 1 shows the resulting changes in the real and imaginary components of the electroacoustic impedance of the QCM as a function of time following addition of the vesicle solution. Similar results were obtained in more than ten replicate experiments. Several features are apparent. First the overall timescale for the observed changes is of the order of 1 h, with the changes in ΔXL (15–20 Ω) being several times larger than those in the real component of the electroacoustic impedance, ΔR (4–5 Ω). Following the addition of the vesicle solution there is a rapid (ca. 10 s) increase in ΔR of 0.8 Ω and a significantly larger, and slightly slower, increase in ΔXL of 4.0 Ω. We attribute this rapid change in ΔR to an increase in the viscosity of the bulk solution following the addition of the vesicles. Assuming this to be the case and that the additivity condition is valid for the QCM impedance (see above) there will be a corresponding and equal increase in ΔXL caused by the change in solution viscosity. Subtracting this from the observed change in ΔXL leaves a change of 3.2 Ω which is then consistent with the adsorption of a rigid layer of phospholipid with a mass of ca. 150 ng cm−2 onto the 1-decanethiol surface (for our crystals a change in ΔXL of 1 Ω corresponds to a mass change of 46.6 ng cm−2 according to the Sauerbrey equation). This is comparable with the value estimated for a close packed monolayer of DOPG of 227 to 265 ng cm−2 calculated assuming a cross sectional area of 0.6 to 0.7 nm2 for the lipid34 and a surface roughness of 1.2 for the crystal as determined by AFM measurement. | ||
Fig. 1 Change in the response of the quartz crystal during the deposition of DOPG from vesicle solution (30 μg cm−3) in TRIS (0.1 M, pH 8.0)–NaCl (0.1 M) electrolyte onto a 1-decanethiol self-assembled monolayer coated gold electrode at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oC. (a) The change in real, ΔR, and imaginary, ΔXL, components of the electroacoustic impedance, ΔZ with time, (b) The corresponding complex plane plot. oC. (a) The change in real, ΔR, and imaginary, ΔXL, components of the electroacoustic impedance, ΔZ with time, (b) The corresponding complex plane plot. | ||
Following the rapid change in the electroacoustic parameters for the crystal there is a slower increase in (ΔXL−ΔR) over the next 1500 s corresponding to a total increase in mass of approximately 560 ng cm−2 after 1 h. This further increase in mass appears to be due to the formation of a further bilayer of DOPG on top of the initially deposited monolayer since the total mass uptake is equivalent to 3 monolayers of DOPG. We also note that both ΔR and ΔXL also appear to drift upwards linearly over the course of the experiment.
Further insight into the process is provided by the experiment shown in Fig. 2. In this case the vesicle solution was added to the cell containing the 1-decanethiol coated crystal in pure water without any added buffer or electrolyte at time zero. Then after 1170 s TRIS buffer and NaCl were added to bring the concentration to 0.1 M TRIS and 0.1 M NaCl at pH 8.0. It is notable that in the absence of the electrolyte and buffer there is no upward drift in ΔXL and ΔR but when the electrolyte and buffer are added to the cell there is a further significant increase in ΔXL and ΔR and the upward drift in these two parameters appears. These results clearly show that the behavior is dependent on the composition of the solution. The initial change in both ΔXL and ΔR for the addition of the vesicle solution in pure water at time zero is as for the electrolyte case shown in Fig. 1; the response is fast (<10 s) and the magnitudes of the changes in ΔXL and ΔR are the same. These two parameters are then steady for the next 1000 s until the electrolyte and buffer are added indicating that there is no thermal or other drift occurring in the experiment and that the layer initially formed on the 1-decanethiol surface is stable. When the electrolyte and buffer are added a second, slower, change in the electroacoustic impedance of the crystal occurs leading to an overall increase in ΔXL after 2500 s of 16 Ω. Note that both ΔXL and ΔR drift upwards in the presence of the electrolyte and buffer and that the rate of this upward drift is very similar to that observed in experiment shown in Fig. 1. This indicates that the change is due to a change in the properties of the interface and not the result of background drift.
 | ||
Fig. 2 Effect of the electrolyte solution on the deposition of DOPG onto a 1-decanethiol self-assembled monolayer coated gold electrode at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. (a) The change in real, ΔR, and imaginary, ΔXL, components of the electroacoustic impedance with respect to time. Initially the deposition was from a vesicle solution (30 μg cm−3) with no added electrolyte; at 1200 s sufficient electrolyte was added to bring the concentration in the cell to 0.1 M TRIS (pH 8.0), 0.1 M NaCl. (b) The corresponding complex plane plot. °C. (a) The change in real, ΔR, and imaginary, ΔXL, components of the electroacoustic impedance with respect to time. Initially the deposition was from a vesicle solution (30 μg cm−3) with no added electrolyte; at 1200 s sufficient electrolyte was added to bring the concentration in the cell to 0.1 M TRIS (pH 8.0), 0.1 M NaCl. (b) The corresponding complex plane plot. | ||
The results of these QCM experiments are consistent with the rapid formation of a lipid monolayer on the 1-decanethiol surface followed by the slower deposition of a bilayer on top of the lipid monolayer. This subsequent deposition of a lipid bilayer onto the lipid monolayer coated crystal appears to require the presence of electrolyte and buffer in the solution. This is not unreasonable because the DOPG head groups are negatively charged at pH 8 and therefore, in the absence of added electrolyte, we can expect the electrostatic repulsion between the DOPG monolayer deposited onto the 1-decanethiol surface and the DOPG vesicles to prevent the formation of a further DOPG bilayer on top of the lipid monolayer. Addition of electrolyte will act to screen the electrostatic repulsion allowing the bilayer to form on top of the lipid monolayer.
Electrochemical impedance spectroscopy
Electrochemical impedance spectroscopy is a useful technique to characterize thin insulating films at electrode surfaces and can be particularly sensitive to the presence of pores or pin-holes in the films. Fig. 3 shows complex plane electrochemical impedance plots in the absence of any redox species for a 1-decanethiol coated gold electrode before and after the deposition of DOPG on to the surface from vesicle solution containing buffer and electrolyte. Using a simple equivalent circuit of a resistor and capacitance in series to analyse the data (from 1 to 10 kHz) we obtain capacitances of 3.9 μF cm−2 for the 1-decanethiol layer and 1.4 μF cm−2 for 1-decanethiol coated with the phospholipid layer with corresponding uncompensated solution resistances of 25 and 40 Ω cm2 respectively. Then assuming a simple series capacitance model for the 1-decanethiol layer and the phospholipid we obtain a capacitance of 2.2 μF cm−2 for the phospholipid layer alone. The capacitance is related to the ratio of the permittivity of the film to the thickness according to C=εεr/df. The measured value of the capacitance for the phospholipid layer obtained in our experiments could correspond to either a monolayer of lipid (df = 2 nm) with a relative permittivity of 5 or a monolayer of lipid coated with a lipid bilayer, a trilayer structure (df = 6 nm), having a relative permittivity of 15. Both estimates of the relative permittivity are significantly larger than the accepted literature values for lipid layers of 2 to 3.5,35 However these studies relate to lipids with zwitterionic head groups and it may be that for films of charged lipids, such as DOPG, the permittivity is larger due to solvation and charge repulsion effects. In addition the electrochemical impedance of the film is sensitive to contributions from pinholes and defects which tend to make C larger and hence the permittivity appear larger. Finally in the case of the three layer structure there would be water and cations present within the layer between the lipid monolayer and the overlying bilayer and this would contribute to the overall permittivity of the film. Hence it is impossible to distinguish between the monolayer and trilayer models for the lipid based on the electrochemical impedance measurements alone. | ||
Fig. 3 Complex electrochemical impedance plane plot for the 1-decanethiol-coated gold electrode (solid) and the same electrode following DOPG deposition onto the self-assembled monolayer (dashed). The inset shows the relative position of the impedance data point measured at 90 Hz for each case. The measurements were carried out in a TRIS (0.1 M, pH 8.0)–NaCl (0.1 M) aqueous electrolyte, at +100 mV vs. Ag/AgCl and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
The impedance spectroscopy measurements were made by sweeping the frequency and recording the impedance of the electrode. In order to follow the dynamic changes accompanying the deposition of the DOPG layer we made measurements at a single frequency (90 Hz, see inset in Fig. 3) as a function of time, again in the absence of any redox species. Fig. 4 shows the change in the real, Z′, and imaginary, Z″, components of the electrochemical impedance at 90 Hz as a function of time following the addition of the DOPG vesicle solution. There is a rapid increase in Z′ and −Z″ during the first 100 s. This is followed by an increase in −Z″ with no significant change in Z′ until approximately 1000 s after addition of the vesicle solution at which time there is a further increase in −Z″ accompanied by a decrease in Z′. These coupled changes in the real and imaginary components of the impedance indicate that there are associated changes in both the resistance and the capacitance of the film as the process proceeds. If we assume a simple RC series circuit we can convert these changes in Z at 90 Hz into changes in the apparent resistance and capacitance, Fig. 5. The results show a rapid increase in the apparent resistance, R, over the first 200 s followed by a much slower decrease over the next 6000 s. These changes in R mirror the changes and timescales of the effects seen in the QCM experiments carried out under the same conditions (Fig. 1) and indicate that the situation is more complex than a simple RC series circuit where R is identified exclusively with the uncompensated solution resistance and the lipid layer is assumed to be totally blocking. In contrast the capacitance, C, shows a simple monotonic decrease following addition of the vesicle solution. This decrease in C can be described by a biexponential function with time constants of 147 and 1700 s, values which are consistent with the timescales of the biphasic behavior seen in the QCM experiments. Interestingly biexponential kinetics for the changes in C on formation of a lipid film on an alkanethiol coated surface were also reported by Mirsky et al.9 although they assume that a lipid monolayer is formed in their experiments.
 | ||
Fig. 4 Change in the electrochemical impedance response measured at 90 Hz during the deposition of DOPG onto a 1-decanethiol self-assembled monolayer-coated electrode. The inset shows a magnification of the impedance change with respect to the real component of the impedance, Z′. The measurements were carried out in a TRIS (0.1 M, pH 8.0)–NaCl (0.1 M) aqueous electrolyte, at +100 mV vs. Ag/AgCl and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. °C. | ||
 | ||
| Fig. 5 Change in the apparent values of the resistance, R, and the capacitance, C, as a function of time calculated from the data in Fig. 4 assuming a simple series RC model where Z = R − (j/2πfC). | ||
Ellipsometry
We have also used ellipsometry to study the changes which accompany the deposition of the DOPG layer on to the 1-decanethiol surface. Fig. 6 and the inset show the change in the ellipsometric parameters, Δ and Ψ, with time following the addition of the vesicle solution. There is an initial rapid change in Δ and Ψ over the first 200 s followed by a slower change in Δ which appears to stabilize after about 1 h (although the signal is noisy). | ||
| Fig. 6 Change in the ellipsometric parameters, Δ and Ψ, during the deposition of DOPG from vesicle solution (5 μg cm−3) in a TRIS (0.1 M, pH 8.0)–NaCl (0.1 M) electrolyte onto a 1-decanethiol self-assembled monolayer coated gold electrode. The inset shows the change in each parameter with time. | ||
In principle we should be able to obtain an estimate of the thickness of the DOPG film deposited on to the 1-decanethiol layer from analysis of the ellipsometry data by using the Drude equations36 for thin films. This assumes that changes in Δ and ψ are linear with the film thickness, eqns. (8) and (9),
 | (8) |
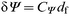 | (9) |
Atomic force microscopy
We have used intermittent contact atomic force microscopy to image the DOPG coated 1-decanethiol films. For these experiments flame annealed gold on glass surfaces was used as the substrate. This surface preparation produces surfaces which are atomically flat over large areas and have predominantly a gold (111) surface. In our experiments we found significant surface damage to the samples caused by the AFM tip even with the intermittent contact mode and low surface forces (of the order of 1 nN) for our measurements. Fig. 7 shows a typical AFM image for the DOPG coated 1-decanethiol surface. Similar observations have been made for other liquid phase phospholipid films.26 In separate experiments we have shown that under the same conditions the 1-decanethiol itself surface is not damaged by the AFM tip. Fig. 7 also shows the results for a linescan taken across the image at the position shown by the line. From linescan measurements taken at different places in the image we obtain an estimate of the thickness of the phospholipid layer of 5.6±0.9 nm (based on an average of 15 individual measurements). This is clearly greater than the expected value for a monolayer of DOPG (ca. 2 nm) and corresponds most closely to a of trilayer of the phospholipid. Thus we interpret the image as showing patches of the trilayer DOPG film on top of the 1-decanethiol surface. It is also noticeable that directly adjacent to clean areas of 1-decanethiol the overlayer appears to be thicker (up to 12 nm). This could be due to build up of phospholipid that has been swept along and deposited by the tip or it could be an imaging artifact. | ||
| Fig. 7 Intermittent contact AFM image of a DOPG film on a 1-decanethiol coated flame annealed gold substrate. The image was recorded with a tip oscillation frequency of 89 Hz and tip force of around 1 nN at room temperature in air. The topography of the film, shown in the cross section below the image, is obtained from the linescan taken at the position of the white line at the bottom of the AFM image. | ||
Conclusion
Our experiments show that for each of the four techniques that we have used to study the deposition of DOPG films onto 1-decanethiol coated gold surfaces from lipid solutions there are different problems in the interpretation of the data. For the quartz crystal microbalance there are problems with rigorously accounting for the coupled effects of changes in the solution viscosity accompanying the addition of the vesicles to the solution. In addition there is an, as yet, unexplained drift in the electroacoustic parameters in the presence of buffer and background electrolyte. Nevertheless the sensitivity and time resolution of the technique is well suited to these types of study and by analysing the electroacoustic impedance changes we can go some way to separating the effects of changes in solution viscosity, viscoelastic effect within the film and film loading. For the electrochemical impedance spectroscopy measurements although experimentally simpler the analysis of the data is problematic. Simple series RC equivalent circuit models are not appropriate because of the effects of pinholes and defects in the films. As a consequence the technique is not well suited to differentiating between monolayer and multilayer coverage of the electrode since changes in df and εr are not distinguished and because the capacitance depends inversely on the film thickness. More sophisticated models should be used to analyse the experimental data as a function of frequency; this will form the subject of a separate publication. Ellipsometry is also suitable for the in situ study of the formation of lipid films at surfaces but again the quantitative interpretation of the data is not straightforward and is model dependent. Finally atomic force microscopy can be used to image small regions of the surface of these films but it is not, in general, a non-invasive technique and the tip can cause significant changes in the film structure.In comparing the results from the different techniques note should also be taken of the differences in the types of the gold surface that are available for each of the techniques. With the exception of the AFM substrate all samples were polycrystalline. For the AFM measurements it is necessary to have an atomically flat surface in order clearly to resolve the different organic overlayers, therefore flame annealed gold surfaces of predominantly (111) orientation were used. Electrochemical impedance spectroscopy and ellipsometry measurements were made on optically smooth, although not atomically flat, polycrystalline gold surfaces. For the quartz crystal microbalance measurements rougher electrodes (surface roughness of 1.2) were used in order to ensure adhesion of the gold electrode to the quartz surface and to avoid the need for a chromium adhesion layer which causes corrosion problems in electrochemical experiments. Thus although comparable there are differences between the gold surfaces used for each technique which could affect the results.
Despite the problems with the quantitative interpretation of the data from the different techniques a consistent picture does emerge when the results from the four techniques are considered together. For the deposition of the DOPG films we find that in 0.1 M TRIS buffered solution at pH 8 containing 0.1 M NaCl the deposition proceeds in two stages with the initial deposition of a monolayer of DOPG on to the 1-decanethiol surface over about 200 s followed by the deposition of a further bilayer of DOPG on top of this monolayer over the succeeding 3000 s. This subsequent step is not observed when the process is carried out in pure water, presumably because of the effects of electrostatic repulsion between the DOPG monolayer and the vesicles. It will be of interest to conduct similar experiments with lipids with zwitterionic headgroups to see if the same effects are observed. Our experiments indicate that the common assumption that the vesicle deposition method for the formation of lipid films onto hydrophobic surface produces supported lipid monolayers may not always be justified.
Acknowledgements
This work was supported by a grant from Fundacion Antorchas and the British Council. We thank Dr X. Q. Tong of Molecular Imaging for assistance with AFM measurement and Dr R. Greef for assistance with ellipsometry measurements.References
- O. Pierrat, N. Lechat, C. Bourdillon and J. M. Laval, Langmuir, 1997, 13, 4112 CrossRef CAS.
- B. A. Cornell, V. L. B. Braach-Maksvytis, L. G. King, P. D. J. Osman, B. Raguse, L. Wieczorek and R. J. Pace, Nature (London), 1997, 387, 580 CrossRef CAS.
- A. T. A. Jenkins, R. J. Bushby, N. Boden, S. D. Evans, P. F. Knowles, Q. Liu, R. E. Miles and S. D. Ogier, Langmuir, 1998, 14, 4675 CrossRef CAS.
- A. L. Plant, Langmuir, 1993, 9, 2764 CrossRef CAS.
- A. Plant, M. Gueguetchkeri and W. Yap, Biophys. J., 1994, 67, 1126 Search PubMed.
- S. Gritsch, P. Nollert, F. Jähnig and E. Sackmann, Langmuir, 1998, 14, 3118 CrossRef CAS.
- S. Terrettaz, T. Stora, C. Duschl and H. Vogel, Langmuir, 1993, 9, 1361 CrossRef CAS.
- M. Stelzle, G. Weissmüller and E. Sackmann, J. Phys. Chem., 1993, 97, 2974 CrossRef CAS.
- V. M. Mirsky, M. Mass, C. Krause and O. S. Wolfbeis, Anal. Chem., 1998, 70, 3674 CrossRef CAS.
- Liposomes: a practical approach, ed. R. R. C. New, IRL Press, Oxford, 1990, p. 8. Search PubMed.
- B. Lindholm-Sethson, Langmuir, 1996, 12, 3305 CrossRef CAS.
- Y. Ebara, H. Ebato, K. Ariga and Y. Okahata, Langmuir, 1994, 10, 2267 CrossRef CAS.
- K. Watamatsu, K. Hosoda, H. Mitomo, M. Ohya, Y. Okahata and K. Yasunaga, Anal. Chem., 1995, 67, 3336 CrossRef.
- M. Liebau, G. Bendas, U. Rothe and R. H. H. Neubert, Sensors Actuators B, 1998, 47, 239 CrossRef.
- M. Rodahl, F. Höök, C. Fredriksson, C. A. Keller, A. Krozer, P. Brzezinski, M. Voinova and B. Kasemo, Faraday Discuss. R. Soc. Chem., 1997, 107, 229 Search PubMed.
- D. Johannsmann, J. Gruner, J. Wesser, K. Mathauer, G. Wegner and W. Knoll, Thin Solid Films, 1992, 210/211, 662 CrossRef.
- R. Naumann, A. Jonczyk, R. Kopp, J. v Esch, H. Ringsdorf, W. Knoll and P. Gräber, Angew. Chem., Int. Ed. Engl., 1995, 34, 2056 CrossRef CAS.
- M. A. Cooper, D. H. Williams and Y. R. Cho, Chem. Commun., 1997, 1625 RSC.
- M. A. Cooper, A. C. Try, J. Carroll, D. J. Ellar and D. H. Williams, Biochim. Biophys. Acta, 1998, 1373, 101 CrossRef CAS.
- N. Bunjes, E. K. Schmidt, A. Jonczyk, F. Rippmann, D. Beyer, H. Ringsdorf, P. Gräber, W. Knoll and R. Naumann, Langmuir, 1997, 13, 6188 CrossRef CAS.
- L. M. Williams, S. D. Evans, T. M. Flynn, A. Marsh, P. F. Knowles, R. J. Bushby and N. Boden, Langmuir, 1997, 13, 751 CrossRef CAS.
- C. Striebel, A. Brecht and G. Gauglitz, Biosensors Bioelectronics, 1994, 9, 139 CrossRef CAS.
- Y. F. Dufrêne, W. R. Barger, J.-B. D. Green and G. U. Lee, Langmuir, 1997, 13, 4779 CrossRef CAS.
- Y. F. Dufrêne, T. Boland, J. W. Schneider, W. R. Barger and G. U. Lee, Faraday Discuss. R. Soc. Chem., 1998, 111, 79 Search PubMed.
- J. A. N. Zasadzinski, C. A. Helm, M. L. Longo, A. L. Weisenhorn, S. A. C. Gould and P. K. Hansma, Biophys. J., 1991, 59, 755 Search PubMed.
- S. W. Hui, R. Viswanathan, J. A. Zasadzinski and J. N. Israelachvili, Biophys. J., 1995, 68, 171 Search PubMed.
- E. J. Calvo, C. Danilowicz and R. Etchenique, J. Chem. Soc., Faraday Trans., 1995, 91, 4083 RSC.
- E. J. Calvo, R. Etchenique, P. N. Bartlett, K. Singhal and C. Santamaria, Faraday Discuss. R. Soc. Chem., 1997, 107, 141 Search PubMed.
- P. S. Hauge and F. H. Dill, Optics Commun., 1975, 14, 431 CrossRef.
- W. Han, A. M. Lindsay and T. Jing, Appl. Phys. Lett., 1996, 69, 4111 CrossRef CAS.
- R. A. Etchenique and E. J. Calvo, Anal. Chem., 1997, 64, 4833 CrossRef CAS.
- S. J. Martin, V. E. Granstaff and G. C. Frye, Anal. Chem., 1991, 63, 2272 CrossRef CAS.
- V. E. Granstaff and S. J. Martin, J. Appl. Phys., 1994, 75, 1319 CrossRef CAS.
- D. Marsh, Biochim. Biophys. Acta, 1996, 1286, 183 CrossRef CAS.
- M. R. Moncelli, R. Herrero, L. Becucci and R. Guidelli, J. Phys. Chem., 1995, 99, 9940 CrossRef CAS.
- T. G. HarlandA user's guide to ellipsometry, Academic Press, San Diego, 1993. Search PubMed.
- L. A. Sklar, B. S. Hudson, M. Peterson and J. Diamond, Biochemistry, 1977, 16, 813 CrossRef CAS.
Footnote |
| † Basis of a presentation given at Materials Chemistry Discussion No. 2, 13–15 September 1999, University of Nottingham, UK. |
| This journal is © The Royal Society of Chemistry 2000 |
