Multivariate investigation of matrix effects in inductively coupled plasma atomic emission spectrometry using pneumatic or ultrasonic nebulization

Abstract

A multivariate interference study was carried out using a low power inductively coupled plasma atomic emission spectrometer, after optimization of operating parameters in order to achieve both plasma robustness and maximum signal to background ratios. The method, based on the empirical modelling and experimental design concepts, provided a multivariate quantification of interferences caused by complex matrices containing Na, K, Ca, Al and Fe, at concentration levels ranging from 10 to 5000 µg ml⁻¹, deducing the complex relationships between interfering effects and matrix composition. In order to test the plasma excitation conditions, the Mg II 280.270 nm to Mg I 285.213 nm line intensity ratio was measured for each combination of matrix elements. Both Meinhard and ultrasonic nebulization were considered for comparison.

---

Introduction

The problem of matrix interferences in inductively coupled plasma atomic emission spectrometry (ICP-AES) continues to receive considerable attention. The matrix effect most extensively studied^1–38 is that caused by high concentrations of easily ionized elements (EIEs), such as Na, K and Li, the presence of which may result either in an enhancement or a depression of the analyte signal intensity, depending on the operating conditions, particularly on the observation height, rf power and carrier gas flow rate.

Several explanations were suggested to account for the EIE effect, mainly related to processes occurring in the plasma, such as changes in the atomization step,^1–12 shifts in excitation and ionization equilibria,^{6,8,9,12–15} lateral diffusion events,^5,16 volatilization,⁵ enhanced electron impact excitation,¹⁷ changes in plasma thermal conductivity,¹⁸ collision processes and ambipolar diffusion.^5,12,19–23 Also, matrix-induced changes in the aerosol formation and transport were suggested, indicating the significant contribution of the sample introduction system to the EIE effects.^14,24–29

Non-EIE elements were also studied,^11,40–42 mainly calcium, whose effect under usual analytical conditions is even greater than that due to alkali metals. The interfering effect of calcium is strongly related to changes in the plasma excitation conditions, as proved by the interactive power adjustment experiments performed by Thompson et al.⁴² Changes in the excitation plasma conditions induced by calcium were also reported by Budic,⁴³ using an ultrasonic nebulizer.

The concept of “robustness" was introduced to describe the capability of an analytical system to tolerate any change in matrix composition.^13,14,44 The robustness is linked to the capability of the plasma to accept a matrix change without a change in the plasma conditions, such as temperature and electron number density. Since ionic lines are more sensitive to any change in plasma conditions than atomic lines, the easiest way to evaluate the robustness of the plasma is to measure the Mg II 280.270 nm to Mg I 285.213 nm line intensity ratio. It was estimated that a ratio >8 in the normal viewing zone corresponds to robust conditions. In these conditions, any observed effect can be assigned to a change in the efficiency of aerosol formation and transport, i.e. to the sample introduction system.

The introduction of the ultrasonic nebulizer (USN) stimulated further investigations on matrix effects in ICP-AES.^45–48 Brenner et al.^46,47 studied the interference effects of Na and Ca in axially and radially viewed ICPs, using both cross-flow and ultrasonic nebulizers. They found that severe interferences may occur, especially with USN. The interferences due to calcium were stronger than those caused by sodium and both of them depended on the robustness of the plasma. Budic⁴³ studied the matrix interferences due to the presence of calcium, potassium and composite matrices containing Na, K, Ca and P, using a USN. Generally, suppression of the analyte emission in the presence of the matrix was observed. These effects were attributed both to a reduction of transport efficiency and to a change in plasma excitation conditions. Finally, matrix interferences in trace element analysis of environmental samples by USN-ICP-AES were considered by Hoenig et al.⁴⁸ It was found that a matrix composed of K, Ca, Na, Mg and P drastically affected the determination of several analytes, leading to poor recoveries, especially in the presence of high contents of matrix elements and low concentrations of analyte (50–100 ng ml⁻¹).

Owing to the complexity of the processes related to matrix effects in ICP-AES, almost all the cited studies were performed considering one interfering element at a time, and only few papers^43,48,49 dealt with the effect of a composite matrix. However, when a specific analytical determination is considered, it is important to quantify accurately the matrix effects in order to: (i) estimate the expected accuracy; (ii) compare various instrumental systems (e.g. different nebulizers); and (iii) choose the proper strategy for overcoming interferences (e.g. matrix matching vs. internal standardization). A multivariate approach, based on the empirical modelling and experimental design concepts, was successfully applied for the investigation and quantification of interferences in graphite furnace atomic absorption spectrometry^50–52 and inductively coupled plasma mass spectrometry.⁵³

In this paper, a similar method was applied in order to obtain a multivariate quantification of interferences caused by complex matrices containing Na, K, Ca, Al and Fe, at concentration levels ranging from 10 to 5000 µg ml⁻¹. In order to distinguish between chemical and physical interfering effects, the Mg II/Mg I intensity ratio was measured for each combination of matrix elements. The operating conditions (rf power and sheathing gas flow rate) were optimized in order to obtain both plasma robustness and greater signal to background ratios (SBRs), favourable for trace element determinations in real samples.

Experimental

Instrumentation and operating conditions

All measurements were performed using a Jobin-Yvonn (Longjumeau, France) JY-24 ICP emission spectrometer, having the following features: rf power supplied by a 40.60 MHz generator (JY 2300 model); sequential monochromator with a 640 mm focal length equipped with a highly dispersive holographic grating (2400 grooves mm⁻¹); and IBM personal computer interfaced by a Spectralink microprocessor.

Two sample introduction systems were used: (i) a concentric pneumatic nebulizer, Meinhard (Santa Anna, CA, USA) model, with a Scott spray chamber; and (ii) an ultrasonic nebulizer, CETAC (Omaha, NB, USA) U-5000 AT model, consisting of an air-cooled piezoelectric transducer, an aerosol chamber, a temperature-controlled heated U-tube and a temperature-controlled condenser.

The operating conditions are listed in Table 1. The observation height was set in order to maximize the Mg II/Mg I intensity ratio.

Table 1 Operating parameters for ICP-AES measurements using pneumatic (MPN) or ultrasonic (USN) nebulization

	MPN	USN
^aOptimized in order to obtain both plasma robustness and maximum SBRs.
Rf power/W	900^a	800^a
Outer gas flow rate/l min^−1	14	14
Intermediate gas flow rate/l min^−1	0.1^a	0.2^a
Nebulizer gas flow rate/l min^−1	0.35	0.7
Nebulizer pressure/bar	3.2	1.0
Sample uptake/ml min^−1	1.0	1.0
Solvent load/mg min^−1	39	18
Integration time/s	1.0	1.0
Heating temperature/°C	—	140
Cooling temperature/°C	—	3

---

The emission lines were selected in order to cover a wide range of excitation and ionization energies, including the lines suggested by Romero et al.¹⁴ for studying the Na effect (Table 2).

Table 2 Selected emission lines and their characteristics

Analyte	Wavelength/nm	Ionization energy/eV	Excitation energy/eV
Zn II	202.548	9.39	6.12
Pb II	220.353	7.42	7.37
Ni II	231.604	7.64	6.39
Ba II	233.527	5.21	6.01
Mn II	257.610	7.44	4.81
Cr II	267.716	6.76	6.15
Mg II	280.270	7.65	4.42
Mg I	285.213	—	4.30
V II	292.402	6.74	4.63

---

Reagents and materials

Standard solutions (10 mg ml⁻¹) of Na, K, Ca, Al and Fe, as nitrates (BDH Chemicals, Poole, Dorset, UK), were used as matrix stock solutions. Standard solutions (1 mg ml⁻¹) of Zn, Pb, Ba, Ni, Mn, Cr, Mg and V, as nitrates (BDH Chemicals), were used as analyte stock solutions.

Synthetic samples and standards for the multivariate interference study were prepared daily by the addition of appropriate aliquots of the above-mentioned standard solutions and by dilution with Milli-Q water (Millipore, El Paso, TX, USA). The concentration of the analytes was set at 1 mg l⁻¹, while the concentration of the concomitant elements ranged from 10 to 5000 µg l⁻¹, according to the experimental plan (Table 3).

Table 3 Experimental design

	Coded values					Real values/µg ml^−1
Run	Na	K	Ca	Al	Fe	Na	K	Ca	Al	Fe
1	−1	−1	−1	−1	+1	56	56	56	56	900
2	+1	−1	−1	−1	−1	900	56	56	56	56
3	−1	+1	−1	−1	−1	56	900	56	56	56
4	+1	+1	−1	−1	+1	900	900	56	56	900
5	−1	−1	+1	−1	−1	56	56	900	56	56
6	+1	−1	+1	−1	+1	900	56	900	56	900
7	−1	+1	+1	−1	+1	56	900	900	56	900
8	+1	+1	+1	−1	−1	900	900	900	56	56
9	−1	−1	−1	+1	−1	56	56	56	900	56
10	+1	−1	−1	+1	+1	900	56	56	900	900
11	−1	+1	−1	+1	+1	56	900	56	900	900
12	+1	+1	−1	+1	−1	900	900	56	900	56
13	−1	−1	+1	+1	+1	56	56	900	900	900
14	+1	−1	+1	+1	−1	900	56	900	900	56
15	−1	+1	+1	+1	−1	56	900	900	900	56
16	+1	+1	+1	+1	+1	900	900	900	900	900
17	−	0	0	0	0	10	224	224	224	224
18	+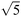	0	0	0	0	5000	224	224	224	224
19	0	−	0	0	0	224	10	224	224	224
20	0	+	0	0	0	224	5000	224	224	224
21	0	0	−	0	0	224	224	10	224	224
22	0	0	+	0	0	224	224	5000	224	224
23	0	0	0	−	0	224	224	224	10	224
24	0	0	0	+	0	224	224	224	5000	224
25	0	0	0	0	−	224	224	224	224	10
26	0	0	0	0	+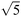	224	224	224	224	5000
27–32	0	0	0	0	0	224	224	224	224	224

---

Standard solutions for Mg II/Mg I intensity ratio and SBR measurements contained the analytes at a concentration of 1 mg l⁻¹. All solutions were in 20% (v/v) HNO₃ of suprapur grade (Merck, Darmstadt, Germany).

Multivariate experiments and data processing

Optimization of the operating parameters was carried out according to a Doehlert experimental design,⁵⁴ in which the intermediate gas flow rate and rf power were selected as independent variables and the Mg II/Mg I intensity ratio or the SBR measured at 292.402 nm (V^II emission line) were considered as responses.

The multivariate study of matrix effects was performed according to a method previously reported.⁵¹ The adopted experimental design is presented in Table 3. According to this, each variable is studied at five levels (coded as −√5, −1, 0, +1, +√5); the experiments are performed on a spherical domain, at the vertices of the hypercube corresponding to a 2^{5 − 1} fractional design (points 1–16), at the so-called “star points" (points 17–26) and at the centre of the domain (points 27–32). The replicates at the centre point give the estimate of the experimental variance, taking into account both the instrumental precision and the sample preparation procedure.

By fixing the ranges of the variables (10–5000 µg ml⁻¹) and considering a logarithmic scale, the coded values were replaced by real values and the experimental plan was obtained (Table 3). According to this, 32 standard solutions were prepared and analysed by ICP-AES at the operating conditions previously optimized and reported in Table 1.

Data were processed by performing a multiple linear regression (MLR) analysis in which the concentrations of five matrix elements were considered as independent variables and the analytical error chosen as response:

where C_theoretical is the added analyte concentration and C_measured is the analyte concentration calculated using a calibration curve based on standard solutions in 20% (v/v) nitric acid.

The quality of the MLR analyses was tested by performing the “cross-validation" procedure.⁵⁵ According to this, each experiment was removed from the training set and the model recalculated. Then, the predicted value of the missing experiment was computed by the new model and compared with the true one. This procedure was repeated for all the experiments and the explained variance (EV) was calculated:

where y_i is the experimental value of experiment i, y^a_i is the predicted value and N is the number of experiments.

MLR analyses and other statistical calculations were performed using the package of programs PARVUS 1.2.⁵⁶

Results and discussion

It is well known that matrix effects strongly depend on the operating conditions and that ideal plasma robustness, which results in the absence of variation of the analyte signal for any change in the matrix composition, can be approached by the combination of high power, usually more than 1200 W, and a long residence time.⁴⁴ However, an increase in power could lead to a decrease in the SBRs, as reported by Brenner et al.⁴⁷ Therefore, before performing the interference study, some preliminary experiments were carried out in order to choose the optimal operating conditions, taking into account both plasma robustness and SBRs.

Effect of operating conditions on plasma robustness

In order to evaluate the effect of the rf power and sheathing gas flow rate on the plasma excitation conditions, a Doehlert experimental study was designed (Table 4) and the Mg II/Mg I intensity ratio considered as response. The calculated effects are shown in Figs. 1 and 2 for pneumatic and ultrasonic nebulization, respectively. The plotted response surfaces fit the experimental data well, being characterized by MLR coefficients equal to 0.996 and 0.997, respectively. It can be seen that, for both sample introduction systems, an increase in the intermediate gas flow rate causes a decrease in the Mg II/Mg I intensity ratio, indicating a degradation of the energy transfer between the plasma and the sample. Moreover, the effect was sharper when using a pneumatic nebulizer, while with the ultrasonic nebulization system an intermediate gas flow rate up to 0.2 l min⁻¹ could be used without a significant change in the plasma excitation conditions.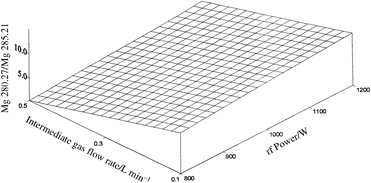

Fig. 1 Effect of sheathing gas flow rate and rf power on Mg II 280.27 nm/Mg I 285.21 nm line intensity ratio, using pneumatic nebulization.

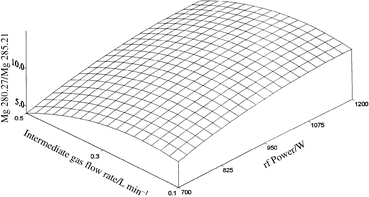Fig. 2 Effect of sheathing gas flow rate and rf power on Mg II 280.27 nm/Mg I 285.21 nm line intensity ratio, using ultrasonic nebulization.

Table 4 Doehlert experimental design and levels of variables fixed for pneumatic (MPN) or ultrasonic (USN) nebulization

Run	Variable 1 (coded unit)	Variable 2 (coded unit)	Intermediate gas flow rate/ml min^−1	Rf power/W
				MPN	USN
1	0.866	−0.5	0.5	900	825
2	0.866	0.5	0.5	1100	1075
3	0	1	0.3	1200	1200
4	−0.866	0.5	0.1	1100	1075
5	−0.866	−0.5	0.1	900	825
6	0	−1	0.3	800	700
7	0	0	0.3	1000	950

---

Concerning the effect of the rf power, the expected increase in plasma robustness with increasing power was found. However, the Mg II/Mg I intensity ratio was sufficiently high even at low power, indicating that the energy transfer was efficient. This result is in agreement with previously reported measurements carried out with the same instrument,^55,56 and can be explained considering that: (i) the inner diameter of the injector was 3 mm, while other instruments are equipped with injectors having smaller diameters; and (ii) a low carrier gas flow rate was used (0.35 l min⁻¹ and 0.7 l min⁻¹ with pneumatic and ultrasonic nebulization, respectively). Both of these factors ensure a long residence time and, consequently, more robust conditions were obtained.

Effect of operating conditions on signal to background ratios

The effect of the rf power and sheathing gas flow rate on the SBR measured at 292.402 nm (V^II emission line) was studied by applying a Doehlert experimental design (Table 4). The calculated effects are shown in Figs. 3 and 4 for pneumatic and ultrasonic nebulization, respectively. The response surfaces, characterized by MLR coefficients equal to 0.997 and 0.967, respectively, show that an increase in rf power caused a sharp decrease in the SBR. This trend is typical of all the analyte spectral lines studied (except Zn when using USN), as shown in Table 5, where the SBRs measured at different power levels are reported.

Fig. 3 Effect of sheathing gas flow rate and rf power on V II 292.402 nm SBR, using pneumatic nebulization.

Fig. 4 Effect of sheathing gas flow rate and rf power on V II 292.402 nm SBR, using ultrasonic nebulization.

Table 5 Signal to background ratios measured by analysing a multielement standard solution (1 mg l⁻¹) at different power levels^a

Pneumatic nebulization	Rf power/W
Emission line	1200	1100	1000	900	Enhancement^b
^aAn intermediate gas flow rate of 0.1 l min^−1 was used. ^bIncreased percentage of SBR obtained by varying the power from higher to lower level.
Zn II 202.548	29	31	37	42	45
Pb II 220.353	2.1	2.1	2.5	2.7	29
Ni II 231.604	5.3	5.5	6.5	8.2	55
Mn II 257.610	55	62	84	106	93
Cr II 267.716	8.7	9.9	12.3	14.9	71
V II 292.402	5.2	5.8	7.3	9.1	75
Cu I 324.754	5.6	7.1	9.7	13.0	132
Ultrasonic nebulization	Rf power/W
Emission line	1150	1000	850	700	Enhancement^b
Zn II 202.548	146	144	99.2	112	−23
Pb II 220.353	7.90	8.91	9.72	11.8	49
Ni II 231.604	18.9	22.2	24.3	28.1	49
Mn II 257.610	246	326	347	358	46
Cr II 267.716	37.0	42.6	47.8	56.7	53
V II 292.402	20.4	22.8	28.1	34.3	68
Cu I 324.754	21.4	29.1	33.6	44.8	109

---

Concerning the effect of the sheathing gas flow rate on SBR, a different trend depending on the nebulization system was found. When using a pneumatic nebulizer a sharp decrease in the SBR with increasing gas flow rate was observed (Fig. 3). Remembering that a similar effect on plasma robustness had been found, this can be attributed to a degradation of plasma excitation conditions.

With ultrasonic nebulization, an increase in the intermediate gas flow rate caused an initial increase in the SBR, until a maximum was reached. A further increase in this parameter led to a decrease in the SBR (Fig. 4). This trend can be explained considering that a moderate flow of sheathing gas improves the analyte transport efficiency without altering the plasma properties, while higher gas flow rates (higher than 0.2 l min⁻¹) cause a degradation of plasma conditions, as previously found (Fig. 2).

Multivariate study of matrix effects

In order to obtain an accurate estimation of the expected interferences due to a specific matrix, it is necessary to investigate the relationship between the interfering effect and the concentrations of all the elements composing the matrix, including all the potential interactions between matrix elements. Therefore, the following equation was postulated: where Y is the parameter used to quantify the interferences, x_i are the concentrations of the i elements which compose the matrix and b_i are the coefficients of the model. In the present study, we have considered five common matrix elements (Na, K, Ca, Al and Fe) and investigated their effects on several analytical emission lines, listed in Table 2 together with their characteristics.

To quantify the matrix effects in ICP-AES, different parameters were considered, such as the total interfering effect,⁴⁹ intensity ratio with/without matrix,^29,43,46 recovery or error per cent referred to the added analyte concentration.^28,48 In order to quantify immediately the analytical error due to matrix effects, we chose as response [Y in eqn. (3)] the error per cent, defined by eqn. (1).

In order to estimate the coefficients of the model, MLR analysis was performed, according to the method previously reported in the experimental section. The results of the MLR analyses are shown in Tables 6 and 7. The calculated effects are expressed as mean values and 95% confidence intervals (only significant terms are reported).

Table 6 Multivariate effects of sodium, potassium, calcium, aluminium and iron on analytical error (mean values and 95% confidence intervals) (Meinhard nebulization)

Coefficient	Factor	Zn 202.548	Pb 220.353	Ni 231.604	Ba 233.527	Mn 257.610	Cr 267.716	V 292.402
Intercept
b0	Mean	−8.35 ± 1.56	−15.6 ± 1.2	−12.7 ± 1.8	−21.5 ± 1.5	−16.8 ± 1.1	−16.0 ± 1.6	−13.8 ± 1.5
Main effects
b1	(Na)	—	—	—	−3.36 ± 1.81	−3.10 ± 0.81	−3.87 ± 1.16	−2.50 ± 1.09
b2	(K)	−3.04 ± 1.19	−3.58 ± 1.00	−2.46 ± 1.33	−3.54 ± 1.81	−3.41 ± 0.81	−3.61 ± 1.16	−4.41 ± 1.09
b3	(Ca)	−2.46 ± 0.97	−1.45 ± 0.81	−2.35 ± 1.09	−4.35 ± 1.62	−3.96 ± 0.63	−5.08 ± 0.92	−4.62 ± 0.85
b4	(Al)	—	−4.57 ± 0.91	−1.85 ± 1.22	—	−1.31 ± 0.72	−1.25 ± 1.04	−1.74 ± 0.98
b5	(Fe)	—	2.14 ± 0.91	−2.15 ± 1.09	−1.88 ± 1.62	−2.28 ± 0.63	−2.29 ± 0.92	−2.67 ± 0.85
Quadratic effects
b11	(Na)^2	—	−1.02 ± 0.82	—	—	−0.70 ± 0.68	—	−1.12 ± 0.92
b22	(K)^2	−1.66 ± 1.06	−2.64 ± 0.90	−1.67 ± 1.19	—	−1.40 ± 0.68	−1.21 ± 0.99	−2.23 ± 0.92
b33	(Ca)^2	−0.90 ± 0.76	—	−1.14 ± 0.86	—	−0.69 ± 0.48	−0.97 ± 0.70	−0.89 ± 0.64
b44	(Al)^2	—	—	—	—	—	—	—
b55	(Fe)^2	−1.37 ± 0.76	—	−2.41 ± 0.86	—	−1.26 ± 0.48	−1.11 ± 0.70	−1.61 ± 0.64
Two-factor interactions
b12	(Na)(K)	—	—	—	—	—	—	—
b13	(Na)(Ca)	—	—	—	—	—	—	−1.23 ± 1.12
b14	(Na)(Al)	—	—	—	—	—	—	—
b15	(Na)(Fe)	—	—	—	—	—	—	—
b23	(K)(Ca)	—	—	—	—	—	—	—
b24	(K)(Al)	—	—	—	—	—	—	—
b25	(K)(Fe)	—	—	—	—	—	—	−1.58 ± 1.12
b34	(Ca)(Al)	1.58 ± 1.24	1.51 ± 1.03	1.61 ± 1.38	—	−1.03 ± 0.83	−1.74 ± 1.19	−1.48 ± 1.12
b35	(Ca)(Fe)	—	−1.38 ± 1.03	—	—	−1.62 ± 0.83	−1.79 ± 1.19	−1.80 ± 1.12
b45	(Al)(Fe)	—	—	—	—	—	—	—
Multiple linear regression coefficient
		0.885	0.963	0.919	0.853	0.982	0.970	0.975
Cross-validation explained variance
		70%	81%	65%	64%	85%	74%	78%

---

Table 7 Multivariate effects of sodium, potassium, calcium, aluminium and iron on analytical error (mean values and 95% confidence intervals) (ultrasonic nebulization)

Coefficient	Factor	Zn 202.548	Pb 220.353	Ni 231.604	Ba 233.527	Mn 257.610	Cr 267.716	V 292.402
Intercept
b0	Mean	−4.79 ± 2.79	−15.4 ± 2.4	−13.6 ± 2.3	−15.2 ± 3.5	−17.5 ± 2.4	−15.7 ± 2.6	−16.8 ± 3.1
Main effects
b1	(Na)	—	−2.67 ± 2.23	−6.25 ± 1.96	−3.40 ± 2.60	−3.53 ± 2.07	−4.66 ± 2.10	−5.43 ± 2.40
b2	(K)	—	—	−4.31 ± 1.96	−2.63 ± 2.60	—	−2.93 ± 2.10	−3.42 ± 2.40
b3	(Ca)	−7.25 ± 1.85	−3.41 ± 2.42	−4.34 ± 1.56	−3.41 ± 2.73	−3.36 ± 1.87	−3.11 ± 1.90	−4.01 ± 1.69
b4	(Al)	—	−4.23 ± 2.18	—	—	−2.02 ± 1.68	−1.79 ± 1.90	−2.79 ± 1.96
b5	(Fe)	−7.44 ± 1.85	−3.83 ± 1.91	−7.22 ± 1.19	−6.03 ± 2.16	−4.88 ± 1.46	−5.87 ± 1.46	−5.57 ± 1.69
Quadratic effects
b11	(Na)^2	—	—	−2.73 ± 1.41	−	−1.88 ± 1.66	−1.95 ± 1.65	−2.58 ± 1.89
b22	(K)^2	—	—	−1.59 ± 1.41	−	−	−1.41 ± 1.65	−1.92 ± 1.89
b33	(Ca)^2	−2.56 ± 1.36	−4.18 ± 2.05	−4.42 ± 1.27	−4.48 ± 2.28	−4.64 ± 1.58	−4.69 ± 1.57	−2.46 ± 1.27
b44	(Al)^2	2.71 ± 1.74	—	2.74 ± 1.13	2.12 ± 2.06	—	—	—
b55	(Fe)^2	−2.76 ± 1.36	—	−3.12 ± 0.89	−2.88 ± 1.60	−3.01 ± 1.09	−2.82 ± 1.08	−3.07 ± 1.27
Two-factor interactions
b12	(Na)(K)	—	—	−2.74 ± 1.95	—	—	—	—
b13	(Na)(Ca)	—	—	—	—	—	—	—
b14	(Na)(Al)	—	—	—	—	—	—	—
b15	(Na)(Fe)	—	—	—	—	—	—	—
b23	(K)(Ca)	—	—	—	—	—	—	—
b24	(K)(Al)	−3.04 ± 2.46	—	—	—	—	—	—
b25	(K)(Fe)	—	—	—	—	—	—	—
b34	(Ca)(Al)	—	—	—	—	—	—	—
b35	(Ca)(Fe)	—	—	3.15 ± 1.61	—	—	—	—
b45	(Al)(Fe)	—	—	—	—	—	—	—
Multiple linear regression coefficient
		0.951	0.909	0.986	0.923	0.961	0.968	0.949
Cross-validation explained variance
		79%	67%	89%	58%	76%	84%	55%

---

The MLR coefficients and EV values [see eqn. (2)] were also computed. From them, it was concluded that all the models are satisfactory both to fit the experimental data and to predict the response inside the experimental domain.

The values of b₀ (corresponding to the estimate of the response at the central point, when all the matrix elements have a concentration of 224 µg ml⁻¹, coded as 0) furnish an evaluation of the mean analytical error due to the whole matrix. In addition, the coefficients of the models allow an estimation of all the individual and mutual effects, providing a multivariate quantification of interferences arising from the considered matrix elements.

Tables 6 and 7 contain a great deal of information and show how complex the relationships are between interfering effects and matrix composition. In general, all the concomitant elements show a negative effect, except aluminium in the determination of Zn, Ni and Ba with ultrasonic nebulization. Moreover, the matrix effects are often non-linear, since significant quadratic terms were deduced for many elements. This means that the depressive interfering effect sharply increases with increasing matrix element concentration.

Concerning the influence of the sample introduction system on matrix effects, it can be seen that the effects of sodium, calcium and iron are generally greater with USN than MPN, while the effect of potassium is greater when using MPN, except in the determination of nickel. The effect of aluminium strongly depends on the nebulization system, showing a negative linear effect in the determination of Pb, Ni, Mn, Cr and V with MPN, but a positive quadratic effect in the determination of Zn, Ni and Ba with USN. Moreover, significant two-term interactions were deduced and must be considered to obtain a complete quantification of the matrix effects. In particular, a significant mutual effect of calcium and aluminium on the interferences on several lines was deduced when using a Meinhard nebulizer. This codependence might be the result of the formation of a calcium aluminate complex, similar to that which was proven to exist in analytical flame spectrometry.

In order to determine whether the observed interfering effects were due to changes in plasma excitation conditions or to aerosol formation and transport, for each sample considered in the interference study the Mg II/Mg I intensity ratio was measured. From the values found (9.3 ± 0.4 and 9.0 ± 0.6 for Meinhard and ultrasonic nebulization, respectively), it can be concluded that all the samples were analysed under robust plasma conditions and that the observed matrix effects are due to a degradation of the efficiency of sample introduction. This result was expected since the optimization of the operating conditions had been carried out in order to obtain plasma robustness.

Finally, it should be noted that the magnitude of the matrix-induced analytical errors estimated by the models, when considering real analytical determinations, can be significantly high. To highlight this result, the matrix element concentrations in some real samples usually analysed by ICP-AES are reported in Table 8. By inserting these values in the models, it can be easily verified that an underestimation ranging from 10% to 30% is predicted in the determination of the considered trace elements at a concentration of 1 µg ml⁻¹. As outlined by Hoenig et al.,⁴⁸ even greater analytical errors are expected when the analyte concentration is lower. These examples clearly show that optimization of the plasma excitation conditions is not sufficient to remove completely the matrix effects, and there is a need to reduce physical interferences in ICP-AES determinations.

Table 8 Matrix element concentrations in some environmental and geochemical samples, after solubilization (1 g of wet material in 100 ml of solution)

		Matrix element concentrations/µg ml^−1
Sample	Type	Na	K	Ca	Al	Fe
^aCommunity Bureau of Reference, Brussels, Belgium. ^bNational Research Council Canada, Ottawa, Canada.
CRM-414^a	Plankton	83	76	650	18	19
HISS-1^b	Marine sediment	37	33	114	73	25
PACS-1^b	Marine sediment	345	124	197	662	409
BCR-1^a	Basalt	243	140	497	722	941
BCR-280^a	Lake sediment	176	276	169	775	424

---

Conclusions

Although high power plasmas are generally employed for matrix effect investigations in ICP-AES, the use of lower power is more favourable in practical analyses in order to obtain greater signal to background ratios and lower detection limits. However, it has been well established that plasma robustness is a necessary condition in order to minimize matrix-induced changes in the plasma source. A good compromise can be obtained by optimizing the other parameters that affect plasma robustness, such as the viewing height, carrier gas flow rate, sheathing gas flow rate, injector diameter and rf frequency, the last two being characteristic of the adopted instrumentation. Our results clearly prove that, after optimization of the operating parameters, plasma robustness is achieved even with a low power plasma: 900 W and 800 W with MPN and USN, respectively.

In such conditions, a multivariate study of interferences caused by complex matrices containing Na, K, Ca, Al and Fe, at concentration levels ranging from 10 to 5000 µg ml⁻¹, was performed, providing a multivariate quantification of interferences arising from the considered matrix elements and showing how complex the relationships are between interfering effects and matrix composition. The application of the techniques of empirical modelling and experimental design allowed a great deal of information of good statistical quality to be obtained with a relatively limited number of measurements. Therefore, this approach is proposed as a simple and satisfactory method to quantify accurately matrix effects and to investigate interference phenomena.

References

1. G. F. Larson, V. A. Fassel, R. H. Scott and R. N. Kniseley, Anal. Chem., 1975, 47, 238.
2. M. H. Abdallah, J. M. Mermet and C. Trassy, Anal. Chem., 1976, 87, 329.
3. P. W. J. M. Boumans and F. J. De Boer, Spectrochim. Acta, Part B, 1976, 31, 355.
4. G. R. Kornblum and L. de Galan, Spectrochim. Acta, Part B, 1977, 32, 455.
5. M. Blades and G. Horlick, Spectrochim. Acta, Part B, 1981, 36, 861.
6. W. H. Gunter, K. Visser and P. B. Zeeman, Spectrochim. Acta, Part B, 1982, 37, 571.
7. R. Rezaaiyaan and G. M. Hieftje, Anal. Chem., 1985, 57, 412.
8. L. J. Prell, C. Monnig, R. E. Harris and S. R. Koirtyohann, Spectrochim. Acta, Part B, 1985, 40, 1401.
9. D. A. Wilson, A. Yuen and G. M. Hieftje, Anal. Chim. Acta, 1985, 171, 241.
10. G. D. Rayson and G. M. Hieftje, Spectrochim. Acta, Part B, 1986, 41, 683.
11. M. R. Tripkovic and I. D. Holclajtner-Antunovic, J. Anal. At. Spectrom., 1993, 8, 349.
12. M. Blades and G. Horlick, Spectrochim. Acta, Part B, 1981, 36, 881.
13. X. Romero, E. Poussel and J. M. Mermet, Spectrochim. Acta, Part B, 1997, 52, 487.
14. X. Romero, E. Poussel and J. M. Mermet, Spectrochim. Acta, Part B, 1997, 52, 495.
15. S. E. Hobbs and J. W. Olesik, Spectrochim. Acta, Part B, 1997, 52, 353.
16. P. J Galley, M. Glick and G. M. Hieftje, Spectrochim. Acta, Part B, 1993, 48, 769.
17. J. P. Rybarczyk, C. P. Jester, D. A. Yates and S. R. Koirtyohann, Anal. Chem., 1982, 54, 2162.
18. J. M. Mermet, Anal. Chim. Acta, 1991, 250, 85.
19. N. Furuta, Spectrochim. Acta, Part B, 1986, 41, 1115.
20. J. A. Olivares and R. S. Houk, Anal. Chem., 1986, 58, 20.
21. G. D. Rayson and G. M. Hieftje, Spectrochim. Acta, Part B, 1986, 41, 683.
22. D. Beauchemin, J. W. McLaren and S. S. Berman, Spectrochim. Acta, Part B, 1987, 42, 467.
23. S. E. Hobbs and J. W. Olesik, Appl. Spectrosc., 1991, 9, 1939.
24. R. Rezaaiyaan, J. W. Olesik and G. M. Hieftje, Spectrochim. Acta, Part B, 1985, 40, 73.
25. K. O'Hanlon, L. Ebdon and M. Foulkes, J. Anal. At. Spectrom., 1997, 12, 329.
26. B. L. Sharp, J. Anal. At. Spectrom., 1988, 3, 939.
27. C. Debuisson, E. Poussel, J. L. Todolì and J. M. Mermet, J. Anal. At. Spectrom., 1998, 12, 593.
28. C. Dubuisson, E. Poussel and J. M. Mermet, J. Anal. At. Spectrom., 1998, 13, 1265.
29. J. M. Mermet, J. Anal. At. Spectrom., 1998, 13, 419.
30. M. Wu and G. M. Hieftje, Spectrochim. Acta, Part B, 1994, 49, 149.
31. P. J. Galley and G. M. Hieftje, Spectrochim. Acta, Part B, 1994, 49, 703.
32. J. C. Ivaldi and J. F. Tyson, Spectrochim. Acta, Part B, 1995, 50, 1207.
33. G. R. Gillson and G. Horlick, Spectrochim. Acta, Part B, 1986, 41, 619.
34. J. W. Olesik and E. J. Williamsen, Appl. Spectrosc., 1989, 43, 1223.
35. S. E. Hobbs and J. W. Olesik, Appl. Spectrosc., 1991, 45, 1395.
36. G. Horlick and M. W. Blades, Appl. Spectrosc., 1980, 34, 229.
37. J. W. Olesik, Anal. Chem., 1991, 63, 12A.
38. G. M. Hieftje, P. J. Galley, M. Glick and D. S. Hanselman, J. Anal. At. Spectrom., 1992, 7, 769.
39. C. Debuisson, E. Poussel and J. M. Mermet, J. Anal. At. Spectrom., 1998, 12, 63.
40. M. R. Tripkovic and I. D. Holclajtner-Antunovic, J. Anal. At. Spectrom., 1993, 8, 359.
41. M. Thompson and M. H. Ramsey, Analyst, 1985, 110, 1413.
42. M. Thompson, M. H. Ramsey, B. J. Coles and C. M. Du, J. Anal. At. Spectrom., 1987, 2, 185.
43. B. Budic, J. Anal. At. Spectrom., 1998, 13, 869.
44. I. Novotny, J. C. Farinas, W. Jialiang, E. Poussel and J. M. Mermet, Spectrochim. Acta, Part B, 1996, 51, 1517.
45. E. Magi, M. Grotti and A. Mazzucotelli, Annali di Chimica, 1994, 84, 417.
46. I. B. Brenner, M. Zischka, B. Maichin and G. Knapp, J. Anal. At. Spectrom., 1998, 13, 1257.
47. I. B. Brenner, A. Zander, M. Cole and A. Wiseman, J. Anal. At. Spectrom., 1997, 12, 897.
48. M. Hoenig, H. Docekalova and H. Baeten, J. Anal. At. Spectrom., 1998, 13, 195.
49. W. Branagh, C. Whelan and E. D. Salin, J. Anal. At. Spectrom., 1997, 12, 1307.
50. M. Grotti, E. Magi and R. Leardi, Anal. Chim. Acta, 1996, 327, 47.
51. M. Grotti, R. Leardi and R. Frache, Anal. Chim. Acta, 1998, 376, 293.
52. M. Grotti, R. Leardi, C. Gnecco and R. Frache, Spectrochim. Acta, Part B, 1999, 54, 845.
53. M. Grotti, C. Gnecco and F. Bonfiglioli, J. Anal. At. Spectrom., 1999, 14, 1171.
54. D. H. Doehlert, J. R. Statist. Soc., Ser. C, 1970, 19, 231.
55. M. Stone, J. R. Statist. Soc., Ser. B, 1974, 36, 111.
56. M. ForinaS. LanteriC. ArmaninoR. LeardiG. Drava, PARVUS 1.2 An Extendable Package of Programs for Data Explorative Analysis, Classification and Regression Analysis, Dipartimento di Chimica e Tecnologie Farmaceutiche e Alimentari, Università di Genova, Genoa, Italy, 1995..
57. M. Carrè, K. Lebas, M. Marichy, M. Mermet, E. Poussel and J. M. Mermet, Spectrochim. Acta, Part B, 1995, 50, 271.
58. A. Fernandez, M. Murillo, N. Carrion and J. M. Mermet, J. Anal. At. Spectrom., 1994, 9, 217.

---