Copper(I) and silver(I) carbonyls. To be or not to be nonclassical

Abstract

The traditional, or classical, picture of M–CO bonding is not a good model for more than 200 metal carbonyl species with average ν(CO) values greater than 2143 cm⁻¹. These “nonclassical” complexes, exemplified in this Perspective by the cations Cu(CO)_n⁺ and Ag(CO)_n⁺ (n = 1–4), possess M–CO interactions that are best described as M←CO σ bonds having a significant electrostatic component. There is relatively little M→CO π backbonding. However, despite the similarity in ν(CO) values, homologous Cu(CO)_n⁺ and Ag(CO)_n⁺ complexes behave differently when subjected to perturbations such as stretching the metal–carbon bonds or adding a pair of weak ligands to the metal center.

---

Steven H. Strauss

Steve Strauss, shown with his wife and crystallographer Susie M. Miller, is Professor of Chemistry at Colorado State University. He was born in New York City in 1952, received his bachelor’s degree from Franklin & Marshall College and his Ph.D. from Northwestern University (with D. F. Shriver), and was a postdoctoral fellow at Stanford and Harvard Universities (with R. H. Holm). He has been a faculty member at CSU since 1981, where he has received four awards for outstanding teaching and an A. P. Sloan Research Fellowship. His research interests include metal carbonyl chemistry, fluorine chemistry, boron cluster chemistry, and the selective removal and recovery of ionic pollutants from water. In 2001 he will chair the ACS Division of Fluorine Chemistry and the Gordon Research Conference on Inorganic Chemistry.

---

Introduction

Metal carbonyl chemistry is a mature discipline. The first metal carbonyl complex, cis-PtCl₂(CO)₂, was reported in 1870 ¹ and the first homoleptic metal carbonyl, Ni(CO)₄, in 1890.² It is impossible to know how many compounds and materials containing M–C≡O linkages have been prepared since then, but the total is likely to be in the tens of thousands. As any scientifically interesting collection grows over time, it is inevitable that scholars will want to systematize that collection, and some scholars will disagree with others over the degree the systemization that is appropriate.³ Biology, for example, has its taxonomists, who are sometimes known as “splitters” or “lumpers”. As far as metal carbonyl chemistry is concerned, we find ourselves on the side of the splitters, acknowledging the similarities between compounds but choosing to dwell on their differences. For those chemists who design and synthesize new molecules with specific properties, an understanding of the differences is of vital importance.

Listed below are five pairs of statements that students of inorganic chemistry are usually taught about transition metal carbonyls. Although it may seem at first that each pair of statements is merely two ways of expressing the same concept, there are important distinctions that will become obvious shortly.

1a.	CO is a σ donor and a π acceptor ligand;
1b.	M–CO bonds have a significant M←CO σ component and a significant M→CO π component;
2a.	The π component (π backbonding) involves the transfer of electron density from metal dπ orbitals to CO π* orbitals;
2b.	C–O distances (R(CO)) are longer and ν(CO) values are lower for metal carbonyls than for the free CO molecule (1.1282 Å and 2143 cm^−1, respectively);
3a.	Adding a donor ligand L to a metal carbonyl complex increases the electron density at the metal center and enhances M→CO π backbonding;
3b.	Adding a donor ligand L to a metal carbonyl complex results in a stronger, shorter M–CO bond and a weaker, longer C–O bond;
4a.	Substituting an ancillary ligand L with one that is a stronger σ donor enhances M→CO π backbonding;
4b.	Substituting an ancillary ligand L with one that is a stronger σ donor results in a stronger, shorter M–CO bond and a weaker, longer C–O bond;
5a.	The transformation LM(CO)n→LM(CO)n − 1 + CO results in fewer π-acceptor CO ligands competing for the same metal dπ electron density;
5b.	The transformation LM(CO)n→LM(CO)n − 1 + CO results in weaker, longer C–O bonds and lower ν(CO) values.

Statements 1a, 2a, 3a, 4a, and 5a (1a–5a) are universally true. Unbeknownst to most students (and perhaps some instructors), however, there is a growing class of transition metal carbonyls that violate one or more of Statements 1b, 2b, 3b, 4b, and/or 5b (1b–5b). For example, there are now more than two hundred metal carbonyl species with average ν(CO) values higher than 2143 cm⁻¹.⁴ In three cases for which very precise X-ray diffraction data are available, these have been shown to have R(CO) values shorter than 1.1282 Å at the ±3σ level of confidence.^5,6 Furthermore, in at least one case, dissociation of CO from a tricarbonyl complex resulted in a dicarbonyl complex with a higher, not a lower, ν(CO) value.⁷ There are several recent ⁴ as well as older reviews ⁸ of the chemistry of these unusual metal carbonyls.

Discussion

We will now highlight the similarities and differences between the vast majority of metal carbonyls and the ones that violate one or more of Statements 1b–5b by comparing two homologous sets of metal carbonyl cations, Cu(CO)_n⁺ and Ag(CO)_n⁺ (n = 1–4). A wealth of information has been published about these complexes. The mono- and di-carbonyls were previously studied theoretically by several investigators;⁹ more recently, all eight complex cations were studied by Frenking and co-workers at the CCSD(T) level of theory.^4g,10 All eight complexes can be generated in the gas phase, and sequential M–CO bond energies have been measured with good precision by Armentrout and co-workers.¹¹ Seven of the eight complexes have been generated in condensed phases.¹² Using strong protic acids such as BF₃·H₂O and HSO₃F, Souma and co-workers generated Cu(CO)⁺, Cu(CO)₂⁺, Cu(CO)₃⁺, Cu(CO)₄⁺, Ag(CO)⁺, and Ag(CO)₂⁺.^12a,b Zhou and Andrews recently reported IR spectra of the four Cu(CO)_n⁺ cations isolated in Ne/CO matrices at 4 K.^12c Using highly fluorinated anions, Passmore and co-workers prepared the solid compound [Cu(CO)][AsF₆] ^13a and we prepared the solid compounds [Cu(CO)_2,3][AsF₆],^13b [Cu(CO)₄][1-Et-CB₁₁F₁₁],⁶ [Ag(CO)][SbF₆],¹⁴ [Ag(CO)₂][B(OTeF₅)₄],¹⁵ and [Ag(CO)₃][Nb(OTeF₅)₆].⁷ Both [Ag(CO)₂][B(OTeF₅)₆] and [Cu(CO)₄][1-Et-CB₁₁F₁₁] have been structurally characterized. As far as crystalline compounds containing the eight cations Cu(CO)_n⁺ and Ag(CO)_n⁺ are concerned, the above list includes those that have only weak M ⋯ F bonds in addition to the M–CO bonds. Related compounds that contain stronger metal–ligand bonds and have been structurally characterized include Ag(CO)(B(OTeF₅)₄) (two Ag–O(B,Te) bonds),¹⁵ Cu(CO)₂(N(SO₂CF₃)₂) (one Cu–N bond),¹⁶ Cu(CO)₂(1-Bn-CB₁₁F₁₁) (one η² copper–arene bond),⁶ and (Cu,Ag)(CO)(Tp′) (three Cu–N or Ag–N bonds; Tp′ = hydridotris(3,5-bis(trifluoromethyl)pyrazol-1-yl)borate).¹⁷ In addition, there is an extensive literature on the generation of Cu(CO)_n⁺ and Ag(CO)_n⁺ species in a variety of zeolites.¹⁸

How are the cations Cu(CO)_n⁺ and Ag(CO)_n⁺ similar to each other but different than the vast majority of metal carbonyls? It was predicted that all eight cations would have ν(CO) values greater than the value for free CO,^10,12c in harmony with experimental data for the seven cations studied in condensed phases with fluoroanions or in Ne/CO matrices. For example, the sets of cm⁻¹ values {ν_asym(CO), ν_sym(CO)} for the D_∞h Cu(CO)₂⁺ and Ag(CO)₂⁺ cations in [Cu(CO)₂][AsF₆] ¹⁴ and [Ag(CO)₂][Nb(OTeF₅)₆] ¹⁶ are {2164, 2177} and {2196, 2220}, respectively. The average values, 2171 and 2208 cm⁻¹, are 28 and 65 cm⁻¹ higher than 2143 cm⁻¹. As another example, the ν_asym(CO) value for the T_d Cu(CO)₄⁺ cation in [Cu(CO)₄][1-Et-CB₁₁F₁₁] is 2184 cm⁻¹.⁶ In contrast, the ν_asym(CO) values for the isoelectronic species Ni(CO)₄, Co(CO)₄⁻, Fe(CO)₄²⁻, and Mn(CO)₄³⁻ are 2058, 1883, 1729, and 1670 cm⁻¹, respectively, all lower than 2143 cm⁻¹.¹⁹ Relevant IR and Raman data for Cu(CO)_n⁺ and Ag(CO)_n⁺ are listed in Table 1.

Table 1 Carbon–oxygen stretching frequencies

		ν(CO), cm^−1
Complex	Counter ion	IR	Raman	Ref.
Ag(CO)^+	SbF6^−	2185		14
Ag(CO)^+	Nb(OTeF5)6^−	2204	2206	15
Ag(CO)2^+	Nb(OTeF5)6^−	2196	2220	15
Ag(CO)3^+	Nb(OTeF5)6^−	2191		7
Cu(CO)^+	1-Et-CB11F11^−	2175		6
	AsF6^−	2178		13(b)
	Ne/CO matrix	2234		12(c)
Cu(CO)2^+	AsF6^−	2164	2177	13(b)
	Ne/CO matrix	2230		12(c)
Cu(CO)3^+	AsF6^−	2183	2179, 2206	13(b)
	Ne/CO matrix	2211		12(c)
Cu(CO)4^+	1-Et-CB11F11^−	2184		6
	Ne/CO matrix	2202		12(c)
Ni(CO)4	None	2058		19(a)
Co(CO)4^−	Na^+	1883		19(b)
Fe(CO)4^2−	Na^+	1729		19(b)
Mn(CO)4^3−	Na^+	1670		19(c)

---

The CO triple bond is one of the strongest known chemical bonds. Because of the depth of its potential energy well, even a dramatic change in CO bond energy upon coordination to a metal center would result in only a modest change in R(CO). In the past, crystal structures of metal carbonyls were rarely of sufficient precision that derived R(CO) values were significantly different than 1.1282 Å (i.e., significant at the ±3σ level of confidence). However, R(CO) values for [Cu(CO)₄][1-Et-CB₁₁F₁₁], 1.110(3), 1.114(3), 1.109(4), and 1.111(4) Å,⁶ and for Cu(CO)₂(1-Bn-CB₁₁F₁₁), 1.109(3) and 1.115(3) Å,⁶ are all significantly shorter than 1.1282 Å (a related example is Pd(CO)₂(SO₃F )₂,⁵ in which one of the two R(CO) values, 1.102(6) Å, was found to be significantly shorter than 1.1282 Å). Compare, for example, the significantly longer R(CO) values in two recently published metal carbonyl structures, [HL][Co(CO)₄] (L = quinuclidine), with R(CO) = 1.150(2)–1.153(2) Å,²⁰ and [NEt₄][Cr(CO)₄(NHMeCH₂CO₂)], with R(CO) = 1.154(3)–1.165(3) Å.²¹ These and other relevant data are displayed in Fig. 1.

Fig. 1 Top: carbon–oxygen distances (±3σ) for selected compounds: a, [Cu(CO)₄][1-Et-CB₁₁F₁₁] (ref. 6); b, Cu(CO)₂(1-Bn-CB₁₁F₁₁) (ref. 6); c, Pd(CO)₂(SO₃F )₂ (ref. 5); d, Ag(CO)(B(OTeF₅)₄) (ref. 16); e, [(CH₃)₂CHCO][SbCl₆] (ref. 16); f, [HL][Co(CO)₄] (ref. 20); g, [NEt₄][Cr(CO)₄(NHMeCH₂CO₂)] (ref. 21). Middle: structure of the Cu(CO)₄⁺ cation in [Cu(CO)₄][1-Et-CB₁₁F₁₁]. Selected interatomic distances (Å) and angles (°): Cu–C, 1.961(3)–1.968(3); C–Cu–C, 104.3(1)–112.1(6); Cu–C–O, 174.8(3)–178.4(3). Bottom: structure of Cu(CO)₂(1-Bn-CB₁₁F₁₁). Selected interatomic distances (Å) and angles (°): Cu–C1, 1.916(3); Cu–C2, 1.915(3); Cu–C9, 2.218(2); Cu–C10, 2.303(2); C1–Cu–C2, 124.1(1); Cu–C1–O1, 177.7(2); Cu–C2–O2, 177.4(3).

The data just presented highlight the fact that the diatomic molecule CO can respond in two completely different ways when it binds to a metal center. In the vast majority of cases, the response is that R(CO) increases and ν(CO) decreases. This large category of metal carbonyls could be called common, ordinary, or usual; we have chosen to call it classical. Strictly speaking, we should say that metal carbonyls in this category are classical with respect to Statement 2b. The other response is that R(CO) decreases and ν(CO) increases, and we call metal carbonyls in this category nonclassical with respect to Statement 2b. The reason for the nonclassical response, which has been discussed at length in several recent reviews ⁴ and will be summarized below, is that π backbonding is severely limited when the metal center has no d_π electrons, has a high effective nuclear charge, is very electronegative, and/or has an unusually long M–CO distance due to σ repulsion. Fig. 2 displays some of the relevant experimental and theoretical data illustrating the classical (down) and nonclassical (up) responses, with respect to free CO, in a series of one-dimensional graphs. The graph on the right demonstrates that some copper(I) carbonyls are nonclassical and some are classical with respect to Statement 2b. Fig. 3 shows the convolution of σ-bonding, π-bonding, and metal-ion charge effects on ν(CO) or R(CO).^4e Note that π backbonding is less important at long M–CO distances than σ bonding and metal-ion charge. The turning point on the resultant curve (ν(CO)_max or R(CO)_min) represents the M–C distance at which the opposing effects of π backbonding and σ bonding plus charge are equal in magnitude. Every metal carbonyl complex has a unique resultant curve, and the equilibrium M–CO distance for a given complex, R(MC)_eq, may be to the left or to the right of the turning point. A metal carbonyl that is classical with respect to Statement 2b is not only to the left of the turning point on its curve, it is below the horizontal line that represents free CO. Metal carbonyls that are nonclassical with respect to Statement 2b lie above this line on their respective curves.

Fig. 2 One-dimensional graphs showing ΔR(CO), ν(CO), and Δν(CO) as a function of metal complex relative to the free CO molecule. All of the values are experimental except the ΔR(CO) values for Ag(CO)₂⁺, Pd(CO)₂, and Rh(CO)₂⁻, which are theoretical values from ref. 10(a). The Δν(CO) value for Cu(CO)⁺ is for the neon-matrix-isolated species (ref. 11(c)). Abbreviations: X⁻ = 1-Et-CB₁₁F₁₁⁻; Y⁻ = 1-Bz-CB₁₁F₁₁⁻; Z⁻ = Nb(OTeF₅)₆⁻; (Tp′)⁻ = hydridotris(3,5-bis(trifluoromethyl)pyrazol-1-yl)borate); Tp⁻ = hydridotris(pyrazol-1-yl)borate).

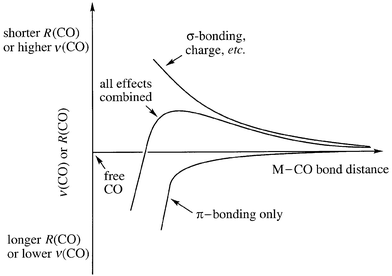Fig. 3 Plots of ν(CO) or R(CO) vs. R(MC) for a generic metal carbonyl complex. The middle curve is the resultant of the upper and lower curves.

Having highlighted above the similar, nonclassical nature of the eight complexes Cu(CO)_n⁺ and Ag(CO)_n⁺ with respect to Statement 2b, it is instructive to point out their differences with respect to Statements 1b, 3b, and 5b. As far as Statement 5b is concerned, the transformation [Ag(CO)₃][Nb(OTeF₅)₆] → [Ag(CO)₂][Nb(OTeF₅)₆] + CO resulted in an increase in ν_asym(CO) (2191 → 2198 cm⁻¹; nonclassical behavior) ⁷ but the transformation [Cu(CO)₃][AsF₆] → [Cu(CO)₂][AsF₆] + CO resulted in a decrease in ν_asym(CO) (2183 → 2164 cm⁻¹; classical behavior).† ^,14 As far as Statement 3b is concerned, the addition of two F⁻ ions at 3 Å along a perpendicular to the C_∞ molecular axis of Ag(CO)₂⁺ and Cu(CO)₂⁺ was predicted to cause an increase in R(AgC) (ΔR(AgC) = 0.036 Å; nonclassical behavior) but a decrease in R(CuC) (ΔR(CuC) = −0.034 Å; classical behavior).^10a As far as Statement 1b is concerned, an infinitesimal lengthening of R(MC) from its equilibrium value (i.e., from R(MC)_eq) was predicted to cause an increase in R(CO) for Ag(CO)⁺ but a decrease in R(CO) for Cu(CO)⁺, as shown in Fig. 4.²² According to one possible definition, “significant” π backbonding for a metal carbonyl occurs whenever R(MC)_eq is to the left of the R(MC)/R(CO) curve maximum for that complex, regardless of whether R(CO)_eq is shorter or longer than the value for free CO. Therefore, Ag(CO)⁺ is nonclassical while Cu(CO)⁺ is classical with respect to Statement 1b.^4e,22

Fig. 4 Theoretical R(MC) vs. ΔR(CO) curves for the monocarbonyl cations Cu(CO)⁺ and Ag(CO)⁺. The open data points indicate the equilibrium R(MC) values.

In these three cases, a single perturbation, dissociation of one CO ligand, addition of F⁻ ligands at 3 Å, or a small extension of the M–C bond, led to two different responses, nonclassical for the silver(I) complex in question and classical for the corresponding copper(I) complex. We are left then, with an interesting dilemma. Are Cu(CO)_n⁺ cations classical or nonclassical? The answer is that it depends on which statement about metal carbonyls is being considered. All four Cu(CO)_n⁺ complexes are nonclassical with respect to Statement 2b, but at least one of the four complexes is classical with respect to Statements 1b, 3b, or 5b. This potential confusion does not diminish the usefulness of the classical/nonclassical distinction. That the phrase “with respect to” is needed to answer the question should be no more disconcerting than the fact that this three-word phrase is also needed to answer questions unambiguously about the stability of compounds. For example, is TaF₄, an as-yet-unknown compound, stable at 25 °C? It depends on which type of stability is being considered. Thermochemical cycles have been used to predict that TaF₄ should be stable with respect to metallic tantalum and diatomic fluorine in their standard states and to predict that TaF₄ should be unstable with respect to disproportionation to the known compound TaF₅ and elemental tantalum.²³ Therefore, it is stable with respect to the elements but unstable with respect to disproportionation. As far as a simple question of “stability” is concerned, the most sensible approach is to designate a compound as “unstable” if it is unstable with respect to at least one set of products, even if it is stable with respect to other possible sets of products. Accordingly, the most sensible way to label metal carbonyls may be as follows: any metal carbonyl complex that violates at least one of Statements 1b–5b is a nonclassical metal carbonyl. Even if a complex violates only one of the five statements, its designation as nonclassical serves to alert other scientists that it is an unusual compound and that careful scrutiny of it might lead to new chemical insights and discoveries.

Interestingly, the IR ν(CO) trend for Cu(CO)₄⁺ → Cu(CO)₃⁺ → Cu(CO)₂⁺ in their crystalline fluoroanion salts, 2184 cm⁻¹ → 2179 cm⁻¹ → 2164 cm⁻¹,^6,13b is reversed for the neon-matrix-isolated cations, 2202 cm⁻¹ → 2211 cm⁻¹ → 2230 cm⁻¹,^12c as shown in Fig. 5. In other words, the isolated cations Cu(CO)₄⁺ → Cu(CO)₃⁺ → Cu(CO)₂⁺ are intrinsically nonclassical with respect to Statement 5b. It is the set of compounds containing these cations and weakly coordinating fluoroanions that is classical with respect to Statement 5b. Our interpretation of the different trends shown in Fig. 5 is that Cu ⋯ F contacts with AsF₆⁻ and 1-Et-CB₁₁F₁₁⁻ fluoroanions lower the effective positive charge on the copper(I) center and induce additional π backbonding relative to the isolated Cu(CO)_n⁺ cations. This is supported by the predicted effect, mentioned above, of the addition of two F⁻ ions at 3 Å along a perpendicular to the C_∞ molecular axis of Cu(CO)₂⁺.^10a Not only was the Cu–C bond distance predicted to be 0.034 Å shorter in Cu(CO)₂⁺·2F⁻ (1.850 Å) than in Cu(CO)₂⁺ (1.884 Å), but the ν_sym(CO) value was predicted to be 32 cm⁻¹ lower in Cu(CO)₂⁺·2F⁻ (2164 cm⁻¹) than in Cu(CO)₂⁺ (2196 cm⁻¹). Both results are clear manifestations of additional π backbonding induced by the presence of weak Cu ⋯ F contacts in [Cu(CO)₂][AsF₆] and [Cu(CO)₃][AsF₆]. Note that the choice of 3 Å for the Cu ⋯ F distance in the computational study was dictated by the observation of Ag ⋯ F distances of 2.75(1)–3.19(1) Å in the structure of [Ag(CO)₂][B(OTeF₅)₄].¹⁵ A drawing of one of the Ag(CO)₂⁺ cations in that structure, with its seven Ag ⋯ F contacts, is shown in Fig. 6. The difference between the neon-matrix IR ν(CO) value and the fluoroanion salt IR ν(CO) value is 66 cm⁻¹ for Cu(CO)₂⁺, 28 cm⁻¹ for Cu(CO)₃⁺, and 18 cm⁻¹ for Cu(CO)₄⁺. This suggests that there are fewer and longer Cu ⋯ F contacts as the number of CO ligands increases, a perfectly sensible result. In fact, there are only two Cu ⋯ F contacts shorter than 3.2 Å in [Cu(CO)₄][1-Et-CB₁₁F₁₁] (3.14 and 3.19 Å); the next two Cu ⋯ F contacts in this salt are 3.48 and 3.55 Å.⁶

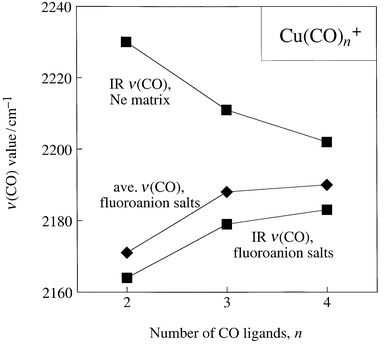Fig. 5 Plots of ν(CO) values for Cu(CO)₄⁺, Cu(CO)₃⁺, and Cu(CO)₂⁺vs. number of CO ligands. Note that the trend for the fluoroanion salts is the same whether IR ν(CO) or average ν(CO) values are considered.

Fig. 6 One of the three unique Ag⁺ coordination spheres in [Ag(CO)₂][B(OTeF₅)₄]. Selected distances (Å) and angles (°): Ag–C, 2.16(4), 2.20(4); C–O, 1.07(5), 1.09(5); Ag ⋯ F, 2.75(1)–3.19(1); Ag–C–O, 173(3), 178(3); C–Ag–C, 169(1).

Let us see what chemical insights are provided by a closer examination of copper(I) and silver(I) M(CO)_n⁺ complexes. The experimental M–CO bond dissociation energies for Cu(CO)⁺ and Ag(CO)⁺ are 36 and 21 kcal mol⁻¹, respectively ¹¹ (the CCSD(T) predicted values are 31 and 21 kcal mol⁻¹, respectively ^10b). The Cu⁺–CO bond is 70% stronger than the Ag⁺–CO bond, a difference much larger than commonly observed for 3d vs. 4d metal–ligand bond energies within a triad. Furthermore, Ag–C distances in silver(I) carbonyls are ca. 0.2 Å longer than Cu–C distances in similar compounds. Compare, for example, the Ag–C distance in Ag(CO)(B(OTeF₅)₄), 2.10(1) Å,¹⁵ with the Cu–C distance in Cu(CO)Cl, 1.86(2) Å,²⁴ or the Ag–C distance in Ag(CO)(Tp′), 2.037(5) Å, with the Cu–C distance in Cu(CO)(Tp′), 1.808(5) Å.¹⁷ One might therefore ask, are Ag⁺–CO bonds long and weak because there is negligible π backbonding or is there negligible π backbonding because Ag⁺–CO bonds are long and weak? The answer is that Ag⁺–ligand σ bonds are intrinsically long and weak relative to Cu⁺–ligand σ bonds because of greater σ repulsion in Ag⁺ complexes. For one- or two-coordinate d¹⁰ metal complexes, σ repulsion is due to the interaction of filled ligand σ MOs with the filled metal d_z² (d_σ) atomic orbital. For these complexes, sd_σ mixing results in a shift of metal electron density from the z axis (the metal–ligand axis) to the xy plane, decreasing the σ repulsion and allowing for shorter, stronger metal–ligand σ bonds.²⁵ The amount of sd_σ mixing depends on the s–d_σ energy gap, and although this cannot be measured directly, others have estimated it to be equal to the lowest energy d⁹s¹←d¹⁰ electronic transition energy.²⁵ The s–d_σ energy gaps ²⁶ and d-subshell energy levels for Cu⁺ and Ag⁺ are depicted in Fig. 7 (the d-subshell energies correspond to the second ionization potentials of the neutral atoms). Note that there would be no corresponding 4d_z² σ repulsion for two-coordinate d⁸ Rh⁺ complexes. For example, ab initio calculations have been used to predict that the Rh⁺–CO bonds in Rh(CO)₂⁺ are ≈50% stronger than the Ag–CO bonds in Ag(CO)₂⁺, a consequence of stronger σ bonding as well as significant π backbonding for Rh⁺ (see below).²⁷ The Ag⁺ ion, with a larger s–d_σ energy gap than Cu⁺, forms considerably weaker metal–ligand σ bonds than Cu⁺. This explanation is consistent with the Ag(CO)⁺ plot in Fig. 4, which suggests that the Ag⁺ ion is, in principle, capable of as much π backbonding to a CO ligand as the Cu⁺ ion for equal M–CO distances. The lack of significant backbonding in Ag(CO)⁺ is primarily because the equilibrium Ag–CO distance is too long to allow for effective Ag–C π overlap.

Fig. 7 Orbital energy diagram for monovalent copper and silver. The d-subshell energies correspond to the second ionization potentials for the neutral atoms. The s–d energy gaps correspond to the lowest energy d⁹s¹←d¹⁰ electronic transition energies for the gas-phase M⁺ cations.

Fig. 7 reveals a second reason why there is little π backbonding in Ag(CO)⁺. In addition to a long Ag–C bond, which is not conducive to effective π backbonding, the second ionization energy of silver atoms is 21.5 eV, the highest value for any metal in the periodic table with the exception of the alkali metals. For comparison, the second ionization energies of copper and rhodium atoms are 20.3 and 18.1 eV, respectively. It is now abundantly clear why CO binds so weakly to Ag⁺ in Ag(CO)⁺. This metal ion has three strikes against it: (i) the relatively large s–d_σ energy gap leads to significant σ repulsion and a weak σ bond; (ii) the weak and long Ag–C bond prevents effective π overlap; and (iii) the high second ionization energy of Ag⁺ signals a very high effective nuclear charge, which also precludes effective π backbonding.

Another important chemical insight concerns Cu(CO)_n⁺ complexes and related copper(I) carbonyl complexes containing ancillary ligands. The right-hand graph in Fig. 2 demonstrates convincingly that Cu⁺ is capable of π backbonding to CO and that the extent of π backbonding is determined by the basicity of the ancillary ligands. By forming moderately strong bonds to CO with some π backbonding, but not too much π backbonding, several copper(I) salts are well suited for the reversible binding of CO. This property has led to the widespread use of supported CuCl and related salts for the industrial purification of CO by reversible pressure-swing or vacuum-swing adsorption/desorption processes.²⁸ In all known adsorbents involving CuCl, the limiting Cu∶CO stoichiometry is 1∶1. An understanding of the structure and bonding of nonclassical Cu(CO)_nX compounds has recently led to the design of improved copper(I)-containing CO adsorbents with Cu∶CO stoichiometries of 1∶2, 1∶3, and even 1∶4.²⁹ A possible design criterion for new reversible adsorbents for CO is the position of a compound on its R(MC) vs. ΔR(CO) curve (see Fig. 4). It is possible that good performance might be found for carbonyls of other metals if they, like Cu(CO)⁺, have positions on their respective curves that are to the left of the curve maximum but above the horizontal line that represents free CO.

How can the position of a complex relative to its curve maximum be determined? In addition to theoretical calculations, there are two potential, if difficult, experimental approaches. The first approach is to determine the sign of the M–C/C–O bond-stretch interaction force constant, F(MC,CO). This should be positive to the left of the curve maximum and negative to the right of the curve maximum. As an example using metal cyanide complexes, F(MC,CN) is 0.31(5) mdyn Å⁻¹ for [Au(CN)₂]⁻ but only 0.02(3) mdyn Å⁻¹ for Hg(CN)₂, and the difference has been attributed to less π backbonding for the Hg²⁺ complex than for the Au⁺ complex.³⁰ A problem with the F(MC,CO) approach is that such interaction force constants are generally small and have relatively large experimental errors. The second approach would involve high-pressure spectroscopy. Compressing a solid sample leads to compression of all bonds in a compound, but M–CO bonds would be especially susceptible to compression since they have relatively low force constants and consequently relatively shallow potential energy surfaces. Compressing the M–C bond or bonds should lead to a negative value of ∂(ν(CO))/∂P to the left of the curve maximum and a positive value of ∂(ν(CO))/∂P to the right of the curve maximum. Of course there are also potential problems with this approach. It will be interesting to see if either approach leads to results that are consistent with theoretical calculations.

Conclusion

We have identified five ways that a metal carbonyl species can deviate from the classical behavior of most metal carbonyls. Accordingly, we have suggested that a metal carbonyl be considered nonclassical if it is shown to violate any one of Statements 1b–5b listed above. Semantics aside, the more important purpose of this Perspective is to highlight the unusual spectroscopic and structural properties of a small but growing class of metal carbonyls, to suggest that unusual (and perhaps useful) chemical properties might be found for new metal carbonyls with limited π backbonding, and to encourage more synthetic chemists to turn their attention to these reactive and fascinating compounds.

Acknowledgements

Our work on nonclassical metal carbonyls has been generously supported by the U.S. National Science Foundation and, in part, by Air Products and Chemicals, Inc. I am very pleased to thank my co-workers and collaborators, whose names can be found in the references, for their enthusiasm, hard work, and keen insight. A special acknowledgement goes to my former student Dr Paul K. Hurlburt, whose discovery of isolable silver(I) carbonyls first kindled my interest in this subject.

References

1. (a) P. Schützenberger, Bull. Soc. Chim. Fr., 1870, 14, 97; (b) P. Schützenberger, C. R. Hebd. Sceances Acad. Sci., 1870, 70, 1134.
2. L. Mond, J. Chem. Soc., 1890, 57, 749.
3. C. Bach, H. Willner, C. Wang, S. J. Rettig, J. Trotter and F. Aubke, Angew. Chem., Int. Ed. Engl., 1996, 35, 1974.
4. (a) F. Aubke and C. Wang, Coord. Chem. Rev., 1994, 137, 483; (b) L. Weber, Angew. Chem., Int. Ed. Engl., 1994, 33, 1077; (c) J. E. Ellis and W. Beck, Angew. Chem., Int. Ed. Engl., 1995, 34, 2489; (d) J. J. Rack and S. H. Strauss, Catal. Today, 1997, 36, 99; (e) S. H. Strauss, Chemtracts: Inorg. Chem., 1997, 10, 77; (f) H. Willner and F. Aubke, Angew. Chem., Int. Ed. Engl., 1997, 36, 2402; (g) A. J. Lupinetti , G. Frenking and S. H. Strauss , Prog. Inorg. Chem.,in press..
5. C. Wang, H. Willner, M. Bodenbinder, R. J. Batchelor, F. W. B. Einstein and F. Aubke, Inorg. Chem., 1994, 33, 3521.
6. S. M. Ivanova, S. V. Ivanov, S. M. Miller, O. P. Anderson, K. A. Solntsev and S. H. Strauss, Inorg. Chem., 1999, 38, 3756.
7. (a) J. J. Rack, B. Moasser, J. D. Gargulak, W. L. Gladfelter, H. D. Hochheimer and S. H. Strauss, J. Chem. Soc., Chem. Commun., 1994, 685; (b) J. J. Rack, O. G. Polyakov, C. M. Gaudinski, J. W. Hammel, P. Kasperbauer, H. D. Hochheimer and S. H. Strauss, Appl. Spectrosc., 1998, 52, 1035.
8. (a) M. I. Bruce, J. Organomet. Chem., 1972, 44, 209; (b) M. Pasquali , and C. Floriani , in Coppper Coordination Chemistry: Biochem. Inorg. Perspect., ed. K. D. Karlin and J. Zubieta, Adenine Press, Guilderland, NY, 1983, p. 311; (c) F. Calderazzo and D. B. Dell’Amico, Pure Appl. Chem., 1986, 58, 561.
9. (a) M. A. Lynn and B. E. Bursten, Inorg. Chim. Acta, 1995, 229, 437; (b) A. Veldkamp and G. Frenking, Organometallics, 1993, 12, 4613; (c) M. Sodupe, C. W. Bauschlicher, Jr. and T. J. Lee, Chem. Phys. Lett., 1992, 189, 266; (d) L. A. Barnes, M. Rosi and C. W. Bauschlicher, Jr., J. Chem. Phys., 1990, 93, 609; (e) P. Y. Morgantini and J. Weber, THEOCHEM, 1988, 43, 247; (f) M. Merchan, I. Nebot-Gil, R. Gonzalez-Luque and E. Orti, J. Chem. Phys., 1987, 87, 1690.
10. (a) A. J. Lupinetti, G. Frenking and S. H. Strauss, Angew. Chem., Int. Ed., 1998, 37, 2113; (b) A. J. Lupinetti, V. Jonas, W. Thiel, S. H. Strauss and G. Frenking, Chem. Eur. J., 1999, 5, 2573.
11. F. Meyer, Y.-M. Chen and P. B. Armentrout, J. Am. Chem. Soc., 1995, 117, 4071.
12. (a) Y. Souma, J. Iyoda and H. Sano, Inorg. Chem., 1976, 15, 968; (b) Q. Xu and Y. Souma, Top. Catal., 1998, 6, 17; (c) M. Zhou and L. Andrews, J. Chem. Phys., 1999, 111, 4548.
13. (a) C. D. Desjardins, D. B. Edwards and J. Passmore, Can. J. Chem., 1979, 57, 2714; (b) J. J. Rack, J. D. Webb and S. H. Strauss, Inorg. Chem., 1996, 35, 277.
14. J. W. Hammel, S. H. Strauss, unpublished work.
15. P. K. Hurlburt, J. J. Rack, J. S. Luck, S. F. Dec, J. D. Webb, O. P. Anderson and S. H. Strauss, J. Am. Chem. Soc., 1994, 116, 10003.
16. O. G. Polyakov, S. M. Ivanova, C. M. Gaudinski, S. M. Miller, O. P. Anderson and S. H. Strauss, Organometallics, 1999, 13, 3769.
17. (a) H. V. R. Dias, H.-J. Kim, H.-L. Lu, K. Rajeshwar, N. R. de Tacconi, A. Derecskei-Kovacs and D. S. Marynick, Organometallics, 1996, 15, 2994; (b) H. V. R. Dias, Z. Wang and W. Jin, Inorg. Chem., 1997, 36, 6205.
18. Leading references (a) J. Baumann, R. Beer, G. Calzaferri and B. Waldeck, J. Phys. Chem., 1989, 93, 2292; (b) L. Frunza, E. Pop, G. Pop, R. Ganea, R. Burjega, L. Milea and I. Fota, Rev. Roum. Chim., 1992, 37, 809; (c) T. Baba, N. Akinaka, M. Nomura and Y. Ono, J. Chem. Soc., Faraday Trans., 1993, 89, 595; (d) M. Iwamoto and Y. Hoshino, Inorg. Chem., 1996, 35, 6918; (e) Y. Kuroda, H. Maeda, Y. Yoshikawa, R. Kumashiro and M. Nagao, J. Phys. Chem. B, 1997, 101, 1312; (f) C. Lamberti, S. Bordiga, A. Zecchina, M. Salvalaggio, F. Geobaldo and C. Otero Areán, J. Chem. Soc., Faraday Trans., 1998, 94, 1519; (g) V. Y. Borovkov, M. Jiang and Y. Fu, J. Phys. Chem. B, 1999, 105, 5010.
19. (a) P. S. Braterman , Metal Carbonyl Spectra, Academic Press, London, 1975;; (b) J. E. Ellis, R. A. Faltynek and S. G. Hentges, J. Organomet. Chem., 1976, 120, 389; (c) J. E. Ellis and R. A. Faltynek, J. Am. Chem. Soc., 1977, 99, 1801.
20. L. Brammer, J. C. Mareque Rivas and D. Zhao, Inorg. Chem., 1998, 37, 5512.
21. D. J. Darensbourg, J. D. Draper and J. H. Reibenspies, Inorg. Chem., 1997, 36, 3648.
22. A. J. Lupinetti, S. Fau, G. Frenking and S. H. Strauss, J. Phys. Chem. A, 1997, 101, 9551.
23. S. H. Strauss, J. Chem. Educ., 1999, 76, 1095.
24. M. Håkansson and S. Jagner, Inorg. Chem., 1990, 29, 5241.
25. L. E. Orgel, J. Chem. Soc., 1958, 4186.
26. C. E. Moore , Atomic Energy Levels, National Bureau of Standards, Washington, DC, 1971..
27. L. A. Barnes, M. Rosi and C. W. Bauschlicher, Jr., J. Chem. Phys., 1990, 93, 609.
28. (a) X. D. Peng, T. C. Golden, R. M. Pearlstein and R. Pierantozzi, Langmuir, 1995, 11, 534and refs. therein; (b) R. Kumar, W. C. Kratz, D. E. Guro and T. C. Golden, Process Technol. Proc., 1994, 11, 383.
29. S. H. Strauss , O. G. Polyakov , J. W. Hammel , S. V. Ivanov , S. M. Ivanova and M. D. Havighurst , Novel Copper Complexes for nCO Adsorption, US Pat. Appl. (assigned to Air Products and Chemicals, Inc.), 1999..
30. L. H. Jones and B. I. Swanson, Acc. Chem. Res., 1976, 9, 128.

---

Footnote

† ν_sym(CO) also decreased for the pair of copper complexes, from 2206 to 1977 cm⁻¹. ν_sym(CO) has not yet been reported for [Ag(CO)₃][Nb(OTeF₅)₆].

---