Photoactive molecular wires based on metal complexes
Francesco Barigelletti and Lucia Flamigni
Istituto FRAE-CNR, Area della Ricerca, Via P. Gobetti 101, I-40129, Bologna, Italy
First published on UnassignedUnassigned11th January 2000
Abstract
Molecular wires incorporating polypyridine metal complexes are amenable to studies of directional energy and electron transfer. The complexes are chromophores mainly based on Ru(II), Os(II), Rh(III), and Re(I) centres, which usually exhibit luminescence and can play as donor (D) or acceptor (A) units. A bridging ligand (B) provides both the structural and electronic connectivity between D and A and the DAB wires are flexible or rigid, depending on the spacers included within the bridge. Developments regarding multicentre systems and stereochemically interesting systems are taken into account.
 Francesco Barigelletti Francesco Barigelletti | Francesco Barigelletti was born in 1944 and got his ‘Laurea’ in Chemistry in 1971. He joined the National Research Council of Italy in 1973, at FRAE, Bologna. His work deals mostly with the spectroscopy of photoinduced energy and electron transfer processes in molecular and supramolecular species. These typically contain photoactive and electroactive Ru(II), Os(II), and Re(I) polypyridyl centres which are assembled into models for the study of energy conversion and storage and may operate as light driven molecular devices. |
 Lucia Flamigni Lucia Flamigni | Lucia Flamigni was born in 1949. She studied at the University of Bologna where she received her ‘Laurea’ in Chemistry in 1973. After postdoctoral experience at the Chemistry Department of the University of Manchester, in the FRAE-CNR Institute of Bologna and at the Center for Fast Kinetic Research of the University of Texas at Austin, she became a researcher at the FRAE-CNR Institute of Bologna. She is presently a senior researcher of the National Research Council of Italy. Her main scientific interests are in the area of photoinduced energy and electron transfer processes in artificial multicomponent systems. |
1 Introduction
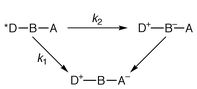
When can a molecular arrangement be termed a wire? The answer has certainly to do with structural (geometric) features, which may be easily identified from the molecular shape. However, some well-defined electronic properties are required if functional expectations are taken into account.1 Thus, the large interest in studies of energy or electron transport schemes has resulted in the preparation of molecular wires (or rods, if these molecules are sufficiently rigid) containing photoactive components, usually placed at the termini of the wire.1–5 These active units, as a consequence of specific interactions with light or after undergoing electrochemical processes, can be the initial and final sites for the temporary storage of energy. Other components, the linkers or bridges, are bound to play a structural role and to provide the electronic connection between the active centres.A family of structurally well defined organic conjugated compounds may serve as a reference example of molecular wiring.1 These compounds incorporate tetracene as an electron donor (D), p-phenylenevinylene oligomers of variable length as bridges (B), and pyromellitimide as the electron acceptor (A). For this paradigmatic case it was found that the electron transfer rate constant, which is of the order of 1010–1011 s−1 over a distance separation up to 40 Å, does not follow a monotonic dependence on the distance between D and A. The authors carefully identify the favourable factors that allow this remarkable performance. These include a good energy matching between the donor and bridge components (at larger and larger distances, the energy difference between excited levels localized on D and B is < 0.1 eV) and relevant steric details at the DB connection. The mechanistic suggestions derived from this study have to do with the interplay of two mechanisms: electron tunnelling and electron hopping,1 see Scheme 1. These come into play depending on the energy levels of the HOMOs and LUMOs involved, in turn affected by the length of B (HOMO and LUMO are the highest occupied and the lowest unoccupied MO, respectively).
 | ||
| Scheme 1 | ||
At short DA distance, k1 >> k2 and the bridge only plays a structural role or, at best, provides an electronic mediation according to a superexchange mechanism. With the more efficient electron hopping, states can be identified whereby a temporary stepping of the electron on the bridge takes place, k2 >> k1. We will see below that similar reference schemes may be useful for both energy and electron transfer within wires based on metal complexes.
In this work, we will survey some recent literature in a field that includes molecular threads incorporating metal complexes of polypyridine ligands.2–5 The optical properties (absorption and luminescence) of these units have been extensively studied and many efforts are devoted to design and synthesise multinuclear complexes in view of their uses for energy storage and transfer schemes,2–5 for sensing the chemical environment,6 and, on general grounds, for information transduction purposes. In these DBA arrays the photoactive units, the metal complexes, can play as energy or electron donors (D) and energy or electron acceptors (A), respectively, and the bridge is usually an organic, in many cases modular component. The complexes can frequently undergo well-defined oxidation and reduction processes, and in the presence of identical metal units (homometallic cases) the conducting properties of the bridge can be evaluated via intervalence studies, which we will not discuss.
We will examine some interesting species from a number of viewpoints which include (i) the role of the energetic and geometric factors for energy and electron transfer processes, (ii) the role of the electronic properties of B and of delocalization of the metal-to-ligand charge transfer (MLCT) excited states, (iii) mechanisms of energy transfer and long-distance transfer, (iv) differences brought about by the use of the tris-bidentate coordination as opposed to bis-tridentate coordination, (v) developments in the field of molecular devices, and (vi) approaches towards the preparation of chiral species.
We notice that, at the moment, in wires based on metal complexes and with respect to electron transfer, the energy transfer process has been more systematically investigated.2–6 This outcome is probably due to practical reasons: for polypyridine complexes it has proved feasible to assemble luminescent D and A components. In this way, for a high number of cases, both luminescence quenching at D and luminescence sensitisation at A (occurring via energy transfer) have been measured by using luminescence spectroscopy.
2 Energy transfer
From a conceptual viewpoint, DBA dyads represent simple systems and some examples are discussed first where the octahedral coordination is provided by bidentate ligands, mostly derived from the basic 2,2′-bipyridine (bpy). In Fig. 1 are shown cases where B is flexible, as in complexes 17 and 2,8 or rigid, as in complex 3.3 | ||
| Fig. 1 Schematic formulae for 1–3. | ||
For 1 and 2, the alkane chain does not provide a good electronic interaction between D and A, and the DA interaction is of the dipole–dipole type.9 This mechanism is describable in terms of a treatment due to Förster.9 The exoergonic Ru→Os energy transfer is moderately fast, ken is 1.7 × 108 and 4.5 × 108 s−1 for 1 and 2, respectively, Table 1. It is useful to compare cases 1 and 2 with case 3. In complex 3 the energetic and spatial (intermetal separation, dMM) parameters are quite similar to those of 1 and 2, however the Ru→Os energy step is faster by two orders of magnitude, Table 1. This behaviour is due to the fact that the alkyne bridge provides an efficient electronic interaction between the D and A centres; accordingly, a through-bond Dexter-type mechanism10 is found to be involved.
| Metal centers | 10−8ken/s−1 | dMM/Å | ΔG/eV | Mechanisma | Ref. | |
|---|---|---|---|---|---|---|
| a Mechanism of energy transfer, Förster (F), Dexter (D). | ||||||
| 1 | RuII/OsII | 1.7 | 13.0 | −0.24 | F | 7 |
| 2 | RuII/OsII | 4.5 | 12.8 | −0.32 | F | 8 |
| 3 | RuII/OsII | 250.0 | 13.8 | −0.34 | D | 3 |
| 4 | RuII/OsII | 5.8 | <18.1 | −0.36 | 5 | |
| 6 | RuII/OsI | >10.0 | 12.8 | 11 | ||
| 7 | RuII/OsII | 2.6 | 16.0 | −0.40 | 5 | |
| 8 | RuII/OsII | 0.4 | 21.0 | −0.38 | 5 | |
| 9 | RuII/OsII | 0.13 | 19.2 | −0.35 | F/D | 12 |
| 10 | RuII/OsII | 0.1 | 13.7 | −0.35 | F/D | 12 |
| 11 | RuII/OsII | 7 | 18.3 | −0.33 | 4 | |
| 15 | RuII/OsII | 6.7 | 24.0 | −0.37 | D | 14 |
| 16 | RuII/OsII | 0.1 | 32.5 | −0.37 | D | 14 |
| 17 | RuII/OsII | 0.013 | 42.0 | −0.37 | D | 14 |
| 21 | RuII/OsII | 500.0 | 16.2 | −0.11 | D | 12 |
| 22 | RuII/OsII | >100.0 | 20.0 | −0.25 | D | 17 |
| 23 | RuII/OsII | 0.044 | 24.0 | −0.25 | 16 | |
| 24 | RuII/OsII | <0.2 | 20.0 | −0.18 | D | 15 |
The series of complexes of Fig. 2 further illustrate the spatial and electronic role of the bridge with respect to Ru→Os energy transfer. In 4 and 5,5 B does not allow complete control of the DA spatial separation, mainly because of rotations about single bonds. By contrast, in 6,117 and 8,5 B ensures a high degree of control of the geometry of the complexes. For 6, B may be viewed as a good electronic conductor as ken > 1×109 s−1 . For 7 and 8, which contain the same type of both unsaturated (conducting) and saturated (isolating) units, the energy transfer rate constant, ken = 2.6 × 108 and 4.0 ×107 s−1, respectively, is clearly related to the intermetal separation, dMM = 16 and 21 Å, respectively.
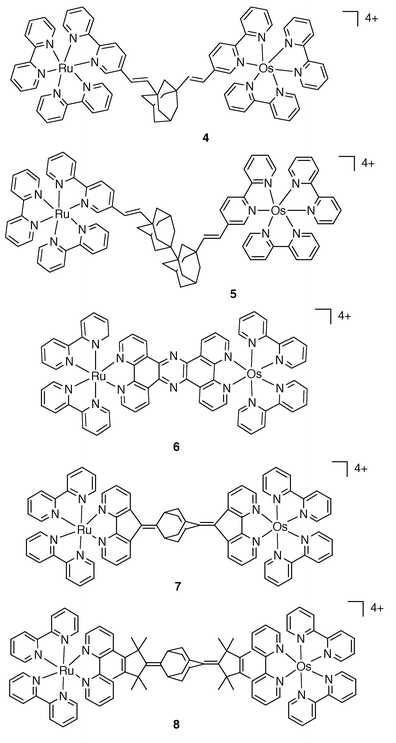 | ||
| Fig. 2 Schematic formulae for 4–8. | ||
The shape of the wire can be controlled to a high degree. Complexes 9 and 10 contain the same D and A centres which are linked in both complexes by a connecting PtII bis(trialkynephosphine) interposed unit, Fig. 3.12
 | ||
| Fig. 3 Schematic formulae for 9 and 10. | ||
In 9 the arrangement is linear while it is L-shaped for 10; this brings about a substantial difference in the dMM separation, 19.2 vs 13.7 Å, respectively, Table 1. The fact that the rate constants in 9 and 10 are very close to each other is ascribed to balanced contributions by both the dipole–dipole and through-bond mechanisms of energy transfer, given that the PtII centre somewhat decouples the terminal units.12
There are DBA cases where an active role for B has been addressed. Fig. 4 compares the behaviour of three related systems in which the bridge contains a phenyl, 11, a naphthyl, 12, and an anthryl, 13, group.4
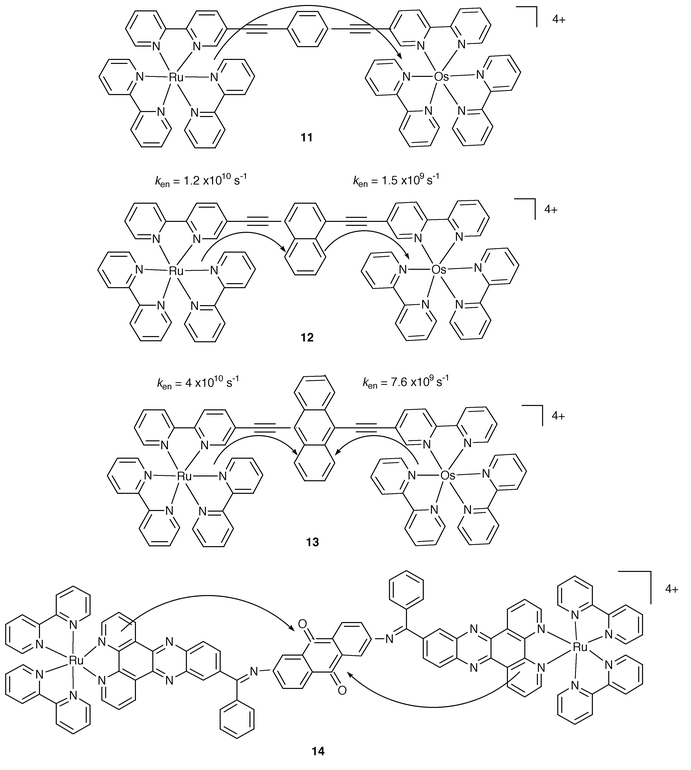 | ||
| Fig. 4 Schematic formulae for 11–14. | ||
A systematic variation of the energy levels of the HOMOs and LUMOs and, as a consequence, of the involved excited states of B is thus designed. Actually, while for 11 B plays the usual mediating role, for 12 a two step energy transfer has been found, with the excitation stepping at the naphthyl component, Fig. 4. For the case of 13, the anthryl group acts as an excitation trap, preventing the Ru→Os transfer of energy. A different case of energy trapping can be identified by looking at the homometallic complex 14,13 where the anthraquinone unit collects the excitation energy from either of the two identical metal centres, Fig. 4
A long distance transfer of excitation occurs in the series of complexes shown in Fig. 5.14 Here the modular approach based on the inclusion within B of a variable number of spacer units allows the construction of dyads 15, 16 and 17, where the photoactive units are separated by 3, 5 and 7 phenylene groups, respectively.
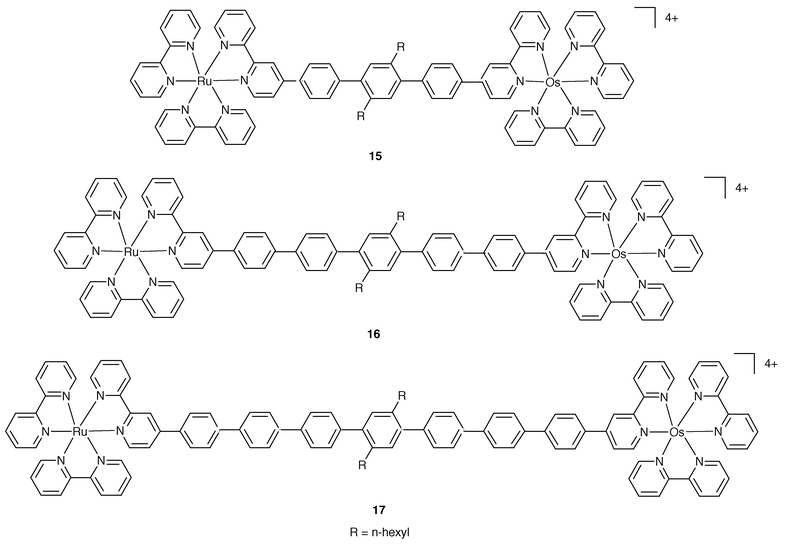 | ||
| Fig. 5 Schematic formulae for 15–17. | ||
The three dyads represent excellent models of rigid systems particularly suited for the study of Ru→Os energy over the remarkable distance of up to 42 Å. For these cases, it has been possible to draw the firm conclusion that the dipole–dipole mechanism cannot be responsible for the energy transfer step. On the other hand, by plotting ln(ken) against the intermetal separation, Fig. 6, a linear dependence is observed, in accord with expectations based on the Dexter approach, eqn. (1).
| ken ∝ exp(−βdMM) | (1) |
 | ||
| Fig. 6 Distance dependence of ken for Ru–B–Os complexes where B contains an n-phenylene chain; circles, n = 0, 1, 2, ref. 15; squares, n = 3, 5, 7, ref. 14. Data points obtained at 77 K. | ||
From these results an attenuation factor β = 0.32 Å−1 has been evaluated,14 while previous work dealing with the effect of polyphenylene spacers15 suggested β = 0.66 Å−1; the data points concerned are also displayed in Fig. 6. It is noteworthy that nearly identical results are obtained at 77 K and at room temperature,14,15 showing that energy transfer, unlike electron transfer, is not affected by temperature or state of the (fluid or frozen) solvent. This probably happens because the reorganization energy, λ, for the energy transfer step is very close to the exhothermicity, −ΔG, of the process.16
A close inspection of the schematic structures for some of the complexes where the photoactive centres are based on the tris-bpy coordination points to a few problems.2,5,17 For instance, the geometry, i.e.dMM, of systems like 4 and 5 may be ill-defined because of rotations about single bonds. A relevant feature related to the tris-bidentate coordination is the possible coexistence of different stereoisomers, which may cause specific difficulties in the study of the photoinduced processes.17 With regard to these aspects, a better choice for the ligand coordination is represented by the bis-tridentate coordination as ensured by use of the 2,2′∶6′,2″-terpyridine ligand (tpy), Fig. 7.
 | ||
| Fig. 7 Schematic formulae for 18–20. | ||
Here, the M(tpy)22+ unit represents an appealing building block via the possible use of the 4′ position of tpy for developing wires. Unfortunately, the basic Ru(tpy)22+ centre, 18, which might be employed as an energy donor in DBA systems, exhibits poor luminescence properties, phi = < 10−5 and τ = 0.25 ns.17 This indicates that in excited 18 the intrinsic deactivation rate is rather fast and that its use as an energy donor is restricted to cases where the competing energy transfer step is even faster (ken > 4 × 109 s−1). Recent studies have revealed reasons for such poor luminescence behaviour, and ways for improving the luminescence performances of Ru-tpy-type units. For instance, this has been documented for complexes 193 and 2018 where the luminescence properties are much improved with respect to 18, basically due to extended conjugation over B.
In Fig. 8, cases are illustrated where the convenient geometric properties of the tpy coordination are combined with the use of polyphenylene spacers, which ensure a high control of the intermetal distance (rigidity).
 | ||
| Fig. 8 Description of energy transfer in terms of dual electron exchange (M-to-M and L-to-L transfers). (a) MLCT transition, (b) L-to-L electron transfer; the concomitant M-to-M electron transfer is not shown. | ||
For 213 and 2217 the Ru→Os energy transfer is very fast, ken > 1010 s−1, which is explained by the role of B in delocalizing the MLCT excitation. By contrast, for 2316 and 2415 the energy transfer rate constant is much lower, Table 1. For 23, studied at T < 200 K, this is ascribed to the insertion of the saturated bicyclooctane unit within B. For 24, this is due to the fact that B is a dianion, which results in the MLCT states being localized on the terminal ligands, as opposed to the cases of 21 and 22 (where B is involved in the delocalization of the MLCT state). In Fig. 8, an illustration is provided of some mechanistic aspects of the energy transfer step, described in terms of two simultaneous electron transfers, M→M and L→L; for the geometrically identical cases of 22 and 24 the different distance associated with the latter step may explain the different rate constants observed,19Table 1.
3 Mechanism of energy transfer
What is the relative importance of the Förster and Dexter mechanisms for the transmission of the excitation along a Ru–B–Os wire? According to a spectroscopic approach based on the luminescence properties of the donor and the absorption properties of the acceptor, and taking care of the dMM separation of the D and A components,9 it is possible to evaluate kenF, the rate constant for the Förster mechanism, see Appendix. In turn, also the contribution of the Dexter mechanism, kenD, can be estimated.Results of model calculations for the couple Ru(bpy)32+ (D) and Os(bpy)32+ (A), as connected by polyphenylene bridges for which β = 0.32 Å−1,14 are shown in Fig. 9, top panel. Results for the analogous case of the Ru(ttp)22+ (D) and Os(ttp)22+ (A) chromophores (ttp = 4′-tolyl-tpy) are also illustrated, bottom panel. Further details are reported in the Appendix.
 | ||
| Fig. 9 Calculated distance dependence of the energy transfer rate constants and efficiencies for Ru–B–Os complexes where B contains an n-phenylene chain: Dexter (full line), Förster (dashed line) and intrinsic (dotted line) contributions. Top: case of Ru(bpy)32+/Os(bpy)32+. Bottom: case of Ru(ttp)22+/Os(ttp)22+. | ||
Relevant points are that (i) kenD is always larger than kenF, and that (ii) the competition with the intrinsic deactivation at the donor unit causes a dramatic drop of the energy transfer efficiency at dMM of ca. 40 and ca. 25 Å, for the M(bpy)32+ and M(ttp)22+ couples, respectively. This suggests that for efficient energy transfer to occur over larger distances, bridges exhibiting a significantly weaker distance dependence (β << 0.32 Å−1) are required.3
4 Electron transfer
In DBA dyads based on metal complexes, photoinduced electron transfer has also been investigated. Frequently, the RuII–B–OsII dyads employed for studies of energy transfer, see above, have been shown to be amenable to investigations of electron transfer after selective oxidation of the OsII centre. This can be performed both with chemical and electrochemical means and relatively stable RuII–B–OsIII species are made available. A few results obtained with complexes 1,74 and 5,5 are collected in Table 2. This series is relatively homogeneous in terms of energetic parameters, while the intermetal separation dMM is varied. Thus, comparison of the rate constants, kel, for the *RuII–B–OsIII → RuIII–B–OsII step (the forward electron transfer) shows that the results are in line with expectations based on the Marcus treatment of the relation among thermodynamic, electronic and kinetic parameters.1,2| Metal centers | 10−9kel/s−1 | dMM/Å | ΔG/eV | Ref. | |
|---|---|---|---|---|---|
| 1 | RuII/OsIII | 5.5 | 13.0 | −1.68 | 7 |
| 4 | RuII/OsIII | 2.8 | <18.1 | −1.61 | 5 |
| 5 | RuII/OsIII | 0.9 | <22.3 | −1.71 | 5 |
| 7 | RuII/OsIII | 0.8 | 16.0 | −1.69 | 5 |
| 25 | RuII/RhIII | 1.7 | 13.5 | 0.1 | 20 |
| 26 | RuII/RhIII | ![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) 3.0 3.0 | 15.5 | 0.1 | 21 |
| 27 | RuII/RhIII | <0.5 | 20.0 | 0.1 | 21 |
An interplay of geometric and energetic factors can also come into play, as illustrated by the sufficiently homogeneous series of complexes 25,2026 and 27,21Fig. 10.
 | ||
| Fig. 10 Schematic formulae for 25–29. | ||
Here the electron transfer step is *RuII–B–RhIII → RuIII–B–RhII, with unfavourable thermodynamics because the process is slightly endoergonic, ΔG = 0.1 eV, Table 2. In fact, electron transfer takes place in 25 and 26 but not in 27, where dMM is the largest in the series.
An interesting case is also illustrated in Fig. 10 and regards the RuII–B–OsIII species 28 and 29.22 In these complexes B contains two different diimides. In the former case, the bridge plays the usual structural role and the RuII→OsIII step is of low efficiency. For 29, a more complicated behaviour is documented because B becomes an active component and the complex behaves like a triad, D–A–A′. Thus, a two-step electron transfer gives rise to the final charge separated state with a production yield of 75%; remarkably, the charge recombination process is relatively slow, kCR = 9.1 × 106 s−1.
5 High nuclearity wires
For the series of Ru-tpy-type complexes in Fig. 11 the increase of the nuclearity has been pursued in view of particular purposes.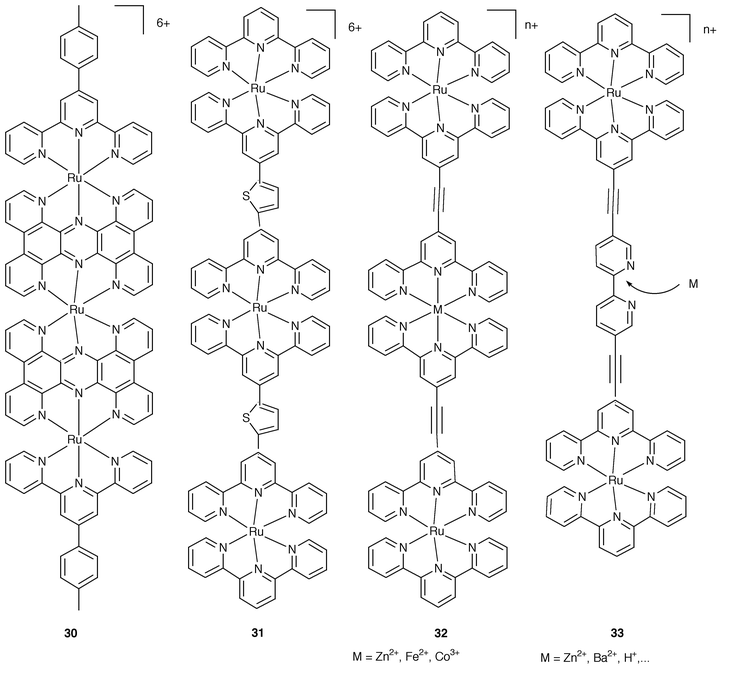 | ||
| Fig. 11 Schematic formulae for 30–33. | ||
Complexes 3023 and 3124 are aimed at the extension of the electronic conjugation over the rod either by using fused bridges (30) or strongly interacting spacers (31). For the latter case, the resulting rod is luminescent, which represents an improvement with respect to the basic non-luminescent mononuclear chromophore 18. Complexes 323 illustrate ways for the building up of nm length rods by using metal-based non-photoactive connectors. In complex 3325 a free bipyridine site is available for the interaction with various cations. The luminescence properties undergo changes in the presence of the guest and this may be taken as an illustration of an useful approach towards molecular-based devices for chemical sensing.6
6 Molecular devices
Metal-based rods prove to be amenable to use within signalling schemes.6 Recent examples include those shown in Fig. 12. In complex 3426 no luminescence can be detected because the intermediate azo group acts as a trap for the excitation based on the two terminal chromophores. | ||
| Fig. 12 Schematic formulae for 34 and 35. | ||
Reduction of the azo group allows the occurrence of Ru→Os energy transfer, so that 34 plays as a redox-responsive molecular switch. In complex 35,27 the energy transfer rate constant is decreased by the presence of the anion, which also represents a signalling event based on the occurrence of energy transfer.
The field of molecular-based devices is expanding broadly. Energy-processing and storing are key events that can be triggered by light. Metal-based wires are finding wider use in molecular-based schemes, as further illustrated by the few examples in Fig. 13. Complex 36 is a wire composed by 5 chromophores based on ReI and RuII centres.28
 | ||
| Fig. 13 Schematic formulae for 36 and 37. | ||
Each component of the wire can absorb light, and an energy excitation cascade, occurring within a fast timescale, leads to localisation of the excitation at one extreme of the wire. The final collection point can be anchored to a wide-bandgap semiconductor, and the wire works as a multi-photon harvesting system.
A two-photon collection scheme can be envisaged by the use of the trimetallic complex 37,29Fig. 13. Through sequential second order steps involving a donor (D, dimethylaniline), the two ligands coordinated to the RhIII metal centre store two electrons, which might be available for subsequent two-electron reduction processes.
7 Chiral complexes
There has been a recent surge of interest in chiral complexes. As noted above, multinuclear species based on the basic bis-tpy octahedral coordination are devoid of stereoisomerism at the metal centre. Conversely, the tris-bpy (or the stereochemically equivalent tris-phen) coordination may result in a rich chemistry associated with chiral properties.30,31 This has generated lines of activity for the setting up of synthetic and separation procedures, in order to gain control over stereoisomers. Successful procedures are frequently based on the assembly of precursors with pre-determined chiralities and on chromatographic techniques, as for the examples in Figs. 14 and 15. | ||
| Fig. 14 Schematic formulae for 38–41. | ||
 | ||
| Fig. 15 Schematic formulae for 42–44. | ||
Thus, the homometallic dinuclear complexes 3832 and 39,33 were prepared via the assembly of enantiomerically pure components. In the former case, the bridge confers a high degree of rigidity to the dinuclear species, while in the latter rotations around single bonds might result in some uncertainty for the dMM separation.
An interesting rod-like arrangement is likewise maintained in complex 40,34 a species which was also prepared by using enantiomerically pure building-blocks. Preparation of 40, and related species, was probably the first example of controlled synthesis of stereochemically defined multinuclear complexes based on RuII centres. The mixed-metal RuII–PdII trinuclear 41,35 is another example of a remarkable nm rod based on enantiomerically pure Ru-centres.
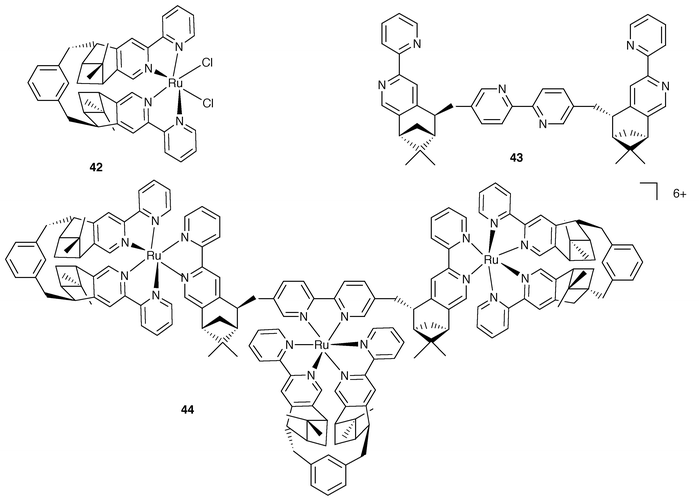
The approach based on the use of enantiomerically pure building blocks has been extended to include the use of metal centres where the predetermined stereochemistry is dictated by chiragen ligands, which can confer the desired metal helicity in a controlled way.36 A relevant example is provided by the case of the trinuclear species 44, Fig. 15.37 In this complex, two types of chiragen ligands are employed. One ligand is the so-called chiragen[0], which allows the preparation of the basic building block 42. The assembling of 44 is then performed based on the use of superchiragen[0] bridging ligand 43.
The study of the excited state properties of chiral transition metal complexes appears very promising,30,31 at the moment however the extension to cases of mixed metal enantiomerically pure complexes does not seem easy. Of course, these complexes would be suitable for energy or electron transfer studies of the type treated above, which would seem to be an appropriate subject for further development.
Appendix. Energy transfer rate constants
The energy transfer rate constant for the dipole–dipole (Förster) mechanism, kenF, can be estimated by using spectroscopic quantities and according to eqns. (A1) and (A2),9,15 | (A1) |
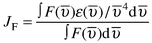 | (A2) |
![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/char_e0d5.gif) ) and the absorption
spectrum of the acceptor, ε(
) and the absorption
spectrum of the acceptor, ε(![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/char_e0d5.gif) ), on an energy scale
(cm−1).
), on an energy scale
(cm−1).In order to estimate the exchange rate constant (Dexter),10kenD, eqns. (A3) and (A4) can be employed in the presence of a weak interaction, H, between the donor and acceptor units, JD is the Dexter integral.
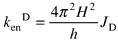 | (A3) |
 | (A4) |
In practice one proceeds through a few calculation steps: (a) JF, JD, kenF and its distance dependence can be evaluated from the photophysical and spectroscopic data; (b) based on kenexp = kenF + kenD, one obtains kenD (and H), if any, at a certain dMM separation; (c) for the distance dependence, kenD = koD exp(−βdMM), β may be available from experiments; in that case the rate constant at van der Waals distance, koD , can also be assessed.
For both cases in Fig. 9, the solvent was aerated acetonitrile and β was taken to be 0.32 Å−1.14 Other used parameters are as follows. For the couple Ru(bpy)32+/Os(bpy)32+ (bpy = 2,2′-bipyridine): K2 = 2/3, Φ = 1.6 ×10−2 and τ = 170 ns; calculations gave JF = 3.8 ×10−14 cm3 M−1 , JD = 1.4 ×10−4 cm and H = 13.7 cm−1 at dMM = 8 Å (estimated VDW distance). For the couple Ru(ttp)22+/Os(ttp)22+ (ttp = 4′-tolyl-2,2′:6’,2″-terpyridine): K2 = 2/3, Φ = 3.5 ×10−5 and τ = 0.95 ns; calculations gave JF = 8.3 ×10−14 cm3 M−1, JD = 2.9 × 10−3 cm and H =14 cm−1 at dMM = 8 Å. Computations were performed with the help of Matlab 5.2 (MatWorks).
References
- W. B. Davies, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60 CrossRef CAS
.
-
(a) V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759 CrossRef CAS
; (b) P. F. H. Scwab, M. D. Levin and J. Michl, Chem. Rev., 1999, 99, 1863 CrossRef CAS
.
- A. Harriman and R. Ziessel, Chem. Commun., 1996, 1707 RSC
.
- R. Ziessel, M. Hissler, A. El-ghayoury and A. Harriman, Coord. Chem. Rev., 1998, 177, 1251 CrossRef
.
- L. De Cola and P. Belser, Coord. Chem. Rev., 1998, 177, 301 and references therein CrossRef
.
- A. P. De Silva, H. Q. N. Gunaratne, T. Gunnlaugson, A. J. M. Huxley, C. P. McCoy, J. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515 CrossRef
.
- B. Gholamkhass, K. Nozaki and T. Ohno, J. Phys. Chem. B, 1997, 101, 9010 CrossRef CAS
.
- M. Furue, T. Yoshidzumi, S. Kinoshita, T. Kushida, S. Nozakura and M. Kamachi, Bull. Chem. Soc. Jpn., 1991, 64, 1632 CAS
.
- Th. Förster, Discuss. Faraday Soc., 1959, 27, 7 RSC
.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836 CrossRef CAS
.
- C. Chiorboli, C. A. Bignozzi, F. Scandola, E. Ishow, A. Gourdon and J.-P. Launay, Inorg. Chem., 1999, 38, 2402 CrossRef CAS
.
- V. Grossheny, A. Harriman, M. Hissler and R. Ziessel, J. Chem. Soc., Faraday Trans., 1996, 92, 2223 RSC
.
- L. Mishra, C.-S. Choi and K. Araki, Chem. Lett., 1997, 447 CrossRef CAS
.
- B. Schlicke, P. Belser, L. De Cola, E. Sabbioni and V. Balzani, J. Am. Chem. Soc., 1999, 121, 4207 CrossRef CAS
.
- F. Barigelletti, L. Flamigni, M. Guardigli, A. Juris, M. Beley, S. Chodorowski-Kimmes, J.-P. Collin and J.-P. Sauvage, Inorg. Chem., 1996, 35, 136 CrossRef CAS
.
- L. Hammarström, F. Barigelletti, L. Flamigni, N. Armaroli, A. Sour, J.-P. Collin and J.-P. Sauvage, J. Am. Chem. Soc., 1996, 118, 11972 CrossRef
.
- J.-P. Sauvage, J.-P. Collin, J.-C. Chambron, S. Guillerez, C. Coudret, V. Balzani, F. Barigelletti, L. De Cola and L. Flamigni, Chem. Rev., 1994, 94, 993 and references therein CrossRef CAS
.
- L. Hammarström, F. Barigelletti, L. Flamigni, M. T. Indelli, N. Armaroli, G. Calogero, M. Guardigli, A. Sour, J.-P. Collin and J.-P. Sauvage, J. Phys. Chem., 1997, 101, 9061 CrossRef
.
- F. Barigelletti, L. Flamigni, J.-P. Collin and J.-P. Sauvage, Chem. Commun., 1997, 333 and references therein RSC
.
- M. T. Indelli, C. A. Bignozzi, A. Harriman, J. R. Schoonover and F. Scandola, J. Am. Chem. Soc., 1994, 116, 3768 CrossRef CAS
.
- M. T. Indelli, F. Scandola, L. Flamigni, J.-P. Collin and J.-P. Sauvage, Inorg. Chem., 1997, 36, 4247 CrossRef CAS
.
- Md. D. Hossain, M.-a. Haga, H. Monjushiro, B. Gholamkhass, K. Nozaki and T. Ohno, Chem. Lett., 1997, 573 CrossRef CAS
.
- P. Bonhôte, A. Lecas and E. Amouyal, Chem. Commun., 1998, 885 RSC
.
- E. C. Constable, C. E. Hosecroft, E. S. Schofield, S. Encinas, N. Armaroli, F. Barigelletti, L. Flamigni, E. Figgemeier and J. G. Vos, Chem. Commun., 1999, 869 RSC
.
- M. Hissler, A. El-ghayoury, A. Harriman and R. Ziessel, Angew. Chem., Int. Ed. Engl., 1998, 37, 1717 CrossRef CAS
.
- J. Otsuki, M. Tsujino, T. Izaki, K. Araki, M. Seno, K. Takatera and T. Watanabe, J. Am. Chem. Soc., 1997, 119, 7895 CrossRef CAS
.
- P. D. Beer, F. Szemes, V. Balzani, C. M. Salá, M. G. Drew, S. W. Dent and M. Maestri, J. Am. Chem. Soc., 1997, 119, 11864 CrossRef CAS
.
- C. A. Bignozzi, J. R. Schoonover and F. Scandola, Progr. Inorg. Chem., 1997, 44, 1 Search PubMed
.
- S. Molnar, G. Nallas, J. S. Bridgewater and K. J. Brewer, J. Am. Chem. Soc., 1994, 116, 5206 CrossRef CAS
.
- F. R. Keene,
Chem. Soc. Rev., 1998, 27,
185; and Coord. Chem. Rev.,
1997, 166,
121. Search PubMed
.
- M. Ziegler and A. Von Zelewsky, Coord. Chem. Rev., 1998, 177, 257 and references therein CrossRef
.
- S. Bodige, A. S. Torres, D. J. Maloney, D. Tate, G. R. Kinsel, A. K. Walker and F. M. MacDonnell, J. Am. Chem. Soc., 1997, 119, 10364 CrossRef CAS
.
- K. Wärnmark, P. N. Baxter and J.-M. Lehn, Chem. Commun., 1998, 993 RSC
.
- D. Tzalis and Y. Tor, J. Am. Chem. Soc., 1997, 119, 852 CrossRef CAS
.
- K. Wärnmark, J. A. Thomas, O. Heyke and J.-M. Lehn, Chem. Commun., 1996, 701 RSC
.
- U. Knopf and A. Von Zelewsky, Angew. Chem. Int. Ed., 1999, 38, 302 and references therein CrossRef
.
- N. C. Fletcher, F. R. Keene, H. Viebrock and A. Von Zelewsky, Inorg. Chem., 1997, 36, 1113 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2000 |
