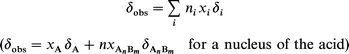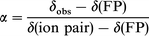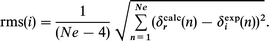Hydrogen-bonded complexes of pentaalkyl guanidines
Maria Rappo-Abiusoa, Marie-France Llaurob, Yves Chevaliera and Pierre Le Perchec*a
aLaboratoire des Matériaux Organiques à Propriétés Spécifiques, UMR 5041 CNRS—Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersité de Sa
ersité de Sa![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) oie, BP 24, 69390, Vernaison, France
oie, BP 24, 69390, Vernaison, France
bSer![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ice de RMN de la “Fédération de Recherche des Polyméristes Lyonnais”, FR 2151, LMOPS—CNRS, BP 24, 69390, Vernaison, France
ice de RMN de la “Fédération de Recherche des Polyméristes Lyonnais”, FR 2151, LMOPS—CNRS, BP 24, 69390, Vernaison, France
First published on 15th December 2000
Abstract
The hydrogen-bonded complexes of strongly basic pentaalkylguanidines (G) with 4-fluorophenol as a proton donor reference (FP) have been studied in CDCl3 solution by means of 13C NMR spectroscopy. The equilibrium constants for formation and the chemical shifts of all the 13C NMR lines of the hydrogen-bonded complexes were determined. This rich spectroscopic characterization of the complexes allowed us to discuss their structure. The guanidines were found to be more basic than triethylamine, the bicyclic ones being the strongest bases, in accordance with expectations. The ion pair character of the hydrogen-bonded complexes was as high as 40% for the strongest bases. In addition to the expected GFP complex, a diassociation complex G(FP)2 was observed at high fluorophenol concentrations. In this latter complex, one fluorophenol molecule is ionized by full proton transfer to the guanidine and the second fluorophenol molecule is bound by hydrogen bonding to the fluorophenate anion. A linear relationship between the 13C NMR chemical shift variations of 4-fluorophenol and log(K1) was found, as in the original work of Gurka and Taft using 19F NMR.
Introduction
Guanidine derivatives are involved in many chemical and biochemical processes as strong hydrogen acceptors.1 They are found in widespread biological compounds (arginine, creatine); their basic properties and their ability to form hydrogen-bonded complexes determine the chemical recognition and catalysis phenomena.2,3 Supramolecular association by means of hydrogen bonding affords the design of new materials.4,5 In quite a different field, the strong basic properties of guanidines enable them to be used as basic catalysts in chemical processes involving hydrogen abstraction steps.1 Most of such organic reactions are carried out in aprotic and nonpolar solvents, or in the bulk.The origin of the strong basic properties of guanidines is the stabilization of the guanidinium cation by delocalization of the positive charge on the three nitrogen and central carbon atoms (“Y-delocalization”).1,6 Another consequence of the charge delocalization is the weakening of the electrostatic attraction to anions,7 enhancing the reactivity of the anions. N-substituted guanidines (Scheme 1), especially pentaalkyl guanidines, are of greater interest in basic catalysis because of their lesser reactivity (but still strong basicity) compared to the non-substituted guanidine.8 However, steric hindrance induces a twisted conformation of the guanidinium cation similar to that of hexaalkylguanidinium cations,9 which impedes the delocalization of the positive charge in the guanidinium cation. Bicyclic guanidines (Scheme 1) are more basic because of the more planar conformation of the cations.
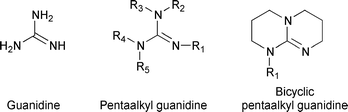 | ||
| Scheme 1 Different types of guanidines. | ||
In aqueous solution, acid–base interactions amount to a simple proton transfer from the acid to the base. Conversely, acid–base interactions in nonpolar aprotic organic solvents generally lead to hydrogen-bonded complexes2,10 where the acid and the base are linked by a hydrogen bond. The scale of basicity in organic solvents is a scale of hydrogen-bonding ability. The scales of basicity in organic solvents and in water are quite distinct and there is no correlation between them.11,12 Such a scale was established by Taft et al.11 based upon formation constants Kf with a reference acid (4-fluorophenol) in carbon tetrachloride solution. This method was extended by Abraham et al.13 who gave linear relationships independent of any reference compound.
In the complex, the hydrogen atom can be either located at an intermediate distance between the acid and the base, or at two distinct positions between them. The potential energy assumes either a single minimum (single-well potential) or two minima (double-well potential) as a function of the position of the H atom.14 The hydrogen atom is generally closer to the acid than to the base, but in the case of strong acid–base interactions, a proton transfer takes place in the complex.15 The former complex is referred to as a hydrogen-bonded complex and the latter as a hydrogen-bonded ion pair. In the case of a double-well potential, an equilibrium between the two types of complexes can be written as
The purpose of this study is to investigate in detail the acid–base interactions of strongly basic pentaalkylguanidines with a reference acid. The aim is to disclose the various equilibria other than the simple hydrogen-bonded complex formation, and to be able to order the studied compounds on a basicity scale.
In favourable cases, the equilibrium constant could be easily measured by means of spectroscopic methods, especially IR spectroscopy.11,1219F NMR was successful when 4-fluorophenol was used as an acid.16 IR spectroscopy was of scarcely any use for the pentaalkylguanidines–phenol series because the band of the OH vibration was very broad, resulting in a continuous background in the IR spectra.17 Zundel et al. ascribed this phenomenon to the large polarizability of the hydrogen bond.18 NMR spectroscopy and more particularly 13C NMR, due to its very large chemical shift range, appeared to be a very appropriate technique because both the substrates can be followed simultaneously. 4-Fluorophenol (FP) was selected as a reference acid. The A–B system (FP–G) was analyzed by observation of the 13C NMR chemical shifts dependence with N = [FP]/[G] mole ratio for both substrates. Supplementary 19F NMR of FP allowed us to make a more direct comparison with previous work by Taft.11 Five pentaalkylguanidines (Scheme 2) have been selected so that the above-mentioned different stages of interactions may be observed. Triethylamine, for which abundant literature data exist, was also studied for the sake of comparison.
 | ||
| Scheme 2 Chemical structures and assignment of the 13C NMR spectra for the compounds studied. | ||
Results and discussion
The formation of a complex species by hydrogen bonding can be written as an equilibrium in the general formThe complex species and the pure acid and base coexist in solution according to the equilibrium. When the reaction rate is slow, the NMR lines of each individual chemical species are observed. Conversely in the case of a fast reaction rate, the lines of a given nucleus present in the complex and the acid (or base) coalesce into a single average line. The chemical shift of this line in the so-called fast exchange limit is then the weighted average of the chemical shifts δi of the pure species:
where xi are the mole fractions of the different chemical species containing the observed nucleus and ni are the numbers of such nuclei present in the i species. The chemical shifts of all the carbons of the pure compounds studied are given in Scheme 2 with their chemical formulae. The chemical shift variations discussed in the following are given with respect to the chemical shift of the pure compound.
Qualitative 13C NMR analysis of the FP–G systems
The binary systems [G + FP] were investigated in CDCl3 as solvent at 300 K. Chemical shift values of both G and FP were dependent on the mole ratio N = [FP]/[G] according to the equilibrium between the free acid (or base) and the hydrogen-bonded complex(es). Of course, many lines are related so that a large part of the 13C NMR data is redundant. The lines of the 13C nuclei located far from the acidic or basic centres show a weaker variation. In the quantitative analysis where the minimum of the difference between calculated and experimental shifts was looked for, only lines having chemical shift variations larger than 0.2 ppm were retained. Including lines having a weak variation results in broader minima of the rms deviation. The complete data are shown in Fig. 1 to 3. Some relevant lines with characteristic behaviour and large variations of chemical shift were selected for the following qualitative discussion. | ||
| Fig. 1 Chemical shift variations with respect to free guanidine as a function of the relative FP content (N) for the CE and CZ carbons of BTBG (left) and TMOG (right): (●) CE; (○) CZ. | ||
![Chemical shift variation with respect to free species as a function of N
=
[FP]/[TMOG] for titration experiments at constant [TMOG] (open symbols) and constant [FP] (filled symbols): (○) Ci; (□) CQ; (▽) C2; (⋄) C1(FP); (△) C4(FP).](/image/article/2001/CP/b008241o/b008241o-f2.gif) | ||
| Fig. 2 Chemical shift variation with respect to free species as a function of N = [FP]/[TMOG] for titration experiments at constant [TMOG] (open symbols) and constant [FP] (filled symbols): (○) Ci; (□) CQ; (▽) C2; (⋄) C1(FP); (△) C4(FP). | ||
![Comparison of the calculated (full lines) and experimental (symbols) values of the chemical shift variations as a function of N
=
[FP]/[G]. Filled symbols are for chemical shifts of 4-fluorophenol carbons with respect to those of free FP: (♦) C1; (●) C4, (★) 19F NMR. Open symbols are for chemical shifts of the base carbons (guanidines or triethylamine) with respect to those of the free base. For guanidines: (□) CQ; (○) Ci; (⋄) CEZ of BTMG, TMOG and C1EZ of BTBG; (△) C3 of MTBD and BTBD; (▽) C6 of MTBD and BTBD, C2 of TMOG and C2EZ of BTBG; (◁) and (▷) C3EZ and C4EZ of BTBG. For triethylamine (TEA): (□) C1; (○) C2.](/image/article/2001/CP/b008241o/b008241o-f3.gif) | ||
| Fig. 3 Comparison of the calculated (full lines) and experimental (symbols) values of the chemical shift variations as a function of N = [FP]/[G]. Filled symbols are for chemical shifts of 4-fluorophenol carbons with respect to those of free FP: (♦) C1; (●) C4, (★) 19F NMR. Open symbols are for chemical shifts of the base carbons (guanidines or triethylamine) with respect to those of the free base. For guanidines: (□) CQ; (○) Ci; (⋄) CEZ of BTMG, TMOG and C1EZ of BTBG; (△) C3 of MTBD and BTBD; (▽) C6 of MTBD and BTBD, C2 of TMOG and C2EZ of BTBG; (◁) and (▷) C3EZ and C4EZ of BTBG. For triethylamine (TEA): (□) C1; (○) C2. | ||
Chemical shift of the Ci and CQ carbons
For the Ci carbons of the Gs located in the α-position of the imino nitrogen, large variations are observed, which are similar for all Gs. As FP is added to the G, the chemical shifts δ(N) (N = [FP]/[G]) show a nearly linear decrease between N = 0 and N = 2–3, above which δ(N) has reached a constant value corresponding to the chemical shift of the complex δ(∞). This suggests the formation of a G–FP complex with a 1:2 stoichiometry.For all Gs, a downfield shift of the central quaternary carbon CQ is observed from N = 0 to N≈2. Beyond this value of N, the chemical shifts fall off instead of being constant as for the Ci carbon. This phenomenon is much more pronounced (Δδ = 1.65 ppm) for the more basic bicyclic Gs MTBD (I) and BTBD (II); this indicates a more complex mechanism than a simple complex formation of 1:1 stoichiometry by means of an acid–base reaction.
Chemical shifts of the CE and CZ carbons
The carbons CE and CZ in the α-position of the amino nitrogens include the methyl carbons of the 1,1,3,3-tetramethyl-2-alkylguanidines BTMG and TMOG (III and IV), the C1 methylene of the butyl residues of BTBG (V). Because of the double bond linking the central carbon CQ and the imino nitrogen, the two amino nitrogens are at the non-equivalent Z- and E-positions with respect to the substituent at the imino nitrogen. The alkyl substituents on these two nitrogen atoms are then also non-equivalent in 13C NMR. In non-cyclic pentaalkylguanidines, the CZ carbons are shifted upfield by ∽1 ppm with respect to the CE E carbons. This non-equivalence is alleviated in the G cations, owing to the free rotation around the C–N bond of the protonated forms and the high exchange rate between the different mesomeric forms. This is actually observed for the non-cyclic BTMG, TMOG and BTBG (Fig. 1) in association with FP. This observation excludes the simple formation of a hydrogen-bonded complex and proves the formation of a guanidinium salt. Increasing the FP content (N), the rate of exchange between the E- and Z-positions increases because of the increasing fraction of guanidinium species and the two lines progressively coalesce into a single resonance. When the acidic compound is too weak, the coalescence of CE and CZ carbons is no longer observed. With TMOG for example, coalescence is observed with both FP and acetic acid but not with ethanol. A weak acid such as ethanol does not allow the hydrogen transfer and although a hydrogen-bonded complex does form the formation of a hydrogen-bonded ion pair remains insignificant. Quantitative analysis of the chemical shift variations can only be carried out on the average line; that is on the peak position which would be observed if the exchange rate was fast. The chemical shift of this hypothetical average line is δCEZ = (δCE + δCZ)/2 (dashed line in Fig. 1).Chemical shift of the carbons and fluorine of fluorophenol
The reading of a variation Δδ of FP as a function of N = [FP]/[G] is different from the above described case for the guanidine lines. Thus, the chemical shift of pure FP is found at N = ∞; there is no data point at N = 0 (no FP) since FP is observed. The data extrapolated to N = 0 gives the chemical shift of FP involved in the complex. A plot of Δδ as a function of 1/N = [G]/[FP] would read in a similar way to a plot of Δδ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. N for the G shifts. Whatever the type of plot, the FP chemical shift increases as G is added, reaches a maximum, and decreases for
further additions of G. Exactly the same behaviour is observed
by means of 19F NMR. This behavior is similar to that
of the CQ carbons of the G described above. In the
case of a simple equilibrium between free FP and a complex, the
chemical shift would vary between that of FP and pure complex.
A single equilibrium can in no way account for a maximum.
Also, an equilibrium between a hydrogen-bonded complex and
a hydrogen-bonded ion pair cannot account for a maximum
because it is not a concentration-dependent equilibrium.
At least two different complex species do form according to the relative amounts of FP and G. The complex formed
at high FP mole ratio (N) is inevitably richer in FP than
the complex formed at lower N.
s. N for the G shifts. Whatever the type of plot, the FP chemical shift increases as G is added, reaches a maximum, and decreases for
further additions of G. Exactly the same behaviour is observed
by means of 19F NMR. This behavior is similar to that
of the CQ carbons of the G described above. In the
case of a simple equilibrium between free FP and a complex, the
chemical shift would vary between that of FP and pure complex.
A single equilibrium can in no way account for a maximum.
Also, an equilibrium between a hydrogen-bonded complex and
a hydrogen-bonded ion pair cannot account for a maximum
because it is not a concentration-dependent equilibrium.
At least two different complex species do form according to the relative amounts of FP and G. The complex formed
at high FP mole ratio (N) is inevitably richer in FP than
the complex formed at lower N.In the experimental method, the Gs were titrated with the FP at a constant concentration of G of 0.15 mol L−1. The concentration of FP, which varies with N, can reach quite high levels (0<N<10). However, the self-association of FP has been ruled out in a separate experiment: the chemical shift of solutions of FP in CDCl3 did not depend significantly on concentration up to 1.2 mol L−1. In order to check against the validity of the titration procedure, the chemical shifts of the TMOG–FP system were measured in two experimental conditions where either the concentration of TMOG or the concentration of FP was kept constant. The results, shown in Fig. 2, are identical within experimental error. Any self-association phenomenon can then be ruled out; the chemical shift variations have to be rationalized by means of complex formation.
The pure complexes cannot be isolated and cannot be observed directly by NMR. The nature of the complex species formed by means of hydrogen bonding, their stoichiometry and the formation equilibrium constants, and the chemical shifts of the nuclei involved in these complexes cannot be directly extracted from the NMR data. A calculation of the chemical shift variation as a function of N according to the complexation equilibria and an adjustment of the free parameters looking to the best fit to the experimental data will provide us with this information.
Quantitative study of association mechanism in binary systems by 13C NMR
The quantitative approach aims to extract the formation equilibrium constants and the chemical shifts of the complexes from the experimental data. The first step is the selection of a suitable set of equilibrated reactions consistent with the experimental data. The preliminary interpretation of the data has indeed shown the occurrence of several complex species.Given a set of equilibria (a model), the chemical shift can be calculated as a function of the acid:base mole ratio N using the values of the equilibrium constants Ki, the chemical shifts δij of the carbons Ci involved in the complex species j, and the (known) overall chemical composition of the solutions. Once this calculation is possible, the unknown parameters Ki and δij are adjusted, looking for the best fit of the calculated chemical shifts to the experimental data. This calculation is given in detail in the appendix for the two-equilibria model which best accounts for the experiments. However the same procedure applies also to the other models which have been tested. The pentaalkylguanidines are represented by (G), the labile hydrogen compound (the acid) by (AH), the hydrogen-bonded complex by (G···H–A), the hydrogen-bonded ion pair by (GH+A−), the di-association complex by (GH+A2H−).
The model which could account correctly for all the experimental data involved the formation of two complexes with (1:1) and (1:2) (G–A) stoichiometries. The 1:1 complex denoted GHA may assume two forms: a hydrogen-bonded complex G···H–A and a hydrogen-bonded ion pair GH+A−.
The second equilibrium where the acid AH binds to the 1:1 complex has often been assumed in order to account for departures from the simple behaviour of 1:1 complex formation. In particular, Zundel et al.17 have shown the formation of such a 1: 2 complex between the MTBD guanidine and several phenols in chloroform by comparison of the IR spectra or 1:1 and 1:2 mixtures of guanidine and phenol. The complete titration curve has not been studied however.
This model was satisfactory since it allowed the calculated chemical shifts to be fitted to the experimental data. The unknown parameters which come out of the fitting process are the two equilibrium constants K1 and K2, and the chemical shifts of each carbon involved in the pure complexes δi(GHA) and δi(GH+A2H−). The chemical shifts of the pure acid and base can be directly observed with the isolated compounds. The detailed procedure for the calculations of the chemical shifts and the search for the best fit by minimization of the errors is presented in the Appendix.
Other models which have been checked against experimental data did not hold. In particular, the sole formation of a (1:1) hydrogen-bonded complex does not account for the data. According to this equilibrium, the chemical shifts of all the NMR lines of G or FP should vary between that of the free species and of the pure complex. This simple model is inconsistent with experimental data which show maxima or minima in most cases. Considering both the hydrogen-bonded complex (G···H–A) and the hydrogen-bonded ion pair (GH+A−) as different complex species having a 1:1 stoichiometry cannot help in accounting for the data.
According to the equilibrium between G···H–A and GH+A−, the fraction of complex present as hydrogen bonded ion pair is α = K′/1 + K′ (K′ being the equilibrium constant), independent of the overall stoichiometry of the mixture (N). For the NMR experiment, the two complex species cannot be distinguished in the fast exchange limit because the average line is observed and because the second equilibrium does not depend on N. The two complexes can be replaced by a single “effective mean complex” noted GHA having the average chemical shift δi = (1 − α)δi(G···HA) + αδi(GH+A−) which could be obtained from the NMR data.
Lastly, it was not possible to account for the experimental data with the stepwise formation of (1:n) hydrogen-bonded complexes assuming an infinite number of complexes with recurrence relationships linking the equilibrium constants19 and identical chemical shifts δi(GH+AnH(n−1)−) for 2<n<∞.
In contrast with most previous studies, the formation of the 1:2 complex was not postulated a priori. Alternative solu tions were also analyzed and discarded by comparison with experiment. The selection of the model results from a comparison with a large set of spectroscopic data. Notice that 13C NMR allows the simultaneous observation of both the lines of the Gs and FP, which is an improvement with regards to 19F NMR of FP.
Titration monitoring by 13C NMR provides the equilibrium constants K1 and K2 and the chemical shifts of the carbons present in the different complex species. The results do not contain any direct information on the nature of the complexes, only the stoichiometry is obtained. The values of the chemical shifts of the complexes and their comparison with literature data allow us to discuss the nature of the complexes and the type of bonds created. The 1:1 complex resulting from the acid–base interaction may be a hydrogen-bonded complex, a hydrogen-bonded ion pair, or an equilibrium between these two limiting forms described by the mole fraction of ion pairs α as defined above. The nature of the bond giving rise to the 1:2 complex has to be elucidated.
Evaluation of the best values of K1, K2, and δi(GHA) and δi(GH+A2H−)
The values of the free parameters of the two-step model were evaluated as giving the best fit to the experimental data. The details of the method are described in the Appendix. The shifts of the most sensitive lines are shown in Fig. 3. The calculated shifts of the lines of the carbons belonging to the different Gs and FP fit the data equally well. Notice that the same analysis was successful for both 13C and 19F NMR. The deduced values of the equilibrium constants K1 and K2 and chemical shifts of the complexes are given in Tables 1 and 2.| Basic compound | K1/L mol−1 | α | K2/L mol−1 |
|---|---|---|---|
| MTBD | 108 | 0.44 | 12 |
| BTBD | 78 | 0.38 | 20 |
| BTMG | 64 | 0.30 | 22 |
| TMOG | 48 | 0.42 | 56 |
| BTBG | 44 | 0.24 | 76 |
| TEA | 27 | 0.17 | 0.9 |
| Chemical shift variation Δδi (ppm) of 4- fluorophenol with respect to pure FP | Chemical shift variation Δδi (ppm) of the guanidines with respect to pure G | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Basic compound | C1 | C2 | C3 | C4 | 19F | CQ | Ci | CEZ | |
| a Rough estimate from the sparse experimental data. | |||||||||
| MTBD | GFP | 6.28 | 0.54 | −0.79 | −2.50 | 0.31 | −2.51 | ||
| G(FP)2 | 10.12 | 1.86 | −1.22 | −3.94 | − 1.68 | −5.32 | |||
| BTBD | GFP | 5.42 | 0.45 | −0.84 | −2.17 | −5.34 | 0.97 | −2.50 | |
| G(FP)2 | 8.43 | 1.54 | −1.11 | −3.32 | −7.86 | −0.73 | −5.37 | ||
| BTMG | GFP | 4.21 | 0.26 | −0.78 | −1.82 | −4.5a | 1.47 | −1.92 | 0.10 |
| G(FP)2 | 7.44 | 1.41 | −0.90 | −3.01 | 0.23 | −4.94 | 0.22 | ||
| TMOG | GFP | 5.98 | 0.41 | −0.84 | −2.40 | 2.77 | −2.71 | 0.20 | |
| G(FP)2 | 7.38 | 1.29 | −0.86 | −2.91 | 1.37 | −4.03 | 0.41 | ||
| BTBG | GFP | 3.41 | 0.10 | −0.96 | −1.55 | −4.5a | 3.53 | −1.98 | −0.30 |
| G(FP)2 | 6.46 | 1.33 | −0.91 | −2.50 | 1.76 | −4.16 | 0.96 | ||
| TEA | GFP | 2.40 | 0.51 | −0.44 | −1.18 | ||||
| G(FP)2 | 6.14 | 3.73 | −0.36 | −2.19 | |||||
The error in the values of the equilibrium constants K1 and K2 is estimated to be 30%. The errors in the chemical shifts of the pure complex species are also of the order of 30% for the lines which experience large shifts (C1 and C4 of FP, CQ and Ci of the Gs); the errors can reach 100% when the chemical shift variations are low. The errors in the parameters pertaining to BTMG are larger than for the other compounds because the experimental data show more scatter.
The concentrations of the different species present in a titration experiment can be calculated from the equilibrium constants. Three examples are shown in Fig. 4: [large K1, small K2]; [small K1, large K2]; [small K1, small K2].
 | ||
| Fig. 4 Calculated concentrations of the different chemical species present in a titration experiment of the base (guanidine or triethylamine) by 4-fluorophenol performed at the constant base concentration of 0.15 mol L−1. Dashed line: free base; dotted line: free FP; solid line: GHA; dash–dot line: G(HA)2. | ||
Discussion
The stoichiometry of the hydrogen-bonded complexes
Several complexes with different stoichiometries have been identified. The 1:1 complex GHA corresponds actually to two complexes which cannot be resolved by 13C NMR at room temperature: the hydrogen-bonded complex G···H–A and the hydrogen-bonded ion pair GH+A−.The diassociation complex (GH+A2H−) involves the formation of a bimolecular anion A2H− associated to the guanidinium cation GH+ as an ion pair. This kind of anion (A2H−) was first postulated in the solid state in 1923 from a structural X-ray study of potassium hydrogen difluoride.20 Since then, several examples of such A2H− dimers isolated in ionic crystals have been reported and studied by crystallography.21 The same species were identified or postulated in both polar and nonpolar organic solutions by means of IR spectroscopy,22 and by combinations of electrical conductivity and potentiometric methods.23 In particular, diassociation complexes of phenol derivatives with MTBD have been reported.17 Most reports deal with carboxylate anions and their parent carboxylic acid. However, carboxylic acids are known to self-associate by hydrogen bonding as a dimer (AH)2, and great confusion results in the literature on the exact chemical nature of the complexes when the methods of investigation do not allow one to analyze the chemical species. Conversely, phenol and its derivatives do not self-associate in solution. Phenolic complexes containing a phenol-phenoxide anion in organic solvents were reported a long time ago.24
It appears that the formation of the diassociation complex involves the hydrogen-bonded ion pair intermediate. Thus, such GH+A2H− species can be observed in cases where the complex has a significant ion pair character. It could be stated that strong bases would be required for that purpose. On the other hand, the formation of the diassociation complex stabilizes the ion pair. If another interaction (different from hydrogen bonding) makes the formation of the diassociation complex thermodynamically more favorable, the second equilibrium (GH+A−⇌GH+A2H−) shifts the hydrogen-bonded (G···H–A⇌GH+A−) equilibrium towards the ion pair form.
The basicity scale
The basic properties influence the first equilibrium and the values of K1 will be used for discussion of the basicity of the different Gs. According to the K1 values of Table 1, the increasing order of basicity is MTBD>BTBD >BTMG>TMOG![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) BTBG>TEA. This is in agreement with well-established chemistry1
since triethylamine is less basic than the guanidines and bicyclic guanidines are found to be much more basic than noncyclic ones. As a general trend, bulky
substituents weaken the basic properties. This should not be ascribed to the steric hindrance acting against the approach of the acid for complex formation. More likely, steric hindrance of the substituents destabilizes the complexes because it imposes a more twisted conformation of the guanidinium cation.
BTBG>TEA. This is in agreement with well-established chemistry1
since triethylamine is less basic than the guanidines and bicyclic guanidines are found to be much more basic than noncyclic ones. As a general trend, bulky
substituents weaken the basic properties. This should not be ascribed to the steric hindrance acting against the approach of the acid for complex formation. More likely, steric hindrance of the substituents destabilizes the complexes because it imposes a more twisted conformation of the guanidinium cation.This basicity scale cannot be compared directly to the tabulated data of Taft et al. or Abraham in CCl4 solvent because our experimental data was collected in CDCl3 as solvent. Chloroform has a weak acidic character and is able to form hydrogen bonds with various bases such as amines.25 Chloroform then competes with FP for hydrogen bonding with the G. The equilibrium constants in CDCl3 are therefore lower than in CCl4.
Since the formation of the diassociation complex is believed to involve a hydrogen-bonded ion pair and because the structure of the 1:1 complex is shifted towards the ion pair form for stronger base, the value of K2 may also provide a basicity scale, however, the value of K2 does not reflect the basicity in a straightforward manner. The values of Table 1 do not show any linear relationship between K1 and K2: K2 is very low for the weakly basic TEA, but decreases also for Gs as their basicity increases. The situation appears complex and a supplementary interaction is probably involved.
The structure of the complexes
The titration data provide the stoichiometry and the equilibrium constants but do not contain any direct structural information. A discussion of the chemical nature and structure of the complexes can be attempted from the values of the chemical shifts of the 13C nuclei involved in the complex species (Table 2) which also came out of the titration data. The discussion is made difficult because there is no general relationship between the electron density at a carbon atom and the chemical shift in 13C NMR.26The chemical shifts of the 19F and 13C lines of FP in the complex of 1:1 stoichiometry provide information on the type of hydrogen bond formed. Owing to the fast equilibrium between the two limiting forms of the GHA complex, the hydrogen-bonded complex G···H–A and the hydrogen-bonded ion pair GH+A−, the shift of GHA is a weighted average of the chemical shifts of the complex in its pure limiting forms: δi = (1 − α)δi(G···HA) + αδi(GH+A−). Following Gurka and Taft,16 the fraction of hydrogen-bonded ion pair, α, can be estimated as the ratio of the 19F NMR observed chemical shift relative to that of FP to the chemical shift difference between 4-fluorophenate and FP:
The underlying assumption in this relationship is that the chemical shift difference between the hydrogen-bonded complex and FP can be neglected as compared to [δ(ion pair) − δ(FP)]. The fraction of ion pair α can be calculated from our 19F NMR data and the chemical shift of the 4-fluorophenate anion measured in DMSO16 (14 ppm upfield from FP), giving α = 0.38 for BTBD. The chemical shifts of the 13C NMR lines of the ion pair complex can then be calculated from the value of α: + 14.3 ppm for C1 and − 5.7 ppm for C4. These values are found to be close to the chemical shift difference between the phenate anion and phenol (+12.7 ppm for C1 and − 6.2 ppm for C4).27 Lastly, the fraction of ion pair α can be estimated for any G from the 13C NMR chemical shifts of the ion pair complex (Table 1). The complex with the most basic MTBD has a 40% ionic character, while α remains low for TEA, as expected.
In the same way as for 19F NMR,16 the 13C NMR chemical shift may provide a measurement of the basicity. Thus, a linear relationship is found between log(K1) and the [δobs − δ(FP)] measured by 13C NMR (Fig. 5). The present range of K1 values is narrow, however. The data of TMOG depart from a linear relationship, indicating an ionic character larger than expected. It can be speculated that the bulky octyl substituent at the imino nitrogen where the complexation reaction takes place, pushes aside the FP molecule which leaves its hydrogen as a proton. In that way, steric hindrance promotes the formation of the ion pair form.
 | ||
| Fig. 5 Linear relationship between Δδ and log(K1) for the 13C NMR lines of FP: (○) C1; (⋄) C4. | ||
The chemical shifts of the 13C lines of FP in the diassociation complex do not depend significantly on the value of K2. This remarkable invariance of the chemical shifts indicates a similar state of the FP molecule in the diassociation complex, whatever the associated base. The values of the chemical shifts (+7.5 ppm for C1 and − 3.0 ppm for C4) are half the values of the shifts of the fluorophenate anion calculated above. This strongly supports the structure of the G(AH)2 complex previously proposed as GH+A2H− where one FP molecule is fully ionized in a hydrogen-bonded ion pair and the second one is involved in a hydrogen-bonded complex with the 1:1 complex. Thus, the ionic character of the GHA complex does not influence the structure of the G(AH)2 complex. Even in the case of TEA where the fraction of ion pair in the 1:1 complex is only 17%, the formation of the diassociation complex forces full hydrogen transfer to the base. The second equilibrium shifts the (GH+A−⇌GH+A2H−) equilibrium towards the ion pair form.
There are clearly several opposing contributions to the 13C NMR chemical shift variations. The chemical shift variations for the CQ and CEZ lines are weak and puzzling. The chemical shifts of the Ci lines do not depend much on the type of G. Upfield shifts Δδ(Ci) from − 2 to − 2.5 ppm and Δδ(Ci) from − 4 to − 5 ppm are found for the GHA and G(HA)2 complexes respectively. The weak variations follow the order of basic character of the Gs, however. The approximately constant values of the chemical shifts of a carbon located close to the reaction centre indicate that the electronic environment does not change significantly upon hydrogen bonding in spite of the different basicities of the Gs. In particular, the chemical shift of the Ci carbon is not sensitive to the degree of proton transfer α. The large cationic charge of the strongly basic Gs is delocalized on the 3 nitrogen atoms since the stabilization of the cation is precisely the origin of the basic properties. The stronger the base, the stronger the delocalization, so that a compensation phenomenon leaves approximately constant partial charge on the imino nitrogen.
The origin of the decrease of K2 as the base strength (K1) increases remains an open question. The information obtained from the chemical shifts does not allow us to discuss this point further. A supplementary interaction may be put forward as the origin of this effect. Gs of moderate basic strength such as BTBG or TMOG have their fractional cationic charge concentrated on the immonium nitrogen whereas this charge is widely delocalized for highly basic guanidines (MTBD, BTBD). An effect of the localized positive charge is also suggested by some observations of the catalytic activity of hexaalkylguanidinium cations. Thus, recent studies of acetal deprotection29 and ring opening of epoxides30 catalyzed by hexabutylguanidinium chloride, have attributed the remarkable catalytic behaviour of this catalyst to the tight associ ation of the guanidinium cation (G+) with the oxygen lone pair of the acetal or epoxide. Similarly, the association of the oxygen lone pair of the second FP with the positive charge of the cation GH+ can be proposed.
Conclusions
The hydrogen-bonded complexes of strongly basic pentaalkylguanidines (G) with 4-fluorophenol as a reference acid (AH) could be studied by means of 13C NMR. Two different complex species with different stoichiometry, namely GHA and G(HA)2, were evidenced and the equilibrium constants of the two equilibria were determined. The equilibrium constant for the formation of the GHA complex (K1) provides a basicity scale: MTBD>BTBD>BTMG >TMOG![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) BTBG>TEA. The bicyclic guanidines are found to be much more basic that the
noncyclic ones and triethylamine. The ion pair character of the GHA complex is quite high (40%). The diassociation complex involves the full formation of an ion pair and the hydrogen-bonding of a second 4-fluorophenol molecule to
the 4-fluorophenate anion; this complex (Scheme 3) is
written as GH+A2H−.
BTBG>TEA. The bicyclic guanidines are found to be much more basic that the
noncyclic ones and triethylamine. The ion pair character of the GHA complex is quite high (40%). The diassociation complex involves the full formation of an ion pair and the hydrogen-bonding of a second 4-fluorophenol molecule to
the 4-fluorophenate anion; this complex (Scheme 3) is
written as GH+A2H−. | ||
| Scheme 3 Proposed structure for the pentaalkylguanidine–4-fluorophenol diassociation complex. | ||
13C NMR proved superior to 19F NMR because several lines were observed simultaneously. In particular, 13C NMR chemical shifts of the 4-fluorophenol involved in the two complex species were quite informative in discussing the structure of the complexes. A linear relationship between the 13C NMR chemical shift variations of 4-fluorophenol and log(K1) was found as in the original work of Gurka and Taft by 19F NMR.16
Experimental
Procedures
The 13C and 19F NMR spectra were recorded at 300 K with a Bruker AC250 spectrometer working at 60.2 MHz and a Bruker AC200 spectrometer working at 188.3 MHz, respectively. CDCl3 was used as solvent. The 13C chemical shift values are given with respect to TMS as an internal reference and the 19F values are given with respect to fluorotrichloromethane; both were determined with ± 0.025 ppm accuracy. The G concentrations were in the range 0.14–0.16 mol L−1. The mole ratio N = [FP]/[G] was varied up to 10 by increasing the concentration of FP.Materials
The 4-fluorophenol, acetic acid and ethyl alcohol used were commercial purum grade products purchased from Aldrich, 1,5,7-triazabicyclo[4.4.0]dec-5-ene (TBD, Aldrich, 98%), 7-methyl-1,5,7-triazabicyclo[4.4.0]dec-5-ene (MTBD, Fluka, >98% were used as received. 1,1,3,3-Tetramethyl-2-octylguanidine (TMOG), 2-benzyl-1,1,3,3-tetramethylguanidine (BTMG), 2-benzyl-1,1,3,3-tetrabutylguanidine (BTBG) and 7-benzyl-1,5,7-triazabicyclo[4.4.0]dec-5-ene (BTBD) were prepared with good yields according to procedures described in the literature.31 The analyses were as follows.![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N) = 1612 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 3.09
(t, 2H, CH2–N
N) = 1612 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 3.09
(t, 2H, CH2–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C), 2.75 (s, 6H, CH3–N
trans), 2.65 (s, 6H, CH3–N
cis), 1.5 (m, 2H, CH2–CH2–N
C), 2.75 (s, 6H, CH3–N
trans), 2.65 (s, 6H, CH3–N
cis), 1.5 (m, 2H, CH2–CH2–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C), 1.3 (m, 10H, CH2–CH2–CH2), 0.9 (m,
3H, CH3–CH2).
C), 1.3 (m, 10H, CH2–CH2–CH2), 0.9 (m,
3H, CH3–CH2).![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N) = 1617 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 2.8
(s, 12H, CH3–N), 4.3 (s, 2H, N–CH2), 7.3 (m, 5H, aromatic).
N) = 1617 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 2.8
(s, 12H, CH3–N), 4.3 (s, 2H, N–CH2), 7.3 (m, 5H, aromatic).![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N) = 1602 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 0.87 (q, 12H, CH3–CH2), 1.24 (m,
6H, –CH2–
cis), 1.43 (m, 6H, –CH2–
trans), 3.02 (t, 4H,
–CH2–N cis), 3.14 (m, 4H, –CH2–N trans), 4.36 (m, 2H, –CH2–), 7.3 (m,
5H, aromatic).
N) = 1602 cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 0.87 (q, 12H, CH3–CH2), 1.24 (m,
6H, –CH2–
cis), 1.43 (m, 6H, –CH2–
trans), 3.02 (t, 4H,
–CH2–N cis), 3.14 (m, 4H, –CH2–N trans), 4.36 (m, 2H, –CH2–), 7.3 (m,
5H, aromatic).![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N) = 1601
cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 4.6 (s, 2H,
CH2–Ar), 3.4 (t, 2H, CH2–N
N) = 1601
cm−1. 1H NMR (250 MHz, CDCl3, ppm from TMS): 4.6 (s, 2H,
CH2–Ar), 3.4 (t, 2H, CH2–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C), 3.1 (m, 6H, CH2–N), 1.85 (m, 4H, CH2–CH2).
C), 3.1 (m, 6H, CH2–N), 1.85 (m, 4H, CH2–CH2).Equilibria and mass action laws:
Material balance for G and AH (N = [FP]°/[G]°):
Chemical shifts of nuclei i in G and nuclei j in AH under fast exchange conditions:
Combination of the mass action laws and material balances gives non-linear equations which were solved numerically, giving the concentrations of all chemical species in a titration experiment as a function of K1 and K2. The equations giving the chemical shifts are linear with respect to the chemical shifts of the pure species. Thus, for a given pair of K1 and K2 values, once the concentrations of all species have been calculated, the chemical shifts δi,j(GHA) and δi,j(G(HA)2) can be determined by a simple linear regression on the experimental data δi,j. In the simple analysis of a single line i, the best fit to the experimental data is obtained for the values of K1 and K2 which minimizes the rms-deviation between the calculated and the experimental chemical shifts as a function of N. Since there are 4 adjustable parameters (K1, K2, δi(GHA) and δi(G(HA)2), the error function for a titration curve with Ne data points is
Given a guanidine, the values of K1 and K2 are unique, but there are several observed lines in the same titration experiment. The data for all the lines have to be analyzed in the same minimization procedure. For a titration experiment with Ne different concentrations of FP and Np NMR lines (of the G and/or FP), the standard deviation is
The minimum of σ is searched over a map of Δ(K1, K2). In such analysis, only the lines which show large variations have been retained. Considering lines with small variations results in the incorporation of data with low signal-to-noise ratio; the consequence is an ill-defined minimum (of low depth) in the Δ(K1, K2) map (Fig. 6). The final error in the values of the equilibrium constants is estimated at 30%.
 | ||
| Fig. 6 Map of the overall standard deviation Δ as a function of K1 and K2 BTBD. | ||
References
- The Chemistry of Amidines and Imidates, ed. S. Patai and Z. Rappoport, Wiley, Chichester, 1991, vol. 2. Search PubMed.
- S. N. Vinogradov and R. H. Linnell, Hydrogen Bonding, van Nostrand Reinhold, New York, 1971. Search PubMed.
- A. D. Ellington, Curr. Biol., 1993, 3, 375 CrossRef CAS.
- G. Varani, Acc. Chem. Res., 1997, 30, 189 CrossRef CAS.
- (a) M. C. Etter, J. Phys. Chem., 1991, 95, 4601 CrossRef CAS; (b) V. A. Russel, M. C. Etter and M. D. Ward, J. Am. Chem. Soc., 1994, 116, 1941 CrossRef; (c) V. A. Russel and M. D. Ward, J. Mater. Chem., 1997, 7, 1123 RSC.
- P. Gund, J. Chem. Educ., 1972, 49, 100 Search PubMed.
- G. Remaud, G. J. Martin and M. L. Martin, J. Phys. Chem., 1985, 89, 2082 CrossRef CAS.
- (a) D. H. R. Barton, J. D. Elliot and S. D. Géro, J. Chem. Soc., Chem. Commun., 1981, 1136 RSC; (b) D. H. R. Barton, J. D. Elliot and S. D. Géro, J. Chem. Soc., Perkin Trans. 1, 1982, 2085 RSC.
- (a) A. V. Santoro and G. Mickevicius, J. Org. Chem., 1979, 44, 117 CrossRef CAS; (b) M. T. Reetz, C. Bingel and K. Harms, J. Chem. Soc., Chem. Commun., 1993, 1558 RSC.
- The Hydrogen Bond, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland, Amsterdam, 1976, vol. 1–3. Search PubMed.
- (a) R. W. Taft, D. Gurka, L. Joris, P. von R. Schleyer and J. W. Rakshys, J. Am. Chem. Soc., 1969, 91, 4801 CrossRef CAS; (b) D. Gurka and R. W. Taft, J. Am. Chem. Soc., 1969, 91, 4794 CrossRef CAS; (c) L. Joris, J. Mitsky and R. W. Taft, J. Am. Chem. Soc., 1972, 94, 3438 CrossRef CAS.
- R. L. Denyer, A. Gilchrist, J. A. Pegg, J. Smith, T. E. Tomlinson and L. E. Sutton, J. Chem. Soc., 1955, 3889 RSC.
-
(a) M. H. Abraham, P. L. Grellier, D. V. Prior, R. W. Taft, J. J. Morris, P. J. Taylor, C. Laurence, M. Berthelot, R. M. Doherty, M. J. Kamlet, J.-L. M. Abboud, K. Sraidi and G. Guihéneuf, J. Am. Chem. Soc., 1988, 110, 8534 CrossRef CAS;
(b) M. H. Abraham, Chem. Soc. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1993, 73 Search PubMed.
., 1993, 73 Search PubMed. -
(a) C. L. Bell and G. M. Barrow, J. Chem. Phys., 1959, 31, 1158 CrossRef CAS;
(b) , J. Emsley, Chem. Soc. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1980, 9, 91 Search PubMed.
., 1980, 9, 91 Search PubMed. - R. L. Denyer, A. Gilchrist, J. A. Pegg, J. Smith, T. E. Tomlinson and L. E. Sutton, J. Chem. Soc., 1955, 3889 RSC.
- (a) D. Gurka, R. W. Taft, L. Joris and P. von R. Schleyer, J. Am. Chem. Soc., 1967, 89, 5957 CrossRef CAS; (b) D. Gurka and R. W. Taft, J. Am. Chem. Soc., 1969, 91, 4794 CrossRef CAS.
- B. Brzezinski and G. Zundel, J. Mol. Structure, 1996, 380, 195 Search PubMed.
- (a) G. Zundel, in The Hydrogen Bond, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland, Amsterdam, 1976, vol. 2, p. 683 Search PubMed; (b) G. Albrecht and G. Zundel, J. Chem. Soc., Faraday Trans., 1984, 80, 553 RSC; (c) R. Krämer, G. Zundel, B. Brzezinski and J. Olejnik, J. Chem. Soc., Faraday Trans., 1992, 88, 1659 RSC; (d) W. Galezowski, A. Jarczewski, M. Stanczyk, B. Brzezinski, F. Bartl and G. Zundel, J. Chem. Soc., Faraday Trans., 1997, 93, 2515 RSC; (e) R. Langner and G. Zundel, J. Chem. Soc., Faraday Trans., 1998, 94, 1805 RSC.
-
(a) F. Garland and S. D. Christian, J. Phys. Chem., 1975, 79, 1247 CrossRef CAS;
(b) M. Lencka and A. Anderko, AIChE J., 1993, 39, 533 Search PubMed;
(c) A. Anderko and J. M. Prausnitz, Fluid Phase Equilib., 1994, 95, 59 CrossRef CAS;
(d) R. B. Martin, Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1996, 96, 3043 Search PubMed.
., 1996, 96, 3043 Search PubMed. - R. M. Bozorth, J. Am. Chem. Soc., 1923, 45, 2128 CrossRef CAS.
-
(a) J. Emsley, Chem. Soc. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1980, 9, 91 Search PubMed;
(b) A. L. MacDonald, J. C. Speakman and D. J. Hadzi, J. Chem. Soc., Perkin 2, 1972, 825 RSC.
., 1980, 9, 91 Search PubMed;
(b) A. L. MacDonald, J. C. Speakman and D. J. Hadzi, J. Chem. Soc., Perkin 2, 1972, 825 RSC. - (a) G. M. Barrow and A. Yerger, J. Am. Chem. Soc., 1954, 76, 5211 CrossRef CAS; (b) A. Yerger and G. M. Barrow, J. Am. Chem. Soc., 1955, 77, 4474 CrossRef; (c) A. Yerger and G. M. Barrow, J. Am. Chem. Soc., 1955, 77, 6206 CrossRef; (d) J. W. Smith and M. C. Victoria, J. Chem. Soc. A, 1968, 2468 RSC; (e) E. A. Arnett and B. Chawla, J. Am. Chem. Soc., 1978, 100, 214 CrossRef CAS.
- (a) I. M. Kolthoff and M. K. Chantooni, Jr., J. Am. Chem. Soc., 1963, 85, 426 CrossRef CAS; (b) I. M. Kolthoff and M. K. Chantooni, Jr., J. Am. Chem. Soc., 1965, 87, 1004 CrossRef CAS; (c) I. M. Kolthoff, M. K. Chantooni, Jr. and S. Bhowmik, J. Am. Chem. Soc., 1966, 88, 5430 CrossRef CAS; (d) I. M. Kolthoff and M. K. Chantooni, Jr., J. Phys. Chem., 1966, 70, 856 CAS; (e) J. A. Carusso and A. I. Popov, J. Phys. Chem., 1968, 72, 918 CrossRef; (f) I. M. Kolthoff, M. K. Chantooni, Jr. and S. Bhowmik, J. Am. Chem. Soc., 1968, 90, 23 CrossRef CAS; (g) I. M. Kolthoff and M. K. Chantooni, Jr., J. Am. Chem. Soc., 1969, 91, 4621 CrossRef.
- (a) G. A. Harlow and D. B. Bruss, Anal. Chem., 1958, 30, 1833 CrossRef CAS; (b) D. B. Bruss and G. A. Harlow, Anal. Chem., 1958, 30, 1836 CrossRef CAS.
- (a) E. Halpern, J. Bouck, H. Finegold and J. Goldenson, J. Am. Chem. Soc., 1955, 77, 4472 CrossRef CAS; (b) J. H. Lady and K. B. Whetsel, J. Phys. Chem., 1964, 68, 1001 CAS; (c) J. H. Lady and K. B. Whetsel, J. Phys. Chem., 1964, 68, 1010.
- G. L. Nelson and E. A. Williams, Prog. Phys. Org. Chem., 1976, 12, 229 Search PubMed.
- D. F. Ewing, Org. Magn. Reson., 1979, 12, 499 Search PubMed.
- (a) H.-O. Kalinowski, S. Berger and S. Braun, Carbon-13 NMR Spectroscopy, Wiley, Chichester, 1988, pp. 241–247 Search PubMed; (b) G. A. Olah and D. J. Dovovan, J. Org. Chem., 1978, 43, 860 CrossRef CAS; (c) A. Olofson, K. Yakushijin and D. A. Horne, J. Org. Chem., 1998, 63, 5787 CrossRef CAS.
- P. Gros, P. Le Perchec and J.-P. Senet, J. Chem. Res., 1995, 196 Search PubMed.
- P. Gros, P. Le Perchec and J.-P. Senet, J. Org. Chem., 1994, 59, 4925 CrossRef CAS.
- G. Bacelo, D. Grenouillat, J.-P. Senet and G. Senyey, Tetrahedron, 1990, 46, 1939.
- E. E. Tucker and E. Lippert, in The Hydrogen Bond, ed. P. Schuster, G. Zundel and C. Sandorfy, North-Holland, Amsterdam, 1976, vol. 2, p. 791. Search PubMed.
| This journal is © the Owner Societies 2001 |