Photocyclization of triphenylamine: an investigation through time-resolved photoacoustic calorimetry

Abstract

Energetics of formation of the intermediate produced during the photocyclization of triphenylamine (TPA) in alkane and alcoholic solvents have been investigated by employing the time-resolved photoacoustic calorimetric technique. The study, in conjugation with flash photolytic observations, confirms that the long lived intermediate N-phenyldihydrocarbazole (NPDHC) is formed through a cascade of processes. The endothermicity for the process of NPDHC formation from TPA was determined to be ∽53 kcal mol⁻¹ in all the environments studied. The nature and structure of NPDHC have been assigned for the first time. The experimental value of the enthalpy of reaction resembles well that calculated from the semi-empirical (AM1-SCI) method.

---

Introduction

The complex and interesting features of the oxidative photocyclization of diphenylamine(s) to carbazole(s) have been the subject of extensive research in a number of laboratories for a long time. The reactions have been studied using both continuous wave and pulsed exciting light sources.^1–6 With the UV irradiation of diphenylamines, such as diphenylamine (DPA), N-methyldiphenylamine (MDPA) and triphenylamine (TPA), an intramolecular cyclization reaction takes place to produce the corresponding carbazoles as the final photoproduct. The complex reaction scheme proposed by Rahn et al., on the basis of nanosecond laser flash photolysis experiments,⁵ has been supported by work in different laboratories.

Although the rates of the individual processes of the complex multi-step reaction have been studied in detail in different solvents, the energetics of the reaction have yet to be established. To the best of our knowledge, there is only one report dealing with the energetics of the photoconversion of DPA in methanol using the time-resolved thermal lensing technique.⁶ However, the photophysical parameters of DPA are markedly different from those of MDPA and TPA, resulting in a remarkable difference in the rate constants of the individual steps of the photoconversion reaction for the former from the other two.⁵ Thus, it still remains interesting to study the energetics of the reactions for TPA and/or MDPA.

In spite of the fact that the involvement of an intermediate is established for the above-mentioned photoreaction, there is controversy regarding the nature of it. While Suzuki et al. proposed a biradical structure for it in its ground state,⁶ Grellmann et al. proposed a zwitterionic structure of the same, although they have not ruled out the possibility of the biradical structure.^7,8 Shizuka et al. proposed that the “610 nm” transient differs from the intermediate “dihydrocarbazole ” for DPA.^4,9 Thus, the nature of the intermediate is yet to be established.

Since time-resolved photoacoustic calorimetry (PAC) detects the time-dependent heat released through radiationless deactivation processes from the different metastable states, this technique allows one to acquire information regarding the energetics of a multi-step photoreaction in detail. In the present work we have exploited this technique to explore a detailed picture of the energetics of the photoreaction of TPA in n-heptane (HEP), methanol (MeOH) and ethanol (EtOH) solutions.

Experimental

TPA (Aldrich) was purified through vacuum sublimation followed by recrystallization from ethanol. Spectroscopic grade n-heptane, methanol and ethanol (Merck) were used as received. 2-Hydroxybenzophenone (HBP, Aldrich) was used as a reference for the PAC experiments.

A Shimadzu UV-2100 spectrophotometer and a Spex Fluorolog 2 spectrofluorimeter were used for the absorption and fluorescence measurements respectively. For our investigation, principally we have used two sets of measurements: flash photolysis for kinetic measurements of the transients and photoacoustic calorimetry for energy measurements for the individual reaction steps. We will describe the two experiments separately. It is pertinent to mention here that as the flash photolysis results are basically a reproduction of the existing literature (confirming the proposed reaction mechanism by Rahn et al.⁵) we will skip the details of them.

Flash photolysis

Our flash photolysis set-up is composed of a Spectra Physics Quanta-Ray GCR-130 Nd-YAG laser, an Applied Photophysics LKS 60 laser flash photolysis spectrometer and a Hewlett-Packard Infinium Oscilloscope (500 MHz, 1 Gsa s⁻¹). The samples were excited with the third harmonic (355 nm, 8 ns FWHM) of the laser. The monitoring light was produced by a 150 W pulsed Xe lamp. The detection of the transient species in the 300–650 nm range was made with a Hamamatsu photomultiplier (model 1P-28). The sample solutions were made with absorbance ≃0.1 at the excitation wave length and were degassed with dry nitrogen prior to their use in the flash experiments.

Photoacoustic calorimetry (PAC)

The PAC apparatus follows the front-face irradiation design described elsewhere.^10,11 The solutions were pumped through a 0.11 mm thick cell at a flow rate of 1 ml min⁻¹ with an SSI chromatography pump (model 300) and irradiated with an unfocussed N₂ laser (PL 2300 from PTI) working at a frequency of 2 Hz. The acoustic waves generated by the non-radiative processes following light absorption in the cell were detected with a 2.25 MHz Panametrics transducer (model A106S), preamplified with a Panametrics ultrasonic preamplifier (model 5676), captured by the transient recorder (Tektronix DSA 601) and transferred to a PC for data analysis. For each sample, reference and pure solvent an average of 100 acoustic waves were collected. Four sets of averaged waves for each of the sample, reference and solvent were used for data analysis at a given laser intensity, and four laser intensities were employed in each experiment. The different laser intensities used in the experiment were obtained by interposing filters with transmissions in the range of 30 to 100%. As oxygen was found to have a strong effect on the PAC signal for the present case, the experiments were performed under an atmosphere of constant purging of solvent-saturated N₂. Before going through the time-resolved PAC we confirmed that the PAC signal was linear with the concentration of sample at least up to a concentration of the solution with absorbance = 0.3 (correlation coefficient = 0.999). However, for the time-resolved PAC experiments we used sample solutions with absorbance ≃0.1. The absorbances of the reference solutions were the same as that of the sample solutions within the limit of the experimental error.

Theory

Although ab initio calculations involving extended basis sets with extensive configuration interaction (CI) have been successful in explaining structures, energetics and reactivities of small molecules in different electronic states, such reports are still limited in number for large molecular systems. However, semi-empirical molecular orbital methods have already established their wide usefulness in this respect. The methods provide acceptable approximations to give results which are quite close to the experimental findings.^12–16 In the present calculations we have used the commercial package Hyperchem 5.01 (Hypercube Inc., Canada). The energies of the various electronic states of the different species (TPA and different possible structures of NPDHC) have been calculated for the optimized structures using the AM1-SCI method.

Results and discussion

Flash photolysis

Our flash photolysis as well as PAC experiments confirm the following scheme (Scheme 1) as proposed by Rahn et al.⁵ TPA is first excited to the S₁ state (¹TPA*) which decays very quickly to the corresponding T₁ state (³TPA*) through intersystem crossing (ISC). Let us designate this step as step I. ³TPA* is then converted into the T₁ state of the intermediate (³NPDHC*). We consider this process as step II. It is important to mention here that in O₂-free solutions of TPA at room temperature all other channels of deactivation of the ³TPA* but its transformation to the intermediate are insignificant.⁸³NPDHC* is then deactivated to its ground singlet state (NPDHC) (step III) which eventually undergoes oxidative dehydrogenation to form N-phenylcarbazole (NPC). We have measured the rates of step II and step III through flash photolysis. Since our flash results do not differ from the literature we only summarize our data in methanol solvent in Table 1 without reproducing other details and figures. NPDHC was, however, found to decay quite slowly with a lifetime of 420 μs in the alcoholic solvents. In n-heptane solvent these rate constants are also quite similar.

Scheme 1 Different steps in the photoreaction of TPA.

Table 1 Rates of the individual steps for the formation of the intermediate during the photoreaction of TPA in MeOH measured by flash photolysis

Monitoring process	Rate constant^a/s^−1
a The data incorporates a 10% error associated with the method.
Step II	Formation of ^3NPDHC*	2.0 × 10^7
(growth of 420 nm band)
Step III	Decay of ^3NPDHC*	2.6 × 10^6
(decay of 420 nm band)
Formation of NPDHC	2.6 × 10^6
(growth of 610 nm band)

---

Photoacoustic calorimetry

Time-resolved photoacoustic calorimetry is based on the measurement of the acoustic wave generated by the heat released in the non-radiative processes following electronic excitation. The experimental wave (E-wave) of the sample is compared with that of the pressure transducer (T-wave). The T-wave is obtained with the calorimetric reference, HBP in the same solvent absorbing the same fraction of light as the sample and releasing it as thermal energy in a time much shorter than the transducer oscillation frequency. The phase and amplitude differences between the T- and E-waves allow for the simultaneous determination of the thermal energy released by the transients (E) and their lifetimes (τ). Typical background-corrected reference and sample signals are shown in Fig. 1.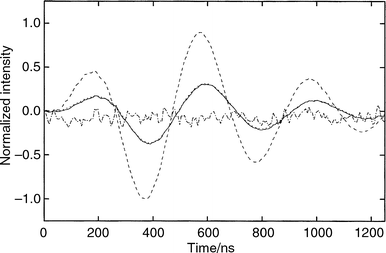

Fig. 1 Typical sample photoacoustic wave (E-wave, ———), reference wave (T-wave, – – –), calculated wave (C-wave, ---) and the residual (multiplied by 10, –-–-). The calculated wave, C-wave, was obtained with three sequential decays with lifetimes τ₁ = 1 ns, τ₂ = 50 ns and τ₃ = 380 ns. Residual = (C-wave) − (E-wave). For details see the text. The E- and T-waves were corrected for the background signal and normalized. The normalization factor is the reciprocal of the largest absolute value of the T-wave. The sample (TPA), reference (HBP) and solvent (methanol) data were obtained under the following experimental conditions: irradiation at 337 nm of N₂ saturated solutions with a filter with 57% transmittance; absorbance of 0.10 for both sample and reference solutions; solution flow rate of 1 ml min⁻¹.

We interpret the waves of the N₂ saturated samples with three sequential exponents. The first one for the formation of the triplet state of TPA (step I), the second one corresponding to the formation of the intermediate in its triplet state (³NPDHC*) (step II) and the third one for its decay to NPDHC (step III) (refer to Scheme 1). Each decay step is described by two parameters: the lifetime of the transient (τ) and the fraction of thermal energy released (ϕ) within that lifetime. The convolution of the reference waves with parameters of the kinetic model for the decay of the transient species gives the calculated E-wave (to be termed C-wave). The appropriateness of the kinetic model and its parameters to describe the observed E-wave can be evaluated by the difference (termed as residual) between the amplitudes and phases of the observed (E-) and calculated (C-) waves at each decay time (Fig. 1). The formation of ³TPA* is faster than the time resolution of our experimental set-up, and we arbitrarily set the lifetime of the first exponential decay to τ₁ = 1 ns, smaller values of τ₁ do not change the other parameters in the deconvolution. For the second and third exponential components we set τ₂ = 50 ns and τ₃ = 380 ns as determined from our flash experiments corresponding to step II and step III. However, when we fix τ₁ ( = 1 ns) and τ₃ ( = 380 ns) and let τ₂ be adjusted by the Marquardt's algorithm employed in the deconvolution, we only get a good fit to the E-wave with τ₂ = 52 ± 2 ns. This is an independent verification of the time windows for the individual steps.

The fractions of laser energy released by each system were measured at four laser intensities. The first fraction was found to vary with laser intensity. We plotted this fraction as a function of laser intensity and obtained linear correlation coefficients greater than 0.96. The difference was assigned to transient–transient absorption and was corrected by extrapolating the fraction of energy released to zero laser intensity. From this laser intensity corrected value of the first fraction of the released heat, the energy of the triplet state of TPA was determined considering the energy of excitation at 337 nm. The energy of the triplet state was, however, corrected for the weak fluorescence of TPA (Φ_f≃0.03).¹⁰ E₂ and E₃ were estimated from the other two fractions of heat released in the other two exponents (E₂ = ϕ₂E_hν, E₃ = ϕ₃E_hν). Table 2 presents the energy of the lowest triplet state of TPA (E_T) and the energies involved for step II (E₂) and step III (E₃) during the photoproduction of NPDHC. The NPDHC species has a very long lifetime (420 μs) and is considered as the dump for our experiments in n-heptane and alcoholic solvents. E_T can also be determined directly from the phosphorescence measurements and the data is available in the literature.¹⁷

Table 2 Triplet state energy of TPA, the amount of energy involved in step II (E₂) and step III (E₃) during the photoreaction of TPA (Scheme 1) and the enthalpy of reaction for the formation of the intermediate in n-heptane and alcoholic solvents

Solvent	ET^a/kcal mol^−1	E2/kcal mol^−1	E3/kcal mol^−1	ΔHTPA → NPDHC^0 /kcal mol^−1
a The literature value is 69.6 kcal mol^−1 in polar solvents.^17
HEP	69.5 ± 1.0	11.5 ± 1.0	3.3 ± 0.6	54.7 ± 1.5
MeOH	70.6 ± 1.0	14.9 ± 1.0	3.9 ± 0.6	51.8 ± 1.5
EtOH	69.2 ± 1.0	12.6 ± 1.0	3.1 ± 0.6	53.5 ± 1.5

---

Table 2 shows that the heat of formation of NPDHC from TPA is 53.3 ± 1.5 kcal mol⁻¹. Thus, the reaction is fairly endothermic. However, the endothermicity of this reaction is reasonably less than that reported for DPA in methanol solvent (62.1 kcal mol⁻¹).⁶

From their observation that the T₁ state of the intermediate of DPA lies closer to the S₀ state and not the S₁ state, Suzuki et al. assumed that the intermediate has, probably, a biradical character in the ground state.⁶ However, there is no direct experimental evidence in favor of the proposition. Had it been a biradical with such a long lifetime (420 μs), it should have been quenched by a spin trap very efficiently.^18,19 However, our flash experiments with two spin traps, [italic v]iz., 5,5-dimethyl-1-pyrroline-N-oxide (DMPO) and N-tert-butyl-α-phenylnitrone (PBN) reflected no change in the lifetime of the 610 nm band for the intermediate, NPDHC, in all solvents. We have also tried with a conjugated triene, [italic v]iz., 1,6-diphenylhexa-1,3,5-triene, to see if there is any quenching in the lifetime of the intermediate as biradicals are susceptible to addition reactions with these substrates. The negative results with all our trials go against a biradical nature for the intermediate.

To assign the structure of the intermediate NPDHC we have calculated the energies of the electronic states for all reasonable structures of it. Out of them, the one that explains the experimental findings best is the trans isomer (with the two hydrogens in a trans arrangement) with a zwitterionic character (the skeleton is shown in Fig. 2). The cis isomer (with the two hydrogens in cis arrangement) has been found to be less stable than the trans isomer. It is interesting to point out here that Grellmann et al. also proposed such zwitterionic structures for the intermediate of MDPA, although they did not exclude the possibility of a biradical.^7,8

Fig. 2 Skeleton of the ground state structure of the intermediate NPDHC. The carbon atoms are numbered in the figure. Charges on the atoms are not shown in the figure as the negative charge has been calculated to be delocalized (Table 3).

It can be seen that in the ground state the nitrogen atom acquires a reasonable positive charge while all the carbon atoms, particularly C5, C3 and C1 (or C8, C10 and C12), acquire partial negative charges. Table 3 gives the net charges on the atoms comprising the skeleton of the intermediate.

Table 3 Net charges on different atoms of NPDHC skeleton

Atom with no. (refer. to Fig. 2)	Net charge
C1	−0.157976
C2	−0.127901
C3	−0.162153
C4	−0.080966
C5	−0.213062
C6	−0.016082
C7	−0.015868
C8	−0.213423
C9	−0.080634
C10	−0.162351
C11	−0.127501
C12	−0.158232
N	+0.131026
C14	+0.000918
C15	−0.111052
C16	−0.126067
C17	−0.115260
C18	−0.126008
C19	−0.110994

---

The simulated electronic spectrum of NPDHC shows a strong absorption (oscillator strength f = 0.33) at 643.6 nm corresponding to the 0–0 transition of S₀ → S₁. Experimentally, a strong absorption band with a broad maximum in the range 610–620 nm is observed, justifying the acceptability of our assigned structure for the transient. We have also calculated the ground state energy of TPA. From the difference of the ground state energies (or from the enthalpies of formation) of TPA and NPDHC we have calculated the enthalpy of reaction for the formation of NPDHC from TPA during the photoreaction. Table 4 represents the experimental as well as the calculated values. From a good agreement between the calculated and the experimental values of the parameters we assign the structure of the intermediate to the one described above.

Table 4 Comparison between the calculated and experimental results

Experimental
Calculated^a	in HEP	in MeOH	in EtOH
a The calculated values are in vacuum ([italic v]ide infra).b The calculated transition has a high oscillator strength of 0.33 that explains the strong absorption observed for the species in this wavelength region.
Enthalpy of reaction for the	50.71	54.7 ± 1.5	51.8 ± 1.5	53.5 ± 1.5
formation of NPDHC/
(kcal mol^−1)
Absorption position/nm^b	643.6 (0–0 transition)	610–620 (broad maximum)
(S0–S1)

---

Conclusion

The present study confirms the proposition of Rahn et al.⁵ that the long lived intermediate NPDHC is formed through a cascade of processes during the photoreaction of the TPA system. The time-resolved PAC study reveals that the formation of the intermediate from TPA is an endothermic process, the endothermicity being ∽53 kcal mol⁻¹ in alkane as well as in alcoholic environments. From the theoretical calculations and their agreement with the experimental results the structure of the intermediate for the photoreaction has been assigned for the first time. The present work reveals that the intermediate, in its ground state, has a partial positive charge on the nitrogen atom.

Acknowledgements

The authors express their sincere thanks to Professor H. D. Burrows and Dr A. A. C. C. Pais for helpful discussions. Financial support from PRAXIS/PCEX/QUI/0108/96 (European Union) and Fundação para a Ciência e a Tecnologia (grant BD/18362/98) are gratefully acknowledged.

References

1. C. A. Parker and W. J. Barnes, Analyst, 1957, 82, 606.
2. E. J. Bowen and J. H. D. Eland, Proc. Chem. Soc. London, 1963, 202.
3. D. Sur, P. Purkayastha and N. Chattopadhyay, J. Photochem. Photobiol. A, 2000, 134, 17.
4. H. Shizuka, Y. Takayama, T. Morita, S. Matsumoto and I. Tanaka, J. Am. Chem. Soc., 1971, 93, 5987.
5. R. Rahn, J. Schroeder, J. Troe and K. H. Grellmann, J. Phys. Chem., 1989, 93, 7841; K. H. Grellmann, G. M. Sherman and H. Linschitz, J. Am. Chem. Soc., 1963, 85, 1881.
6. T. Suzuki, Y. Kajii, K. Shibuya and K. Obi, Bull. Chem. Soc. Jpn., 1992, 65, 1084.
7. K. H. Grellmann, W. Kühnle, H. Weller and T. Wolff, J. Am. Chem. Soc., 1981, 103, 6889.
8. E. W. Förster, K. H. Grellmann and H. Linschitz, J. Am. Chem. Soc., 1973, 95, 3108.
9. H. Shizuka, Y. Takayama, I. Tanaka and T. Morita, J. Am. Chem. Soc., 1972, 92, 727.
10. M. Pineiro, A. L. Carvalho, M. M. Pereira, A. M. d'A. R. Gonsalves, L. G. Arnaut and S. J. Formosinho, Chem. Eur. J., 1998, 4, 2299; J. Seixas de Melo, L. M. Silva, L. G. Arnaut and R. S. Baker, J. Chem. Phys., 1999, 111, 5427.
11. L. G. Arnaut, R. A. Cadwell, J. E. Elbert and L. A. Melton, Re[italic v]. Sci. Instrum., 1992, 63, 5381.
12. T. Arthen-Engeland, T. Bultmann, N. P. Earnsting, M. A. Rodriguez and W. Thiel, Chem. Phys., 1992, 163, 43.
13. J. Catalan, F. Fabero, M. S. Guijarro, R. M. Claramunt, M. D. Santa Maria, M. C. Foces-Foces, F. H. Cano, J. Elguero and R. Sastre, J. Am. Chem. Soc, 1990, 112, 747.
14. B. Dick, J. Phys. Chem., 1990, 94, 5752.
15. P. Purkayastha, P. K. Bhattacharyya, S. C. Bera and N. Chattopadhyay, Phys. Chem. Chem. Phys., 1999, 1, 3253.
16. P. Purkayastha and N. Chattopadhyay, Phys. Chem. Chem. Phys., 2000, 2, 203.
17. S. L. Murov, I. Carmichael and G. L. Hug, Handbook of Photochemistry, Marcel Dekker, New York, 2nd edn., 1993, p. 6..
18. T. J. Kemp, Prog. React. Kinet. Mech., 1999, 24, 287.
19. B. Halliwell and J. M. C. Gutteridge, Free Radicals in Biology and Medicine, Oxford University Press, London, 3rd. edn., 1998, ch. 5..

---